Multi-Band Analysis on Physical Properties of the Quasi-Two-Dimensional Superconductor NbSe₂

Abstract

The discovery of quasi-two-dimensional superconductors bears consequences for both basic research and practical applications. However, the mechanism of superconductivity and the form of order parameters are still controversial problems for the transition metal dichalcogenide NbSe${}_2$ thin film. Under the Neumann boundary condition, the physical properties of this compound are investigated within the two-component Ginzburg–Landau theory. We compute the upper critical field in an arbitrary direction and the temperature dependence of critical supercurrent density through this layered system. All of our theoretical calculations fit the experimental measurements well; thus, this study strongly provides evidence of two-gap s-wave superconductivity in the NbSe${}_2$ thin film.

1. Introduction

The first isolation of graphene in 2004 has generated a resurgence of interest in the investigations on layered systems [1]. NbSe${}_2$ as a transition metal dichalcogenide is one of the most studied van der Waals compounds that exhibit both charge density wave and superconductivity at low temperatures [2]. The crystalline structure of niobium diselenide in turn contains one Nb and two Se layers in the sequence of Se-Nb-Se, featuring a covalent bond between the Nb and Se atoms [3]. Bulk 2H-NbSe${}_2$, which is formed by stacking the monolayers of NbSe${}_2$ with adjacent layers rotated by 180° with respect to one another, is a well-studied type-II superconductor [4,5,6,7]. Meanwhile, superconductivity in atomically thin NbSe${}_2$ ($T_c$∼ 1.7 K) [8,9] and samples down to the monolayer thickness [10] has also been observed. It is noteworthy that this film system has been recognized as an intrinsic superconductor, due to the occurrence of superconductivity without the need for a special substrate [3]. Moreover, band structure calculations in NbSe${}_2$ thin film indicate that the electronic states around the Fermi level are dominated by the $4d_{z^2}$, $4d_{x^2-y^2}$, and $4d_{xy}$ orbitals of the Nb atoms, and the contribution from the Se $4p$ orbitals is small [11].

To date, several explorations have been made on the physical mechanism and the form of order parameters in the superconducting NbSe${}_2$ thin film. The quasi-two-dimensional superconductor NbSe${}_2$ possesses out-of-plane mirror symmetry and broken in-plane inversion symmetry. Meanwhile, the existence of $4d$ transition metal also causes large spin–orbit interactions, which will induce the spin-momentum locking in this system [12,13,14]. In a later study, this Ising pairing scenario was experimentally verified in the magnetotransport measurement of an in-plane upper critical field on NbSe${}_2$ monolayers [15]. In the exploration of the excitation spectrum in this material, Yokoya et al. observed a momentum-averaged gap value of about 1.0 meV with angle-resolved photoemission spectroscopy (ARPES) [16]. However, detailed analyses on the ARPES and scanning tunneling microscopy (STM) results also establish the existence of substantially different gap values on different Fermi surface sheets and give evidence of the presence of multi-band superconductivity in NbSe${}_2$ film [16,17,18]. Meanwhile, the low-temperature specific heat data on a similar system can be accurately characterized using the two-gap model with the gap values at about 1.26 and 0.73 meV respectively [19]. Recently, the angular and temperature dependence of the upper critical field $H_{c2}$ for NbSe${}_2$ films with various thicknesses has been obtained from electrical resistance measurements [9,15]. The experimental measurement of the upper critical field parallel to the $ab$-plane can be explained well by the single-band Werthamer–Helfand–Hohenberg model, while the positive curvature near the critical temperature of $H_{c2}$ data in the c-direction clearly shows the deviation from this simple scenario. Thus, the pairing symmetry of order parameters is still a debatable problem in the quasi-two-dimensional NbSe${}_2$, and further investigations to clarify the problem are necessary.

This paper mainly aims to discuss the physical properties of NbSe${}_2$ films within the two-component Ginzburg–Landau (GL) theory. We first derive the two-band GL equations for the two-gap superconducting film and then calculate the upper critical magnetic field in an arbitrary direction and the temperature dependence of critical supercurrent density through this system. Our computations are in agreement with the experimental measurements and thus indicate that this system is a two-gap s-wave superconductor. Meanwhile, the theoretical results also show that the effective mass anisotropy of this compound is 4.2.

The article is structured as follows: In Section 2, we introduce the two-component GL theory and explain the Neumann boundary condition to the superconducting film. In Section 3, we carry out detailed calculations on the upper critical field in the NbSe${}_2$ thin film. In Section 4, we work out the temperature dependence of in-plane critical supercurrent density through this film. Finally, we summarize this paper in Section 5.

2. Two-Component Ginzburg–Landau Theory

Starting from the two-band Bardeen–Cooper–Schrieffer (BCS) theory [20] and taking into account the multi-gap feature of quasi-two-dimensional superconductor NbSe${}_2$, we can write the weak-coupling GL functional of the two-band superconducting film with a small thickness d in the z (or c)-direction as [21,22,23,24]

$$F={\int }_{-d/2}^{d/2}\left(f_1+f_2+f_{12}+\frac{{\mathbf{H}}^2}{8\pi }\right)dz,$$

(1)

with

$$f_{\gamma }=\frac{{\hslash }^2}{2m_{\gamma }}{\left|\left(\nabla -\frac{2\mathrm{i}e\mathbf{A}}{\hslash c}\right){\Delta }_{\gamma }\right|}^2-{\alpha }_{\gamma }\left(T\right){\left|{\Delta }_{\gamma }\right|}^2+\frac{{\beta }_{\gamma }}{2}{\left|{\Delta }_{\gamma }\right|}^4$$

(2)

and

$$f_{12}=-{ϵ}_{12}({\Delta }_1^{*}{\Delta }_2+\mathrm{c}.\mathrm{c}.).$$

(3)

Here, $f_{\gamma }$ ($\gamma =1,2$) represents the free energy density for band $\gamma$, and $f_{12}$ is the interaction free energy density between these two bands. ${\Delta }_{\gamma }$ is the order parameter in the superconductor. $m_{\gamma }$ denotes the effective mass for each band, and ${ϵ}_{12}$ represents the Josephson coupling constant. ${\alpha }_{\gamma }$ is related to temperature, while the coefficient ${\beta }_{\gamma }$ is independent of temperature. Without considering the interband interaction, the GL functional can be simplified as two independent single-band issues with the corresponding transition temperature $T_{c1}$ and $T_{c2}$ separately. Thus, we can approximately express the coefficient ${\alpha }_{\gamma }$ as ${\alpha }_{\gamma }\left(T\right)={\alpha }_{\gamma 0}{t}_{\gamma }\left(T\right)={\alpha }_{\gamma 0}(1-T/T_{c\gamma })$, where ${\alpha }_{\gamma 0}$ is the proportional constant [25]. $\mathbf{A}$ is the vector potential and $\mathbf{H}=\nabla \times \mathbf{A}$ denotes the external magnetic field.

At this stage, we would like to give a brief explanation of the form of the free energy density in Equations (1)–(3). Since the order parameter evolves continuously from zero below the critical temperature $T_c$, it is natural to expand the free energy density as power series in ${\Delta }_{\gamma }$. Since the order parameter ${\Delta }_{\gamma }$ can be complex, only the terms of even power may enter the expression of the free energy density, and the expansion form will be preserved up to the quartic order. The gradient terms in Equation (2) represent the increase in the free energy density associated with a spatial distortion of order parameters.

In principle, all the parameters in our GL theory can be derived from the two-band BCS model [20,23]. Without losing any generalization, we can set that $T_{c1}$ (or $T_{c2}$) corresponds to the band with the large (or small) gap. The microscopic forms of ${\alpha }_{\gamma }$ can be expanded as linear functions of $t_1\left(T\right)$ with $\ln (T_{c1}/T)\approx t_1\left(T\right)$, and then we can obtain the valuable relation ${\alpha }_{10}$/${\alpha }_{20}$ = $T_{c1}$/$T_{c2}$. Since at low temperatures, the superconducting gaps of quasi-two-dimensional NbSe${}_2$ appear at 1.26 and 0.73 meV from specific heat data [19], we can roughly approximate $T_{c1}$/$T_{c2}$ as $1.26/0.73\approx 1.7$ based on the BCS theory. Moreover, we can also obtain ${\beta }_1={\beta }_2\equiv \beta$ [23] through the microscopic two-band BCS model. Furthermore, we see that the GL free energy density in Equations (1)–(3) keeps invariant under the scale transformation of the scaling factor l: ${\Delta }_{\gamma }\to \sqrt{l}{\Delta }_{\gamma }$, $m_{\gamma }\to l{m}_{\gamma }$, ${\alpha }_{\gamma }\to {\alpha }_{\gamma }/l$, $\beta \to \beta /l^2$, ${ϵ}_{12}\to {ϵ}_{12}/l$. Thus, $m_2$ can be taken as the electron mass $m_e$ for simplicity.

We assume that there is no electric current flowing through the boundary for a smooth nonmagnetic superconductor–insulator or superconductor–vacuum interface. Furthermore, we can then use the Neumann boundary condition on the macroscopic scale. Thus, $\frac{d{\Delta }_{\gamma }}{dz}{|}_{z=\pm d/2}=0$ gives the boundary conditions on both surfaces of the thin film. Hence, the Neumann boundary condition is automatically satisfied when the order parameter ${\Delta }_{\gamma }$ is approximated invariable along the z-axis.

3. The Upper Critical Field of NbSe${}_2$ Film

Now, we would like to solve the issue of the nucleation of superconductivity in the existence of external magnetic field $\mathbf{H}$. Without any loss of generality, we set $\mathbf{H}=\left(Hsin\theta ,0,Hcos\theta \right)$ with $\theta$ the directional angle between the z-axis and the field. It is convenient to choose the vector potential as $\mathbf{A}=\left(0,Hxcos\theta -Hzsin\theta ,0\right)$. Since $\mathbf{A}$ only depends on x and z, the solution can be written with the form ${\Delta }_{\gamma }(x,y,z)={\rho }_{\gamma }(x,z)e^{\mathrm{i}{k}_{y}y}$. After substituting this form into Equations (2) and (3) and omitting the quartic terms, $f_{\gamma }$ and $f_{12}$ can be rewritten as follows:

$$\begin{array}{cc}\hfill f_{\gamma }=& \frac{{\hslash }^2}{2m_{\gamma }}{\left(\frac{\partial {\rho }_{\gamma }}{\partial x}\right)}^2+\frac{{\hslash }^2}{2m_{\gamma }}{\left(\frac{\partial {\rho }_{\gamma }}{\partial z}\right)}^2+[\frac{2e^2{(xcos\theta -zsin\theta )}^2{H}^2}{m_{\gamma }{c}^2}\hfill \\ \hfill -& \frac{2e\hslash k_y(xcos\theta -zsin\theta )H}{m_{\gamma }c}+\frac{{\hslash }^2{k}_y^2}{2m_{\gamma }}-{\alpha }_{\gamma }]{\rho }_{\gamma }^2\hfill \end{array}$$

(4)

and

$$f_{12}=-2{ϵ}_{12}{\rho }_1{\rho }_2.$$

(5)

Meanwhile, according to the applicability of Neumann boundary conditions in the case of thin films, we have the wavefunction ${\rho }_{\gamma }(x,z)\approx {\rho }_{\gamma }\left(x\right)$ in the lowest order. With this approximation, performing the integration on z in Equation (1), we can obtain the form of the total free energy as follows:

$$\begin{array}{c}\hfill \frac{F}{d}=\sum _{\gamma }\left[\frac{{\hslash }^2}{2m_{\gamma }}{\left(\frac{d{\rho }_{\gamma }}{dx}\right)}^2+\frac{1}{2}{m}_{\gamma }{\omega }_{\gamma }^2{(x-x_0)}^2{\rho }_{\gamma }^2+{\sigma }_{\gamma }{\rho }_{\gamma }^2\right]-2{ϵ}_{12}{\rho }_1{\rho }_2+\frac{H^2}{8\pi }.\end{array}$$

(6)

Here, we define

$${\omega }_{\gamma }=\frac{2eHcos\theta }{m_{\gamma }c},x_0=\frac{\hslash c{k}_y}{2eHcos\theta }\mathrm{and}{\sigma }_{\gamma }=\frac{{(edHsin\theta )}^2}{6m_{\gamma }{c}^2}-{\alpha }_{\gamma }.$$

(7)

In the normal metal phase, we have ${\rho }_{\gamma }$ equal to zero, but ${\rho }_{\gamma }$ will be a function of position in the superconducting state. Close to the upper critical field, the free energy F is a functional of ${\rho }_{\gamma }\left(x\right)$, and the spatial distribution of order parameters can be obtained from the variation in F with respect to ${\rho }_{\gamma }\left(x\right)$. Consequently, by minimizing the free energy with ${\rho }_{\gamma }$ in Equation (6), the linearized two-band GL equations in the quasi-two-dimensional system can be written as

$$\left[-\frac{{\hslash }^2}{2m_1}\frac{d^2}{d{x}^2}+\frac{1}{2}{m}_1{\omega }_1^2{(x-x_0)}^2+{\sigma }_1\right]{\rho }_1-{ϵ}_{12}{\rho }_2=0$$

(8)

and

$$\left[-\frac{{\hslash }^2}{2m_2}\frac{d^2}{d{x}^2}+\frac{1}{2}{m}_2{\omega }_2^2{(x-x_0)}^2+{\sigma }_2\right]{\rho }_2-{ϵ}_{12}{\rho }_1=0.$$

(9)

Because $x_0$ only shifts the location of the minimum of the effective potential, the usual method involves setting $x_0=0$.

Without the external magnetic field, ${\rho }_{\gamma }$ can be treated as constant close to the critical temperature, then Equations (8) and (9) are simplified as follows:

$$\left(\begin{array}{ccc}{\alpha }_1& & {ϵ}_{12}\\ {ϵ}_{21}& & {\alpha }_2\end{array}\right)\left(\begin{array}{c}{\rho }_1\\ {\rho }_2\end{array}\right)=0.$$

(10)

In order to obtain a non-zero solution of ${\rho }_{\gamma }$, we can set the determinant of the matrix in Equation (10) as zero. Then, we can obtain

$${ϵ}_{12}^2={\alpha }_1\left(T_c\right){\alpha }_2\left(T_c\right),$$

(11)

which we will use to determine ${ϵ}_{12}$ in our calculations.

Now, we try to work out the upper critical magnetic field $H_{c2}$ of the NbSe${}_2$ thin film under the external magnetic field. At ${ϵ}_{12}=0,$ we can obtain the solution of Equations (8) and (9) immediately by noting that it is the Schrödinger equation for a particle bound in a harmonic oscillator potential for each band. The simple harmonic oscillator is one of the most significant problems in quantum mechanics. It not only elaborates on many of the fundamental concepts and methods of quantum physics but also has great guiding value. Basically, any potential well can be approximated as a simple harmonic oscillator, so it describes different phenomena, from molecular vibrations to nuclear structure. The resulting eigenvalues of this problem are

$$E_{\gamma ,n}=(n+1/2)\hslash {\omega }_{\gamma }+{\sigma }_{\gamma }$$

(12)

with n as a non-negative integer, and the ground wavefunctions corresponding to these two bands take the form of ${({\nu }_0/\pi )}^{1/4}{e}^{-{\nu }_0{x}^2/2}$, with ${\nu }_0=2\pi H/{\mathsf{\Phi }}_0$ and the magnetic flux quantum ${\mathsf{\Phi }}_0=\pi \hslash c/e$.

If ${ϵ}_{12}\ne 0,$ Equations (8) and (9) describe a system of two coupled oscillators. We propose the solution in the form of ${\rho }_{\gamma }=a_{\gamma }{\left({\nu }_0/\pi \right)}^{1/4}{e}^{-{\nu }_0{x}^2/2}$, where $a_{\gamma }$ is constant, in order to obtain the minimum eigenvalue of the coupled oscillators. Thus, for $n=0$, Equations (8) and (9) can be transformed into

$$\left(\frac{1}{2}\hslash {\omega }_1+{\sigma }_1\right)a_1-{ϵ}_{12}{a}_2=0$$

(13)

and

$$\left(\frac{1}{2}\hslash {\omega }_2+{\sigma }_2\right)a_2-{ϵ}_{12}{a}_1=0.$$

(14)

Then, the upper critical field $H_{c2}$ can be derived from Equations (13) and (14) as

$$\left(\frac{1}{2}\hslash {\omega }_1+{\sigma }_1\right)\left(\frac{1}{2}\hslash {\omega }_2+{\sigma }_2\right)={ϵ}_{12}^2$$

(15)

at $H=H_{c2}$.

When $\theta =0^{\circ }$, from Equation (15), the exact expression of the $H_{c2}$ parallel to the z-direction can be obtained as follows:

$$\begin{array}{cc}\hfill H_{c2}^{\Vert }\left(T\right)& =\frac{{\mathsf{\Phi }}_0}{2\pi {\xi }_0^2}\{1.7{\eta }_m{t}_1\left(T\right)+t_2\left(T\right)\hfill \\ & +\sqrt{{\left[1.7{\eta }_m{t}_1\left(T\right)-t_2\left(T\right)\right]}^2+6.8{\eta }_m{t}_1\left(T_c\right)t_2\left(T_c\right)}\}.\hfill \end{array}$$

(16)

Here, ${\xi }_0^2={\hslash }^2/m_2{\alpha }_{20}$ and ${\eta }_m=m_1/m_2$ represent the effective mass anisotropy.

For $\theta ={90}^{\circ }$, the upper critical field perpendicular to the z-direction can be obtained as

$$H_{c2}^{\perp }\left(T\right)=\sqrt{\frac{6{\mathsf{\Phi }}_0{H}_{c2}^{\Vert }\left(T\right)}{\pi d^2}}.$$

(17)

High-quality NbSe${}_2$ thin films can be prepared via a two-step vapor deposition method [9,26]. In this technique, Nb (99% purity) is first deposited as a thin film on SiO${}_2$/Si substrates in vacuum. This procedure is typically carried out at 10${}^{-4}$ Pa, and the evaporation rate is about 0.5 nm/s. Subsequently, the mixture of H${}_2$/N${}_2$ (3% H${}_2$, 300 sccm) is used as a carrier gas to conduct the selenization process in a two-zone furnace at atmospheric pressure. The deposited Nb film is placed in the center of the tubular furnace, and then the alumina boat containing excessive Se powder (99% purity) is positioned upstream at the center of the quartz tube. After blowing with H${}_2$/N${}_2$ at a flow rate of 300 sccm for 10 min, the Se powder and the Nb film are heated to 360 °C and 800 °C respectively, maintained for 1 h. The NbSe₂ thin films are fabricated when the furnace is turned off and cooled to room temperature. Then, the electrical transport and magnetization measurements can be performed in a physical property measurement system (PPMS-16T) and using a SQUID magnetometer (MPMS-XL-5) separately. For NbSe${}_2$ thin films, the experimental measurements of the upper critical field can be obtained following these steps and can be compared with our theoretical calculations.

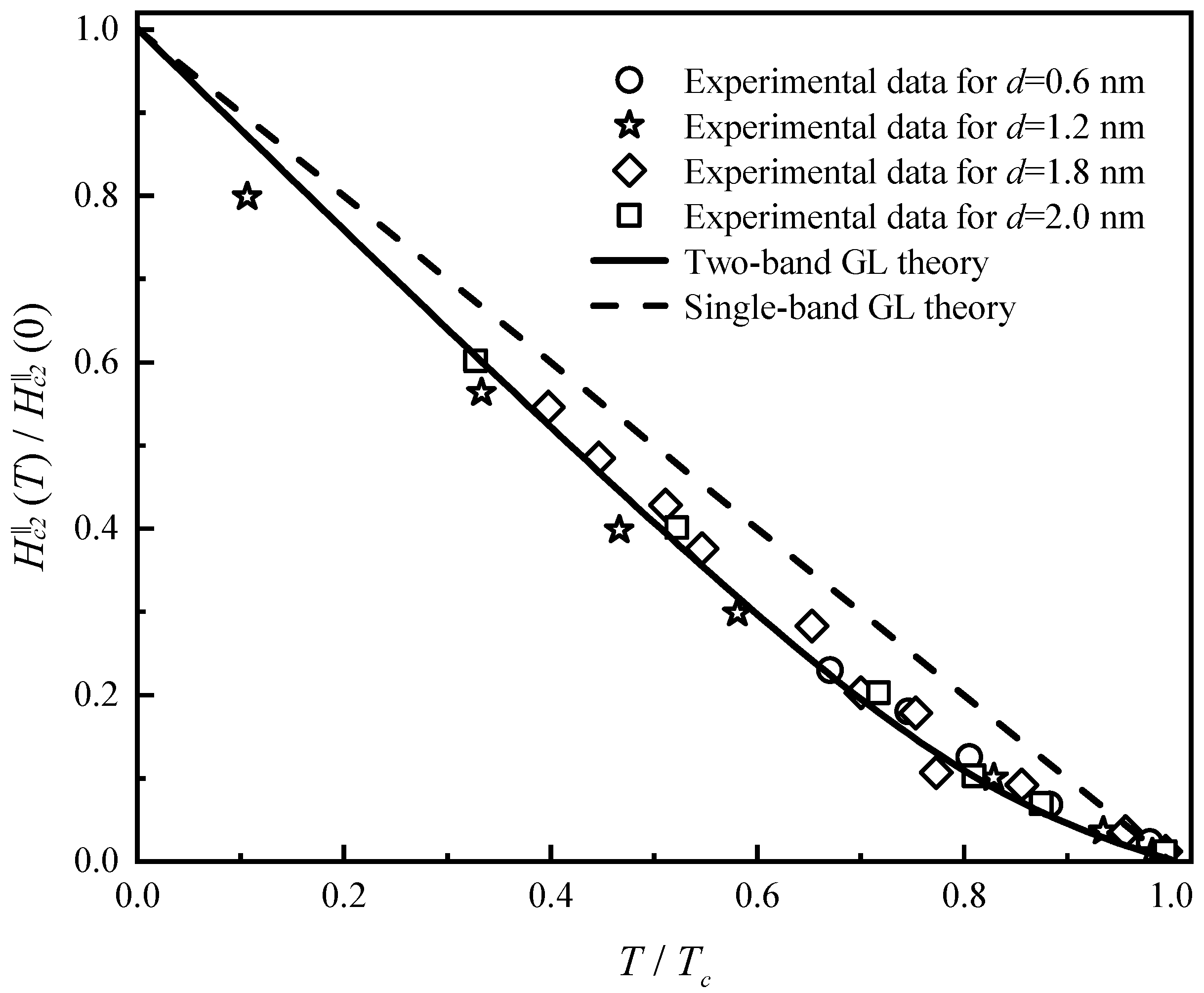
We can easily see from Equations (16) and (17) that the normalized upper critical fields $H_{c2}\left(T\right)/H_{c2}\left(0\right)$ are independent of the film thickness d, and these values can be explicitly computed with two scale-invariant parameters ${\eta }_m$ and ${\eta }_t=T_{c1}/T_c$. We choose ${\eta }_m=4.2$ and ${\eta }_t=0.95$ to match the experimental measurements of the NbSe${}_2$ films and plot the theoretical results in Figure 1 and Figure 2. From Figure 1 and Figure 2, it is shown that our calculations can fit the experimental data well in the whole temperature range. Meanwhile, according to Ref. [27], the exact expressions of $H_{c2}$ parallel and perpendicular to the c-axis based on the single-band GL theory can also be written as $mc\alpha /e\hslash$ and $\sqrt{6m{c}^2\alpha /e^2{d}^2}$, respectively. Here, m denotes the single-band effective mass, and the coefficient $\alpha$ can be approximately written as $\alpha ={\alpha }_0(1-T/T_c)$ with ${\alpha }_0$ the proportionality constant. We also show the single-band computations in Figure 1 and Figure 2 as comparative studies. From Figure 1 and Figure 2, we can see that the two-band model can fit the experimental measurements with the various film thicknesses better than the single-band theory.

Figure 1. The temperature dependence of normalized upper critical magnetic field parallel to the c-axis for the NbSe${}_2$ thin film. The experimental data of the NbSe${}_2$ films with the thickness $d=$ 0.6, 1.2, 1.8, and 2.0 nm are taken from Refs. [9,15].

Figure 2. The temperature dependence of normalized upper critical magnetic field perpendicular to the c-axis for the NbSe${}_2$ thin film. The experimental data of the NbSe${}_2$ with the thickness $d=$ 0.6, 1.2, 1.8, and 2.0 nm are taken from Ref. [9].

In addition, according to Equation (15), we can also calculate the angular dependence of the upper critical field through numerical computations. We then plot our calculations at $T=0.4$ K for the NbSe${}_2$ thin film in Figure 3. Meanwhile, we also show the single-band computations from Ref. [27] in Figure 3. Furthermore, we can see that the upper critical field $H_{c2}$ monotonously increases with angle $\theta$, and our two-band results fit the experimental measurements of the 2.0 nm thick NbSe${}_2$ well. All of our theoretical analyses thus strongly indicate the two-gap s-wave superconductivity in this compound.

Figure 3. The angular ($\theta$) dependence of the upper critical magnetic field at T = 0.4 K for the NbSe${}_2$ thin film, and $\theta$ is in the unit of degree. The experimental data of NbSe${}_2$ with the thickness $d$ = 2.0 nm are taken from Ref. [9].

It is worth noting that from the fitting of our numerical data, the band with the large (or small) gap corresponds to the large (or small) effective mass, and the effective mass anisotropy between these two bands equals 4.2 in this layered system.

4. The In-Plane Critical Supercurrent of NbSe${}_2$ Film

Now, we start to investigate the in-plane critical supercurrent density $j_c$ through the quasi-two-dimensional NbSe${}_2$. No external magnetic field is applied to the layered system in the following discussion. We assume the supercurrent in the x-direction and take the solution of our two-component GL theory as ${\Delta }_{\gamma }\left(x\right)=\left|{\Delta }_{\gamma }\right|e^{\mathrm{i}\varphi {}_{\gamma }\left(x\right)}.$ In order to minimize the interaction free energy density in Equation (3), we have $\varphi {}_1\left(x\right)=\varphi {}_2\left(x\right)$ for ${ϵ}_{12}>0$ or $\varphi {}_1\left(x\right)=\varphi {}_2\left(x\right)+\pi$ for ${ϵ}_{12}<0$. In either case, we can define the supercurrent speed $v_{\gamma }=\frac{\hslash }{m_{\gamma }}\frac{d\varphi {}_{\gamma }}{dx}$ for each band and can easily obtain the same relation $v_2/v_1={\eta }_m$.

The GL free energy Equation (1) can be easily rewritten with the form of ${\Delta }_{\gamma }$ following the standard procedure [28]

$$\frac{F}{d}=\sum _{\gamma }\left(-{\alpha }_{\gamma }{\left|{\Delta }_{\gamma }\right|}^2+\frac{1}{2}{m}_{\gamma }{v}_{\gamma }^2{\left|{\Delta }_{\gamma }\right|}^2+\frac{\beta }{2}{\left|{\Delta }_{\gamma }\right|}^4-2\left|{ϵ}_{12}\right|·\left|{\Delta }_1\right|·\left|{\Delta }_2\right|\right).$$

(18)

In the thin samples, we assume that the amplitude of the order parameter $\left|{\Delta }_{\gamma }\right|$ is constant in space, and the supercurrent is produced through phase variation due to the Josephson relation. Thus, the free energy F is a function of $|{\Delta }_{\gamma }|$ with the fixed $v_{\gamma }$. By minimizing the free energy in Equation (18) with $|{\Delta }_{\gamma }|$, we can write the equations that $|{\Delta }_{\gamma }|$ satisfies as follows:

$$D_1\left|{\Delta }_1\right|+\beta {\left|{\Delta }_1\right|}^3-\left|{ϵ}_{12}\right|·\left|{\Delta }_2\right|=0$$

(19)

and

$$D_2\left|{\Delta }_2\right|+\beta {\left|{\Delta }_2\right|}^3-\left|{ϵ}_{12}\right|·\left|{\Delta }_1\right|=0,$$

(20)

where $D_{\gamma }\left(T\right)=m_{\gamma }{v}_{\gamma }^2/2-{\alpha }_{\gamma }$. Solving Equations (19) and (20) to the cubic order of $|{\Delta }_{\gamma }|$, we can obtain

$${\left|{\Delta }_1\right|}^2=\frac{{ϵ}_{12}^4-{ϵ}_{12}^2{D}_1{D}_2}{\beta ({ϵ}_{12}^2{D}_2+D_1^3)}$$

(21)

and

$${\left|{\Delta }_2\right|}^2=\frac{{ϵ}_{12}^4-{ϵ}_{12}^2{D}_1{D}_2}{\beta ({ϵ}_{12}^2{D}_1+D_2^3)}.$$

(22)

Similar to the single-band circumstance [28], the uniform supercurrent density $j_c\left(T\right)$ can be calculated from the two-component GL theory as follows:

$$\begin{array}{cc}\hfill j\left(T\right)& =2e{\left|{\Delta }_1\right|}^2{v}_1+2e{\left|{\Delta }_2\right|}^2{v}_2\hfill \\ & =\frac{2e}{\beta }\left(\frac{{ϵ}_{12}^4-{ϵ}_{12}^2{D}_1{D}_2}{{ϵ}_{12}^2{D}_2+D_1^3}{v}_1+\frac{{ϵ}_{12}^4-{ϵ}_{12}^2{D}_1{D}_2}{{ϵ}_{12}^2{D}_1+D_2^3}{v}_2\right).\hfill \end{array}$$

(23)

Then the maximum $j\left(T\right)$, i.e., $j_c\left(T\right)$, can be found according to the condition $\frac{dj\left(T\right)}{d{v}_1}{|}_{v_1=v_{1c}}=0$ with Equation (23). We can observe that the normalized critical supercurrent density $j_c\left(T\right)/j_c\left(0\right)$ is independent of $\beta$. With the GL parameter ${\xi }_0=0.28\pm 0.02$ μm, we plot our numerical calculations in Figure 4. For comparison, we also plot the single-band result $j_c\left(T\right)/j_c\left(0\right)={(1-T/T_c)}^{3/2}$ [28] in Figure 4. Furthermore, we can see that our theoretical analysis based on the two-band model is consistent with the experimental measurements for the 2.0 nm thick NbSe${}_2$ film in temperature down to 0.4 $T_c$, which further confirms the multi-band character of the corresponding systems.

Figure 4. The temperature dependence of critical supercurrent density for the NbSe${}_2$ thin film. The experimental data of the 2.0 nm thick NbSe${}_2$ film are taken from Ref. [29].

5. Conclusions

In summary, the experimental measurement of the gap structure at about 1.26 meV and 0.73 meV gives direct evidence of the presence of multi-band superconductivity in the quasi-two-dimensional NbSe${}_2$ system. Based on the two-component GL theory, we first investigated the temperature and angular dependence of the upper critical field in the NbSe${}_2$ film. The results show that the normalized upper critical field as a function of temperature is independent of film thickness, and our calculations are in agreement with the experimental measurements. Furthermore, we also studied the critical supercurrent density through this layered material, which is also in accordance with the experimental measurement. For comparison, we also showed that our two-component model can fit the experimental data better than the single-band theory. Thus, combining all of these facts, our multi-band analyses strongly suggest the NbSe${}_2$ thin film as a two-gap s-wave superconductor. In addition, our mean-field computations also indicate that the band with the large (or small) gap corresponds to the one with the large (or small) effective mass, and the effective mass anisotropy is about 4.2. We hope that our theoretical results will inspire further research on better understanding the pairing symmetry and superconducting properties in this van der Waals layered material.