Analysis of Interlayer Crack Propagation and Strength Prediction of Steel Bridge Deck Asphalt Pavement Based on Extended Finite Element Method and Cohesive Zone Model (XFEM–CZM) Coupling
Abstract
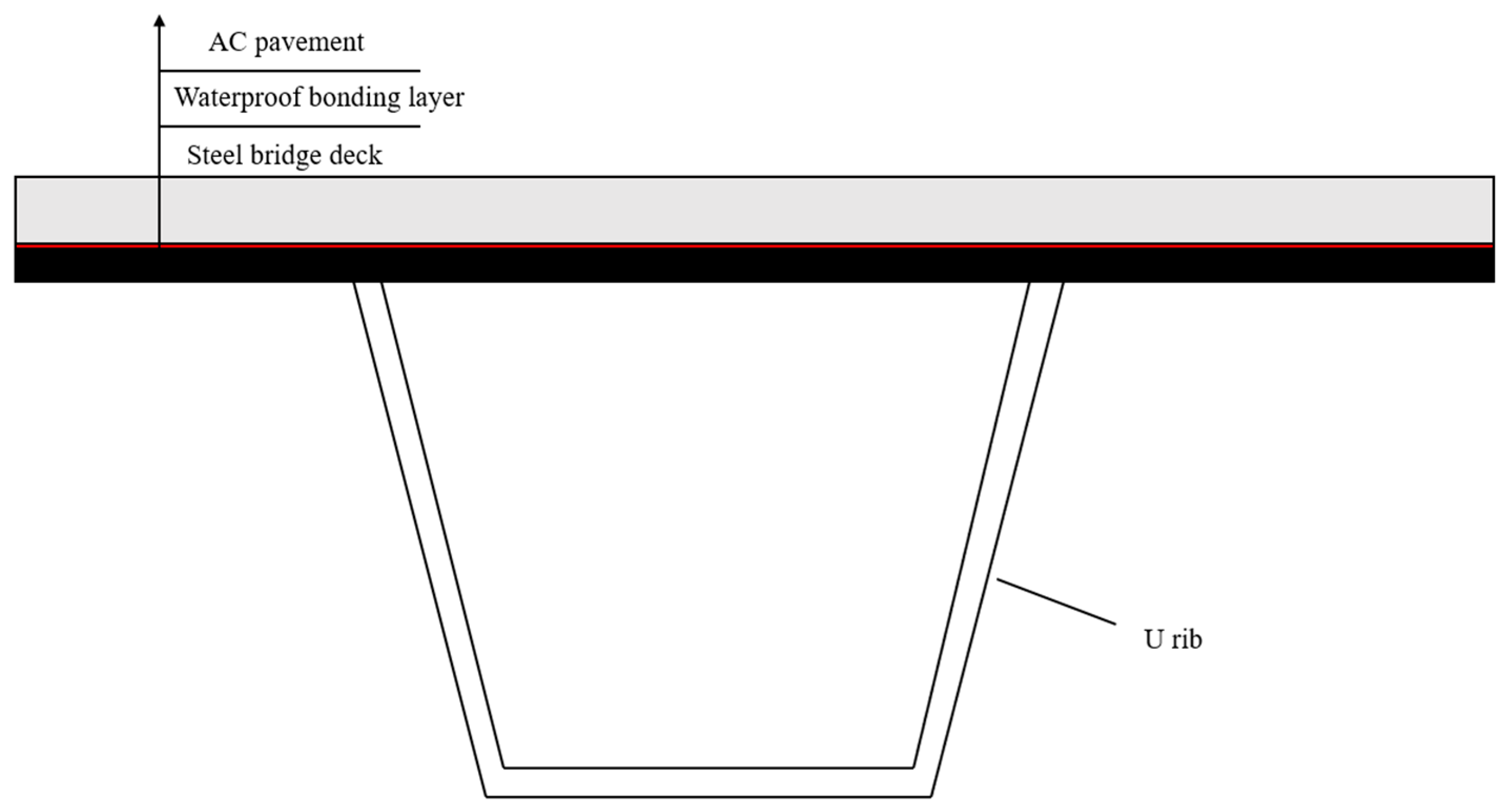
1. Introduction
2. Numerical Methods and Damage Models
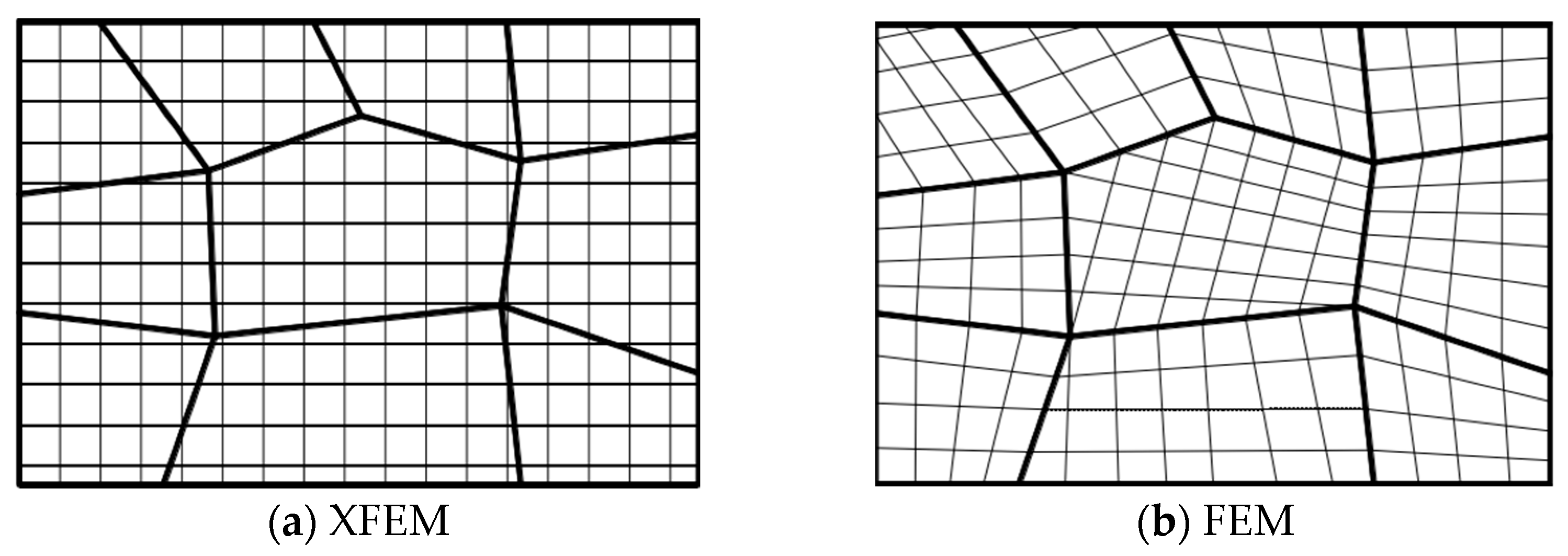
2.1. XFEM
2.2. Crack Initiation Criterion and Expansion Criterion of the Bonded Layer
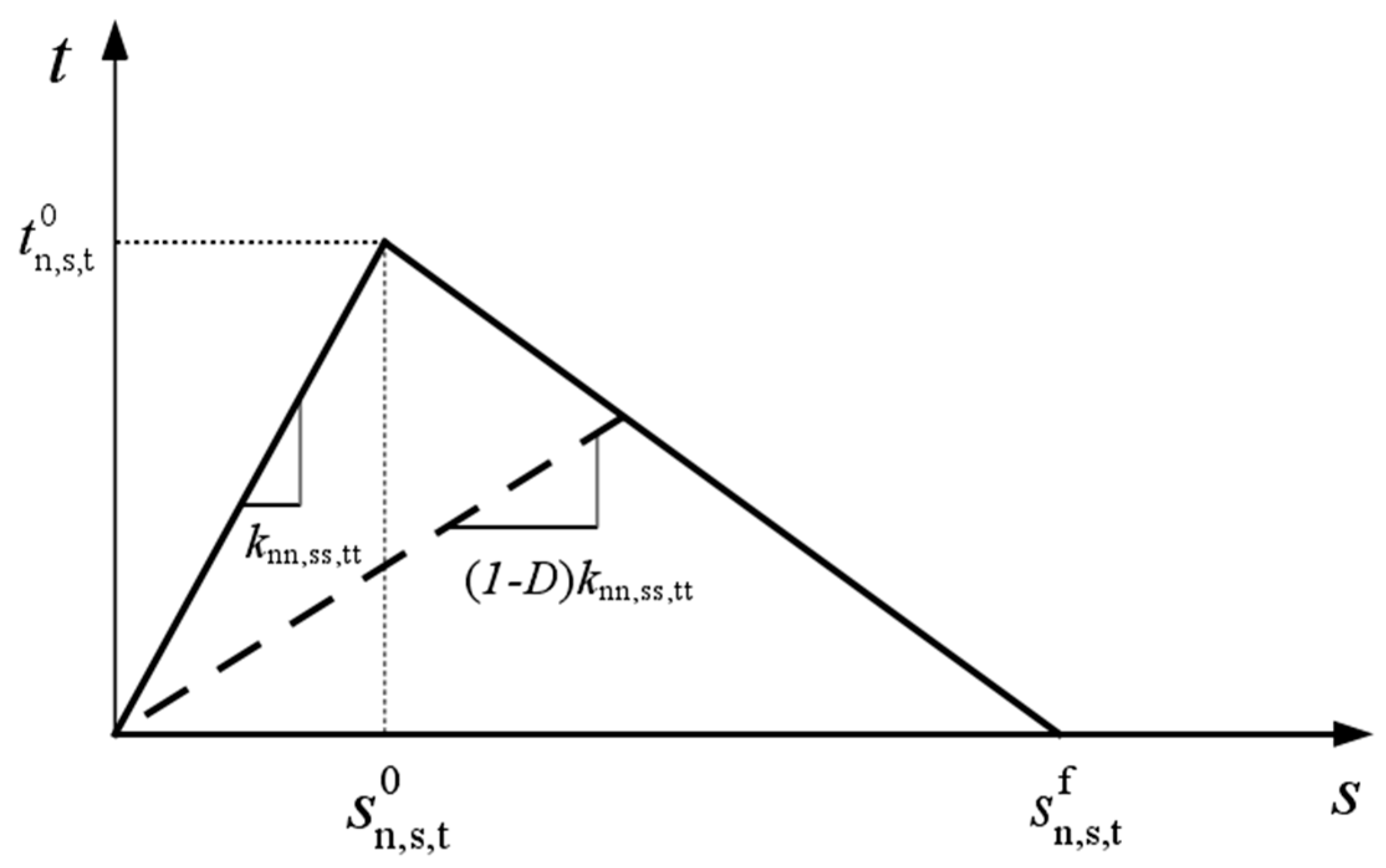
2.3. Interface Damage Model
- (1)
- Injury initiation criterion
- (2)
- Damage evolution
3. Experimental Interlayer Model of a Double Cantilever Beam with a Steel Deck Asphalt Pavement
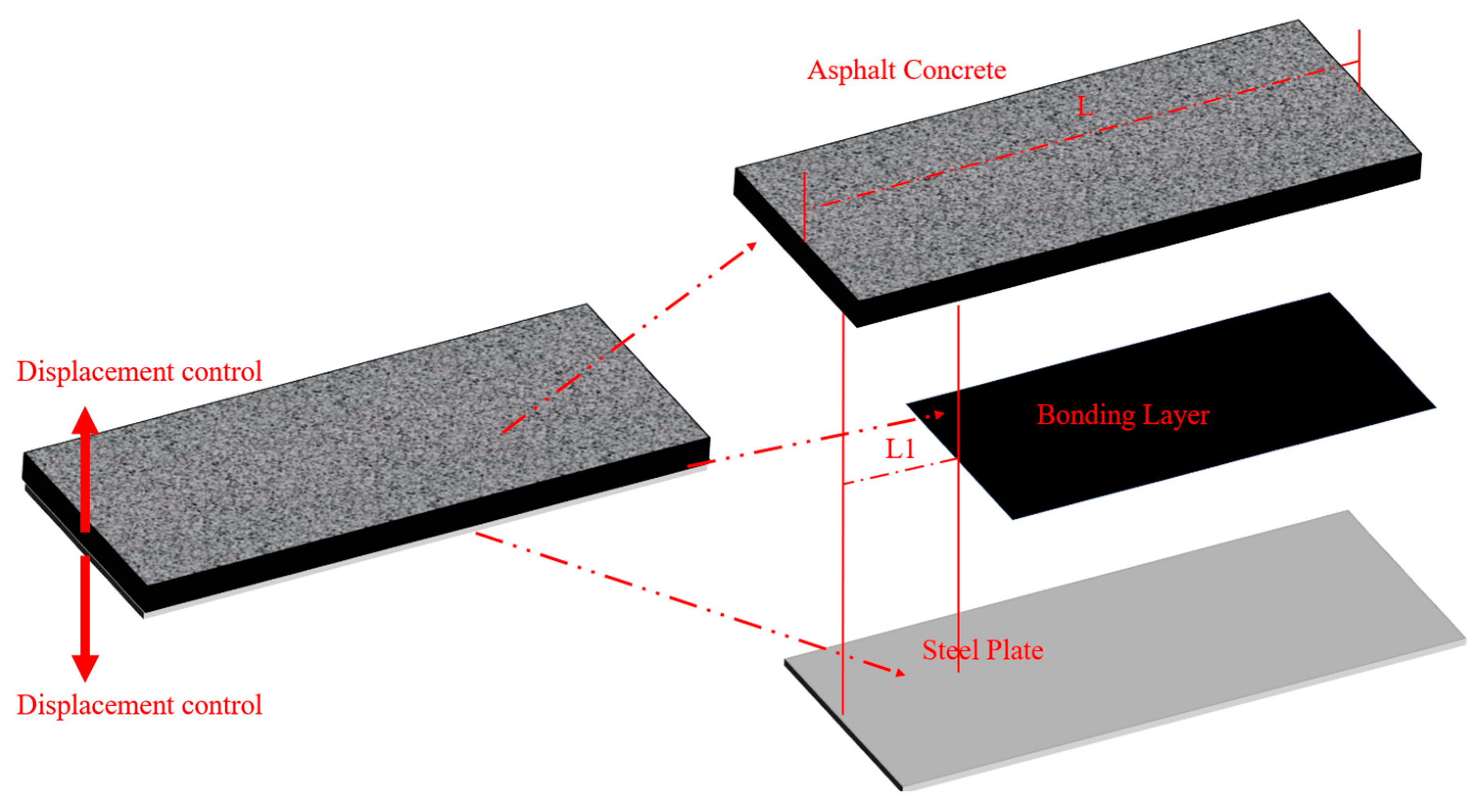
3.1. Experimental Design of Double Cantilever Beam
3.1.1. Specimen Design
3.1.2. Test Piece Fabrication Method
3.2. Finite Element Model
4. Numerical Validation and Parameter Discussion
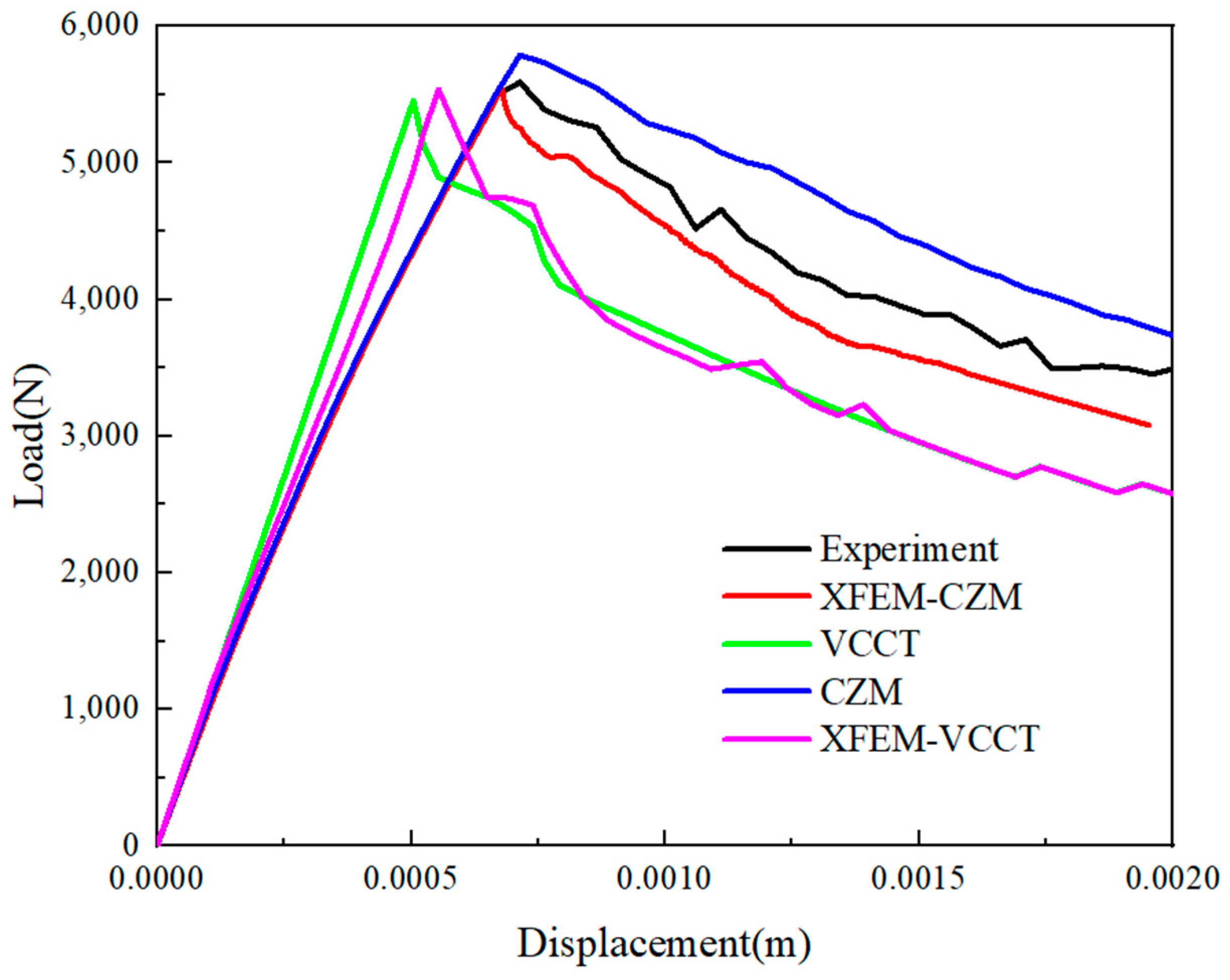
4.1. Numerical Verification
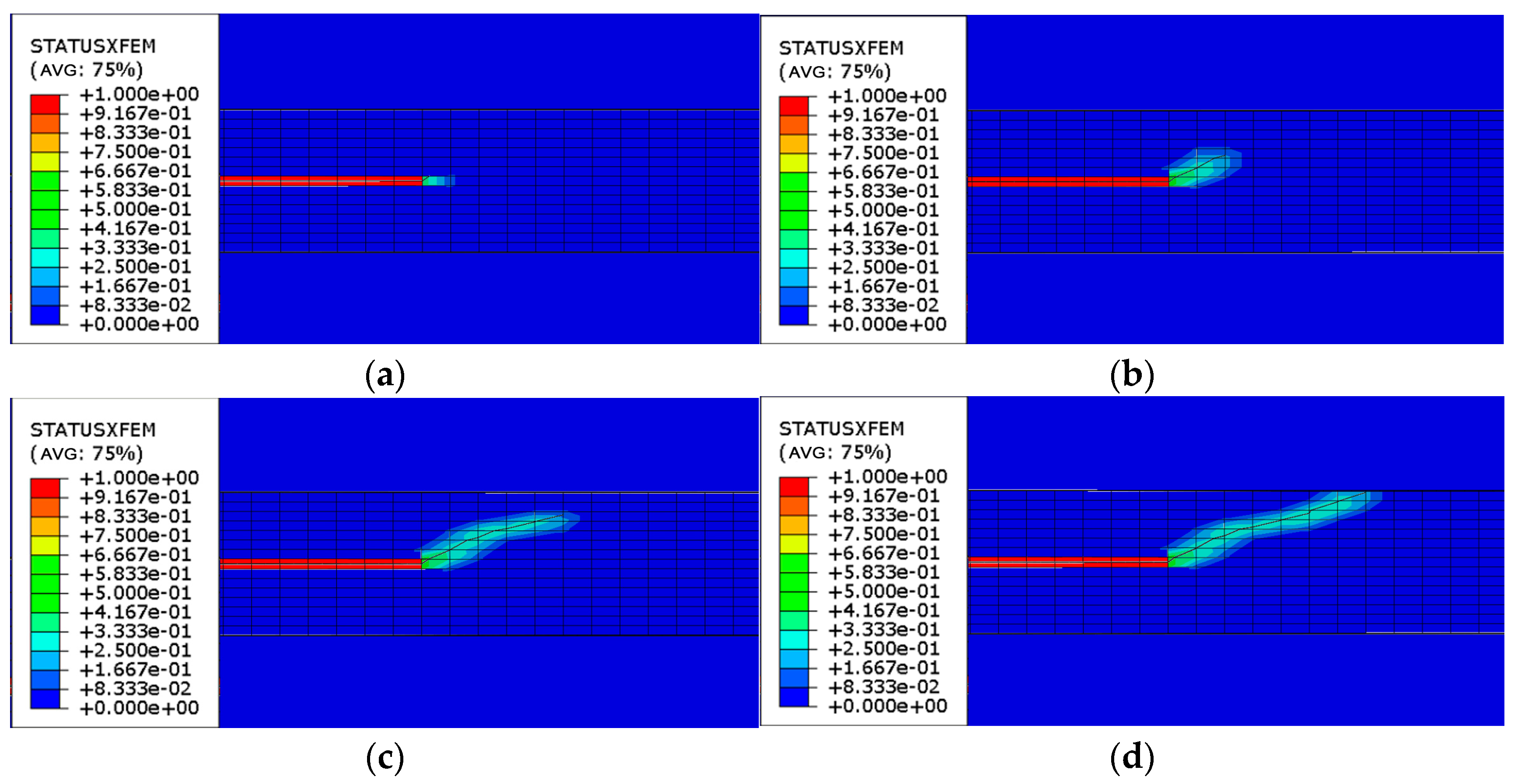
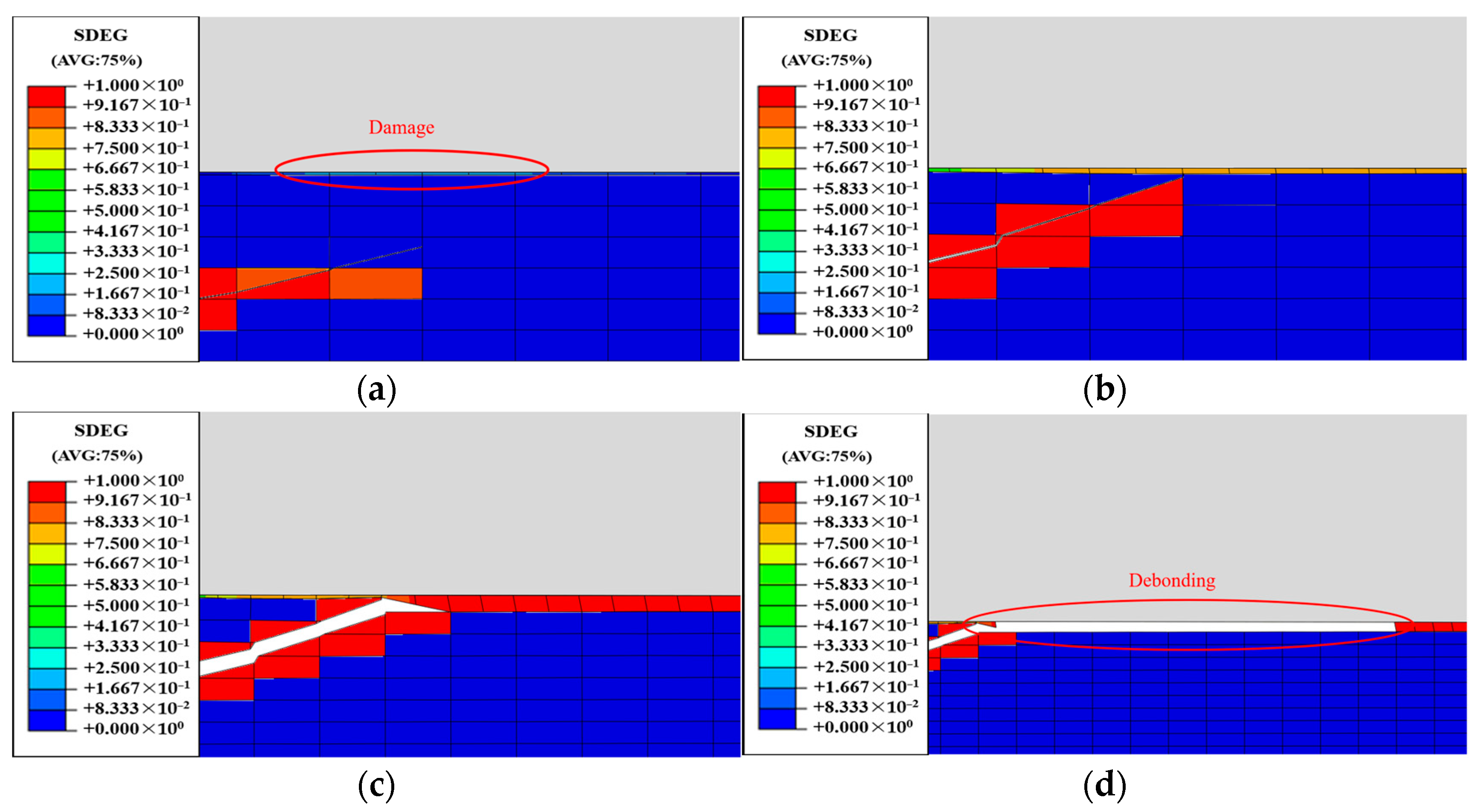
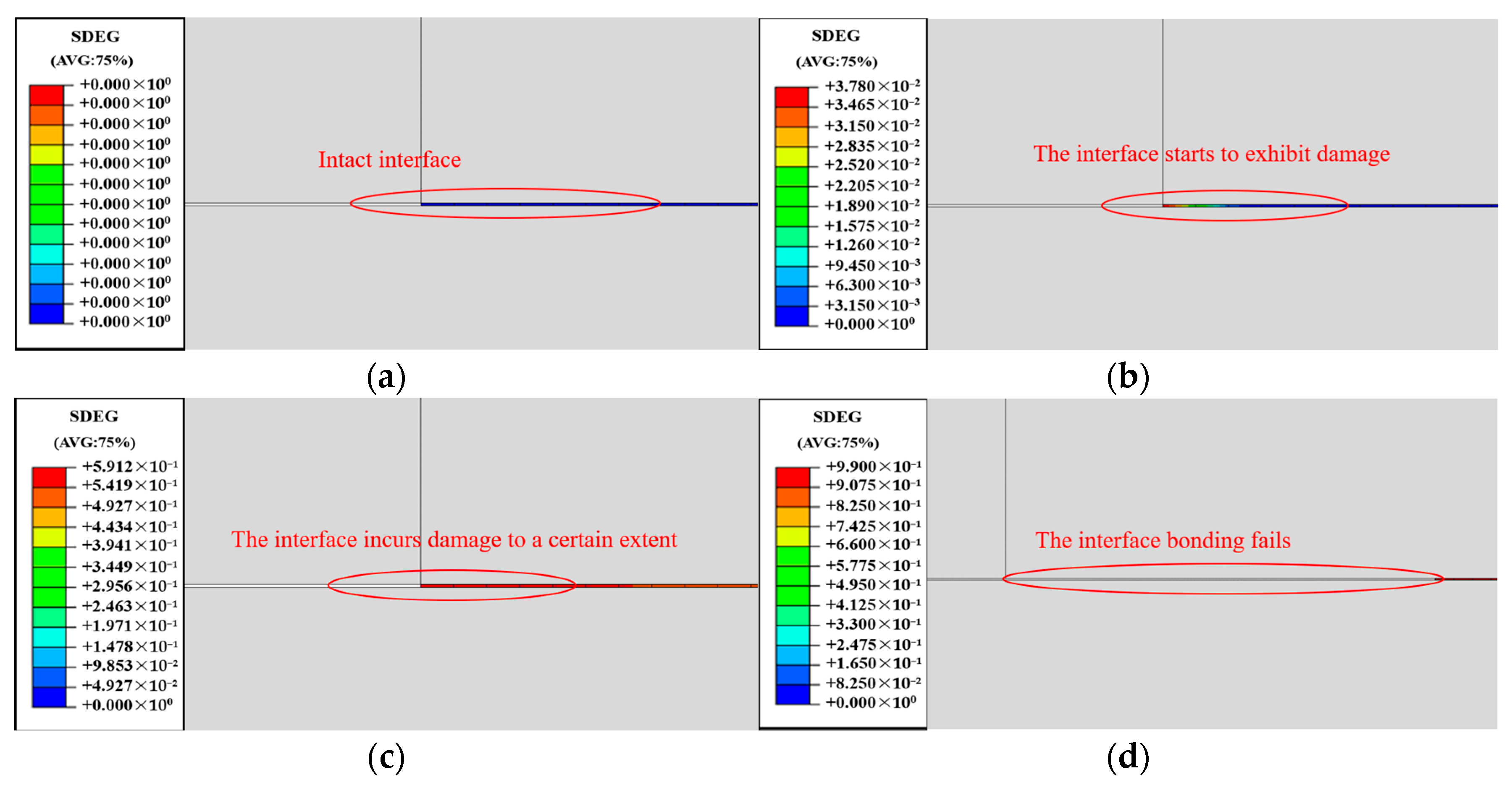
4.2. Crack Extension and Interface Debonding Analysis
4.3. Impact of Parameters
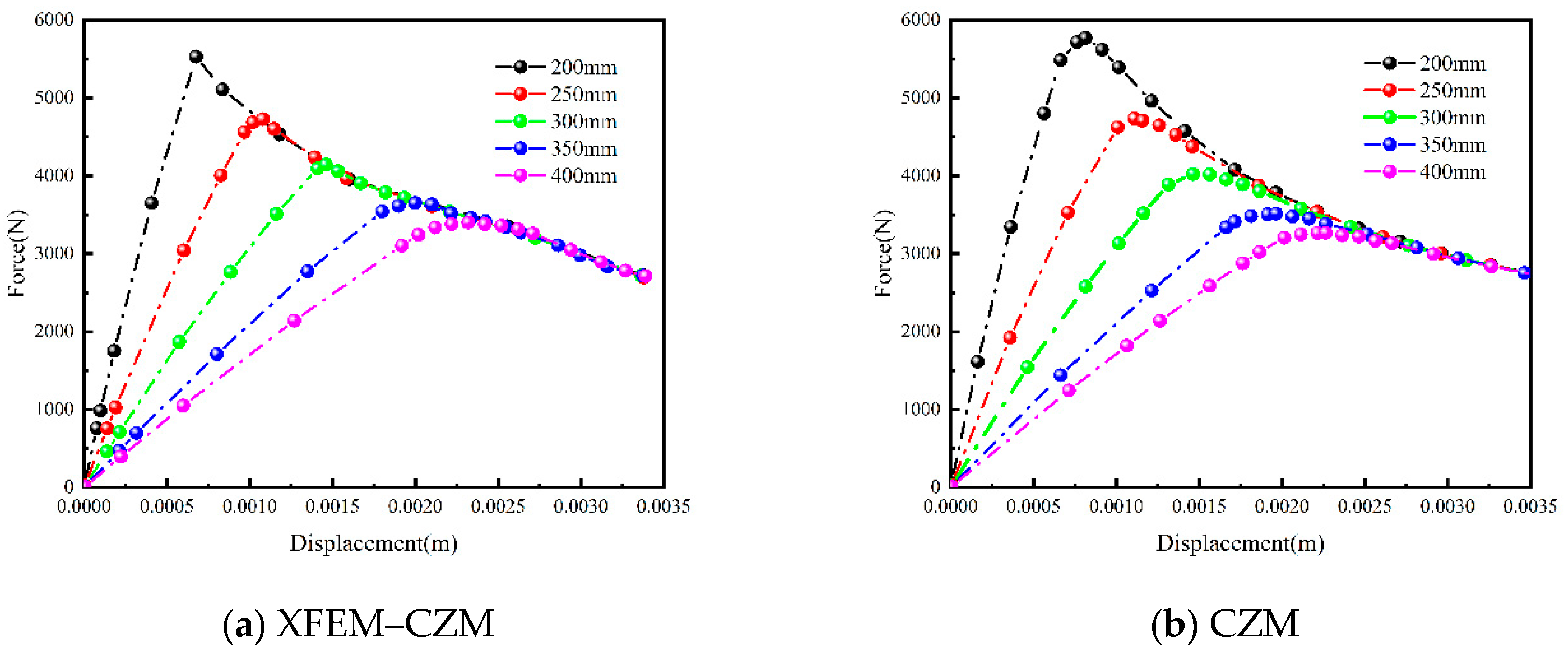
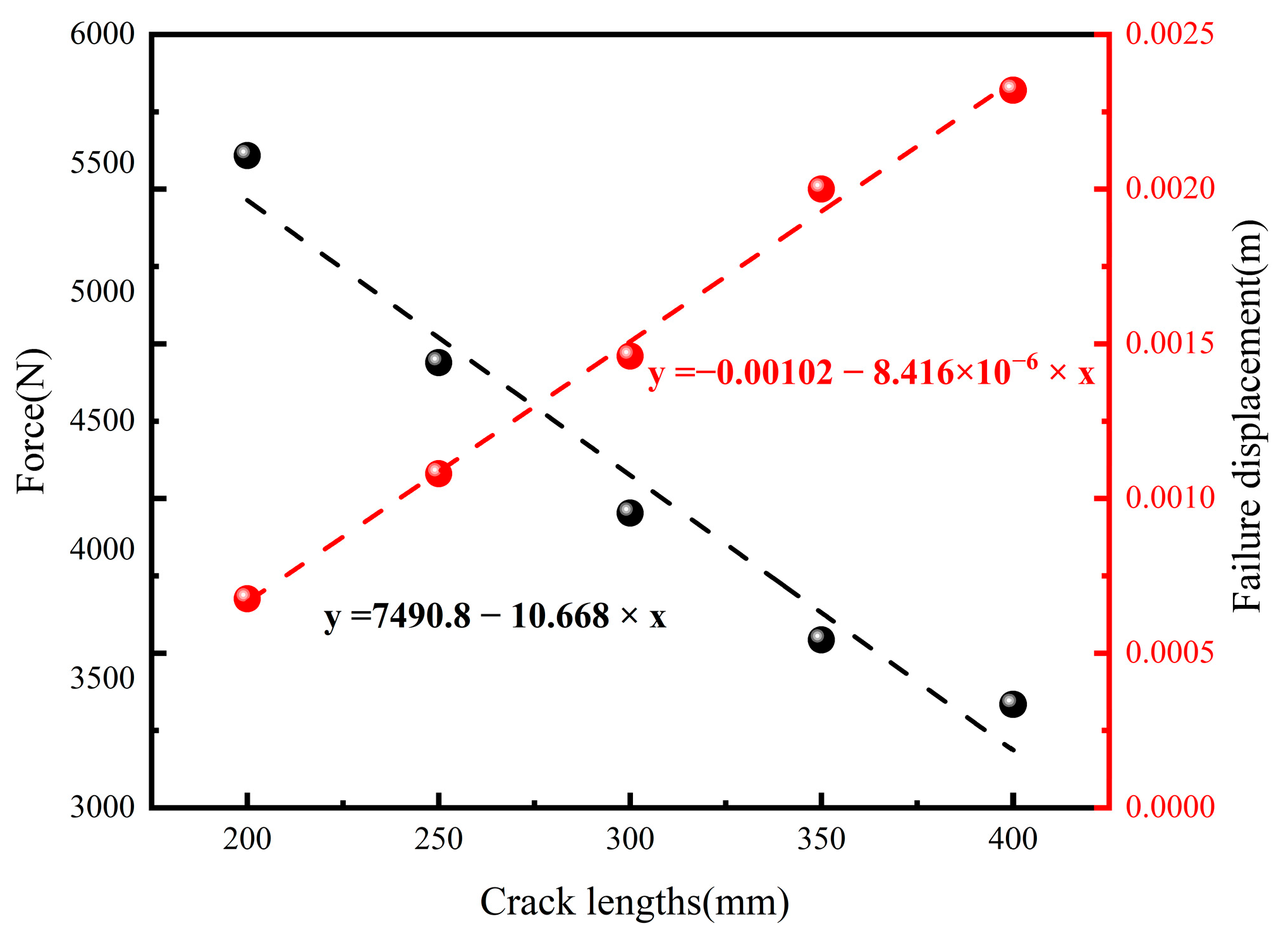
4.3.1. Influence of Initial Crack Length
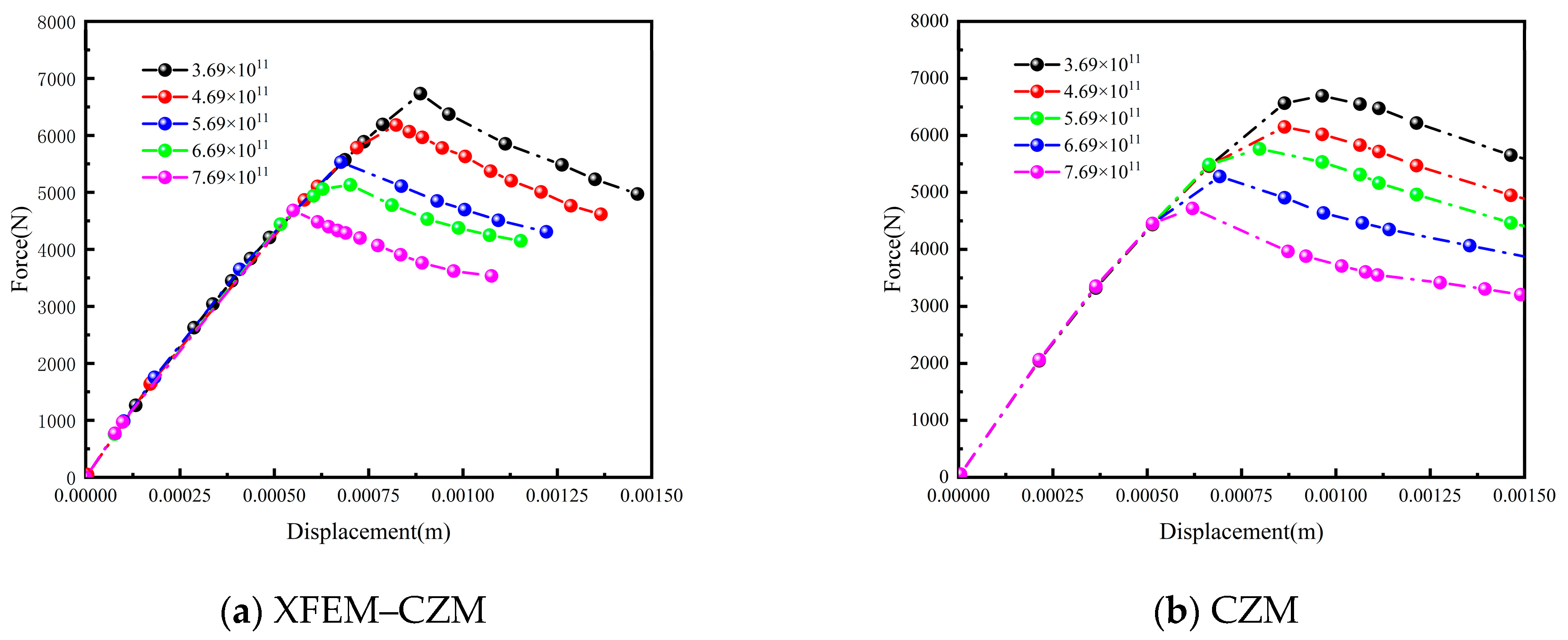
4.3.2. Effect of Interface Parameters
- (1)
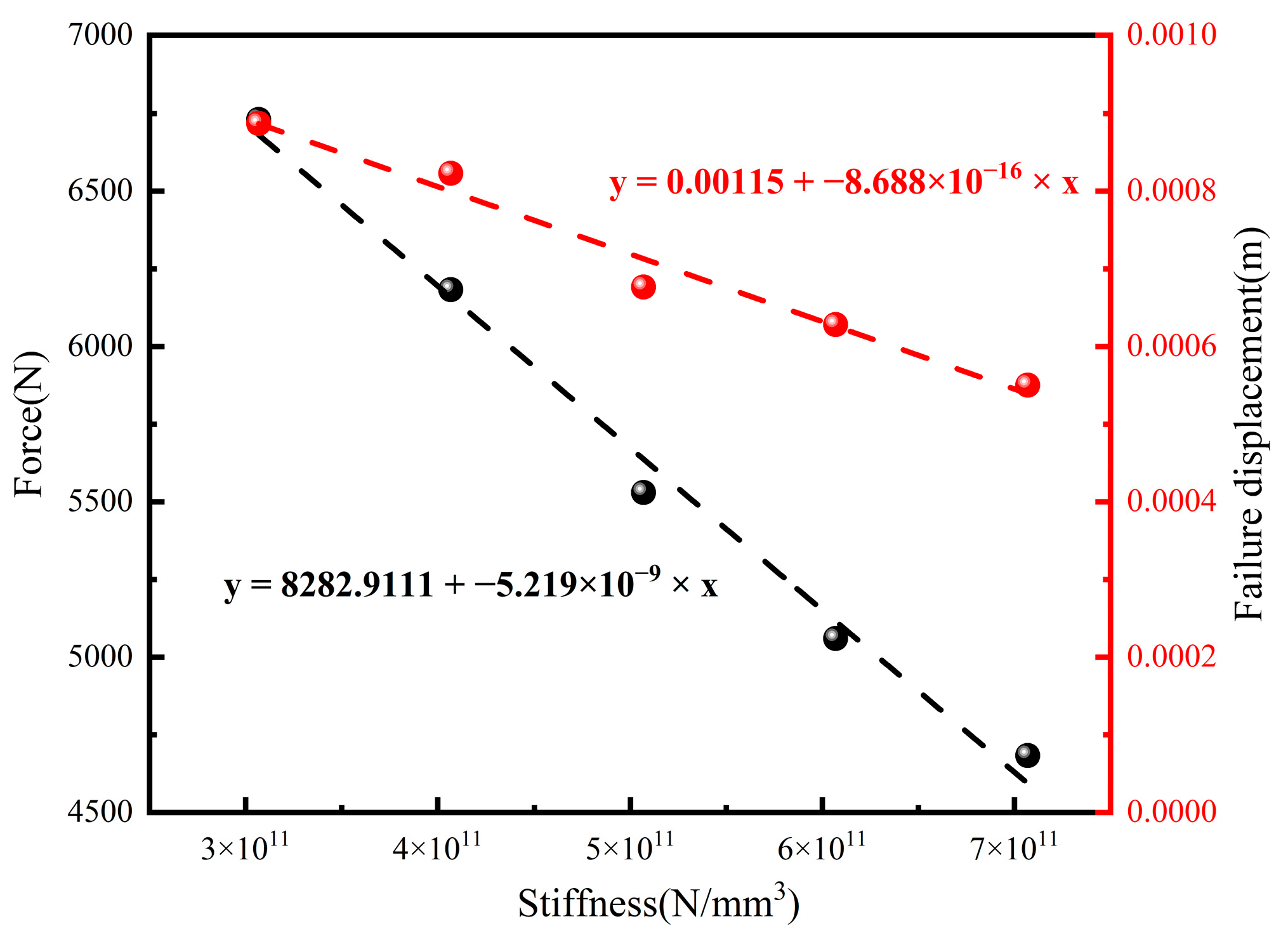
- Influence of Interface Stiffness
- (2)
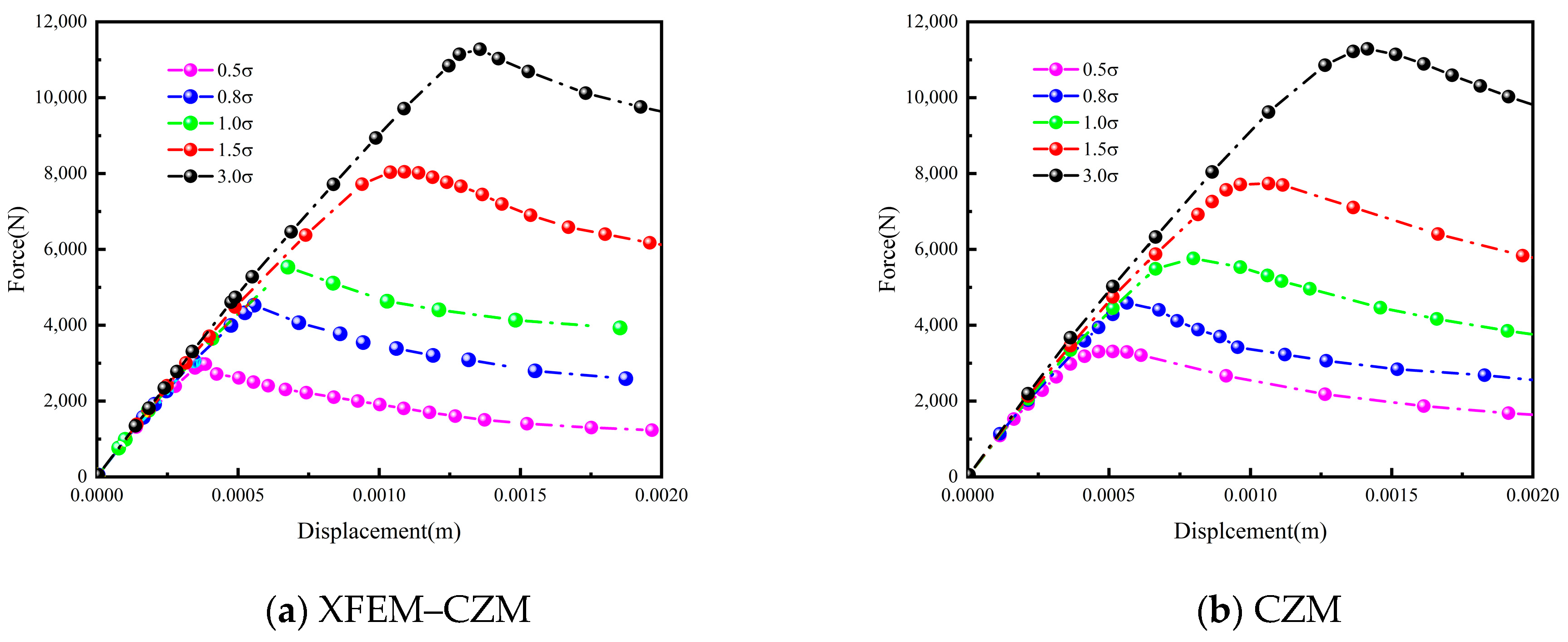
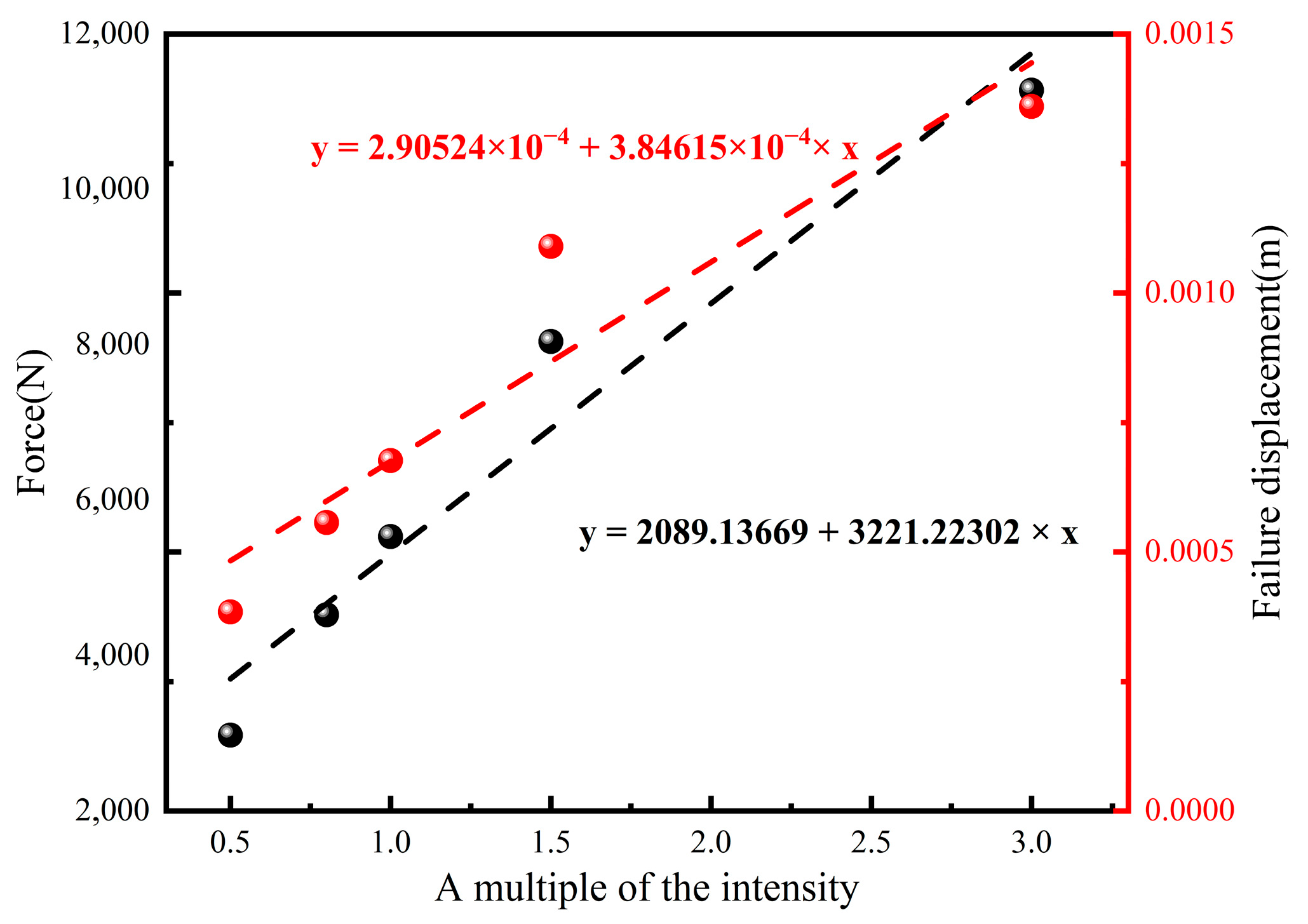
- Influence of Interface Strength
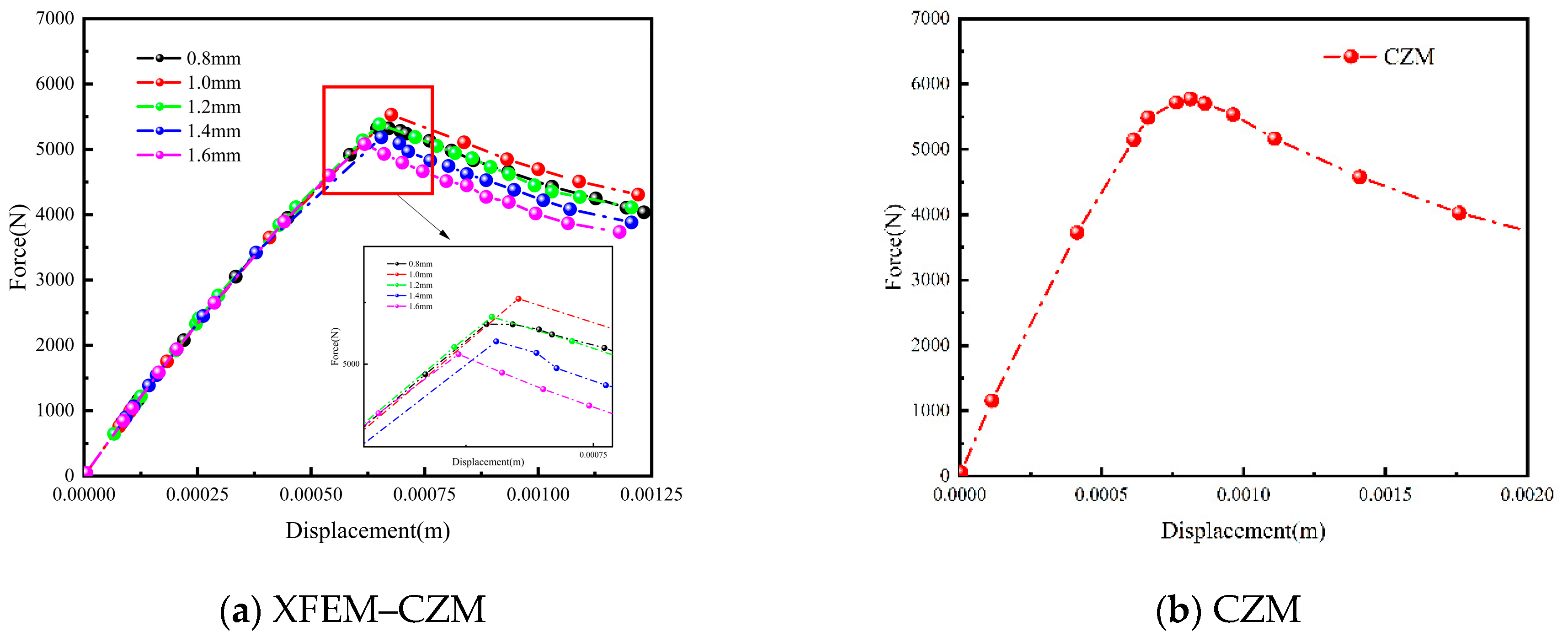
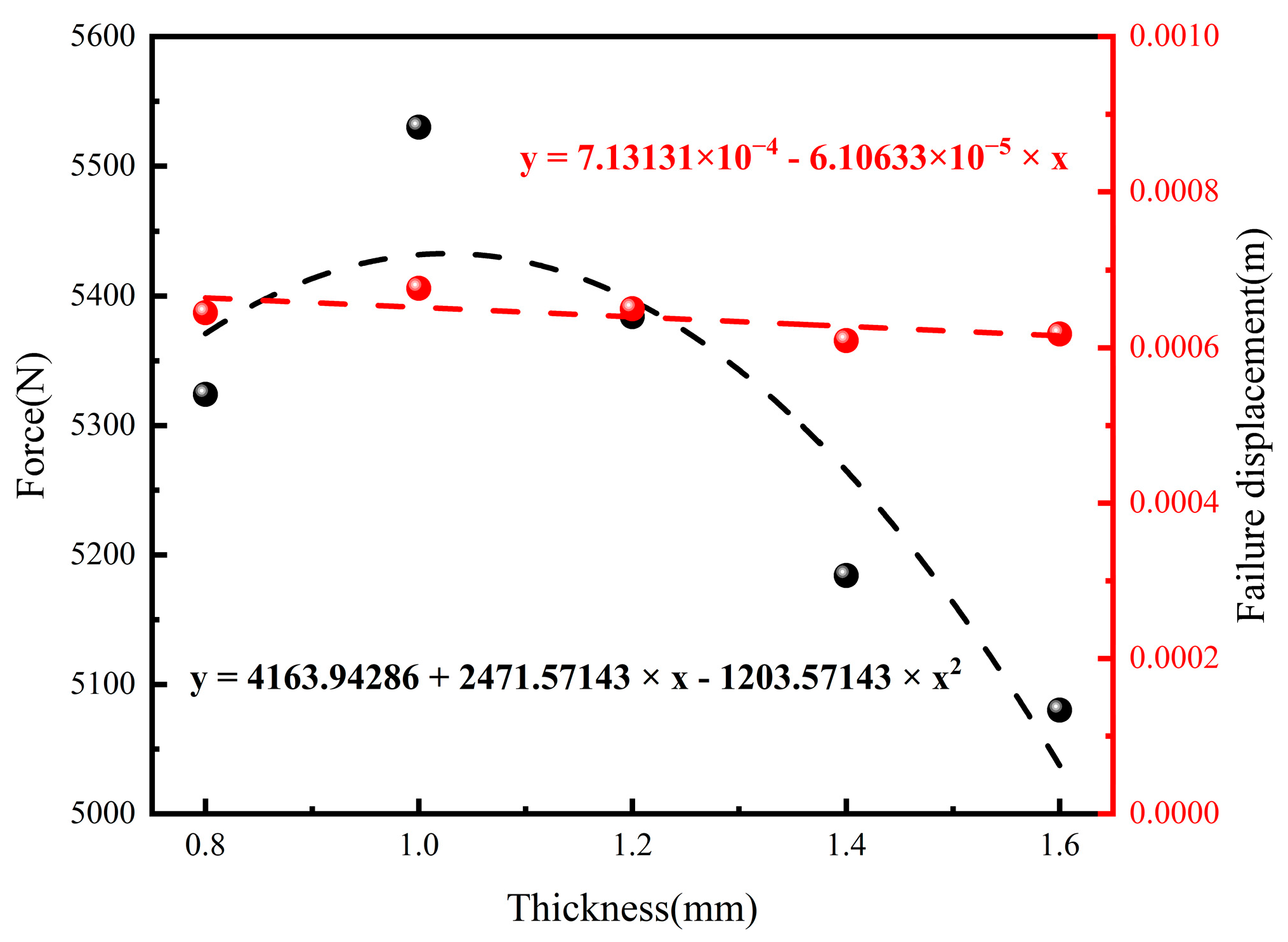
4.3.3. Influence of Bonding Layer Thickness
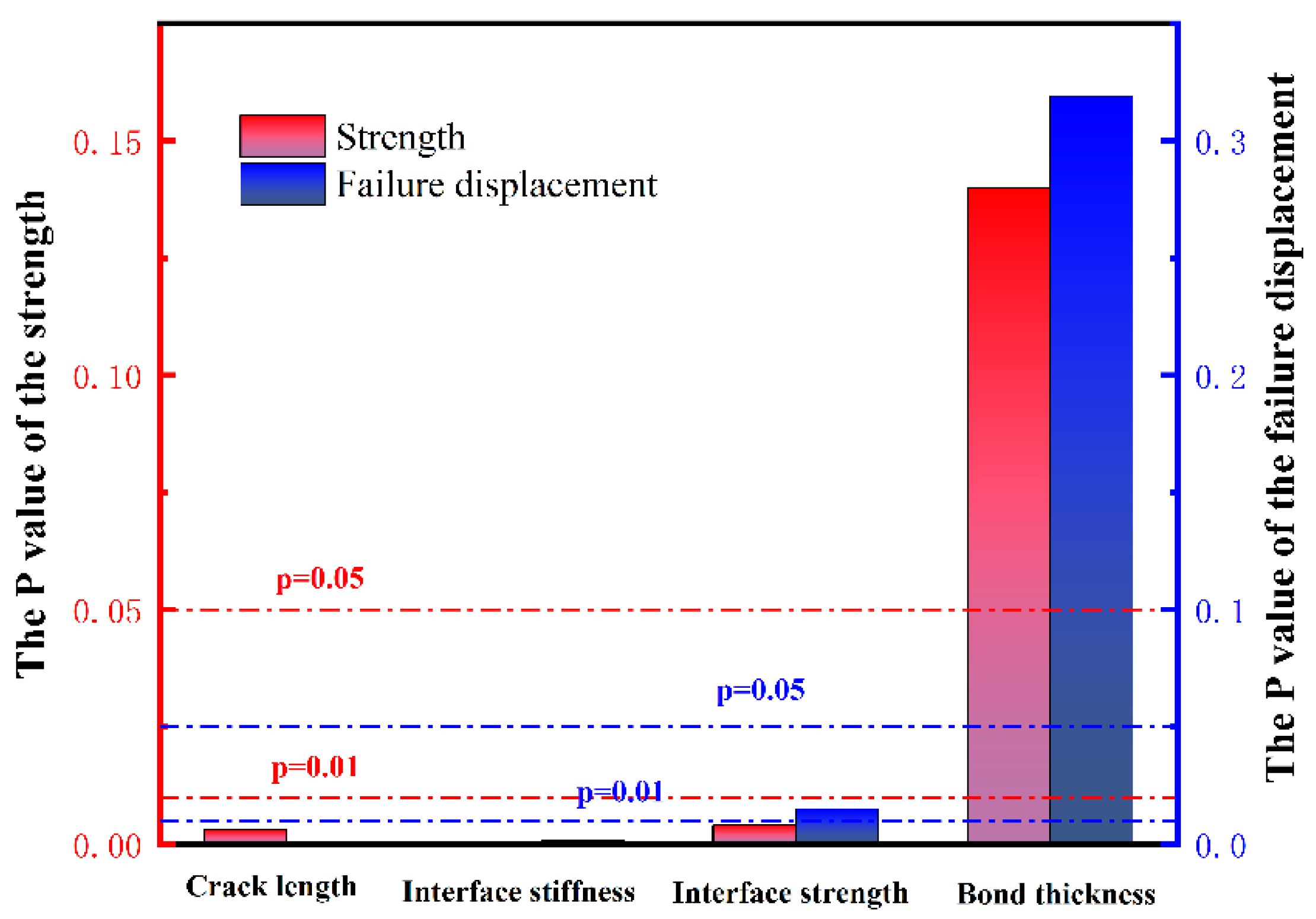
4.3.4. Significance Analysis
5. Conclusions
- Cracks originating within the bonding layer propagated in the direction of the maximum principal stress until they reached the asphalt–bonding layer interface, resulting in interface damage and the occurrence of layering. Similar interface damage was observed between the bonding layer and the steel bridge deck. As displacement loads increased, various layering phenomena manifested at these interfaces.
- Longer crack lengths within the layer led to reduced crack propagation, resulting in diminished strength and increased failure displacement. Increased interfacial stiffness widened the crack propagation path within the layer, consequently reducing strength and augmenting failure displacement. Although the interfacial strength exhibited a minor influence on the crack propagation path, it significantly impacted overall strength and interlayer failure displacement.
- It is worth noting that interface stiffness and strength had minimal effects on the crack propagation path within the layer, but exerted a significant influence on the interlayer bonding strength. Enhanced stiffness diminished the bonding layer strength and failure displacement, while an elevated interface strength fortified the bonding layer strength and augmented failure displacement.
- Variations in the thickness of the bonding layer affected the crack propagation path within the layer. An initial increase in thickness enhanced the bonding strength, but subsequent increments resulted in reduced strength. Our analysis recommended an optimal bonding layer thickness of approximately 1 mm to achieve a higher strength.
- A significance analysis underscored that changes in interface stiffness had the most substantial impact on interlayer strength and failure displacement, followed by the influence of the crack length, interface strength, and bonding layer thickness. These findings shed light on the intricate interplay of parameters that influence crack propagation and interlayer bonding behavior.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Li, G. Study of factors influencing gussasphalt mixture performance. Constr. Build. Mater. 2015, 101, 193–200. [Google Scholar] [CrossRef]
- Ma, Y.; Wang, H.; Zhao, K.; Yan, L.; Yang, D. Study of a Modified Time Hardening Model for the Creep Consolidation Effect of Asphalt Mixtures. Materials 2022, 15, 2710. [Google Scholar] [PubMed]
- Du, H.; Ni, F.; Ma, X. Crack resistance evaluation for In-service asphalt pavements by using SCB tests of layer-core samples. J. Mater. Civ. Eng. 2021, 33, 04020418. [Google Scholar] [CrossRef]
- Zhang, M.; Hao, P.; Li, Y. Interfacial adhesive property in “asphalt mixture-PMA copolymer-steel plate” system: Experimental and molecular dynamics simulation. Constr. Build. Mater. 2021, 281, 122529. [Google Scholar]
- Liu, Y.; Qian, Z.; Gong, M.; Huang, Q.; Ren, H. Inter-layer residual stress analysis of steel bridge deck pavement during gussasphalt pavement paving. Constr. Build. Mater. 2022, 324, 126624. [Google Scholar] [CrossRef]
- Xue, C.; Wan, Y.; Wang, H. Mechanics Property Analysis for A New Steel Bridge Deck Pavement with UTAC—UHPC. For. Eng. 2020, 36, 76–84+93. [Google Scholar]
- Liu, Y.; Qian, Z.; Yin, Y.; Ren, H. Investigation on inter-layer Behaviors of a Double-Layered Heterogeneous Asphalt Pavement Structure for Steel Bridge Deck. J. Mater. Civ. Eng. 2022, 34, 04022062. [Google Scholar] [CrossRef]
- Jin, W.; Zhao, Y.; Wang, W.; He, F. Performance evaluation and optimization of waterproof adhesive layer for concrete bridge deck in seasonal frozen region using AHP. Adv. Mater. Sci. Eng. 2021, 2021, 5555535. [Google Scholar] [CrossRef]
- Fu, J.; Shen, A.; Yuan, Z. Properties of Different Waterproof Bonding Layer Systems for Cement Concrete Bridge Deck Pavement. Coatings 2022, 12, 308. [Google Scholar] [CrossRef]
- Zhang, M.; Hao, P.; Men, G.; Liu, N.; Yuan, G. Research on the compatibility of waterproof layer materials and asphalt mixture for steel bridge deck. Constr. Build. Mater. 2021, 269, 121346. [Google Scholar] [CrossRef]
- Xu, Y.; Lv, X.; Ma, C.; Liang, F.; Qi, J.; Chou, Z.; Xu, S. Shear Fatigue Performance of Epoxy Resin Waterproof Adhesive Layer on Steel Bridge Deck Pavement. Front. Mater. 2021, 7, 618073. [Google Scholar] [CrossRef]
- Ai, C.; Huang, H.; Rahman, A.; An, S. Establishment of a new approach to optimized selection of steel bridge deck waterproof bonding materials composite system. Constr. Build. Mater. 2020, 264, 120269. [Google Scholar] [CrossRef]
- Chen, W.; Hui, B.; Rahman, A. Inter-layer Shear Characteristics of Bridge Deck Pavement through Experimental and Numerical Analysis. Materials 2022, 15, 7001. [Google Scholar] [CrossRef] [PubMed]
- Xu, J.; Li, N.; Xu, T. Temperature changes of interlaminar bonding layer in different seasons and effects on mechanical properties of asphalt pavement. Int. J. Pavement Res. Technol. 2022, 15, 589–605. [Google Scholar] [CrossRef]
- Zhang, W.; Li, Q.; Wang, J.; Meng, Y.; Zhou, Z. Aging Behavior of High-Viscosity Modified Asphalt Binder Based on Infrared Spectrum Test. Materials 2022, 15, 2778. [Google Scholar] [CrossRef]
- Ma, X.; Kan, J.; Liu, S.; Tu, M.; Wang, D. Investigation of the Effect of Filler on Cohesive Bond Strength of Asphalt Mastic Using Binder Bond Strength (BBS) Test. Coatings 2023, 13, 1001. [Google Scholar] [CrossRef]
- Chen, Z.; Xu, W.; Zhao, J.; An, L.; Wang, F.; Du, Z.; Chen, Q. Experimental Study of the Factors Influencing the Performance of the Bonding Interface between Epoxy Asphalt Concrete Pavement and a Steel Bridge Deck. Buildings 2022, 12, 477. [Google Scholar] [CrossRef]
- Liu, Y.; Qian, Z.; Zheng, D.; Zhang, M. Interlaminar thermal effect analysis of steel bridge deck pavement during gussasphalt mixture paving. Int. J. Pavement Eng. 2019, 20, 1323–1335. [Google Scholar] [CrossRef]
- Graczyk, M.; Zbiciak, A.; Michalczyk, R.; Kowalewski, Ł. Numerical modelling of bubbles formation in the bridge asphalt pavement under gas pressure impact. Transp. Res. Procedia 2016, 14, 3925–3934. [Google Scholar] [CrossRef][Green Version]
- Nie, W.; Wang, D.; Sun, Y.; Xu, W.; Xiao, X. Integrated design of structure and material of epoxy asphalt mixture used in steel bridge deck pavement. Buildings 2021, 12, 9. [Google Scholar] [CrossRef]
- Yuya, W.; Yasushi, T.; Futoshi, K.; Kazuhiro, W. Evaluation of the Effect of Interlayer Bonding Condition on the Deterioration of Asphalt Pavement. Transp. Res. Rec. 2023, 2677, 03611981231153649. [Google Scholar] [CrossRef]
- De Santis, Y.; Pasca, D.P.; Aloisio, A.; Stenstad, A.; Mahnert, K.C. Experimental, analytical and numerical investigation on the capacity of composite glulam beams with holes. Eng. Struct. 2023, 285, 115995. [Google Scholar] [CrossRef]
- Koord, J.; Völkerink, O.; Petersen, E.; Hühne, C. Effect of low temperature on mode I and mode II interlaminar fracture toughness of CFRP-steel hybrid laminates. Compos. Part B Eng. 2023, 262, 110773. [Google Scholar] [CrossRef]
- Yao, X.; Li, C.; Xu, T. Interfacial adhesive behaviors between SBS modified bitumen and aggregate using molecular dynamics simulation. Surf. Interfaces 2022, 33, 102245. [Google Scholar] [CrossRef]
- Zhou, W.; Zhang, C.; Gan, S. Crack propagation analysis and strength prediction of glued joints based on XFEM-CZM coupling method. J. Beijing Univ. Aeronaut. Astronaut. 2020, 46, 2121–2130. [Google Scholar]
- Feng, W.; Xu, H.; Yu, H.; Li, M. Adhesive damage and defect analysis of scarf-repaired composite by combining extended finite element method and cohesive zone model. J. Compos. 2018, 35, 1354–1360. [Google Scholar]
- Belytschko, T.; Black, T. Elastic crack growth in finite elements with minimal remeshing. Int. J. Numer. Methods Eng. 1999, 45, 601–620. [Google Scholar] [CrossRef]
- Moës, N.; Dolbow, J.; Belytschko, T. A finite element method for crack growth without remeshing. Int. J. Numer. Methods Eng. 1999, 46, 131–150. [Google Scholar] [CrossRef]
- Zhuo, Z. Extended Finite Element Method; Tsinghua University Press: Beijing, China, 2012; pp. 35–36. [Google Scholar]
- Melenk, J.M.; Babuška, I. The partition of unity finite element method: Basic theory and applications. Comput. Methods Appl. Mech. Eng. 1996, 139, 289–314. [Google Scholar] [CrossRef]
- Gao, L.; Deng, X.; Zhang, Y.; Ji, X.; Li, Q. Fracture parameters and cracking propagation of cold recycled mixture considering material heterogeneity based on extended finite element method. Materials 2021, 14, 1993. [Google Scholar] [CrossRef]
- Heidari-Rarani, M.; Sayedain, M. Finite element modeling strategies for 2D and 3D delamination propagation in composite DCB specimens using VCCT, CZM and XFEM approaches. Theor. Appl. Fract. Mech. 2019, 103, 102246. [Google Scholar] [CrossRef]
- Wu, S. Study on the Interface Characteristics of Steel Deck Pavement with Engineered Cementitious Composites. Ph.D. Thesis, Southeast University, Dhaka, Bangladesh, 2019. [Google Scholar]
- Qian, Z.; Liu, Y. Mechanical analysis of waterproof bonding layer on steel bridge deck under bridge-temperature-load coupling effect. J. Southeast Univ. Nat. Sci. Ed. 2012, 42, 729–733. [Google Scholar]
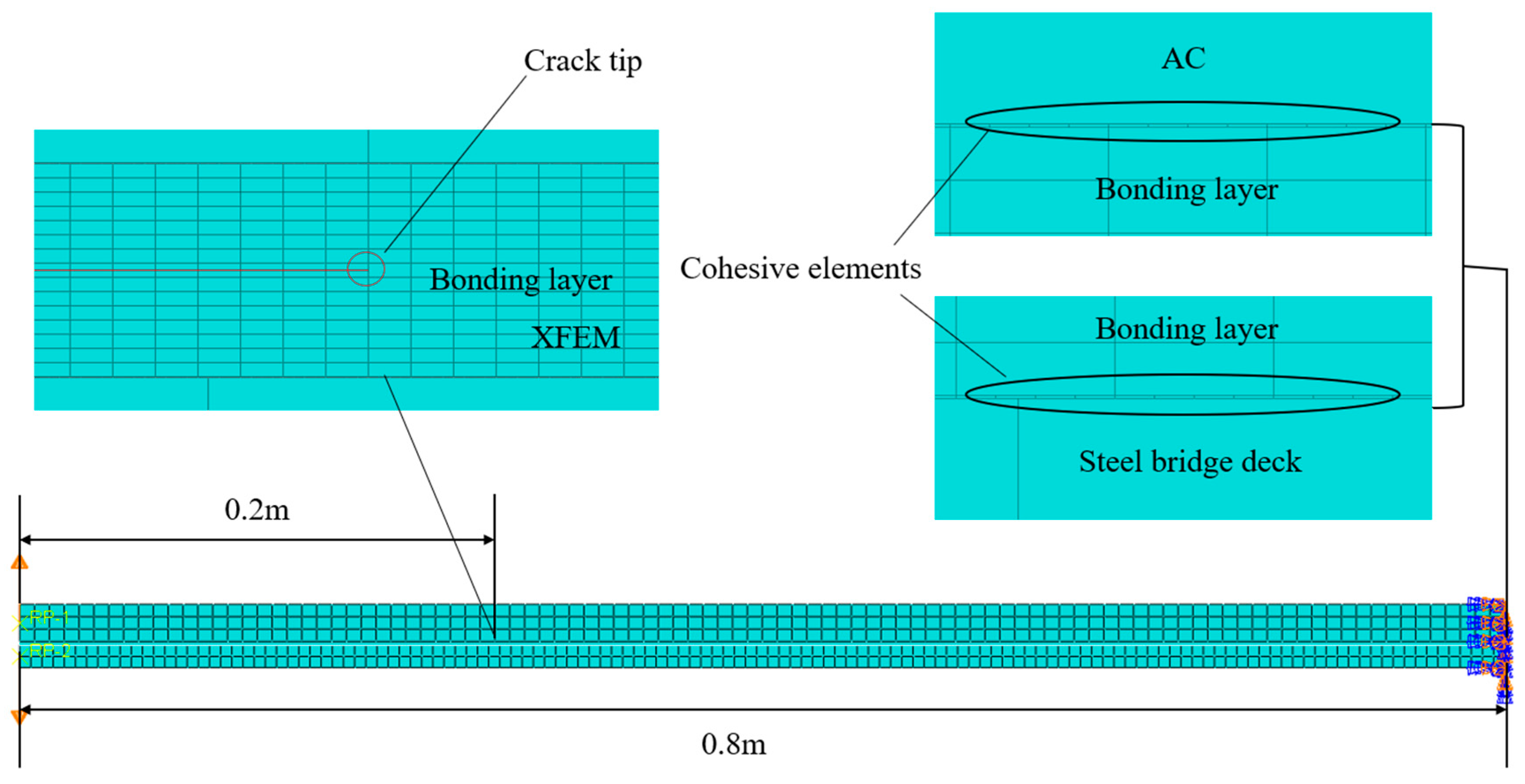

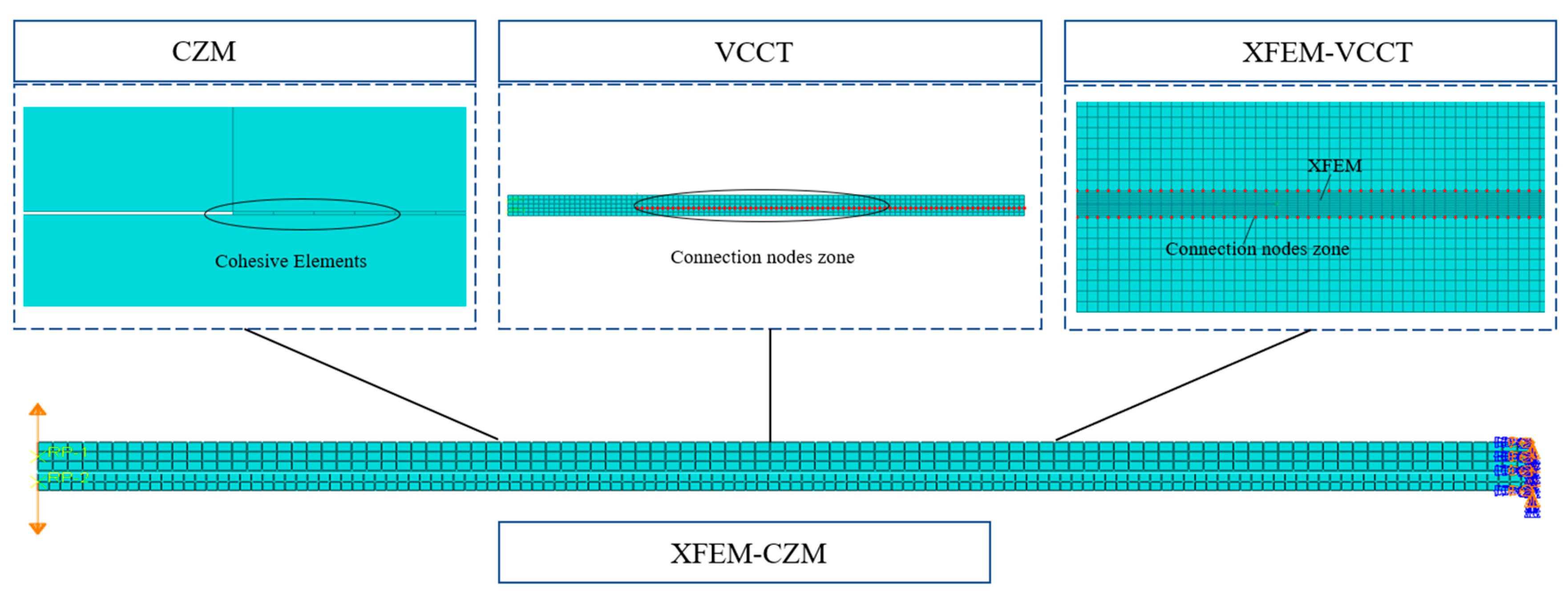






| Materials | Length/m | Width/m | Thickness/m |
|---|---|---|---|
| AC | 0.8 | 0.35 | 0.066 |
| Q345qD | 0.8 | 0.35 | 0.014 |
| Parameters | Steel Plate | AC Layer | Bonding Layer |
|---|---|---|---|
| 210,000 | 4500 | 100 [34] | |
| 0.3 | 0.25 | 0.25 | |
| 0.8 | |||
| 0.5 | |||
| 233 | |||
| 142 |
| Interface Parameters | Numerical Value |
|---|---|
| 5.069 × 1011 | |
| 0.8 | |
| 0.5 | |
| 233 | |
| 142 |
| Element Count | Maximum Load/N | Displacement/mm |
|---|---|---|
| 50,000 | 6248.321 | 0.688 |
| 65,000 | 5882.212 | 0.656 |
| 70,000 | 5652.465 | 0.628 |
| 75,000 | 5544.823 | 0.629 |
| 85,000 | 5642.330 | 0.629 |
| 95,000 | 5598.426 | 0.631 |
| Method | Maximum Load/N | Displacement/mm | Load Error/% | Displacement Error/% |
|---|---|---|---|---|
| Experiment | 5589.130 | 0.713 | 0 | 0 |
| VCCT | 5450.182 | 0.504 | 2.4 | 29.1 |
| XFEM–VCCT | 5536.503 | 0.554 | 0.9 | 22.3 |
| CZM | 5771.36 | 0.713 | 3.2 | 0.1 |
| XFEM–CZM | 5544.17 | 0.688 | 0.8 | 0.3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, C.; Li, W.; Wang, H. Analysis of Interlayer Crack Propagation and Strength Prediction of Steel Bridge Deck Asphalt Pavement Based on Extended Finite Element Method and Cohesive Zone Model (XFEM–CZM) Coupling. Coatings 2023, 13, 1973. https://doi.org/10.3390/coatings13111973
Zhu C, Li W, Wang H. Analysis of Interlayer Crack Propagation and Strength Prediction of Steel Bridge Deck Asphalt Pavement Based on Extended Finite Element Method and Cohesive Zone Model (XFEM–CZM) Coupling. Coatings. 2023; 13(11):1973. https://doi.org/10.3390/coatings13111973
Chicago/Turabian StyleZhu, Chen, Weiwei Li, and Hongchang Wang. 2023. "Analysis of Interlayer Crack Propagation and Strength Prediction of Steel Bridge Deck Asphalt Pavement Based on Extended Finite Element Method and Cohesive Zone Model (XFEM–CZM) Coupling" Coatings 13, no. 11: 1973. https://doi.org/10.3390/coatings13111973
APA StyleZhu, C., Li, W., & Wang, H. (2023). Analysis of Interlayer Crack Propagation and Strength Prediction of Steel Bridge Deck Asphalt Pavement Based on Extended Finite Element Method and Cohesive Zone Model (XFEM–CZM) Coupling. Coatings, 13(11), 1973. https://doi.org/10.3390/coatings13111973







