Mathematical Modeling and Analysis of the Steady Electro-Osmotic Flow of Two Immiscible Fluids: A Biomedical Application
Abstract
:1. Introduction
2. Flow Geometry
2.1. Potential Field for Fluid B
2.2. Governing Equations and the Rheological Model
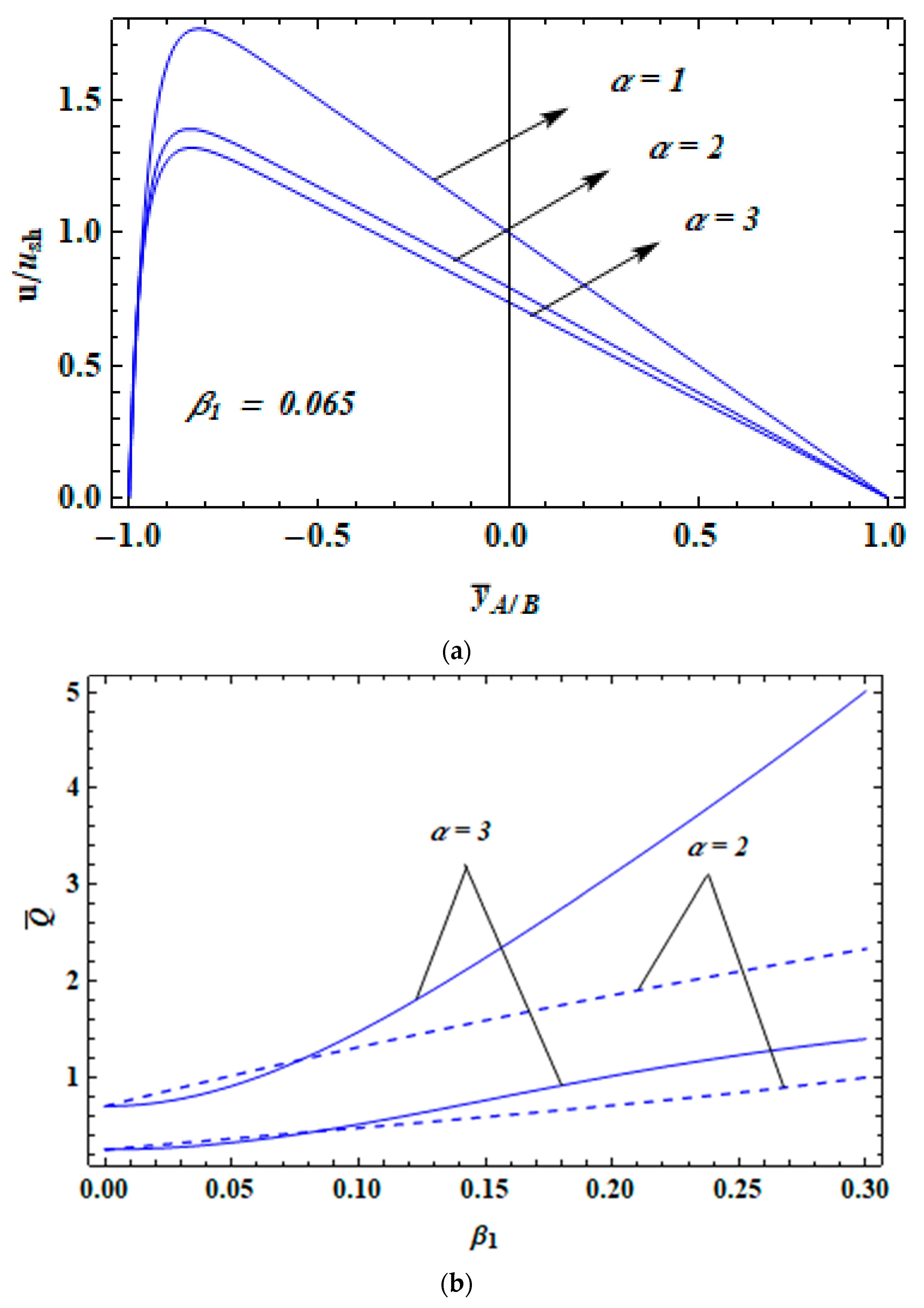
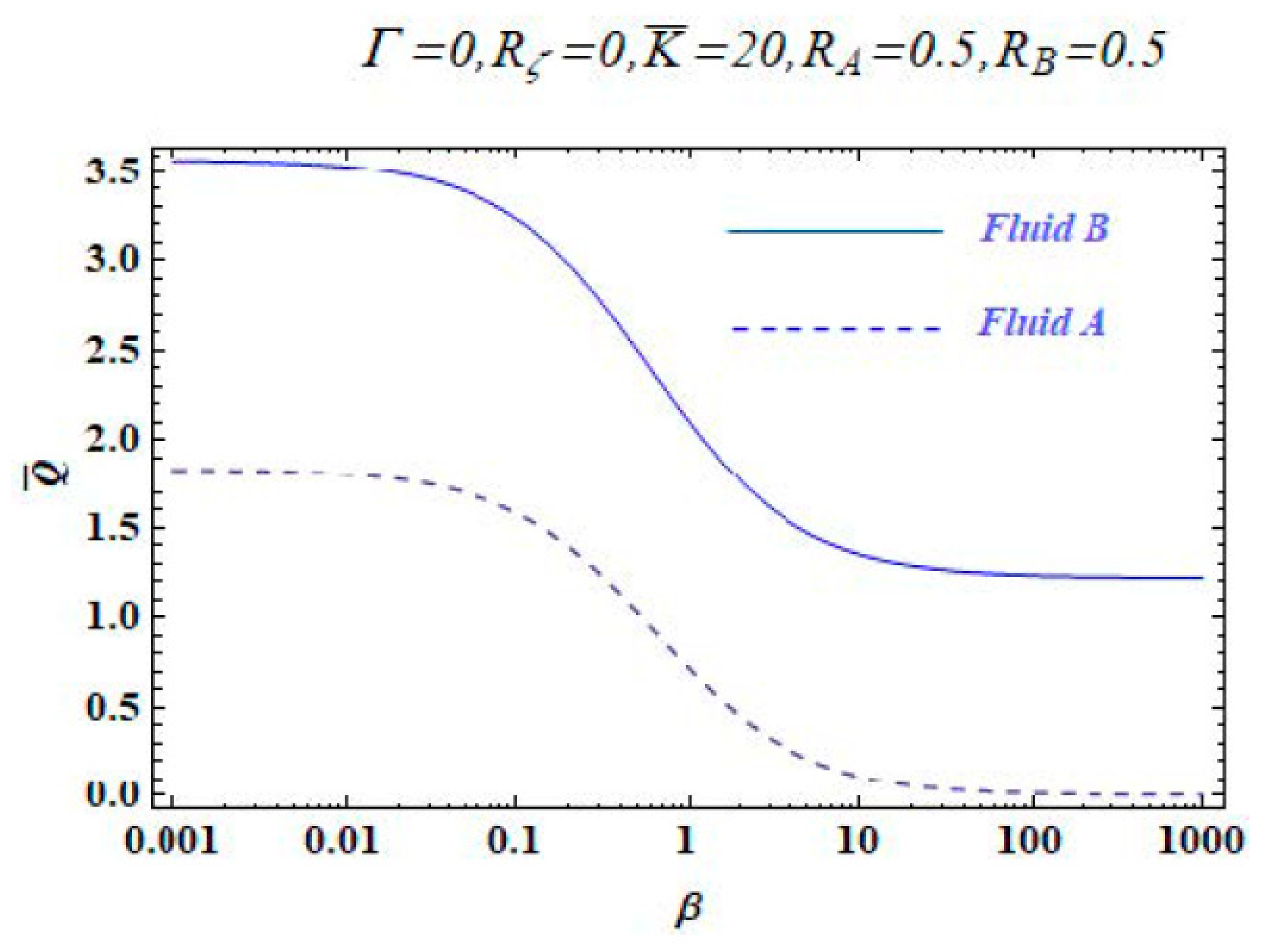
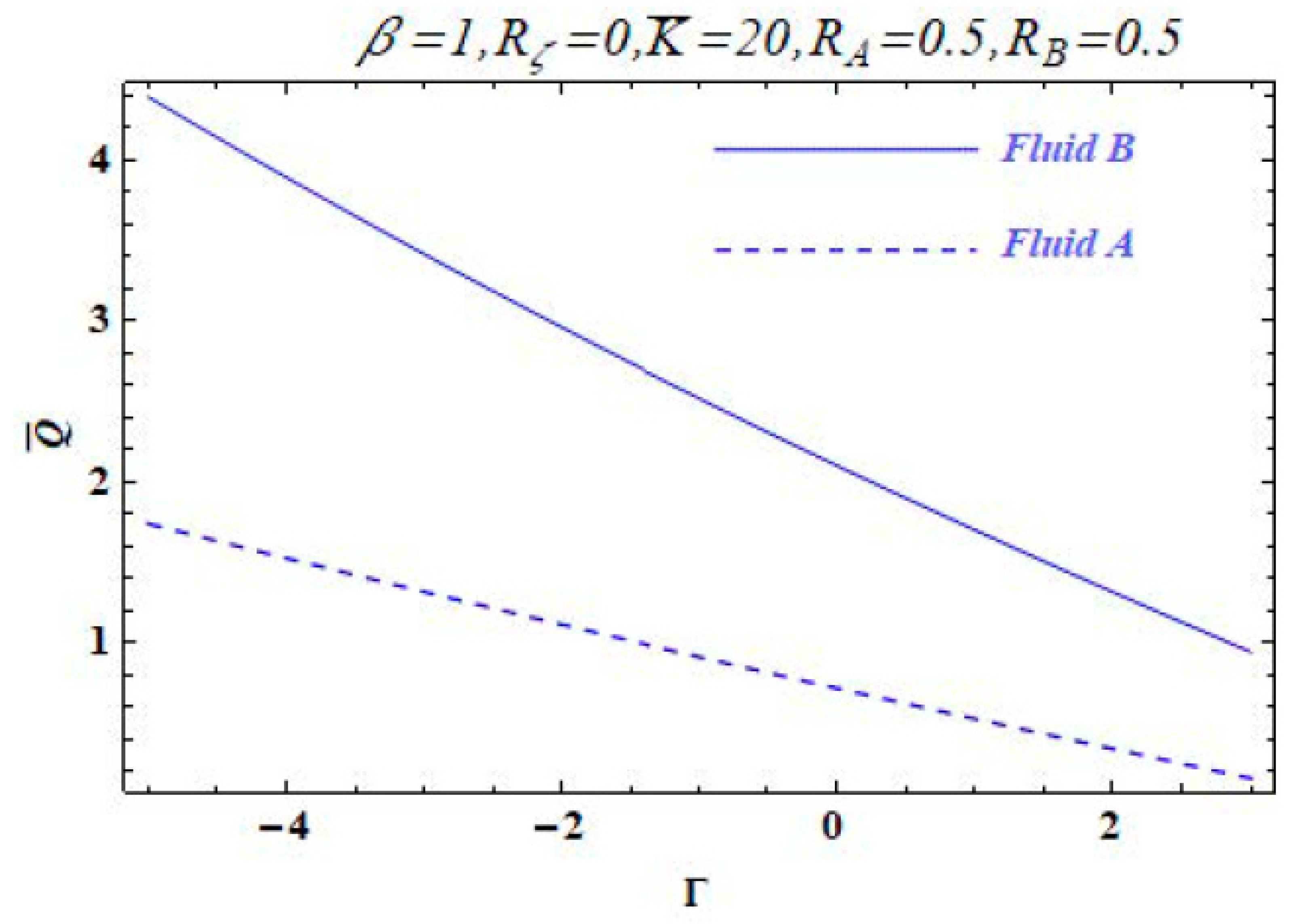
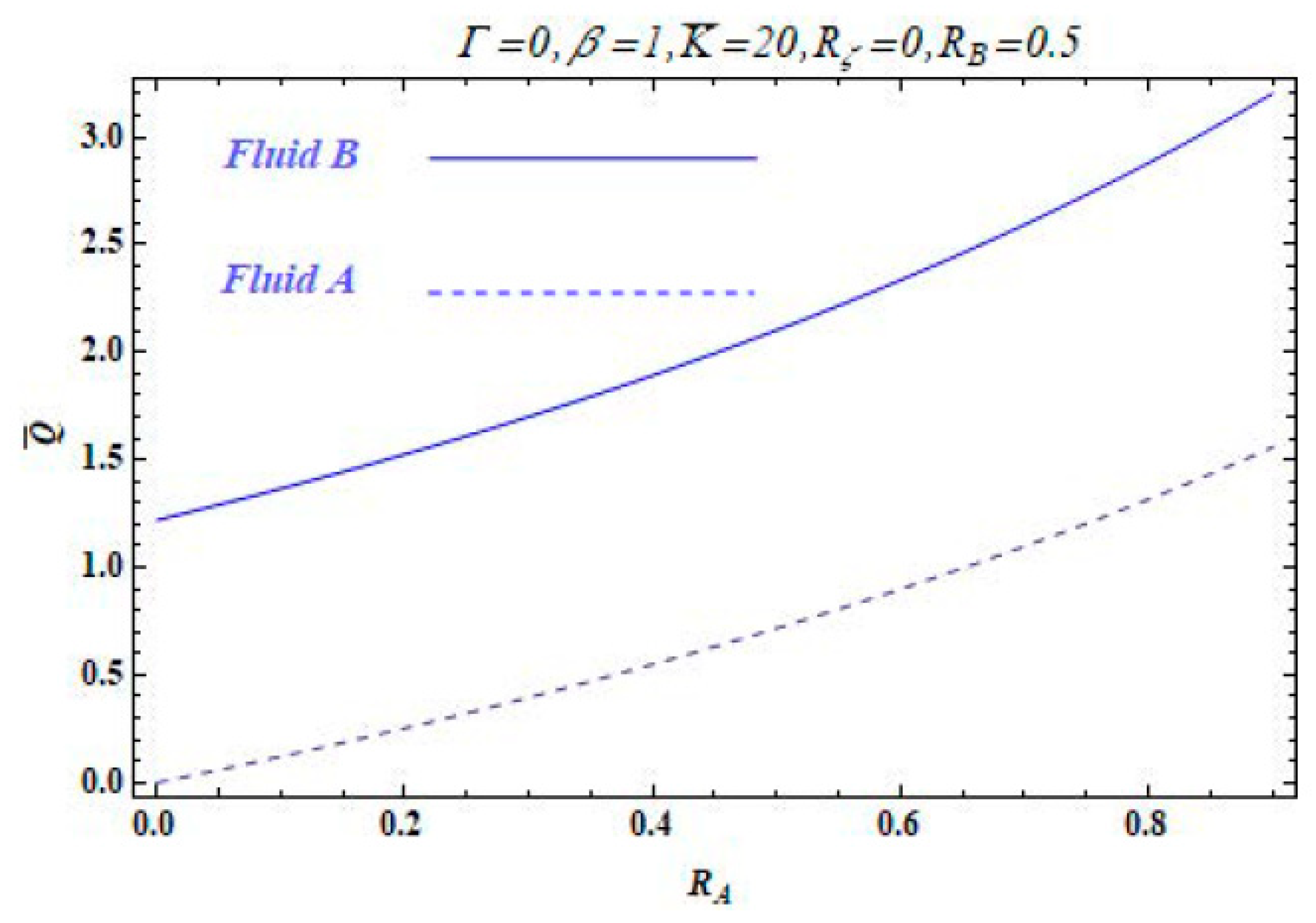
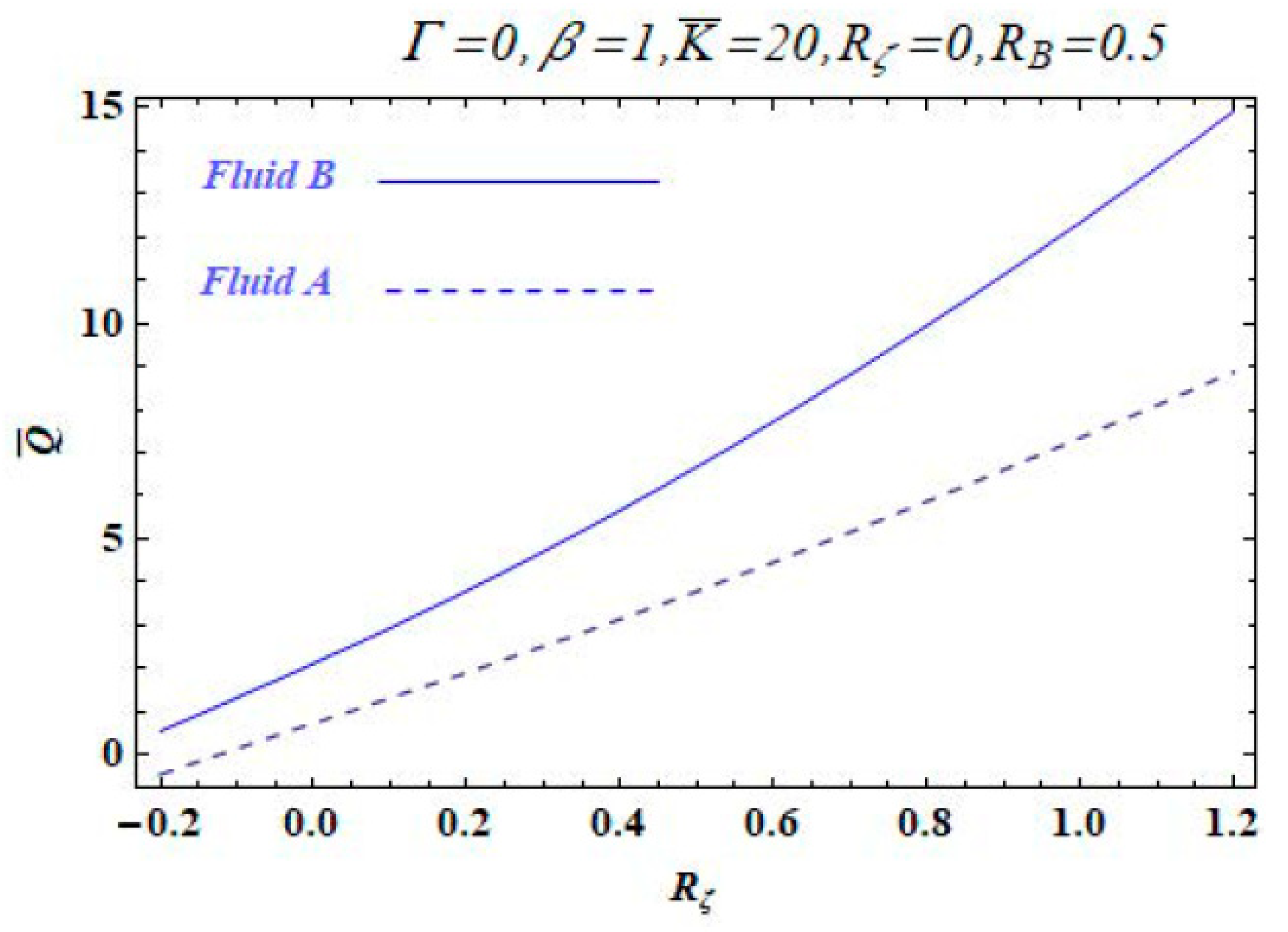
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, X.; Cheng, C.; Wang, S.; Liu, S. Electro-Osmotic Pumps and Their Applications in Microfluidic Systems; Springer: Berlin/Heidelberg, Germany, 2009; Volume 6, pp. 145–162. [Google Scholar]
- Brask, A.; Goranovic, G.; Bruus, H. Electro-osmotic pumping of non-conducting liquids by viscous drag from a secondary conducting liquid. Tech. Proc. Nanotech. 2003, 1, 190–193. [Google Scholar]
- Das, S.; Chakraborty, S. Anal. Chim, Electro-osmotic and pressure driven flow of viscoelastic fluids in micro channel. Acta 2006, 559, 15–24. [Google Scholar]
- Chakraborty, S. Electro-osmotically driven capillary transport of typical non-Newtonian bio fluids in rectangular micro channel. Anal. Chim. Acta 2007, 605, 175–184. [Google Scholar] [CrossRef] [PubMed]
- Afonso, A.; Alves, M.; Phino, F. Analytical solution of mixed electroosmotic/pressure driven flows of viscoelastic fluids in microchannels. J. Non-Newton. Fluid Mech. 2009, 159, 50–63. [Google Scholar] [CrossRef]
- Park, H.; Lee, W. Effect of viscoelasticity on the flow pattern and the volumetric flow rate in electro-osmotic flows through a microchannel. Lab A Chip 2008, 8, 1163–1170. [Google Scholar] [CrossRef] [PubMed]
- Afonso, A.; Alves, M.; Phino, F. Elecro-osmotic flow of viscoelastic fluids in microchannel under asymmetric zeta potentials. J. Eng. Math. 2011, 71, 15–30. [Google Scholar] [CrossRef]
- Sousa, J.; Afonso, A.; Alves, M.; Phino, F. Effect of the skimming layer electroosmotic poiseuille flows of viscoelastic fluids. Microfluid. Nanofluidics 2011, 10, 107–122. [Google Scholar] [CrossRef]
- Dhinakaran, S.; Afonso, A.; Alves, M.; Phino, F. Steady viscoelastic fluid flow between parallel plate under electro-osmotic forces. J. Colloid Interf. Sci. 2010, 344, 513–520. [Google Scholar] [CrossRef] [PubMed]
- Afonso, A.; Alves, M.; Phino, F. Electro-osmosis of viscoelastic and prediction of electro-elastic flow instabilities in a cross slot using a finite-volume method. J. Non-Newton. Fluid Mech. 2012, 179, 55–68. [Google Scholar] [CrossRef]
- Afonso, A.; Alves, M.; Phino, F. Analytical solution of two-fluid electro osmotic flows of viscoelastic fluid. J. Colloid Interface Sci. 2013, 395, 277–286. [Google Scholar] [CrossRef]
- Martínez, L.; Bautista, O.; Escandón, J.; Méndez, F. Electroosmotic flow of a Phan-Thien–Tanner fluid in a wavy-wall microchannel. Colloids Surf. A Physicochem. Eng. Asp. 2016, 498, 7–19. [Google Scholar] [CrossRef]
- Deng, S. Analytical Study of the Electroosmotic Flow of Two Immiscible Power-Law Fluids in a Microchannel. Open J. Fluid Dyn. 2022, 12, 263–276. [Google Scholar] [CrossRef]
- Mustafa, T. Eyring–Powell fluid flow through a circular pipe and heat transfer: Full solutions. Int. J. Numer. Methods Heat Fluid Flow 2020, 30, 4765–4774. [Google Scholar] [CrossRef]
- Javed, M.; Ali, N.; Sajid, M. A theoretical analysis of the calendering of Ellis model. J. Plast. Sheeting 2017, 33, 207–226. [Google Scholar] [CrossRef]
- Hayat, T.; Yasmin, H.; Alsaedi, A. Convective heat transfer analysis for peristaltic flow of power-law fluid in a channel. J. Braz. Soc. Mech. Sci. Eng. 2015, 37, 463–477. [Google Scholar] [CrossRef]
- Yasmin, H.; Iqbal, N. Convective mass/heat analysis of an electroosmotic peristaltic flow of ionic liquid in a symmetric porous microchannel with soret and dufour. Mathe. Prob. Eng. 2021, 2021, 2638647. [Google Scholar] [CrossRef]
- Balachandran, P. Fundamental of Compressible Fluid Dynamics; Phi Publishers: Delhi, India, 2006. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alyousef, H.A.; Yasmin, H.; Shah, R.; Shah, N.A.; El-Sherif, L.S.; El-Tantawy, S.A. Mathematical Modeling and Analysis of the Steady Electro-Osmotic Flow of Two Immiscible Fluids: A Biomedical Application. Coatings 2023, 13, 115. https://doi.org/10.3390/coatings13010115
Alyousef HA, Yasmin H, Shah R, Shah NA, El-Sherif LS, El-Tantawy SA. Mathematical Modeling and Analysis of the Steady Electro-Osmotic Flow of Two Immiscible Fluids: A Biomedical Application. Coatings. 2023; 13(1):115. https://doi.org/10.3390/coatings13010115
Chicago/Turabian StyleAlyousef, Haifa A., Humaira Yasmin, Rasool Shah, Nehad Ali Shah, Lamiaa S. El-Sherif, and Samir A. El-Tantawy. 2023. "Mathematical Modeling and Analysis of the Steady Electro-Osmotic Flow of Two Immiscible Fluids: A Biomedical Application" Coatings 13, no. 1: 115. https://doi.org/10.3390/coatings13010115
APA StyleAlyousef, H. A., Yasmin, H., Shah, R., Shah, N. A., El-Sherif, L. S., & El-Tantawy, S. A. (2023). Mathematical Modeling and Analysis of the Steady Electro-Osmotic Flow of Two Immiscible Fluids: A Biomedical Application. Coatings, 13(1), 115. https://doi.org/10.3390/coatings13010115







