Fatigue and Life Prediction of S135 High-Strength Drill Pipe Steel under Tension–Torsion Multiaxial Loading
Abstract
:1. Introduction
2. Experimental Section
2.1. Materials
2.2. Fatigue Test
3. Results and Discussion
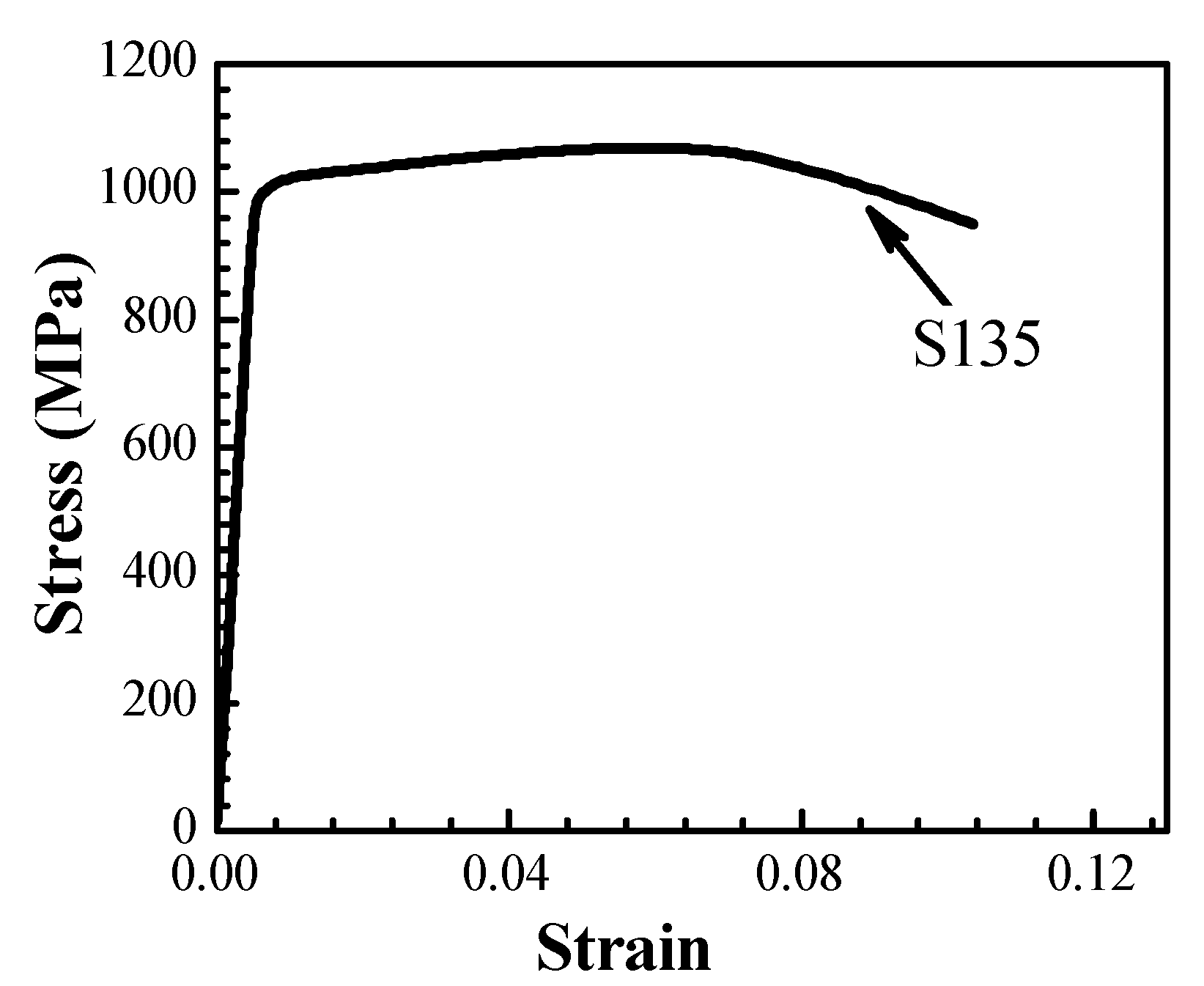
3.1. Stress–Strain Curve
3.2. Proportional Tension–Torsion Loading
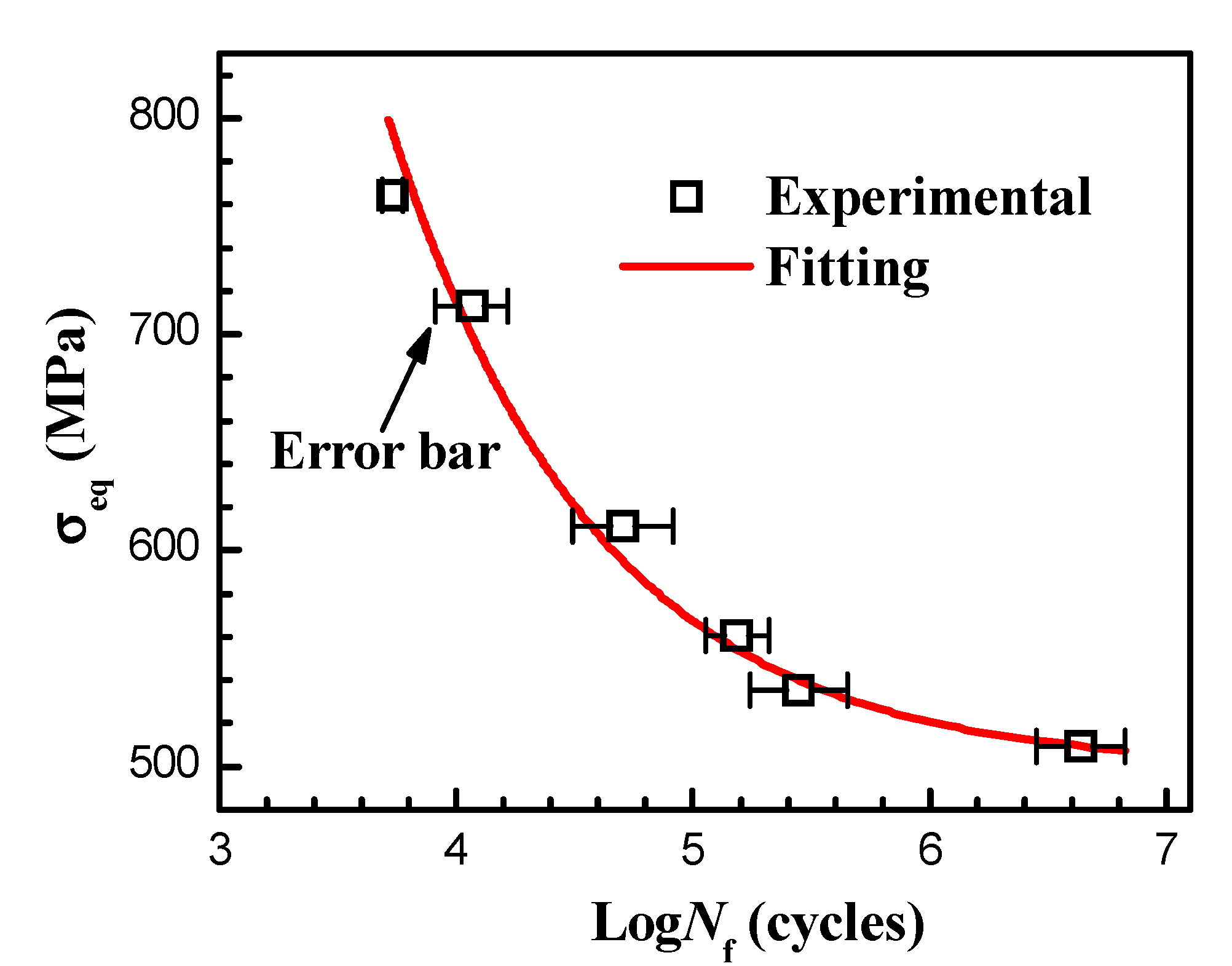
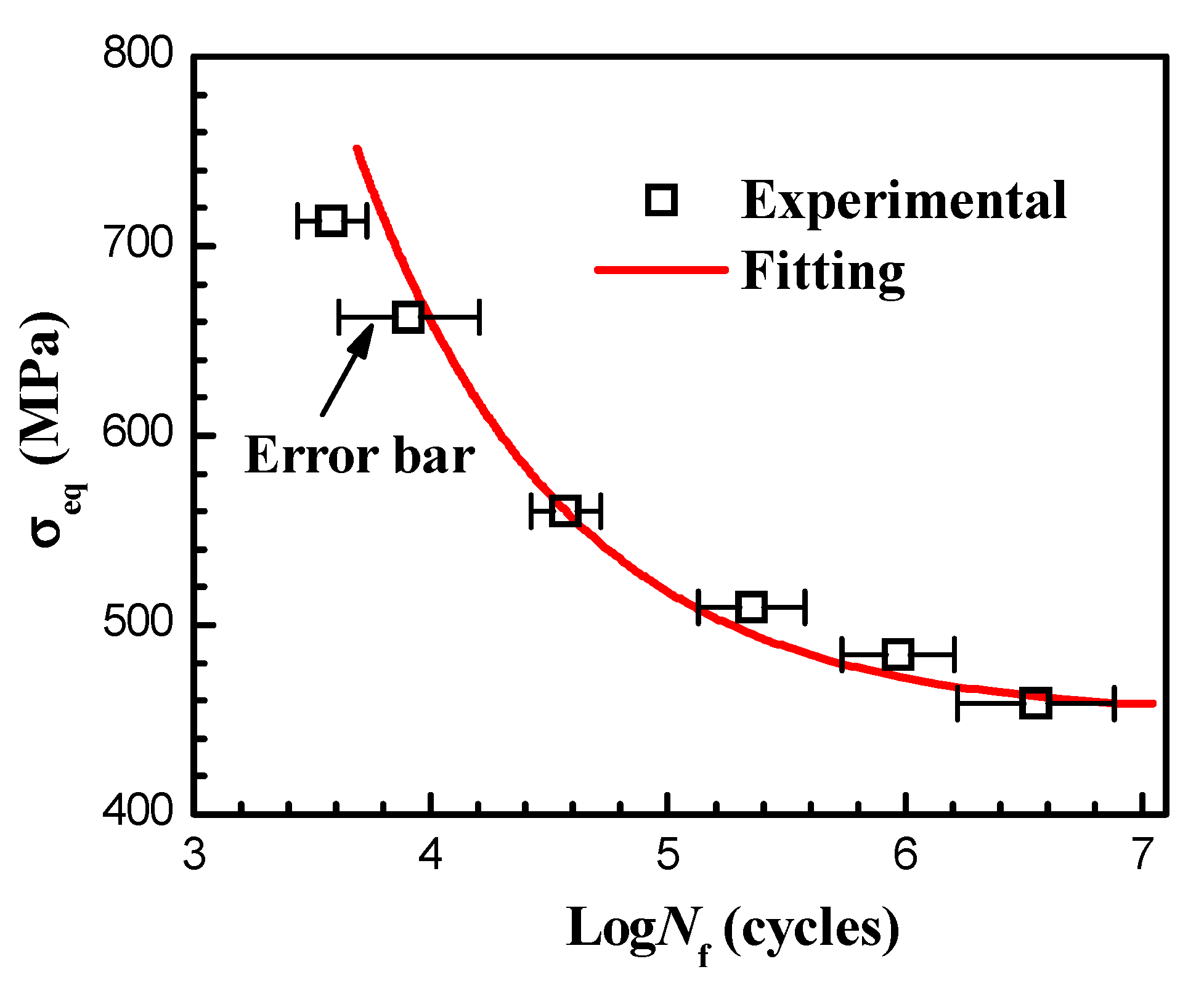
3.2.1. Fatigue Life and S-N Curve
3.2.2. Fatigue Fracture Mechanisms
3.3. Non-Proportional Tension–Torsion Loading
3.3.1. Fatigue Life and S–N Curve
3.3.2. Fatigue Fracture Mechanisms
3.4. Fatigue Quantitative Model
3.4.1. Basic Assumptions
3.4.2. Fatigue Critical Plane
3.4.3. Proportional Fatigue Life Equation
3.4.4. Non-Proportional Fatigue Life Equation
3.4.5. Contrastive Analysis
4. Conclusions
- (1)
- The fatigue model of the S135 steel under the combined loading of tension–torsion is established: , and the method to determine the weight and the non-proportional sensitivity coefficient is given. The specific expressions are for proportional tension–torsion loading, and for non-proportional tension–torsion loading;
- (2)
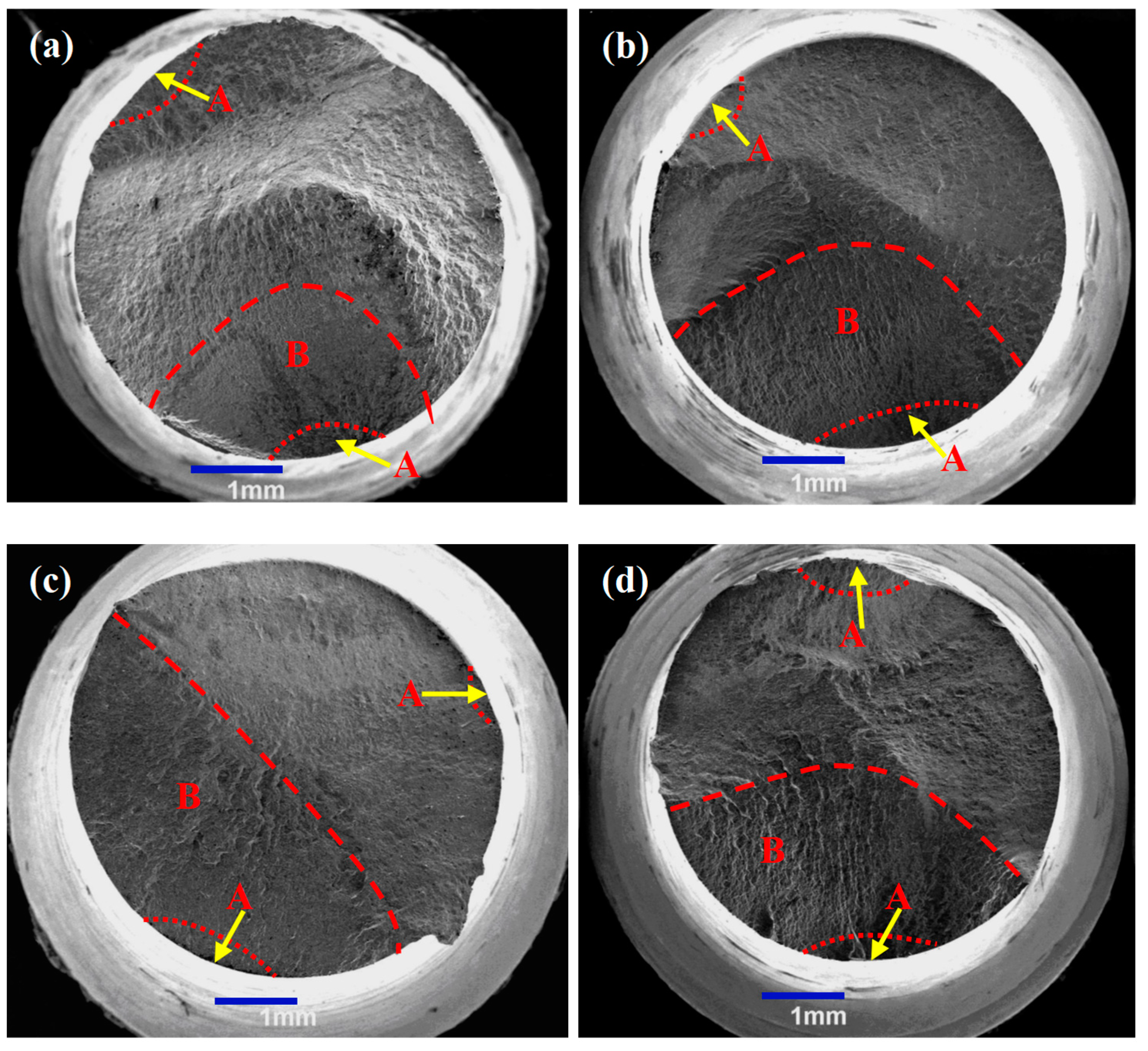
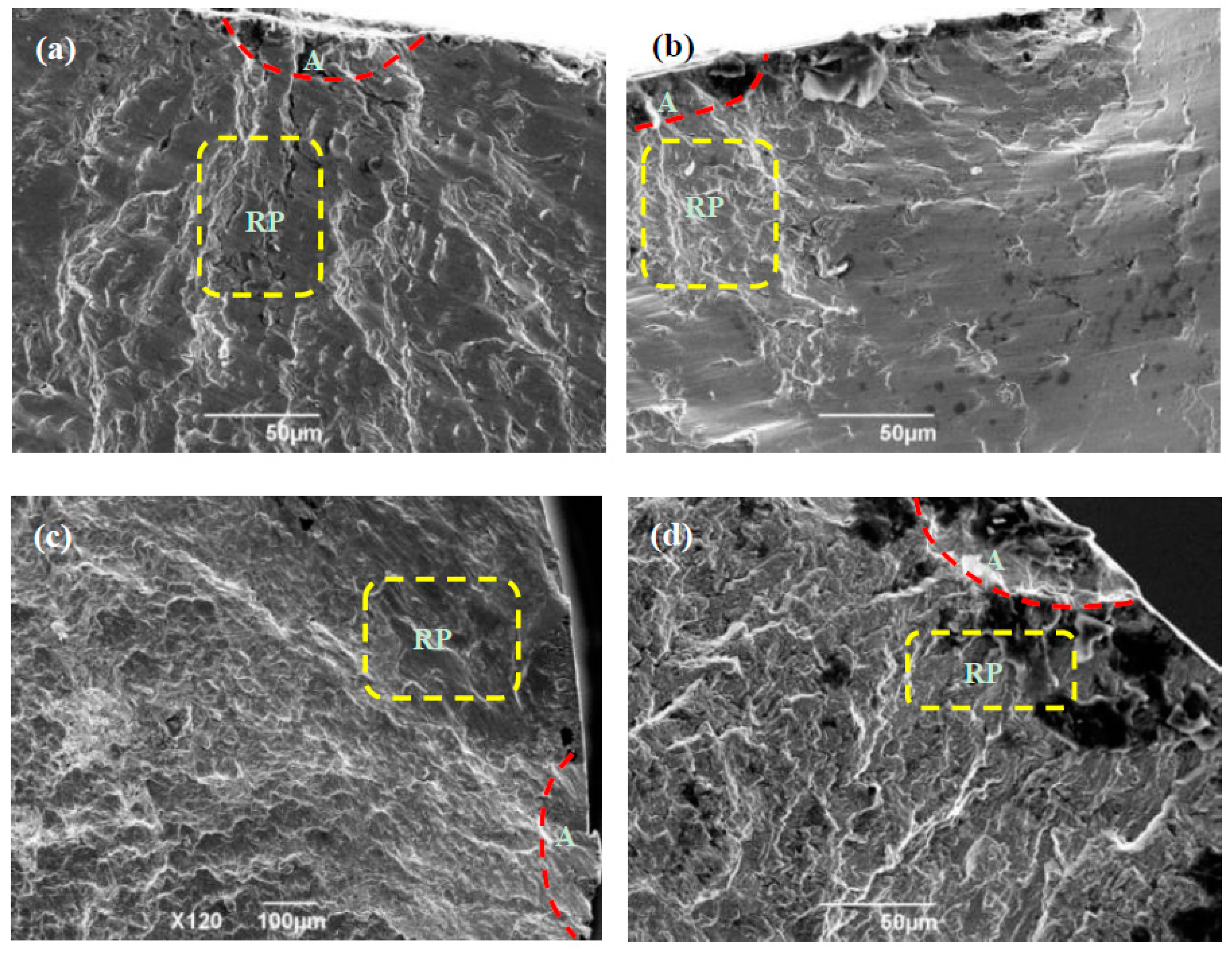
- Under the proportional tension–torsion loading, the fatigue crack initiates on the surface of the specimen and propagates to the interior, which is often caused by multiple fatigue initiations that connect to form the so-called “ridge” feature; Under the condition of 90° non-proportional tension–torsion loading, the fatigue crack initiates at the maximum equivalent stress site of the specimen surface, and the fatigue crack often appears from multiple sources;
- (3)
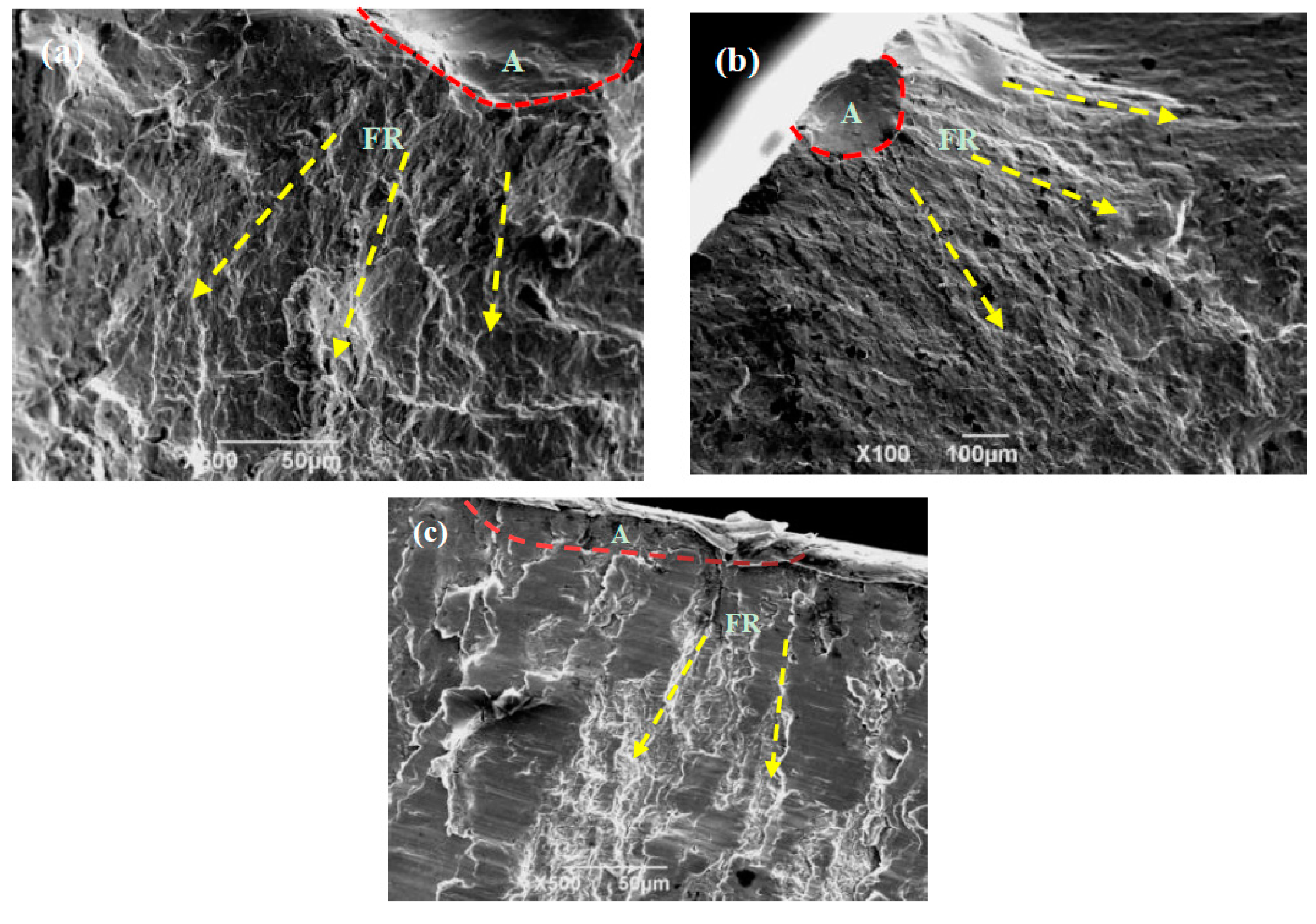
- The fracture source area of the proportional tension–torsion loading is characterized as an obvious fluvial pattern, and the crack propagation zone is characterized as fatigue striations and ripple patterns; the fracture source area of the 90° non-proportional tension–torsion loading is characterized as cleavage, the stable growth area is characterized as the tear edges formed by the connection between different fracture surfaces, and the tear edges are relatively flat.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Far, A.H.; Anijdan, S.M.; Abbasi, S.M. The effect of increasing Cu and Ni on a significant enhancement of mechanical properties of high strength low alloy, low carbon steels of HSLA-100 type. Mater. Sci. Eng. A 2019, 746, 384–393. [Google Scholar] [CrossRef]
- Rahi, A. Lateral Vibration of a Micro Overhung Rotor-Disk Subjected to an Axial Load Based on the Modified Strain Gradient Theory. Mech. Adv. Mater. Struct. 2018, 18, 1850114. [Google Scholar] [CrossRef]
- Rajabinezhad, M.; Bahrami, A.; Mousavinia, M.; Seyedi, S.J.; Taheri, P. Corrosion-Fatigue Failure of Gas-Turbine Blades in an Oil and Gas Production Plant. Materials 2020, 13, 900. [Google Scholar] [CrossRef] [Green Version]
- Bisong, M.; Sivtsev, P.; Lepov, V. Numerical Analysis of Stress-Strain State and Crack Propagation in Welded Samples. Solid State Phenom. 2017, 265, 507–512. [Google Scholar] [CrossRef]
- Sabzi, M.; Dezfuli, S.M. Drastic improvement in mechanical properties and weldability of 316L stainless steel weld joints by using electromagnetic vibration during GTAW process. J. Manuf. Process. 2018, 33, 74–85. [Google Scholar] [CrossRef]
- Antsiferov, S.; Sammal, A.; Deev, P. Stress state estimation in multilayer support of vertical shafts, considering off-design cross-sectional deformation. IOP Conf. Ser. Earth Environ. Sci. 2018, 134, 012001. [Google Scholar] [CrossRef] [Green Version]
- Khorsov, P.; Laas, R.; Surzhikov, A.P. The Application of Reverberation in Method of Mechanoelectrical Transformations for Estimation of Stress-Strain State in Solid Dielectrical Matter. Mater. Sci. Forum 2019, 970, 47–54. [Google Scholar] [CrossRef]
- Tarasov, B.G.; Sadovskii, V.M.; Sadovskaya, O.V.; Cassidy, M.J.; Randolph, M.F. Modelling the static stress-strain state around the fan-structure in the shear rupture head. Appl. Math. Model. 2018, 57, 268–279. [Google Scholar] [CrossRef]
- Yan, Q.; Luo, M.; Tang, K. Multi-axis variable depth-of-cut machining of thin-walled workpieces based on the workpiece deflection constraint. Comput.-Aided Des. 2018, 100, 14–29. [Google Scholar] [CrossRef]
- Tian, Y.Z.; Sun, S.J.; Lin, H.R.; Zhang, Z.F. Fatigue behavior of CoCrFeMnNi high-entropy alloy under fully reversed cyclic deformation. J. Mater. Sci. Technol. 2018, 35, 334–340. [Google Scholar] [CrossRef]
- Mironov, V.I.; Ogorelkov, D.A.; Lukashuk, O.A. Analysis of Fatigue Damage Accumulation in Structural Materials under Quasi-Random Load. Solid State Phenom. 2020, 299, 1178–1183. [Google Scholar] [CrossRef]
- Luo, S.; Liu, M.; Shen, Y.; Lin, X. Sulfide Stress Corrosion Cracking Behavior of G105 and S135 High-Strength Drill Pipe Steels in H2S Environment. J. Mater. Eng. Perform. 2019, 28, 1707–1718. [Google Scholar] [CrossRef]
- Zeng, D.; Li, H.; Tian, G.; Liu, F.; Li, B.; Yu, S.; Ouyang, Z.; Shi, T. Fatigue behavior of high-strength steel S135 under coupling multi-factor in complex environments. Mater. Sci. Eng. A 2018, 724, 385–402. [Google Scholar] [CrossRef]
- Zhao, T.; Liu, Z.; Du, C.; Dai, C.; Li, X.; Zhang, B. Corrosion fatigue crack initiation and initial propagation mechanism of E690 steel in simulated seawater. Mater. Sci. Eng. A 2017, 708, 181–192. [Google Scholar] [CrossRef]
- Han, L.; Liu, M.; Luo, S.; Lu, T.J. Fatigue and corrosion fatigue behavior of G105 and S135 high-strength drill pipe steels in air and H2S environment. Process Saf. Environ. Prot. 2019, 124, 63–74. [Google Scholar] [CrossRef]
- Liu, W.; Liu, Y.; Chen, W.; Shi, T.; Singh, A.; Lu, Q. Longitudinal crack failure analysis of box of S135 tool joint in ultra-deep well. Eng. Fail. Anal. 2015, 48, 283–296. [Google Scholar] [CrossRef]
- Medjo, B.; Rakin, M.; Gubeljak, N.; Matvienko, Y.; Arsić, M.; Šarkoćević, Ž.; Sedmak, A. Failure resistance of drilling rig casing pipes with an axial crack. Eng. Fail. Anal. 2015, 58, 429–440. [Google Scholar] [CrossRef]
- May, M.E.; Saintier, N.; Palin-Luc, T.; Devos, O.; Brucelle, O. Modelling of corrosion fatigue crack initiation on martensitic stainless steel in high cycle fatigue regime. Corros. Sci. 2018, 133, 397–405. [Google Scholar] [CrossRef]
- Farhangdoost, K.; Siahpoosh, M. On The Fatigue Life Prediction of Die-Marked Drillpipes [C]. In Proceedings of the 2006 ASME Pressure Vessels and Piping Division Conference, Vancouver, BC, Canada, 23–27 July 2006; Volume 7, pp. 1–8. [Google Scholar]
- Feng, M.; Ding, F.; Jiang, Y. A study of loading path influence on fatigue crack growth under combined loading. Int. J. Fatigue 2006, 28, 19–27. [Google Scholar] [CrossRef]
- Luo, S.; Liu, M.; Wen, N.; Shen, Y.; Liu, Y.M.; Lin, X.Z. Effect of pre-corrosion on electrochemical corrosion and fatigue behavior of S135 high-strength drill pipe steel in marine environment. Int. J. Electrochem. Sci. 2019, 14, 2589–2605. [Google Scholar] [CrossRef]
- Liu, M.; Luo, S.; Shen, Y. Corrosion fatigue crack propagation behaviour of S135 high-strength drill pipe steel in H2S environment. Eng. Fail. Anal. 2019, 97, 493–505. [Google Scholar] [CrossRef]
- Luo, S.; Liu, M.; Zheng, X. Characteristics and life expression of fatigue fracture of drilling pipe steels for API G105 and S135 grade. Eng. Fail. Anal. 2020, 116, 104705. [Google Scholar] [CrossRef]
- Zheng, X.-L.; Lu, B.; Jiang, H. Determination of probability distribution of fatigue strength and expressions of P–S–N curves. Eng. Fract. Mech. 1995, 50, 483–491. [Google Scholar] [CrossRef]
- Wang, R. Corrosion Fatigue of Metallic Materials [M]; Xi’an Northwestern Polytechnical University Press: Xi’an, China, 2001. [Google Scholar]
- Zheng, X.L.; Wang, R. Overload effects on corrosion fatigue crack initiation life and life prediction of aluminum notched elements under variable amplitude loading. Eng. Fract. Mech. 1999, 57, 557–572. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Dhar, S.; Acharyya, S.K.; Gupta, S.K. Modelling of non-proportional hardening by dislocation based latent effects for SA333 Grade-6 C-Mn Steel. Mater. Res. Express 2019, 6, 086562. [Google Scholar] [CrossRef]
- Borodii, M.V. Determination of the Non-Proportional Cyclic Hardening Coefficient Sensitive to the Loading Amplitude. Strength Mater. 2021, 52, 919–929. [Google Scholar] [CrossRef]
- Zhang, Q.; Hu, X.; Zhang, Z.; Sun, T.; Wu, J.; Li, Y.; Ren, T. The mean stress and phase angle effect on multiaxial fatigue behavior of a TiAl alloy: Failure analysis and life modeling. Int. J. Mech. Sci. 2021, 193, 106123. [Google Scholar] [CrossRef]
- Amjadi, M.; Fatemi, A. Multiaxial Fatigue Behavior of Thermoplastics Including Mean Stress and Notch Effects: Experiments and Modeling. Int. J. Fatigue 2020, 136, 105571. [Google Scholar] [CrossRef]
- Zhao, B.; Xie, L.; Wang, L.; Hu, Z.; Zhou, S.; Bai, X. A new multiaxial fatigue life prediction model for aircraft aluminum alloy. Int. J. Fatigue 2021, 143, 105993. [Google Scholar] [CrossRef]
- Shu, D.L. Mechanical Properties of Engineering Materials; China Machine Press: Beijing, China, 2007. [Google Scholar]
- Luo, S.-J.; Wang, R.; Zhao, K. Investigations of fatigue performance of S135 drill pipe steel under uniaxial loading. Adv. Mater. Res. 2013, 716, 418–422. [Google Scholar] [CrossRef]
- Carpinteri, A.; Spagnoli, A. Multiaxial high-cycle fatigue criterion for hard metals. Int. J. Fatigue 2001, 23, 135–145. [Google Scholar] [CrossRef]
- Findley, W.N. A theory for the effect of mean stress on fatigue of metals under combined torsion and axial load or bending. J. Eng. Ind. 1959, 81, 301–306. [Google Scholar] [CrossRef]
- Matake, T. An explanation on fatigue limit under combined stress. Bull. JSME 1977, 141, 257–263. [Google Scholar] [CrossRef]
- Park, J.; Nelson, D. Evaluation of an energy-based approach and a critical plane approach for predicting constant amplitude multiaxial fatigue life. Int. J. Fatigue 2000, 22, 23–39. [Google Scholar] [CrossRef]
- Freitas, M.D.; Li, B.; Santos, J.L. A numerical approach for high-cycle fatigue life prediction with multiaxial loading. In Multiaxial Fatigue and Deformation: Testing and Prediction; Kalluri, S., Bonacuse, P., Eds.; ASTM: West Conshohocken, PA, USA, 2000; pp. 139–156. [Google Scholar]




| No. | Pmax/kN | ||||
|---|---|---|---|---|---|
| 1 | 15 | 763.0 | 13.125 | 535.03 | 4785 |
| 2 | 15 | 763.0 | 13.125 | 535.03 | 5673 |
| 3 | 15 | 763.0 | 13.125 | 535.03 | 8974 |
| 4 | 14 | 713.3 | 12.25 | 499.4 | 8705 |
| 5 | 14 | 713.3 | 12.25 | 499.4 | 17,250 |
| 6 | 14 | 713.3 | 12.25 | 499.4 | 10,456 |
| 7 | 12 | 611.5 | 10.5 | 428.0 | 83,155 |
| 8 | 12 | 611.5 | 10.5 | 428.0 | 49,646 |
| 9 | 12 | 611.5 | 10.5 | 428.0 | 31,087 |
| 10 | 11 | 560.5 | 9.625 | 392.3 | 163,603 |
| 11 | 11 | 560.5 | 9.625 | 392.3 | 109,413 |
| 12 | 11 | 560.5 | 9.625 | 392.3 | 201,298 |
| 13 | 10.5 | 535.0 | 9.1875 | 375.0 | 261,066 |
| 14 | 10.5 | 535.0 | 9.1875 | 375.0 | 180,658 |
| 15 | 10.5 | 535.0 | 9.1875 | 375.0 | 461,559 |
| 16 | 10 | 509.6 | 8.75 | 356.7 | 2.65 × 106, fracture |
| 17 | 10 | 509.6 | 8.75 | 356.7 | 5.21 × 106, fracture |
| 18 | 10 | 509.6 | 8.75 | 356.7 | 5.90 × 106, fracture |
| No. | Pmax/kN | ||||
|---|---|---|---|---|---|
| 1 | 14 | 713.3 | 12.25 | 499.4 | 5230 |
| 2 | 14 | 713.3 | 12.25 | 499.4 | 3972 |
| 3 | 14 | 713.3 | 12.25 | 499.4 | 2685 |
| 4 | 13 | 662.4 | 11.375 | 467.3 | 4138 |
| 5 | 13 | 662.4 | 11.375 | 467.3 | 16,230 |
| 6 | 13 | 662.4 | 11.375 | 467.3 | 7835 |
| 7 | 11 | 560.5 | 9.625 | 392.3 | 36,720 |
| 8 | 11 | 560.5 | 9.625 | 392.3 | 26,478 |
| 9 | 11 | 560.5 | 9.625 | 392.3 | 52,467 |
| 10 | 10 | 509.6 | 8.75 | 356.7 | 143,852 |
| 11 | 10 | 509.6 | 8.75 | 356.7 | 199,838 |
| 12 | 10 | 509.6 | 8.75 | 356.7 | 394,570 |
| 13 | 9.5 | 486 | 8.3125 | 338.9 | 1.58×106 |
| 14 | 9.5 | 486 | 8.3125 | 338.9 | 524,780 |
| 15 | 9.5 | 486 | 8.3125 | 338.9 | 981,740 |
| 16 | 9 | 458.6 | 7.875 | 321.0 | 1.52 × 106, fracture |
| 17 | 9 | 458.6 | 7.875 | 321.0 | 6.23 × 106, fracture |
| 18 | 9 | 458.6 | 7.875 | 321.0 | 6.48 × 106, fracture |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, S.; Liu, M.; Han, L.; Xue, Y. Fatigue and Life Prediction of S135 High-Strength Drill Pipe Steel under Tension–Torsion Multiaxial Loading. Coatings 2022, 12, 1222. https://doi.org/10.3390/coatings12081222
Luo S, Liu M, Han L, Xue Y. Fatigue and Life Prediction of S135 High-Strength Drill Pipe Steel under Tension–Torsion Multiaxial Loading. Coatings. 2022; 12(8):1222. https://doi.org/10.3390/coatings12081222
Chicago/Turabian StyleLuo, Sheji, Ming Liu, Lihong Han, and Yuna Xue. 2022. "Fatigue and Life Prediction of S135 High-Strength Drill Pipe Steel under Tension–Torsion Multiaxial Loading" Coatings 12, no. 8: 1222. https://doi.org/10.3390/coatings12081222
APA StyleLuo, S., Liu, M., Han, L., & Xue, Y. (2022). Fatigue and Life Prediction of S135 High-Strength Drill Pipe Steel under Tension–Torsion Multiaxial Loading. Coatings, 12(8), 1222. https://doi.org/10.3390/coatings12081222







