Experimental Research on the Fluctuation Characteristics of Water Film Driven by Wind
Abstract
:1. Introduction
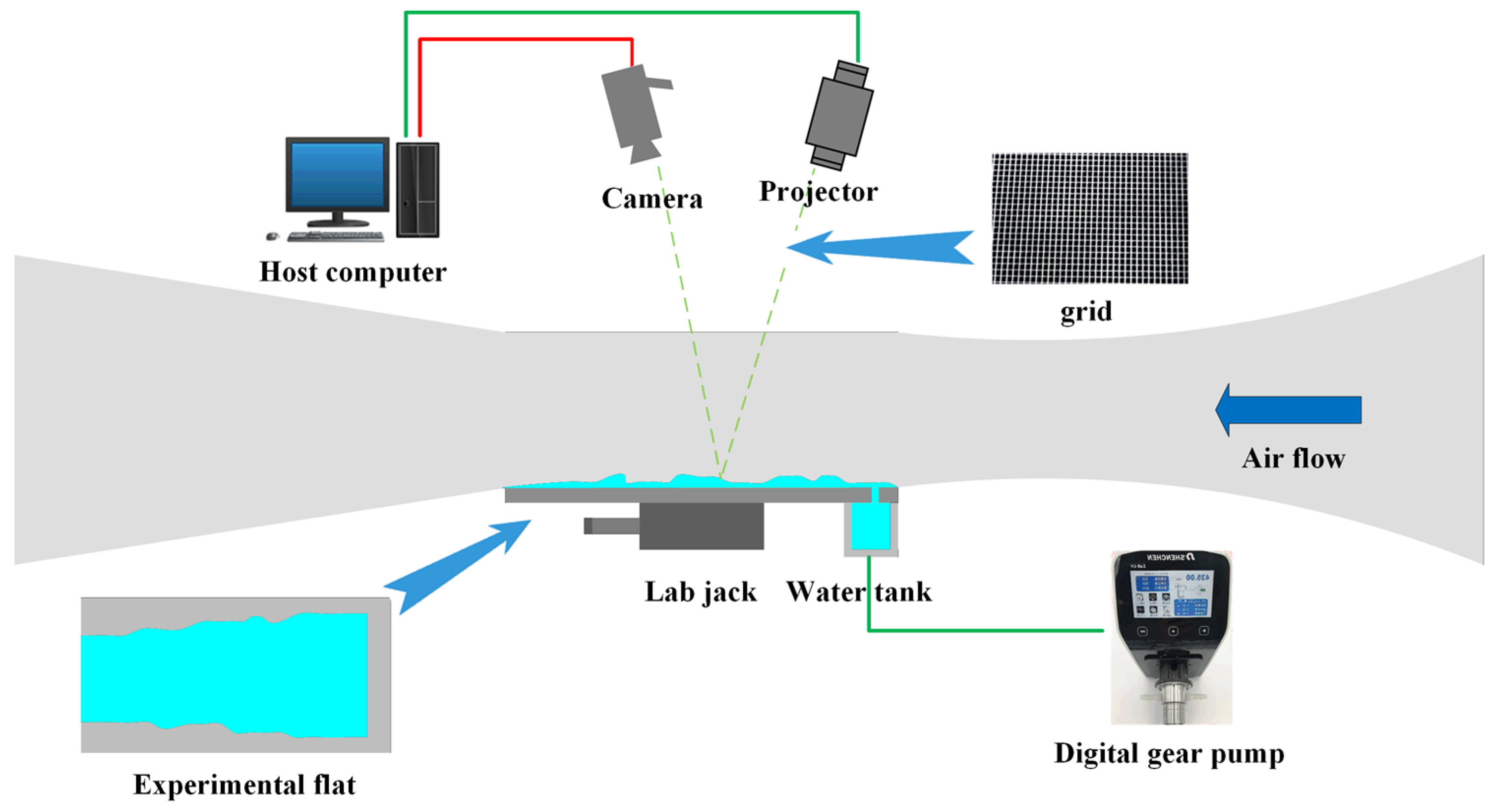
2. Experimental Setup
2.1. Construction of Measurement System
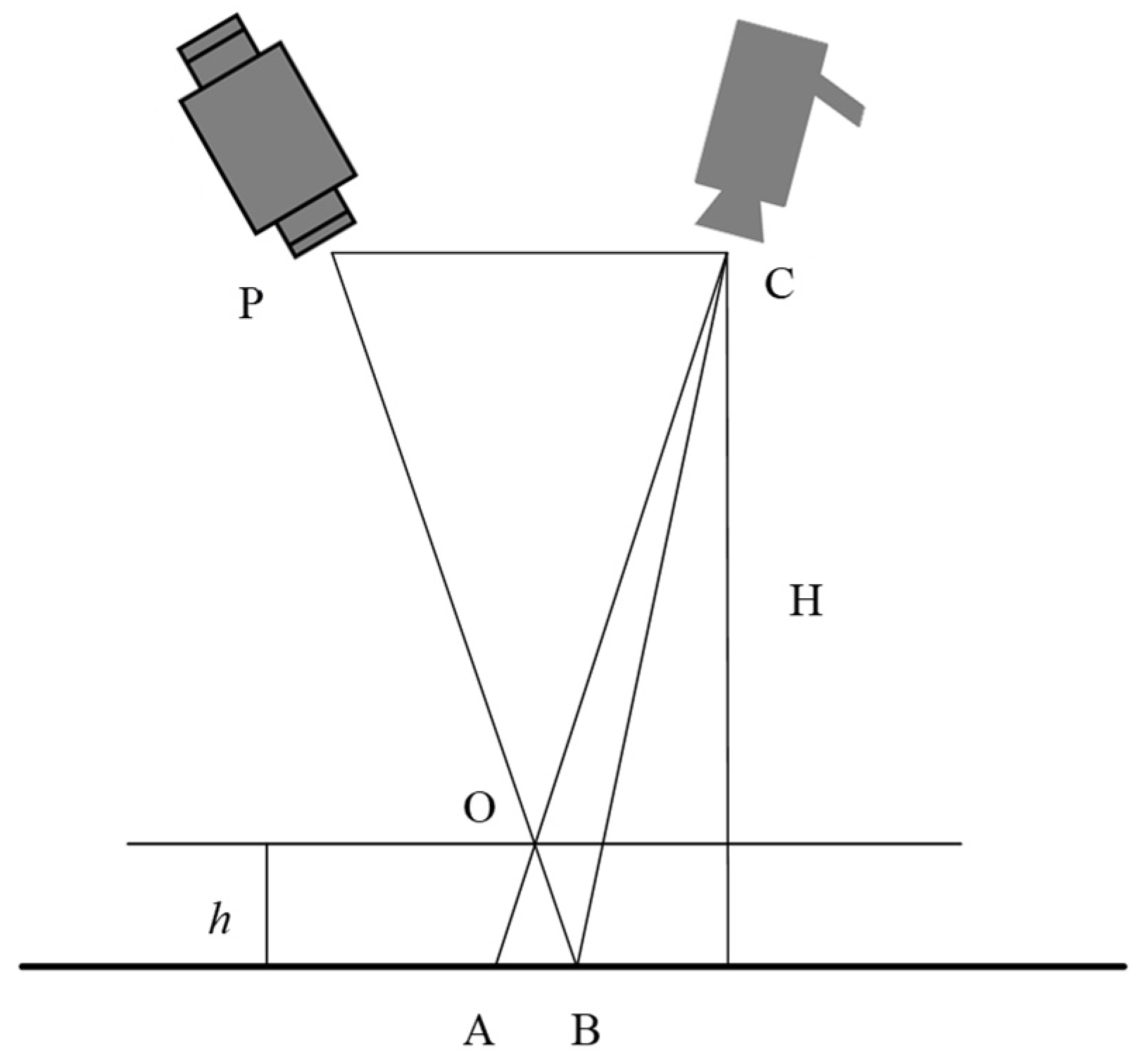
2.2. Principle of the DIP Measurement Technology
2.3. Calibration and Measurement of Experimental System
2.4. Measurement Results Processing Method
3. Results and Analysis
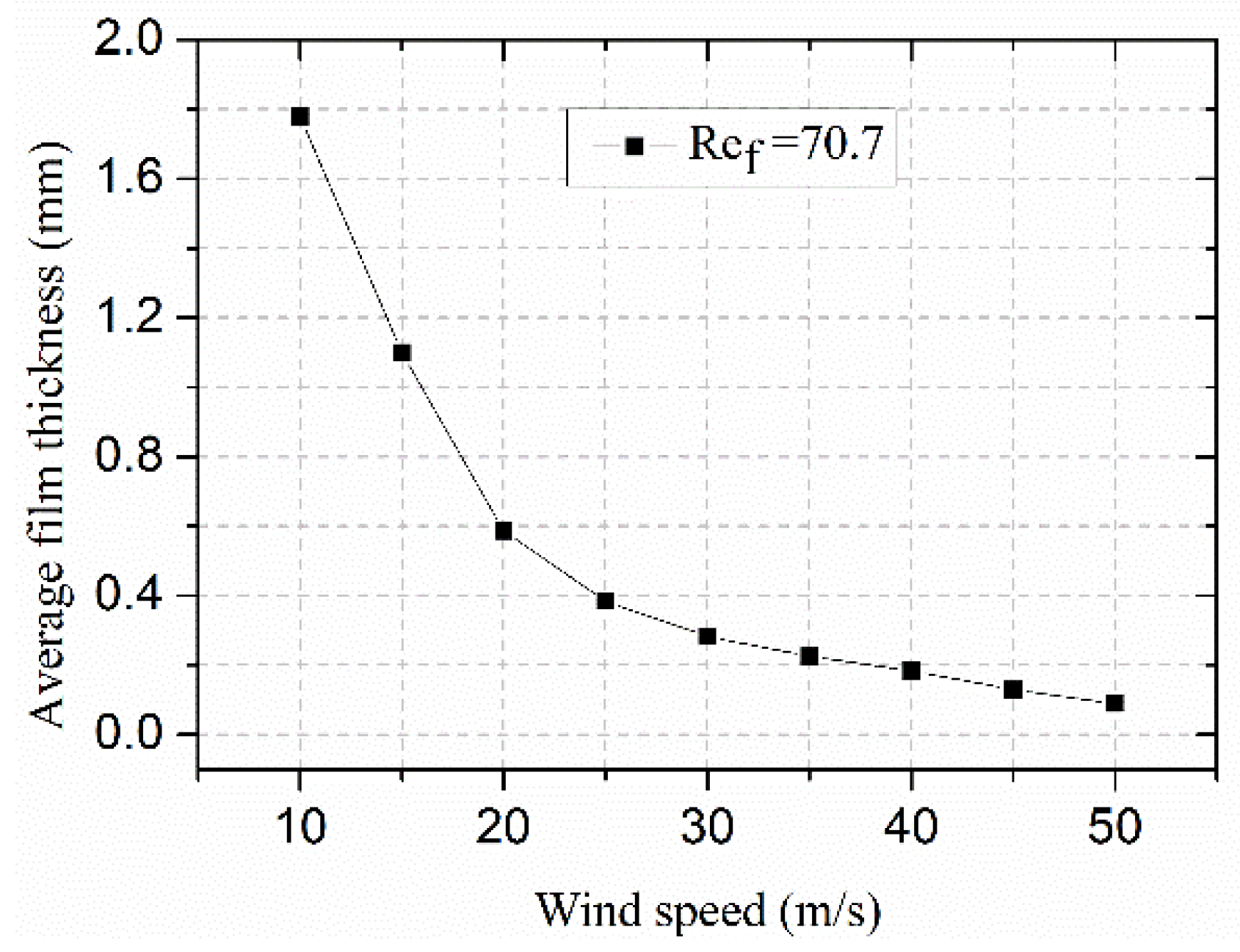
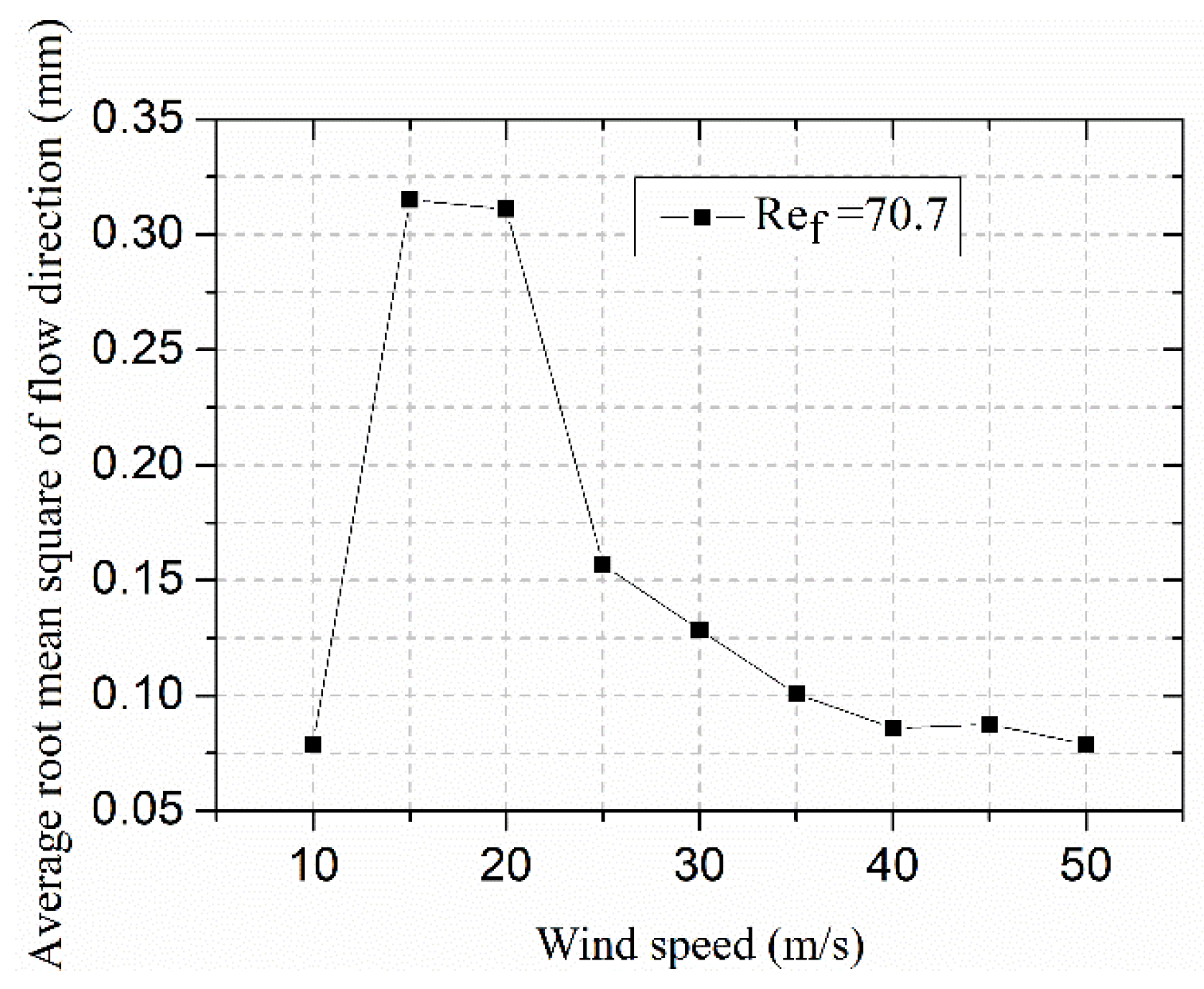
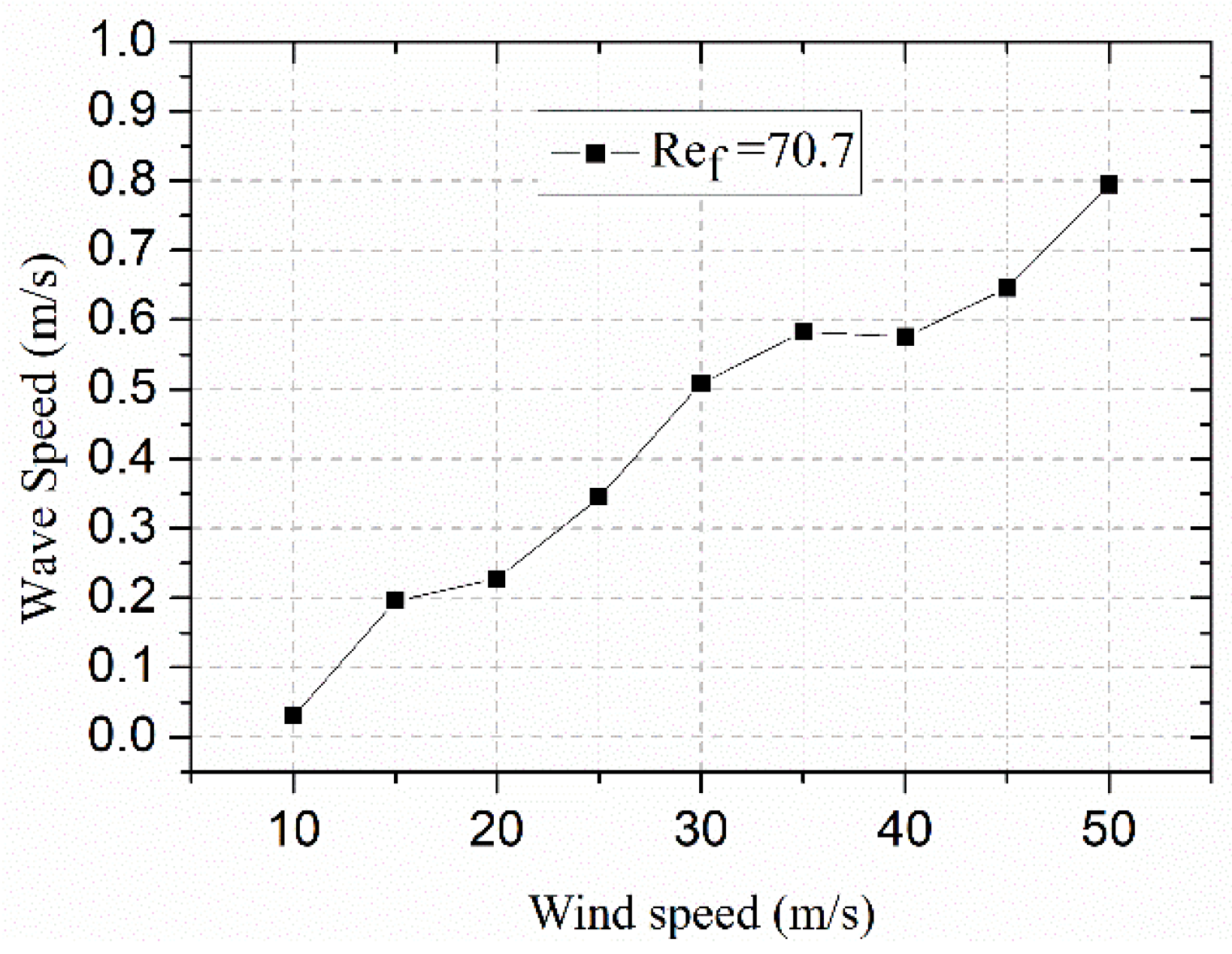
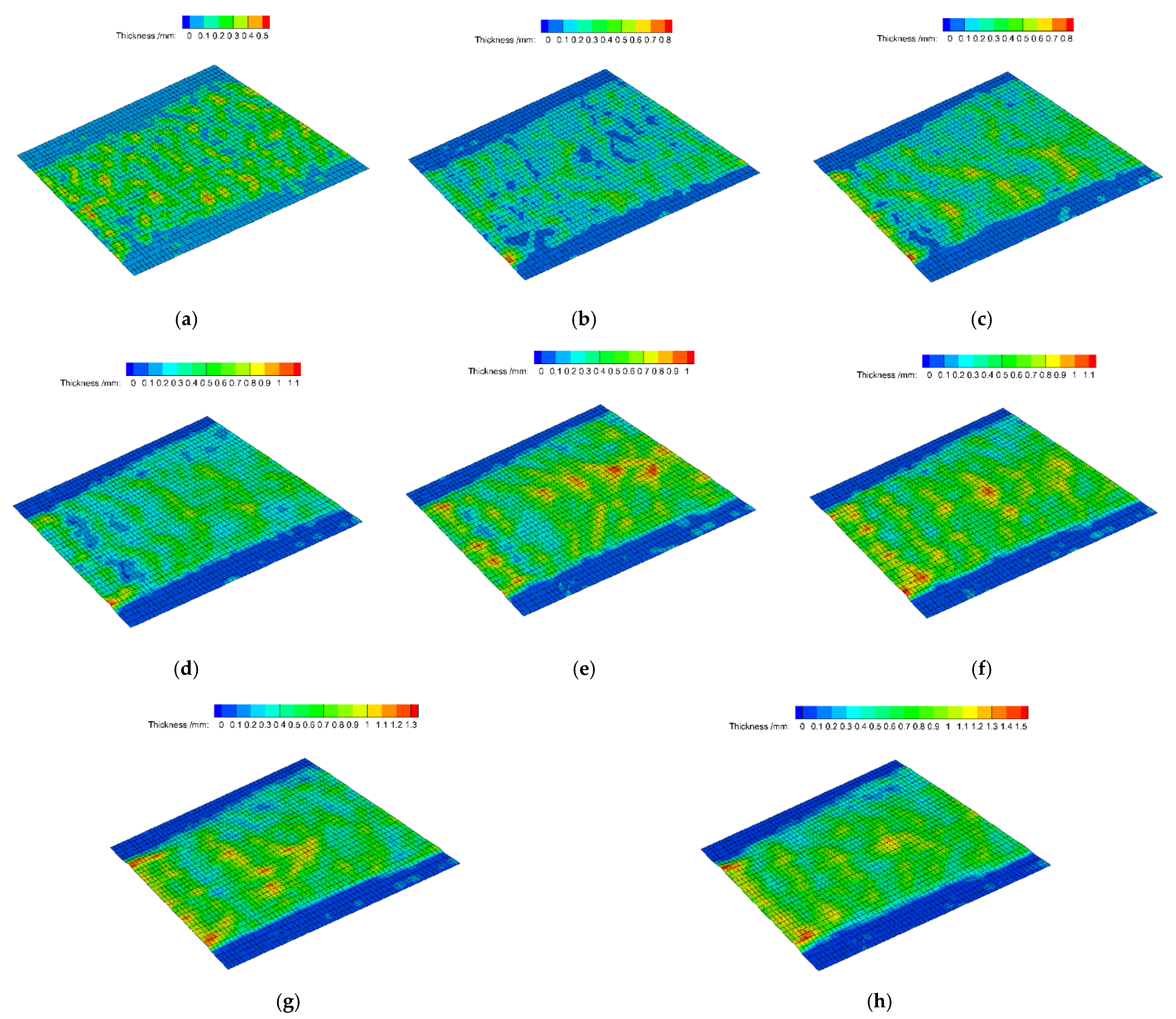
3.1. Effect of Wind Speed on the Water Film Flow
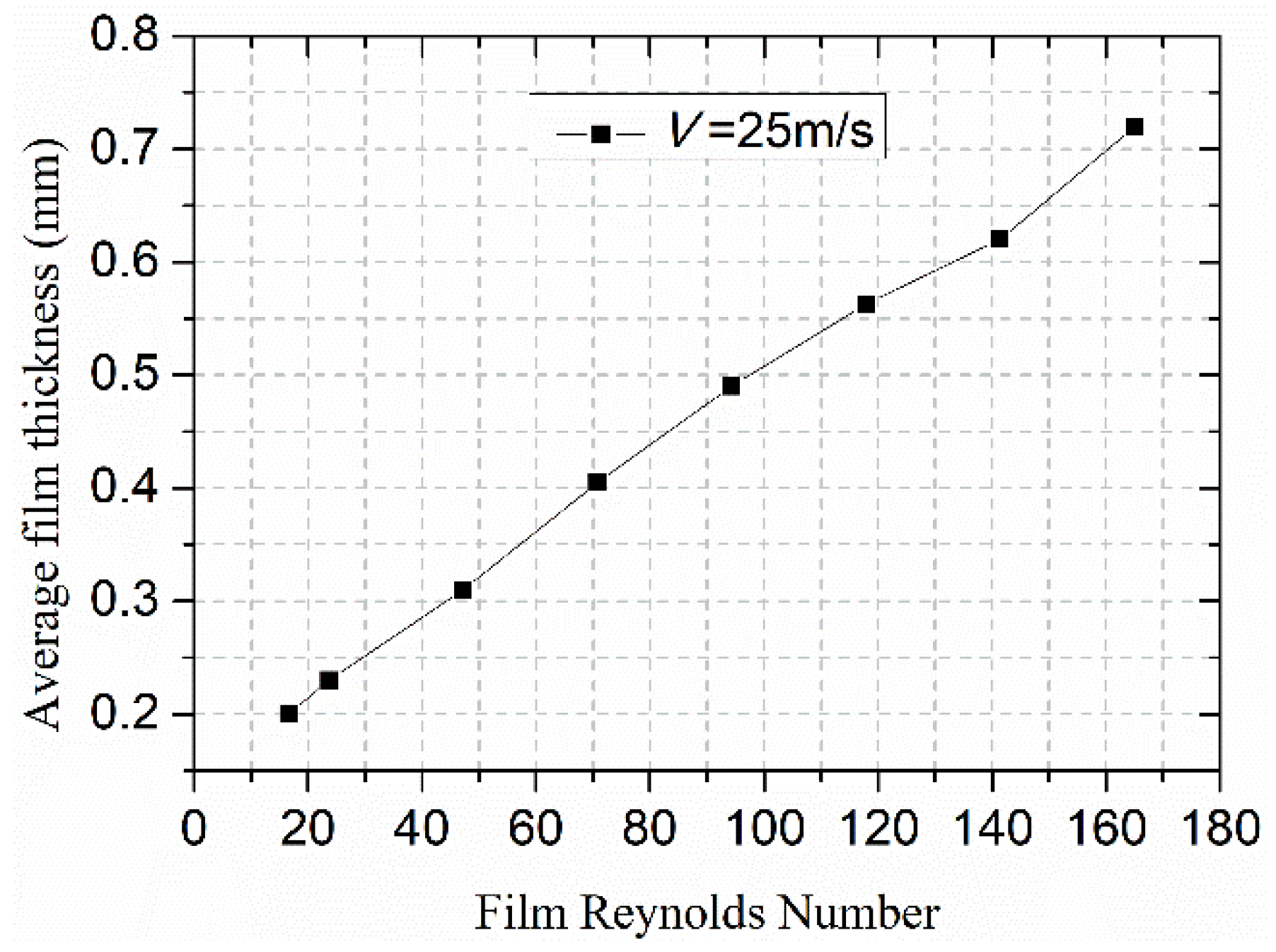
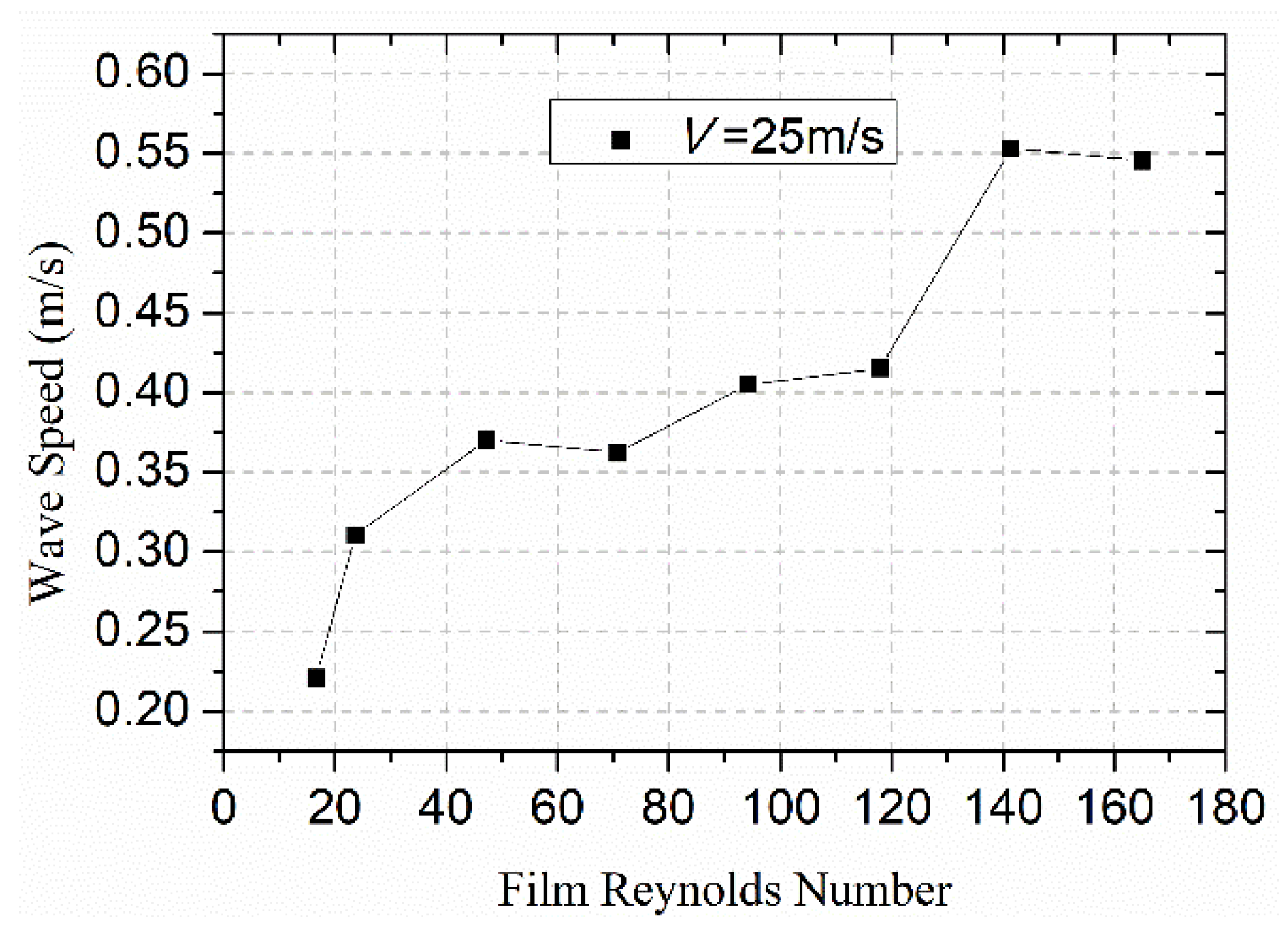
3.2. Effect of Reynolds Number on the Water Film Flow
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dai, H.; Zhu, C.; Zhao, H.; Liu, S. A New Ice Accretion Model for Aircraft Icing Based on Phase-Field Method. Appl. Sci. 2021, 11, 5693. [Google Scholar] [CrossRef]
- Wang, Z.; Zhao, H.; Liu, S. Numerical Simulation of Aircraft Icing under Local Thermal Protection State. Aerospace 2022, 9, 84. [Google Scholar] [CrossRef]
- Holl, M.; Pátek, Z.; Smrcek, L. Wind Tunnel Testing of Performance Degradation of Ice Contaminated Airfoils. In Proceedings of the 22nd International Congress of Aeronautical Sciences, Harrogate, UK, 27 August–1 September 2000. [Google Scholar]
- Otta, S.P.; Rothmayer, A.P. Instability of Stagnation Line Icing. Comput. Fluids 2009, 38, 273–283. [Google Scholar] [CrossRef]
- Rothmayer, A.P.; Hu, H. Linearized Solutions of Three-Dimensional Condensed Layer Films. In Proceedings of the 5th AIAA Atmospheric and Space Environments Conference, AIAA, San Diego, CA, USA, 24–27 June 2013. [Google Scholar]
- Rothmayer, A.P.; Matheis, B.D.; Timoshin, S.N. Thin Liquid Films Flowing over External Aerodynamic Surfaces. J. Eng. Math. 2002, 42, 341–357. [Google Scholar] [CrossRef]
- Wang, G.; Rothmayer, A.P. Thin Water Films Driven by Air Shear Stress Through Roughness. Comput. Fluids 2009, 38, 235–246. [Google Scholar] [CrossRef]
- Planquart, P.; Riethmuller, M.; Joly, A.; Detry, J.M. Real Time Optical Detection and Characterisation of Water Model Free Surfaces—Application to the Study of the Mold. In Proceedings of the 4th European Continuous Casting Conference, Birmingham, UK, 14–16 October 2002. [Google Scholar]
- Touron, F.; Labraga, L.; Keirsbulck, L.; Bratec, H. Measurements of Liquid Film Thickness of a Wide Horizontal Co-current Stratified Air-Water Flow. Therm. Sci. 2015, 19, 521–530. [Google Scholar] [CrossRef]
- Cherdantsev, A.V.; Hann, D.B.; Azzopardi, B.J. Study of Gas-Sheared Liquid Film in Horizontal Rectangular Duct Using High-Speed LIF Technique: Three-Dimensional Wavy Structure and Its Relation to Liquid Entrainment. Int. J. Multiph. Flow 2014, 67, 52–64. [Google Scholar] [CrossRef]
- Zhang, K.; Zhang, S.; Rothmayer, A.P.; Hu, H. Development of a Digital Image Projection Technique to Measure Wind-Driven Water Film Flows. In Proceedings of the 51st AIAA Aerospace Sciences Meeting AIAA, Grapevine, TX, USA, 7–10 January 2013. [Google Scholar]
- Zhang, K.; Blake, J.; Rothmayer, A.P.; Hu, H. An Experimental Investigation on Wind-Driven Rivulet/Film Flows over a NACA0012 Airfoil by Using Digital Image Projection Technique. In Proceedings of the 52nd Aerospace Sciences Meeting, AIAA, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar]
- Zhang, K.; Tian, W.; Hu, H. An Experimental Investigation on the Surface Water Transport Process over an Airfoil by Using a Digital Image Projection Technique. Exp. Fluids 2015, 56, 173. [Google Scholar] [CrossRef]
- Chang, S.; Yu, W.; Song, M.; Leng, M.; Shi, Q. Investigation on Wavy Characteristics of Shear-Driven Water Film Using the Planar Laser Induced Fluorescence Method. Int. J. Multiph. Flow 2019, 118, 242–253. [Google Scholar]
- Leng, M.; Chang, S.; Wu, H. Experimental Investigation of Shear-Driven Water Film Flows on Horizontal Metal Plate. Exp. Therm. Fluid Sci. 2018, 94, 134–147. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Zhu, C.; Zhao, N.; Zhu, C.; Wang, Z. Experimental Research on the Influence of Roughness on Water Film Flow. Aerospace 2021, 8, 225. [Google Scholar] [CrossRef]




Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, H.; Dai, H.; Zhu, D.; Zhao, N.; Zhu, C.; Liu, S.; Zhu, C. Experimental Research on the Fluctuation Characteristics of Water Film Driven by Wind. Coatings 2022, 12, 1040. https://doi.org/10.3390/coatings12081040
Zhao H, Dai H, Zhu D, Zhao N, Zhu C, Liu S, Zhu C. Experimental Research on the Fluctuation Characteristics of Water Film Driven by Wind. Coatings. 2022; 12(8):1040. https://doi.org/10.3390/coatings12081040
Chicago/Turabian StyleZhao, Huanyu, Hao Dai, Dongyu Zhu, Ning Zhao, Chengxiang Zhu, Senyun Liu, and Chunling Zhu. 2022. "Experimental Research on the Fluctuation Characteristics of Water Film Driven by Wind" Coatings 12, no. 8: 1040. https://doi.org/10.3390/coatings12081040
APA StyleZhao, H., Dai, H., Zhu, D., Zhao, N., Zhu, C., Liu, S., & Zhu, C. (2022). Experimental Research on the Fluctuation Characteristics of Water Film Driven by Wind. Coatings, 12(8), 1040. https://doi.org/10.3390/coatings12081040








