All-Dielectric Refractive Index Sensor Based on Multiple Fano Resonance with High Sensitivity in the Long-Wave Infrared Region
Abstract
:1. Introduction
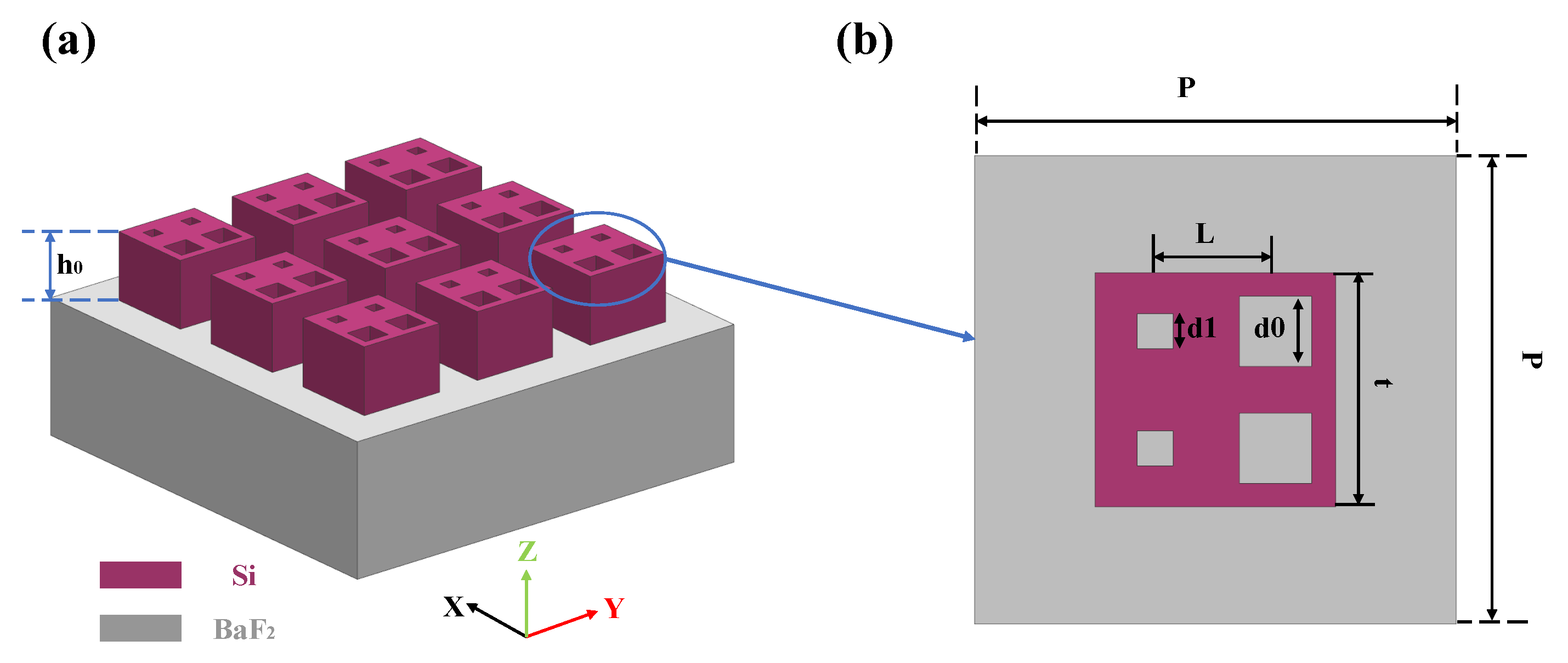
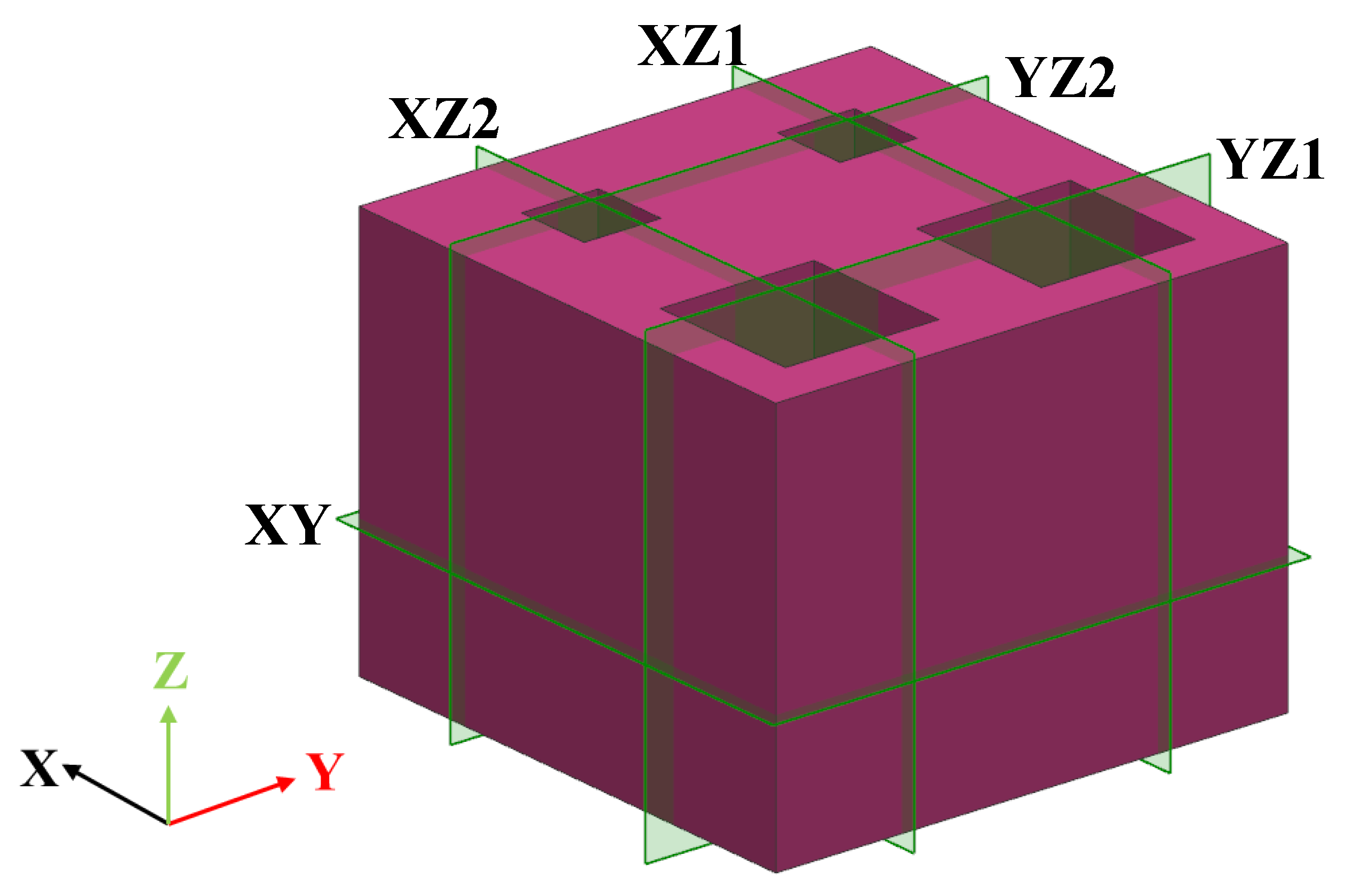
2. Unit Structure and Simulation Methods
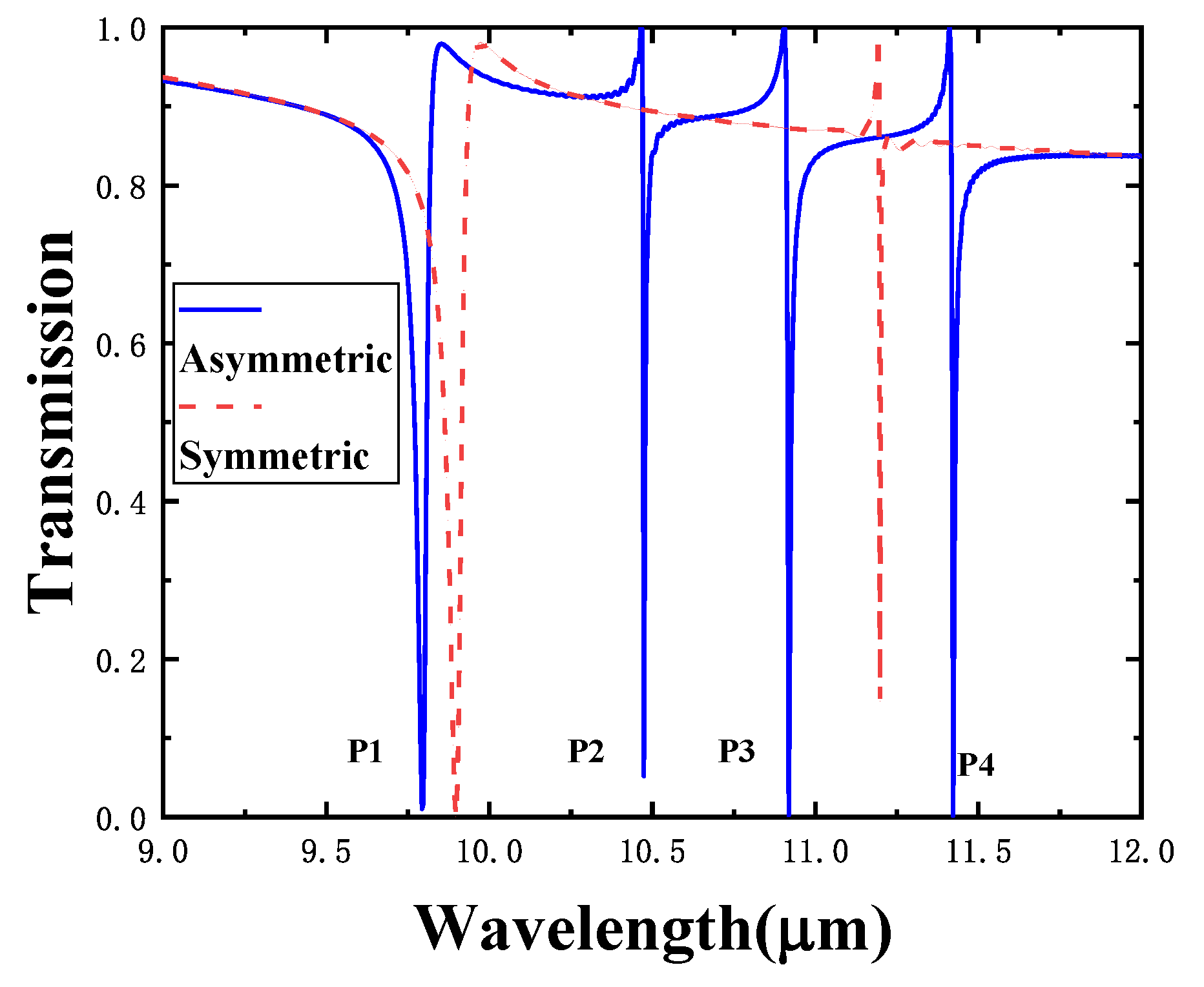
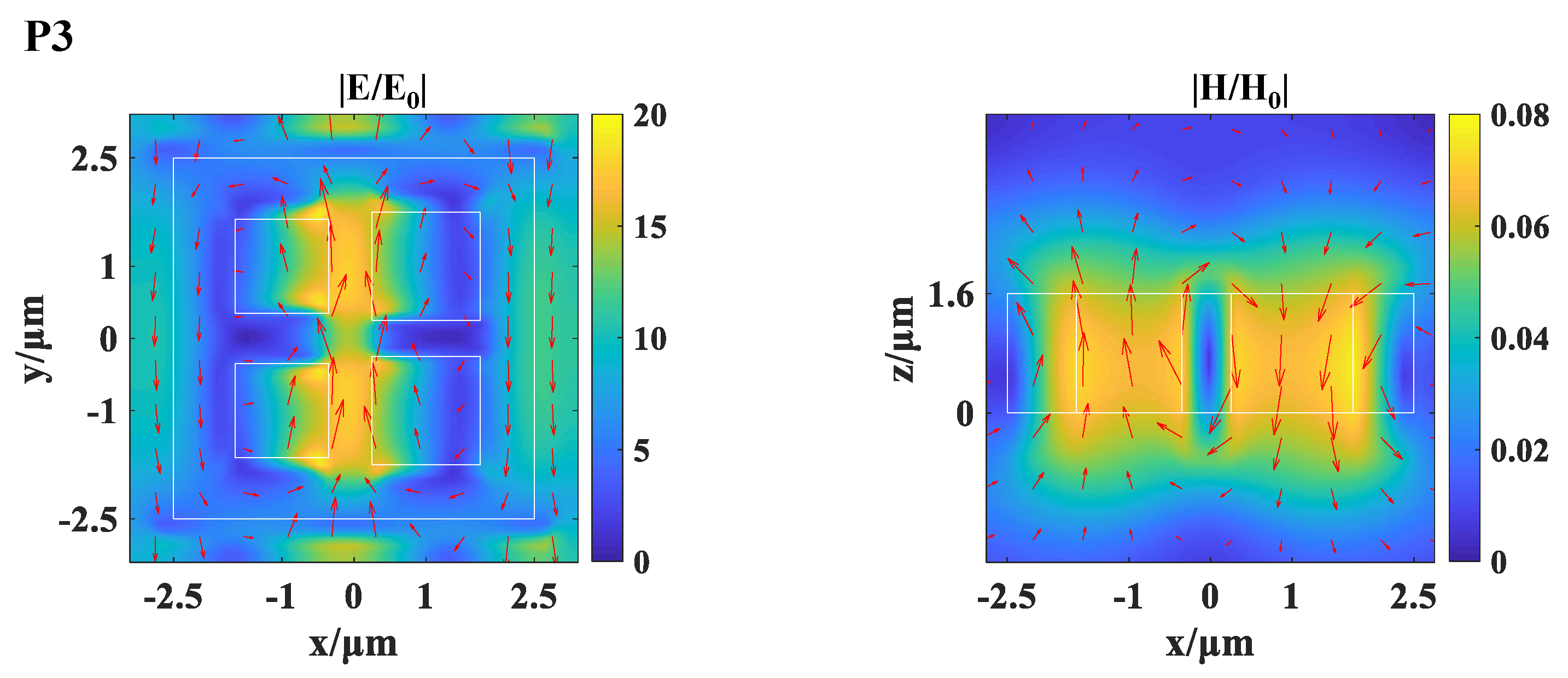
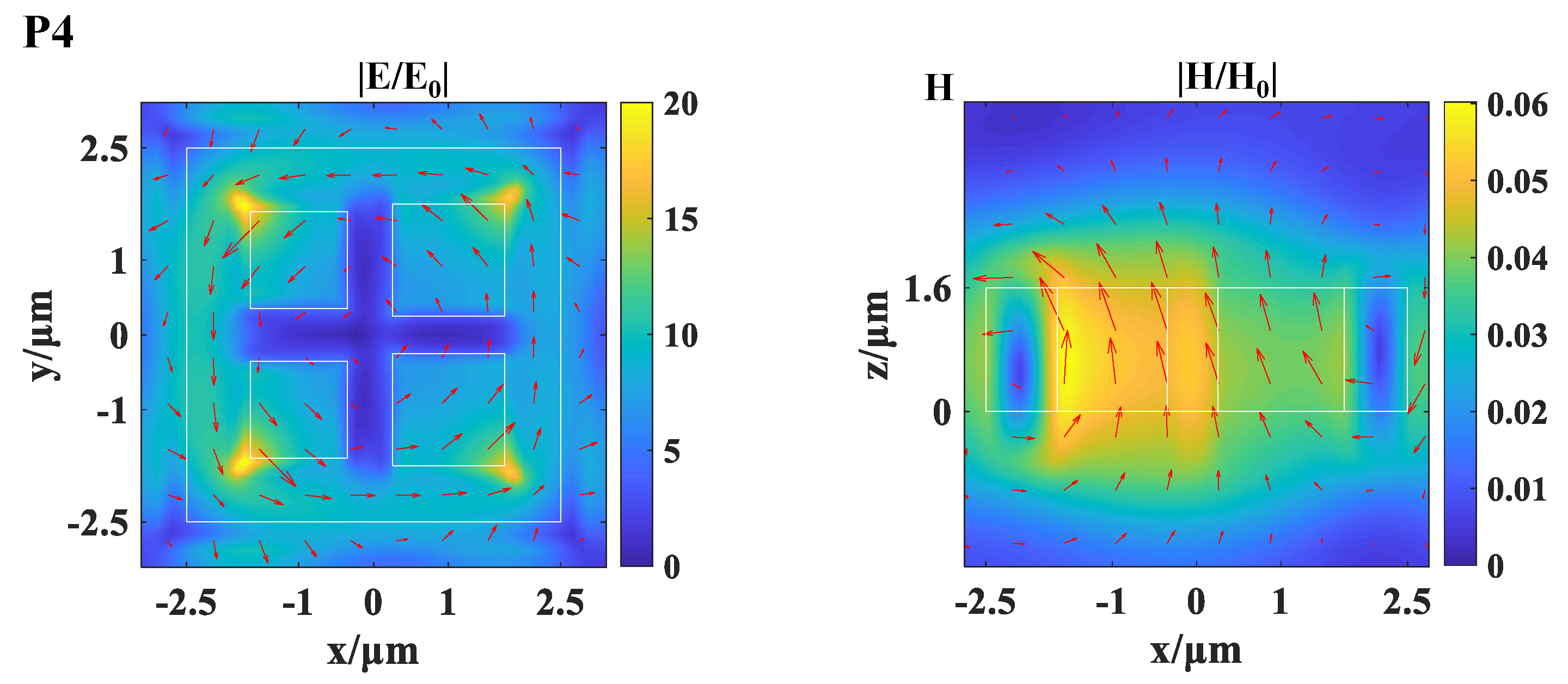
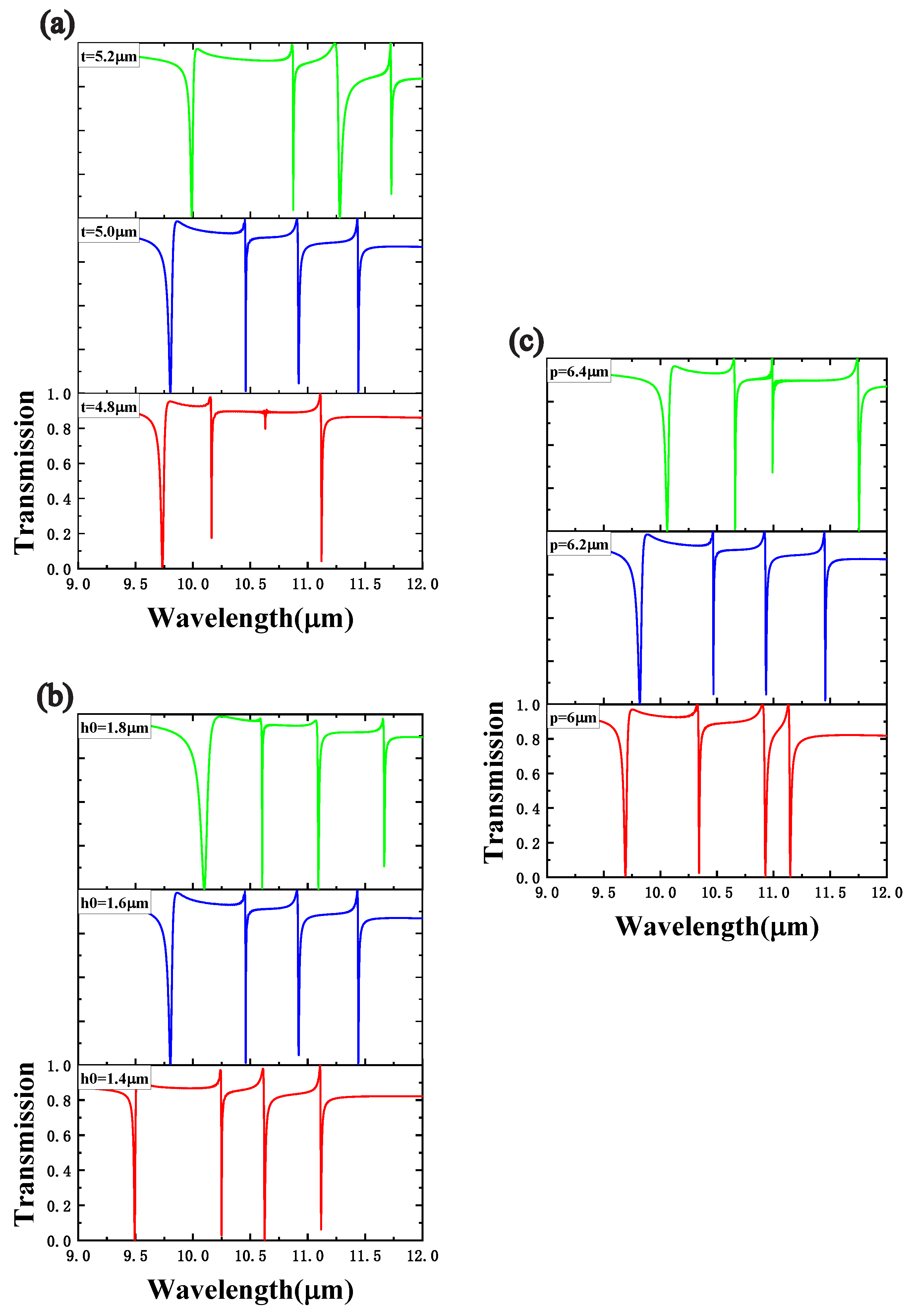
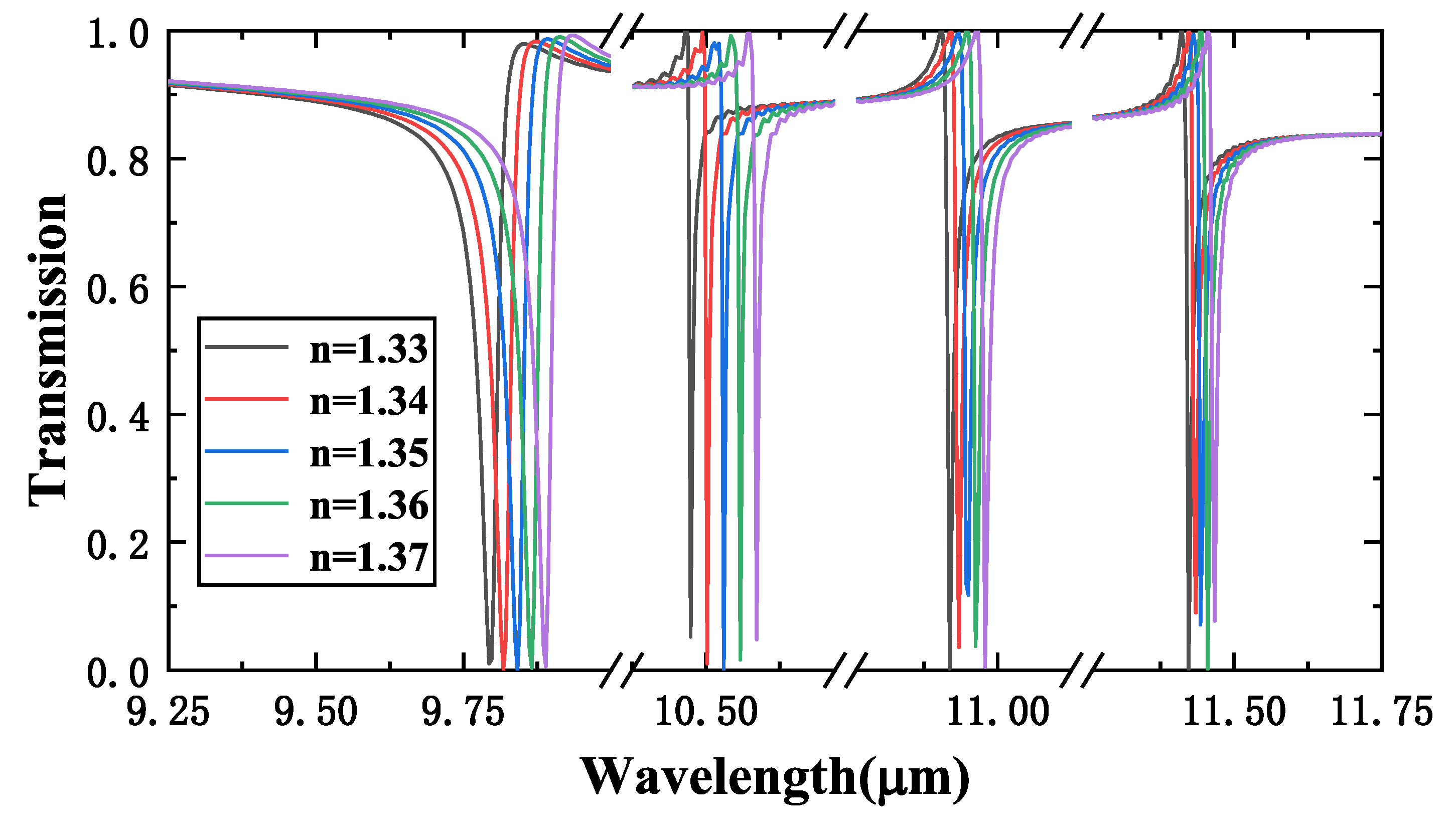
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Liyanage, T.; Alharbi, B.; Quan, L.; Esquela-Kerscher, A.; Slaughter, G. Plasmonic-Based Biosensor for the Early Diagnosis of Prostate Cancer. ACS Omega 2022, 7, 2411–2418. [Google Scholar] [CrossRef]
- Hajshahvaladi, L.; Kaatuzian, H.; Danaie, M. A high-sensitivity refractive index biosensor based on Si nanorings coupled to plasmonic nanohole arrays for glucose detection in water solution. Opt. Commun. 2022, 502, 127421. [Google Scholar] [CrossRef]
- Zhang, Q.; Yan, H.H.; Ru, C.; Zhu, F.; Zou, H.Y.; Gao, P.F.; Huang, C.Z.; Wang, J. Plasmonic biosensor for the highly sensitive detection of microRNA-21 via the chemical etching of gold nanorods under a dark-field microscope. Biosens. Bioelectron. 2022, 201, 113942. [Google Scholar] [CrossRef] [PubMed]
- Hu, J.; Lang, T.T.; Shi, G.H. Simultaneous measurement of refractive index and temperature based on all-dielectric metasurface. Opt. Express 2017, 25, 15241. [Google Scholar] [CrossRef] [PubMed]
- Yesilkoy, F.; Terborg, R.A.; Pello, J.; Belushkin, A.A.; Jahani, Y.; Pruneri, V.; Altug, H. Phase-sensitive plasmonic biosensor using a portable and large field-of-view interferometric microarray imager. Light Sci. Appl. 2018, 7, 17152. [Google Scholar] [CrossRef]
- Danila, O.; Manaila-Maximean, D. Bifunctional Metamaterials Using Spatial Phase Gradient Architectures: Generalized Reflection and Refraction Considerations. Materials 2021, 14, 2201. [Google Scholar] [CrossRef] [PubMed]
- Dănilă, O.; Bărar, A.; Vlădescu, M.; Mănăilă-Maximean, D. An Extended k-Surface Framework for Electromagnetic Fields in Artificial Media. Materials 2021, 14, 7842. [Google Scholar] [CrossRef]
- Wang, K.; Xiong, Y.; Li, Q.; Wang, Y.C.; Zhang, J.; Liu, H.; Liu, Z.; Wang, T.T.; Shen, Z.F.; Wang, X.K.; et al. Near-infrared narrow-band minus filter based on a Mie magnetic dipole resonance. Opt. Express 2022, 30, 22830–22837. [Google Scholar] [CrossRef]
- Bontempi, N.; Chong, K.E.; Orton, H.W.; Staude, I.; Choi, D.Y.; Alessandri, I.; Kivshar, Y.S.; Neshev, D.N. Highly sensitive biosensors based on all-dielectric nanoresonators. Nanoscale 2017, 9, 4912–4980. [Google Scholar] [CrossRef]
- Yavas, O.; Svedendahl, M.; Dobosz, P.; Sanz, V.; Quidant, R. On-a-chip biosensing based on all-dielectric nanoresonators. Nano Lett. 2017, 17, 4421–4426. [Google Scholar] [CrossRef] [Green Version]
- He, J.N.; Fan, C.Z.; Wang, J.Q.; Ding, P.; Cai, G.W.; Cheng, Y.G.; Zhu, S.M.; Liang, E.J. A giant localized field enhancement and high sensitivity in an asymmetric ring by exhibiting Fano resonance. J. Opt.-UK 2013, 15, 025007. [Google Scholar] [CrossRef]
- Zhu, Z.; You, O.; Li, Q.; Fan, S. Fano resonance boosted cascaded optical field enhancement in a plasmonic nanoparticle-in-cavity nanoantenna array and its SERS application. Light Sci. Appl. 2015, 4, e296. [Google Scholar] [CrossRef]
- Zhang, Y.H.; Liang, Z.Z.; Meng, D.J.; Qin, Z.; Fan, Y.D.; Shi, X.Y.; Smith, D.R.; Hou, E.Z. All-dielectric refractive index sensor based on Fano resonance with high sensitivity in the mid-infrared region. Results Phys. 2021, 24, 104129. [Google Scholar] [CrossRef]
- Gao, Z.X.; Yao, B.C.; Qin, C.Y.; Yang, R.; Guo, Y.H.; Zhang, Y.F.; Wu, Y.; Bi, L.; Chen, Y.F.; Xie, Z.D.; et al. Biochemical sensing in graphene-enhanced microfiber resonators with individual molecule sensitivity and selectivity. Light Sci. Appl. 2019, 8, 107. [Google Scholar]
- Lu, H.; Liu, X.M.; Mao, D.; Wang, G.X. Plasmonic nanosensor based on Fano resonance in waveguide-coupled resonators. Opt. Lett. 2012, 37, 3780. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Flach, S.; Kivshar, Y.S. Fano resonances in nanoscale structures. Rev. Mod. Phys. 2010, 82, 2257–2298. [Google Scholar] [CrossRef] [Green Version]
- Nejad, F.Z.; Fleury, R. Topological Fano Resonances. Phys. Rev. Lett. 2019, 122, 014301. [Google Scholar] [CrossRef]
- Nazari, F.; Bender, N.; Ramezani, H.; Moravvej-Farshi, M.K.; Christodoulides, D.N.; Kottos, T. Optical isolation via pt-symmetric nonlinear Fano resonances. Opt. Express 2014, 22, 9574. [Google Scholar] [CrossRef] [Green Version]
- Zhou, H.J.; Su, S.J.; Qiu, W.B.; Zhao, Z.Y.; Lin, Z.L.; Qiu, P.P.; Kan, Q. Multiple Fano Resonances with Tunable Electromagnetic Properties in Graphene Plasmonic Metamolecules. Nanomaterials 2020, 10, 236. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Yu, S.L.; Yang, L.; Zhao, T.G. High Q-factor multi-Fano resonances in all-dielectric double square hollow metamaterials. Opt. Laser Technol. 2021, 140, 107072. [Google Scholar] [CrossRef]
- Zhang, Y.B.; Liu, W.W.; Li, Z.C.; Li, Z.; Cheng, H.; Chen, S.Q.; Tian, J.G. High-quality-factor multiple Fano resonances for refractive index sensing. Opt. Lett. 2018, 43, 1842–1845. [Google Scholar] [CrossRef] [PubMed]
- Chau, Y.F.C.; Chou Chao, C.T.; Jumat, S.Z.B.H.; Kooh, M.R.R.; Thotagamuge, R.; Lim, C.M.; Chiang, H.P. Improved Refractive Index-Sensing Performance of Multimode Fano-Resonance-Based Metal-Insulator-Metal Nanostructures. Nanomaterials 2021, 11, 2097. [Google Scholar] [CrossRef] [PubMed]
- Chou Chao, C.T.; Chau, Y.F.C.; Chiang, H.P. Multiple Fano resonance modes in an ultra-compact plasmonic waveguide-cavity system for sensing applications. Results Phys. 2021, 27, 104527. [Google Scholar] [CrossRef]
- Su, W.; Chen, X.Y.; Geng, Z.; Luo, Y.L. Multiple Fano resonances in all-dielectric elliptical disk-ring metasurface for high-quality refractive index sensing. Results Phys. 2020, 18, 103340. [Google Scholar] [CrossRef]
- Zhang, S.P.; Bao, K.; Halas, N.J.; Xu, H.X. Substrate-Induced Fano Resonances of a Plasmonic: Nanocube: A Route to Increased-Sensitivity Localized Surface Plasmon Resonance Sensors Revealed. Nano Lett. 2011, 11, 1657–1663. [Google Scholar] [CrossRef]
- Fan, K.B.; Shadrivov, l.V.; Padilla, W.J. Dynamic bound states in the continuum. Optica 2019, 6, 169. [Google Scholar] [CrossRef]
- Garmon, S.; Noba, K.; Ordonez, G.E.; Segal, D. Non-Markovian dynamics revealed at a bound state in the continuum. Phys. Rev. A 2019, 99, 010102. [Google Scholar] [CrossRef] [Green Version]
- Ndangali, F.R.; Shabanov, S.V. Electromagnetic bound states in the radiation continuum for periodic double arrays of subwavelength dielectric cylinders. J. Math. Phys. 2010, 51, 102901. [Google Scholar] [CrossRef] [Green Version]
- Hsu, C.W.; Zhen, B.; Stone, A.D.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef] [Green Version]
- Sadrieva, Z.F.; Sinev, I.S.; Koshelev, K.L.; Samusev, A.; Iorsh, I.V.; Takayama, O.; Malureanu, R.; Bogdanov, A.A.; Lavrinenko, A.V. Transition from Optical Bound States in the Continuum to Leaky Resonances: Role of Substrate and Roughness. ACS Photonics 2017, 4, 723–727. [Google Scholar] [CrossRef]
- Li, B.; Yao, J.; Zhu, H.; Cai, G.; Liu, H.Q. Asymmetric excitations of toroidal dipole resonance and the magnetic dipole quasi-bound state in the continuum in an all-dielectric metasurface. Opt. Mater. Express 2021, 11, 2359. [Google Scholar] [CrossRef]
- Jerrard, H.G. Handbook of optical constant of solids. Opt. Laser Technol. 1986, 18, 142–149. [Google Scholar] [CrossRef]
- Zou, S.; Liu, J.S.; Wang, K.J. Microwave transmission properties of metamaterials with double sets of square holes. Sci. Bull. 2012, 57, 3769–3772. [Google Scholar] [CrossRef] [Green Version]
- Xu, L.; Kamali, K.Z.; Huang, L.; Rahmani, M.; Smirnov, A.; Camacho-Morales, R.; Ma, Y.; Zhang, G.; Woolley, M.; Neshev, D.; et al. Dynamic Nonlinear Image Tuning through Magnetic Dipole Quasi-BIC Ultrathin Resonators. Adv. Sci. 2019, 6, 1802119. [Google Scholar] [CrossRef] [Green Version]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric Metasurfaces with High- Q Resonances Governed by Bound States in the Continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef] [Green Version]
- Sadrieva, Z.; Frizyuk, K.; Petrov, M.; Kivshar, Y.; Bogdanov, A. Multipolar origin of bound states in the continuum. Phys. Rev. B 2019, 100, 115303. [Google Scholar] [CrossRef] [Green Version]
- Koshelev, K.; Bogdanov, A.; Kivshar, Y. Meta-optics and bound states in the continuum. Sci. Bull. 2019, 64, 836–842. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.L.; Han, Z.H.; Du, Y.; Qin, J.Y. Ultrasensitive terahertz sensing with high-Q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface. Nanophotonics 2021, 10, 1295–1307. [Google Scholar] [CrossRef]
- Cao, Y.; Liu, H.; Tong, Z.; Yuan, S.; Zhao, S. Simultaneous measurement of temperature and refractive index based on a core-offset Mach-Zehnder interferometer cascaded with a long-period fiber grating. Optoelectron. Lett. 2015, 11, 69–72. [Google Scholar] [CrossRef]
- Xu, Y.; Bai, P.; Zhou, X.; Akimov, Y.; Png, C.E.; Ang, L.K.; Knoll, W.; Wu, L. Optical Refractive Index Sensors with Plasmonic and Photonic Structures: Promising and Inconvenient Truth. Adv. Opt. Mater. 2019, 7, 1801433. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Wang, Y.; Wang, X.; Wang, X.; Gao, J.; Yang, H. All-Dielectric Refractive Index Sensor Based on Multiple Fano Resonance with High Sensitivity in the Long-Wave Infrared Region. Coatings 2022, 12, 970. https://doi.org/10.3390/coatings12070970
Wang K, Wang Y, Wang X, Wang X, Gao J, Yang H. All-Dielectric Refractive Index Sensor Based on Multiple Fano Resonance with High Sensitivity in the Long-Wave Infrared Region. Coatings. 2022; 12(7):970. https://doi.org/10.3390/coatings12070970
Chicago/Turabian StyleWang, Kai, Yansong Wang, Xiaokun Wang, Xiaoyi Wang, Jinsong Gao, and Haigui Yang. 2022. "All-Dielectric Refractive Index Sensor Based on Multiple Fano Resonance with High Sensitivity in the Long-Wave Infrared Region" Coatings 12, no. 7: 970. https://doi.org/10.3390/coatings12070970
APA StyleWang, K., Wang, Y., Wang, X., Wang, X., Gao, J., & Yang, H. (2022). All-Dielectric Refractive Index Sensor Based on Multiple Fano Resonance with High Sensitivity in the Long-Wave Infrared Region. Coatings, 12(7), 970. https://doi.org/10.3390/coatings12070970





