Simulation Analysis of Organic–Inorganic Interface Failure of Scallop under Ultra-High Pressure
Abstract
:1. Introduction
2. Mechanical Model of Failure at the Interface of Organic–Inorganic Composites of Scallops under Ultra-High Pressure
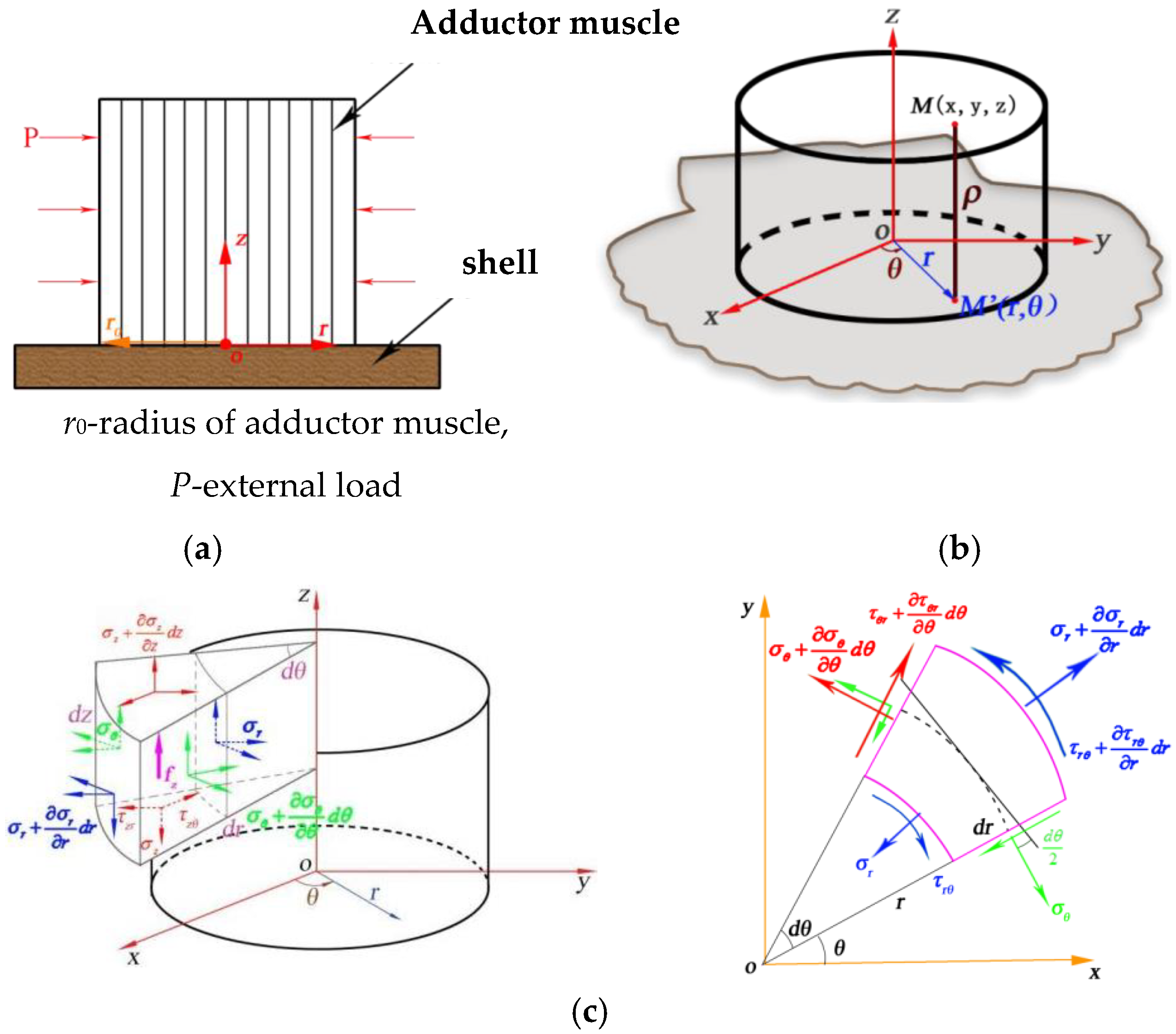
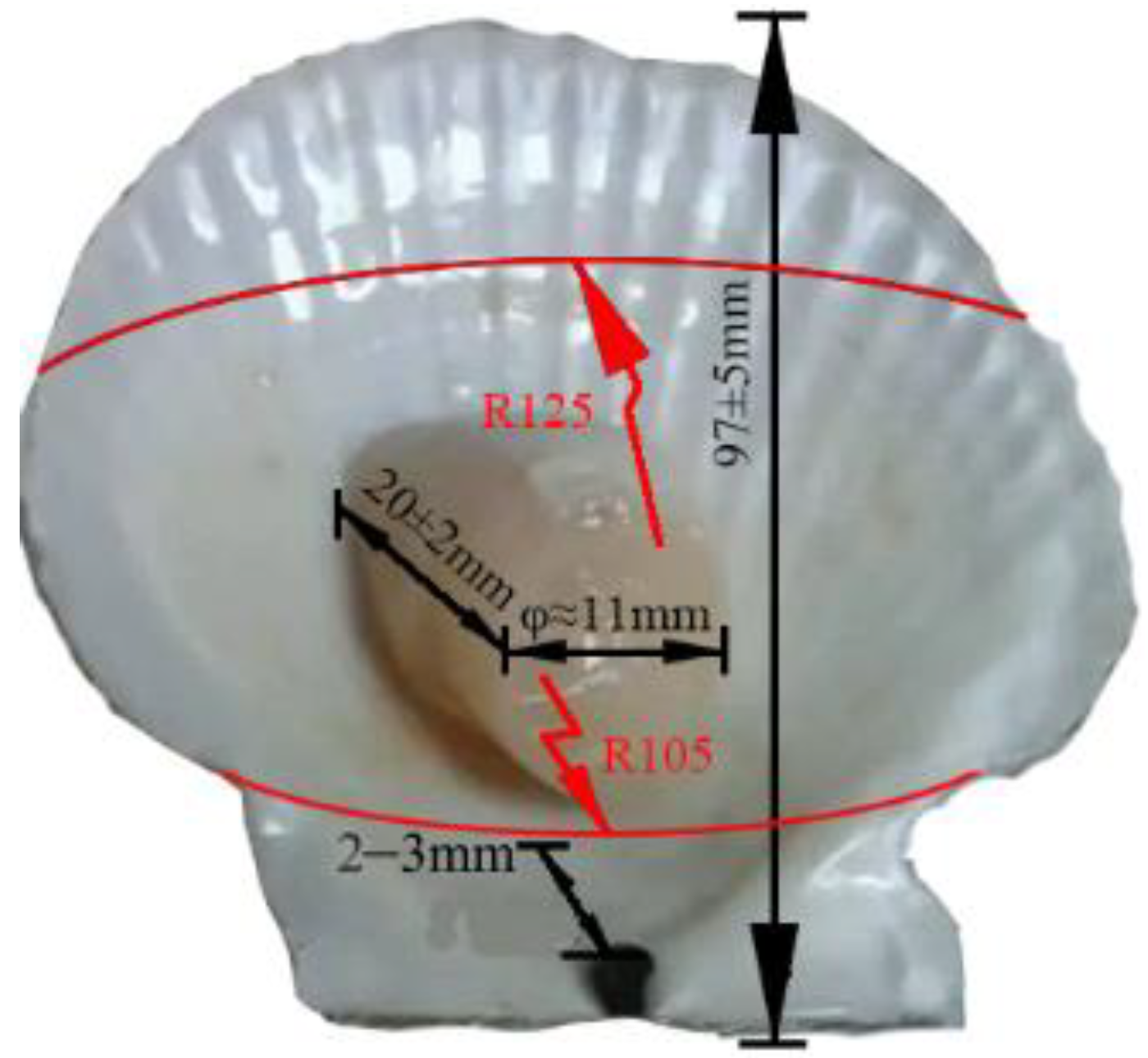
2.1. Simplified Model Analysis of the Scallop Organic–Inorganic Composite Interface
2.2. Construction of a Failure Mechanics Model for the Organic–Inorganic Interface of Scallops
2.2.1. Scallop Organic Interface Material Force Analysis
2.2.2. Establishment of the Ontological Equations for Scallop Organic Interfacial Materials
2.3. Mechanical Model of Scallop Organic–Inorganic Composite Interface Failure under the Action of Ultra-High Pressure
3. Simulation Analysis of Organic–Inorganic Interface Failure of Scallops under Ultra-High Pressure
3.1. Influence of the Angle between the Organic–Inorganic Interface Materials of Scallops on the Stress Distribution
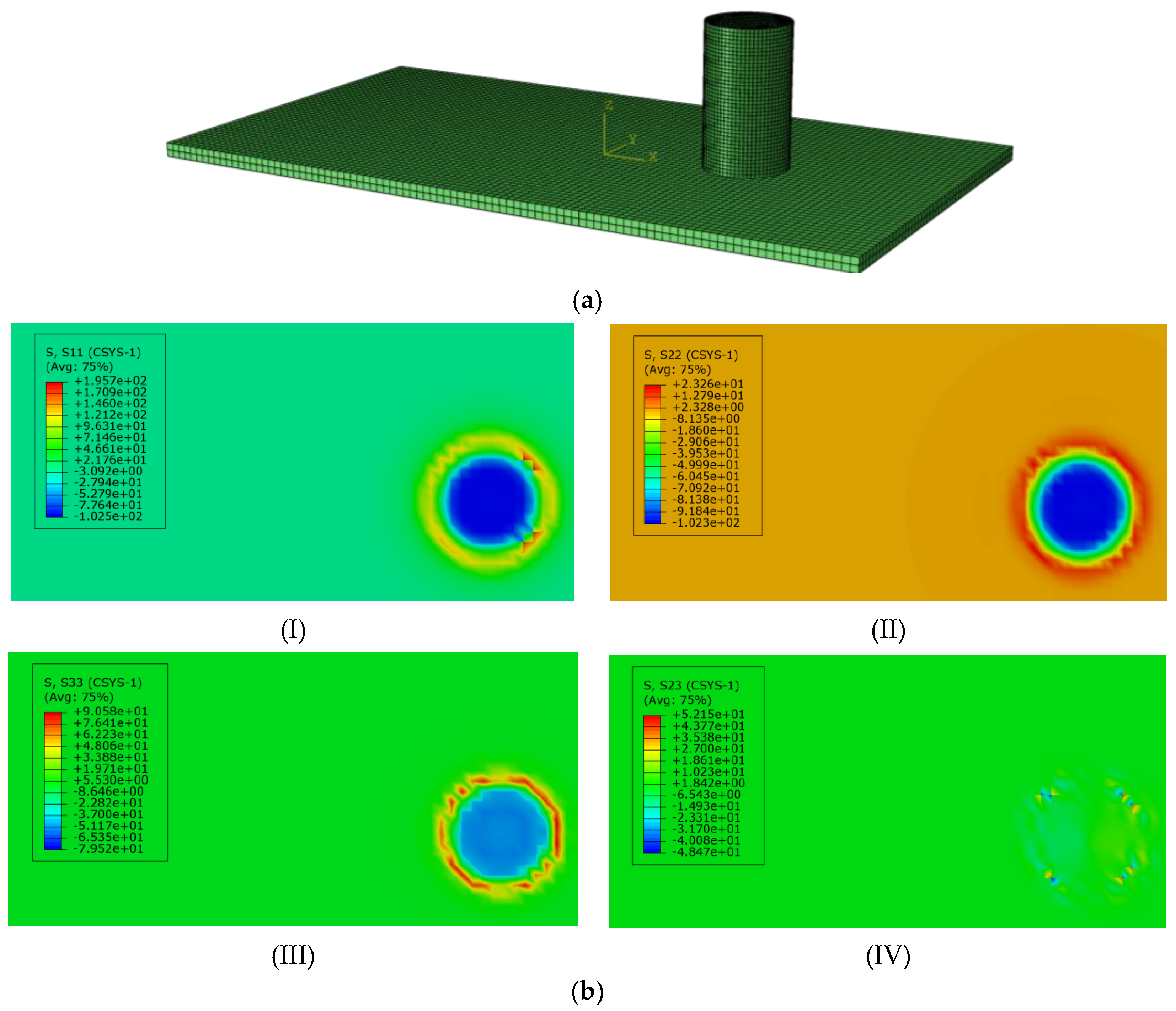
Stress Distribution of Organic–Inorganic Composites of Scallops in Vertical Contact with Smooth Surfaces
3.2. Effect of the Organic–Inorganic Interface State on Yield Stress Distribution of Scallop
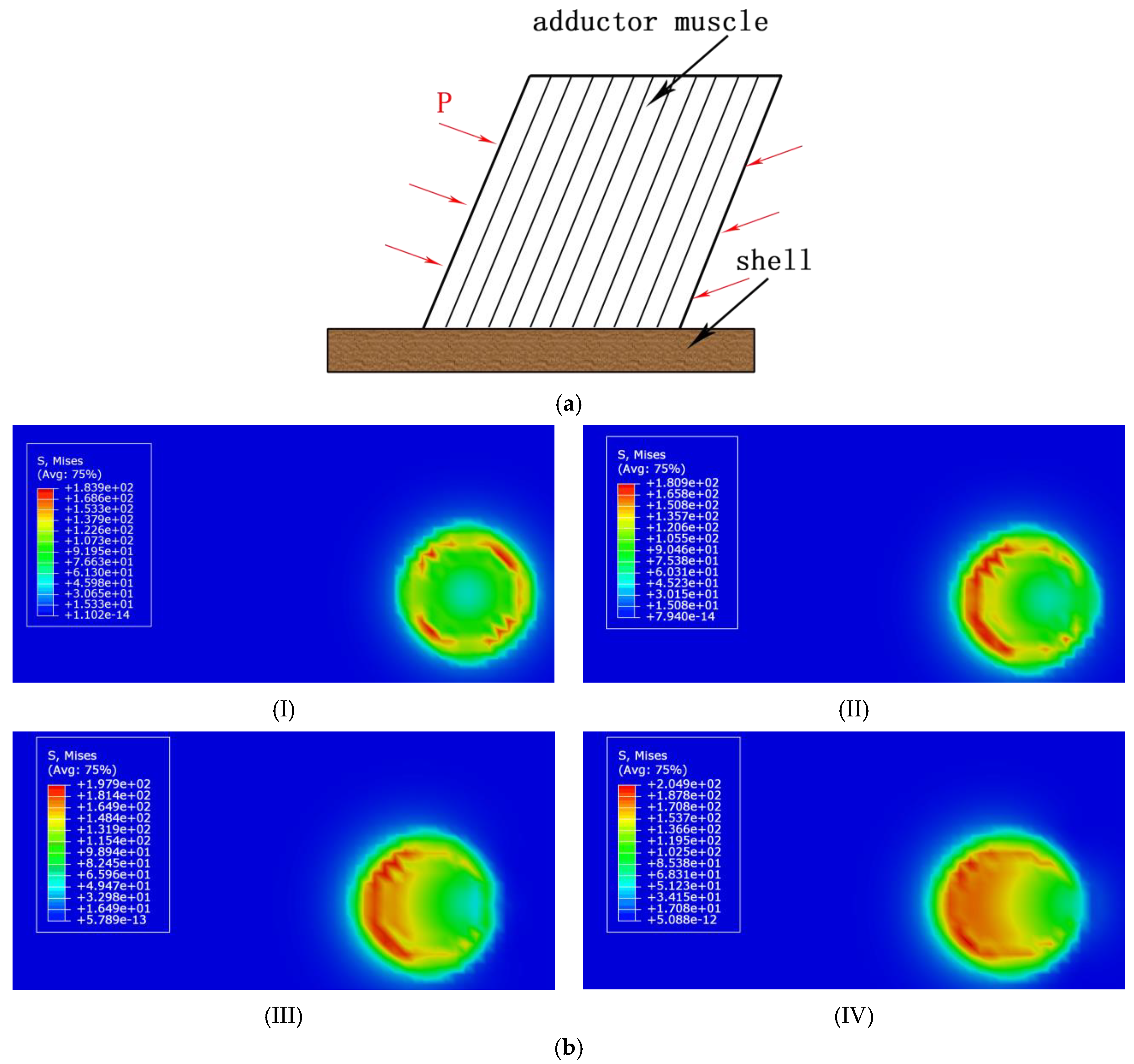
3.2.1. Stress Distribution of the Organic–Inorganic Interface of Scallop with Angular Contact
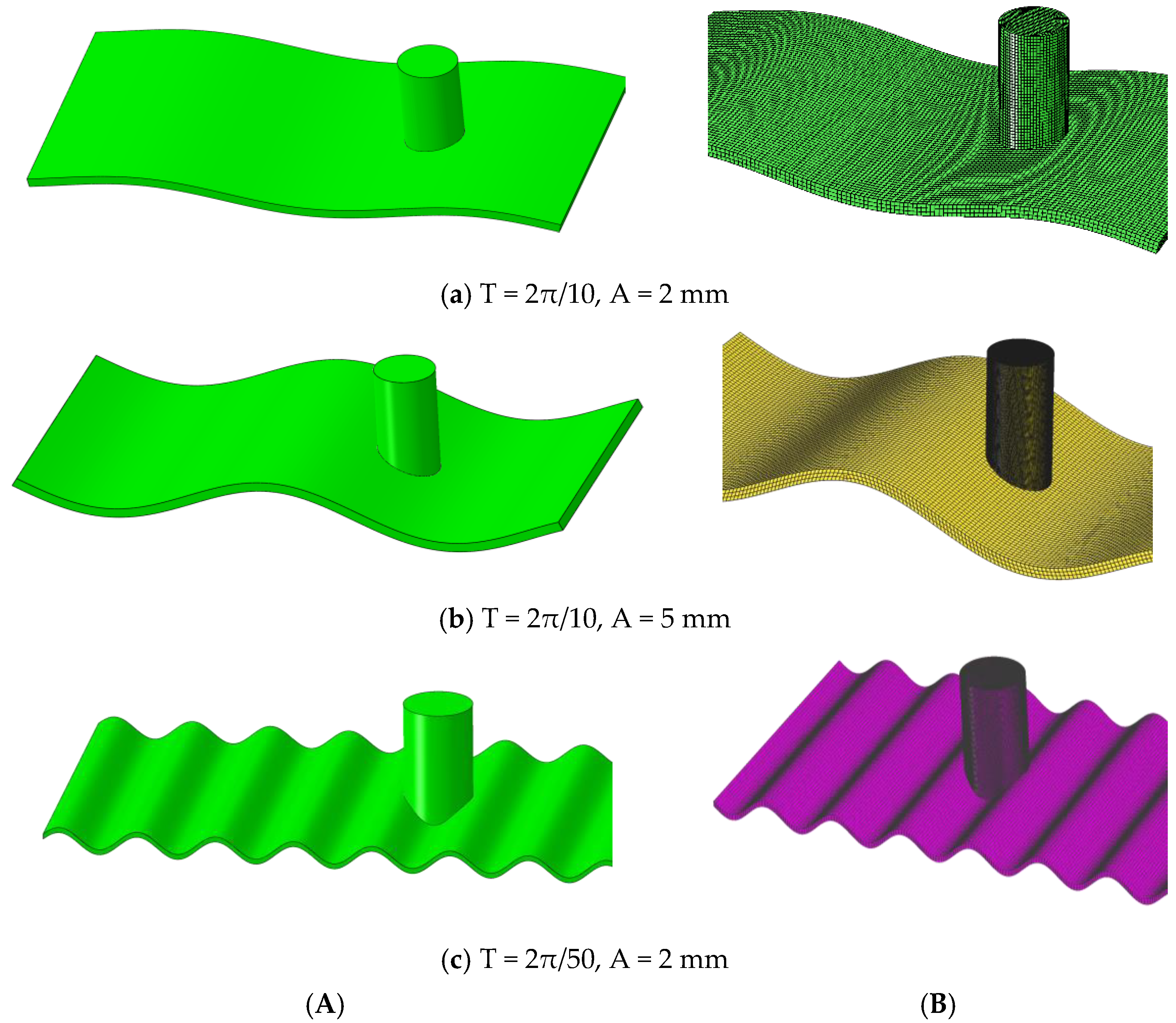
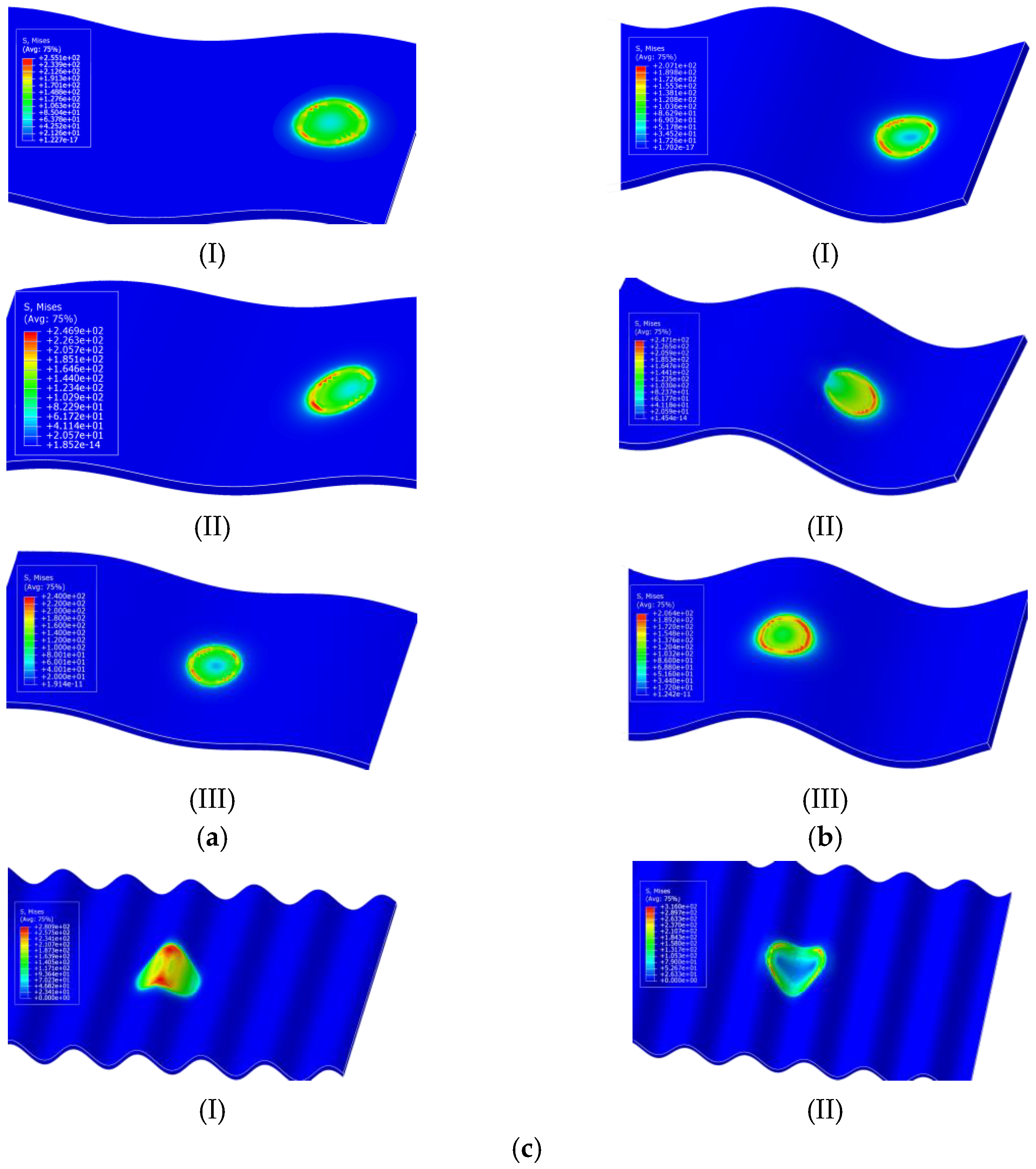
3.2.2. Influence of Surface Undulation Degree on the Stress Distribution of Scallop Shell
4. Structural Stress Distribution at the Organic-Inorganic Interface of Scallops
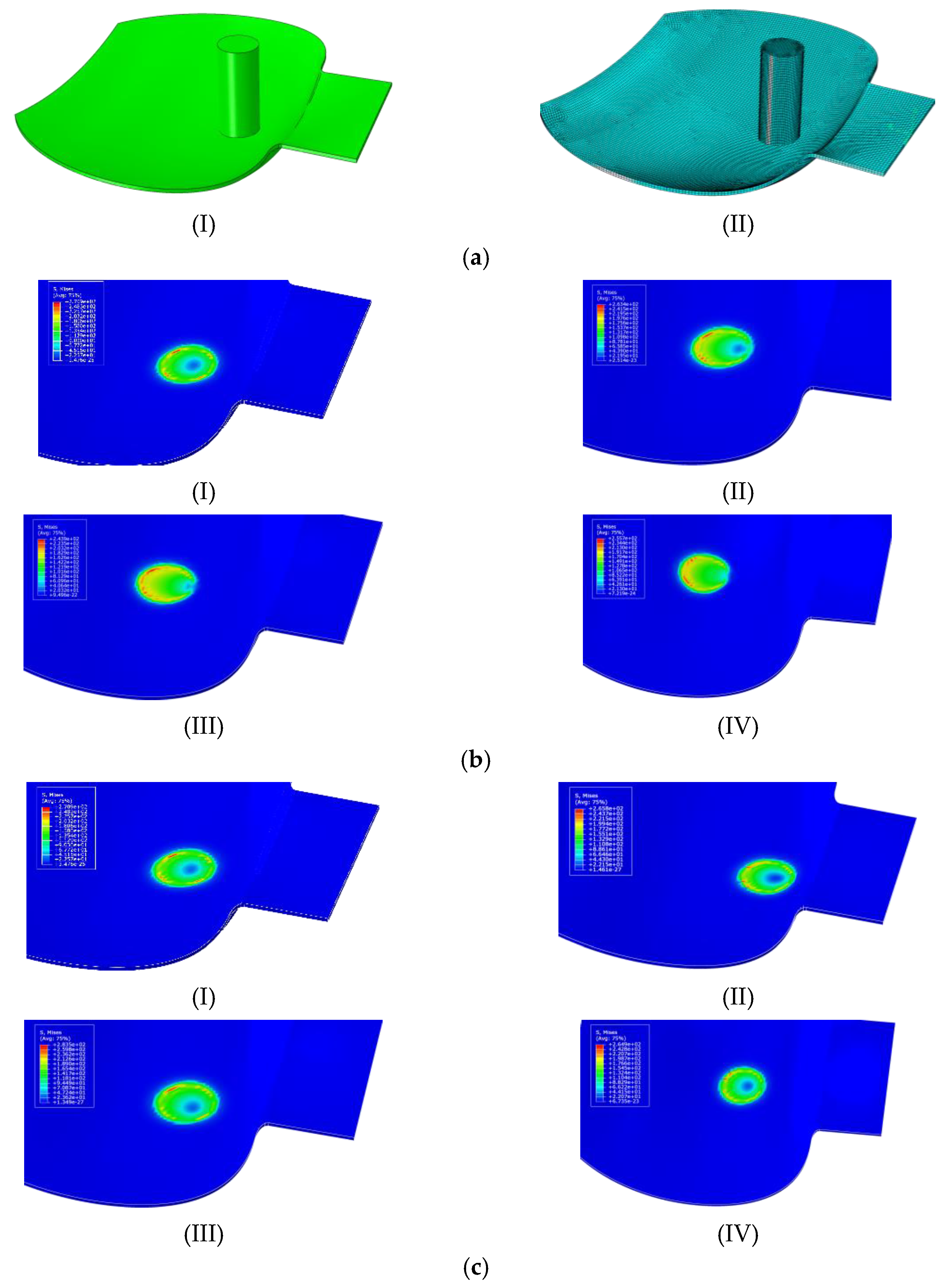
4.1. Influence of the Scallop Interface Material Clamping Angle on the Interface Stress Distribution
4.2. Influence of Relative Position of Scallop Interface Material on Stress Distribution
4.3. The Mechanism of Scallop Organic–Inorganic Interface Fracture Failure under Ultra-High Pressure
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Inglis, S.D.; Kristmundsson, A.; Freeman, M.A.; Levesque, M.; Stokesbury, K. Gray meat in the Atlantic sea scallop, Placopecten magellanicus, and the identification of a known pathogenic scallop apicomplexan. J. Invertebr. Pathol. 2016, 141, 66–75. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.L.; Zheng, Y.; Liu, H.H.; Zhang, Q.; Song, Y.; Tian, Y.Y.; Liu, J.R. Activity and characteristics of superoxide dismutase in adductor muscle of live dry-storaged yesso scallop Patinopecten yessoensis. J. Dalian Ocean. Univ. 2018, 33, 651–657. [Google Scholar] [CrossRef]
- Gong, X.; Chang, J.; Li, D.T.; Sun, Z.H. Effect of ultrahigh pressure on the structure of scallop adductor muscle. Food Sci. 2021, 42, 87–93. [Google Scholar] [CrossRef]
- Zhang, Y.J.; Zhang, S.M.; Cao, P.L. The polypeptide in Chlamys farreri can protect human dermal fibroblasts from ultraviolet B damage. Chin. J. Oceanol. Limnol. 2005, 23, 357–362. [Google Scholar] [CrossRef]
- Song, Y.; Zhang, Q.; Zhou, Y.L. Protein distribution and physicochemical properties in striated muscle and smooth muscle of Patinopecten yessoensis. J. Fish. China 2017, 41, 357–362. [Google Scholar] [CrossRef]
- Kennedy, V.S.; Newell, R.I.E.; Eble, A.F. Process of Eastern Oyster: Crassostrea Virginica; University of Maryland Sea Grant College: College Park, MD, USA, 1996. [Google Scholar]
- Wang, Q.; Yuan, T.; He, M.X. Rearch progress of culture and genetic breeding of noble scallop Chlamys nobilis. South China Fish. Sci. 2011, 7, 73–80. [Google Scholar] [CrossRef]
- Lee, S.W.; Jang, Y.N.; Kim, J.C. Characteristics of the aragonitic layer in adult oyster shells, crassostreagigas: Structural study of myostracum including the adductor muscle scar. Evid.-Based Compl. Alt. 2011, 2011, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Song, Y.F.; Lu, Y.; Ding, H.; Lv, H.H.; Gao, G.H.; Sun, C.J. Structural characteristics at the adductor muscle and shell interface in mussel. Appl. Biochem. Biotech. 2013, 171, 1203–1211. [Google Scholar] [CrossRef]
- Zhao, L.P.; Xu, H.Z.; Chen, D. Microstructure and spectral analysis of Mytilus coruscus shell. J. Zhejiang Univ. Sci. Ed. 2015, 42, 339–346. [Google Scholar] [CrossRef]
- Liao, Z.; Sun, Q.; Jiang, Y.T. Molecular composition and mechanism of muscle-shell attachment of shellfish. J. Zhejiang Ocean. Univ. Nat. Sci. 2018, 37, 313–319. [Google Scholar]
- Ansboro, S.; Greiser, U.; Barry, F. Strategies for improved targeting of therapeutic cells: Implications for tissue repair. Eur. Cells Mater. 2012, 23, 310–318. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.; Li, L.; Zhou, D.J. Unconventional evaluation methods for interface bonding strength of layered materials. Mater. Rep. 2017, 31, 59–67. [Google Scholar] [CrossRef]
- Jessica, F.; Jan, H.; Alexander, G.; Nina, R.; Silvia, B. Tissue-scale biomechanical testing of brain tissue for the calibration of nonlinear material models. Curr. Protoc. 2022, 2, 1–73. [Google Scholar] [CrossRef]
- Justin, S.; Abbas, S.; Jonathan, B.; Donald, B.P. MR validation of soft tissue mimicing phantom deformation as modeled by nonlinear fifinite element analysis. Med. Phys. 2002, 29, 65–72. [Google Scholar] [CrossRef]
- Sun, J.; Bhushan, B. Hierarchical structure and mechanical porperties of nacre: A review. RSC Adv. 2012, 2, 7617–7632. [Google Scholar] [CrossRef]
- Yamamoto, Y.; Nishimura, T.; Sugawara, A.; Inoue, H.; Nagasawa, H.; Kato, T. Effects of peptides on CaCO3 Crystallization: Mineralization properties of an acidic peptide isolated from exoskeleton of crayfish and its derivatives. Cryst. Growth Des. 2008, 8, 4062–4065. [Google Scholar] [CrossRef]
- Fu, H.; Chen, J.L.; Wang, K. Effects of heat treatments on the interfacial crystallization and mechanical properties of carbon fiber/polyamide 6 composites. Acta Mater. Compos. Sinica. 2013, 5, 816–822. [Google Scholar] [CrossRef]
- Jia, P.R.; Jiao, G.P. Stress analyses of fiber-matrix interface and interface failure. Acta Mater. Compos. Sinica. 1999, 16, 93–97. [Google Scholar]
- Bi, J.Z.; Lu, C.M.; Wang, Y.Z. Microstructure experiment and calcination characteristics of shells. J. Chem. Ind. Eng. China 2002, 53, 1228–1232. [Google Scholar]
- Gerlien, V.; Hendrik, H.; Katrin, K.; Kerth, G.; Brede, M.; Haase, M. Testing the adaptive value of gastropod shell morphology to flow: A multidisciplinary approach based on morphometrics, computational fluid dynamics and a flow tank experiment. Zool Lett. 2019, 5, 5. [Google Scholar] [CrossRef]
- Ján, B. Estimation of young’s modulus of elesticity by the form finding of grid shell structures by the dynamic relaxation method. Slovak J. Civil. Eng. 2015, 23, 25–30. [Google Scholar] [CrossRef] [Green Version]
- Ye, T.; Cao, Y.W.; Wang, Y. Realizing ultrahigh modulus and high strength of macroscopic graphene oxide papers through crosslinking of mussel-inspired polymers. Adv. Mater. 2013, 25, 2980–2983. [Google Scholar] [CrossRef]
- Xu, Z.L. Elasticity; Higher Education Press: Beijing, China, 2016. [Google Scholar]
- Zhao, T.; Ren, L.Q.; Liu, Q.P.; Liu, T.R. Morphological and confocal laser scanning microscopic investigations of the adductor muscle-shell interface in scallop. Microsc. Res. Tech. 2015, 78, 761–770. [Google Scholar] [CrossRef] [PubMed]
- Timoshenko, S.P.; Goodier, J.N. Theory of Elasticity, 3rd ed.; Mc Grow-Hill: New York, NY, USA, 1970. [Google Scholar]
- Drozdov, A.D. Finite Elasticity and Viscoelasticity; World Scientific: Singapore, 1996. [Google Scholar]
- Yan, X.Q. Automated simulation of fatigue crack propagation for two-dimensional linear elastic fracture mechanics problems by boundary element method. Eng. Fract. Mech. 2007, 74, 2225–2246. [Google Scholar] [CrossRef]
- Li, J.Q.; Liu, H.Z.; Wang, Z.M. Review on the linearcostitutive equation and its dynamics application stoviscoelastic materials. J. Vib. Shock. 2005, 24, 116–121. [Google Scholar] [CrossRef]
- Eric, F.; Gilles, L. Identification of the parameters of an elastic material model using the constitutive equation gap method. Comput. Mech. 2010, 46, 521–531. [Google Scholar] [CrossRef]
- Lu, X.P.; Zhang, H.W.; Liang, H.Y. Aninvestigation of functional relationship between potential and displacement Love numbers. Sci. Surv. Mapp. 2009, 34, 36–38. [Google Scholar] [CrossRef]
- Yang, E.J.; Yang, X.F.; Dong, Q.; Li, J. Conditional diagnosability of hypermeshes under the comparison model. Inf. Process. Lett. 2011, 111, 188–193. [Google Scholar] [CrossRef]
- Yang, E.J.; Yang, X.F.; Dong, Q.; Li, J. Conditional diagnosability of hypermesh optical multiprocessor systems under the PMC model. Int. J. Comput. Math. 2011, 88, 2275–2284. [Google Scholar] [CrossRef]
- Chaudhari, S.V.; Chakrabarti, M.A. Modeling of concrete for nonlinear analysis Using Finite Element Code ABAQUS. Int. J. Comput. 2012, 44, 14–18. [Google Scholar]
- Diao, X.M. Experimental Study on Normal and Biomechanical Properties of Finger Flexor after Anastomosis; Jinlin University: Jinlin, China, 2006; pp. 6–18. [Google Scholar]
- Yang, W. Investigation on the Mechanical Properties of Saxidomus Purpuratus Shells; Northeast University: Shenyang, China, 2010; pp. 79–89. [Google Scholar]
- Nhung, N.; Anthony, M.W. Nonlinear, finite deformation, finite element analysis. Z. Angew. Math. Phys. 2016, 67, 35–58. [Google Scholar] [CrossRef]
- Gong, X.; Chang, J.; Li, D.T.; Sun, Z.H. Ultra high-pressure preservation technology and parameter optimization of scallop. Ekoloji. 2018, 27, 1697–1704. [Google Scholar]
- Gong, X. Experimental study on texture changes of scallop shell under ultra-high pressure. Digit. Print. 2020, 1, 64–76. [Google Scholar] [CrossRef]
- Gong, X. Experimental study on structural change of scallop shell connecting interface under ultra high pressure. Packag. Eng. 2021, 42, 19–24. [Google Scholar] [CrossRef]
| Mechanical Parameters | Adductor Muscle | Shells |
|---|---|---|
| Young’s modulus/MPa | 25 | 65,000 |
| Poisson’s ratio | 0.45 | 0.25 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chang, J.; Gong, X.; Zhang, Y.; Sun, Z.; Xia, N.; Zhang, H.; Wang, J.; Zhang, X. Simulation Analysis of Organic–Inorganic Interface Failure of Scallop under Ultra-High Pressure. Coatings 2022, 12, 963. https://doi.org/10.3390/coatings12070963
Chang J, Gong X, Zhang Y, Sun Z, Xia N, Zhang H, Wang J, Zhang X. Simulation Analysis of Organic–Inorganic Interface Failure of Scallop under Ultra-High Pressure. Coatings. 2022; 12(7):963. https://doi.org/10.3390/coatings12070963
Chicago/Turabian StyleChang, Jiang, Xue Gong, Yinglei Zhang, Zhihui Sun, Ning Xia, Huajiang Zhang, Jing Wang, and Xiang Zhang. 2022. "Simulation Analysis of Organic–Inorganic Interface Failure of Scallop under Ultra-High Pressure" Coatings 12, no. 7: 963. https://doi.org/10.3390/coatings12070963
APA StyleChang, J., Gong, X., Zhang, Y., Sun, Z., Xia, N., Zhang, H., Wang, J., & Zhang, X. (2022). Simulation Analysis of Organic–Inorganic Interface Failure of Scallop under Ultra-High Pressure. Coatings, 12(7), 963. https://doi.org/10.3390/coatings12070963







