Changes in the Structural Parameters and Effective Magnetic Moment of Eu2−xCexCuO4+α−δ by Zn Substitution
Abstract
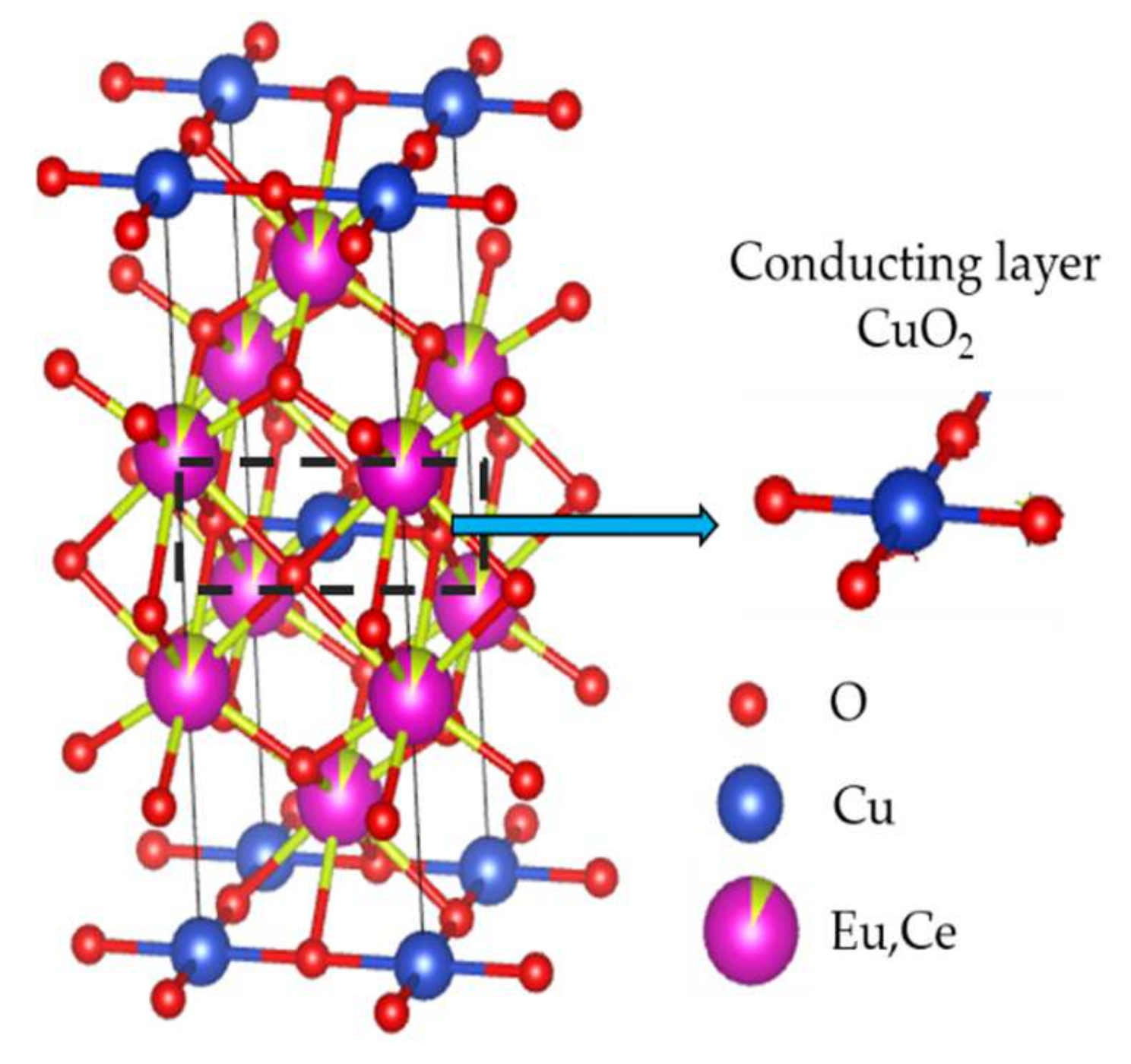
:1. Introduction
2. Materials and Methods
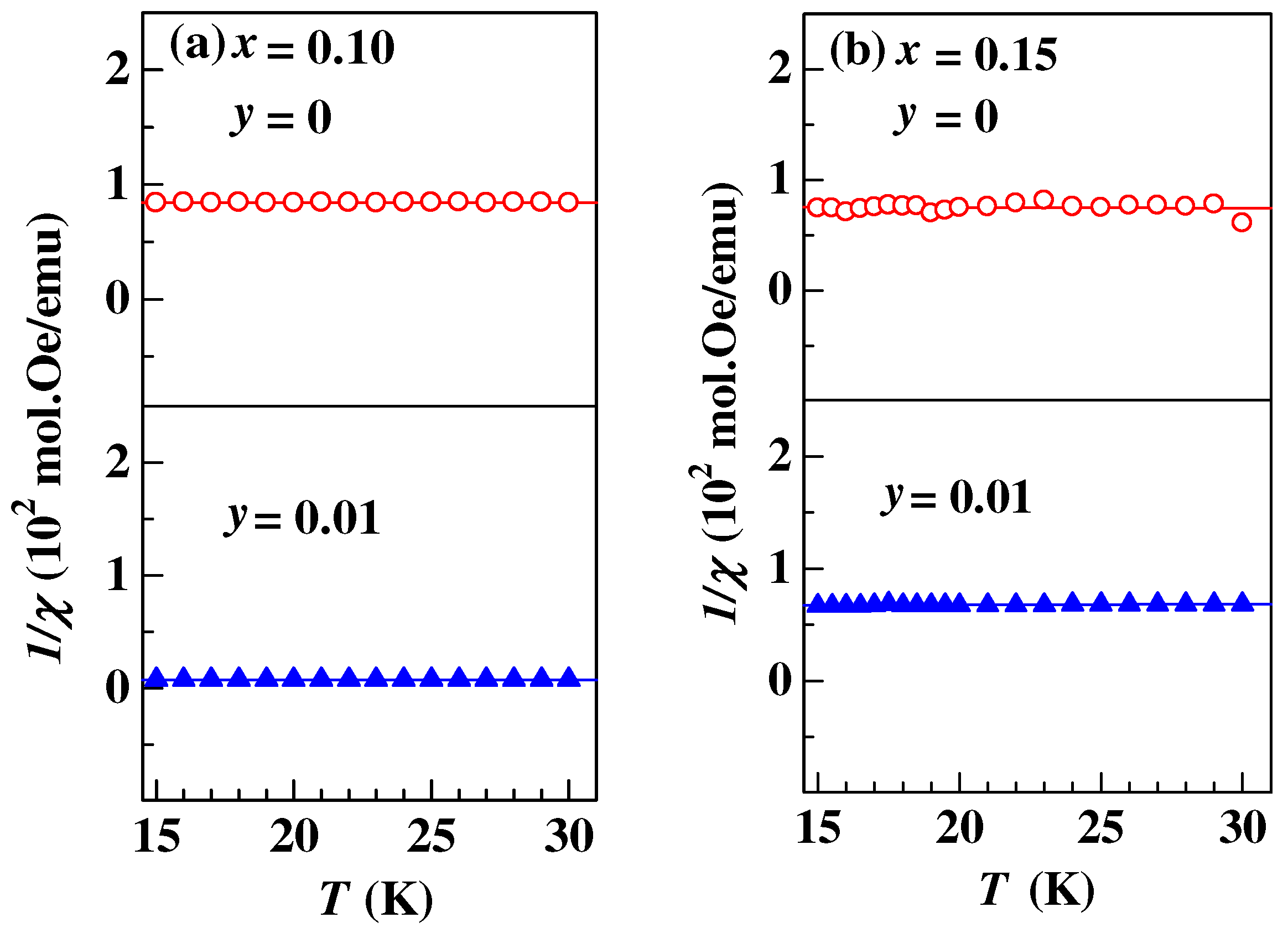
3. Results and Discussion
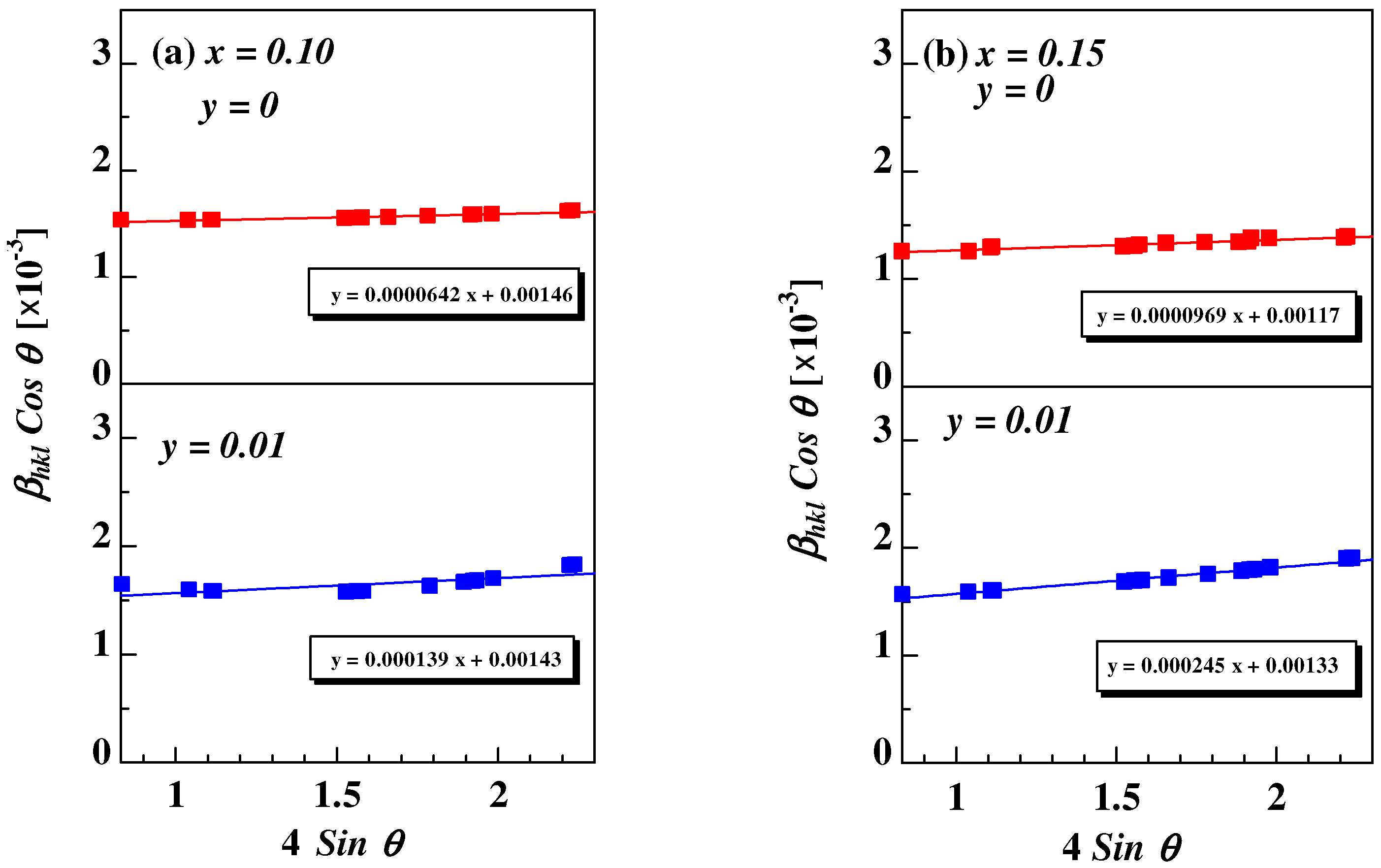
3.1. X-ray Diffraction Analysis
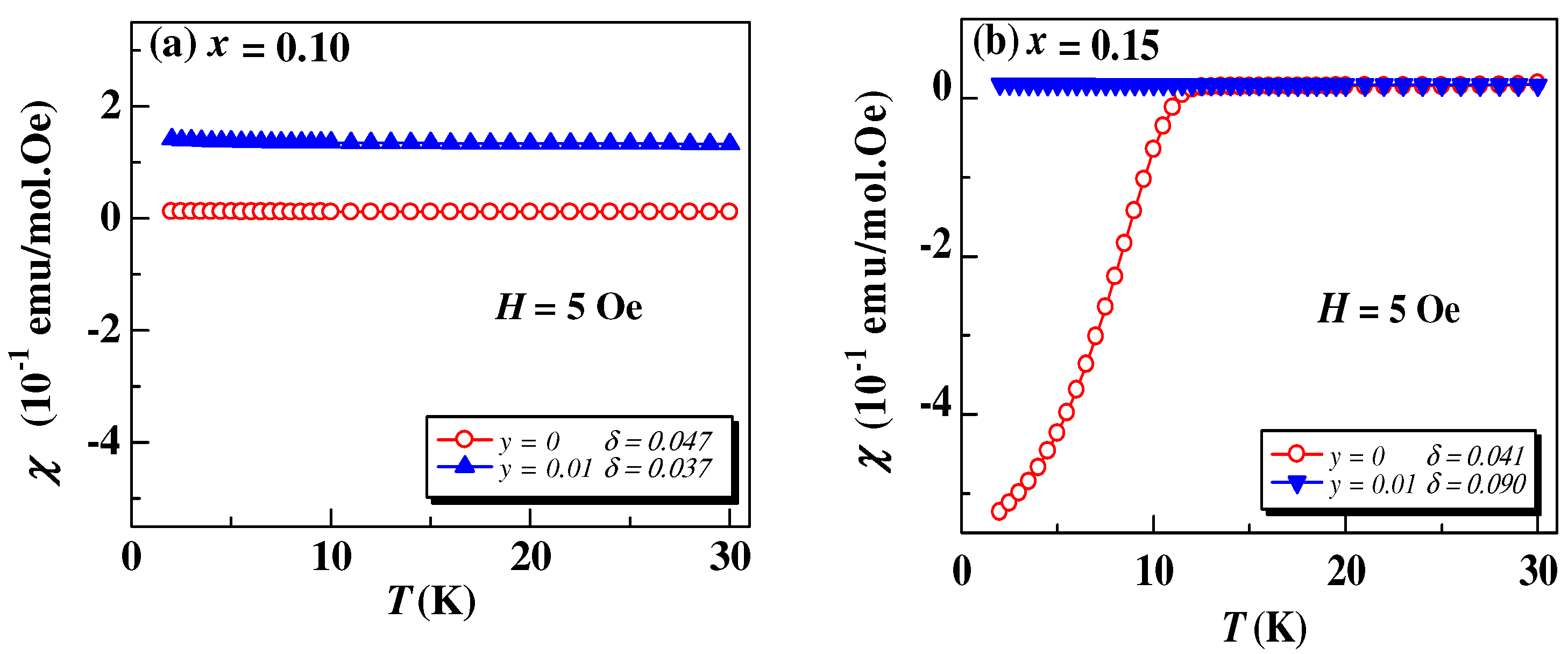
3.2. Susceptibility Analysis
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Niedermayer, C.; Bernhard, C.; Blasius, B.; Golnik, A.; Moodenbaugh, A.; Budnick, J. Common phase diagram for antiferromagnetism in La2−xSrxCuO4 and Y1−xCaxBa2Cu3O6 as seen by muon spin rotation. Phys. Rev. Lett. 1998, 80, 3843. [Google Scholar] [CrossRef]
- Yakhmi, J.V.; Gopalakrishnan, I.K.; Gupta, L.C.; Umarji, A.M.; Vijayaraghavan, R.; Iyer, R.M. Bulk superconductivity at 36 K in La1.8Sr0.2CuO4. Phys. Rev. B 1987, 35, 7122–7123. [Google Scholar] [CrossRef]
- Fournier, P. T′ and infinite-layer electron-doped cuprates. Phys. C Supercond. Its Appl. 2015, 514, 314–338. [Google Scholar] [CrossRef]
- Takagi, H.; Uchida, S.; Tokura, Y. Superconductivity produced by electron doping in CuO2-layered compounds. Phys. Rev. Lett. 1989, 62, 1197–1200. [Google Scholar] [CrossRef]
- Dagan, Y.; Greene, R.L. Quantum criticality in the electron doped cuprates. Phys. C Supercond. Its Appl. 2007, 460–462, 1109–1110. [Google Scholar] [CrossRef]
- Panagopoulos, C.; Petrovic, A.P.; Hillier, A.D.; Tallon, J.L.; Scott, C.A.; Rainford, B.D. Exposing the spin-glass ground state of the nonsuperconducting La2−xSrxCu1−yZnyO4 high-Tc oxide. Phys. Rev. B Condens. Matter Mater. Phys. 2004, 69, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Risdiana, R.; Tanabe, Y.; Omori, K.; Suzuki, T.; Watanabe, I.; Koda, A.; Higemoto, W.; Koike, Y. Cu spin dynamics in the overdoped regime of La2−xSrxCu1−yZnyO4 probed by muon spin relaxation. Phys. Rev. B 2008, 77, 054516. [Google Scholar] [CrossRef] [Green Version]
- Tanabe, Y.; Adachi, T.; Noji, T.; Koike, Y. Superconducting volume fraction in overdoped regime of La2−xSrxCuO4: Implication for phase separation from magnetic-susceptibility measurement. Phys. Soc. Japan 2005, 74, 2893–2896. [Google Scholar] [CrossRef] [Green Version]
- Croft, T.P.; Lester, C.; Senn, M.S.; Bombardi, A.; Hayden, S.M. Charge density waves fluctuations in La2−xSrxCuO4 and their competition with superconductivity. Phys. Rev. B 2014, 89, 224513. [Google Scholar] [CrossRef] [Green Version]
- Nakano, T.; Momono, N.; Matsuzaki, T.; Nagata, T.; Yokoyama, M.; Oda, M.; Ido, M. Effects of Zn substitution on magnetic properties and superconductivity in La2-xSrxCuO4. Phys. C Supercond. its Appl. 1999, 317–318, 575–578. [Google Scholar] [CrossRef]
- Tarascon, J.M.; Greene, L.H.; Barboux, P.; McKinnon, W.R.; Hull, G.W.; Orlando, T.P.; Delin, K.A.; Foner, S.; McNiff, J.E.J. 3d-metal doping of the high-temperature superconducting perovskites La-Sr-Cu-O and Y-Ba-Cu-O. Phys. Rev. B 1987, 36, 8393. [Google Scholar] [CrossRef] [Green Version]
- Tranquada, J.M.; Sternlieb, B.J.; Axe, J.D.; Uchida, S. Evidence for stripe correlations of spins and holes in copper oxide. Nature 1995, 375, 561–563. [Google Scholar] [CrossRef]
- Koike, Y.; Kobayashi, A.; Kawaguchi, T.; Kato, M.; Noji, T.; Ono, Y.; Hikita, T.; Saito, Y. Anomalous x dependence of Tc and possibility of low-temperature structural phase transition in La2−xSrxCu0.99M0.01O4 (M = Ni, Zn, Ga). Solid State Commun. 1992, 82, 889–893. [Google Scholar] [CrossRef]
- Koike, Y.; Takeuchi, S.; Hama, Y.; Sato, H.; Adachi, T.; Kato, M. Possibility of the pinning of the stripe pattern of holes and spins by Zn in La2−xSrxCu1−yZnyO4 with x ~ 0.115. Physica C 1997, 1233, 282–287. [Google Scholar] [CrossRef]
- Koike, Y.; Akoshima, M.; Adachi, T.; Kakinuma, N.; Noji, T.; Ono, Y.; Nishizaki, T.; Kobayashi, N.; Watanabe, I.; Nagamine, K. 1/8 problems in the La-, Bi- and Y-based cuprates and new anomalies in the overdoped region of the La-based cuprate. Int. J. Mod. Phys. B 1999, 13, 3546. [Google Scholar] [CrossRef]
- Adachi, T.; Noji, T.; Sato, H.; Koike, Y.; Nishizaki, T.; Kobayashi, N. Transport anomalies in the Zn-substituted La2−xSrxCu1−yZnyO4 with x ~ 0.115; Possibility of the pinning of CDW and SDW by Zn. J. Low Temp. Phys. 1999, 117, 1151. [Google Scholar] [CrossRef]
- Koike, Y.; Mikuni, H.; Watanabe, I.; Adachi, T.; Yairi, S.; Nagamine, K. 1/8 anomaly in the excess-oxygen-doped La2−xAxCuO4+δ (A = Nd, Bi, Pr). J. Low Temp. Phys. 2003, 837, 131. [Google Scholar]
- Mikuni, H.; Adachi, T.; Yairi, S.; Kato, M.; Koike, Y.; Watanabe, I.; Nagamine, K. 1/8 anomaly in the excess-oxygen-doped La1.8Nd0.2Cu1−yZnyO4+δ. Phys. Rev. B 2003, 68, 024524. [Google Scholar] [CrossRef] [Green Version]
- Adachi, T.; Yairi, S.; Koike, Y.; Watanabe, I.; Nagamine, K. Muon-spin-relaxation and magnetic-susceptibility studies of the effects of the magnetic impurity Ni on the Cu-spin dynamics and superconductivity in La2−xSrxCu1−yNiyO4 with x = 0.13. Phys. Rev. B 2004, 70, 060504. [Google Scholar] [CrossRef] [Green Version]
- Adachi, T.; Yairi, S.; Takahashi, K.; Koike, Y.; Watanabe, I.; Nagamine, K. Muon spin relaxation and magnetic susceptibility studies of the effects of nonmagnetic impurities on the Cu spin dynamics and superconductivity in La2−xSrxCu1−yZnyO4 around x = 0.115. Phys. Rev. B 2004, 69, 184507. [Google Scholar] [CrossRef] [Green Version]
- Adachi, T.; Koike, Y.; Risdiana; Oki, N.; Mikuni, H.; Watanabe, I.; Pratt, F.L. μSR study of effects of rare-earth moments on the 1/8 anomaly in the excess-oxygen-doped high-Tc cuprates La2−xAxCuO4+δ (A = Eu, Pr). Physica C 2007, 1169, 460–462. [Google Scholar] [CrossRef]
- Risdiana, M.; Manawan, M.; Safriani, L.; Saragi, T.; Aprilia, A.; Syakir, N.; Hidayat, S.; Bahtiar, A.; Fitlilawati, F.; Siregar, R.E. Study of structure and resistivity of electron-doped superconducting cuprates Eu1.85Ce0.15Cu1−yZnyO4+α−δ. J. Phys. Conf. Ser. 2018, 1091, 012019. [Google Scholar] [CrossRef]
- Adachi, T.; Mori, Y.; Takasahi, A.; Kato, M.; Nishizaki, T.; Sasaki, T.; Kobayashi, N.; Koike, Y. Evolution of the electronic state through the reduction annealing in electron-doped Pr1.3−xLa0.7CexCuO4+δ (x = 0.10) single crystals: Antiferromagnetism, kondo effect, and superconductivity. J. Phys. Soc. Japan 2013, 82, 063713. [Google Scholar] [CrossRef] [Green Version]
- Risdiana, T.; Adachi, N.; Oki, Y.; Koike, T.; Suzuki, T.; Watanabe, I. Muon spin relaxation study of the Cu spin dynamics in electron-doped high-Tc superconductor Pr0.86LaCeO0.14Cu1−yZnyO4. Phys. Rev. B 2010, 82, 014506. [Google Scholar] [CrossRef] [Green Version]
- Risdiana, M.; Manawan, M.; Safriani, L.; Saragi, T.; Somantri, W.A.; Aprilia, A.; Syakir, N.; Hidayat, S.; Bahtiar, A.; Fitrilawati, F.; et al. Study of transport and magnetic properties of electron-doped superconducting cuprates Eu1.85Ce0.15Cu1−yZnyO4+α−δ. Phys. C Supercond. Its Appl. 2019, 557, 41–43. [Google Scholar] [CrossRef]
- Syakuur, M.A.; Maryati, Y.; Saragi, T.; Risdiana, R. The effect of partial substitution of non-magnetic impurity Zn on the magnetic moments of Eu1.88Ce0.12Cu1−yZnyO4+α−δ. Mater. Sci. Forum 2021, 1028, 15–20. [Google Scholar] [CrossRef]
- Armitage, N.P.; Fournier, P.; Greene, R.L. Progress and perspective on electron-doped cuprates. Rev. Mod. Phys. 2010, 82, 2421–2487. [Google Scholar] [CrossRef]
- Kern, A.; Coelho, A.A.; Cheary, R.W. Convolution Based Profile Fitting. Springer Ser. Mater. Sci. 2004, 28, 17–50. [Google Scholar]
- Toby, B.H. R factors in Rietveld analysis: How good is good enough? Powder Differ. 2006, 21, 67–70. [Google Scholar] [CrossRef] [Green Version]
- Uzumaki, T.; Hashimoto, K.; Kamehara, N. Raman scattering and X-ray diffraction study in layered cuprates. Phys. C Supercond. Its Appl. 1992, 202, 175–187. [Google Scholar] [CrossRef]
- Muniz, F.T.L.; Miranda, M.A.R.; Morilla dos Santos, C.; Sasaki, J.M. The Scherrer Equation and The Dynamical Theory of X-ray Diffraction. Acta Crystallogr. Sect. A Found. Adv. 2016, 72, 385–390. [Google Scholar] [CrossRef] [PubMed]
- Mote, V.; Purushotham, Y.; Dole, B. Williamson-Hall analysis in estimation of lattice strain in nanometer-sized ZnO particles. J. Theor. Appl. Phys. 2012, 6, 2–9. [Google Scholar] [CrossRef] [Green Version]
- Zhu, J.; Zhao, Z.; Xiao, D.; Li, J.; Yang, X.; Wu, Y. Characterization and catalytic activity in NO decomposition of La2−xSrxCuO4 (0 ≤ x ≤1) compounds with T* phase structure. Mater. Chem. Phys. 2005, 94, 257–260. [Google Scholar] [CrossRef]
- Sukumar, M.; John Kennedy, L.; Judith Vijaya, J.; Al-Najar, B.; Bououdina, M. Facile microwave assisted combustion synthesis, structural, optical and magnetic properties of La2−xSrxCuO4 (0 ≤ x ≤ 0.5) perovskite nanostructures. J. Magn. Magn. Mater. 2018, 465, 48–57. [Google Scholar] [CrossRef]
- Renaudin, G.; Gomes, S.; Nedelec, J.M. First-row transition metal doping in calcium phosphate bioceramics: A detailed crystallographic study. Materials 2017, 10, 92. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hira, U.; Sher, F. Structural, magnetic and high-temperature thermoelectric properties of La0.4Bi0.4Ca0.2Mn1−xCOxO3 0 ≤ x ≤ 0.3 perovskites. Magn. Magn. Mater. 2017, 452, 64–72. [Google Scholar] [CrossRef]
- Yamada, K.; Kudo, E.; Endoh, Y.; Hidaka, Y.; Oda, M.; Suzuki, M.; Murakami, T. The effect of the heat treatments on the antiferromagnetism in La2CuO4−δ single crystals. Solid State Commun. 1987, 64, 753–756. [Google Scholar] [CrossRef]
- Risdiana; Safriani, L.; Somantri, W.A.; Saragi, T.; Adachi, T.; Kawasaki, I.; Watanaber, I.; Koike, Y. Possible existence of the stripe correlations in electron-doped superconducting cuprates Eu1.85Ce0.15Cu1−yNiyO4+α−δ studied by muon-spin-relaxation. Adv. Mater. Res. 2014, 896, 354–357. [Google Scholar]
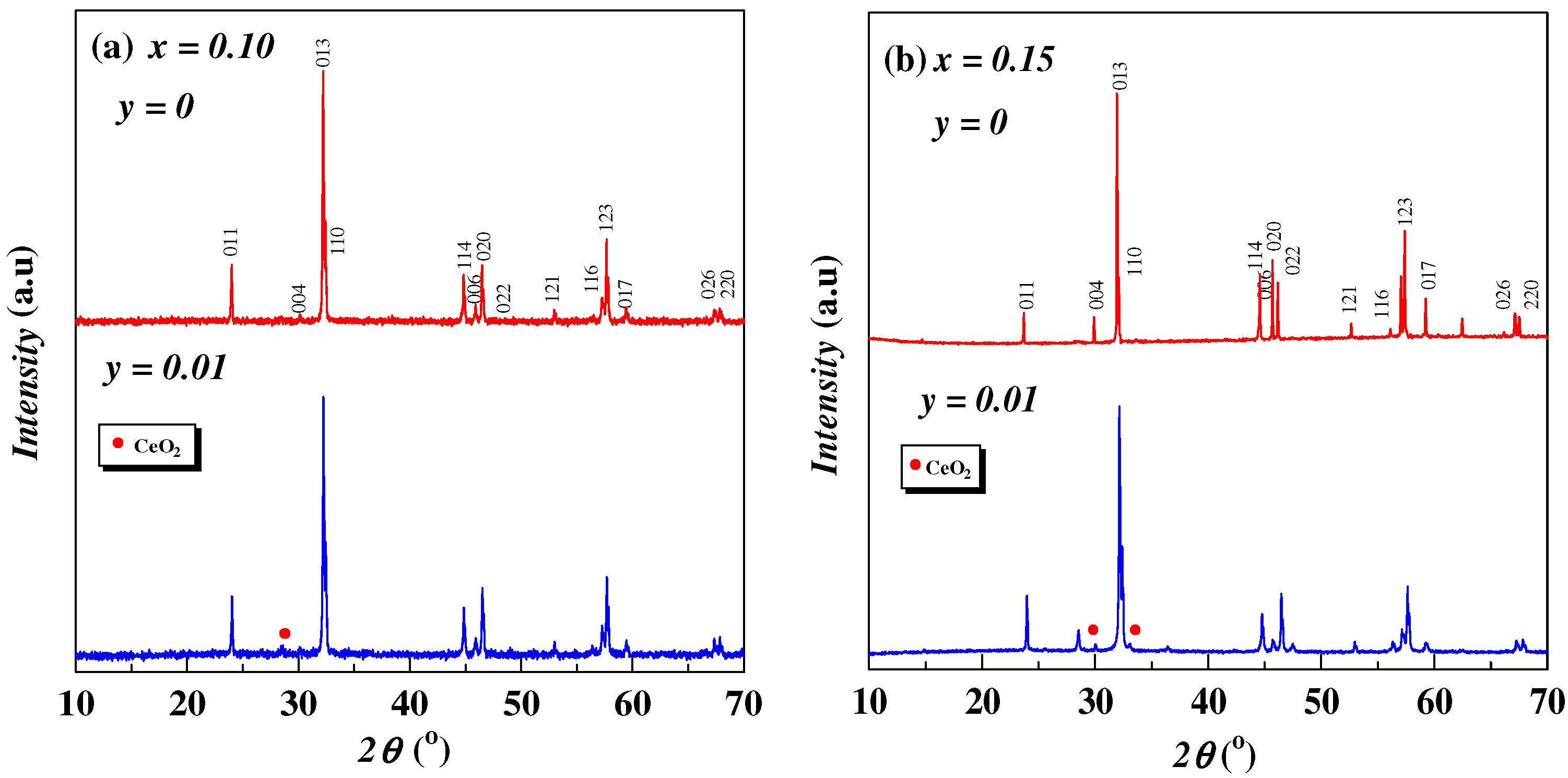
| Samples Eu2−xCexCu1−yZnyO4+α−δ | x = 0.10 | x = 0.15 | ||
|---|---|---|---|---|
| y = 0 | y = 0.01 | y = 0 | y = 0.01 | |
| Space group | I4/mmm | I4/mmm | I4/mmm | I4/mmm |
| Structure | Tetragonal | Tetragonal | Tetragonal | Tetragonal |
| Lattice Parameters | ||||
| 3.9056 (1) | 3.9058 (1) | 3.9070 (1) | 3.9033 (1) | |
| 11.8656 (5) | 11.8721 (6) | 11.8369 (3) | 11.8914 (3) | |
| 180.996 (10) | 181.118 (11) | 180.693 (8) | 181.176 (7) | |
| Bond Length | ||||
| 1.95281 (6) | 1.95293 (8) | 1.95166 (4) | 1.95354 (5) | |
| 2.29122 (6) | 2.29167 (7) | 2.29032 (5) | 2.29161 (4) | |
| 2.63424 (7) | 2.63498 (9) | 2.63190 (5) | 2.63597 (5) | |
| Crystallite Size | ||||
| Debye–Scherrer (D (nm)) | 88.61 (1) | 84.02 (3) | 104.66 (2) | 80.66 (5) |
| W-H Plot (D (nm)) | 94.83 (5) | 97.12 (25) | 118.56 (5) | 104.43 (1) |
| 0.642 × 10−4 | 0.139 × 10−4 | 0.970 × 10−4 | 0.245 × 10−4 | |
| Reliability Factors | ||||
| Goodness of Fit (GoF) | 1.1 | 1.2 | 1.4 | 1.1 |
| x | y | |||
|---|---|---|---|---|
| 0.10 | 0 | 0.06 | 0.02 | 0.01 |
| 0.01 | 0.01 | 0.02 | 0.01 | |
| 0.15 | 0 | 0.02 | 0.01 | 0.02 |
| 0.01 | 0.05 | 0.02 | 0.06 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pratama, R.; Saragi, T.; Maulana, T.; Winarsih, S.; Maryati, Y.; Syakuur, M.A.; Widyaiswari, U.; Sari, D.P.; Manawan, M.; Risdiana, R. Changes in the Structural Parameters and Effective Magnetic Moment of Eu2−xCexCuO4+α−δ by Zn Substitution. Coatings 2022, 12, 789. https://doi.org/10.3390/coatings12060789
Pratama R, Saragi T, Maulana T, Winarsih S, Maryati Y, Syakuur MA, Widyaiswari U, Sari DP, Manawan M, Risdiana R. Changes in the Structural Parameters and Effective Magnetic Moment of Eu2−xCexCuO4+α−δ by Zn Substitution. Coatings. 2022; 12(6):789. https://doi.org/10.3390/coatings12060789
Chicago/Turabian StylePratama, Rosaldi, Togar Saragi, Trisna Maulana, Suci Winarsih, Yati Maryati, Muhammad Abdan Syakuur, Utami Widyaiswari, Dita Puspita Sari, Maykel Manawan, and Risdiana Risdiana. 2022. "Changes in the Structural Parameters and Effective Magnetic Moment of Eu2−xCexCuO4+α−δ by Zn Substitution" Coatings 12, no. 6: 789. https://doi.org/10.3390/coatings12060789
APA StylePratama, R., Saragi, T., Maulana, T., Winarsih, S., Maryati, Y., Syakuur, M. A., Widyaiswari, U., Sari, D. P., Manawan, M., & Risdiana, R. (2022). Changes in the Structural Parameters and Effective Magnetic Moment of Eu2−xCexCuO4+α−δ by Zn Substitution. Coatings, 12(6), 789. https://doi.org/10.3390/coatings12060789








