Simulation of Resonant Cavity-Coupled Colloidal Quantum-Dot Detectors with Polarization Sensitivity

Abstract

Infrared detectors with polarization sensitivity could extend the information dimension of the detected signals and improve target recognition ability. However, traditional infrared polarization detectors with epitaxial semiconductors usually suffer from low extinction ratio, complexity in structure and high cost. Here, we report a simulation study of colloidal quantum dot (CQD) infrared detectors with monolithically integrated metal wire-grid polarizer and optical cavity. The solution processibility of CQDs enables the direct integration of metallic wire-grid polarizers with CQD films. The polarization selectivity of HgTe CQDs with resonant cavity-enhanced wire-grid polarizers are studied in both short-wave and mid-wave infrared region. The extinction ratio in short-wave and mid-wave region can reach up to 40 and 60 dB, respectively. Besides high extinction ratio, the optical cavity enhanced wire-grid polarizer could also significantly improve light absorption at resonant wavelength by a factor of 1.5, which leads to higher quantum efficiency and better spectral selectivity. We believe that coupling CQD infrared detector with wire-grid polarizer and optical cavity can become a promising way to realize high-performance infrared optoelectronic devices.

1. Introduction

Polarization imaging technology plays an increasingly important role in target recognition and detection. The polarization state of light results from the interaction between light and objects at the microscopic level. When the surface topography, states and observation orientation are different, the specular polarization information of the object will change accordingly [1,2]. Therefore, when the temperature difference between the observed objects and the surrounding environment is relatively small, infrared thermal imaging fails to give high-contrast images, whereas polarization imaging can provide a new information dimension for target discrimination with high contrast between the targets and the surrounding background [3,4]. Therefore, polarization imaging technology has become an powerful imaging technology besides traditional intensity imaging and spectral imaging, which has a wide prospective application in military infrared anti-counterfeiting equipment [5], remote sensing, astronomical observation [6] and medical diagnosis [7].

Traditional polarization imaging techniques are mainly divided into time-sharing polarization imaging [8,9], amplitude polarization imaging and aperture polarization imaging. However, they rely on moving optics, registration and sophisticated calibration procedures, which greatly increase their complexity and cost.

With the increasing demands for high sensitivity, low cost and scalable polarized infrared detector equipment, there is a trend to directly couple the polarizers such as metal wire-grid polarizer with infrared detector on pixel level. High sensitivity, compact structure and wide bandwidth have been demonstrated with different processing technology [10,11]. Despite their high performance, these detectors are still limited by the high cost of epitaxial semiconductors [12]. It is advantageous to find a method that has both high polarization sensitivity and low cost. With the continuous progress, the maximum absorption wavelength of colloidal quantum dots (CQDs) has been extended from near infrared to longer wavelength, which provides a promising alternative for bulk infrared semiconductors such as HgCdTe, InSb and type II superlattice. Among all colloidal nano materials, mercury telluride (HgTe) CQDs has shown the highest spectral tunability so far; from short-wave infrared and mid-wave infrared to long-wave infrared and terahertz (THz) regions, we can control the reaction time and temperature to obtain colloidal quantum dots with different particle sizes for different infrared regions [13]. The solution workability and broad spectral tunability of colloidal quantum dots inspire a variety of inexpensive, high-performance optoelectronic devices [14]. Therefore, coupling metal nanowire-grid polarizer with colloidal quantum dot detector seems to be a suitable method to solve this challenge.

In this work, a high-performance polarization-sensitive infrared detector is designed by integrating HgTe CQDs photovoltaic detector with wire-grid polarizer and optical cavity. Finite element analysis of HgTe CQDs polarization-sensitive detectors was systematically conducted covering short-wave infrared and mid-wave infrared. The simulation results show that this detector has high polarization selectivity in both short-wave infrared and mid-wave infrared. The extinction ratio in short-wave and mid-wave region can reach up to 40 and 60 dB, respectively. Besides high extinction ratio, the optical cavity enhanced wire-grid polarizer could also significantly improve light absorption at resonant wavelength by a factor of 1.5, which leads to higher quantum efficiency and better spectral selectivity.

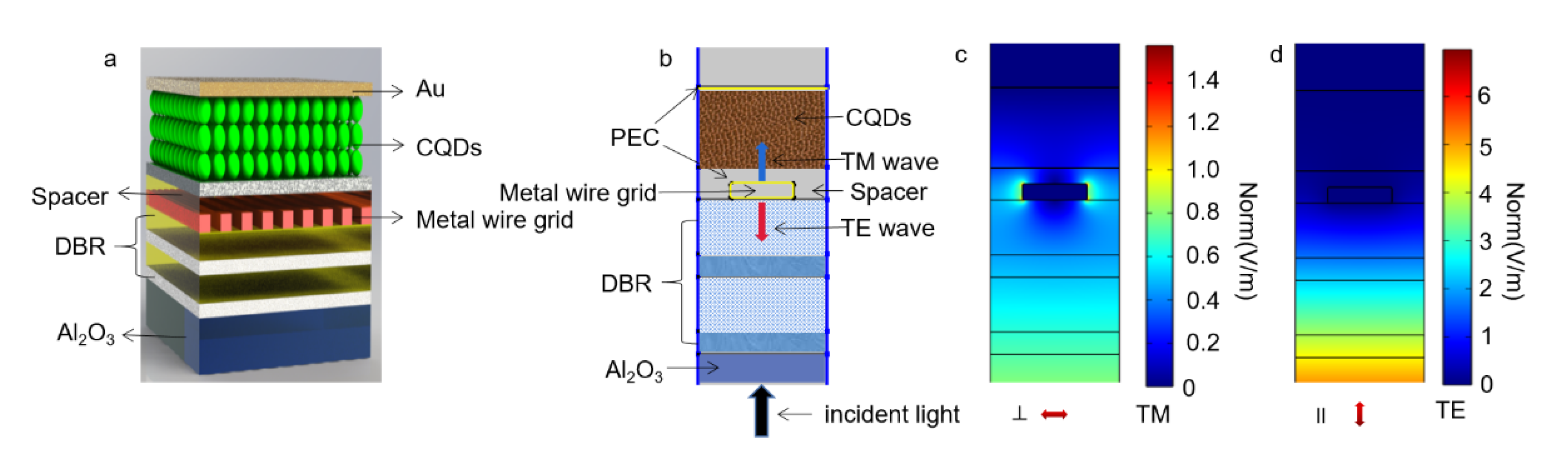
2. Modeling and Simulation

The structure of the proposed HgTe CQDs detector with resonant cavity-coupled wire-grid polarizer is illustrated in Figure 1a. Distributed Bragg reflectors (DBRs) are set on an Al₂O₃ substrate, on top of which subwavelength wire-grid polarizers are added. The reflectivity of DBR is determined by the number of the alternating layers and their difference in refractive index [15]. The polarization selectivity of the metal wire grid is originated from the structural asymmetry. The transverse wave (TE polarized light) in which the electric vector is parallel to the direction of the wire grids can excite the electrons to oscillate along the grid, so TE polarized light will be reflected, and the transverse magnetic wave (TM polarized light) with electric vector perpendicular to the wires cannot excite free electron oscillations and therefore shows high optical transmission [12]. On top of the metal wire-grid polarizer, HgTe CQDs photodiodes are constructed with indium tin oxide and gold as bottom and top contacts. The DBR and top gold contact forms a resonant cavity.

COMSOL Multiphysics is used to conduct the simulation in our study. To save computation resources, a two-dimensional (2D) simulation is used, as shown in Figure 1b. The light is incident from the bottom with controlled power of 1 W. The left and right sides are set as “Periodic boundary condition”. The substrate material is chosen to be Al₂O₃ with a refractive index of 1.3 + 0i. Low refraction SiO₂ material with a refractive index of 1.4 + 0i and high refractive index Si material with a refractive index of 3.42 + 0i are selected for Bragg mirror, and SiO₂ material is also selected as optical spacer. For HgTe CQDs, the refractive index is 2.3 + 0.1i [16], and the rest of the model is set to be air with a refractive index of 1 + 0i. The wire-grid polarizer and the top electrode are set as perfect electrical conductors (PEC). The electric field distribution of TM wave and TE wave obtained by simulation is shown in Figure 1c,d, and it can be seen that the structure has strong polarization selectivity. The index of refraction of CQDs films is measured before simulation. Based on the measured index of refraction, the simulation fraction f_simulation can be estimated by using different effective medium approximations, including the Maxwell-Garnett (MG) model and Bruggeman (BG) model:

$$\mathrm{MG}\mathrm{model}:\frac{{\epsilon }_{eff}-{\epsilon }_{CQD}}{{\epsilon }_{eff}+2{\epsilon }_{CQD}}=(1-f_{simulation})\frac{{\epsilon }_m-{\epsilon }_{CQD}}{{\epsilon }_m+2{\epsilon }_{CQD}}$$

(1)

$$\mathrm{BG}\mathrm{model}:f_{simulation}\frac{{\epsilon }_{CQD}-{\epsilon }_{eff}}{{\epsilon }_{CQD}+2{\epsilon }_{eff}}+(1-f_{simulation})\frac{{\epsilon }_m-{\epsilon }_{eff}}{{\epsilon }_m+2{\epsilon }_{eff}}=0$$

(2)

where ε_eff is the effective dielectric constant, which is obtained by the measured index of refraction n, ε_CQDs is the dielectric constant of CQDs, and ε_m is the dielectric constant of medium. For HgTe, ε_CQDs is taken as 15.1. ε_m is taken to be 1, since the CQDs are surrounded by air. According to the thickness of colloidal quantum dot film, the approximate refractive index is 2.3 + 0.1i; in previous studies, this value has also been proved to be reliable [14,16].

3. Results and Discussions

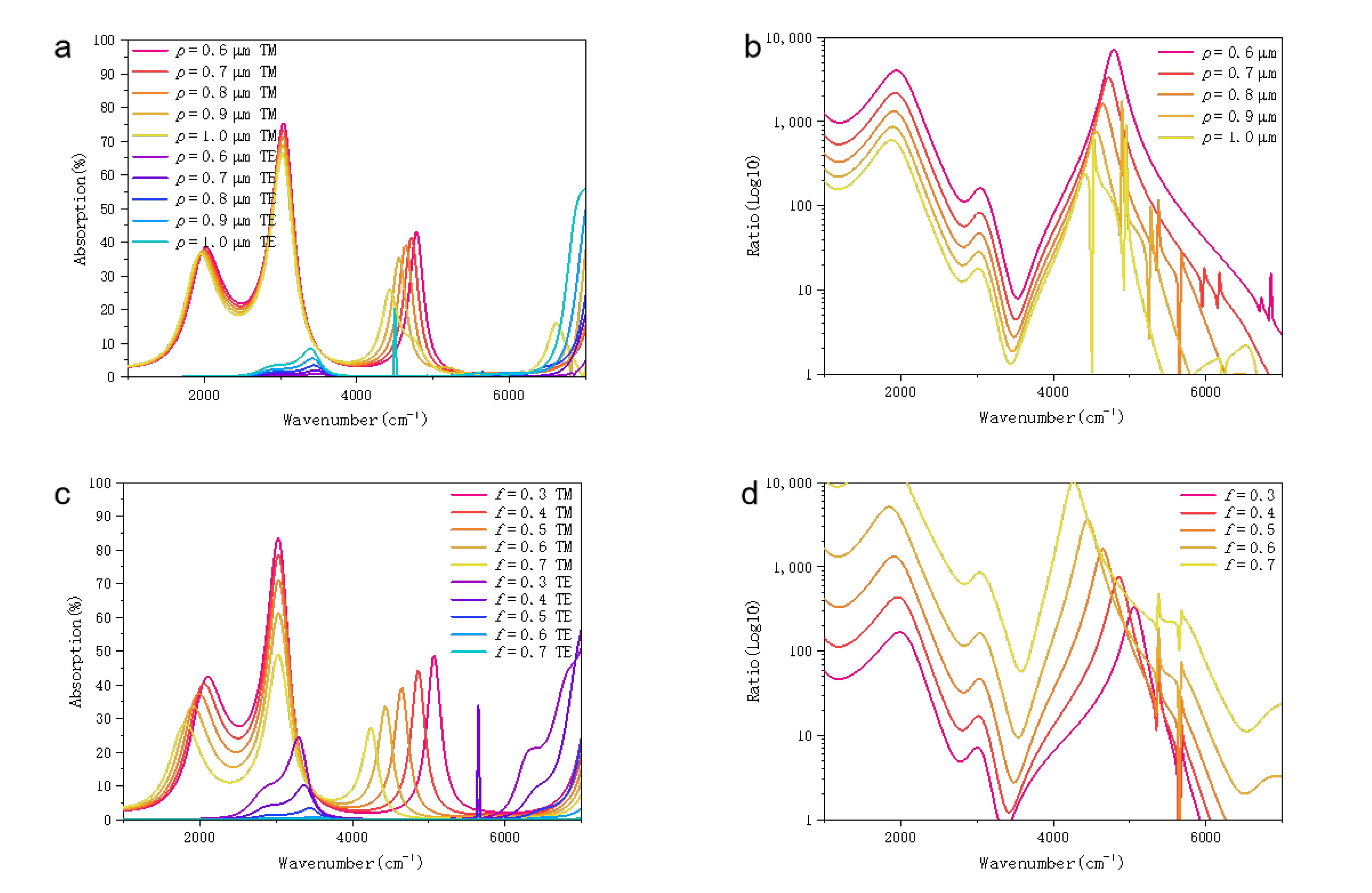
3.1. Effects of Period and Duty Cycle

The center wavelength λ_center of Bragg mirror defined the operation spectral ranges of resonant cavity, and it can be expressed as

$${\lambda }_{center}=4n_l{d}_l=4n_h{d}_h,$$

(3)

where n₁ and n_h are the refractive index of the two materials, and d₁ and d_h are the thickness of the two materials. Bragg mirrors are formed by two alternating layers with different refractive index. By changing the thickness of each layer in the simulation, the reflection window can be controlled. When the response of the detector is in short-wave infrared, the center wavelength is set to be 2 μm, so the thickness of SiO₂ and Si is calculated to be 340 nm and 140 nm, respectively. When the detector works in the mid-wave region, the center wavelength is about 4 μm, and the thickness of SiO₂ and Si is set to be 700 nm and 280 nm [17].

For wire-grid polarizer, the period and duty cycle are two key parameters that influence its spectral extinction ratio [18]. The duty cycle f is defined as: f = b/p, where p is the period of the wire grid, and b is the width of wire grid. The polarization performance of polarizer is usually characterized by extinction ratio, that is, ER = 10 log(TM/TE). In our simulation, the extinction ratio is defined by the absorption ratio of CQDs under TM and TE wave incidence.

When short-wave infrared plane waves are incident and the period of metal wire grid increases from 0.6 μm to 1.0 μm, the spectral absorption characteristic curves of HgTe CQDs is simulated, as shown in Figure 2a. The corresponding extinction ratio of absorption is shown in Figure 2b. The HgTe CQDs demonstrate clear polarization-dependent absorption. With decreasing period from 1.0 to 0.6 µm, the extinction ration increases by almost three orders of magnitude. Duty cycle of wire grid is another important structural parameter. When the plane wave is incident vertically, the absorption characteristic curves of HgTe CQDs with wire grids with different duty cycles are simulated in the short-wave region (Figure 2c). When the duty cycle of the grid increases from 0.3 to 0.7, the absorption rate of TM wave decreases gradually and redshifts, whereas that of TE decreases significantly, and the extinction ratio increases (Figure 2d). In the mid-wave region, when the period increase from 0.6 μm to 1.0 μm, the absorption characteristic curve of HgTe CQDs with metal wire grid is simulated, as shown in Figure 3a,b. When duty cycle changes from 0.3 to 0.7, the absorption rate of TM wave in the mid-wave region redshifts. (Figure 3c). The simulation results show that the extinction ratio of the CQDs detector in the mid-wave region is much larger than that in the short-wave region (Figure 3d). Thus, the detector will be more suitable in the mid-wave region than the short-wave region according to the simulation results.

The extinction ratio in short-wave and mid-wave region according to our simulation results can reach 40 and 60 dB, respectively, through coupling the single-layer wire grid and Bragg mirror, which are higher than that of other similar structures [10,19,20]. Although the extinction ratio using multi-layers wire grid is larger than ours, the complicated structure is difficult for mass production [12]. Compared with previous studies, our structure has considerable extinction ratio on the basis of its simpler structure, which makes the detector easier to manufacture. Therefore, the coupling of colloidal quantum dot detector and nano metal wire grid will be a promising method for the development of high-performance polarization photodetectors.

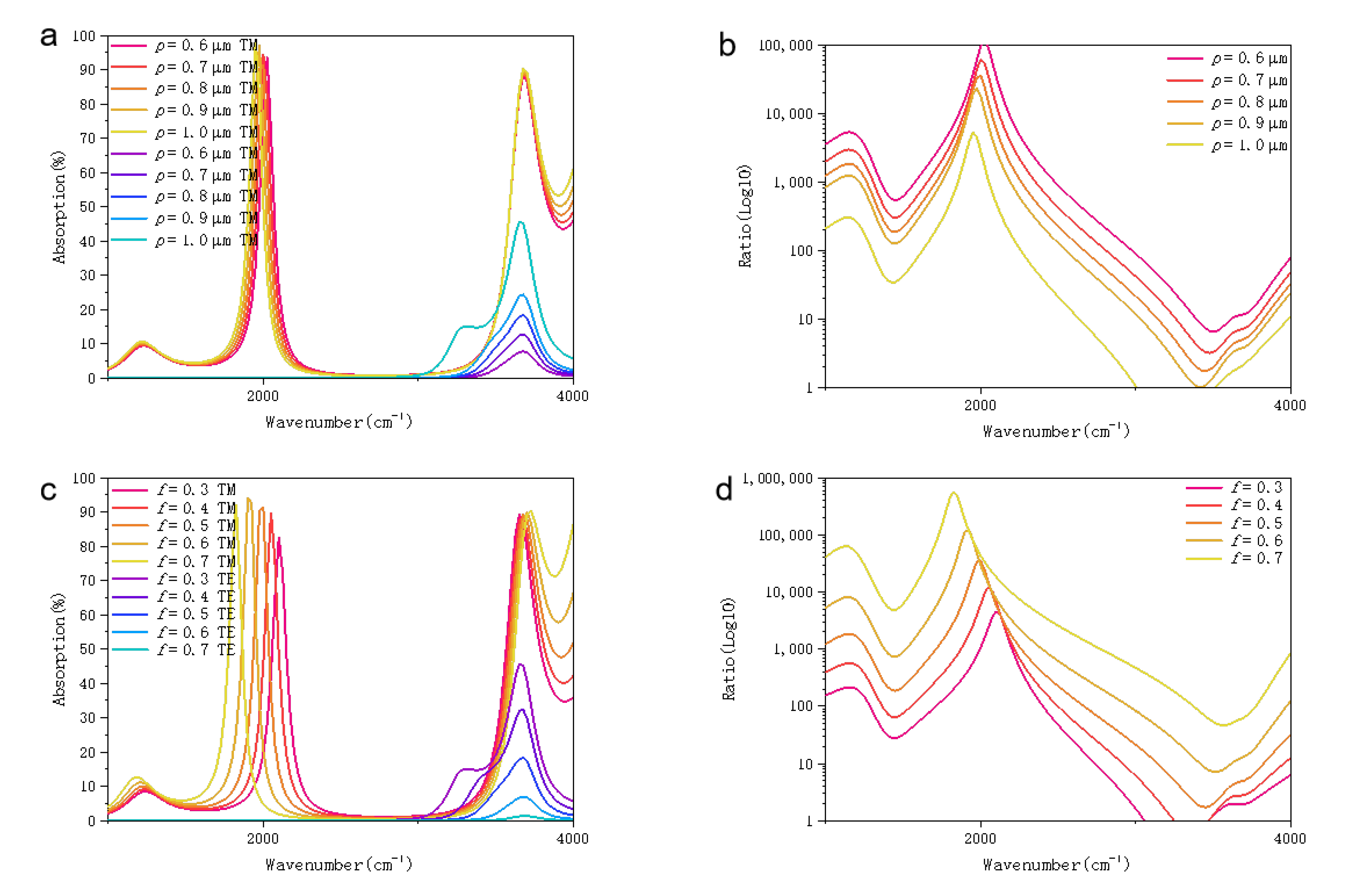
3.2. Effects of Optical Spacer Thickness

The optical spacer above the wire-grid polarizer is composed of SiO₂. The role of the resonator is to select the light with a desired wavelength and suppress the light with other wavelength [21]. Therefore, the desired wavelength of TM absorption peak can be selected by adjusting the thickness of the SiO₂ layer. The wavelength of the peak absorption for a resonant cavity can be expressed by

$$\lambda =\frac{2\pi l\sqrt{n^2-{\sin }^2\theta }}{\pi m-\varphi }$$

(4)

where $l$ is the optical path, $n$ is the index of refraction of the optical spacer, $\theta$ is the angle of incidence, $m$ is the order of interference, and $\varphi$ is the phase shift of light between the two reflective surfaces. Therefore, by changing the thickness of the optical spacer (SiO₂), the spectra can be tuned accordingly.

In the short-wave region and mid-wave infrared, the absorption curves of TM wave and TE wave with various thickness of the optical spacer are shown in Figure 4a,b. The black curve is the reflection window of the distributed Bragg mirror, and the TM absorption peak redshifts with the increased thickness of the optical spacer. For short-wave infrared HgTe detectors, the TM absorption peak decreases gradually with the decrease in wavelength, whereas the magnitude of absorption remains almost unchanged in the mid-wave infrared region. After the addition of optical spacer, the CQD detectors remain sensitive to the polarization direction with high absorption under TM incidence in short-wave region and mid-wave region (Figure 4c,d).

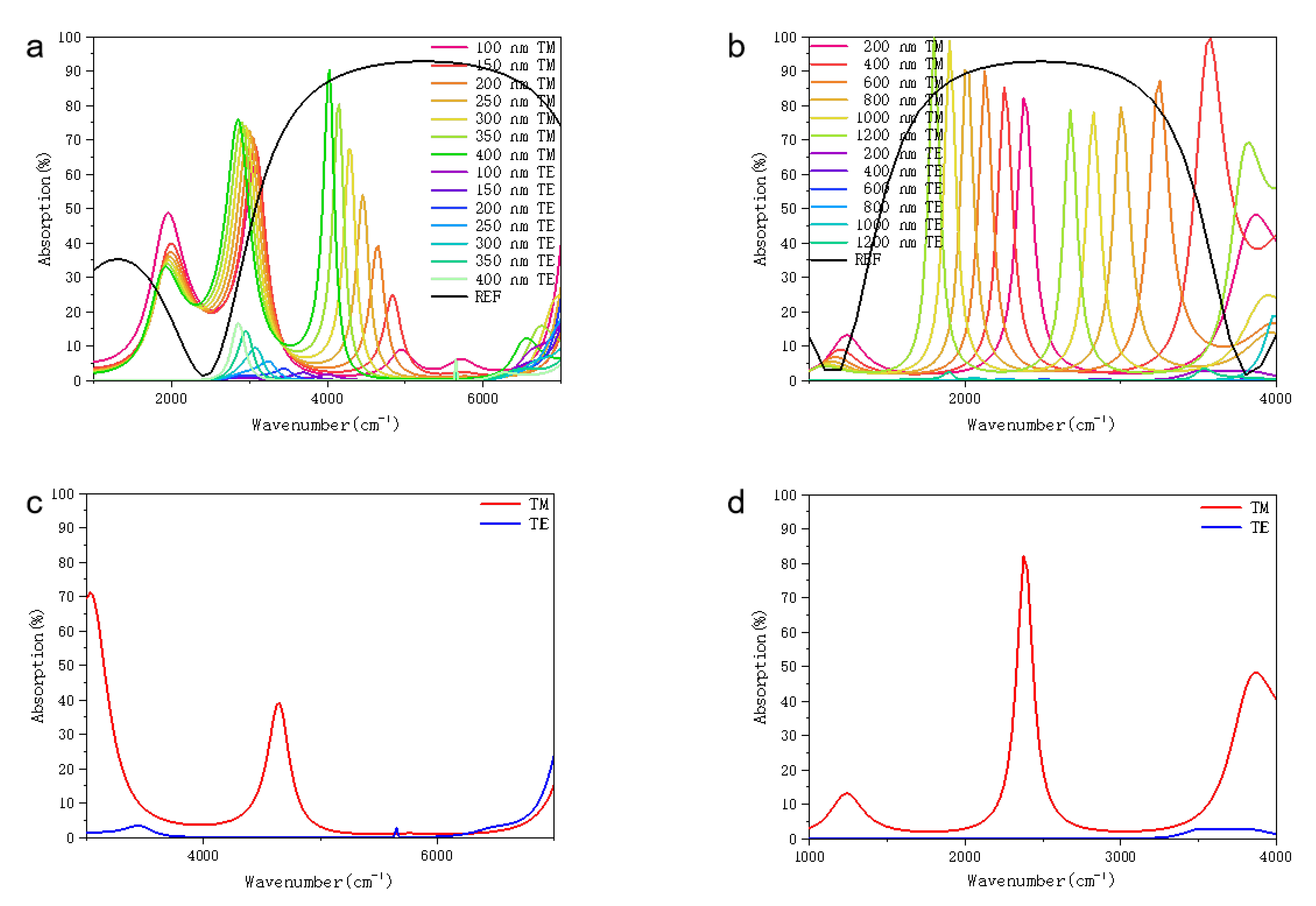
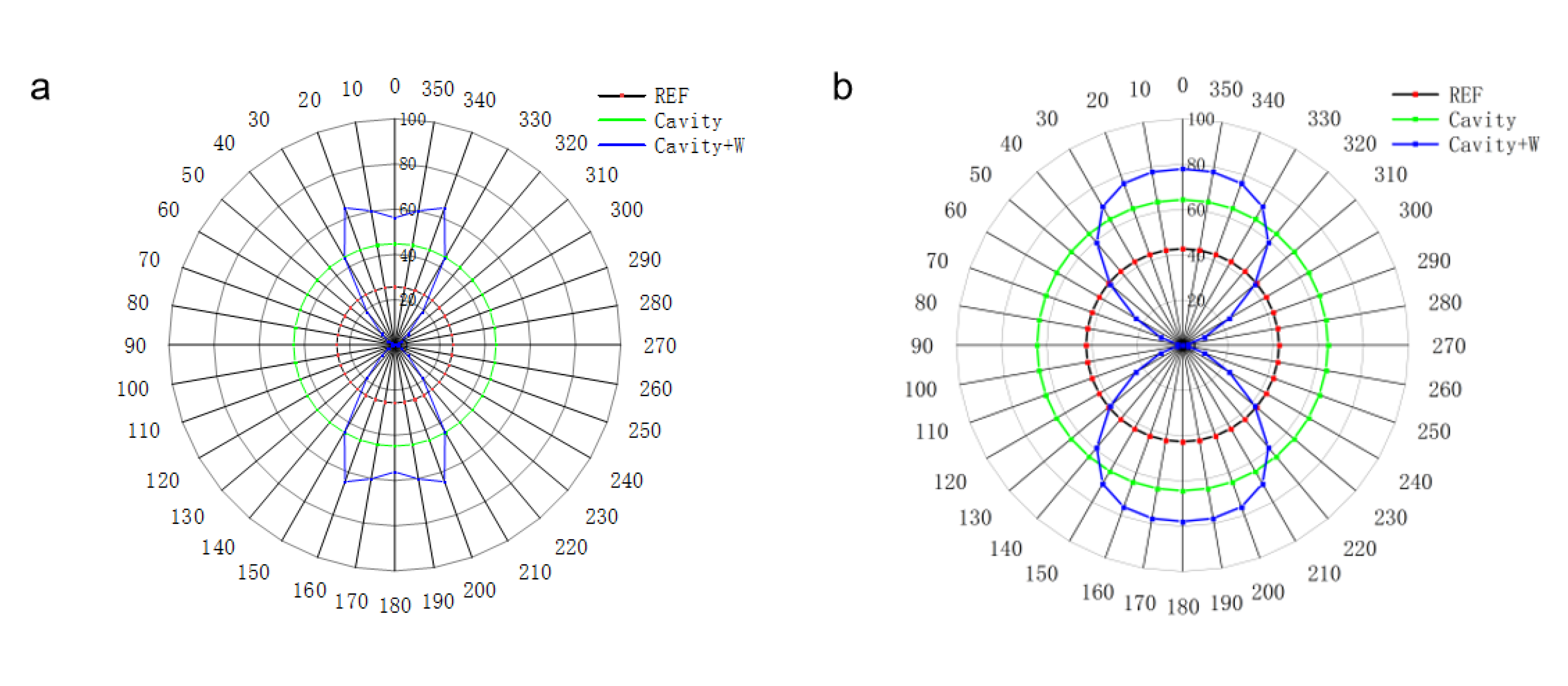
3.3. Effects of Plasmon Resonance by Wire Grid

Compared to HgTe detectors without resonant cavity, the cavity can significantly improve light absorption at targeted wavelength, resulting in the enhancement of quantum efficiency [22]. Moreover, our simulation shows that the metal wire grid provides surface plasmon resonance effect which leads to further increase in the infrared absorption of detector. The absorption of light at different polarization angles by the CQDs infrared detector with resonant cavity and wire-grid polarizer in the short-wave region and mid-wave infrared is shown in Figure 5a,b. The integration of HgTe CQD photovoltaic detector, wire-grid polarizer and resonant cavity can not only provide polarization-sensitivity, but also significantly increases CQDs film absorption.

It can be seen that the proposed resonant cavity-enhanced wire-grid polarizers not only show excellent polarization selectivity, but also give enhanced absorption with high spectral selectivity, which provides a promising method to improve the spectral resolution of infrared polarization detector.

4. Conclusions

In conclusion, we proposed the design of HgTe CQDs photodetectors with resonant cavity-enhanced wire-grid polarizer, providing a theoretical study for designing low-cost polarization infrared detectors in the future. The simulation results show that the detector can work in both short-wave region and mid-wave region with high extinction ratio up to 40 dB and 60 dB. Our simulation shows that the metal wire grid provides surface plasmon resonance effect which leads to further increase in the infrared absorption of detector. Benefitting from CQDs’ solution processibility, HgTe CQDs could be directed integrated with the wire-grid polarizers. Therefore, we believe that the simulation results have important implications for the focal plane array polarization imaging.