Nanomechanical Concepts in Magnetically Guided Systems to Investigate the Magnetic Dipole Effect on Ferromagnetic Flow Past a Vertical Cone Surface
Abstract
:1. Introduction
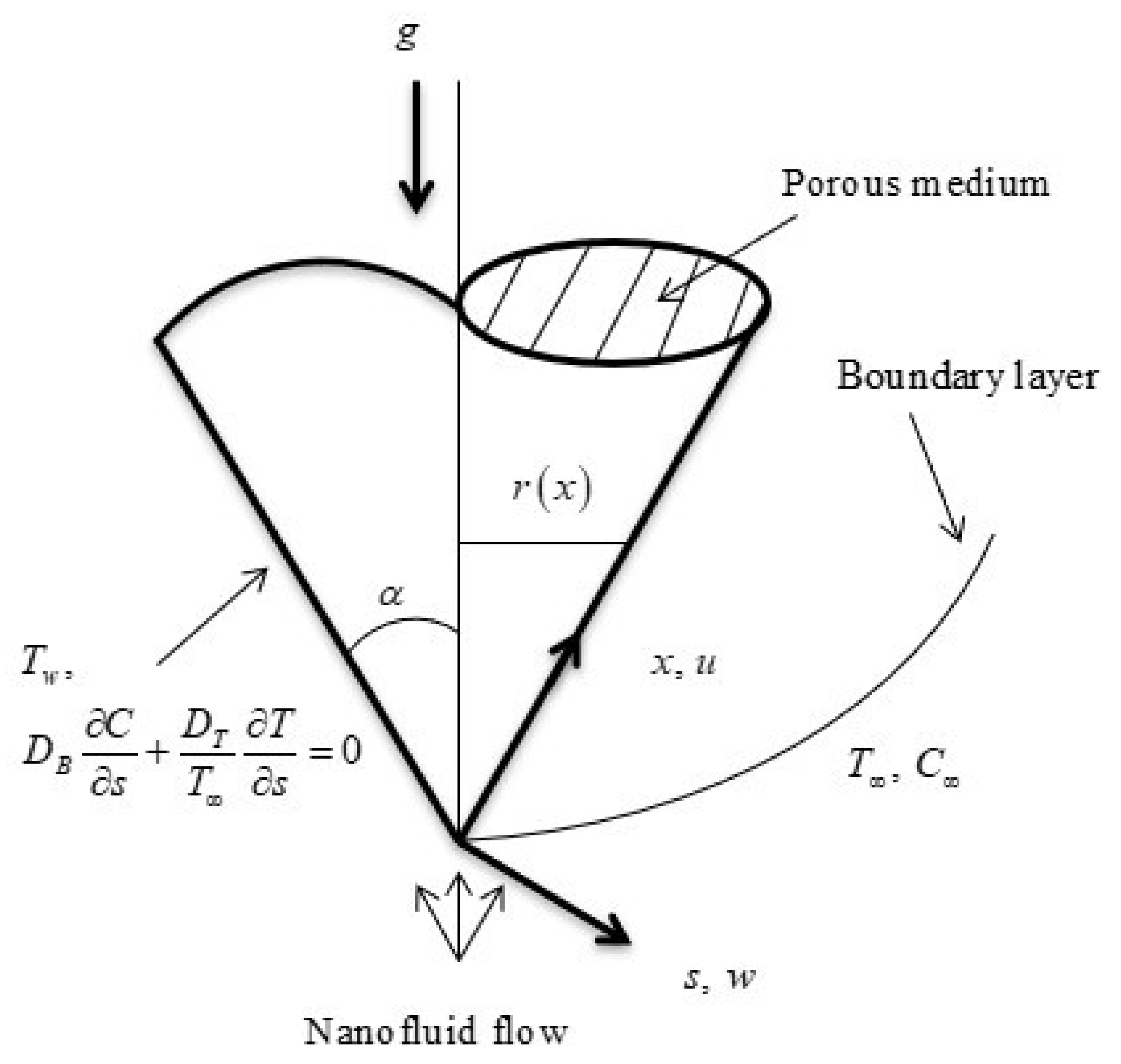
2. Materials and Methods
Magnetic Dipole
3. HAM Solutions Methodology
4. Analysis of Convergence of the Solutions
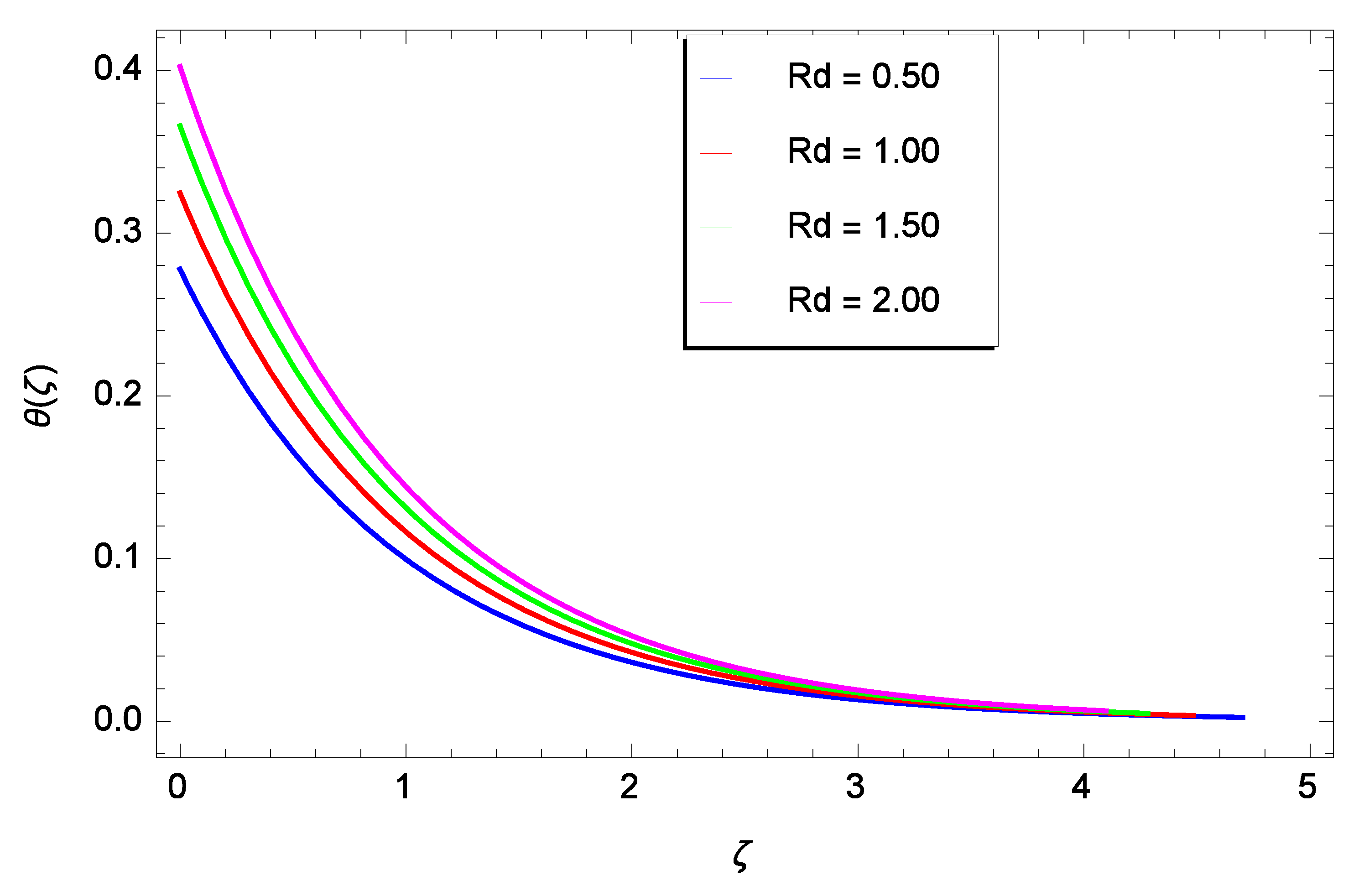
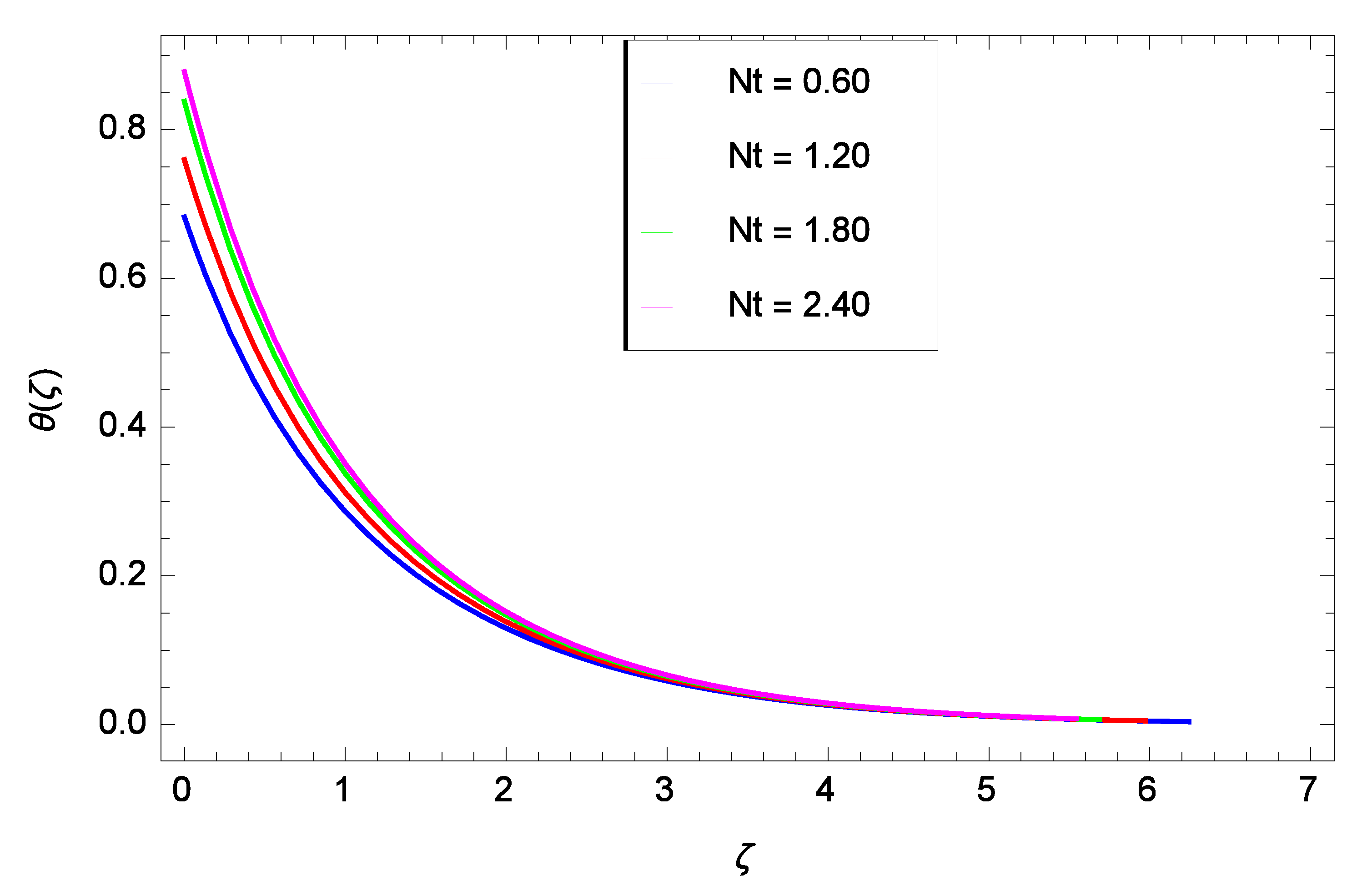
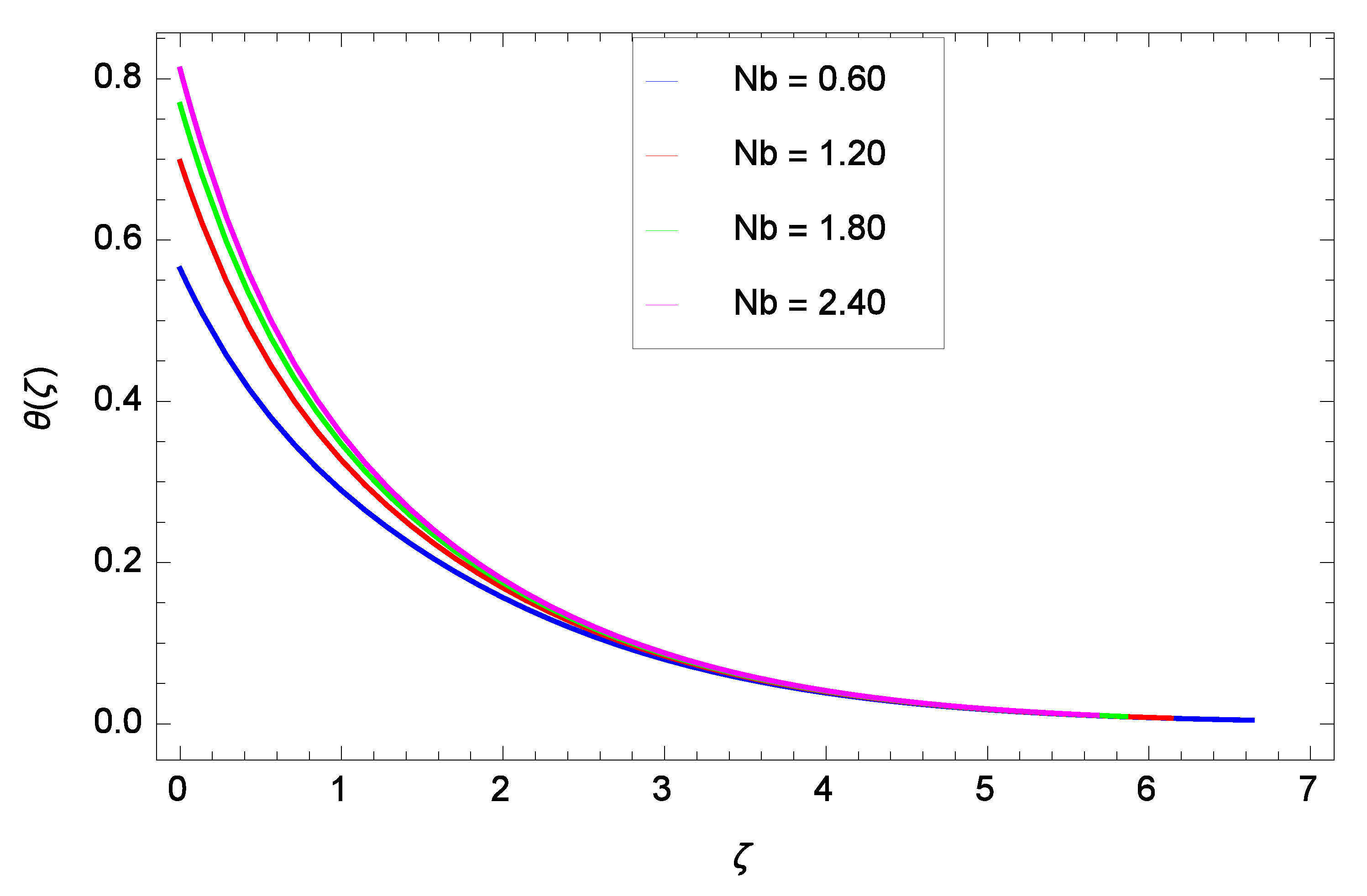
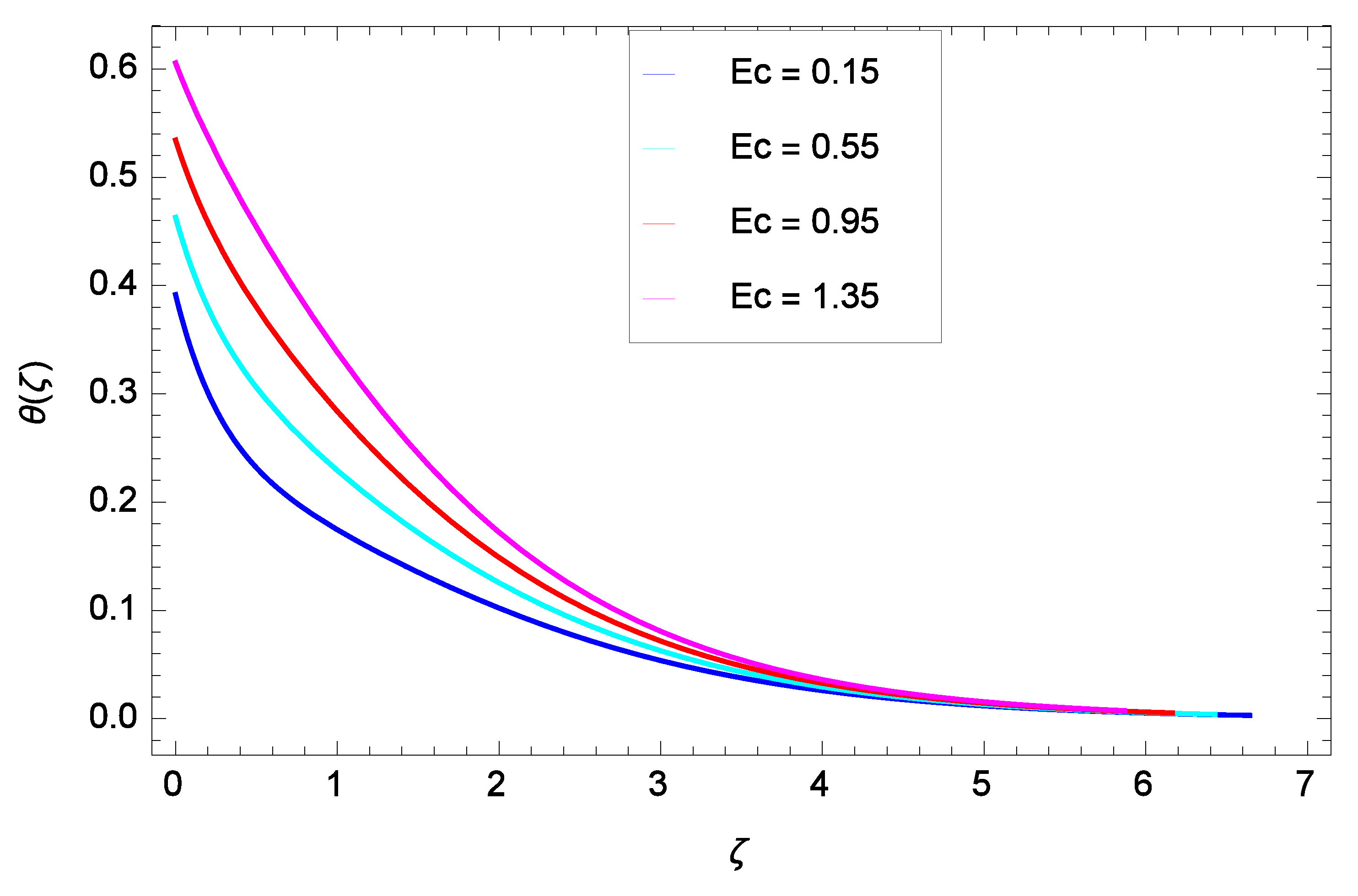
5. Results and Discussion
6. Conclusions
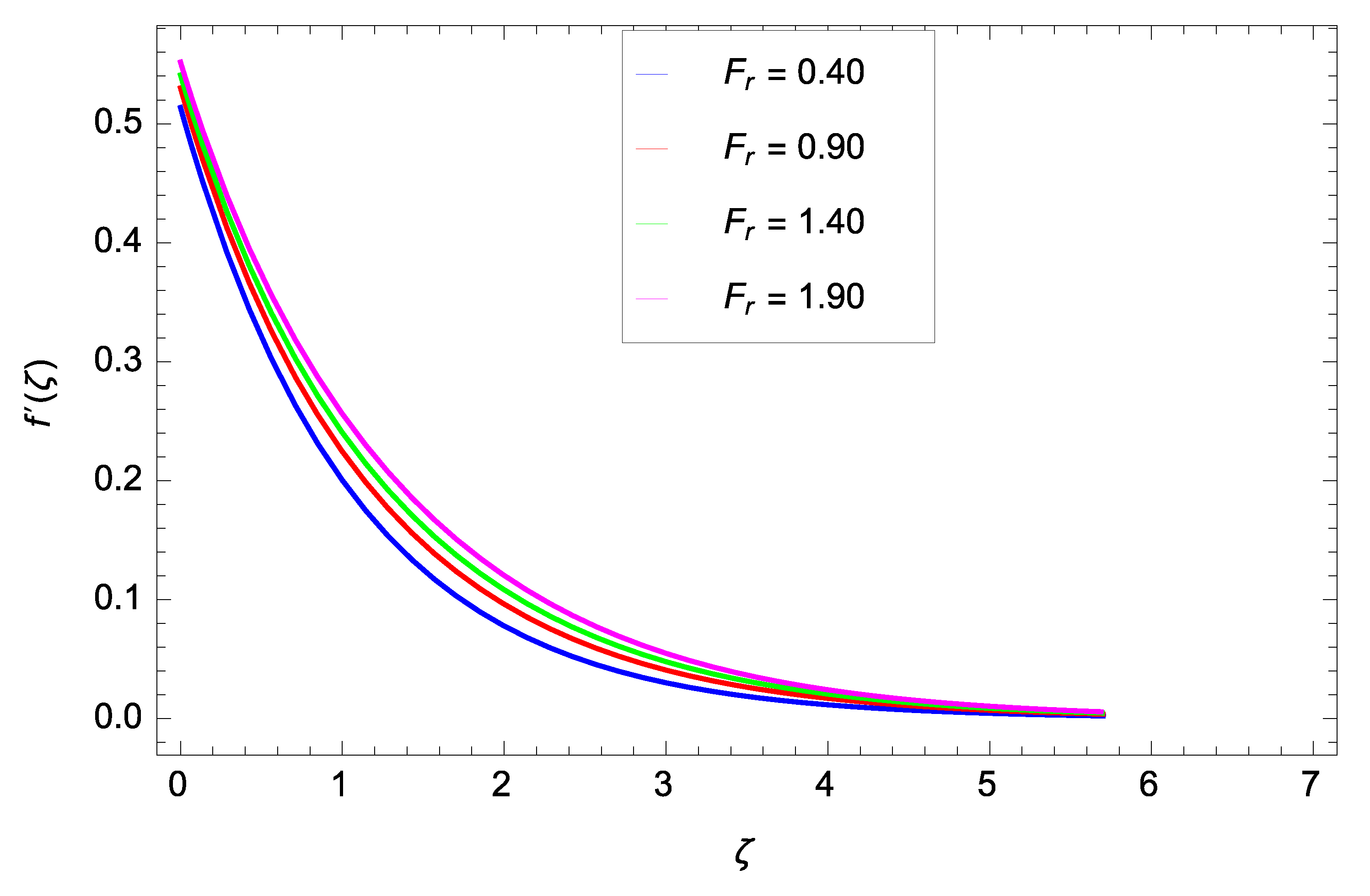
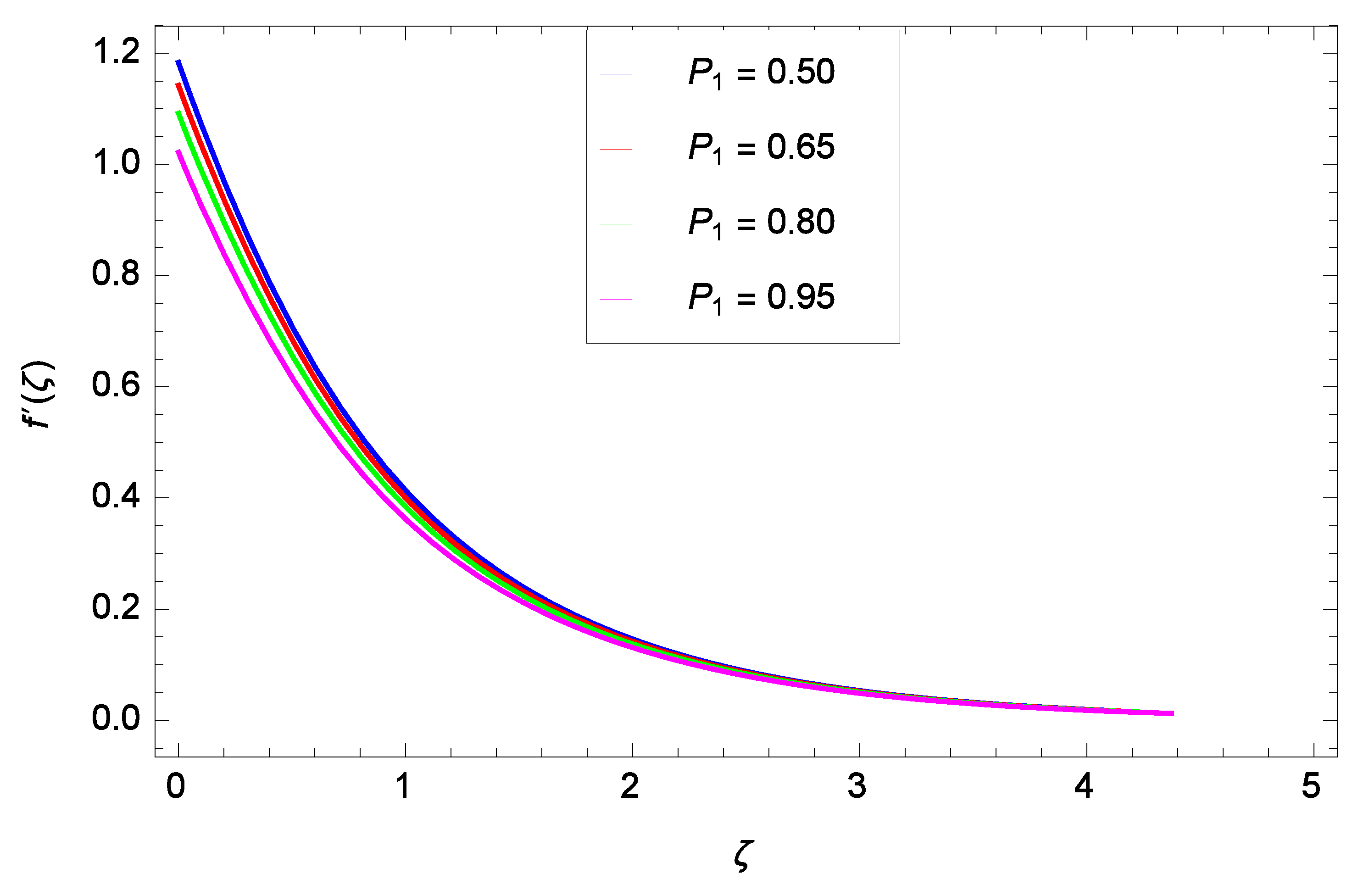
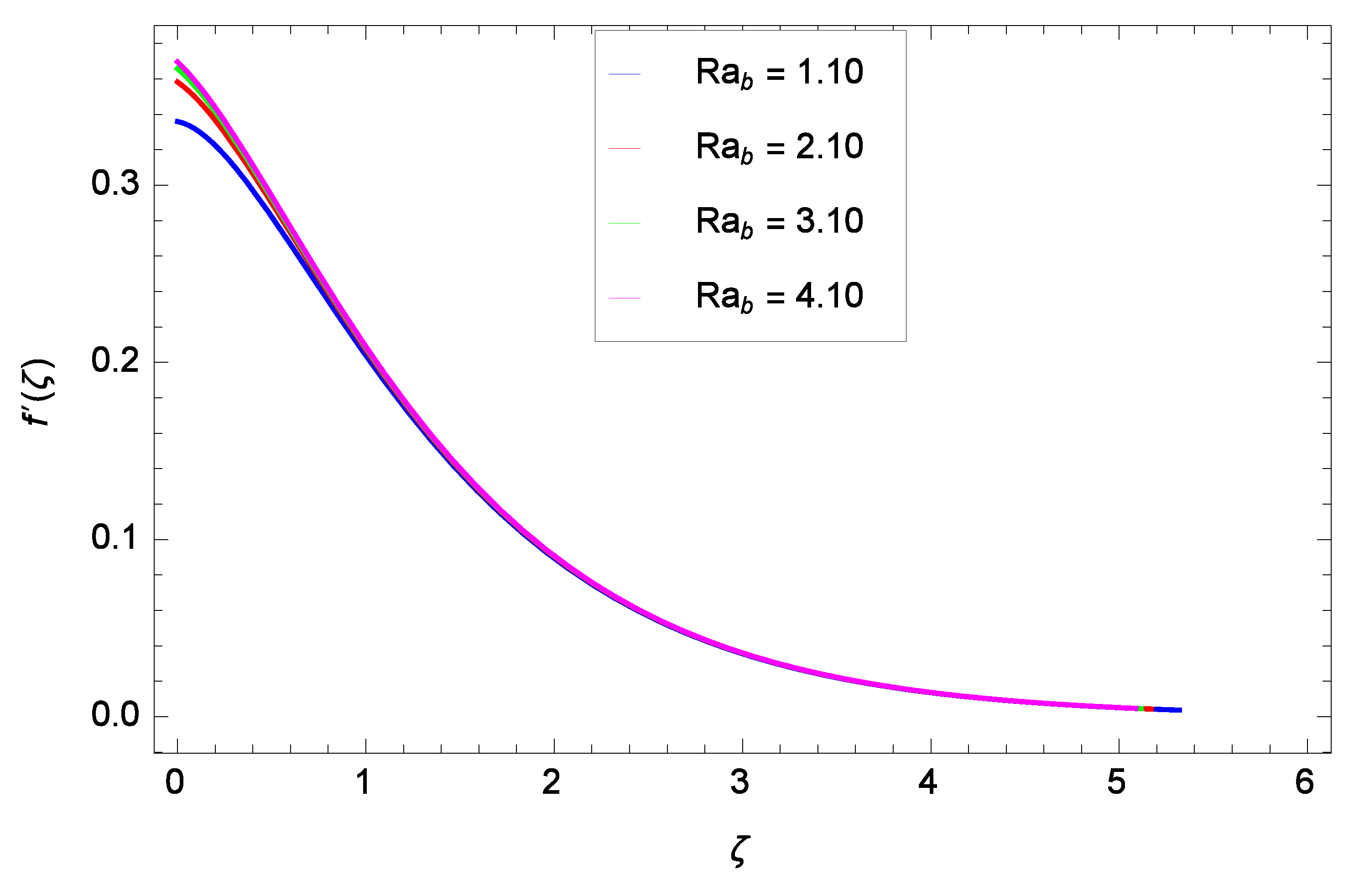
- The velocity decreases as the ferromagnetic interaction parameter, porosity parameter, and local inertia parameter increase.
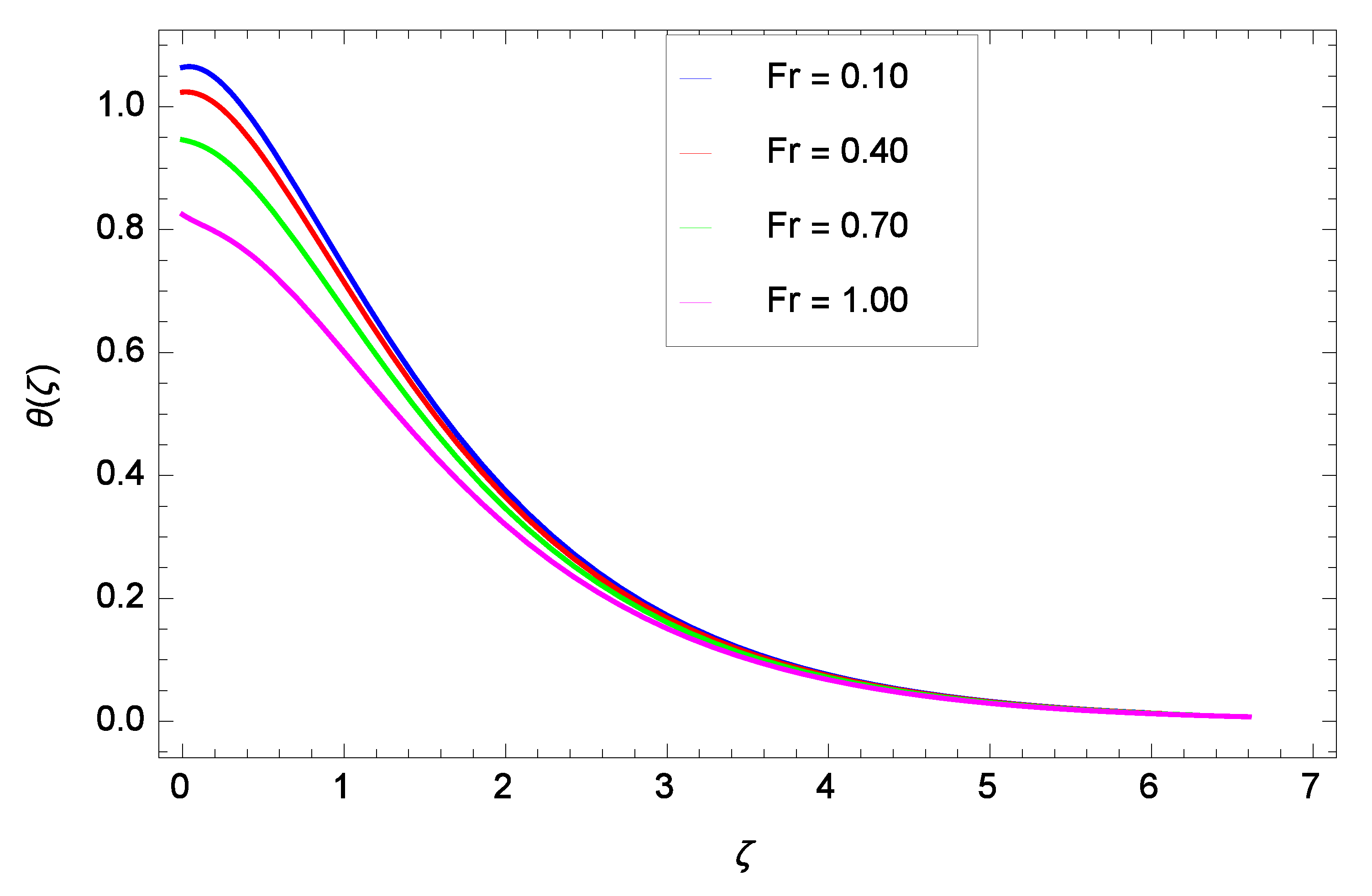
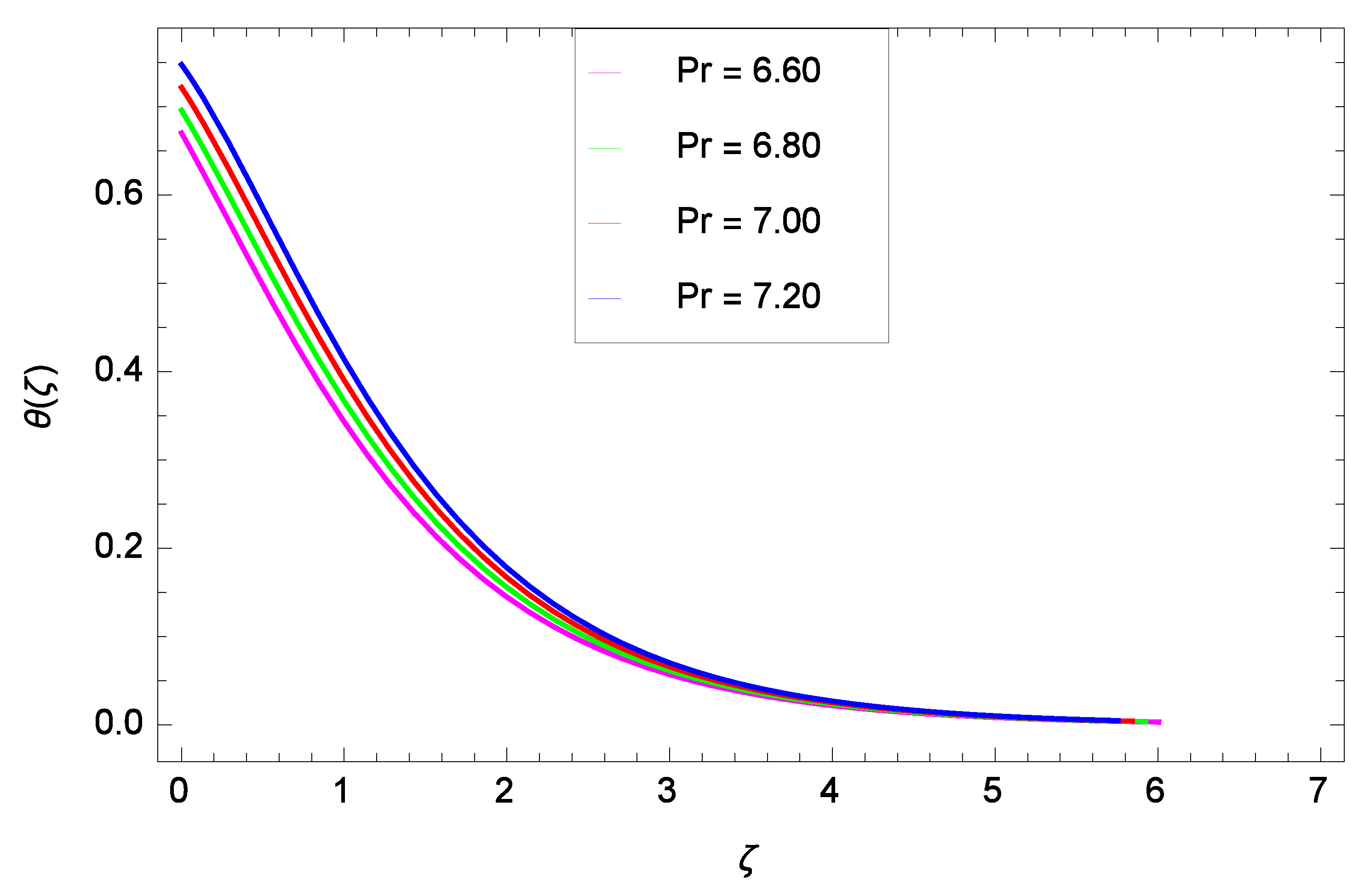
- The temperature rises as the ferromagnetic interaction, heat dissipation, injection, thermal radiation parameters and Eckert number are raised, and reduces when the Prandtl number and sunction parameter are raised.
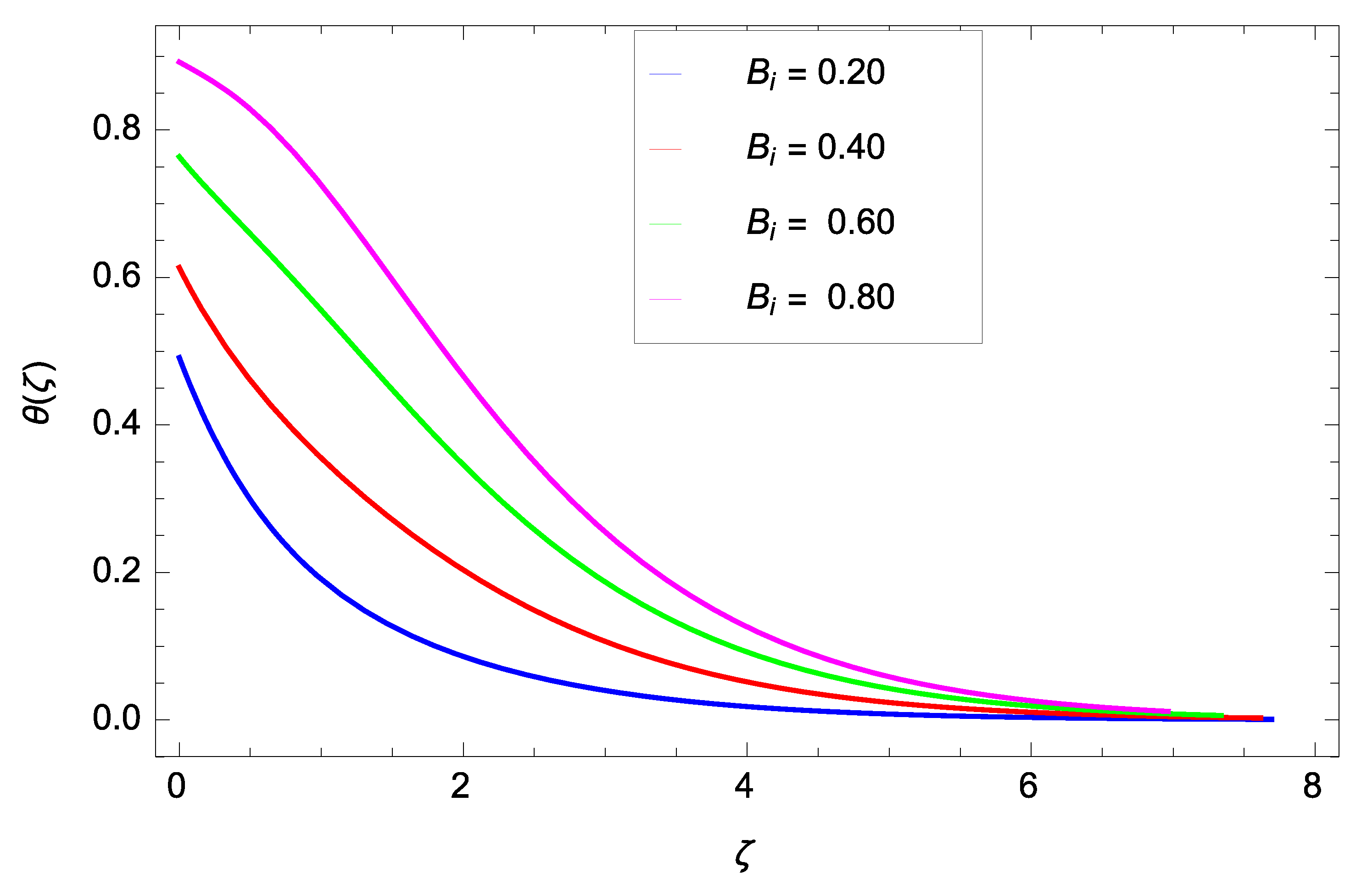
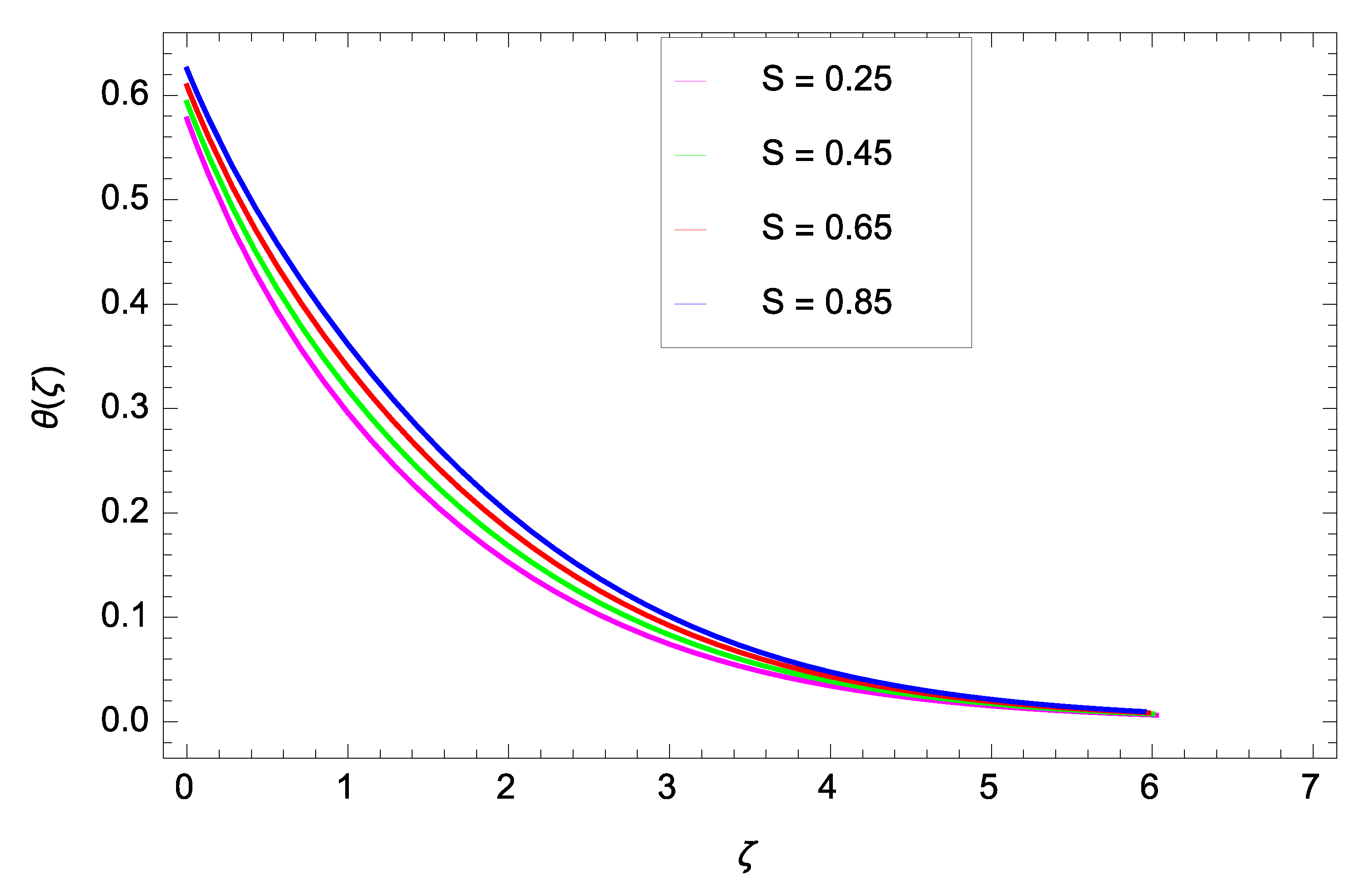
- When the Brownian motion, chemical reaction parameters and Schmidt number increase, the concentration decreases, while it increases when the thermophoresis parameter increases.
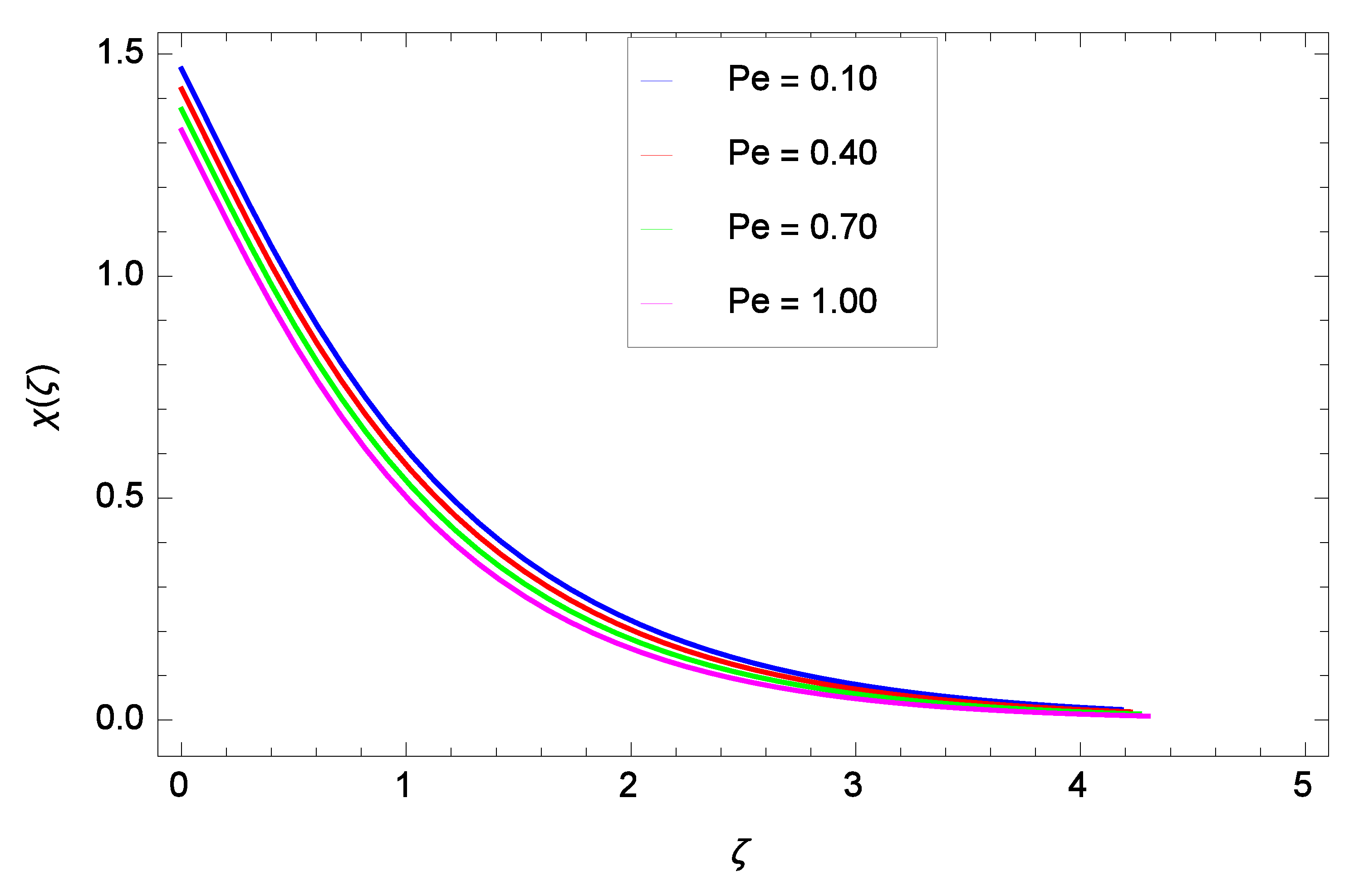
- The motile microorganism density decreases through raising the Peclet number and bioconvection Lewis number.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Raj, K.; Moskowitz, R. Commercial applications of ferrofluids. J. Magn. Magn. Mater. 1990, 85, 233–245. [Google Scholar] [CrossRef]
- Goldman, A. Handbook of Modern Ferromagnetic Materials; Springer Science and Business Media: Berlin, Germany, 2012. [Google Scholar]
- Hathway, D.B. dB-sound. Eng. Mag. 1979, 13, 42–44. [Google Scholar]
- Andersson, H.I.; Valnes, O.A. Flow of a heated ferrofluid over a stretching sheet in the presence of a magnetic dipole. Acta Mech. 1998, 128, 39–47. [Google Scholar] [CrossRef]
- Zeeshan, A.; Majeed, A.; Ellahi, R.; Zia, Q.M.Z. Mixed convection flow and heat transfer in ferromagnetic fluid over a stretching sheet with partial slip effects. Therm. Sci. 2018, 22, 2515–2526. [Google Scholar] [CrossRef]
- Hayat, T.; Ahmad, S.; Khan, M.I.; Alsaedi, A. Exploring magnetic dipole contribution on radiative flow of ferromagnetic Williamson fluid. Results Phys. 2018, 8, 545–551. [Google Scholar] [CrossRef]
- Choi, S.U.; Eastman, J.A. Enhancing Thermal Conductivity of Fluids with Nanoparticles; Argonne National Lab: Lemont, IL, USA, 1995.
- Ellahi, R. The effects of MHD and temperature dependent viscosity on the flow of non-Newtonian nanofluid in a pipe: Analytical solutions. Appl. Math. Model. 2013, 37, 1451–1467. [Google Scholar] [CrossRef]
- Ellahi, R.; Raza, M.; Akbar, N.S. Study of peristaltic flow of nanofluid with entropy generation in a porous medium. J. Porous Media 2017, 20, 461–478. [Google Scholar] [CrossRef]
- Hayat, T.; Ahmad, S.; Khan, M.I.; Alsaedi, A. Modeling and analyzing flow of third grade nanofluid due to rotating stretchable disk with chemical reaction and heat source. Phys. B Condens. Matter. 2018, 537, 116–126. [Google Scholar] [CrossRef]
- Awais, M.; Shah, Z.; Perveen, N.; Ali, A.; Kumam, P.; Thounthong, P. MHD effects on ciliary-induced peristaltic flow coatings with rheological hybrid nanofluid. Coatings 2020, 10, 186. [Google Scholar] [CrossRef] [Green Version]
- Reddy, P.S.; Sreedevi, P.; Chamkha, A.J. MHD natural convection boundary layer flow of nanofluid over a vertical cone with chemical reaction and suction/injection. Comput. Therm. Sci. Int. J. 2017, 9, 165–182. [Google Scholar] [CrossRef]
- Alsaedi, A.; Khan, M.I.; Farooq, M.; Gull, N.; Hayat, T. Magnetohydrodynamic (MHD) stratified bioconvective flow of nanofluid due to gyrotactic microorganisms. Adv. Powder Technol. 2017, 28, 288–298. [Google Scholar] [CrossRef]
- Hayat, T.; Bashir, Z.; Qayyum, S.; Alsaedi, A. Nonlinear radiative flow of nanofluid in presence of gyrotactic microorganisms and magnetohydrodynamic. Int. J. Numer. Methods Heat Fluid Flow 2019, 29, 3039–3055. [Google Scholar] [CrossRef]
- Nadeem, S.; Ijaz, M.; El-Kott, A.; Ayub, M. Rosseland analysis for ferromagnetic fluid in presence of gyrotactic microorganisms and magnetic dipole. Ain Shams Eng. J. 2020, 11, 1295–1308. [Google Scholar] [CrossRef]
- Bhatti, M.M.; Michaelides, E.E. Study of Arrhenius activation energy on the thermo-bioconvection nanofluid flow over a Riga plate. J. Therm. Anal. Calorim. 2021, 143, 2029–2038. [Google Scholar] [CrossRef]
- Waqas, H.; Khan, S.A.; Alghamdi, M.; Alqarni, M.S.; Muhammad, T. Numerical simulation for bio-convection flow of magnetized non-Newtonian nanofluid due to stretching cylinder/plate with swimming motile microorganisms. Eur. Phys. J. Spec. Top. 2021, 230, 1239–1256. [Google Scholar] [CrossRef]
- Ingham, D.B.; Pop, I. (Eds.) Transport Phenomena in Porous Media III; Elsevier: Oxford, UK, 2005; Volume 3. [Google Scholar]
- Zeng, Z.; Grigg, R. A criterion for non-Darcy flow in porous media. Transp. Porous Media 2006, 63, 57–69. [Google Scholar] [CrossRef]
- Kumar, B.R.; Sivaraj, R. MHD viscoelastic fluid non-Darcy flow over a vertical cone and a flat plate. Int. Commun. Heat Mass Transf. 2013, 40, 1–6. [Google Scholar] [CrossRef]
- Chamkha, A.; Abbasbandy, S.; Rashad, A.M. Non-Darcy natural convection flow for non-Newtonian nanofluid over cone saturated in porous medium with uniform heat and volume fraction fluxes. Int. J. Numer. Method Heat Fluid Flow 2015, 25, 422–437. [Google Scholar] [CrossRef]
- Mallikarjuna, B.; Rashad, A.M.; Hussein, A.K.; Raju, S.H. Transpiration and thermophoresis effects on Non-Darcy convective flow past a rotating cone with thermal radiation. Arab. J. Sci. Eng. 2016, 41, 4691–4700. [Google Scholar] [CrossRef]
- Durairaj, M.; Ramachandran, S.; Mehdi, R.M. Heat generating/absorbing and chemically reacting Casson fluid flow over a vertical cone and flat plate saturated with non-Darcy porous medium. Int. J. Numer. Method Heat Fluid Flow 2017, 27, 156–173. [Google Scholar] [CrossRef]
- Pătrulescu, F.O.; Groşan, T.; Pop, I. Natural convection from a vertical plate embedded in a non-Darcy bidisperse porous medium. J. Heat Transf. 2020, 142, 012504. [Google Scholar] [CrossRef]
- Liao, S.J. The Proposed Homotopy Analysis Method for the Solution of Nonlinear Problems. Ph.D. Thesis, Shanghai Jiao Tong University, Shanghai, China, 1992. [Google Scholar]
- Liao, S.J. An explicit, totally analytic approximate solution for Blasius viscous flow problems. Int. J. Non-Linear Mech. 1999, 34, 759–778. [Google Scholar] [CrossRef]
- Liao, S. Beyond Perturbation: Introduction to the Homotopy Analysis Method; CRC Press: Boca Raton, FL, USA, 2003. [Google Scholar]
- Irfan, M.; Khan, M.; Khan, W.A.; Sajid, M. Thermal and solutal stratifications in flow of Oldroyd-B nanofluid with variable conductivity. Appl. Phys. A 2018, 124, 674. [Google Scholar] [CrossRef]
- Tlili, I.; Waqas, H.; Almaneea, A.; Khan, S.U.; Imran, M. Activation energy and second order slip in bioconvection of Oldroyd-B nanofluid over a stretching cylinder: A proposed mathematical model. Processes 2019, 7, 914. [Google Scholar] [CrossRef] [Green Version]
- Usman, A.H.; Khan, N.S.; Humphries, U.W.; Ullah, Z.; Shah, Q.; Kumam, P.; Thounthong, P.; Khan, W.; Kaewkhao, A.; Bhaumik, A. Computational optimization for the deposition of bioconvection thin Oldroyd-B nanofluid with entropy generation. Sci. Rep. 2021, 11, 11641. [Google Scholar] [CrossRef] [PubMed]
- Hayat, T.; Waqas, M.; Shehzad, S.A.; Alsaedi, A. Mixed convection flow of viscoelastic nanofluid by a cylinder with variable thermal conductivity and heat source/sink. Int. J. Numer. Method Heat Fluid Flow 2016, 26, 214–234. [Google Scholar] [CrossRef]


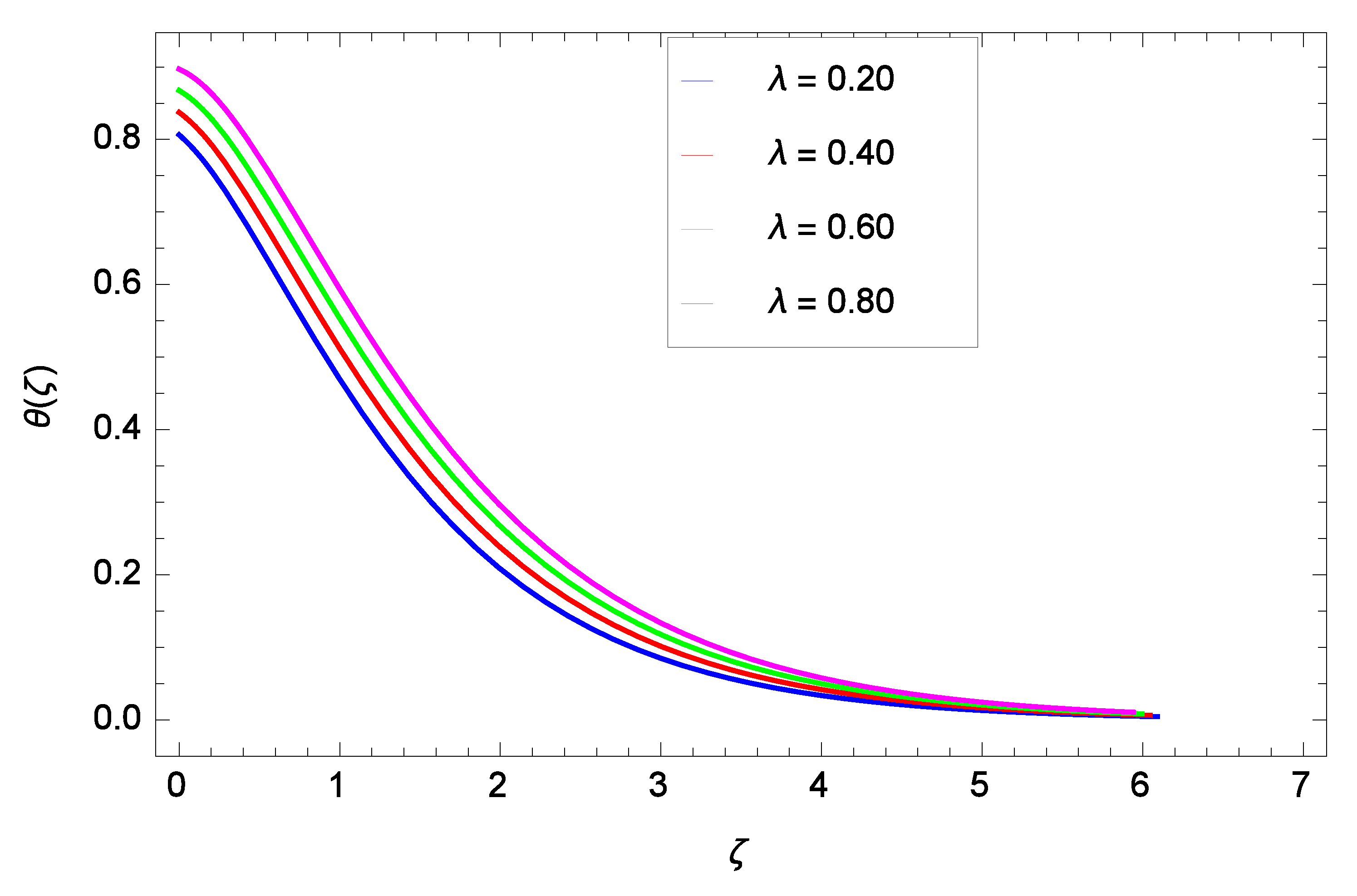





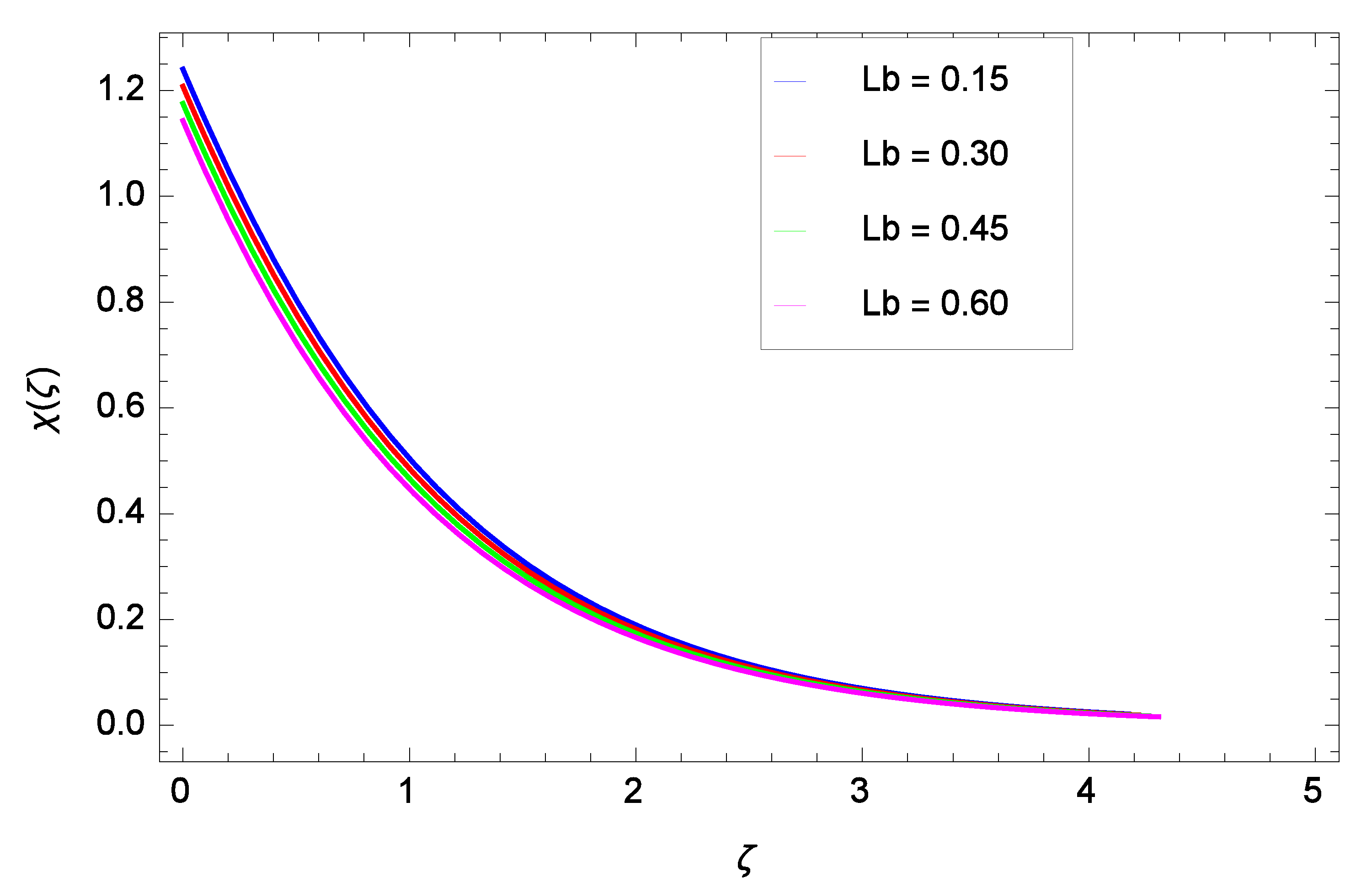
| Order of Approximations | ||||
|---|---|---|---|---|
| 1 | 1.87633 | 0.6333 | 1.12222 | 0.69596 |
| 5 | 1.93521 | 0.76748 | 1.12327 | 0.69583 |
| 10 | 1.93385 | 0.76804 | 1.12349 | 0.69575 |
| 15 | 1.93135 | 0.7658 | 1.12354 | 0.69575 |
| 25 | 1.93026 | 0.7658 | 1.12354 | 0.69575 |
| 30 | 1.93026 | 0.7658 | 1.12354 | 0.69575 |
| 35 | 1.93026 | 0.7658 | 1.12354 | 0.69575 |
| Present | Present | |||
|---|---|---|---|---|
| Reddy et al. [12] | Reddy et al. [12] | |||
| 0.1 | 0.32598 | 0.32601 | 1.48394 | 1.48381 |
| 0.2 | 0.32405 | 0.32411 | 1.46789 | 1.46801 |
| 0.3 | 0.32229 | 0.32231 | 1.45214 | 1.45215 |
| 0.4 | 0.32125 | 0.32129 | 1.43598 | 1.43594 |
| 0.5 | 0.31868 | 0.31867 | 1.41938 | 1.41940 |
| S | ||||||||
|---|---|---|---|---|---|---|---|---|
| 0.2 | 0.3 | 0.2 | 0.4 | 0.3 | 0.2 | 0.1 | 0.7 | 0.44701 |
| 0.3 | 0.43167 | |||||||
| 0.5 | 0.40752 | |||||||
| 0.4 | 0.39766 | |||||||
| 0.5 | 0.38914 | |||||||
| 0.6 | 0.37245 | |||||||
| 0.5 | 0.45806 | |||||||
| 0.8 | 0.45739 | |||||||
| 1.1 | 0.45623 | |||||||
| 0.8 | 1.03123 | |||||||
| 1.2 | 0.87433 | |||||||
| 1.6 | 0.64876 | |||||||
| 0.5 | 0.45342 | |||||||
| 0.7 | 0.44534 | |||||||
| 0.9 | 0.43998 | |||||||
| 0.6 | 0.64554 | |||||||
| 1.0 | 0.63854 | |||||||
| 1.4 | 0.61291 | |||||||
| 0.3 | 0.38453 | |||||||
| 0.5 | 0.38123 | |||||||
| 0.7 | 0.37941 | |||||||
| 6.7 | 0.75651 | |||||||
| 7.7 | 0.80612 | |||||||
| 8.7 | 0.86432 |
| 0.2 | 0.3 | 0.5 | 1.28733 |
| 0.4 | 1.26931 | ||
| 0.6 | 1.24887 | ||
| 0.5 | 1.32742 | ||
| 0.7 | 1.31022 | ||
| 0.9 | 1.30271 | ||
| 1.0 | 1.33075 | ||
| 1.5 | 1.41186 | ||
| 2.0 | 1.47572 |
| Pe | Lb | |||
|---|---|---|---|---|
| 0.1 | 0.3 | 0.3 | 0.2 | 0.57238 |
| 0.2 | 0.56103 | |||
| 0.3 | 0.55271 | |||
| 0.5 | 0.42714 | |||
| 1 | 0.45102 | |||
| 1.5 | 0.49327 | |||
| 0.5 | 0.53185 | |||
| 1 | 0.62386 | |||
| 1.5 | 0.66671 | |||
| 0.3 | 0.75408 | |||
| 0.4 | 0.76965 | |||
| 0.5 | 0.77121 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Usman, A.H.; Shah, Z.; Kumam, P.; Khan, W.; Humphries, U.W. Nanomechanical Concepts in Magnetically Guided Systems to Investigate the Magnetic Dipole Effect on Ferromagnetic Flow Past a Vertical Cone Surface. Coatings 2021, 11, 1129. https://doi.org/10.3390/coatings11091129
Usman AH, Shah Z, Kumam P, Khan W, Humphries UW. Nanomechanical Concepts in Magnetically Guided Systems to Investigate the Magnetic Dipole Effect on Ferromagnetic Flow Past a Vertical Cone Surface. Coatings. 2021; 11(9):1129. https://doi.org/10.3390/coatings11091129
Chicago/Turabian StyleUsman, Auwalu Hamisu, Zahir Shah, Poom Kumam, Waris Khan, and Usa Wannasingha Humphries. 2021. "Nanomechanical Concepts in Magnetically Guided Systems to Investigate the Magnetic Dipole Effect on Ferromagnetic Flow Past a Vertical Cone Surface" Coatings 11, no. 9: 1129. https://doi.org/10.3390/coatings11091129
APA StyleUsman, A. H., Shah, Z., Kumam, P., Khan, W., & Humphries, U. W. (2021). Nanomechanical Concepts in Magnetically Guided Systems to Investigate the Magnetic Dipole Effect on Ferromagnetic Flow Past a Vertical Cone Surface. Coatings, 11(9), 1129. https://doi.org/10.3390/coatings11091129









