Prediction of Thermal Barrier Coatings Microstructural Features Based on Support Vector Machine Optimized by Cuckoo Search Algorithm
Abstract
1. Introduction
2. Experimental Procedures and Modeling Methods
2.1. Coatings Fabrication and Microstructural Features Characterization
2.2. Methodological Background and Model Construction
2.2.1. Support Vector Machine
2.2.2. Cuckoo Search Algorithm
2.2.3. SVM Parameter Optimization Based on CS
- The SVM parameters determine the learning and generalization ability of the SVM model. Two crucial and decisive RBF parameters are C and , respectively. The former determines the balance between the complexity of the SVM model and empirical error, the latter determines the complexity of the sample data distribution. Hence, in this study, MATLAB software (R2017a, MathWorks. Inc) is used for modeling implementation, the CS algorithm is applied to optimize the SVM model parameters C and as follows [34]: Gather the training set samples, and preprocess the training set samples to acquire SVM learning samples. As a matter of experience, set the value range of SVM parameters C and , the minimum step and the maximum step of the CS algorithm, and the number of iterations N [34].
- Set the probability Pa = 0.25 and the number of nests n = 20 from the beginning, stochastically generate the position of the n nests, each nest corresponds to a set of parameters , calculate the fitness evaluation function of each set of nest positions corresponding to the training set, and find the optimum nest position and fitness evaluation function at present.
- Keep the position of the optimal nest of the previous generation, calculate the Levy flight step length according to Equations (5) and (6), use the Levy flight to update the positions of other nests to acquire a new set of nest positions, and calculate their fitness evaluation function F.
- According to the fitness evaluation function F, the position of the new bird’s nest is compared with the position Pi−1 of the previous generation bird’s nest, and the poorer bird’s nest position is replaced with a better bird’s nest position to acquire a new set of bird’s nest position .
- Use random number r to compare with , keep the bird’s nest with the smaller probability of being found in Pt, update the bird’s nest with the higher probability of discovery, calculate the fitness evaluation function of the new nest, and make comparison with the fitness evaluation function of the position Pt, and replace the bad position with a better bird’s nest position to get a set of the latest and better bird’s nest position Pt.
- Find the optimal nest position b in Step (5), determine whether the fitness evaluation function F is up to the standard. If it is up to the standard, the search is stopped, and output the global best fitness evaluation function F and its optimal nest t; if it is not up to the mustard, return back to Step (3) to continue the optimization.
- Set the SVM parameters according to the optimal parameters corresponding to the optimal bird’s nest position .
2.2.4. Model Performance Indicators
3. Results and Discussion
3.1. Microstructure Features
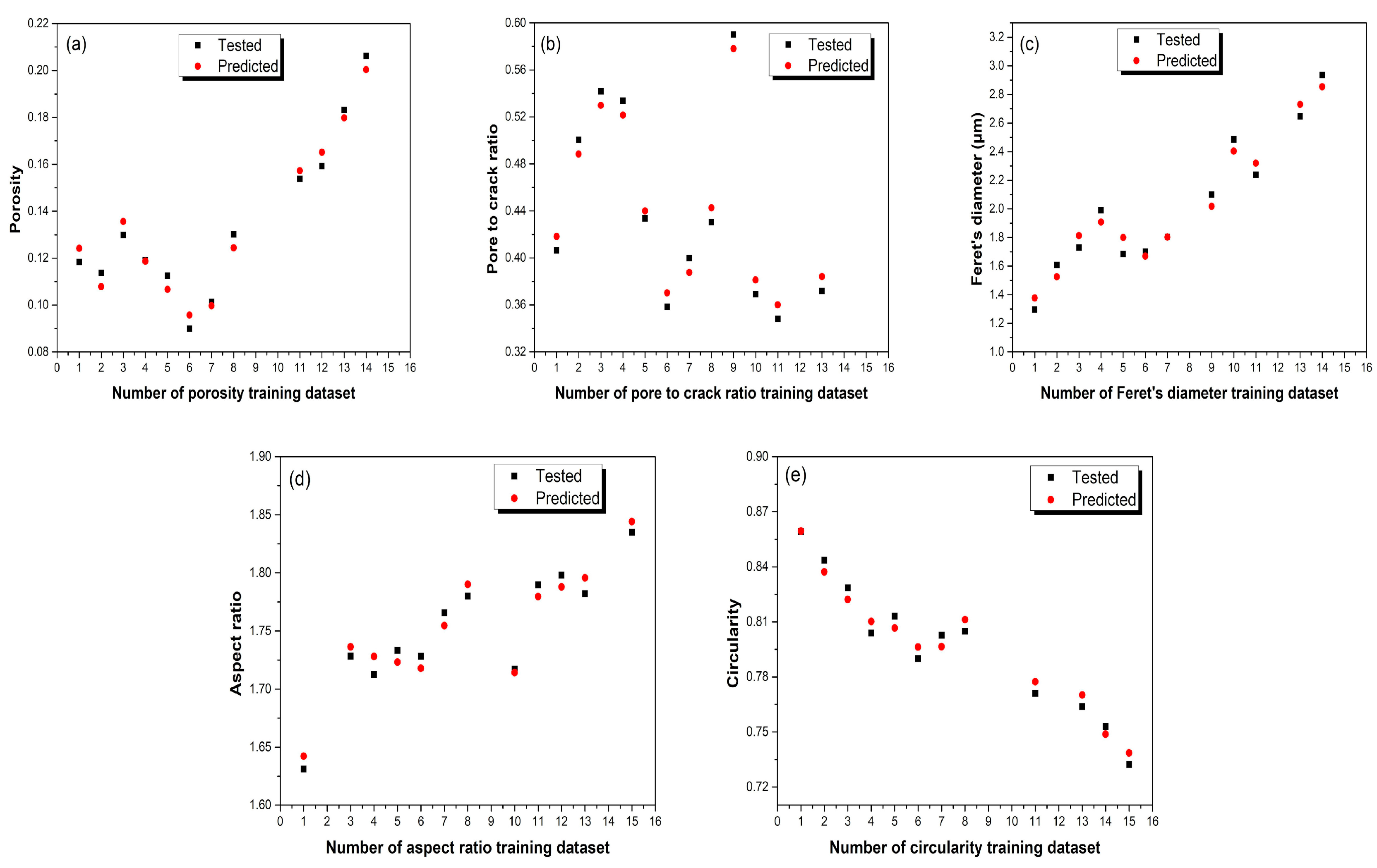
3.2. Analysis of the Training and Prediction Process of CS-SVM Model
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Clarke, D.R.; Levi, C.G. Materials design for the next generation thermal barrier coatings. Annu. Rev. Mater. Sci. 2003, 33, 383–417. [Google Scholar] [CrossRef]
- Padture, N.P.; Gell, M.; Jordan, E.H. Thermal barrier coatings for gas-turbine engine applications. Science 2002, 296, 280–284. [Google Scholar] [CrossRef] [PubMed]
- Ye, D.; Wang, W.; Huang, J.; Lu, X.; Zhou, H. Nondestructive interface morphology characterization of thermal barrier coatings using terahertz time-domain spectroscopy. Coatings 2019, 9, 89. [Google Scholar] [CrossRef]
- Clarke, D.R.; Phillpot, S.R. Thermal barrier coating materials. Mater. Today 2005, 8, 22–29. [Google Scholar] [CrossRef]
- Gizynski, M.; Chen, X.; Dusautoy, N.; Araki, H.; Kuroda, S.; Watanabe, M.; Pakiela, Z. Comparative study of the failure mechanism of atmospheric and suspension plasma sprayed thermal barrier coatings. Surf. Coat. Technol. 2019, 370, 163–176. [Google Scholar] [CrossRef]
- Pia, G.; Casnedi, L.; Sanna, U. Porosity and pore size distribution influence on thermal conductivity of Yttria-stabilized zirconia: Experimental findings and model predictions. Ceram. Int. 2016, 42, 8. [Google Scholar] [CrossRef]
- Huang, Y.; Hu, N.; Zeng, Y.; Song, X.; Lin, C.; Liu, Z.; Zhang, J. Effect of different types of pores on thermal conductivity of YSZ thermal barrier coatings. Coatings 2019, 9, 138. [Google Scholar] [CrossRef]
- Cernuschi, F.; Bison, P.G.; Marinetti, S.S.; Scardi, P. Thermophysical, mechanical and microstructural characterization of aged free-standing plasma-sprayed zirconia coatings. Acta Mater. 2008, 56, 4477–4488. [Google Scholar] [CrossRef]
- Curry, N.; Markocsan, N.; Li, X.H.; Tricoire, A.; Dorfman, M. Next generation thermal barrier coatings for the gas turbine industry. J. Therm. Spray Technol. 2011, 20, 108–115. [Google Scholar] [CrossRef]
- Paul, S. Assessing coating reliability through pore architecture evaluation. J. Therm. Spray Technol. 2010, 19, 779–786. [Google Scholar] [CrossRef]
- Fauchais, P.; Vardelle, M.; Goutier, S. Latest researches advances of plasma spraying: From splat to coating formation. J. Therm. Spray Technol. 2016, 25, 1534–1553. [Google Scholar] [CrossRef]
- Mutter, M.; Mauer, G.; Mücke, R.; Guillon, O.; Vaßen, R. Correlation of splat morphologies with porosity and residual stress in plasma-sprayed YSZ coatings. Surf. Coat. Technol. 2017, 318, 157–169. [Google Scholar] [CrossRef]
- Kumar, D.; Pandey, K.N. Optimization of the process parameters in generic thermal barrier coatings using the Taguchi method and grey relational analysis. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2015, 231, 600–610. [Google Scholar] [CrossRef]
- Praveen, A.S.; Sarangan, J.; Suresh, S.; Channabasappa, B.H. Optimization and erosion wear response of NiCrSiB/WC–Co HVOF coating using Taguchi method. Ceram. Int. 2016, 42, 1094–1104. [Google Scholar] [CrossRef]
- Zhang, B.C.; Chen, K.; Baddour, N.; Patnaik, P.C. Failure and life evaluation of EB-PVD thermal barrier coatings using temperature-process-dependent model parameters. Corros. Sci. 2019, 156, 1–9. [Google Scholar] [CrossRef]
- Li, M.; Christofides, P.D. Modeling and control of High-Velocity Oxygen-Fuel (HVOF) thermal spray: A tutorial review. J. Therm. Spray Technol. 2009, 18, 753–768. [Google Scholar] [CrossRef]
- Ranjbar-Far, M.; Absi, J.; Mariaux, G. Finite element modeling of the different failure mechanisms of a plasma sprayed thermal barrier coatings system. J. Therm. Spray Technol. 2012, 21, 1234–1244. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, D.; Lee, K.; Kim, A.S.; Raju, L.; Cai, W. Compounding meta-atoms into metamolecules with hybrid artificial intelligence techniques. Adv. Mater. 2019, 1904790. [Google Scholar] [CrossRef]
- Liu, M.; Yu, Z.; Zhang, Y.; Wu, H.; Liao, H.; Deng, S. Prediction and analysis of high velocity oxy fuel (HVOF) sprayed coating using artificial neural network. Surf. Coat. Technol. 2019, 378, 124988. [Google Scholar] [CrossRef]
- Ye, D.; Wang, W.; Zhou, H.; Fang, H.; Huang, J.; Li, Y.; Gong, H.; Li, Z. Characterization of thermal barrier coatings microstructural features using terahertz spectroscopy. Surf. Coat. Technol. 2020, 394, 125836. [Google Scholar] [CrossRef]
- Kutner, M.H.; Nachtsheim, C.J.; Neter, J.; Li, W. Applied Linear Statistical Models; McGraw-Hill Irwin: Boston, MA, USA, 2005. [Google Scholar]
- Chen, M. Matlab Neural Network Principle and Example Solution; Tsinghua University Press: Beijing, China, 2013. [Google Scholar]
- Gao, Y.; Pan, J.; Ji, G.; Gao, F. A time-series modeling method based on the boosting gradient-descent theory. Sci. China Technol. Sci. 2011, 54, 1325. [Google Scholar] [CrossRef]
- Wang, K.C. The Grey-Based Artificial Intelligence Modeling of Thermal Error for Machine Tools. J. Grey Syst. 2010, 22, 353–366. [Google Scholar]
- Kim, S.; Yu, Z.; Kil, R.M.; Lee, M. Deep learning of support vector machines with class probability output networks. Neural Netw. 2015, 64, 19–28. [Google Scholar] [CrossRef] [PubMed]
- Ge, H.; Jiang, Y.; Xu, Z.; Lian, F.; Zhang, Y.; Xia, S. Identification of wheat quality using THz spectrum. Opt. Express 2014, 22, 12533–12544. [Google Scholar] [CrossRef]
- Peng, Y.; Shi, C.; Xu, M.; Kou, T.; Wu, X.; Song, B.; Ma, H.; Guo, S.; Liu, L.; Zhu, Y. Qualitative and quantitative identification of components in mixture by Terahertz spectroscopy. IEEE Trans. Terahertz Sci. Technol. 2018, 8, 696–701. [Google Scholar] [CrossRef]
- Suganyadevi, M.V.; Babulal, C.K. Support Vector Regression Model for the prediction of Loadability Margin of a Power System. Appl. Soft Comput. 2014, 24, 304–315. [Google Scholar] [CrossRef]
- Li, X.Z.; Kong, J.M. Application of GA–SVM method with parameter optimization for landslide development prediction. Nat. Hazards Earth Syst. Sci. 2014, 14, 525–533. [Google Scholar] [CrossRef]
- Bessedik, S.A.; Hadi, H. Prediction of flashover voltage of insulators using least squares support vector machine with particle swarm optimisation. Electr. Power Syst. Res. 2013, 104, 87–92. [Google Scholar] [CrossRef]
- Cheng, J.; Fang, J.; Wu, W.; Li, J. Temperature drift modeling and compensation of RLG based on PSO tuning SVM. Measurement 2014, 55, 246–254. [Google Scholar] [CrossRef]
- Barthelemy, P.; Bertolotti, J.; Wiersma, D.A. Lévy flight for light. Nature 2008, 453, 495–498. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via levy flights. arXiv 2010, arXiv:1003.1594. Available online: https://arxiv.org/abs/1003.1594 (accessed on 23 July 2020).
- Jiang, M.; Luo, J.; Jiang, D.; Xiong, J.; Song, H.; Shen, J. A Cuckoo Search-Support Vector Machine Model for Predicting Dynamic Measurement Errors of Sensors. IEEE Access 2016, 4, 5030–5037. [Google Scholar] [CrossRef]
- Sobhanverdi, R.; Akbari, A. Porosity and microstructural features of plasma sprayed Yttria stabilized zirconia thermal barrier coatings. Ceram. Int. 2015, 41, 14517–14528. [Google Scholar] [CrossRef]
- Ghai, R.S.; Chen, K.; Baddour, N. Modelling thermal conductivity of porous thermal barrier coatings. Coatings 2019, 9, 101. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory; Springer: Berlin, Germany, 2000. [Google Scholar]
- Cristianini, N.; Shawe-Taylor, J. An Introduction to Support Vector Machines and Other Kernel-Based Learning Methods; Cambridge University Press: Cambridge, UK, 2000; pp. 93–124. [Google Scholar]
- Smola, A.J.; Scholkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Arunnehru, J.; Kalaiselvi Geetha, M. Difference intensity distance group pattern for recognizing actions in video using Support Vector Machines. Pattern Recognit. Image Anal. 2016, 26, 688–696. [Google Scholar] [CrossRef]
- Özorhan, M.O.; Toroslu, İ.H.; Şehitoğlu, O.T. A strength-biased prediction model for forecasting exchange rates using support vector machines and genetic algorithms. Soft Comput. 2017, 21, 6653–6671. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via lévy flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Yang, X.S.; Deb, S. Multiobjective cuckoo search for design optimization. Comput. Oper. Res. 2013, 40, 1616–1624. [Google Scholar] [CrossRef]
- Long, W.; Liang, X.; Huang, Y.; Chen, Y. An effective hybrid cuckoo search algorithm for constrained global optimization. Neural. Comput. Appl. 2014, 25, 911–926. [Google Scholar] [CrossRef]
- Bai, Y.; Zhao, L.; Qu, Y.; Fu, Q.; Wang, Y.; Liu, K.; Tang, J.; Li, B.; Han, Z. Particle in-flight behavior and its influence on the microstructure and properties of supersonic-atmospheric-plasma-sprayed nanostructured thermal barrier coatings. J. Alloys Compd. 2015, 644, 873–882. [Google Scholar] [CrossRef]
- Liu, K.; Tang, J.; Bai, Y.; Yang, Q.; Wang, Y.; Kang, Y.; Zhao, L.; Zhang, P.; Han, Z. Particle in-flight behavior and its influence on the microstructure and mechanical property of plasma sprayed La2Ce2O7 thermal barrier coatings. Mater. Sci. Eng. A 2015, 625, 177–185. [Google Scholar] [CrossRef]

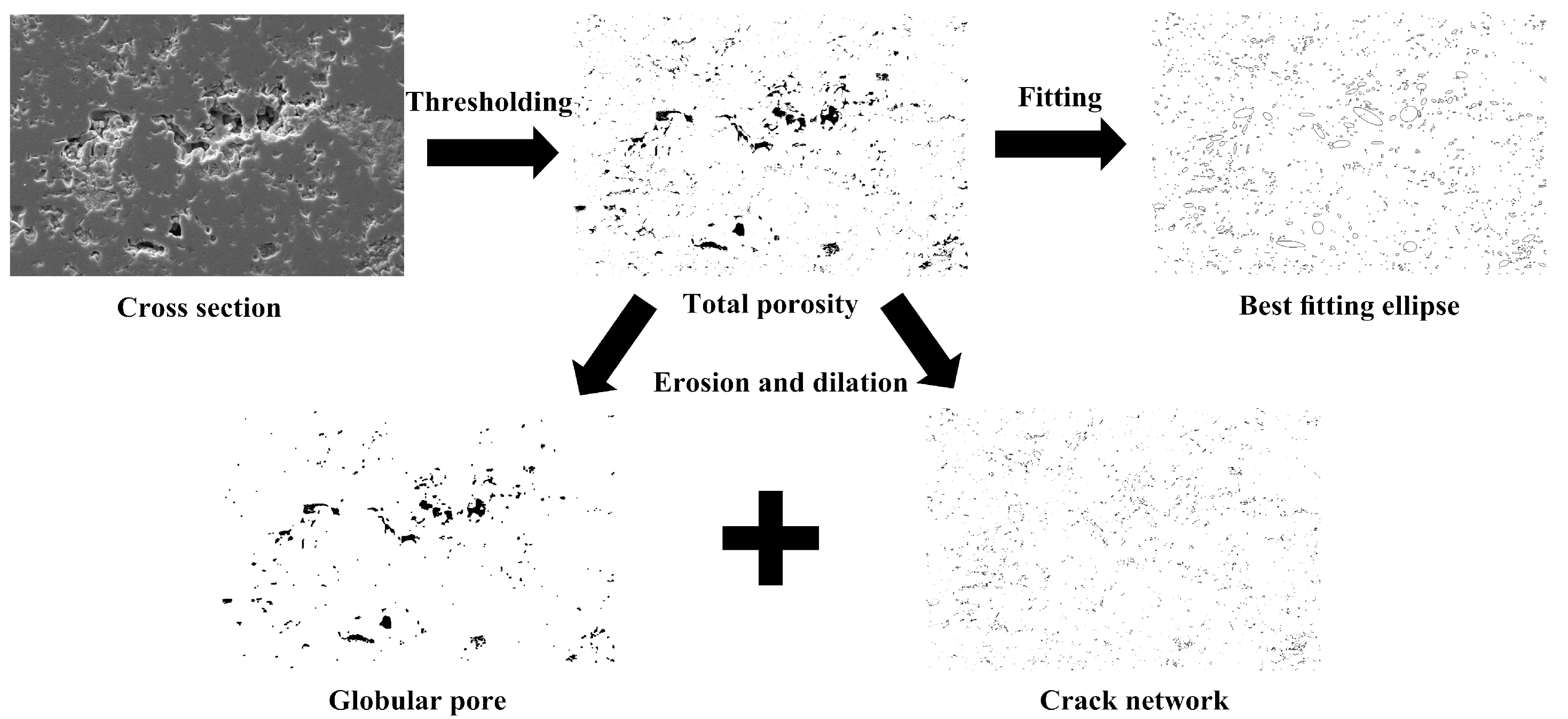

| APS Parameters | Optional Indicators |
|---|---|
| Particle size (μm) | 40–96, 15–55 |
| Spray distance L (mm) | 70, 80, 90, 100, 110, and 120 |
| Spray power (kW) | 24, 30, 33, and 36 |
| Powder feed rate (L/min) | 10 |
| gun speed (cm/s) | 15 |
| Microstructure Feature | Definition | Symbol |
|---|---|---|
| Porosity | The volume percent of pore | ω |
| Pore-to-crack ratio | The ratio of the globular pore area to crack network area | k |
| Maximum Feret’s diameter | Maximum distance between two points on the boundary | Df |
| Circularity | 4πA/p2 (A is the pore area and p is the pore perimeter) | Cr |
| Aspect ratio | Ratio of the longest diameter to shortest diameter (best fitting ellipse) | AR |
| No. | APS Process Parameters | Microstructural Features (Average Value) | ||||||
|---|---|---|---|---|---|---|---|---|
| Particle Size (μm) | Spray Distance (mm) | Spray Power (kW) | Porosity | Pore-to-Crack Ratio | Maximum Feret’s Diameter (μm) | Aspect Ratio | Circularity | |
| 1 | 15–55 | 70 | 36 | 11.83% ± 1.04% | 0.4062 ± 0.0222 | 1.2949 ± 0.2160 | 1.6312 ± 0.0519 | 0.8591 ± 0.0231 |
| 2 | 15–55 | 80 | 36 | 11.37% ± 1.63% | 0.5005 ± 0.0479 | 1.6076 ± 0.3802 | 1.6983 ± 0.0517 | 0.8436 ± 0.0130 |
| 3 | 15–55 | 90 | 24 | 12.98% ± 1.98% | 0.5419 ± 0.0278 | 1.7304 ± 0.1842 | 1.7283 ± 0.0136 | 0.8286 ± 0.0115 |
| 4 | 15–55 | 90 | 30 | 11.91% ± 1.02% | 0.5337 ± 0.0346 | 1.9900 ± 0.1723 | 1.7126 ± 0.0155 | 0.8039 ± 0.0052 |
| 5 | 15–55 | 90 | 33 | 11.25% ± 1.65% | 0.4336 ± 0.0517 | 1.6842 ± 0.3143 | 1.7333 ± 0.0431 | 0.8130 ± 0.0048 |
| 6 | 15–55 | 90 | 36 | 8.99% ± 0.96% | 0.3582 ± 0.0387 | 1.7011 ± 0.0591 | 1.7281 ± 0.0297 | 0.7899 ± 0.0134 |
| 7 | 15–55 | 100 | 36 | 10.14% ± 1.92% | 0.3998 ± 0.0301 | 1.8026 ± 0.1241 | 1.7658 ± 0.0295 | 0.8028 ± 0.0078 |
| 8 | 15–55 | 110 | 36 | 13.02% ± 1.44% | 0.4305 ± 0.0147 | 1.8072 ± 0.1407 | 1.7800 ± 0.0131 | 0.8049 ± 0.0049 |
| 9 | 15–55 | 120 | 36 | 16.83% ± 2.05% | 0.5902 ± 0.0271 | 2.0997 ± 0.2245 | 1.8294 ± 0.0384 | 0.7968 ± 0.0083 |
| 10 | 40–96 | 70 | 36 | 15.02% ± 1.77% | 0.3690 ± 0.0571 | 2.4856 ± 0.1337 | 1.7172 ± 0.0271 | 0.7899 ± 0.0163 |
| 11 | 40–96 | 80 | 36 | 15.38% ± 1.56% | 0.3480 ± 0.0194 | 2.2385 ± 0.1580 | 1.7898 ± 0.0167 | 0.7710 ± 0.0254 |
| 12 | 40–96 | 90 | 36 | 15.93% ± 1.85% | 0.3620 ± 0.0201 | 2.6294 ± 0.2081 | 1.7981 ± 0.0635 | 0.7811 ± 0.0169 |
| 13 | 40–96 | 100 | 36 | 18.31% ± 2.23% | 0.3720 ± 0.0288 | 2.6478 ± 0.2335 | 1.7821 ± 0.0215 | 0.7638 ± 0.0140 |
| 14 | 40–96 | 110 | 36 | 20.62% ± 1.79% | 0.3990 ± 0.0302 | 2.9361 ± 0.3542 | 1.8054 ± 0.0457 | 0.7529 ± 0.0234 |
| 15 | 40–96 | 120 | 36 | 23.01% ± 2.42% | 0.4100 ± 0.0256 | 3.0536 ± 0.2861 | 1.8350 ± 0.0529 | 0.7322 ± 0.0134 |
| Range Analysis | Particle Size (Factor A) | Spray Distance (Factor B) | Spray Power (Factor C) | Influence Rank |
|---|---|---|---|---|
| Porosity | 0.0601 | 0.0771 | 0.0379 | B > A > C |
| Pore-to-crack ratio | 0.0894 | 0.1142 | 0.1298 | C > B > A |
| Maximum Feret’s diameter | 0.9188 | 0.6865 | 0.5078 | A > B > C |
| Aspect ratio | 0.0538 | 0.1580 | 0.0508 | B > A > C |
| Circularity | 0.0506 | 0.0600 | 0.7907 | C > B > A |
| Training Results | R2 | RMSE | MAE | MAPE |
|---|---|---|---|---|
| Porosity | 0.9773 | 0.0050 | 0.0046 | 0.0360 |
| Pore-to-crack ratio | 0.9900 | 0.0118 | 0.0117 | 0.0273 |
| Maximum Feret’s diameter (μm) | 0.9709 | 0.0794 | 0.0739 | 0.0382 |
| Aspect ratio | 0.9569 | 0.0106 | 0.0102 | 0.0058 |
| Circularity | 0.9759 | 0.0059 | 0.0057 | 0.0072 |
| Prediction Results | R2 | RMSE | MAE | MAPE |
|---|---|---|---|---|
| Porosity | 0.9922 | 0.0061 | 0.0057 | 0.0303 |
| Pore-to-crack ratio | 0.9798 | 0.0076 | 0.0063 | 0.0159 |
| Maximum Feret’s diameter (μm) | 0.9955 | 0.0954 | 0.0943 | 0.0408 |
| Aspect ratio | 0.9767 | 0.0140 | 0.0130 | 0.0074 |
| Circularity | 0.9953 | 0.0061 | 0.0047 | 0.0059 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ye, D.; Wang, W.; Xu, Z.; Yin, C.; Zhou, H.; Li, Y. Prediction of Thermal Barrier Coatings Microstructural Features Based on Support Vector Machine Optimized by Cuckoo Search Algorithm. Coatings 2020, 10, 704. https://doi.org/10.3390/coatings10070704
Ye D, Wang W, Xu Z, Yin C, Zhou H, Li Y. Prediction of Thermal Barrier Coatings Microstructural Features Based on Support Vector Machine Optimized by Cuckoo Search Algorithm. Coatings. 2020; 10(7):704. https://doi.org/10.3390/coatings10070704
Chicago/Turabian StyleYe, Dongdong, Weize Wang, Zhou Xu, Changdong Yin, Haiting Zhou, and Yuanjun Li. 2020. "Prediction of Thermal Barrier Coatings Microstructural Features Based on Support Vector Machine Optimized by Cuckoo Search Algorithm" Coatings 10, no. 7: 704. https://doi.org/10.3390/coatings10070704
APA StyleYe, D., Wang, W., Xu, Z., Yin, C., Zhou, H., & Li, Y. (2020). Prediction of Thermal Barrier Coatings Microstructural Features Based on Support Vector Machine Optimized by Cuckoo Search Algorithm. Coatings, 10(7), 704. https://doi.org/10.3390/coatings10070704





