Molecular Dynamics Study of Anti-Wear Erosion and Corrosion Protection of PTFE/Al2O3 (010) Coating Composite in Water Hydraulic Valves
Abstract
1. Introduction
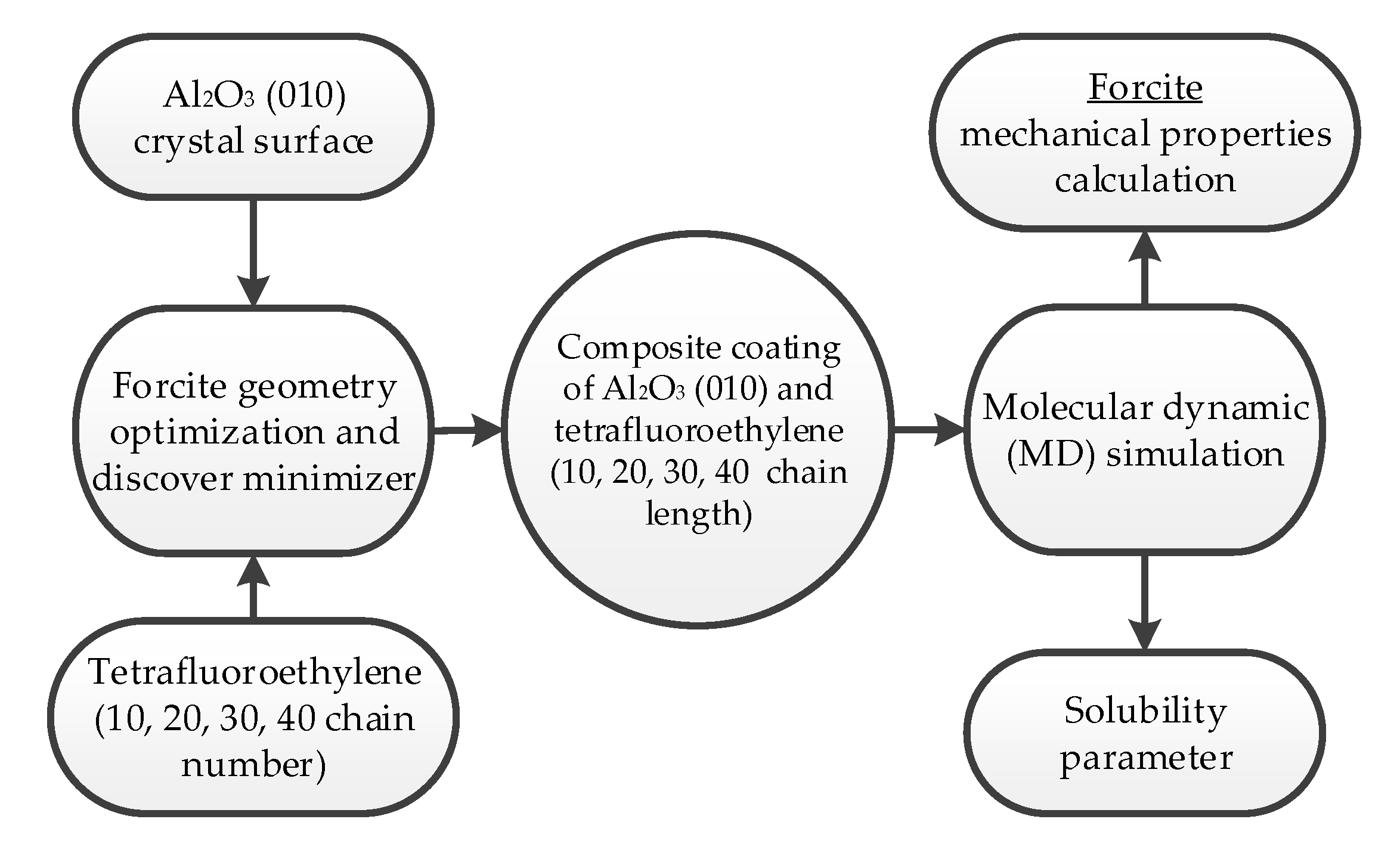
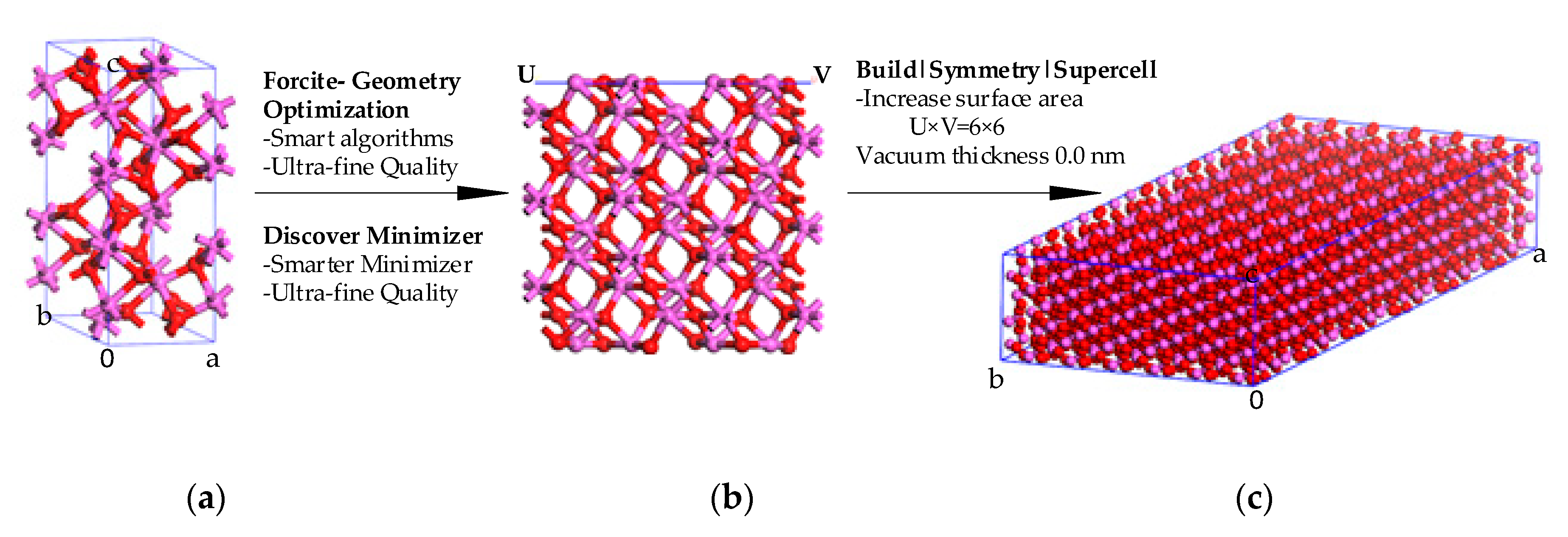
2. Method and Approach
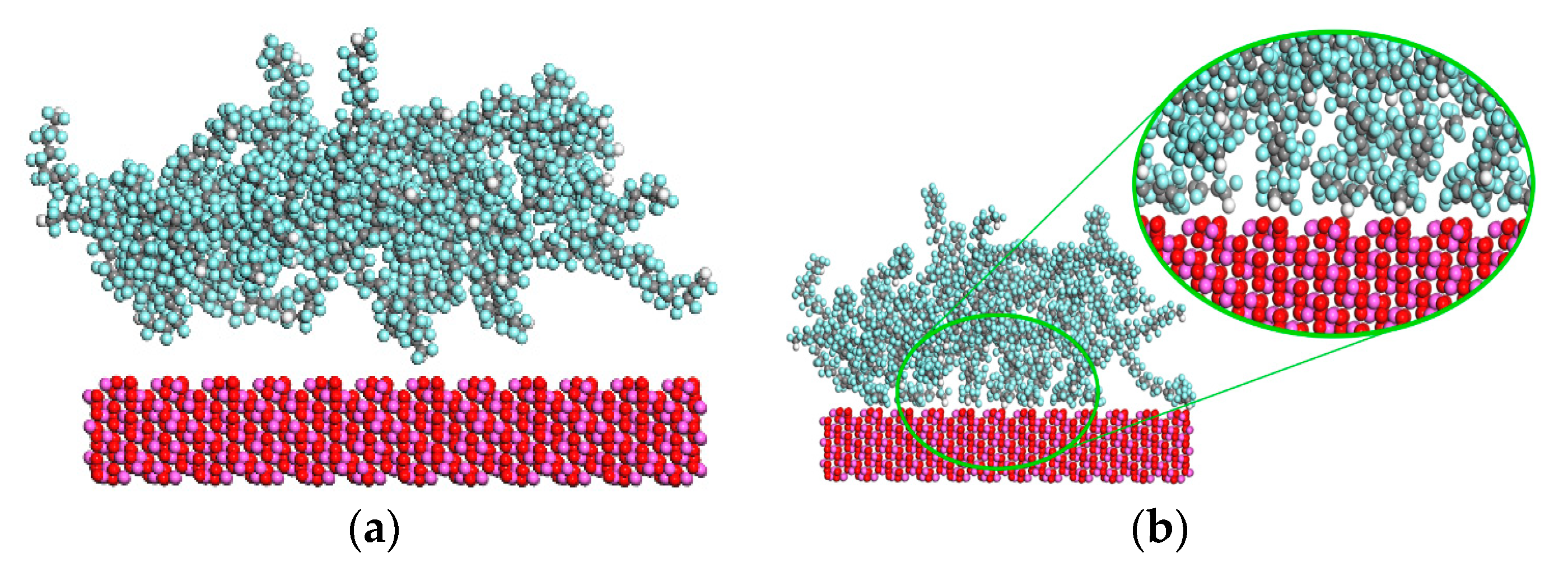
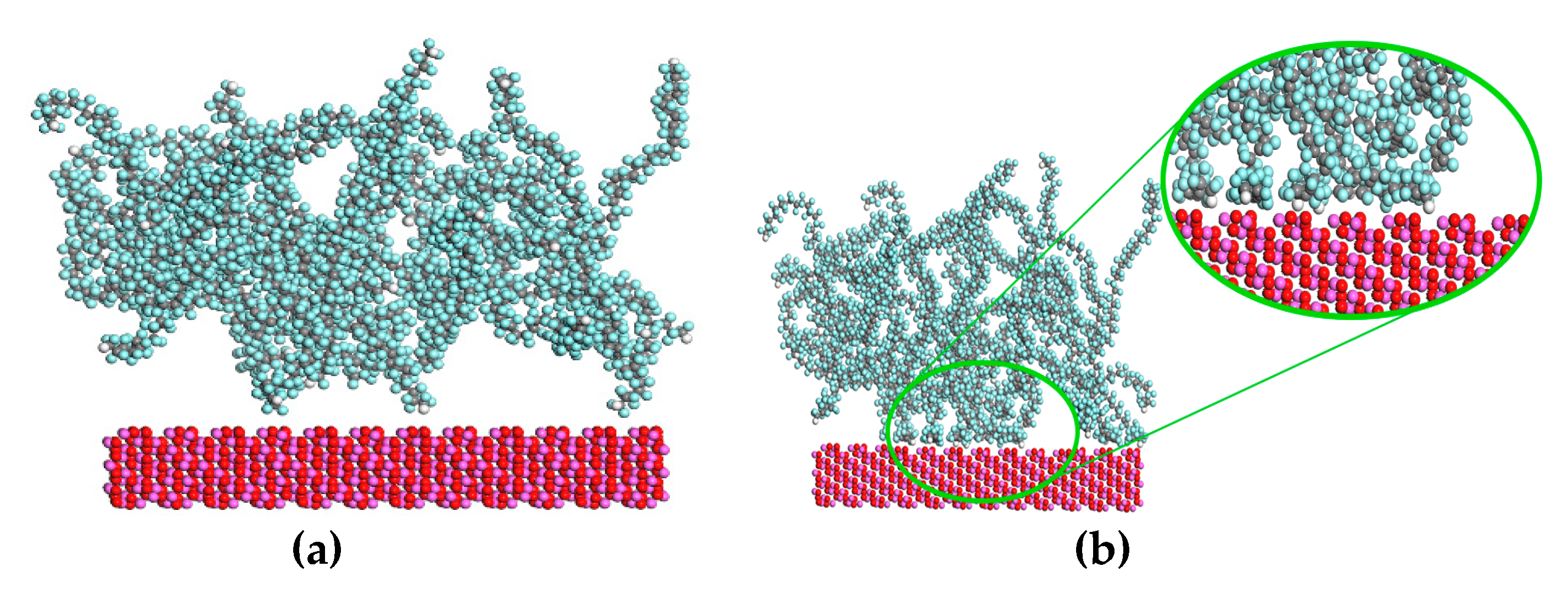
Molecular Dynamics (MD) Simulation and Properties Calculation
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Micu, L.M.; Lazar, I.; Circiumaru, A.; Bordeasu, I.; Pirvulescu, L.D.; Hluscu, M. New results regarding cavitation behavior of polymers modified with anorganic substances coated on bronze surfaces. Mater. Plast. 2018, 55, 460–463. [Google Scholar] [CrossRef]
- Zheng, H.-W.; Shu, X.-Y.; Li, Y.; Zhao, J.-P. Mechanical properties of Fe-based amorphous–crystalline composite: A molecular dynamics simulation and experimental study. Rare Met. 2018. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, H.; Yang, J.; Liu, R.; Zhou, Z.; Hao, T.; Nie, Y. Molecular simulations of microscopic mechanism of the effects of chain length on stereocomplex formation in polymer blends. Comput. Mater. Sci. 2020, 172, 109297. [Google Scholar] [CrossRef]
- Chen, B.; O’Mahony, J.A. Impact of glucose polymer chain length on heat and physical stability of milk protein-carbohydrate nutritional beverages. Food Chem. 2016, 211, 474–482. [Google Scholar] [CrossRef] [PubMed]
- Zhao, J.; Lu, L.; Rabczuk, T. The tensile and shear failure behavior dependence on chain length and temperature in amorphous polymers. Comput. Mater. Sci. 2015, 96, 567–572. [Google Scholar] [CrossRef]
- Pacułt, J.; Rams-Baron, M.; Chrząszcz, B.; Jachowicz, R.; Paluch, M. Effect of polymer chain length on the physical stability of amorphous drug–polymer blends at ambient pressure. Mol. Pharm. 2018, 15, 2807–2815. [Google Scholar] [CrossRef] [PubMed]
- Mlela, M.K.; Xu, H.; Sun, F.; Wang, H.; Madenge, G.D. Material analysis and molecular dynamics simulation for cavitation erosion and corrosion suppression in water hydraulic valves. Materials 2020, 13, 453. [Google Scholar] [CrossRef]
- Li, H.; Bahuleyan, B.K.; Johnson, R.P.; Shchipunov, Y.A.; Suh, H.; Ha, C.-S.; Kim, I. Morphology-tunable architectures constructed by supramolecular assemblies of α-diimine compound: Fabrication and application as multifunctional host systems. J. Mater. Chem. 2011, 21, 17938–17945. [Google Scholar] [CrossRef]
- Sun, H.; Jin, Z.; Yang, C.; Akkermans, R.L.C.; Robertson, S.H.; Spenley, N.A.; Miller, S.; Todd, S.M. COMPASS II: Extended coverage for polymer and drug-like molecule databases. J. Mol. Model. 2016, 22, 47. [Google Scholar] [CrossRef]
- Wang, J.; Jin, S.; Chen, S.; Li, L.; Wang, D.; Lu, Z.; Wang, N.; Wang, J. Molecular dynamic simulations for FOX-7 and FOX-7 based PBXs. J. Mol. Model. 2018, 24, 145. [Google Scholar] [CrossRef]
- Chung, D.H.; Buessem, W.R. The Voigt-Reuss-Hill (VRH) Approximation and the Elastic Moduli of Polycrystalline ZnO, TiO2 (Rutile), and α-Al2O3. J. Appl. Phys. 1968, 39, 2777–2782. [Google Scholar] [CrossRef]
- Hua, X.; Wang, L.; Yang, S.J.P. Molecular dynamics simulation of improving the physical properties of polytetrafluoroethylene cable insulation materials by boron nitride nanoparticle under moisture-temperature-electric fields conditions. Polymers 2019, 11, 971. [Google Scholar] [CrossRef] [PubMed]
- Muhammad, I.D.; Awang, M.; Mamat, O.; Shaari, Z.B. First-principles calculations of the structural, mechanical and thermodynamics properties of cubic zirconia. World J. Nano Sci. Eng. 2014, 4, 97. [Google Scholar] [CrossRef]
- Greaves, G.N.; Greer, A.L.; Lakes, R.S.; Rouxel, T. Poisson’s ratio and modern materials. Nat. Mater. 2011, 10, 823–837. [Google Scholar] [CrossRef]
- Rosato, D.; Rosato, D. DESIGN PARAMETER. In Plastics Engineered Product Design; Elsevier Science: Amsterdam, The Netherlands, 2003; pp. 161–197. [Google Scholar]
- Polymer Properties Database. Relationship between Moduli of Elasticity. 2020. Available online: http://polymerdatabase.com/polymer%20physics/Moduli.html (accessed on 2 July 2020).
- Gatt, R.; Grima, J. Negative compressibility. Phys. Status Solidi (RRL)-Rapid Res. Lett. 2008, 2, 236–238. [Google Scholar] [CrossRef]
- Lakes, R.; Wojciechowski, K.W. Negative compressibility, negative Poisson’s ratio, and stability. Phys. Status Solidi (B) 2008, 245, 545–551. [Google Scholar] [CrossRef]
- Cairns, A.B.; Goodwin, A.L. Negative linear compressibility. Phys. Chem. Chem. Phys. 2015, 17, 20449–20465. [Google Scholar] [CrossRef]
- Schuëller, G.I. Computational Methods in Stochastic Dynamics, 1st ed.; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Corrosionpedia. Mass Density. 2019. Available online: https://www.corrosionpedia.com/definition/1562/mass-density (accessed on 24 May 2020).
- Zhou, X.; Hu, G. Analytic model of elastic metamaterials with local resonances. Phys. Rev. B 2009, 79, 195109. [Google Scholar] [CrossRef]
- Karimi, A.; Martin, J.L. Cavitation erosion of materials. Int. Met. Rev. 1986, 31, 1–26. [Google Scholar] [CrossRef]
- Wang, Y.; Lakes, R. Composites with inclusions of negative bulk modulus: Extreme damping and negative Poisson’s ratio. J. Compos. Mater. 2005, 39. [Google Scholar] [CrossRef]
- Moore, B.; Jaglinski, T.; Stone, D.S.; Lakes, R.S. Negative incremental bulk modulus in foams. Philos. Mag. Lett. 2006, 86, 651–659. [Google Scholar] [CrossRef]
- Su, Y.C.; Sun, C.T. Design of double negativity elastic metamaterial. Int. J. Smart Nano Mater. 2015, 6, 1–12. [Google Scholar] [CrossRef][Green Version]
- Wu, Y.; Lai, Y.; Zhang, Z.-Q. Elastic metamaterials with simultaneously negative effective shear modulus and mass density. Phys. Rev. Lett. 2011, 107, 105506. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.H.; Lee, S.B. The Hildebrand solubility parameters, cohesive energy densities and internal energies of 1-alkyl-3-methylimidazolium-based room temperature ionic liquids. Chem. Commun. 2005, 27, 3469–3471. [Google Scholar] [CrossRef] [PubMed]



| Chain Length (K) | Number of Chains | Number of Configuration | Amorphous Cell Parameter (nm) |
|---|---|---|---|
| 10 | 10 | 2 | a = 7.795, b = 2.855, c = 0.747 |
| 20 | 10 | 2 | a = 7.795, b = 2.855, c = 1.493 |
| 30 | 10 | 2 | a = 7.795, b = 2.855, c = 2.239 |
| 40 | 10 | 2 | a = 7.795, b = 2.855, c = 2.985 |
| Coating of an Amorphous Cell of K10 Chain Length of PTFE on Al2O3 (010) | ||||||
| Cij (GPa) | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | −1276.94 | −2274.16 | −3758.69 | −627.14 | 333.72 | −253.96 |
| 2 | −2274.16 | −3386.35 | −4816.39 | −490.81 | 411.54 | −323.10 |
| 3 | −3758.69 | −4816.39 | −6567.59 | −520.05 | 478.95 | −328.83 |
| 4 | −627.14 | −490.81 | −520.05 | 72.10 | 14.45 | 75.11 |
| 5 | 333.72 | 411.54 | 478.95 | 14.4466 | −21.22 | 2.47 |
| 6 | −253.96 | −323.10 | −328.83 | 75.11 | 2.47 | −127.57 |
| Coating of an Amorphous Cell of K20 Chain Length of PTFE on Al2O3 (010) | ||||||
| Cij (GPa) | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 407.85 | 1468.53 | −1695.44 | 2793.44 | −587.12 | 1229.29 |
| 2 | 1468.54 | 2051.47 | −81.20 | 2679.19 | −532.33 | 851.38 |
| 3 | −1695.44 | −81.20 | −4798.43 | 3515.44 | −712.54 | 1884.61 |
| 4 | 2793.44 | 2679.19 | 3515.45 | 158.28 | 35.72 | −171.47 |
| 5 | −587.12 | −532.33 | −712.53 | 35.72 | −29.93 | −23.67 |
| 6 | 1229.29 | 851.38 | 1884.61 | −171.47 | −23.67 | −422.33 |
| Coating of an Amorphous Cell of K30 Chain Length of PTFE on Al2O3 (010) | ||||||
| Cij (GPa) | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 6455.40 | 2093.16 | 368.40 | −344.27 | 2804.84 | −7985.71 |
| 2 | 2093.16 | −2217.00 | −4349.66 | −15.84 | 2656.07 | −7700.60 |
| 3 | 368.34 | −4349.66 | −9322.88 | −122.49 | 3771.29 | −9737.98 |
| 4 | −344.27 | −15.83 | −122.49 | −15.789 | −34.00 | 414.38 |
| 5 | 2804.84 | 2656.07 | 3771.29 | −34.009 | −47.43 | −144.01 |
| 6 | −7985.71 | −7700.60 | −9737.98 | 414.38 | −144.01 | 531.12 |
| Coating of an Amorphous cell of K40 chain Length of PTFE on Al2O3 (010) | ||||||
| Cij (GPa) | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 685.48 | 587.11 | −111.84 | −1777.92 | 892.86 | −448.15 |
| 2 | 587.11 | 453.74 | −440.53 | −1917.85 | 969.05 | −419.62 |
| 3 | −111.84 | −440.53 | −1064.19 | −1594.49 | 880.50 | −540.85 |
| 4 | −1777.92 | −1917.85 | −1594.49 | 131.19 | −7.49 | −61.23 |
| 5 | 892.86 | 969.05 | 880.50 | −7.49 | −90.60 | 81.79 |
| 6 | −448.15 | −419.62 | −540.84 | −61.23 | 81.79 | 102.39 |
| Property | K10 Chain Length | K20 Chain Length | K30 Chain Length | K40 Chain Length |
|---|---|---|---|---|
| Binding Energy, Eb (kJ/mol) | 6267.16 | 4271.05 | 3428.92 | 590.58 |
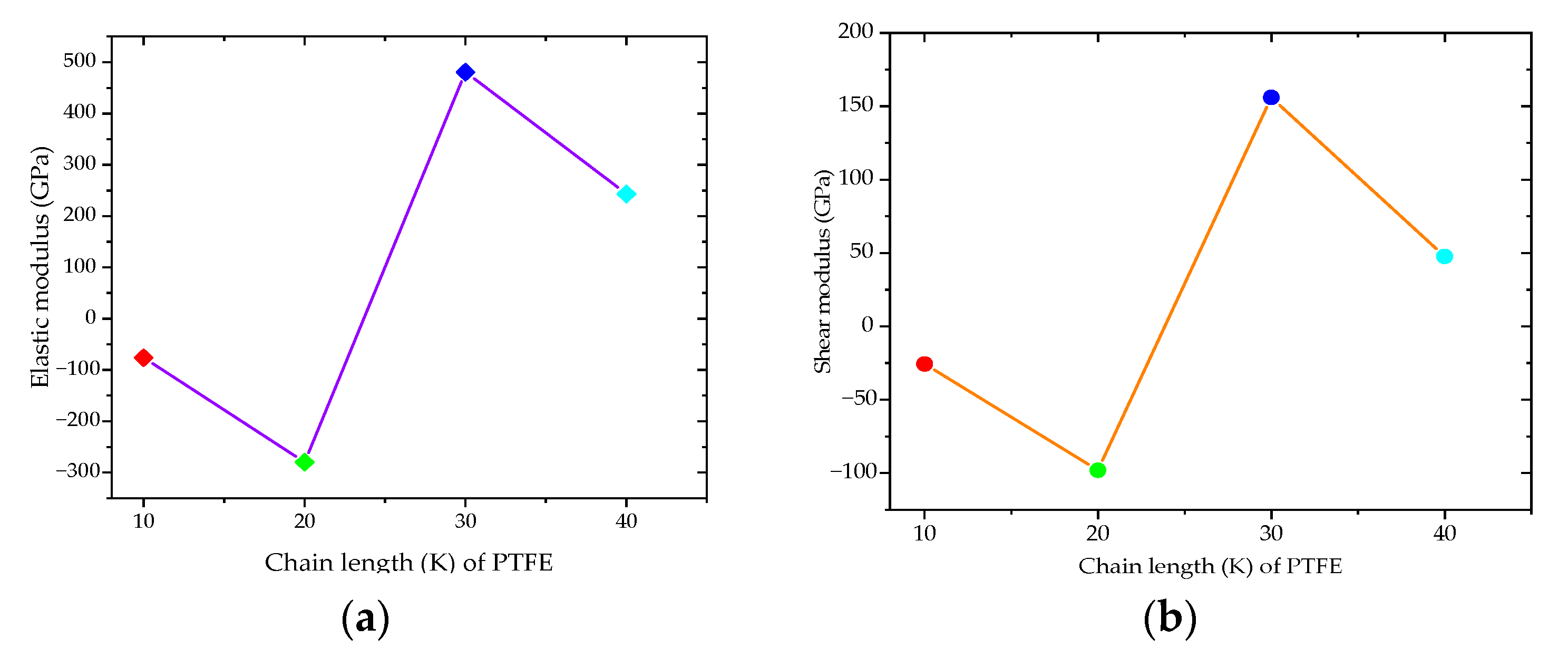
| Elastic Modulus, E (GPa) | −76.52 | −279.89 | 481.04 | 243.28 |
| Shear Modulus, G (GPa) | −25.56 | −97.99 | 155.96 | 47.66 |
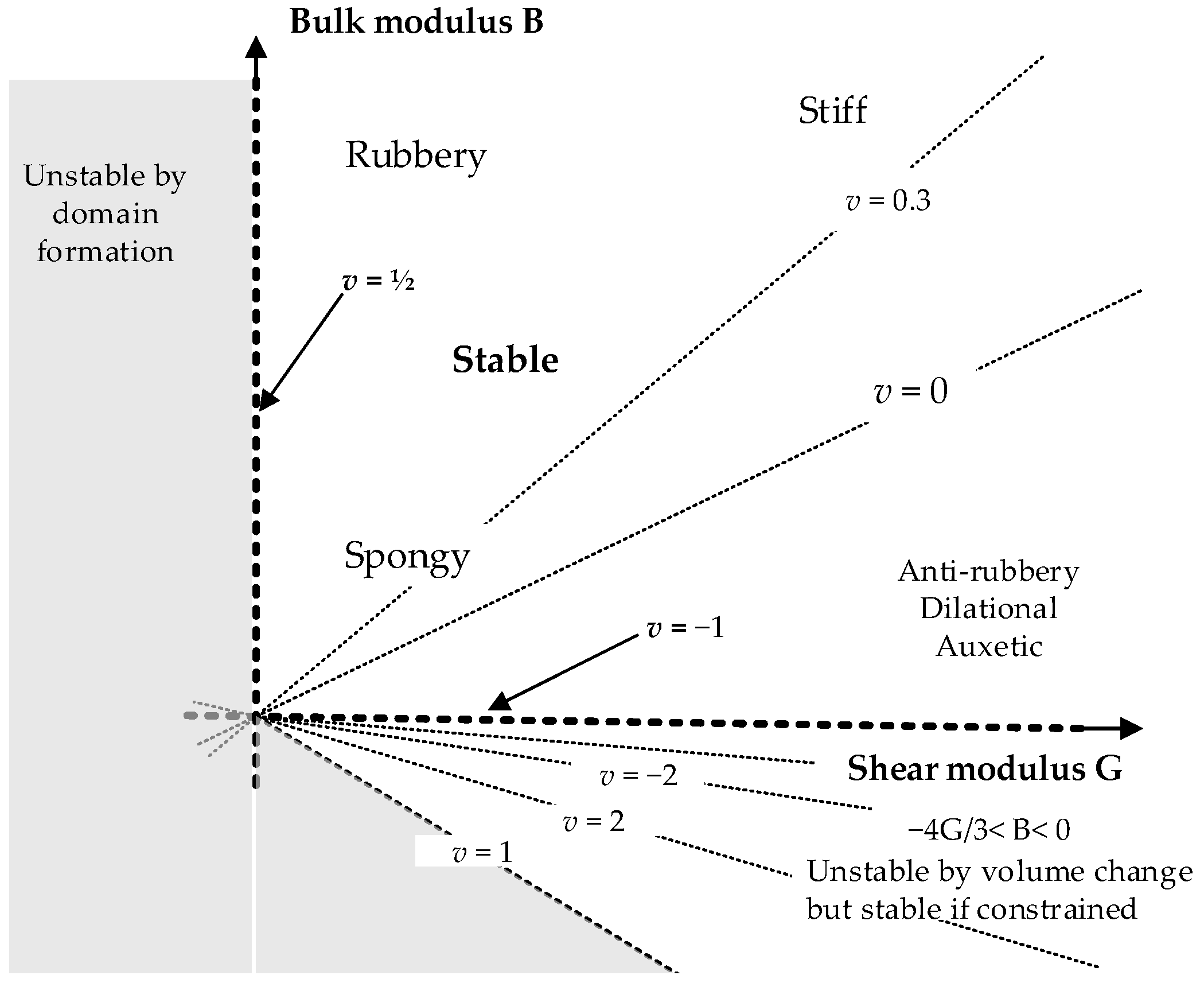
| Bulk Modulus, B (GPa) | −3709.54 | −649.04 | −1902.78 | −38.54 |
| Poisson’s Ratio, v (GPa) | 0.49 | 0.42 | 0.54 | 1.55 |
| Chain Length (K) | CED (J/m3) × 109 | Solubility Parameter (J/cm3)0.5 |
|---|---|---|
| 10 | 6.885 ± 0.00076 | 82.974 ± 0.005 |
| 20 | 4.370 ± 0.00104 | 66.110 ± 0.008 |
| 30 | 2.691 ± 0.00077 | 51.876 ± 0.007 |
| 40 | 0.9 ± 0.00078 | 30.000 ± 0.013 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mlela, M.K.; Xu, H.; Wang, H. Molecular Dynamics Study of Anti-Wear Erosion and Corrosion Protection of PTFE/Al2O3 (010) Coating Composite in Water Hydraulic Valves. Coatings 2020, 10, 1214. https://doi.org/10.3390/coatings10121214
Mlela MK, Xu H, Wang H. Molecular Dynamics Study of Anti-Wear Erosion and Corrosion Protection of PTFE/Al2O3 (010) Coating Composite in Water Hydraulic Valves. Coatings. 2020; 10(12):1214. https://doi.org/10.3390/coatings10121214
Chicago/Turabian StyleMlela, Masoud Kamoleka, He Xu, and Haihang Wang. 2020. "Molecular Dynamics Study of Anti-Wear Erosion and Corrosion Protection of PTFE/Al2O3 (010) Coating Composite in Water Hydraulic Valves" Coatings 10, no. 12: 1214. https://doi.org/10.3390/coatings10121214
APA StyleMlela, M. K., Xu, H., & Wang, H. (2020). Molecular Dynamics Study of Anti-Wear Erosion and Corrosion Protection of PTFE/Al2O3 (010) Coating Composite in Water Hydraulic Valves. Coatings, 10(12), 1214. https://doi.org/10.3390/coatings10121214





