Modeling and Optimization Approaches of Laser-Based Powder-Bed Fusion Process for Ti-6Al-4V Alloy
Abstract
:1. Introduction
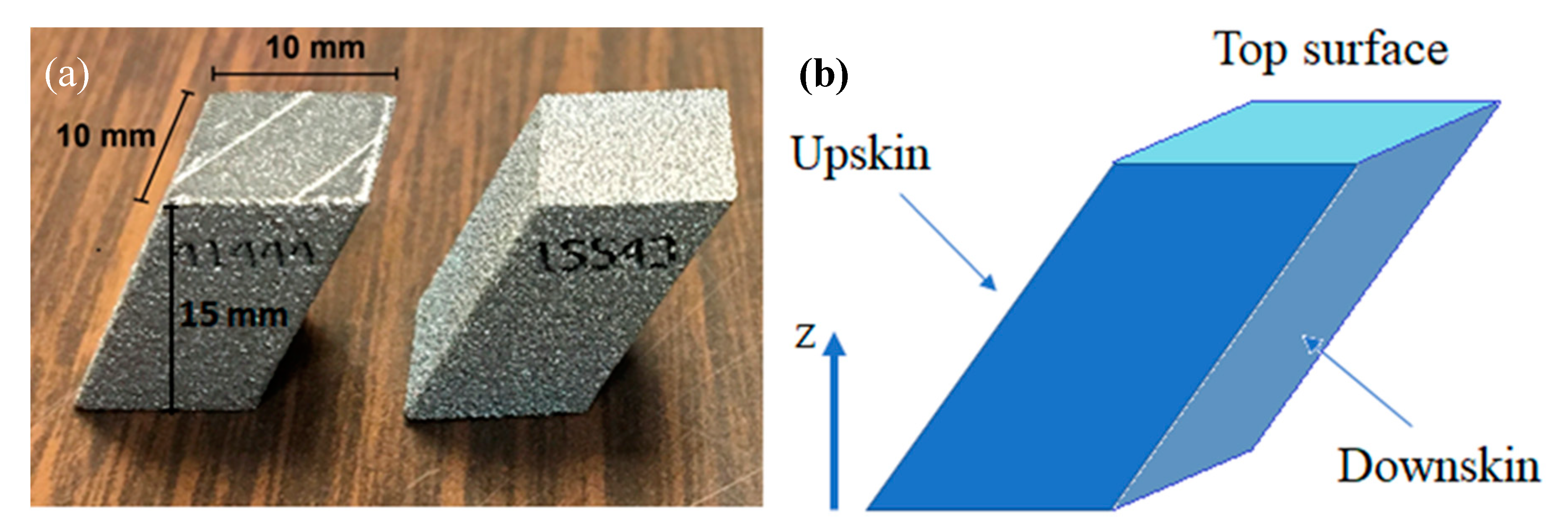
2. Materials and Methods
3. DoE for the L-PBF Process Parameters
3.1. Taguchi Method
3.2. Response Surface Method
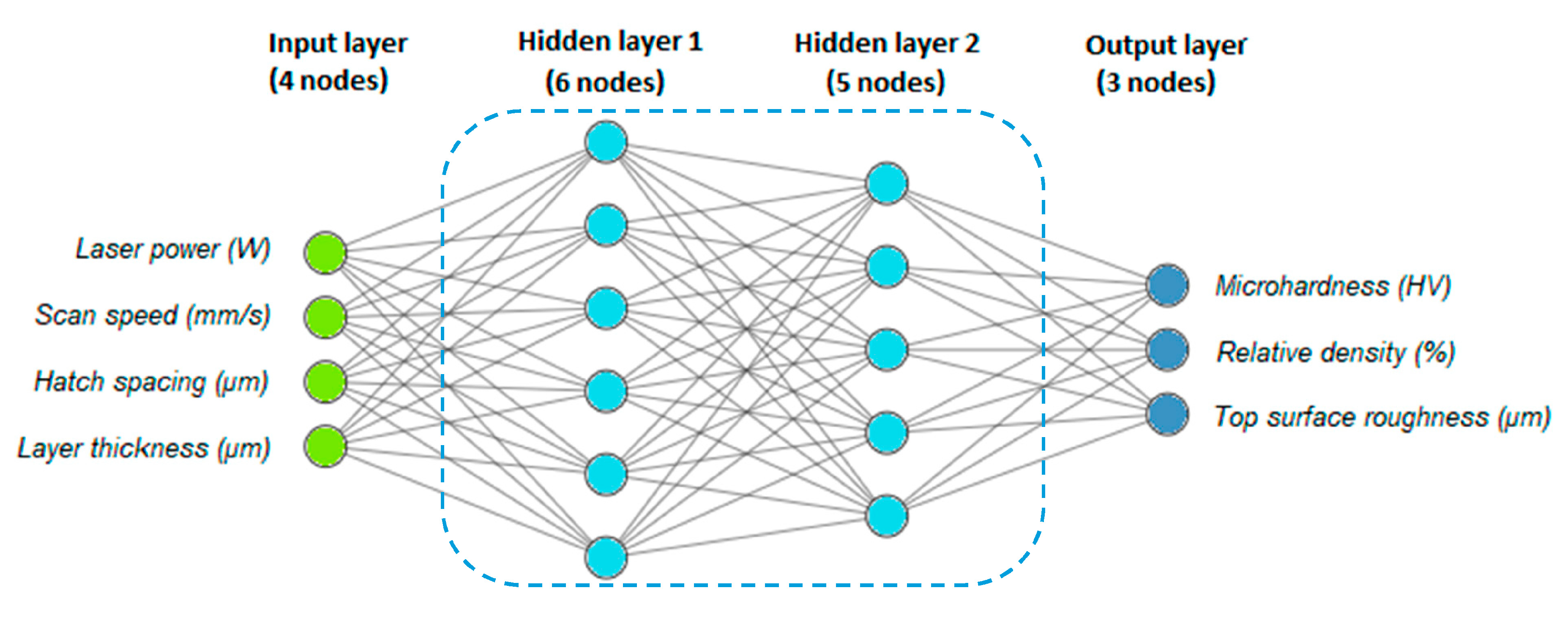
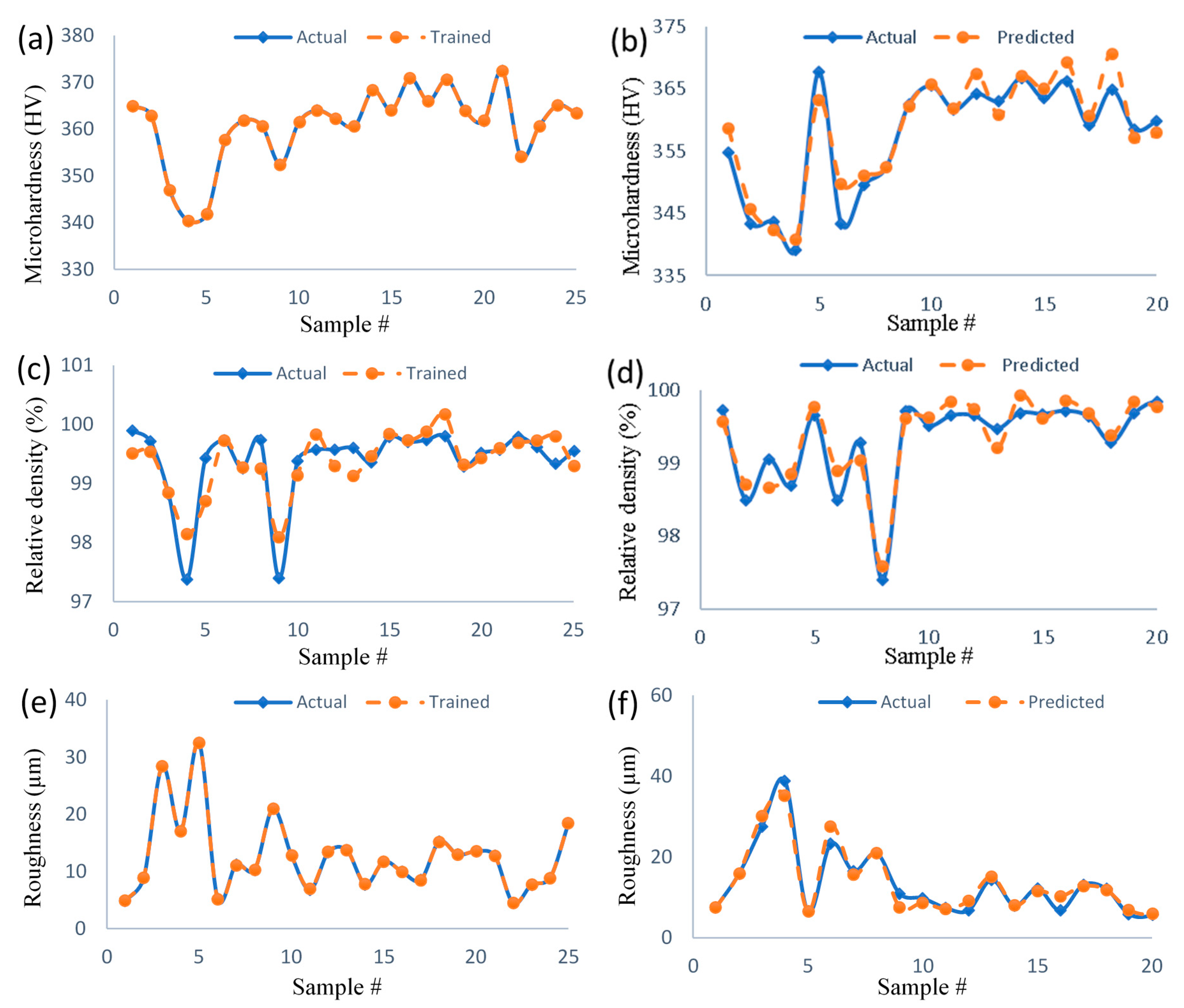
3.3. Artificial Neural Network
4. Results and Discussions
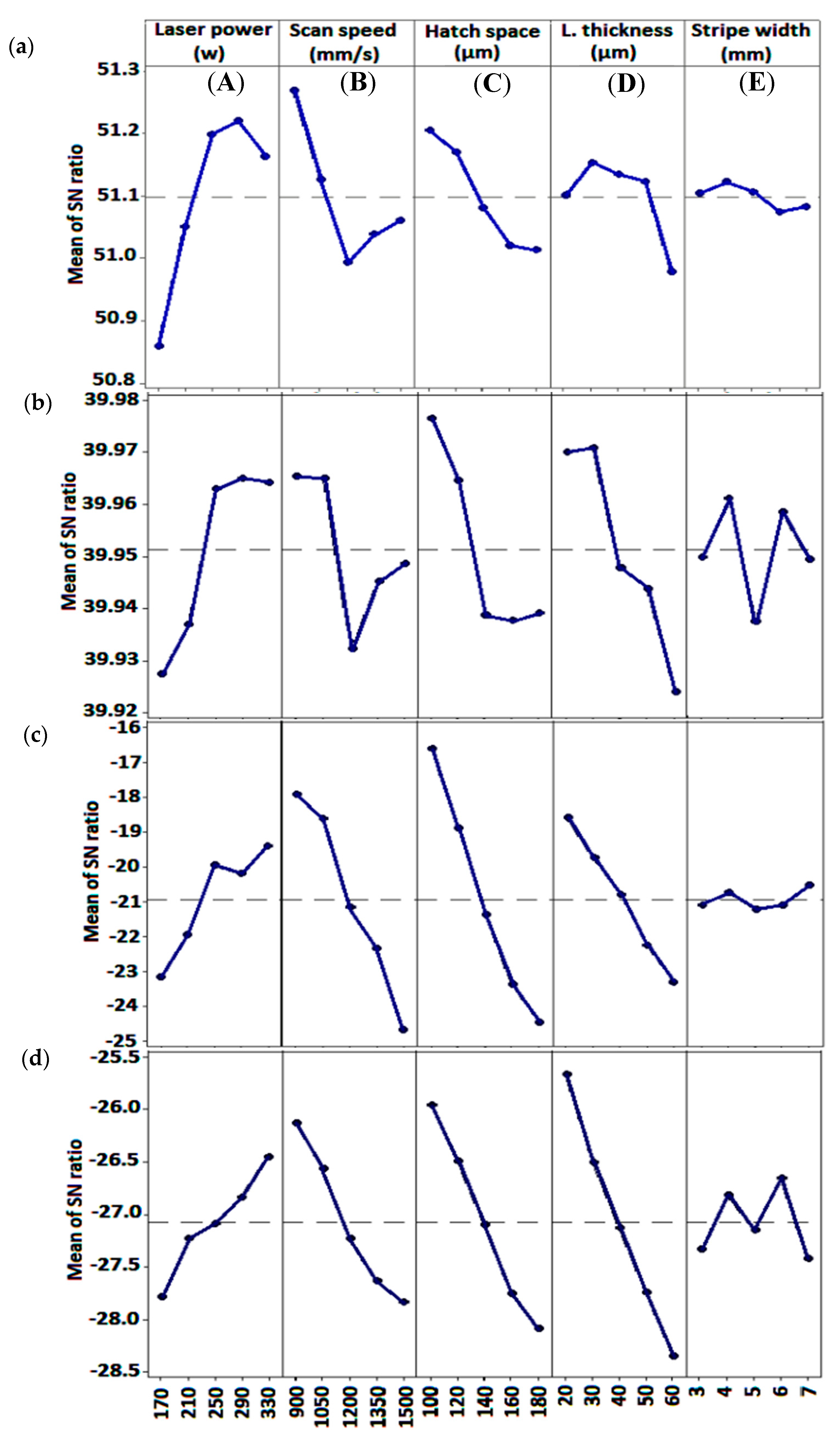
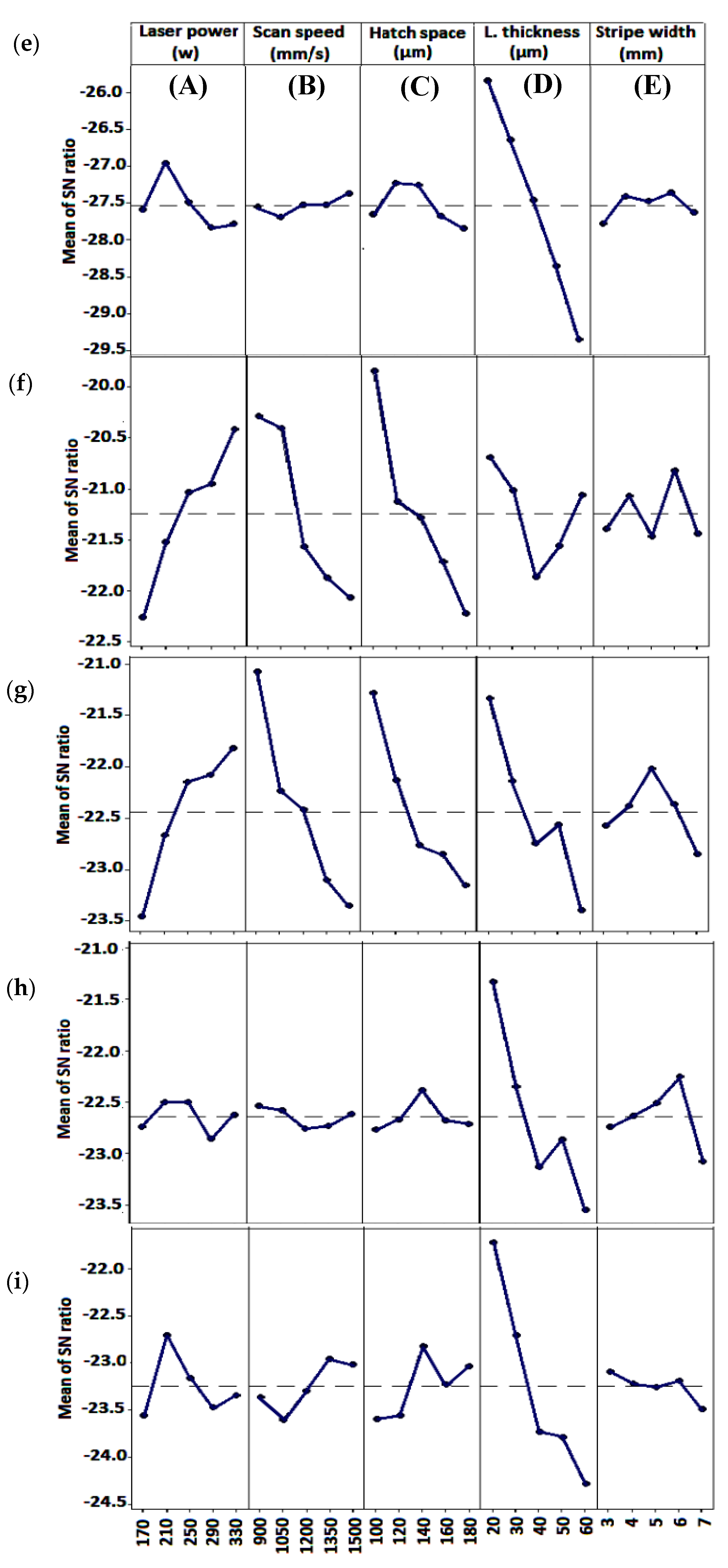
4.1. Taguchi Method
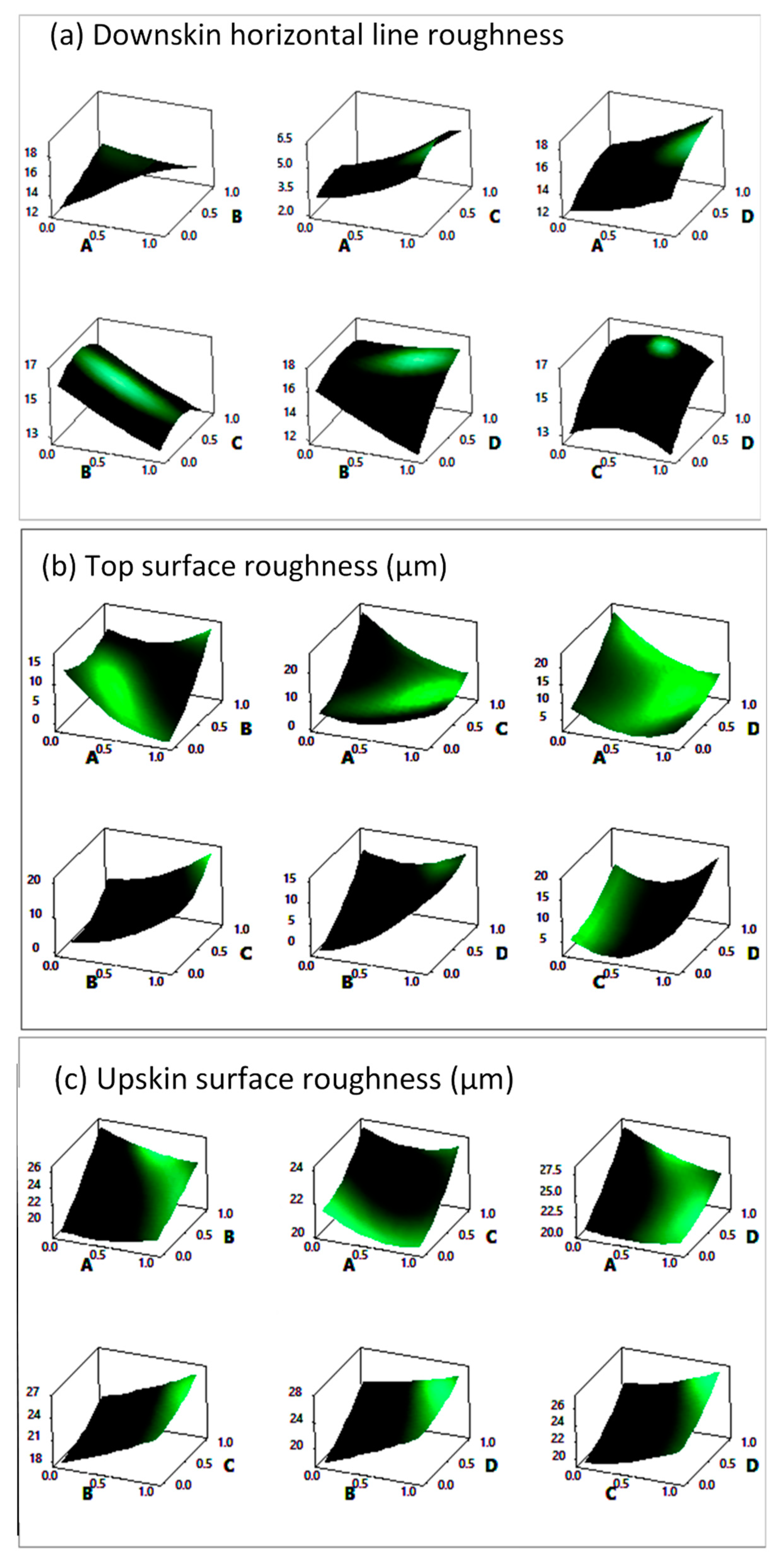
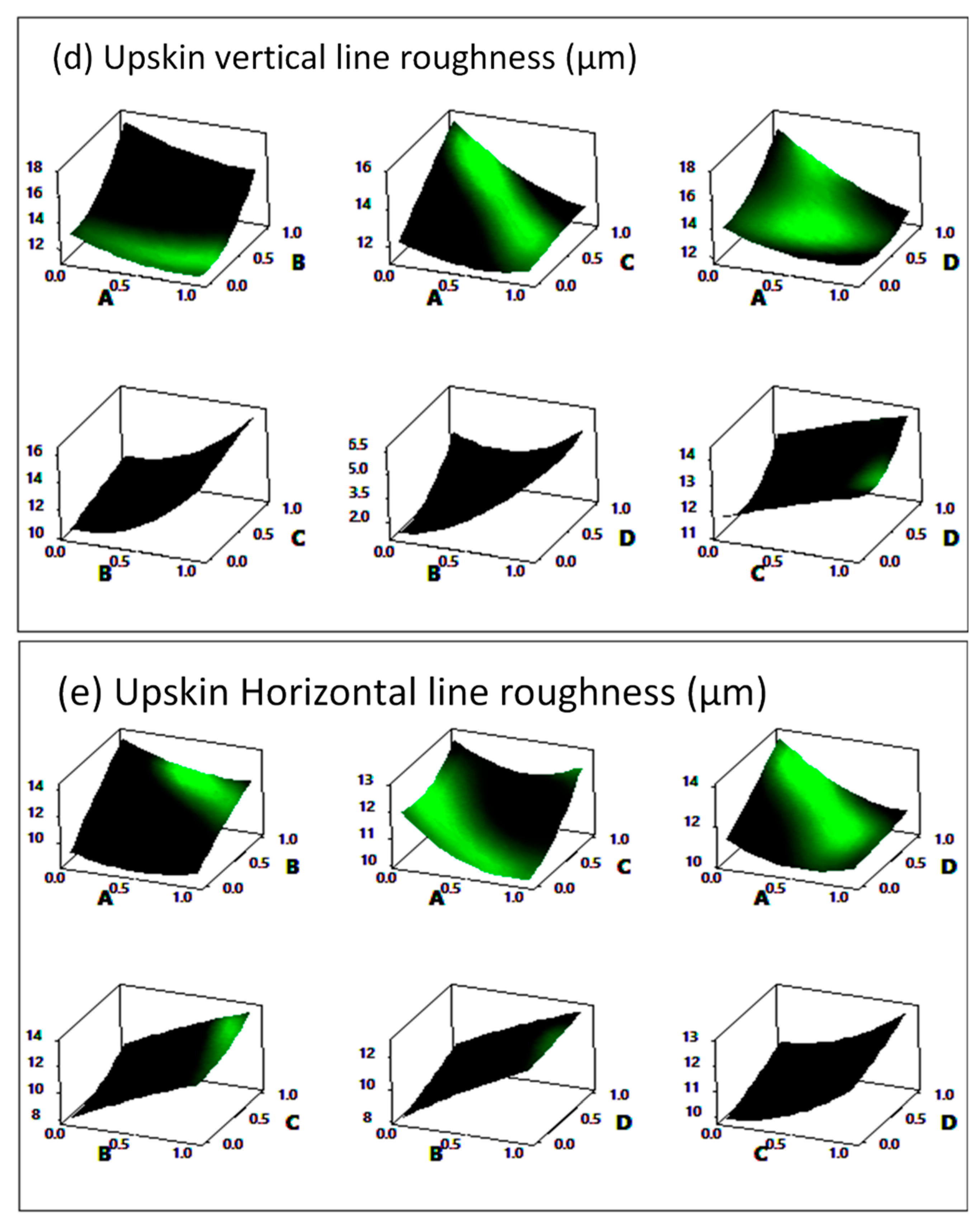
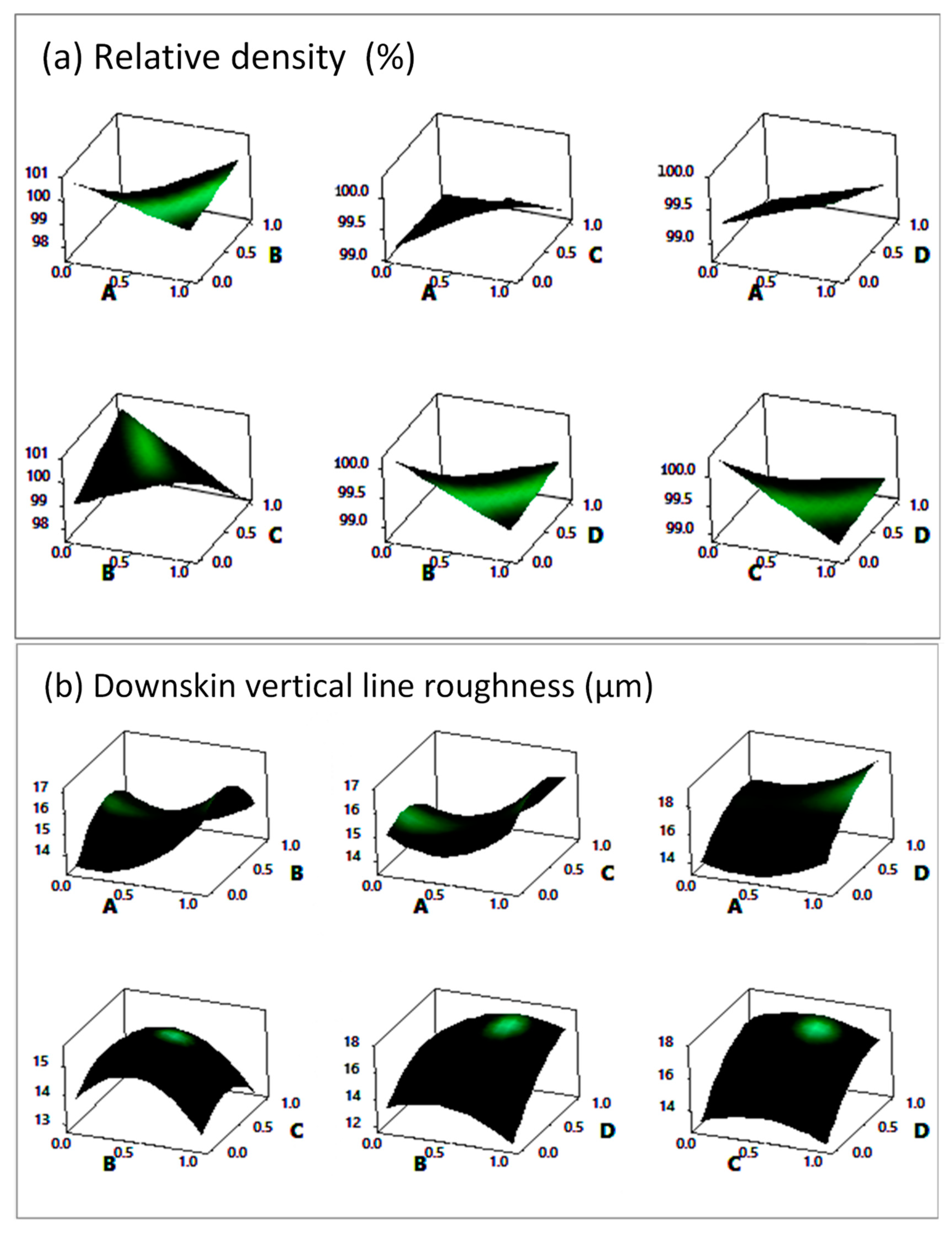
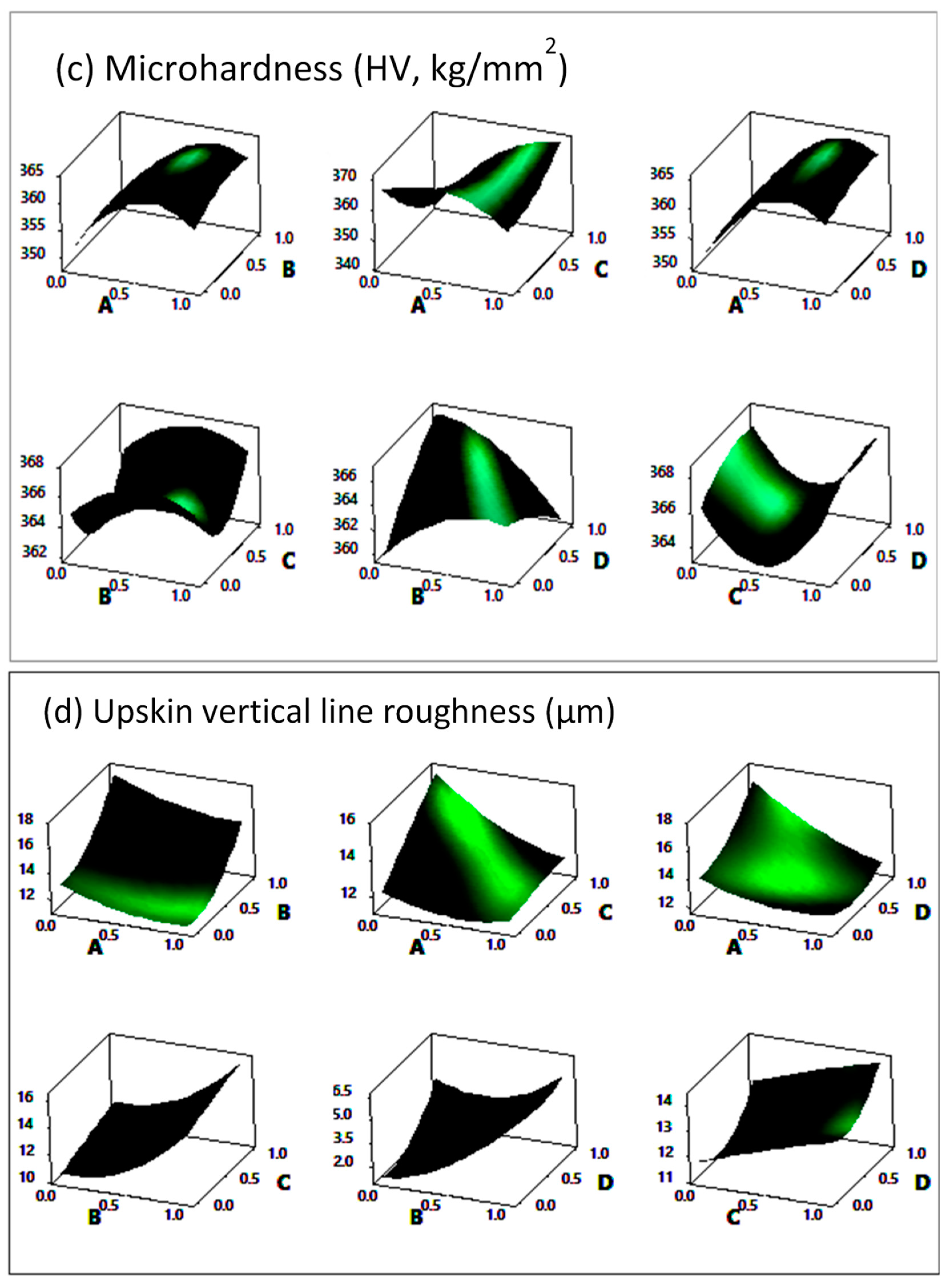
4.2. Response Surface Method
4.3. Artificial Neural Network
4.4. Comparison of the Predictions from the Taguchi Method, the Response Surface Method, and the Artificial Neural Network
5. Conclusions
- Both Taguchi and RSM approaches were successful in capturing the correlations between the L-PBF processing parameters and responses by using only 1/125th of the observations in full factorial experiments.
- The Taguchi results showed that the layer thickness was the most significant factor in determining all the three downskin roughness responses, in which the optimum layer thickness was the smallest value, i.e., 20 µM. Therefore, the layer thickness-related mechanisms, such as stair-stepping effect, were the dominant factors influencing the downskin roughness in the L-PBF process.
- The Taguchi method recommends the highest energy density level to obtain the smallest roughness values for the upskin and top surface roughness of L-PBF-manufactured parts, regardless of all the other properties.
- Similarly, the parameter combinations recommended by the RSM resulting in the smoothest up-facing surfaces in L-PBF-manufactured parts yields the highest energy densities.
- Using RSM results, we were able to assess whether two input parameters are independent in determining a response. The results showed that the interaction between the laser power and hatch spacing in predicting microhardness and relative density was the most significant among the two-way interactions between the other parameters. However, in the upskin roughness properties, the most significant interaction was between laser power and layer thickness.
- A multi-response optimization of all nine properties with the same weights is performed to obtain a single set of L-PBF processing parameters for optimizing all the response properties. The applied weight on each response can be altered based on their importance to the specific application of the L-PBF-manufactured component.
- Overall, the present analyses by both Taguchi and RSM methods showed that the layer thickness was the dominant factor controlling the downskin surface roughness parameters and was a significant factor influencing the top surface and upskin roughness parameters.
- The contribution of stripe width on most responses was negligible, which was attributed to its local importance near the boundaries of parts.
- The microhardness and relative density were both influenced by the energy density calculated based on the laser power, scanning speed, layer thickness, and hatch spacing. However, laser power played a more dominant role on the microhardness response than on the relative density response.
- The trained ANN model exhibited very good accuracy and performance in predicting the true response values based on the given input processing parameters.
- The comparison of the prediction errors corresponding to the ANN, the RSM, and the Taguchi method showed that all the three models exhibited reasonable predictive capabilities.
- Among the three models, the Taguchi method showed the least desirable performance in predicting each and all the response properties. We can conclude that nonlinearity exists in the behavior of the tested response properties of PBF-manufactured parts that the Taguchi method was not able to capture as accurately as the quadratic models.
- Although the RSM performed slightly better than the ANN in predicting microhardness values, the ANN showed much better performance in predicting the other properties. Therefore, it can be concluded that the ANN outperformed the predictive capabilities of the RSM and the Taguchi method.
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Experiment No. | Processing Parameter Level | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 | 1 | 1 |
| 3 | 0 | 2 | 2 | 2 | 2 |
| 4 | 0 | 3 | 3 | 3 | 3 |
| 5 | 0 | 4 | 4 | 4 | 4 |
| 6 | 1 | 0 | 1 | 2 | 3 |
| 7 | 1 | 1 | 2 | 3 | 4 |
| 8 | 1 | 2 | 3 | 4 | 0 |
| 9 | 1 | 3 | 4 | 0 | 1 |
| 10 | 1 | 4 | 0 | 1 | 2 |
| 11 | 2 | 0 | 2 | 4 | 1 |
| 12 | 2 | 1 | 3 | 0 | 2 |
| 13 | 2 | 2 | 4 | 1 | 3 |
| 14 | 2 | 3 | 0 | 2 | 4 |
| 15 | 2 | 4 | 1 | 3 | 0 |
| 16 | 3 | 0 | 3 | 1 | 4 |
| 17 | 3 | 1 | 4 | 2 | 0 |
| 18 | 3 | 2 | 0 | 3 | 1 |
| 19 | 3 | 3 | 1 | 4 | 2 |
| 20 | 3 | 4 | 2 | 0 | 3 |
| 21 | 4 | 0 | 4 | 3 | 2 |
| 22 | 4 | 1 | 0 | 4 | 3 |
| 23 | 4 | 2 | 1 | 0 | 4 |
| 24 | 4 | 3 | 2 | 1 | 0 |
| 25 | 4 | 4 | 3 | 2 | 1 |
| Experiment No. | Processing Parameter Level | ||||
|---|---|---|---|---|---|
| A | B | C | D | E | |
| 1 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 | 2 | 3 |
| 3 | 0 | 2 | 2 | 4 | 1 |
| 4 | 0 | 3 | 3 | 1 | 4 |
| 5 | 0 | 4 | 4 | 3 | 2 |
| 6 | 1 | 0 | 1 | 1 | 1 |
| 7 | 1 | 1 | 2 | 3 | 4 |
| 8 | 1 | 2 | 3 | 0 | 2 |
| 9 | 1 | 3 | 4 | 2 | 0 |
| 10 | 1 | 4 | 0 | 4 | 3 |
| 11 | 2 | 0 | 2 | 2 | 2 |
| 12 | 2 | 1 | 3 | 4 | 0 |
| 13 | 2 | 2 | 4 | 1 | 3 |
| 14 | 2 | 3 | 0 | 3 | 1 |
| 15 | 2 | 4 | 1 | 0 | 4 |
| 16 | 3 | 0 | 3 | 3 | 3 |
| 17 | 3 | 1 | 4 | 0 | 1 |
| 18 | 3 | 2 | 0 | 2 | 4 |
| 19 | 3 | 3 | 1 | 4 | 2 |
| 20 | 3 | 4 | 2 | 1 | 0 |
| 21 | 4 | 0 | 4 | 4 | 4 |
| 22 | 4 | 1 | 0 | 1 | 2 |
| 23 | 4 | 2 | 1 | 3 | 0 |
| 24 | 4 | 3 | 2 | 0 | 3 |
| 25 | 4 | 4 | 3 | 2 | 1 |
| Sample Code * | Relative Density (%) | Hardness (HV) | Roughness (µm) | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Top Surface | Upskin Surface | Upskin Hor. Line | Upskin Ver. Line | Downskin Surface | Downskin Hor. Line | Downskin Ver. Line | |||
| 11111 | 99.893 | 364.91 | 4.86 | 16.63 | 9.14 | 9.85 | 20.52 | 12.18 | 12.99 |
| 12222 | 99.726 | 354.80 | 7.54 | 19.55 | 11.62 | 13.86 | 19.73 | 13.00 | 14.63 |
| 12234 | 99.712 | 362.83 | 8.85 | 21.97 | 11.79 | 14.65 | 20.85 | 12.07 | 15.31 |
| 13333 | 98.493 | 343.40 | 15.86 | 23.72 | 13.72 | 14.67 | 22.30 | 13.28 | 15.08 |
| 13352 | 98.824 | 346.91 | 28.42 | 27.79 | 13.30 | 16.27 | 24.70 | 14.79 | 15.61 |
| 14425 | 97.379 | 340.33 | 17.09 | 24.46 | 12.75 | 15.95 | 20.30 | 14.00 | 14.64 |
| 14444 | 99.053 | 343.74 | 27.52 | 30.08 | 15.03 | 17.09 | 26.73 | 13.27 | 15.07 |
| 15543 | 99.431 | 341.80 | 32.52 | 32.27 | 17.12 | 21.52 | 28.18 | 15.54 | 15.10 |
| 15555 | 98.685 | 339.18 | 38.84 | 38.19 | 16.83 | 21.44 | 32.74 | 17.36 | 18.02 |
| 21222 | 99.732 | 357.64 | 5.26 | 18.96 | 7.74 | 12.66 | 23.64 | 15.26 | 13.14 |
| 21234 | 99.650 | 367.69 | 6.52 | 19.48 | 11.35 | 11.74 | 22.57 | 14.45 | 16.37 |
| 22345 | 99.258 | 361.82 | 11.23 | 24.02 | 11.15 | 14.51 | 24.29 | 14.14 | 14.68 |
| 23413 | 99.734 | 360.61 | 10.26 | 18.69 | 10.67 | 12.52 | 16.63 | 11.00 | 11.58 |
| 23451 | 98.493 | 343.4 | 23.30 | 30.04 | 13.63 | 16.58 | 27.03 | 15.02 | 14.56 |
| 24512 | 99.277 | 349.54 | 16.51 | 21.21 | 12.13 | 13.44 | 18.29 | 11.02 | 10.65 |
| 24531 | 97.399 | 352.40 | 20.98 | 26.77 | 13.65 | 14.84 | 24.70 | 14.99 | 16.37 |
| 25123 | 99.712 | 362.52 | 10.93 | 21.47 | 11.49 | 12.27 | 20.32 | 12.48 | 12.77 |
| 25154 | 99.383 | 361.53 | 12.83 | 26.63 | 14.11 | 15.21 | 25.48 | 16.45 | 15.91 |
| 31333 | 99.571 | 363.98 | 6.81 | 19.67 | 8.22 | 11.03 | 24.48 | 14.52 | 14.85 |
| 31352 | 99.503 | 365.48 | 9.81 | 23.61 | 10.04 | 12.70 | 28.47 | 13.81 | 15.31 |
| 32413 | 99.650 | 361.67 | 7.42 | 20.87 | 10.94 | 11.21 | 21.58 | 12.15 | 13.66 |
| 32451 | 99.573 | 362.20 | 13.39 | 25.31 | 11.62 | 15.71 | 27.59 | 15.37 | 16.12 |
| 33524 | 99.602 | 360.59 | 13.72 | 22.69 | 11.75 | 13.16 | 21.55 | 12.85 | 13.07 |
| 34135 | 99.646 | 364.18 | 6.79 | 22.11 | 11.86 | 13.48 | 22.60 | 14.97 | 15.11 |
| 34142 | 99.358 | 368.30 | 7.74 | 26.43 | 12.17 | 13.87 | 27.13 | 16.52 | 16.63 |
| 35215 | 99.789 | 364.02 | 11.74 | 25.00 | 12.59 | 17.80 | 19.41 | 12.19 | 11.94 |
| 35241 | 99.470 | 363.05 | 14.38 | 23.99 | 11.86 | 13.64 | 24.81 | 13.07 | 14.98 |
| 41425 | 99.684 | 366.77 | 7.96 | 19.36 | 9.68 | 11.12 | 22.39 | 13.23 | 14.40 |
| 41444 | 99.702 | 370.83 | 9.95 | 22.43 | 11.55 | 12.32 | 29.14 | 18.46 | 16.36 |
| 42512 | 99.735 | 365.98 | 8.54 | 23.54 | 11.36 | 14.14 | 24.15 | 14.66 | 13.68 |
| 42531 | 99.669 | 363.44 | 12.17 | 24.94 | 12.78 | 14.27 | 27.09 | 14.50 | 15.44 |
| 43135 | 99.801 | 370.56 | 15.24 | 19.02 | 10.35 | 10.46 | 24.93 | 14.97 | 15.63 |
| 43142 | 99.714 | 366.28 | 6.78 | 21.74 | 10.55 | 11.41 | 29.16 | 15.82 | 17.98 |
| 44253 | 99.286 | 363.92 | 13.00 | 25.16 | 11.50 | 13.91 | 28.96 | 15.70 | 16.69 |
| 45314 | 99.632 | 359.07 | 13.11 | 19.37 | 11.53 | 13.16 | 17.79 | 10.90 | 11.07 |
| 45321 | 99.516 | 361.75 | 13.55 | 23.36 | 11.83 | 14.93 | 23.58 | 13.75 | 13.48 |
| 51543 | 99.283 | 364.92 | 12.16 | 22.96 | 11.73 | 11.37 | 26.21 | 13.40 | 14.84 |
| 51555 | 99.570 | 372.44 | 12.78 | 25.81 | 10.37 | 13.27 | 31.39 | 17.78 | 15.67 |
| 52123 | 99.787 | 354.08 | 4.49 | 17.81 | 8.18 | 10.49 | 26.96 | 15.38 | 14.29 |
| 52154 | 99.681 | 358.51 | 5.83 | 17.92 | 6.97 | 11.25 | 29.87 | 13.65 | 17.58 |
| 53215 | 99.830 | 359.80 | 5.69 | 18.29 | 10.64 | 11.05 | 20.04 | 12.10 | 12.96 |
| 53241 | 99.615 | 360.61 | 7.69 | 25.32 | 11.88 | 13.62 | 39.59 | 20.22 | 20.96 |
| 54314 | 99.338 | 365.06 | 8.89 | 22.76 | 12.13 | 13.51 | 24.00 | 14.23 | 16.04 |
| 54321 | 99.600 | 361.15 | 9.55 | 22.83 | 11.81 | 13.81 | 23.74 | 14.02 | 13.58 |
| 55432 | 99.551 | 363.42 | 18.46 | 23.81 | 12.41 | 14.63 | 23.76 | 14.61 | 14.91 |
| Weight | Bias | |||
|---|---|---|---|---|
| −0.817226931 | 1.2743454058 | −0.4373294332 | −0.2543893758 | 0.0672884998 |
| −0.1742719803 | 0.0407326757 | −0.9436160018 | −0.076517916 | 0.7709497912 |
| 0.4618549711 | 0.1455196574 | −0.2580787273 | −0.8655356556 | −0.1703290546 |
| 0.4420987284 | 0.9007528946 | 1.051149895 | 0.7140146312 | 0.5015783122 |
| 0.9768443561 | −0.4022851406 | −0.6007116257 | −0.078794974 | 0.9597908008 |
| 0.3804623429 | −0.8645048849 | 0.279432945 | −0.4744703392 | 0.5012114738 |
| Weight | Bias | |||||
|---|---|---|---|---|---|---|
| 0.69163044 | −0.29082017 | −0.68915516 | 0.01657495 | 0.53058497 | 0.62056222 | −0.29844372 |
| −0.4943906 | 0.56887031 | −0.02349223 | −0.7047001 | −1.19140218 | 0.17356839 | −0.17197129 |
| −0.1946129 | −0.09454516 | 0.01747523 | −1.2967566 | 0.12582357 | 0.47763527 | −0.12213046 |
| 0.22637272 | 0.11649799 | −0.09655429 | 0.84722914 | −0.74640528 | 0.25596798 | −0.30446552 |
| −0.2527528 | 0.746188496 | 0.899036494 | 0.83378385 | 0.256524716 | −0.0999083 | −0.0819088467 |
| Weight | Bias | ||||
|---|---|---|---|---|---|
| −0.0951860163 | −0.5847561682 | 0.2450872866 | −0.5658932656 | −0.0712814703 | 0.280699756 |
| 0.8474751074 | −1.3345236156 | 0.6504012392 | −0.3931396363 | 0.0672525452 | −0.47777086 |
| −0.9487583799 | −0.3165275189 | −0.8272228144 | −0.5577874479 | −1.0364007486 | −0.26500424 |
References
- Qiu, C.; Al Kindi, M.; Aladawi, A.S.; Al Hatmi, I. A Comprehensive Study on Microstructure and Tensile Behaviour of a Selectively Laser Melted Stainless Steel. Sci. Rep. 2018, 8, 1–16. [Google Scholar] [CrossRef]
- Charles, A.; Elkaseer, A.; Thijs, L.; Hagenmeyer, V.; Scholz, S.G. Effect of Process Parameters on the Generated Surface Roughness of Down-Facing Surfaces in Selective Laser Melting. Appl. Sci. 2019, 9, 1256. [Google Scholar] [CrossRef] [Green Version]
- Perevoshchikova, N.; Rigaud, J.; Sha, Y.; Heilmaier, M.; Finnin, B.; Labelle, E.; Wu, X. Optimisation of Selective Laser Melting Parameters for the Ni-Based Superalloy IN-738 LC Using Doehlert’s Design. Rapid Prototyp. J. 2017, 23, 881–892. [Google Scholar] [CrossRef] [Green Version]
- Fox, J.C.; Moylan, S.P.; Lane, B. Effect of Process Parameters on the Surface Roughness of Overhanging Structures in Laser Powder Bed Fusion Additive Manufacturing. Procedia CIRP 2016, 45, 131–134. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z. Understanding of the Modeling Method in Additive Manufacturing. IOP Conf. Ser. Mater. Sci. Eng. 2020, 711. [Google Scholar] [CrossRef]
- Fisher, R.A. Design of Experiments. BMJ 1936, 1, 554. [Google Scholar] [CrossRef]
- Nath, R.; Murugesan, K. Optimization of Double Diffusive Mixed Convection in a Bfs Channel Filled With Alumina Nanoparticle Using Taguchi Method and Utility Concept. Sci. Rep. 2019, 9, 1–19. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, C.; Liu, W.; Ma, Y.; Tang, S.; Liang, C.; Cai, Q.; Zhang, C. Optimization of Parameters in Laser Powder Deposition AlSi10Mg Alloy Using Taguchi Method. Opt. Laser Technol. 2019, 111, 470–480. [Google Scholar] [CrossRef]
- Manjunath, B.; Vinod, A.; Abhinav, K.; Verma, S.; Sankar, M.R. Optimisation of Process Parameters for Deposition of Colmonoy Using Directed Energy Deposition Process. Mater. Today Proc. 2020, 26, 1108–1112. [Google Scholar] [CrossRef]
- Yang, B.; Lai, Y.; Yue, X.; Wang, D.; Zhao, Y. Parametric Optimization of Laser Additive Manufacturing of Inconel 625 Using Taguchi Method and Grey Relational Analysis. Scanning 2020, 2020, 1–10. [Google Scholar] [CrossRef]
- Cherkia, H.; Kar, S.; Singh, S.S.; Satpathy, A. Fused Deposition Modelling and Parametric Optimization of ABS-M30. In Advances in Materials and Manufacturing Engineering; Springer: Singapore, 2020; pp. 1–15. [Google Scholar]
- Dontsov, Y.V.; Panin, S.; Buslovich, D.G.; Berto, F. Taguchi Optimization of Parameters for Feedstock Fabrication and FDM Manufacturing of Eear-Resistant UHMWPE-Based Composites. Materials 2020, 13, 2718. [Google Scholar] [CrossRef]
- Jiang, H.-Z.; Li, Z.-Y.; Feng, T.; Wu, P.-Y.; Chen, Q.-S.; Feng, Y.-L.; Li, S.-W.; Gao, H.; Xu, H.-J. Factor Analysis of Selective Laser Melting Process Parameters With Normalised Quantities and Taguchi Method. Opt. Laser Technol. 2019, 119, 105592. [Google Scholar] [CrossRef]
- Campanelli, S.; Casalino, G.; Contuzzi, N.; Ludovico, A. Taguchi Optimization of the Surface Finish Obtained by Laser Ablation on Selective Laser Molten Steel Parts. Procedia CIRP 2013, 12, 462–467. [Google Scholar] [CrossRef]
- Calignano, F.; Manfredi, D.; Ambrosio, E.P.; Iuliano, L.; Fino, P. Influence of Process Parameters on Surface Roughness of Aluminum Parts Produced by DMLS. Int. J. Adv. Manuf. Technol. 2013, 67, 2743–2751. [Google Scholar] [CrossRef] [Green Version]
- Rathod, M.K.R.; Karia, M.M.C. Experimental Study for Effects of Process Parameters of Selective Laser Sintering for alsi10mg. Int. J. Technol. Res. Eng. 2020, 7, 6957–6960. [Google Scholar]
- Joguet, D.; Costil, S.; Liao, H.; Danlos, Y. Porosity Content Control of CoCrMo and Titanium Parts by Taguchi Method Applied to Selective Laser Melting Process Parameter. Rapid Prototyp. J. 2016, 22, 20–30. [Google Scholar] [CrossRef]
- Sathish, S.; Anandakrishnan, V.; Dillibabu, V.; Muthukannan, D.; Balamuralikrishnan, N. Optimization of Coefficient of Friction for Direct Metal Laser Sintered Inconel 718. Adv. Manuf. Technol. 2019, 371–379. [Google Scholar] [CrossRef]
- Dong, G.; Marleau-Finley, J.; Zhao, Y.F. Investigation of Electrochemical Post-Processing Procedure for Ti-6AL-4V Lattice Structure Manufactured by Direct Metal Laser Sintering (DMLS). Int. J. Adv. Manuf. Technol. 2019, 104, 3401–3417. [Google Scholar] [CrossRef]
- Kuo, C.-C.; Yang, X.-Y. Optimization of Direct Metal Printing Process Parameters for Plastic Injection Mold With Both Gas Permeability and Mechanical Properties Using Design of Experiments Approach. Int. J. Adv. Manuf. Technol. 2020, 109, 1219–1235. [Google Scholar] [CrossRef]
- Gunst, R.F.; Mason, R.L. Fractional Factorial Design. Wiley Interdiscip. Rev. Comput. Stat. 2009, 1, 234–244. [Google Scholar] [CrossRef]
- Dada, M.; Popoola, P.; Mathe, N.; Pityana, S.; Adeosun, S. Parametric Optimization of Laser Deposited High Entropy Alloys Using Response Surface Methodology (RSM). Int. J. Adv. Manuf. Technol. 2020, 109, 2719–2732. [Google Scholar] [CrossRef]
- Pant, P.; Chatterjee, D.; Nandi, T.; Samanta, S.K.; Lohar, A.K.; Changdar, A. Statistical Modelling and Optimization of Clad Characteristics in Laser Metal Deposition of Austenitic Stainless Steel. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 283. [Google Scholar] [CrossRef]
- Read, N.; Wang, W.; Essa, K.; Attallah, M.M. Selective Laser Melting of ALSi10Mg Alloy: Process Optimisation and Mechanical Properties Development. Mater. Des. 2015, 65, 417–424. [Google Scholar] [CrossRef] [Green Version]
- El-Sayed, M.A.; Ghazy, M.; Youssef, Y.; Essa, K. Optimization of SLM Process Parameters for Ti6Al4V Medical Implants. Rapid Prototyp. J. 2019, 25, 433–447. [Google Scholar] [CrossRef] [Green Version]
- Gajera, H.M.; Darji, V.; Dave, K. Application of Fuzzy Integrated JAYA Algorithm for the Optimization of Surface Roughness of DMLS Made Specimen: Comparison with GA. In Advances in Intelligent Systems and Computing; Springer Science and Business Media LLC: Amsterdam, The Netherlands, 2019; Volume 949, pp. 137–152. [Google Scholar]
- Bartolomeu, F.; Faria, S.; Carvalho, O.; Pinto, E.; Alves, N.; Silva, F.S.; Miranda, G. Predictive Models for Physical and Mechanical Properties of Ti6Al4V Produced by Selective Laser Melting. Mater. Sci. Eng. A 2016, 663, 181–192. [Google Scholar] [CrossRef]
- Krishnan, M.; Atzeni, E.; Canali, R.; Calignano, F.; Manfredi, D.G.; Ambrosio, E.P.; Iuliano, L. On the Effect of Process Parameters on Properties of AlSi10Mg Parts Produced by DMLS. Rapid Prototyp. J. 2014, 20, 449–458. [Google Scholar] [CrossRef]
- Pawlak, A.; Rosienkiewicz, M.; Chlebus, E. Design of Experiments Approach in AZ31 Powder Selective Laser Melting Process Optimization. Arch. Civ. Mech. Eng. 2017, 17, 9–18. [Google Scholar] [CrossRef]
- Marmarelis, M.G.; Ghanem, R.G. Data-Driven Stochastic Optimization on Manifolds for Additive Manufacturing. Comput. Mater. Sci. 2020, 181, 109750. [Google Scholar] [CrossRef]
- Wang, G.; Huang, L.; Liu, Z.; Qin, Z.; He, W.; Liu, F.; Chen, C.; Nie, Y. Process Optimization and Mechanical Properties of Oxide Dispersion Strengthened Nickel-Based Superalloy by Selective Laser Melting. Mater. Des. 2020, 188, 108418. [Google Scholar] [CrossRef]
- Okaro, I.A.; Jayasinghe, S.; Sutcliffe, C.; Black, K.; Paoletti, P.; Green, P.L. Automatic Fault Detection for Laser Powder-Bed Fusion Using Semi-Supervised Machine Learning. Addit. Manuf. 2019, 27, 42–53. [Google Scholar] [CrossRef]
- Nguyen, D.S.; Park, H.-S.; Lee, C.-M. Optimization of Selective Laser Melting Process Parameters for Ti-6Al-4V Alloy Manufacturing Using Deep Learning. J. Manuf. Process. 2020, 55, 230–235. [Google Scholar] [CrossRef]
- Qi, X.; Chen, G.; Li, Y.; Cheng, X.; Li, C. Applying Neural-Network-Based Machine Learning to Additive Manufacturing: Current Applications, Challenges, and Future Perspectives. Engineering 2019, 5, 721–729. [Google Scholar] [CrossRef]
- Sood, A.K.; Ohdar, R.K.; Mahapatra, S.S. Experimental Investigation and Empirical Modelling of FDM Process for Compressive Strength Improvement. J. Adv. Res. 2012, 3, 81–90. [Google Scholar] [CrossRef] [Green Version]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Zhang, Y.; Hong, G.S.; Ye, D.; Zhu, K.; Fuh, J. Extraction and Evaluation of Melt Pool, Plume and Spatter Information for Powder-Bed Fusion AM Process Monitoring. Mater. Des. 2018, 156, 458–469. [Google Scholar] [CrossRef]
- Paul, A.; Mozaffar, M.; Yang, Z.; Liao, W.-K.; Choudhary, A.; Cao, J.; Agrawal, A. A Real-Time Iterative Machine Learning Approach for Temperature Profile Prediction in Additive Manufacturing Processes. In Proceedings of the 2019 IEEE International Conference on Data Science and Advanced Analytics (DSAA), Washington, DC, USA, 5–8 October 2019; pp. 541–550. [Google Scholar]
- Caggiano, A.; Zhang, J.; Alfieri, V.; Caiazzo, F.; Gao, R.X.; Teti, R. Machine Learning-Based Image Processing for on-Line Defect Recognition in Additive Manufacturing. CIRP Ann. 2019, 68, 451–454. [Google Scholar] [CrossRef]
- Shevchik, S.A.; Kenel, C.; Leinenbach, C.; Wasmer, K. Acoustic Emission for in Situ Quality Monitoring in Additive Manufacturing Using Spectral Convolutional Neural Networks. Addit. Manuf. 2018, 21, 598–604. [Google Scholar] [CrossRef]
- Ali, T.K.; Balasubramanian, E. Study on Compressive Strength Characteristics of Selective Inhibition Sintered UHMWPE Specimens Based on ANN and RSM Approach. CIRP J. Manuf. Sci. Technol. 2020. [Google Scholar] [CrossRef]
- Li, M.; Han, Y.; Zhou, M.; Chen, P.; Gao, H.; Zhang, Y.; Zhou, H. Experimental Investigating and Numerical Simulations of the Thermal Behavior and Process Optimization for Selective Laser Sintering of PA6. J. Manuf. Process. 2020, 56, 271–279. [Google Scholar] [CrossRef]
- Guo, Y.; Lu, W.F.; Fuh, J. Semi-Supervised Deep Learning Based Framework for Assessing Manufacturability of Cellular Structures in Direct Metal Laser Sintering Process. J. Intell. Manuf. 2020, 1–13. [Google Scholar] [CrossRef]
- Zhang, M.; Sun, C.-N.; Zhang, X.; Goh, P.C.; Wei, J.; Hardacre, D.; Li, H. High Cycle Fatigue Life Prediction of Laser Additive Manufactured Stainless Steel: A Machine Learning Approach. Int. J. Fatigue 2019, 128, 105194. [Google Scholar] [CrossRef]
- Li, L.; Anand, S. Hatch Pattern Based Inherent Strain Prediction Using Neural Networks for Powder Bed Fusion Additive Manufacturing. J. Manuf. Process. 2020, 56, 1344–1352. [Google Scholar] [CrossRef]
- Yan, J. 3D Printing Optimization Algorithm Based on Back-Propagation Neural Network. J. Eng. Des. Technol. 2020, 18, 1223–1230. [Google Scholar] [CrossRef]
- Marrey, M.; Malekipour, E.; El-Mounayri, H.; Faierson, E.J. A Framework for Optimizing Process Parameters in Powder Bed Fusion (PBF) Process Using Artificial Neural Network (ANN). Procedia Manuf. 2019, 34, 505–515. [Google Scholar] [CrossRef]
- Tran, H.-C.; Lo, Y.-L. Systematic Approach for Determining Optimal Processing Parameters to Produce Parts With High Density in Selective Laser Melting Process. Int. J. Adv. Manuf. Technol. 2019, 105, 4443–4460. [Google Scholar] [CrossRef]
- Lo, Y.-L.; Liu, B.-Y.; Tran, H.-C. Optimized Hatch Space Selection in Double-Scanning Track Selective Laser Melting Process. Int. J. Adv. Manuf. Technol. 2019, 105, 2989–3006. [Google Scholar] [CrossRef]
- Rahimi, M.H.; Shayganmanesh, M.; Noorossana, R.; Pazhuheian, F. Modelling and Optimization of Laser Engraving Qualitative Characteristics of Al-SiC Composite Using Response Surface Methodology and Artificial Neural Networks. Opt. Laser Technol. 2019, 112, 65–76. [Google Scholar] [CrossRef]
- Mehrpouya, M.; Gisario, A.; Rahimzadeh, A.; Nematollahi, M.; Baghbaderani, K.S.; Elahinia, M. A Prediction Model for Finding the Optimal Laser Parameters in Additive Manufacturing of NiTi Shape Memory Alloy. Int. J. Adv. Manuf. Technol. 2019, 105, 4691–4699. [Google Scholar] [CrossRef]
- Khorasani, A.M.; Gibson, I.; Ghasemi, A.; Ghaderi, A. Modelling of Laser Powder Bed Fusion Process and Analysing the Effective Parameters on Surface Characteristics of Ti-6Al-4V. Int. J. Mech. Sci. 2020, 168, 105299. [Google Scholar] [CrossRef]
- Akhil, V.; Raghav, G.; Arunachalam, N.; Srinivasu, D.S. Image Data-Based Surface Texture Characterization and Prediction Using Machine Learning Approaches for Additive Manufacturing. J. Comput. Inf. Sci. Eng. 2020, 20, 1–39. [Google Scholar] [CrossRef]
- Hiren, M.; Gajera, M.E.; Dave, K.G.; Jani, V.P. Experimental Investigation and Analysis of Dimensional Accuracy of Laser-Based Powder Bed Fusion Made Specimen by Application of Response Surface Methodology. Prog. Addit. Manuf. 2019, 4, 371–382. [Google Scholar] [CrossRef]
- Fotovvati, B.; Etesami, S.A.; Asadi, E. Process-Property-Geometry Correlations for Additively-Manufactured Ti–6Al–4V Sheets. Mater. Sci. Eng. A 2019, 760, 431–447. [Google Scholar] [CrossRef]
- Fotovvati, B.; Asadi, E. Size Effects on Geometrical Accuracy for Additive Manufacturing of Ti-6Al-4V ELI Parts. Int. J. Adv. Manuf. Technol. 2019, 104, 2951–2959. [Google Scholar] [CrossRef]
- ASTM B311-17. Standard Test Method for Density of Powder Metallurgy (PM) Materials Containing Less Than Two Percent Porosity; ASTM International: West Conshohocken, PA, USA, 2017; Available online: www.astm.org (accessed on 26 October 2020).
- Wu, C.-F.; Hamada, M. Experiments: Planning, Analysis, and Optimization; Wiley: Hoboken, NJ, USA, 2009; ISBN 9780471699460. [Google Scholar]
- Beale, H.D.; Demuth, H.B.; Hagan, M.T. Neural Network Design; Pws: Boston, MA, USA, 1996. [Google Scholar]
- Wasserstein, R.L.; Lazar, N.A. The ASA Statement on p-Values: Context, Process, and Purpose. Am. Stat. 2016, 70, 129–133. [Google Scholar] [CrossRef] [Green Version]
- Debroy, T.; Wei, H.; Zuback, J.; Mukherjee, T.; Elmer, J.; Milewski, J.; Beese, A.; Wilson-Heid, A.; De, A.; Zhang, W. Additive Manufacturing of Metallic Components–Process, Structure and Properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar] [CrossRef]
- Sun, J.; Yang, Y.; Wang, D. Parametric Optimization of Selective Laser Melting for Forming Ti6Al4V Samples by Taguchi Method. Opt. Laser Technol. 2013, 49, 118–124. [Google Scholar] [CrossRef]
- Fotovvati, B.; Wayne, S.F.; Lewis, G.; Asadi, E. A Review on Melt-Pool Characteristics in Laser Welding of Metals. Adv. Mater. Sci. Eng. 2018, 2018, 1–18. [Google Scholar] [CrossRef] [Green Version]
| Process Parameter | Symbol | Level 0 | Level 1 | Level 2 | Level 3 | Level 4 |
|---|---|---|---|---|---|---|
| Laser power (W) | A | 170 | 210 | 250 | 290 | 330 |
| Scan speed (mm/s) | B | 900 | 1050 | 1200 | 1350 | 1500 |
| Hatch spacing (µM) | C | 100 | 120 | 140 | 160 | 180 |
| Layer thickness (µM) | D | 20 | 30 | 40 | 50 | 60 |
| Stripe width (mm) | E | 3 | 4 | 5 | 6 | 7 |
| Response | The Best Combination of L-PBF Parameters * | Energy Density (J/mm3) | Significance Ranking | ||||
|---|---|---|---|---|---|---|---|
| Microhardness | A4 290 | B1 900 | C1 100 | D2 30 | E2 4 | 107.4 | A > B > C > D > E |
| Relative density | A4 290 | B1 900 | C1 100 | D2 30 | E2 4 | 107.4 | D > C > A > B > E |
| Top surface roughness | A5 330 | B1 900 | C1 100 | D1 20 | E5 7 | 183.3 | C > B > D > A > E |
| Upskin surface roughness | A5 330 | B1 900 | C1 100 | D1 20 | E4 6 | 183.3 | D > C > B > A > E |
| Downskin surface roughness | A2 210 | B5 1500 | C2 120 | D1 20 | E4 6 | 58.3 | D > A > C > E > B |
| Upskin H. line roughness | A5 330 | B1 900 | C1 100 | D1 20 | E4 6 | 183.3 | C > A > B > D > E |
| Upskin V. line roughness | A5 330 | B1 900 | C1 100 | D1 20 | E3 5 | 183.3 | B > D > C > A > E |
| Downskin H. line roughness | A2 210 | B1 900 | C3 140 | D1 20 | E4 6 | 83.3 | D > E > A > C > B |
| Downskin V. line roughness | A2 210 | B4 1350 | C3 140 | D1 20 | E1 3 | 55.6 | D > A > C > B > E |
| Parameter | Microhardness | Relative Density | Top Surface Roughness | |||
| p-Value | Contribution (%) | p-Value | Contribution (%) | p-Value | Contribution (%) | |
| A (laser power) | 0.071 | 45.3 | 0.103 | 22.6 | 0.004 | 19.0 |
| B (scan speed) | 0.185 | 23.3 | 0.197 | 14.1 | 0.002 | 27.7 |
| C (hatch spacing) | 0.334 | 13.9 | 0.098 | 23.5 | 0.001 | 33.6 |
| D (layer thickness) | 0.542 | 7.9 | 0.075 | 28.0 | 0.004 | 17.6 |
| E (stripe width) | 0.984 | 0.7 | 0.464 | 6.2 | 0.282 | 1.3 |
| Error | − | 8.8 | − | 5.6 | − | 0.7 |
| Parameter | Upskin Surface | Upskin Horizontal Line | Upskin Vertical Line | |||
| p-Value | Contribution (%) | p-Value | Contribution (%) | p-Value | Contribution (%) | |
| A (laser power) | 0.304 | 11.4 | 0.192 | 22.6 | 0.035 | 20.4 |
| B (scan speed) | 0.196 | 16.6 | 0.15 | 27.3 | 0.02 | 28.2 |
| C (hatch spacing) | 0.114 | 24.8 | 0.131 | 30.0 | 0.034 | 20.8 |
| D (layer thickness) | 0.065 | 35.9 | 0.5 | 8.8 | 0.029 | 22.8 |
| E (stripe width) | 0.624 | 4.7 | 0.878 | 2.5 | 0.258 | 5.2 |
| Error | − | 6.6 | − | 8.8 | − | 2.6 |
| Parameter | Downskin Surface | Downskin Horizontal Line | Downskin Vertical Line | |||
| p-Value | Contribution (%) | p-Value | Contribution (%) | p-Value | Contribution (%) | |
| A (laser power) | 0.646 | 5.6 | 0.956 | 2.9 | 0.694 | 7.6 |
| B (scan speed) | 0.996 | 0.3 | 0.99 | 1.2 | 0.879 | 3.6 |
| C (hatch spacing) | 0.772 | 3.7 | 0.972 | 2.2 | 0.705 | 7.3 |
| D (layer thickness) | 0.024 | 81.2 | 0.141 | 64.7 | 0.071 | 66.9 |
| E (stripe width) | 0.974 | 0.9 | 0.769 | 9.0 | 0.966 | 1.6 |
| Error | − | 8.3 | − | 20.0 | − | 13.0 |
| Parameter | Micro-Hardness | Rel. Density | Top Surface | Upskin Surface | Upskin Hor. Line | Upskin Ver. Line | Downskin Surface | Downskin Hor. Line | Downskin Ver. Line |
|---|---|---|---|---|---|---|---|---|---|
| Constant | 364.05 | 100.31 | 4.72 | 16.44 | 8.572 | 10.55 | 19.32 | 11.66 | 12.15 |
| A | 16.1 | 1.45 | −15.78 | −1.25 | −3.16 | −1.74 | 3.59 | 3.89 | −2.13 |
| B | 7.1 | −0.23 | −9.3 | 6.98 | 5.91 | 0.43 | −5.4 | 0.31 | 5.82 |
| C | −35.3 | −2.13 | 0.35 | 0.07 | −1.06 | 3.87 | 5.73 | 2.83 | 2.20 |
| D | 7.2 | −0.26 | 13.31 | 6.11 | 2.78 | 1.67 | 2.55 | 2.80 | 4.88 |
| A2 | −26.74 | −2.007 | 14.67 | 2.61 | 2.70 | 2.31 | 7.44 | 1.79 | 3.97 |
| B2 | −6.7 | −0.77 | 11.42 | 1.21 | −0.74 | 5.15 | 2.12 | 0.72 | −5.43 |
| C2 | 12.3 | 0.50 | 20.1 | 2.43 | 1.94 | −0.29 | −1.75 | 3.77 | −3.43 |
| D2 | −2.65 | 0.417 | 7.31 | 2.62 | 0.31 | 3.58 | −0.49 | −3.19 | −3.97 |
| AB | 5.4 | 1.21 | 18.8 | −3.27 | −1.60 | −0.49 | −3.85 | −7.38 | −2.49 |
| AC | 34.3 | 1.89 | −21.6 | 1.03 | 1.48 | −3.03 | −8.07 | 1.02 | 1.35 |
| AD | 3.79 | −0.277 | −10.62 | −3.90 | −2.22 | −3.28 | 4.07 | 1.45 | 1.48 |
| BD | −11.2 | −0.50 | −11.94 | −2.95 | −0.89 | −3.85 | 6.71 | 4.74 | 2.90 |
| Downskin Ver. Line | Cont. % | - | 13.5 | 0.9 | 0.9 | 27.7 | 5.9 | 6.8 | 1.6 | 3.8 | 0.8 | 0.3 | 0.9 | 1.9 | Fitting coefficients | 70.7 | 41.4 | ||||||||||
| p-Value | 0.070 | 0.052 | 0.578 | 0.584 | 0.009 | 0.180 | 0.152 | 0.466 | 0.274 | 0.599 | 0.758 | 0.586 | 0.428 | ||||||||||||||
| Downskin Hor. Line | Cont. % | - | 32.1 | 0.2 | 0.5 | 19.4 | 1.1 | 0.1 | 1.8 | 2.3 | 6.9 | 0.2 | 0.8 | 4.8 | 76.9 | 53.8 | |||||||||||
| p-Value | 0.024 | 0.004 | 0.776 | 0.650 | 0.016 | 0.517 | 0.836 | 0.406 | 0.358 | 0.122 | 0.808 | 0.578 | 0.189 | ||||||||||||||
| Downskin Surface | Cont. % | - | 31.2 | 1.6 | 0.0 | 29.6 | 3.8 | 0.2 | 0.1 | 0.0 | 0.4 | 1.9 | 1.3 | 1.9 | 77.8 | 55.6 | |||||||||||
| p-Value | 0.020 | 0.003 | 0.417 | 0.980 | 0.004 | 0.223 | 0.778 | 0.857 | 0.946 | 0.695 | 0.381 | 0.472 | 0.379 | ||||||||||||||
| Upskin Ver. Line | Cont. % | - | 19.5 | 23.0 | 9.4 | 5.9 | 1.4 | 4.5 | 0.0 | 2.3 | 0.0 | 1.1 | 3.3 | 2.5 | 81.5 | 63.0 | |||||||||||
| p-Value | 0.008 | 0.012 | 0.008 | 0.065 | 0.131 | 0.440 | 0.186 | 0.952 | 0.337 | 0.919 | 0.506 | 0.253 | 0.314 | ||||||||||||||
| Upskin Hor. Line | Cont. % | - | 10.1 | 47.6 | 9.0 | 7.7 | 3.1 | 0.1 | 0.6 | 0.0 | 0.4 | 0.4 | 2.3 | 0.2 | 87.8 | 75.5 | |||||||||||
| p-Value | 0.001 | 0.025 | 0.000 | 0.032 | 0.045 | 0.180 | 0.765 | 0.544 | 0.899 | 0.619 | 0.620 | 0.241 | 0.719 | ||||||||||||||
| Upskin Surface | Cont. % | - | 3.7 | 26.5 | 10.4 | 30.5 | 1.0 | 0.1 | 0.3 | 0.6 | 0.5 | 0.1 | 2.4 | 0.8 | 85.4 | 70.8 | |||||||||||
| p-Value | 0.002 | 0.192 | 0.003 | 0.039 | 0.002 | 0.494 | 0.801 | 0.695 | 0.579 | 0.603 | 0.859 | 0.287 | 0.541 | ||||||||||||||
| Top Surface | Cont. % | - | 14.5 | 6.0 | 19.9 | 17.9 | 5.7 | 2.1 | 4.0 | 0.9 | 3.4 | 5.3 | 3.3 | 2.4 | 86.7 | 73.4 | |||||||||||
| p-Value | 0.001 | 0.004 | 0.045 | 0.002 | 0.002 | 0.049 | 0.206 | 0.092 | 0.398 | 0.116 | 0.057 | 0.120 | 0.186 | ||||||||||||||
| RelativeDensity | Cont. % | - | 19.9 | 15.1 | 8.5 | 1.5 | 16.3 | 0.8 | 0.3 | 0.5 | 2.1 | 3.2 | 0.4 | 0.8 | 71.7 | 37.7 | |||||||||||
| p-Value | 0.123 | 0.029 | 0.051 | 0.127 | 0.501 | 0.044 | 0.615 | 0.772 | 0.685 | 0.426 | 0.329 | 0.726 | 0.630 | ||||||||||||||
| Micro-Hardness | Cont. % | - | 30.6 | 1.3 | 7.7 | 0.1 | 19.8 | 0.8 | 1.6 | 0.1 | 0.3 | 13.9 | 0.4 | 2.2 | 87.0 | 73.9 | |||||||||||
| p-Value | 0.001 | 0.001 | 0.405 | 0.059 | 0.781 | 0.006 | 0.521 | 0.366 | 0.794 | 0.692 | 0.016 | 0.626 | 0.290 | ||||||||||||||
| Source | Model | A | B | C | D | A2 | B2 | C2 | D2 | AB | AC | AD | BD | R2 (%) | R2adj (%) | ||||||||||||
| Response | Parameters Combination | Optimized Response | Energy Density | SE Fit | 90% CI | |||
|---|---|---|---|---|---|---|---|---|
| A | B | C | D | |||||
| Microhardness | 330 | 1024 | 180 | 54 | 372.5 | 33.2 | 3.72 | (365.88, 379.15) |
| Relative Density | 170 | 900 | 180 | 20 | 99.99 | 52.5 | 1.69 | (97.07, 103.17) |
| Top surface Roughness | 250 | 900 | 138 | 20 | 0.1 | 100.6 | 3.77 | (−6.59, 6.83) |
| Upskin Surface Roughness | 208 | 900 | 100 | 20 | 16.29 | 115.6 | 1.49 | (13.65, 18.94) |
| Upskin Horizontal Line Roughness | 262 | 900 | 104 | 20 | 7.64 | 140.0 | 0.893 | (6.051, 9.233) |
| Upskin Vertical Line Roughness | 230 | 900 | 100 | 20 | 10.23 | 127.8 | 1.20 | (8.08, 12.37) |
| Downskin Surface Roughness | 173 | 1500 | 180 | 20 | 16.08 | 32.0 | 4.07 | (7.71, 24.45) |
| Downskin Horizontal Line Roughness | 170 | 900 | 180 | 20 | 10.32 | 52.5 | 4.38 | (2.51, 18.13) |
| Downskin Vertical Line Roughness | 236 | 1500 | 180 | 20 | 10.64 | 43.7 | 1.56 | (6.84, 14.43) |
| Micro-Hardness (HV) | Rel. Density (%) | Top Surface (µm) | Upskin Surface (µm) | Upskin Hor. Line (µm) | Upskin Ver. Line (µm) | Downskin Surface (µm) | Downskin Hor. Line (µm) | Downskin Ver. Line (µm) |
|---|---|---|---|---|---|---|---|---|
| 362.9 | 99.89 | 7.76 | 18.18 | 10.44 | 11.22 | 17.57 | 10.95 | 10.75 |
| Method | Mean Fractional Error of Prediction in Percentage (95% CI) | |||
|---|---|---|---|---|
| Microhardness | Relative Density | Top Surface Roughness | All | |
| Taguchi | 1.68 (1.15, 2.21) | 0.41 (0.19, 0.62) | 32.59 (15.54, 49.65) | 11.56 (4.8, 18.32) |
| RSM | 1.06 (0.68, 1.44) | 0.30 (0.20, 0.39) | 30.16 (16.73, 43.59) | 10.51 (4.85, 16.16) |
| ANN | 1.16 (0.78, 1.54) | 0.23 (0.13, 0.32) | 10.80 (4.80, 16.80) | 4.06 (1.75, 6.38) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fotovvati, B.; Balasubramanian, M.; Asadi, E. Modeling and Optimization Approaches of Laser-Based Powder-Bed Fusion Process for Ti-6Al-4V Alloy. Coatings 2020, 10, 1104. https://doi.org/10.3390/coatings10111104
Fotovvati B, Balasubramanian M, Asadi E. Modeling and Optimization Approaches of Laser-Based Powder-Bed Fusion Process for Ti-6Al-4V Alloy. Coatings. 2020; 10(11):1104. https://doi.org/10.3390/coatings10111104
Chicago/Turabian StyleFotovvati, Behzad, Madhusudhanan Balasubramanian, and Ebrahim Asadi. 2020. "Modeling and Optimization Approaches of Laser-Based Powder-Bed Fusion Process for Ti-6Al-4V Alloy" Coatings 10, no. 11: 1104. https://doi.org/10.3390/coatings10111104
APA StyleFotovvati, B., Balasubramanian, M., & Asadi, E. (2020). Modeling and Optimization Approaches of Laser-Based Powder-Bed Fusion Process for Ti-6Al-4V Alloy. Coatings, 10(11), 1104. https://doi.org/10.3390/coatings10111104






