Cerebrospinal Pharmacokinetic Modeling and Pharmacodynamic Simulation of High-Dose Cefazolin for Meningitis Caused by Methicillin-Susceptible Staphylococcus aureus
Abstract
1. Introduction
2. Results
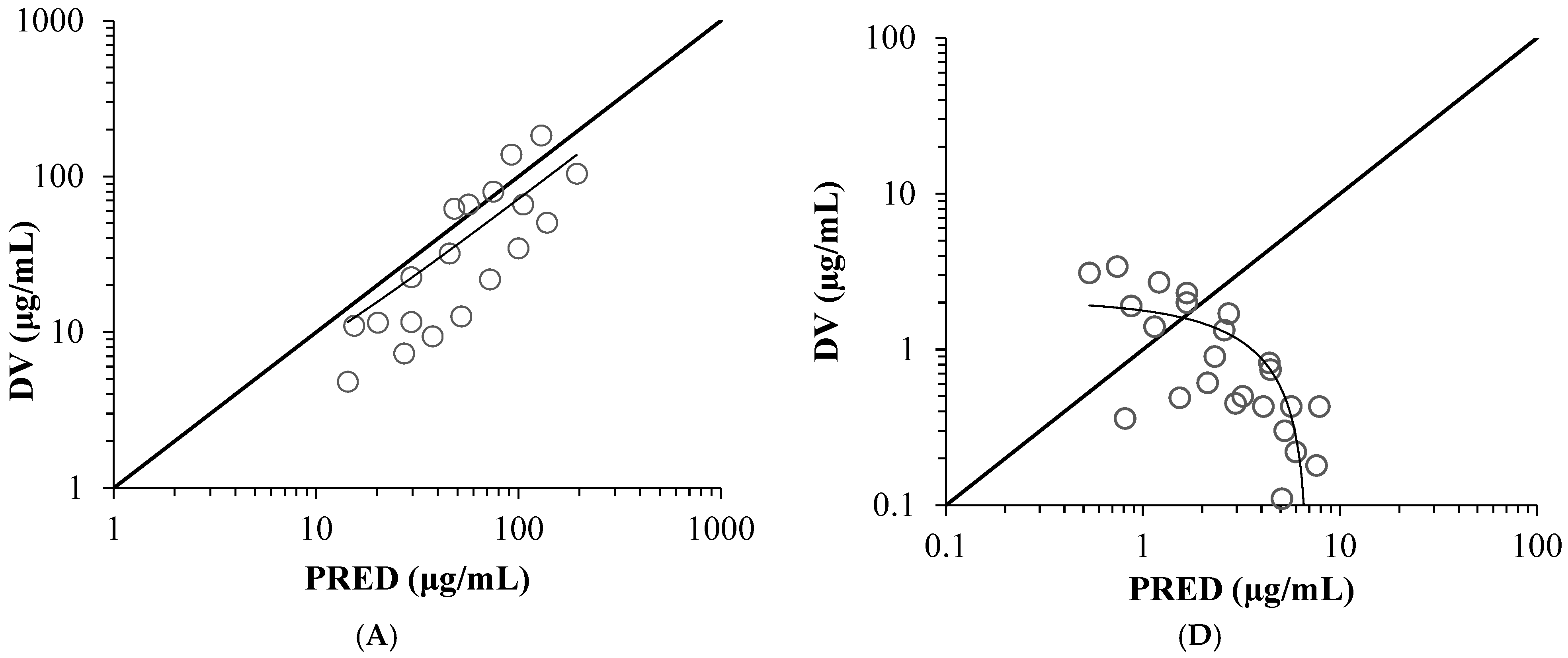
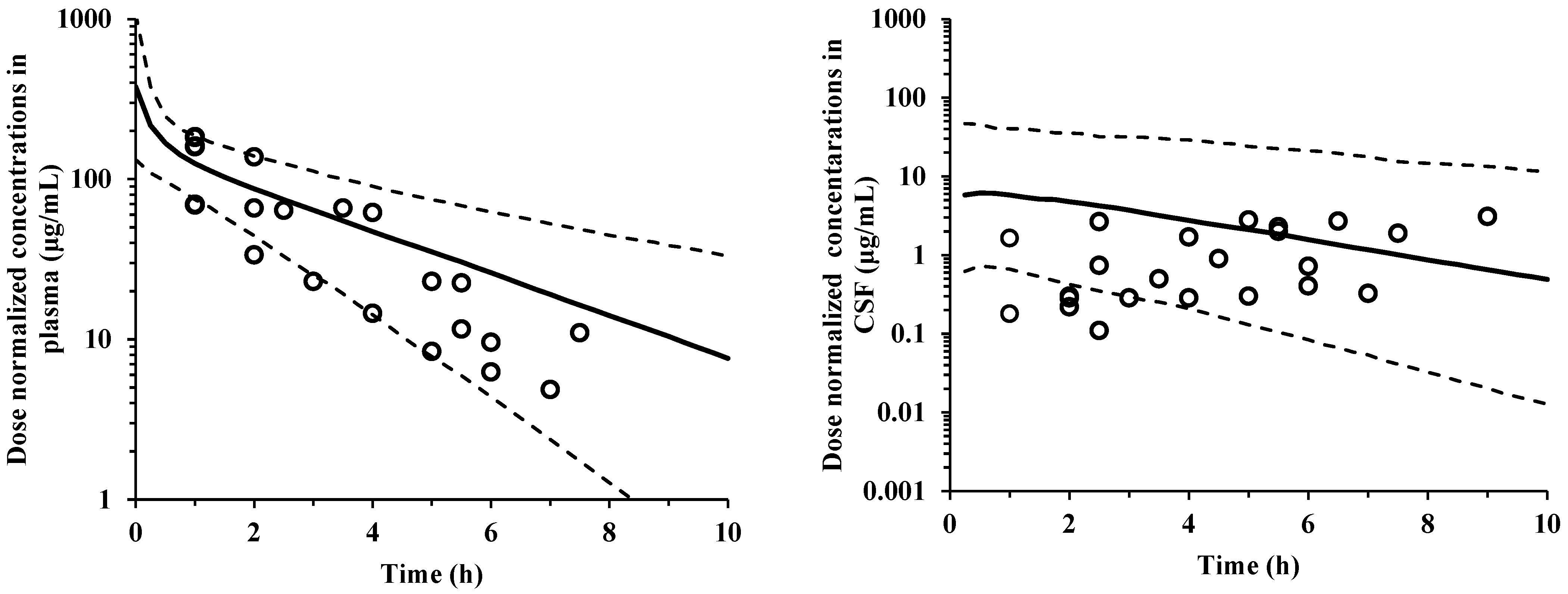
2.1. Model Validation
2.2. PK/PD Evaluation
3. Discussion
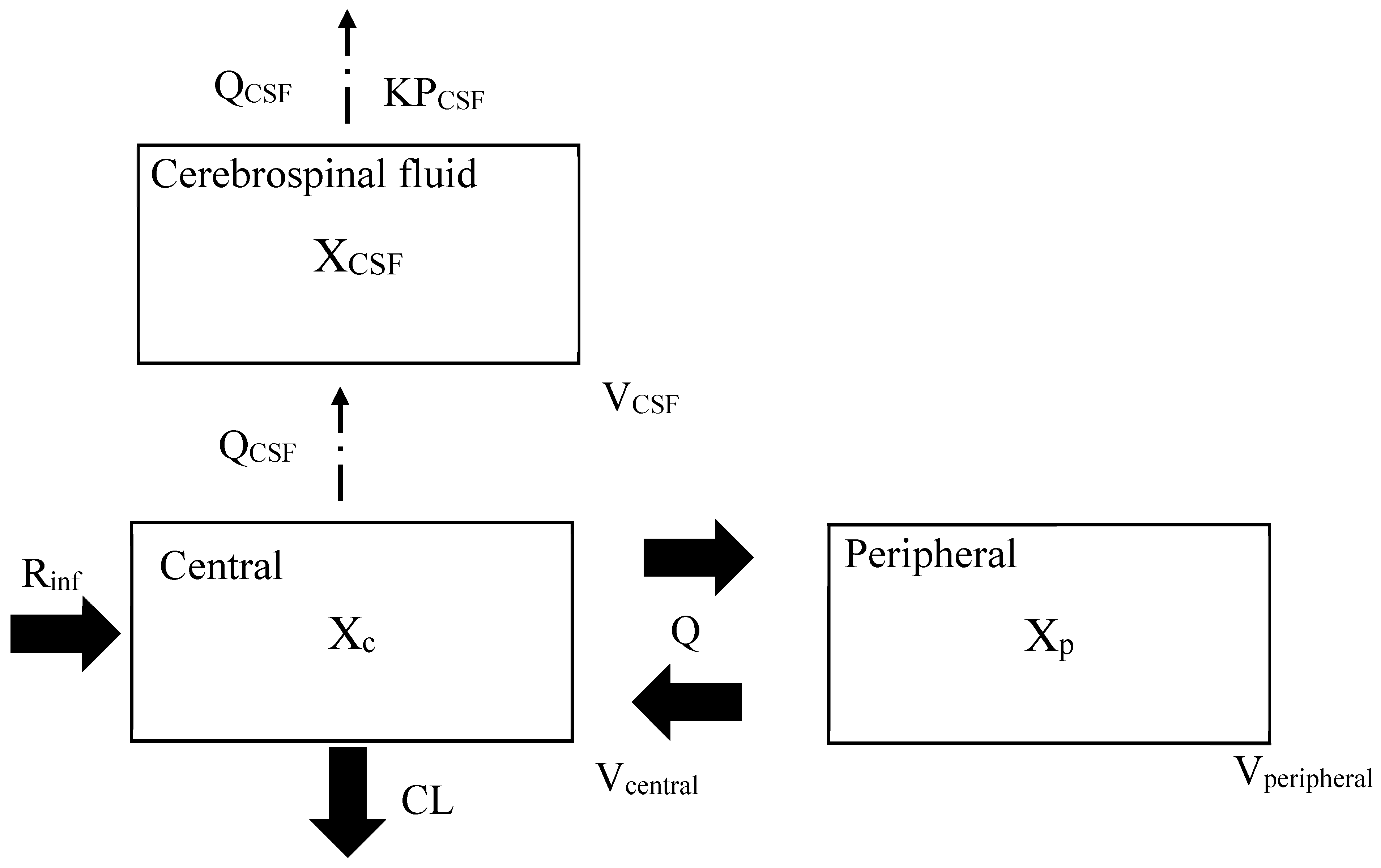
4. Materials and Methods
4.1. Cerebrospinal PK Modeling
4.2. Estimation of CSF/Serum Concentration Ratio
4.3. Model Validation
4.4. PK/PD Simulation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| CNS | Central nervous system |
| CSF | Cerebrospinal fluid |
| CLcr | Creatinine clearance |
| PRED | Population-predicted concentration |
| CWRES | Conditional weighted residuals |
| MSSA | Methicillin-susceptible Staphylococcus aureus |
| PK | Pharmacokinetic |
| PD | Pharmacodynamic |
| MIC | Minimum inhibitory concentration |
| KPCSF | CSF-to-plasma partition coefficient |
| QCSF | CSF flow |
| VCSF | CSF volume |
| CL | Clearance |
| Vcentral | Volumes of distribution volumes of the central |
| Q | central–peripheral intercompartmental clearance |
| Vperipheral | Volumes of distribution volumes of the peripheral |
References
- Gilbert, D.N.; Chambers, H.F.; Saag, M.S.; Pavia, A.T.; Boucher, H.W. The Sanford Guide to Antimicrobial Therapy, 51st ed.; Sanford Guide: Sperryville, VA, USA, 2021. [Google Scholar]
- Tunkel, A.R.; Hasbun, R.; Bhimraj, A.; Byers, K.; Kaplan, S.L.; Scheld, W.M.; van de Beek, D.; Bleck, T.P.; Garton, H.J.L.; Zunt, J.R. 2017 Infectious Diseases Society of America’s Clinical Practice Guidelines for Healthcare-Associated Ventriculitis and Meningitis. Clin. Infect. Dis. 2017, 64, e34–e65. [Google Scholar]
- Tunkel, A.R.; Hartman, B.J.; Kaplan, S.L.; Kaufman, B.A.; Roos, K.L.; Scheld, W.M.; Whitley, R.J. Practice guidelines for the management of bacterial meningitis. Clin. Infect. Dis. 2004, 39, 1267–1284. [Google Scholar] [CrossRef]
- Nafcillin; Package Insert; Baxter Healthcare Corporation: Deerfield, IL, USA, 2007.
- Li, J.; Echevarria, K.L.; Hughes, D.W.; Cadena, J.A.; Bowling, J.E.; Lewis, J.S., 2nd. Comparison of cefazolin versus oxacillin for treatment of complicated bacteremia caused by methicillin-susceptible Staphylococcus aureus. Antimicrob. Agents Chemother. 2014, 58, 5117–5124. [Google Scholar] [CrossRef]
- McDanel, J.S.; Roghmann, M.C.; Perencevich, E.N.; Ohl, M.E.; Goto, M.; Livorsi, D.J.; Jones, M.; Albertson, J.P.; Nair, R.; O’Shea, A.M.J.; et al. Comparative Effectiveness of Cefazolin Versus Nafcillin or Oxacillin for Treatment of Methicillin-Susceptible Staphylococcus aureus Infections Complicated by Bacteremia: A Nationwide Cohort Study. Clin. Infect. Dis. 2017, 65, 100–106. [Google Scholar] [CrossRef] [PubMed]
- Loubet, P.; Burdet, C.; Vindrios, W.; Grall, N.; Wolff, M.; Yazdanpanah, Y.; Andremont, A.; Duval, X.; Lescure, F.X. Cefazolin versus anti-staphylococcal penicillins for treatment of methicillin-susceptible Staphylococcus aureus bacteraemia: A narrative review. Clin. Microbiol. Infect. 2018, 24, 125–132. [Google Scholar] [CrossRef] [PubMed]
- Shi, C.; Xiao, Y.; Zhang, Q.; Li, Q.; Wang, F.; Wu, J.; Lin, N. Efficacy and safety of cefazolin versus antistaphylococcal penicillins for the treatment of methicillin-susceptible Staphylococcus aureus bacteremia: A systematic review and meta-analysis. BMC Infect. Dis. 2018, 18, 508. [Google Scholar] [CrossRef] [PubMed]
- Weis, S.; Kesselmeier, M.; Davis, J.S.; Morris, A.M.; Lee, S.; Scherag, A.; Hagel, S.; Pletz, M.W. Cefazolin versus anti-staphylococcal penicillins for the treatment of patients with Staphylococcus aureus bacteraemia. Clin. Microbiol. Infect. 2019, 25, 818–827. [Google Scholar] [CrossRef]
- Thys, J.P.; Vanderkelen, B.; Klastersky, J. Pharmacological study of cefazolin during intermittent and continuous infusion: A crossover investigation in humans. Antimicrob. Agents Chemother. 1976, 10, 395–398. [Google Scholar] [CrossRef]
- Grégoire, M.; Gaborit, B.; Deschanvres, C.; Lecomte, R.; Deslandes, G.; Dailly, É.; Ambrosi, X.; Bellouard, R.; Asseray, N.; Lakhal, K.; et al. High-Dosage Cefazolin Achieves Sufficient Cerebrospinal Diffusion to Treat an External Ventricular Drainage-Related Staphylococcus aureus Ventriculitis. Antimicrob. Agents Chemother. 2019, 63, e01844-18. [Google Scholar]
- Le Turnier, P.; Gregoire, M.; Deslandes, G.; Lakhal, K.; Deschanvres, C.; Lecomte, R.; Talarmin, J.P.; Dubée, V.; Bellouard, R.; Boutoille, D.; et al. NAMAP study group. Should we reconsider cefazolin for treating staphylococcal meningitis? A retrospective analysis of cefazolin and cloxacillin cerebrospinal fluid levels in patients treated for staphylococcal meningitis. Clin. Microbiol. Infect. 2020, 26, 1415.e1–1415.e4. [Google Scholar]
- Novak, A.R.; Krsak, M.; Kiser, T.H.; Neumann, R.T.; Cava Prado, L.; Molina, K.C.; Mueller, S.W. Pharmacokinetic Evaluation of Cefazolin in the Cerebrospinal Fluid of Critically Ill Patients. Open Forum Infect. Dis. 2021, 9, ofab649. [Google Scholar] [CrossRef] [PubMed]
- Antosz, K.; Battle, S.; Chang, J.; Scheetz, M.H.; Al-Hasan, M.; Bookstaver, P.B. Cefazolin in the treatment of central nervous system infections: A narrative review and recommendation. Pharmacotherapy 2023, 43, 85–95. [Google Scholar]
- Onita, T.; Ishihara, N.; Yano, T. PK/PD-Guided Strategies for Appropriate Antibiotic Use in the Era of Antimicrobial Resistance. Antibiotics 2025, 14, 92. [Google Scholar]
- Craig, W.A. Pharmacokinetic/pharmacodynamic parameters: Rationale for antibacterial dosing of mice and men. Clin. Infect. Dis. 1998, 26, 1–10. [Google Scholar] [CrossRef]
- Craig, W.A. Does the dose matter? Clin. Infect. Dis. 2001, 33, S233–S237. [Google Scholar] [CrossRef]
- Ikuno, H.; Nin, K.; Nishimura, S. Penetration of cefazolin into cerebrospinal fluid and brain tissue. Med. Consult. New Remedies 1977, 14, 457–464. [Google Scholar]
- Pitcock, C.; Burgess, D.S.; Olney, K.B. Optimizing cefazolin dosing for central nervous system infections: Insights from population pharmacokinetics and Monte Carlo simulations. Antimicrob. Agents Chemother. 2025, 69, e0185724. [Google Scholar] [CrossRef] [PubMed]
- Bechtel, T.P.; Slaughter, R.L.; Moore, T.D. Seizures associated with high cerebrospinal fluid concentrations of cefazolin. Am. J. Hosp. Pharm. 1980, 37, 271–273. [Google Scholar] [PubMed]
- Ohata, Y.; Tomita, Y.; Sunakawa, K.; Drusano, G.L.; Tanigawara, Y. Cerebrospinal pharmacokinetic and pharmacodynamic analysis of efficacy of meropenem in paediatric patients with bacterial meningitis. Int. J. Antimicrob. Agents 2019, 54, 292–300. [Google Scholar] [CrossRef]
- Onita, T.; Ikawa, K.; Nakamura, K.; Nishikawa, G.; Kobayashi, I.; Ishihara, N.; Tamaki, H.; Yano, T.; Naora, K.; Morikawa, N. Prostatic Pharmacokinetic/Pharmacodynamic Evaluation of Ampicillin-Sulbactam for Bacterial Prostatitis and Preoperative Prophylaxis. J. Clin. Pharmacol. 2021, 61, 820–831. [Google Scholar] [CrossRef]
- Onita, T.; Ikawa, K.; Ishihara, N.; Tamaki, H.; Yano, T.; Naora, K.; Morikawa, N. Pulmonary Pharmacokinetic and Pharmacodynamic Evaluation of Ampicillin/Sulbactam Regimens for Pneumonia Caused by Various Bacteria, including Acinetobacter baumannii. Antibiotics 2023, 12, 303. [Google Scholar] [CrossRef] [PubMed]
- Onita, T.; Nakamura, K.; Nishikawa, G.; Ishihara, N.; Tamaki, H.; Yano, T.; Naora, K.; Morikawa, N.; Ikawa, K. Prostatic Pharmacokinetic and Pharmacodynamic Analysis of Ceftazidime: Dosing Strategy for Bacterial Prostatitis. J. Clin. Pharmacol. 2025, 65, 121–131. [Google Scholar] [CrossRef] [PubMed]
- Lanoiselée, J.; Chaux, R.; Hodin, S.; Bourayou, S.; Gibert, A.; Philippot, R.; Molliex, S.; Zufferey, P.J.; Delavenne, X.; Ollier, E. Population pharmacokinetic model of cefazolin in total hip arthroplasty. Sci. Rep. 2021, 11, 19763. [Google Scholar] [CrossRef]
- Cutler, R.W.P.; Page, L.; Galicich, J.; Watters, G.V. Formation and absorption of cerebrospinal fluid in man. Brain 1968, 91, 707–720. [Google Scholar] [CrossRef]
- Chan Kwong, A.H.P.; Calvier, E.A.M.; Fabre, D.; Gattacceca, F.; Khier, S. Prior information for population pharmacokinetic and pharmacokinetic/pharmacodynamic analysis: Overview and guidance with a focus on the NONMEM PRIOR subroutine. J. Pharmacokinet. Pharmacodyn. 2020, 47, 431–446. [Google Scholar] [CrossRef]
- Marshall, S.; Macintyre, F.; James, I.; Krams, M.; Jonsson, N.E. Role of mechanistically-based pharmacokinetic/pharmacodynamic models in drug development: A case study of a therapeutic protein. Clin. Pharmacokinet. 2006, 45, 177–197. [Google Scholar]
- Lindbom, L.; Ribbing, J.; Jonsson, E.N. Perl-speaks-NONMEM (PsN)—A Perl module for NONMEM related programming. Comput. Methods Programs Biomed. 2004, 75, 85–94. [Google Scholar] [PubMed]
- Four Academic Societies Joint Antimicrobial Susceptibility Surveillance Program. Available online: https://www.3ssp.jp/database/surgical/mic-5090/ (accessed on 12 February 2025).

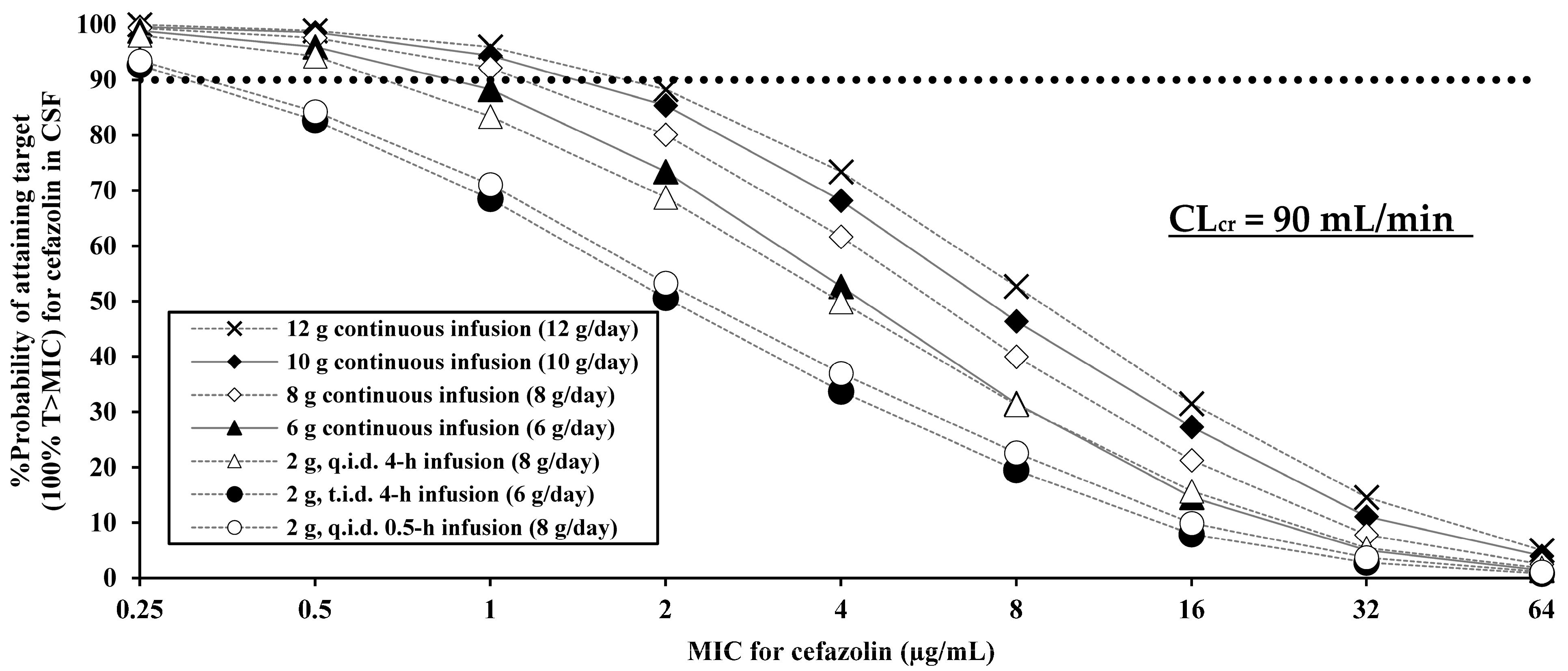
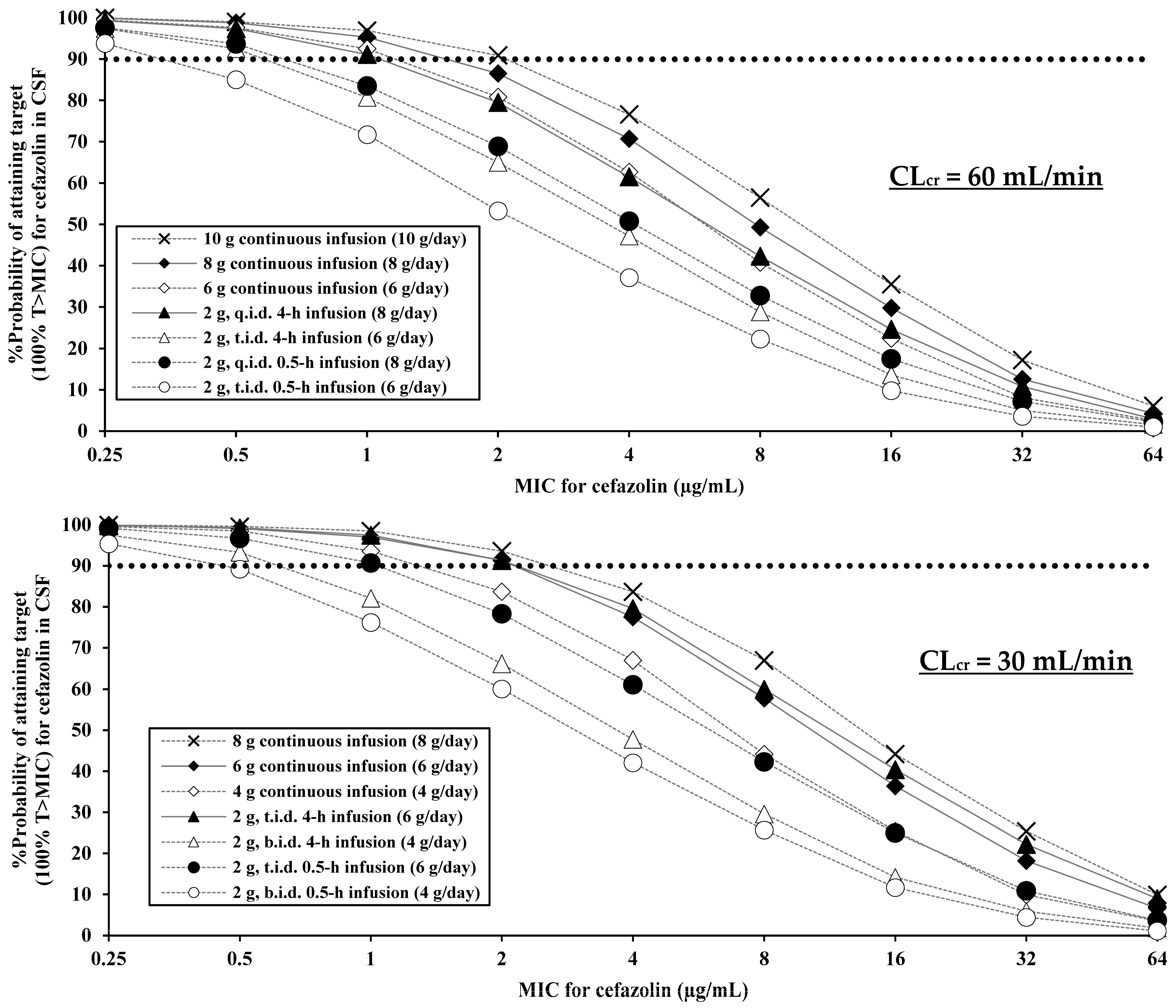
| Cefazolin Regimen | PK/PD Breakpoint (100% T > MIC) |
|---|---|
| CLcr = 90 mL/min | |
| 2 g q.i.d. 0.5 h infusion (8 g/day) | 0.25 |
| 2 g t.i.d. 4 h infusion (6 g/day) | 0.25 |
| 2 g q.i.d. 4 h infusion (8 g/day) | 0.5 |
| 6 g continuous infusion (6 g/day) | 0.5 |
| 8 g continuous infusion (8 g/day) | 1 |
| 10 g continuous infusion (10 g/day) | 1 |
| 12 g continuous infusion (12 g/day) | 1 |
| CLcr = 60 mL/min | |
| 2 g t.i.d. 0.5 h infusion (6 g/day) | 0.25 |
| 2 g q.i.d. 0.5 h infusion (8 g/day) | 0.5 |
| 2 g t.i.d. 4 h infusion (6 g/day) | 0.5 |
| 2 g q.i.d. 4 h infusion (8 g/day) | 1 |
| 6 g continuous infusion (6 g/day) | 1 |
| 8 g continuous infusion (8 g/day) | 1 |
| 10 g continuous infusion (10 g/day) | 2 |
| CLcr = 30 mL/min | |
| 2 g b.i.d. 0.5 h infusion (4 g/day) | 0.25 |
| 2 g t.i.d. 0.5 h infusion (6 g/day) | 1 |
| 2 g b.i.d. 4 h infusion (4 g/day) | 0.5 |
| 2 g t.i.d. 4 h infusion (6 g/day) | 2 |
| 4 g continuous infusion (4 g/day) | 1 |
| 6 g continuous infusion (6 g/day) | 2 |
| 8 g continuous infusion (8 g/day) | 2 |
| Estimate | (RSE %) | 95%CI | |
|---|---|---|---|
| Fix effects parameter | |||
| CL(L/h) a = θCL × (CLcr/80)θCLcr on CL | |||
| θCL(L/h) | 2.86 Fixed | - | - |
| θCLcr on CL | 0.79 Fixed | - | - |
| Vcentral (L) a = θVc | 5.2 Fixed | - | - |
| Q (L/h) a = θQ | 10.9 Fixed | - | - |
| Vperipheral (L) a = θVp | 4.56 Fixed | - | - |
| KPCSF b = θKPCSF | 0.0525 Fixed | - | - |
| QCSF (L/h) c = θQCSF | 0.021 Fixed | - | - |
| VCSF (L) c = θVCSF | 0.092 Fixed | - | - |
| Interindividual variability (exponential error model) | |||
| ηCL a | 0.102 Fixed | - | - |
| ηVcentral a | 0.325 Fixed | - | - |
| ηQ a | 0.437 Fixed | - | - |
| ηVperipheral a | 0.01 Fixed | - | - |
| ηKPCSF | 1.39 | (203.0) | 0.0188–43.6 |
| ηQCSF c | 1.22 | (0.75) | 0.00245–172.7 |
| ηVCSF c | 1.22 | (0.38) | 0.00443–178.4 |
| Residual variability (proportion error model) | |||
| εproportional a | 0.0144 Fixed | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onita, T.; Ikawa, K.; Ishihara, N.; Tamaki, H.; Yano, T. Cerebrospinal Pharmacokinetic Modeling and Pharmacodynamic Simulation of High-Dose Cefazolin for Meningitis Caused by Methicillin-Susceptible Staphylococcus aureus. Antibiotics 2025, 14, 1008. https://doi.org/10.3390/antibiotics14101008
Onita T, Ikawa K, Ishihara N, Tamaki H, Yano T. Cerebrospinal Pharmacokinetic Modeling and Pharmacodynamic Simulation of High-Dose Cefazolin for Meningitis Caused by Methicillin-Susceptible Staphylococcus aureus. Antibiotics. 2025; 14(10):1008. https://doi.org/10.3390/antibiotics14101008
Chicago/Turabian StyleOnita, Tetsushu, Kazuro Ikawa, Noriyuki Ishihara, Hiroki Tamaki, and Takahisa Yano. 2025. "Cerebrospinal Pharmacokinetic Modeling and Pharmacodynamic Simulation of High-Dose Cefazolin for Meningitis Caused by Methicillin-Susceptible Staphylococcus aureus" Antibiotics 14, no. 10: 1008. https://doi.org/10.3390/antibiotics14101008
APA StyleOnita, T., Ikawa, K., Ishihara, N., Tamaki, H., & Yano, T. (2025). Cerebrospinal Pharmacokinetic Modeling and Pharmacodynamic Simulation of High-Dose Cefazolin for Meningitis Caused by Methicillin-Susceptible Staphylococcus aureus. Antibiotics, 14(10), 1008. https://doi.org/10.3390/antibiotics14101008





