Shining a Light on Spectrophotometry in Bacteriology
Abstract
1. Introduction
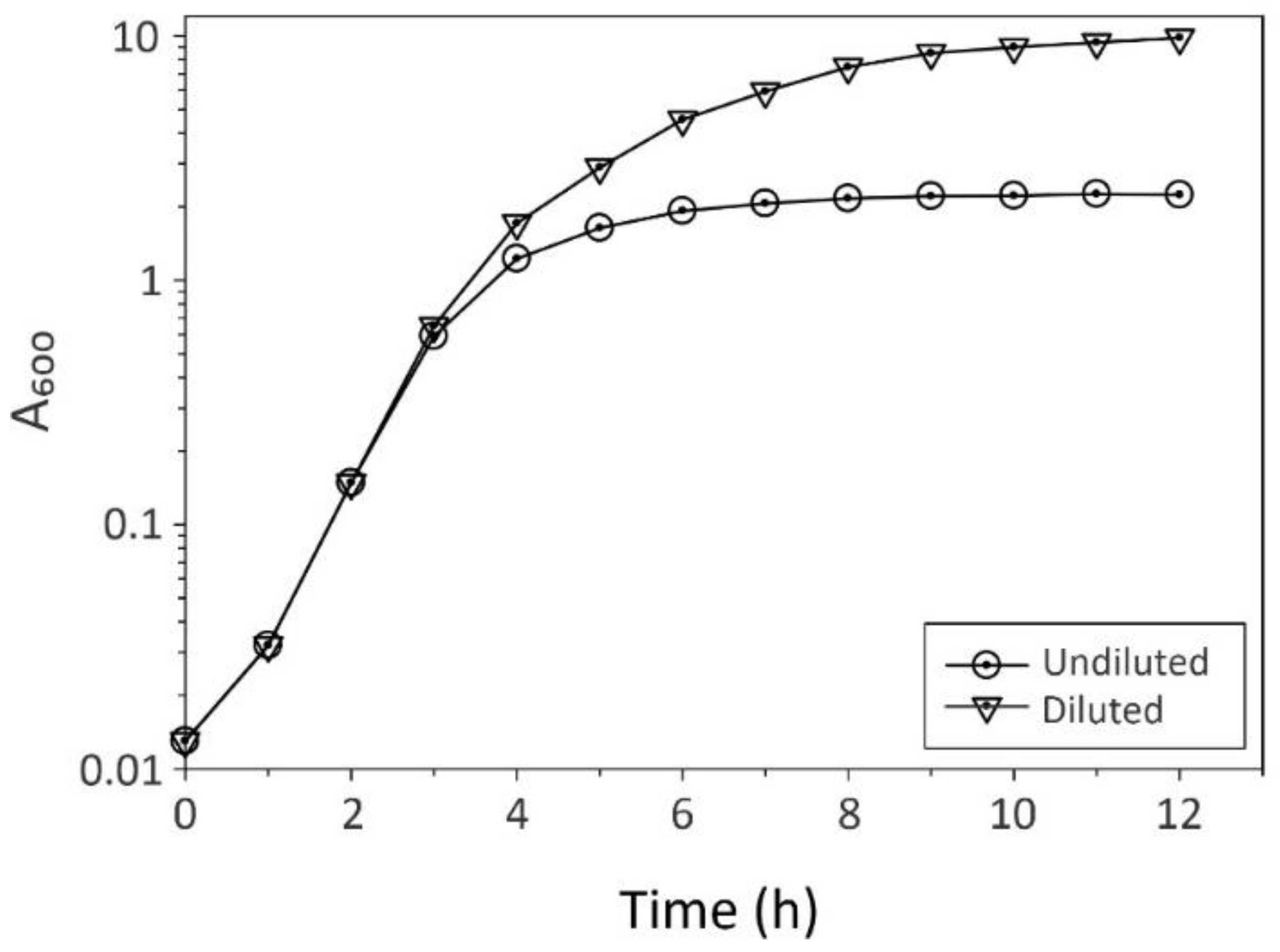
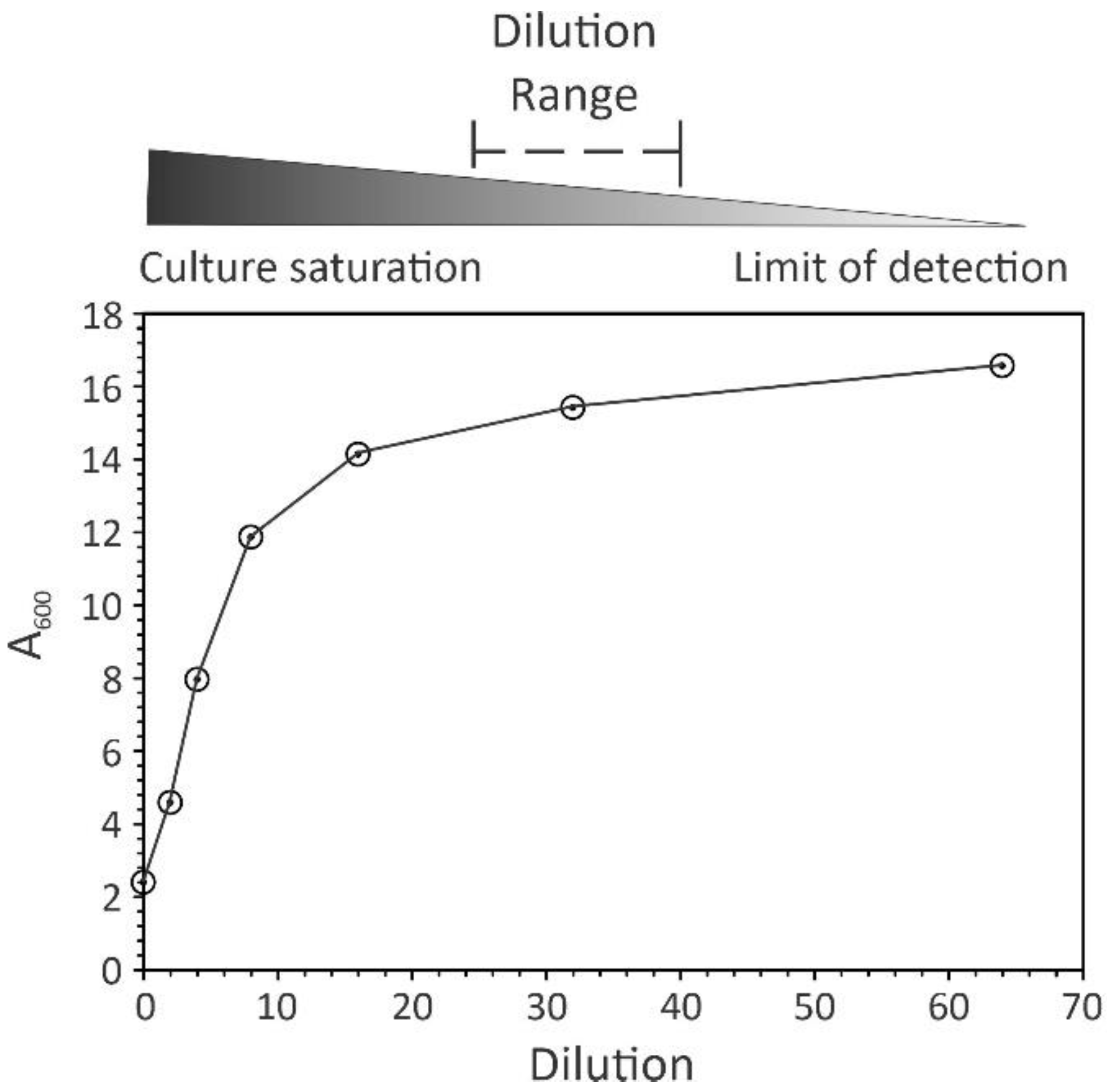
2. Practical Considerations
3. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
References
- Bouguer, P. Essai D’optique, sur la Gradation de la Lumière; Claude Jombert: Paris, France, 1729; p. 193. [Google Scholar]
- Lambert, J.H.; Anding, E. Lamberts Photometrie: [Photometria, Sive de Mensura et Gradibus Luminus, Colorum et Umbrae]; Ostwalds Klassiker der exakten Wissenschaften; Leipzig, W. Engelmann: Lemgo, Germany, 1892; Volume 31–33, p. 433. [Google Scholar]
- Beer, A. Bestimmung der Absorption des rothen Lichts in farbigen Flüssigkeiten. Ann. Phys. Chem. 1852, 88, 78–88. [Google Scholar] [CrossRef]
- Cantor, C.R.; Schimmel, P.R. Biophysical Chemistry: Part II: Techniques for the Study of Biological Structure and Function; W. H. Freeman: Leipzig, Germany, 1980. [Google Scholar]
- Segel, I.H. Biochemical Calculations: How to Solve Mathematical Problems in General Biochemistry; Wiley: Hoboken, NJ, USA, 1976. [Google Scholar]
- Robertson, A.R. Standardization in Transmission Spectrophotometry in the Visible and Ultraviolet Spectral Regions. J. Res. Natl. Bur. Stand. A Phys. Chem. 1976, 80A, 625–630. [Google Scholar] [CrossRef]
- Stevenson, K.; McVey, A.F.; Clark, I.B.; Swain, P.S.; Pilizota, T. General calibration of microbial growth in microplate readers. Sci. Rep. 2016, 6, 38828. [Google Scholar] [CrossRef]
- Strutt, J.W. On the scattering of light by small particles. Lond. Edinb. Dublin Philos. Mag. J. Sci. 1871, 41, 447–454. [Google Scholar] [CrossRef]
- Mie, G. Beiträge zur Optik trüber Medien, speziell kolloidaler Metallösungen. Ann. Phys. 1908, 330, 377–445. [Google Scholar] [CrossRef]
- van de Hulst, H.C. Light Scattering by Small Particles; Wiley: Hoboken, NJ, USA, 1957; p. 470. [Google Scholar]
- Kotlarchyk, M.; Chen, S.H.; Asano, S. Accuracy of RGD approximation for computing light scattering properties of diffusing and motile bacteria. Appl. Opt. 1979, 18, 2470–2479. [Google Scholar] [CrossRef] [PubMed]
- Koch, A.L. Some calculations on the turbidity of mitochondria and bacteria. Biochim. Biophys. Acta 1961, 51, 429–441. [Google Scholar] [CrossRef]
- Mira, P.; Yeh, P.; Hall, B.G. Estimating microbial population data from optical density. PLoS ONE 2022, 17, e0276040. [Google Scholar] [CrossRef] [PubMed]
- Winslow, C.E.; Walker, H.H. The earlier phases of the bacterial culture cycle. Bacteriol. Rev. 1939, 3, 147–186. [Google Scholar] [CrossRef] [PubMed]
- Brauner, A.; Fridman, O.; Gefen, O.; Balaban, N.Q. Distinguishing between resistance, tolerance and persistence to antibiotic treatment. Nat. Rev. Microbiol. 2016, 14, 320–330. [Google Scholar] [CrossRef] [PubMed]
- Stokes, J.M.; Lopatkin, A.J.; Lobritz, M.A.; Collins, J.J. Bacterial Metabolism and Antibiotic Efficacy. Cell Metab. 2019, 30, 251–259. [Google Scholar] [CrossRef] [PubMed]
- Summerson, W.H. A simplified test-tube photoelectric colorimeter, and the use of the photoelectric colorimeter in colorimetric analysis. J. Biol. Chem. 1939, 130, 149–166. [Google Scholar] [CrossRef]
- Somerville, G.A.; Proctor, R.A. Cultivation conditions and the diffusion of oxygen into culture media: The rationale for the flask-to-medium ratio in microbiology. BMC Microbiol. 2013, 13, 9. [Google Scholar] [CrossRef] [PubMed]
- Somerville, G.A.; Powers, R. Growth and preparation of Staphylococcus epidermidis for NMR metabolomic analysis. In Methods in Molecular Biology; Fey, P.D., Ed.; Humana Press: New York, NY, USA, 2014; pp. 71–91. [Google Scholar]
- Dennis, P.P.; Bremer, H. Macromolecular composition during steady-state growth of Escherichia coli B-r. J. Bacteriol. 1974, 119, 270–281. [Google Scholar] [CrossRef] [PubMed]
- Youmans, G.P.; Youmans, A.S. A Method for the Determination of the Rate of Growth of Tubercle Bacilli by the Use of Small Inocula. J. Bacteriol. 1949, 58, 247–255. [Google Scholar] [CrossRef]
- Youmans, G.P.; Youmans, A.S. The growth of recently isolated strains of Mycobacterium tuberculosis var. hominis in liquid media. J. Bacteriol. 1950, 60, 569–572. [Google Scholar] [CrossRef] [PubMed]
- Arnold, M.; Goldschmitt, M.; Rigotti, T. Dealing with information overload: A comprehensive review. Front. Psychol. 2023, 14, 1122200. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Montesinos-Cruz, V.; Somerville, G.A. Shining a Light on Spectrophotometry in Bacteriology. Antibiotics 2024, 13, 1164. https://doi.org/10.3390/antibiotics13121164
Montesinos-Cruz V, Somerville GA. Shining a Light on Spectrophotometry in Bacteriology. Antibiotics. 2024; 13(12):1164. https://doi.org/10.3390/antibiotics13121164
Chicago/Turabian StyleMontesinos-Cruz, Veronica, and Greg A. Somerville. 2024. "Shining a Light on Spectrophotometry in Bacteriology" Antibiotics 13, no. 12: 1164. https://doi.org/10.3390/antibiotics13121164
APA StyleMontesinos-Cruz, V., & Somerville, G. A. (2024). Shining a Light on Spectrophotometry in Bacteriology. Antibiotics, 13(12), 1164. https://doi.org/10.3390/antibiotics13121164




