Penicillins’ Solubility in Supercritical Carbon Dioxide: Modeling by Cubic Equations of States Revisited
Abstract
1. Introduction
2. Modeling and Thermodynamic Basis
3. cEoSs Needed
- Redlich-Kwong (RK cEoS):
- Soave-Redlich-Kwong (SRK cEoS):
- Peng-Robinson (PR cEoS):where is the acentric factor and and are the critical and reduced temperatures, respectively. The conventional mixing rules of van der Waals and combination mixing rules of Lorentz-Berthelot are given below [40]:
4. Review and Discussion of Literature Results
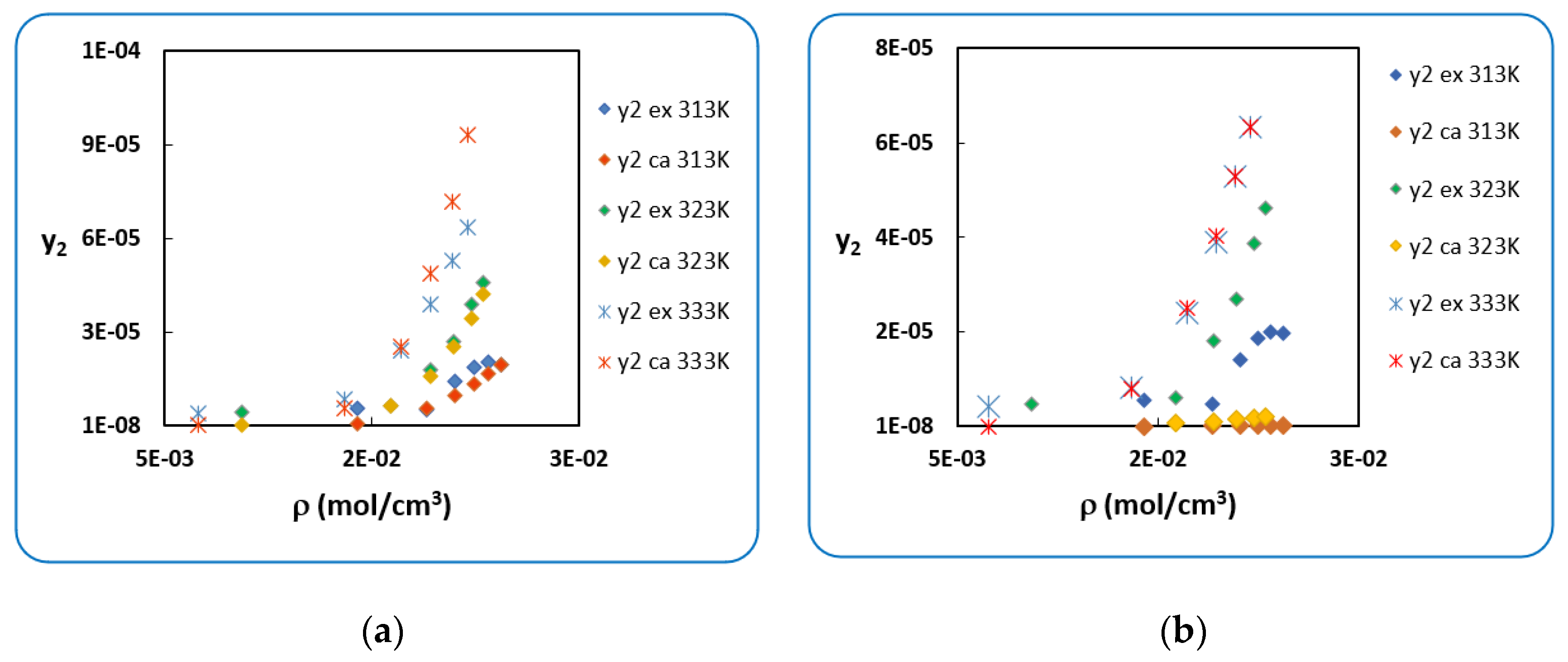
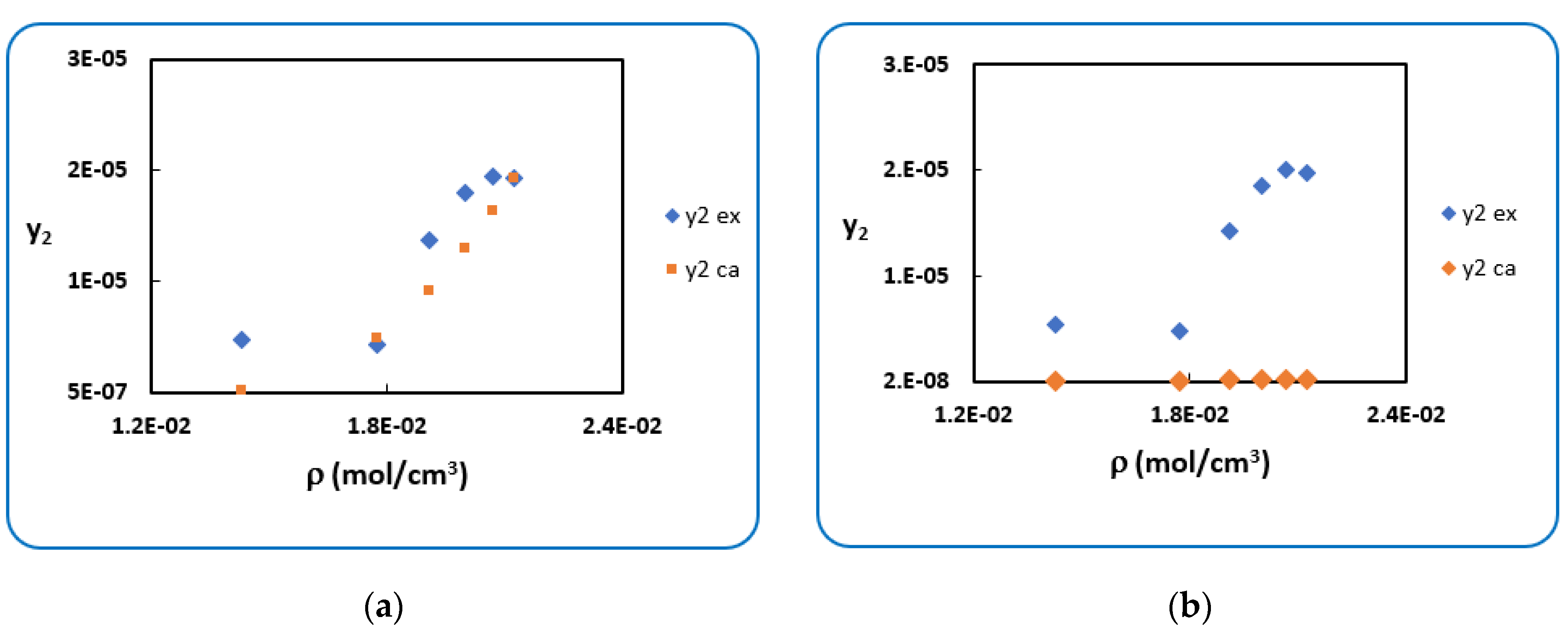
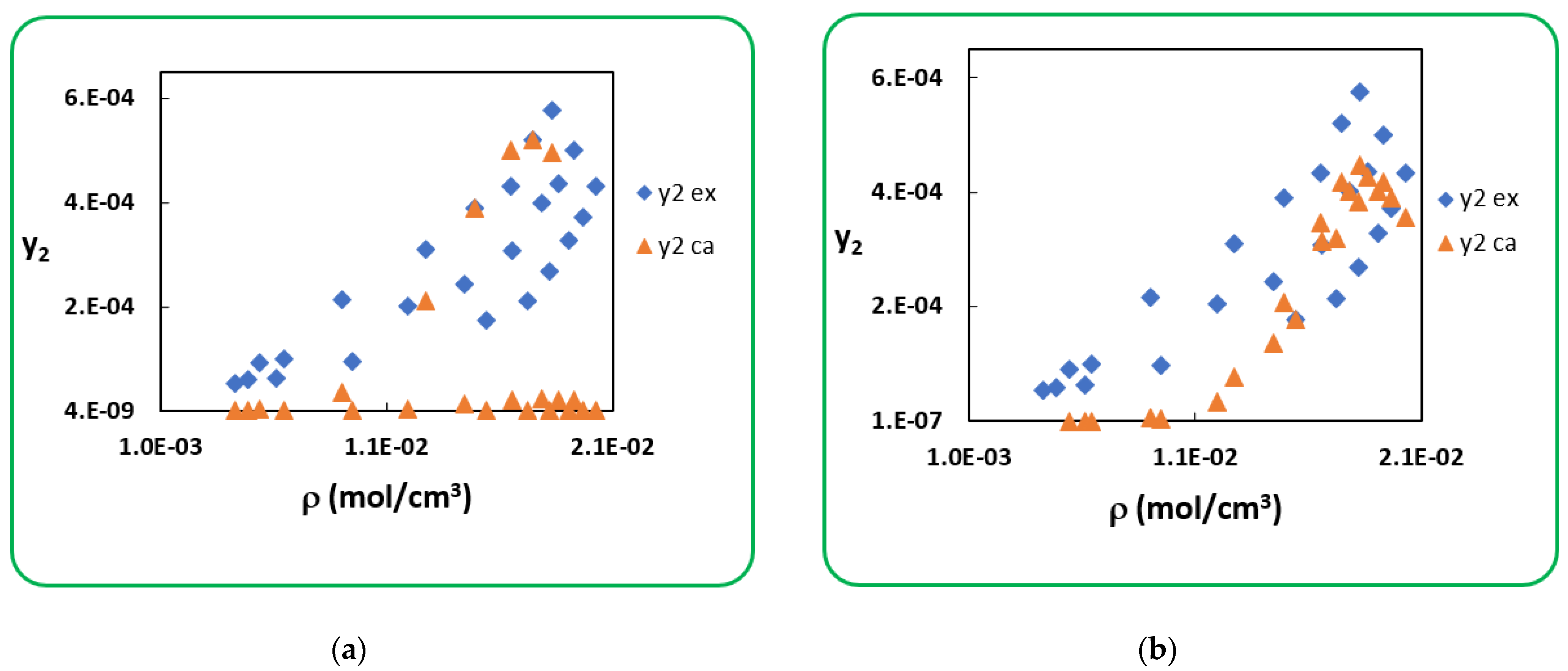
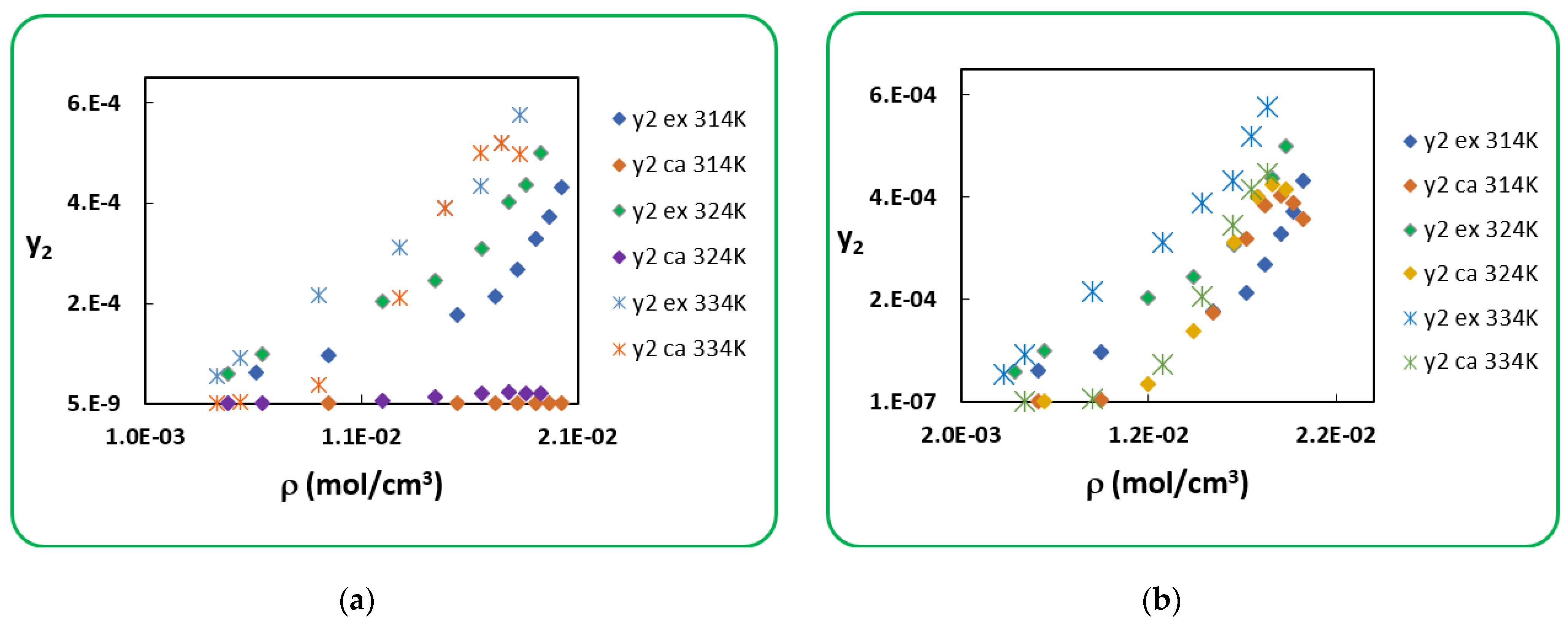
4.1. Penicillin G
4.2. Penicillin V
5. Schmitt and Reid Modified PR cEoS
- Regression of the experimental data (N = 18) for Penicillin G with modified PR cEoS is done by the implementation of , one of whichis obtained by SRK cEoS (-SRK) and the other is obtained by RK cEoS(-RK). The results are presented in Table 3.
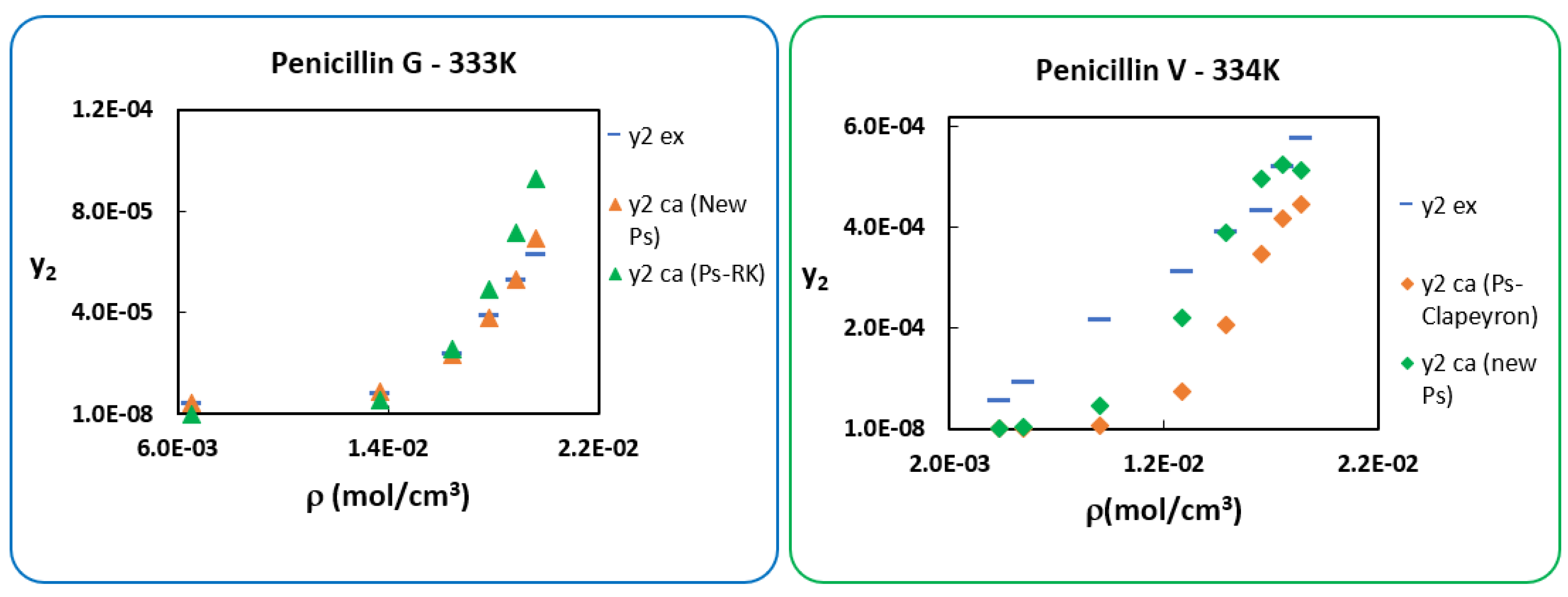
6. Use of New Sublimation Pressure
7. Conclusions
Funding
Conflicts of Interest
References
- Ashour, I.; Almehaideb, R.; Fateen, S.; Aly, G. Representation of solid-supercritical fluid phase equilibria using cubic equations of state. Fluid Phase Equilib. 2000, 167, 41–61. [Google Scholar] [CrossRef]
- Su, C.; Chen, Y. Correlation for the solubilities of pharmaceutical compounds in supercritical carbon dioxide. Fluid Phase Equilib. 2007, 254, 167–173. [Google Scholar] [CrossRef]
- Khamda, M.; Hosseini, M.H.; Rezaee, M. Measurement and correlation solubility of cefixime trihydrate and oxymetholone in supercritical carbon dioxide (CO2). J. Supercrit. Fluids 2013, 73, 130–137. [Google Scholar] [CrossRef]
- Issaoui, A.; Ksibi, H.; Ksibi, M. Supercritical fluid extraction of triterpenes and aliphatic hydrocarbons from olive tree derivatives. Arab. J. Chem. 2017, 10, S3967–S3973. [Google Scholar] [CrossRef]
- Chronopoulou, L.; Bosco, C.; Caprio, F.; Prosini, L.; Gentili, A.; Pagnanelli, F.; Palocci, C. Extraction of carotenoids and fat-soluble vitamins from Tetradesmus obliquus microalgae: An optimized approach by using supercritical CO2. Molecules 2019, 24, 2581. [Google Scholar] [CrossRef]
- Abdul Aziz, A.; Putra, N.; Kong, H.; Yunus, M.C. Supercritical Carbon Dioxide Extraction of Sinensetin, Isosinensetin, and Rosmarinic Acid from Orthosiphon stamineus Leaves: Optimization and Modeling. Arab. J. Sci. Eng. 2020, 45, 7467–7476. [Google Scholar] [CrossRef]
- Sodeifian, G.; Nasri, L.; Razmimanesh, F.; Abadian, M. Measuring and modeling the solubility of an antihypertensive drug (losartan potassium, Cozaar) in supercritical carbon dioxide. J. Mol. Liq. 2021, 331, 115745. [Google Scholar] [CrossRef]
- Abdul Aziz, A.; Putra, N.R.; Zaini, A.S.; Idham, Z.; Muhammad Zulhilmi, A.; Che Yunus, M.A. Solubility of sinensetin and isosinensetin from Cat’s Whiskers (Orthosiphon stamineus) leaves in ethanol-assisted supercritical carbon dioxide extraction: Experimental and modeling. Chem. Pap. 2021, 75, 6557–6563. [Google Scholar] [CrossRef]
- Sodeifian, G.; Sajadian, S.A.; Razmimanesh, F.; Hazaveie, S.M. Solubility of Ketoconazole (antifungal drug) in SC-CO2 for binary and ternary systems: Measurements and empirical correlations. Sci. Rep. 2021, 11, 1–13. [Google Scholar]
- Gordillo, M.D.; Blanco, M.A.; Pereyra, C.; Mart, E.J. Thermodynamic modelling of supercritical fluid—Solid phase equilibrium data. Comput. Chem. Eng. 2005, 29, 1885–1890. [Google Scholar] [CrossRef]
- Sodeifian, G.; Sajadian, S.A.; Derakhsheshpour, R. Experimental measurement and thermodynamic modeling of Lansoprazole solubility in supercritical carbon dioxide: Application of SAFT-VR EoS. Fluid Phase Equilib. 2020, 507, 112422. [Google Scholar] [CrossRef]
- Wexler, P. (Ed.) Encyclopedia of Toxicology, 3rd ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Fatima, S.; Rasool, A.; Sajjad, N.; Bhat, E.A.; Hanafiah, M.M.; Mahboob, M. Analysis and evaluation of penicillin production by using soil fungi. Biocatal. Agric. Biotechnol. 2019, 21, 101330. [Google Scholar] [CrossRef]
- Katritzky, A.R.; Ramsden, C.A.; Scriven, E.F.V.; Taylor, R.J.K. Comprehensive Heterocyclic Chemistry III, 1st ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2008; Volume 1. [Google Scholar]
- Andersen, S.J.; Frisvad, J.C. Penicillin production by Penicillium nalgiovense. Lett. Appl. Microbiol. 1994, 19, 486–488. [Google Scholar] [CrossRef]
- Ferech, M.; Coenen, S.; Malhotra-Kumar, S.; Dvorakova, K.; Hendrickx, E.; Suetens, C. European surveillance of antimicrobial consumption (ESAC): Outpatient antibiotic use in Europe. J. Antimicrob. Chemother. 2006, 58, 401–407. [Google Scholar] [CrossRef] [PubMed]
- Quinn, R. Rethinking antibiotic research and development: World War II and the penicillin collaborative. Am. J. Public Health 2013, 103, 426–434. [Google Scholar] [CrossRef] [PubMed]
- Doble, M.; Kruthiventi, A.K. Green Chemistry and Engineering; Elsevier Inc.: Amsterdam, The Netherlands, 2007. [Google Scholar]
- Asiabi, H.; Yamini, Y.; Latifeh, F.; Vatanara, A. Solubilities of four macrolide antibiotics in supercritical carbon dioxide and their correlations using semi-empirical models. J. Supercrit. Fluids 2015, 104, 62–69. [Google Scholar] [CrossRef]
- Tabernero, A.; del Valle, E.M.M.; Galán, M.A. Supercritical fluids for pharmaceutical particle engineering: Methods, basic fundamentals and modelling. Chem. Eng. Process. Process. Intensif. 2012, 60, 9–25. [Google Scholar] [CrossRef]
- Colussi, S.; Elvassore, N.; Kikic, I. A comparison between semi-empirical and molecular-based equations of state for describing the thermodynamic of supercritical micronization processes. J. Supercrit. Fluids 2006, 38, 18–26. [Google Scholar] [CrossRef]
- Alessi, P.; Cortesi, A.; Kikic, I.; Foster, N.R.; Macnaughton, S.J.; Colombo, I. Particle Production of Steroid Drugs Using Supercritical Fluid Processing. Ind. Eng. Chem. Res. 1996, 35, 4718–4726. [Google Scholar] [CrossRef]
- Jung, J.; Perrut, M. Particle design using supercritical fluids: Literature and patent survey. J. Supercrit. Fluids 2001, 20, 179–219. [Google Scholar] [CrossRef]
- Sodeifian, G.; Sajadian, S.A. Utilization of ultrasonic-assisted RESOLV(US-RESOLV) with polymeric stabilizers for production of amiodaronehydrochloride nanoparticles: Optimization of the process parameters. Chem. Eng. Res. Des. 2019, 142, 268–284. [Google Scholar] [CrossRef]
- Sodeifian, G.; Sajadian, S.A.; Ardestani, N.S.; Razmimanesh, F. Production of Loratadine drug nanoparticles using ultrasonic-assisted Rapid expansion of supercritical solution into aqueous solution (US-RESSAS). J. Supercrit. Fluids 2019, 147, 241–253. [Google Scholar] [CrossRef]
- Franco, P.; de Marco, I. Supercritical antisolvent process for pharmaceutical applications: A review. Processes 2020, 8, 938. [Google Scholar] [CrossRef]
- Campardelli, R.; Reverchon, E.; de Marco, I. Dependence of SAS particle morphologies on the ternary phase equilibria. J. Supercrit. Fluids 2017, 130, 273–281. [Google Scholar] [CrossRef]
- Campardelli, R.; Reverchon, E.; de Marco, I. PVP microparticles precipitation from acetone-ethanol mixtures using SAS process: Effect of phase behavior. J. Supercrit. Fluids 2019, 143, 321–329. [Google Scholar] [CrossRef]
- Brennecke, J.F.; Eckert, C.A. Phase Equilibria for Supercritical Fluid Process Design. AIChE J. 1989, 35, 1409–1427. [Google Scholar] [CrossRef]
- Johnston, K.P.; Peck, D.G.; Kim, S. Modeling Supercritical Mixtures: How Predictive Is It? Ind. Eng. Chem. Res. 1989, 28, 1115–1125. [Google Scholar] [CrossRef]
- Coutsikos, P.; Magoulas, K.; Kontogeorgis, G.M. Prediction of solid-gas equilibria with the Peng-Robinson equation of state. J. Supercrit. Fluids 2003, 25, 197–212. [Google Scholar] [CrossRef]
- Kontogeorgis, G.M.; Liang, X.; Arya, A.; Tsivintzelis, I. Equations of state in three centuries. Are we closer to arriving to a single model for all applications? Chem. Eng. Sci. X 2020, 7, 1060. [Google Scholar] [CrossRef]
- Sodeifian, G.; Razmimanesh, F.; Sajadian, S.A.; Panah, H.S. Solubility measurement of an antihistamine drug (Loratadine) in supercritical carbon dioxide: Assessment of qCPA and PCP-SAFT equations of state. Fluid Phase Equilib. 2018, 472, 147–159. [Google Scholar] [CrossRef]
- Zuknik, M.H.; Nik Norulaini, N.A.; Wan Nursyazreen Dalila, W.S.; Ali, N.R.; Omar, A.K.M. Solubility of virgin coconut oil in supercritical carbon dioxide. J. Food Eng. 2016, 168, 240–244. [Google Scholar] [CrossRef]
- Coelho, J.A.P.; Filipe, R.M.; Naydenova, G.P.; Yankov, D.S.; Stateva, R.P. Semi-Empirical models and a cubic equation of state for correlation of solids solubility in scCO2: Dyes and calix[4]arenes as illustrative examples. Fluid Phase Equilib. 2016, 426, 1–10. [Google Scholar] [CrossRef]
- Prausnitz, J.M.; Lichtenthaler, R.M.; De Azevedo, A.G. Molecular Thermodynamics of Fluid Phase Equilibria, 3rd ed.; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Ksibi, H. The Solvent-Solute Interaction in Supercritical Solution at Equilibrium: Modeling and Related Industrial Applications. Int. J. Thermodyn. 2004, 7, 131–140. [Google Scholar]
- Fotouh, K.; Shukla, K. A comparative study of numerical methods for calculating phase equilibria in fluid mixtures from an equation of state. Chem. Eng. Sci. 1996, 51, 3763–3771. [Google Scholar] [CrossRef]
- Issaoui, A.; Moussa, A.B.; Ksibi, H. Correlation of the binary interaction factor for polar solutes dissolved in supercritical carbon dioxide. Int. J. Thermodyn. 2011, 14, 37–42. [Google Scholar]
- Gordillo, M.; Blanco, M.A.; Molero, A.; Martinez de la Ossa, E. Solubility of the antibiotic penicillin G in supercritical carbon dioxide. J. Supercrit. Fluids 1999, 15, 183–190. [Google Scholar] [CrossRef]
- Reverchon, E.; Porta, G.D.; Taddeo, R.; Pallado, P.; Stassi, A. Solubility and Micronization of Griseofulvin in Supercritical CHF3. Ind. Eng. Chem. Res. 1995, 34, 4087–4091. [Google Scholar] [CrossRef]
- Redlich, O.; Kwong, J.N.S. On the Thermodynamics of Solutions. V: An Equation of State. Fugacities of Gaseous Solutions. Chem. Rev. 1949, 44, 233. [Google Scholar] [CrossRef]
- Soave, G. Equilibrium Constants from a Modified Redlich-Kwong Equation of State. Chem. Eng. Sci. 1972, 27, 1197. [Google Scholar] [CrossRef]
- Valderrama, J.O.; Alvarez, V.H. Correct Way of Reporting Results when Modeling Supercritical Phase Equilibria using Equations of State. Can. J. Chem. Eng. 2005, 83, 578–581. [Google Scholar] [CrossRef]
- Nasri, L. Modified Wilson’s Model for Correlating Solubilities in Supercritical Fluids of Some Polycyclic Aromatic Solutes. Polycycl. Aromat. Compd. 2016, 38, 244–256. [Google Scholar] [CrossRef]
- Ko, M.; Shah, V.; Bienkowski, P.R.; Cochran, H.D. Solubility of the antibiotic penicillin V in supercritical CO2. J. Supercrit. Fluids 1991, 4, 32–39. [Google Scholar] [CrossRef]
- Vafai, S.; Drake, B.D.; Smith, R.L. Solid Molar Volumes of Interest to Supercritical Extraction at 298 K: Atropine, Berberine Hydrochloride Hydrate, Brucine Dihydrate, Capsaicin, Ergotamine Tartrate Dihydrate, Naphthalene, Penicillin V, Piperine, Quinine, Strychnine, Theobromine, Theophylli. J. Chem. Eng. Data 1993, 38, 125–127. [Google Scholar] [CrossRef]
- Schmitt, W.J.; Reid, R.C. Solubility of Monofunctional Organic Solids in Chemically diverse Supercritical Fluids. J. Chem. Eng. Data 1986, 31, 204–212. [Google Scholar] [CrossRef]
- Nasri, L. Modified Equation of State and Sublimation Pressure of Antibiotic Penicillin G. In Proceedings of the 2019 10th International Renewable Energy Congress (IREC), Sousse, Tunisia, 26–28 March 2019; pp. 1–4. [Google Scholar]
- Jahromi, S.A.; Roosta, A. Estimation of critical point, vapor pressure and heat of sublimation of pharmaceuticals and their solubility in supercritical carbon dioxide. Fluid Phase Equilib. 2019, 488, 1–8. [Google Scholar] [CrossRef]
- Huang, Z.; Kawi, S.; Chiew, Y.C. Solubility of cholesterol and its esters in supercritical carbon dioxide with and without cosolvents. J. Supercrit. Fluids 2004, 30, 25–39. [Google Scholar] [CrossRef]
- Housaindokht, M.R.; Bozorgmehr, M.R. Calculation of solubility of methimazole, phenazopyridine and propranolol in supercritical carbon dioxide. J. Supercrit. Fluids 2008, 43, 390–397. [Google Scholar] [CrossRef]
- Wichterle, I. Phase equilibria with supercritical components. Pure Appl. Chem. 1993, 65, 1003–1008. [Google Scholar] [CrossRef][Green Version]
- Sodeifian, G.; Detakhsheshpour, R.; Sajadian, S.A. Experimental study and thermodynamic modeling of Esomeprazole (proton-pump inhibitor drug for stomach acid reduction) solubility in supercritical carbon dioxide. J. Supercrit. Fluids 2019, 154, 104606. [Google Scholar] [CrossRef]
- Sodeifian, G.; Ardestani, N.S.; Sajadian, S.A.; Golmohammadi, M.R.; Fazlali, A. Prediction of Solubility of Sodium Valproate in Supercritical Carbon Dioxide: Experimental Study and Thermodynamic Modeling. ACS Appl. Mater. Interfaces 2020, 65, 1747–1760. [Google Scholar] [CrossRef]
- Lopez-Echeverry, J.S.; Reif-Acherman, S.; Araujo-Lopez, E. Peng-Robinson equation of state: 40 years through cubics. Fluid Phase Equilib. 2017, 447, 39–71. [Google Scholar] [CrossRef]
- Kautz, C.B.; Wagner, B.; Schneider, G.M. High-Pressure solubility of 1,4-bis-(n-alkylamino)-9,10-anthraquinones in near- and supercritical carbon dioxide. J. Supercrit. Fluids 1998, 13, 43–47. [Google Scholar] [CrossRef]
- Li, S.; Varadarajan, G.S.; Hartland, S. Solubilities of theobromine and caffeine in supercritical carbon dioxide: Correlation with density-based models. Fluid Phase Equilib. 1991, 68, 263–280. [Google Scholar] [CrossRef]
- Mackay, D.; Bobra, A.; Chan, D.W.; Shiu, W.Y. Vapor-Pressure correlations for low-volatility environmental chemicals. Environ. Sci. Technol. 1982, 16, 645–649. [Google Scholar] [CrossRef]
- Gordillo, M.D.; Pereyra, C.; de la Ossa, E.J.M. Solubility Estimations for Disperse Blue14 in Supercritical Carbon Dioxide Dyes. Dye. Pigment. 2005, 67, 167–173. [Google Scholar] [CrossRef]
- Nasri, L. About consistency of Solid’s solubility data in supercritical CO2 and some thermodynamic properties estimation. Sustain. Chem. Pharm. 2019, 13, 100145. [Google Scholar] [CrossRef]
- Barton, C.A.; Botelho, M.A.; Kaiser, M.A. Solid vapor pressure and enthalpy of sublimation for ammonium perfluorooctanoate. J. Chem. Eng. Data 2009, 54, 752–755. [Google Scholar] [CrossRef]
- Méndez-Santiago, J.; Teja, A.S. The solubility of solids in supercritical fluids. Fluid Phase Equilib. 1999, 158–160, 501–510. [Google Scholar] [CrossRef]
- Bartle, K.D.; Clifford, A.A.; Jafar, S.; Shilstone, G.F. Solubilities of solids and liquids of low volatility in supercritical carbon dioxide. J. Phys. Chem. Ref. Data 1991, 20, 731–756. [Google Scholar] [CrossRef]
- Garmroodi, A.; Hassan, J.; Yamini, Y. Solubilities of the drugs benzocaine, metronidazole benzoate, and naproxen in supercritical carbon dioxide. J. Chem. Eng. Data 2004, 49, 709–712. [Google Scholar] [CrossRef]
- Vatanara, A.; Najafabadi, A.R.; Khajeh, M.; Yamini, Y. Solubility of some inhaled glucocorticoids in supercritical carbon dioxide. J. Supercrit. Fluids 2005, 33, 21–25. [Google Scholar] [CrossRef]
- Xiang, S.T.; Chen, B.Q.; Kankala, R.K.; Wang, S.B.; Chen, A.Z. Solubility measurement and RESOLV-assisted nanonization of gambogic acid in supercritical carbon dioxide for cancer therapy. J. Supercrit. Fluids 2019, 150, 147–155. [Google Scholar] [CrossRef]
- Pishnamazi, M.; Zabihi, S.; Jamshidian, S.; Hezaveh, H.Z.; Hezave, A.Z.; Shirazian, S. Measuring solubility of a chemotherapy-anti cancer drug (busulfan) in supercritical carbon dioxide. J. Mol. Liq. 2020, 317, 113954. [Google Scholar] [CrossRef]
- Sodeifian, G.; Garlapati, C.; Razmimanesh, F.; Sodeifian, F. The solubility of Sulfabenzamide (an antibacterial drug) in supercritical carbon dioxide: Evaluation of a new thermodynamic model. J. Mol. Liq. 2021, 335, 116446. [Google Scholar] [CrossRef]
- Shojaee, S.A.; Hezave, A.Z.; Aftab, S.; Lashkarbolooki, M.; Esmaeilzadeh, F. Solubility of gabapentin in supercritical carbon dioxide. J. Supercrit. Fluids 2013, 78, 1–6. [Google Scholar] [CrossRef]
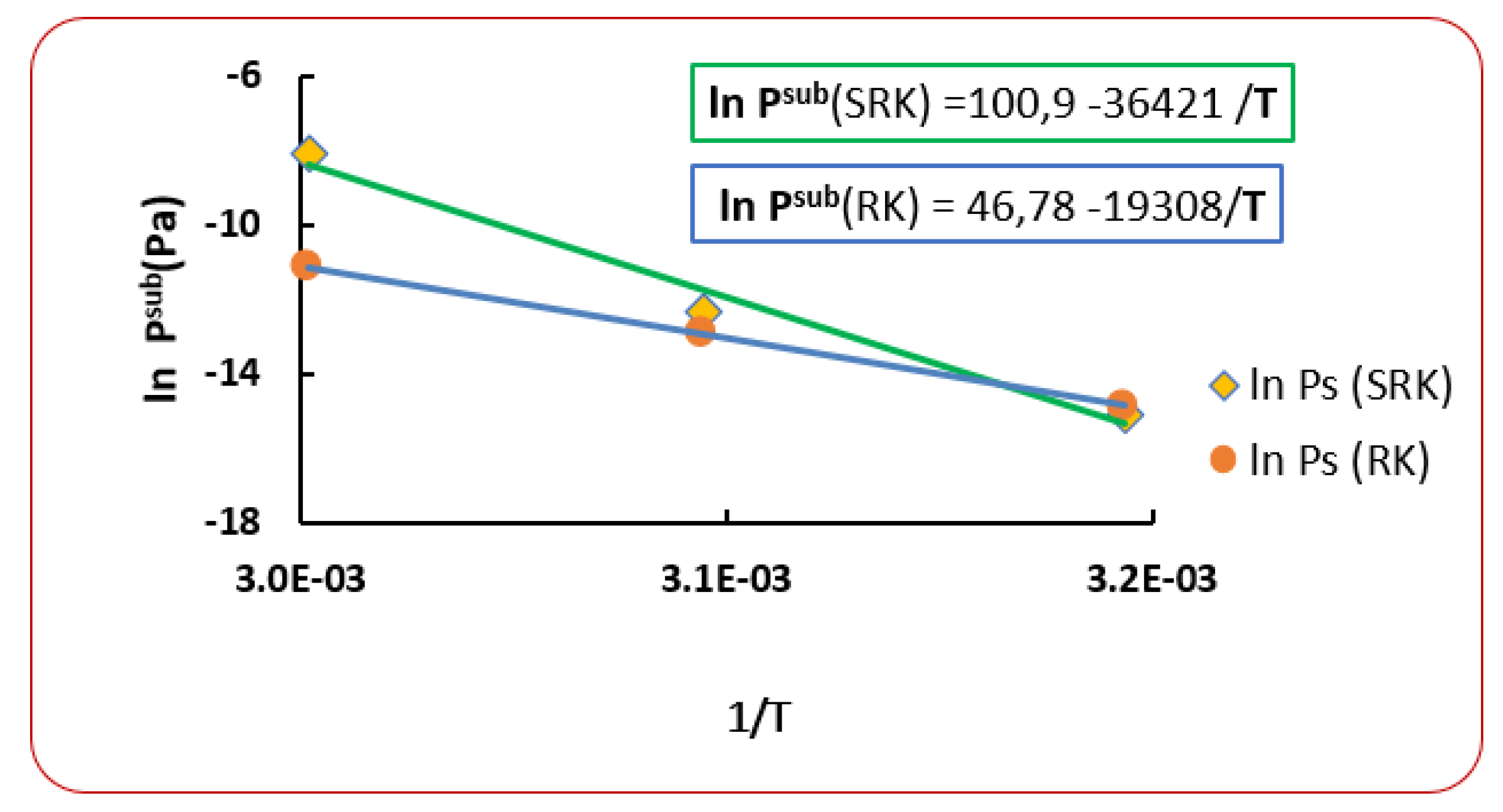
| T (K) | RK [40] | AARD (%) [40] | SRK [40] | AARD (%) [40] | |
|---|---|---|---|---|---|
| 313.15 | 23 | 21 | 26% | ||
| 323.15 | 23 | 21 | 51% | ||
| 333.15 | 23 | 21 | 95% |
| T(K) | Clausius [46] | AARD (%) | PR [46] | AARD (%) | |
|---|---|---|---|---|---|
| 314.85 | 37.85 | 36.23 | 381% | ||
| 324.85 | 42.46 | 40.25 | 83% | ||
| 334.85 | 54.38 | 41.30 | 99% |
| 1.63 × 10−4 | 2.19 × 10−4 | |
| 1.89 × 10−4 | 1.98 × 10−4 | |
| (AARD %) global | 70.86 | 27.98 |
| (AARD%) for 313 K | 98.58 | 28.61 |
| (AARD%) for 323 K | 95.04 | 23.10 |
| (AARD%) for 333 K | 18.95 | 41.51 |
| 1.87 × 10−4 | 2.80 × 10−4 | |
| 2.72 × 10−4 | 2.93 × 10−4 | |
| (AARD %) global | 79.5 | 48.5 |
| (AARD%) for 314.85 K | 99.5 | 41.7 |
| (AARD%) for 324.85 K | 100.1 | 43.4 |
| (AARD%) for 334.85 K | 48.1 | 60.3 |
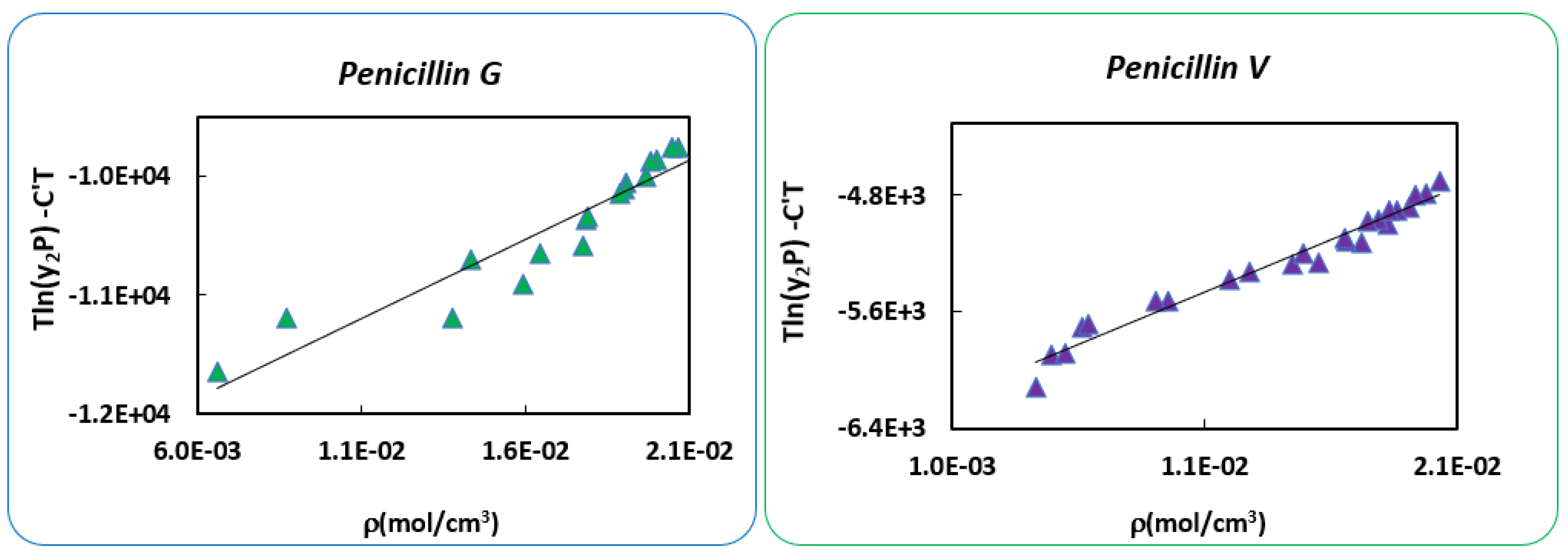
| Mendez-Santiago-Teja Model | Bartle’s Model | ||||
|---|---|---|---|---|---|
| Penicillin G | Penicillin V | Penicillin G | Penicillin V | ||
| A’= | −11,475.4 | −5495.9 | a = | 25.1 | 12.6 |
| B’= | 165,852.2 | 73,223.7 | b = | −10,260.3 | −5049.7 |
| C’= | 26.2 | 12.8 | c = | 1.2 × 10−2 | 5.05 × 10−3 |
| AARD% = | 24.6 | 17.01 | AARD% = | 16.9 | 16.1 |
| estimated (kJ/mol) | 85.3 | 41.9 | |||
| Penicillin G: | Penicillin V: | ||||
| AARD% (Penicillin G) | AARD% (Penicillin V) | ||||
|---|---|---|---|---|---|
| T = 313.15 K | 27.4 | 28.6 | T = 314.85 K | 26.7 | 41.7 |
| T = 323.15 K | 11.1 | 23.1 | T = 324.85 K | 26.4 | 43.4 |
| T = 333.15 K | 4.0 | 41.5 | T = 334.85 K | 40.6 | 60.3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasri, L. Penicillins’ Solubility in Supercritical Carbon Dioxide: Modeling by Cubic Equations of States Revisited. Antibiotics 2021, 10, 1448. https://doi.org/10.3390/antibiotics10121448
Nasri L. Penicillins’ Solubility in Supercritical Carbon Dioxide: Modeling by Cubic Equations of States Revisited. Antibiotics. 2021; 10(12):1448. https://doi.org/10.3390/antibiotics10121448
Chicago/Turabian StyleNasri, Loubna. 2021. "Penicillins’ Solubility in Supercritical Carbon Dioxide: Modeling by Cubic Equations of States Revisited" Antibiotics 10, no. 12: 1448. https://doi.org/10.3390/antibiotics10121448
APA StyleNasri, L. (2021). Penicillins’ Solubility in Supercritical Carbon Dioxide: Modeling by Cubic Equations of States Revisited. Antibiotics, 10(12), 1448. https://doi.org/10.3390/antibiotics10121448





