Design and Parameter Study of Integrated Microfluidic Platform for CTC Isolation and Enquiry; A Numerical Approach
Abstract
1. Introduction
2. Materials and Methods
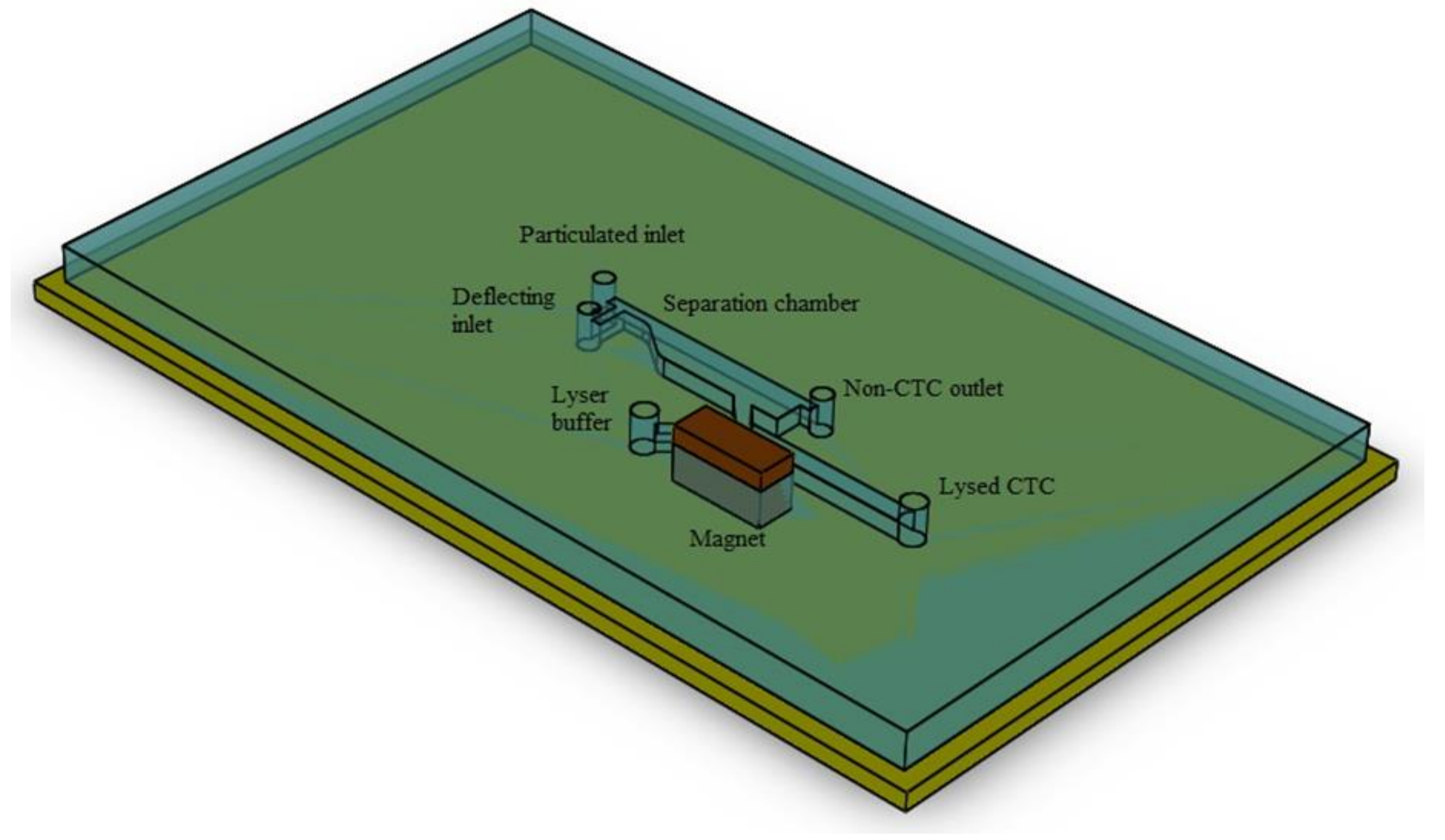
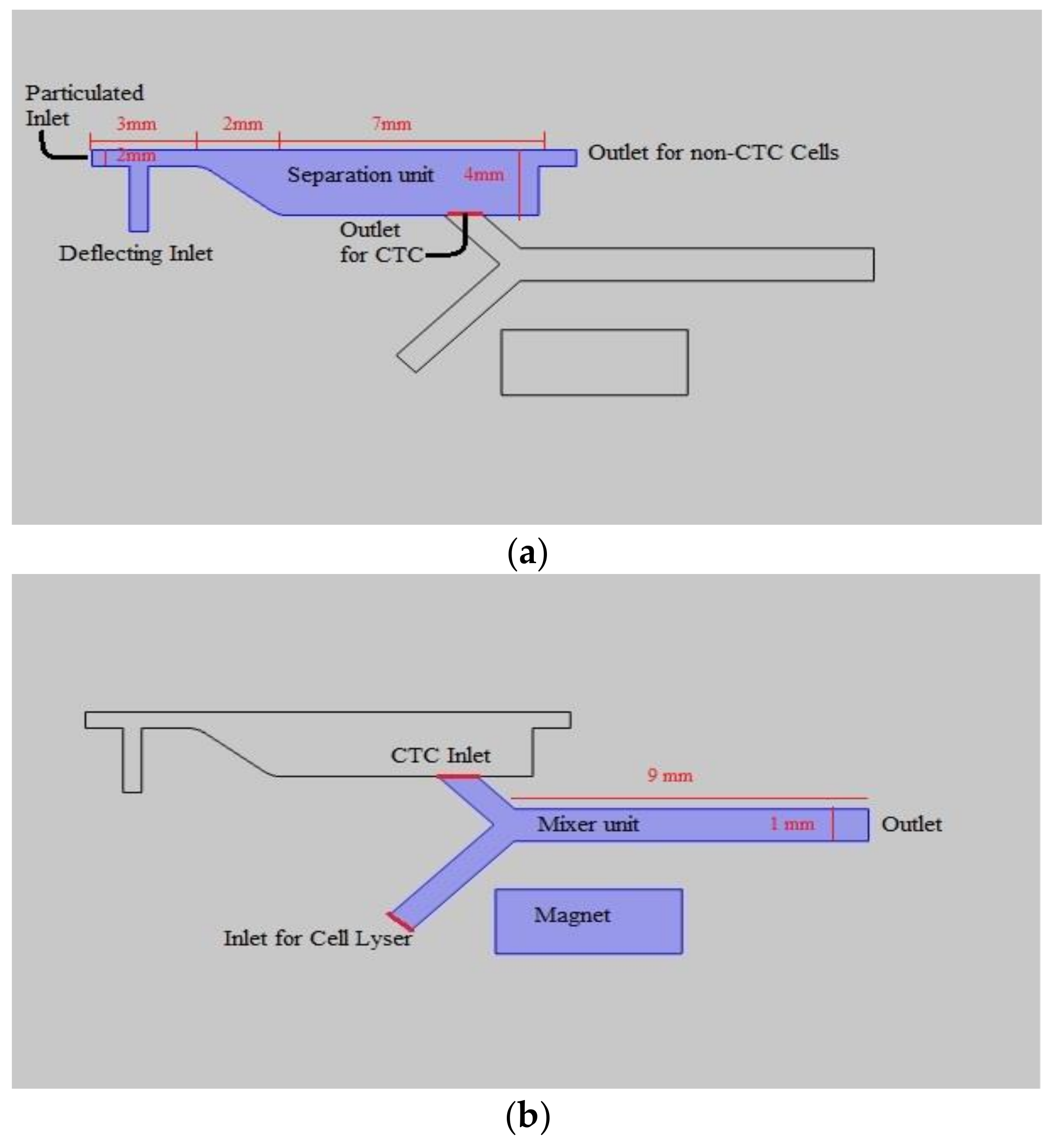
2.1. Description of Geometry and Function of Each Unit
2.2. Description of Separation Mechanism
2.3. Sample Preprocessing
2.4. Separation Unit Governing Equations
2.4.1. Attaining Velocity and Pressure Field
2.4.2. Solving for Magnetic Field Distribution
2.4.3. Assessing Particle Deflection and Separation Efficacy
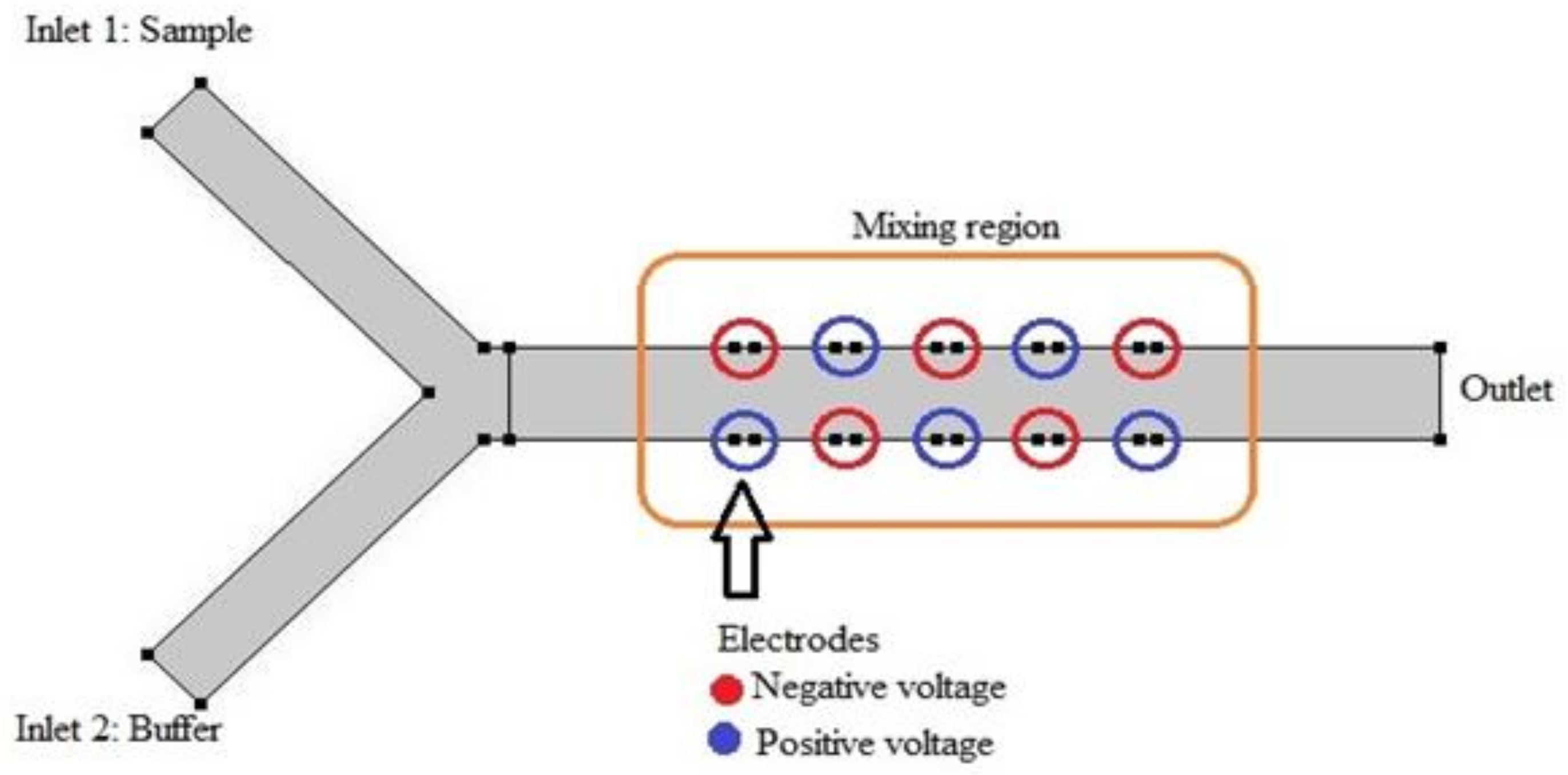
2.5. Governing Equations for Mixing Subunit
2.5.1. Assessment of Fluid Field Variable
2.5.2. Solving for Electric Field
2.5.3. Acquisition of Transport Characteristics within Channel
2.5.4. Evaluation of Mixing Quality
3. Results
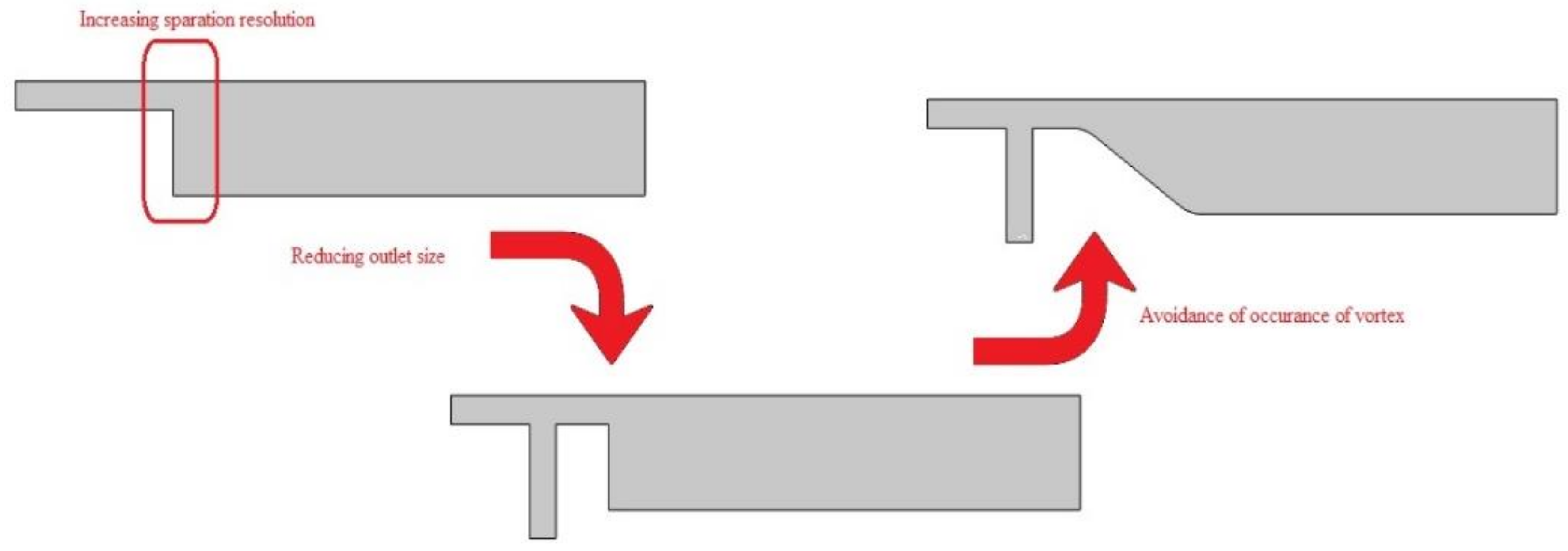
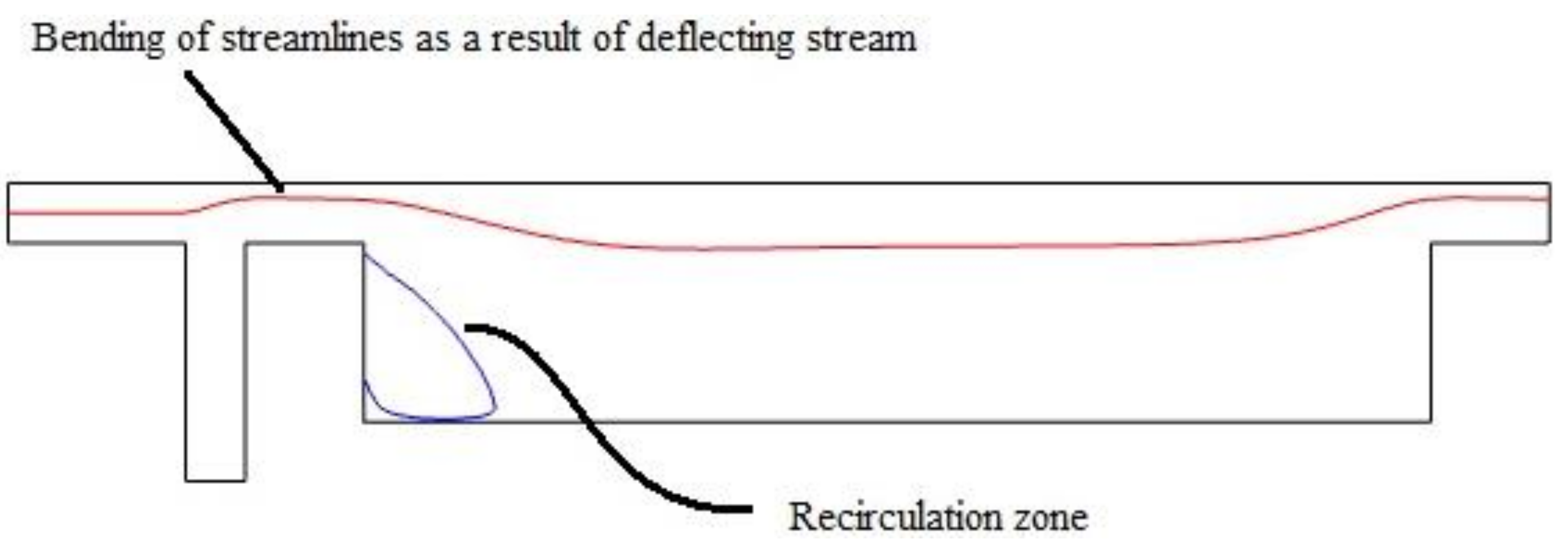
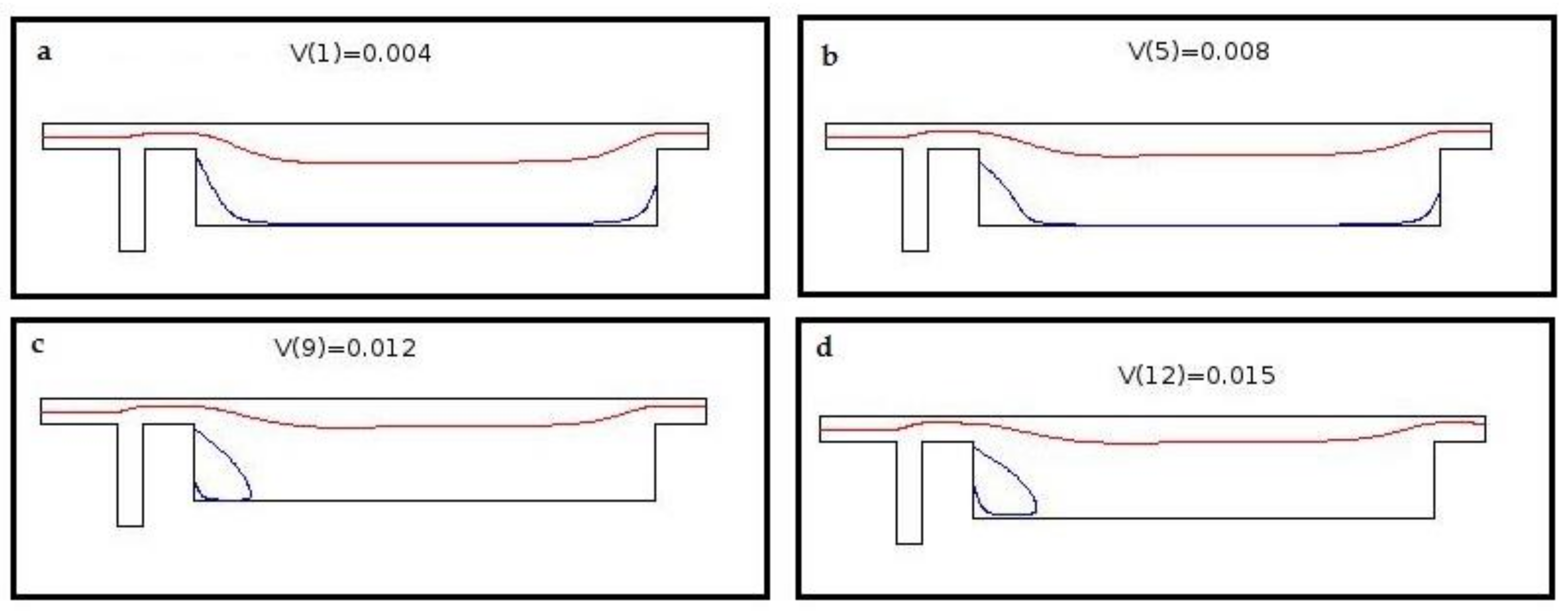
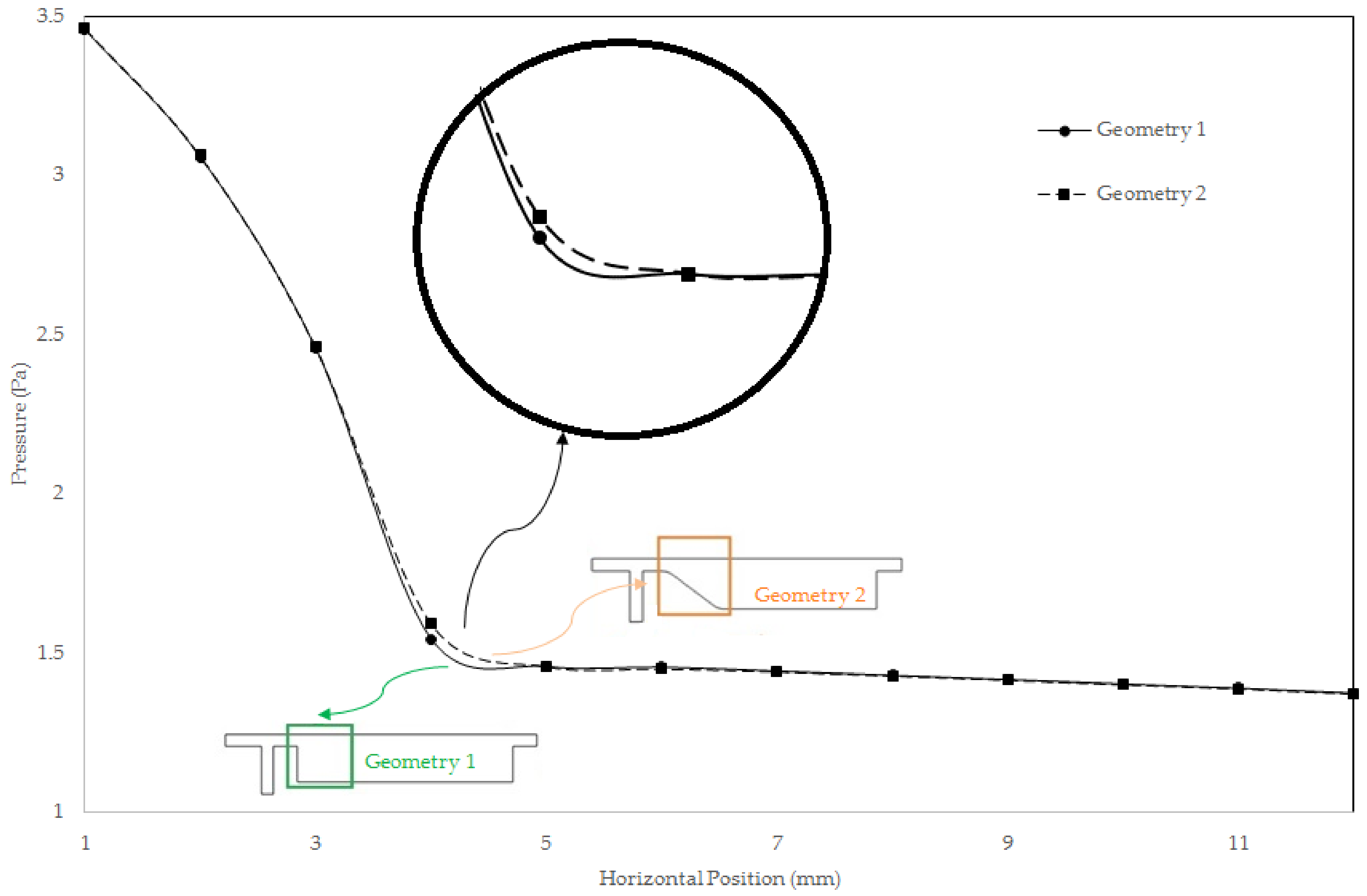
3.1. Geometry Evolution of the Separation Subunit
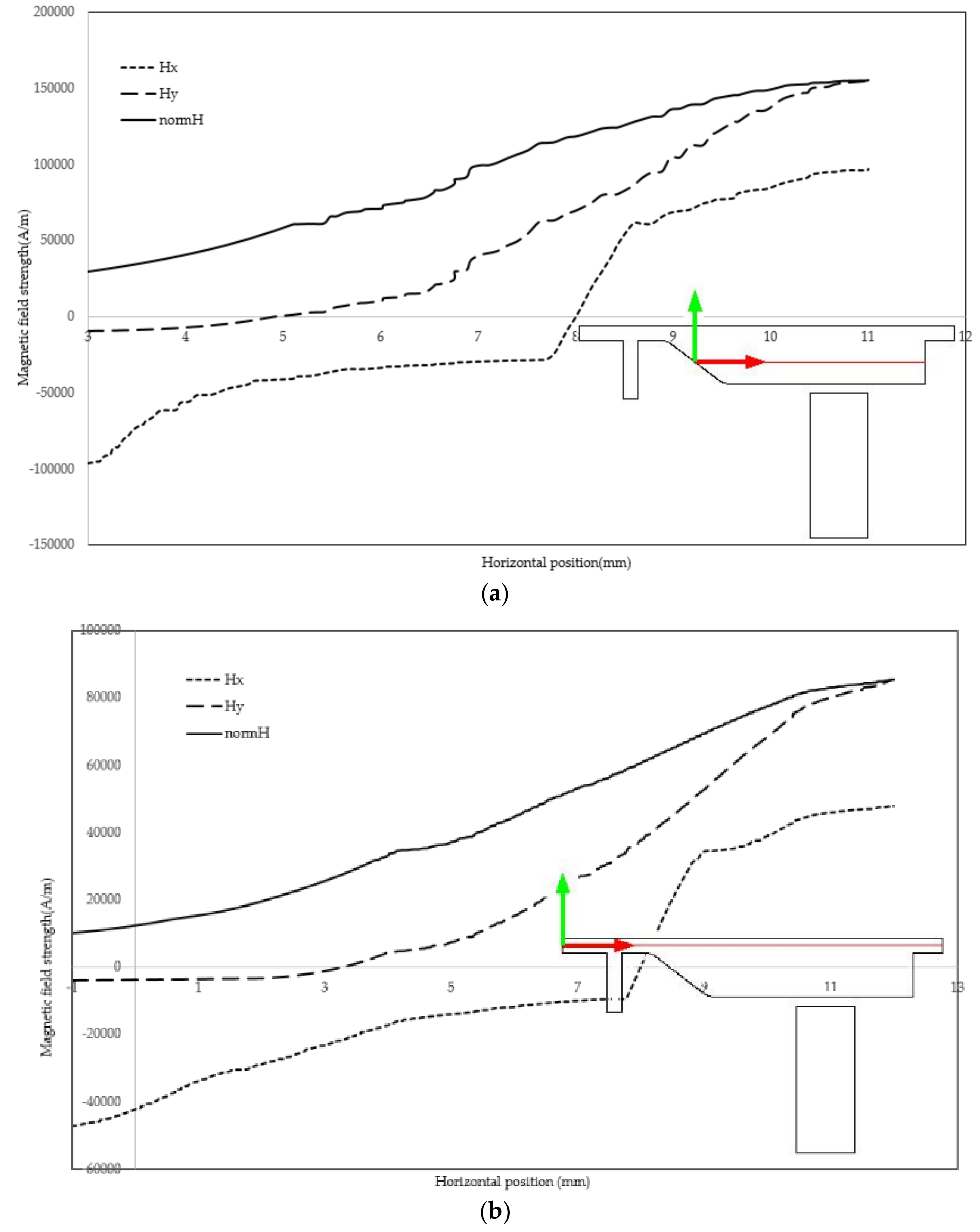
3.2. Velocity and Magnetic Field within the Confined Geometry
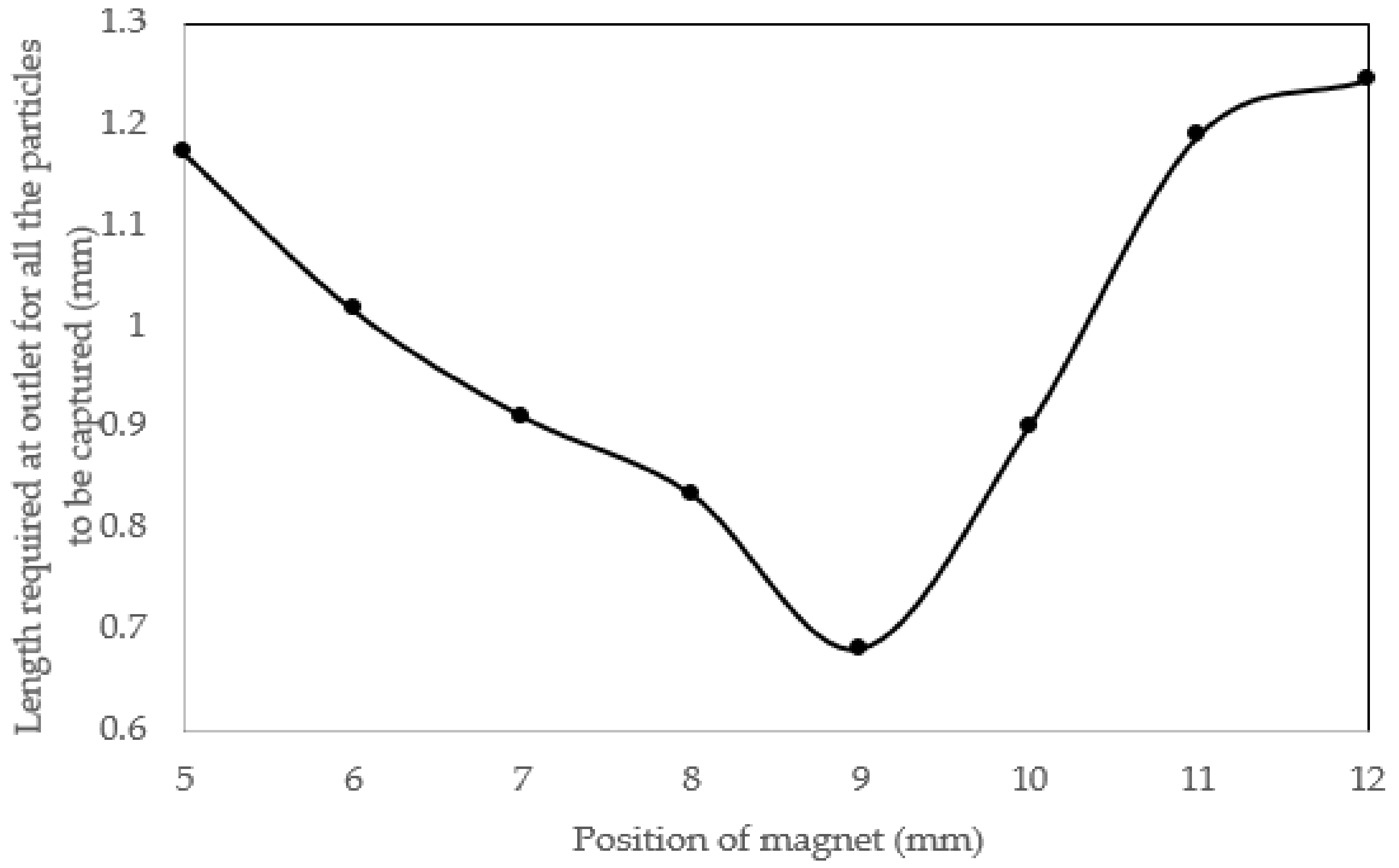
3.3. Attaining the Optimized Position for Magnet
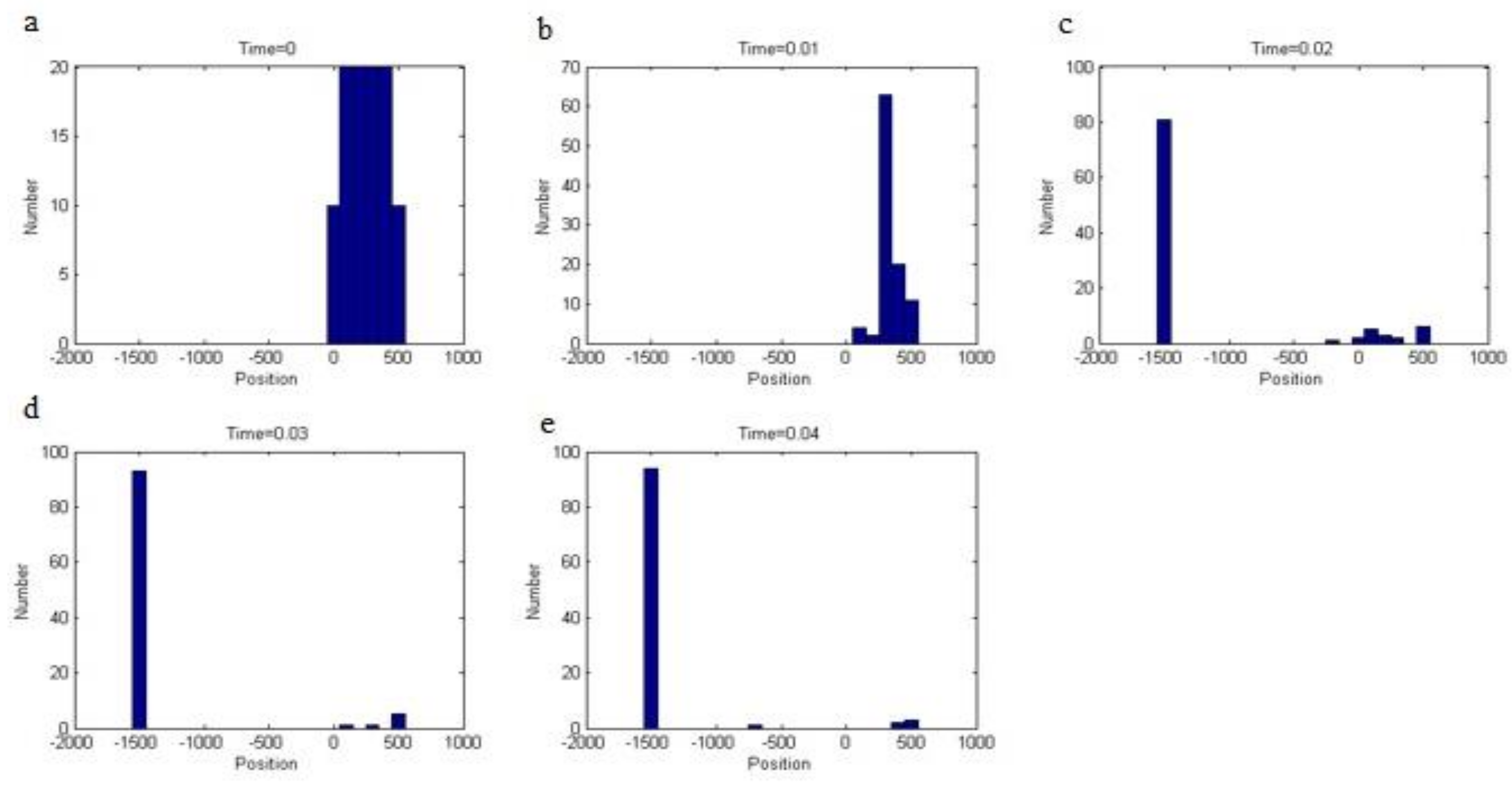
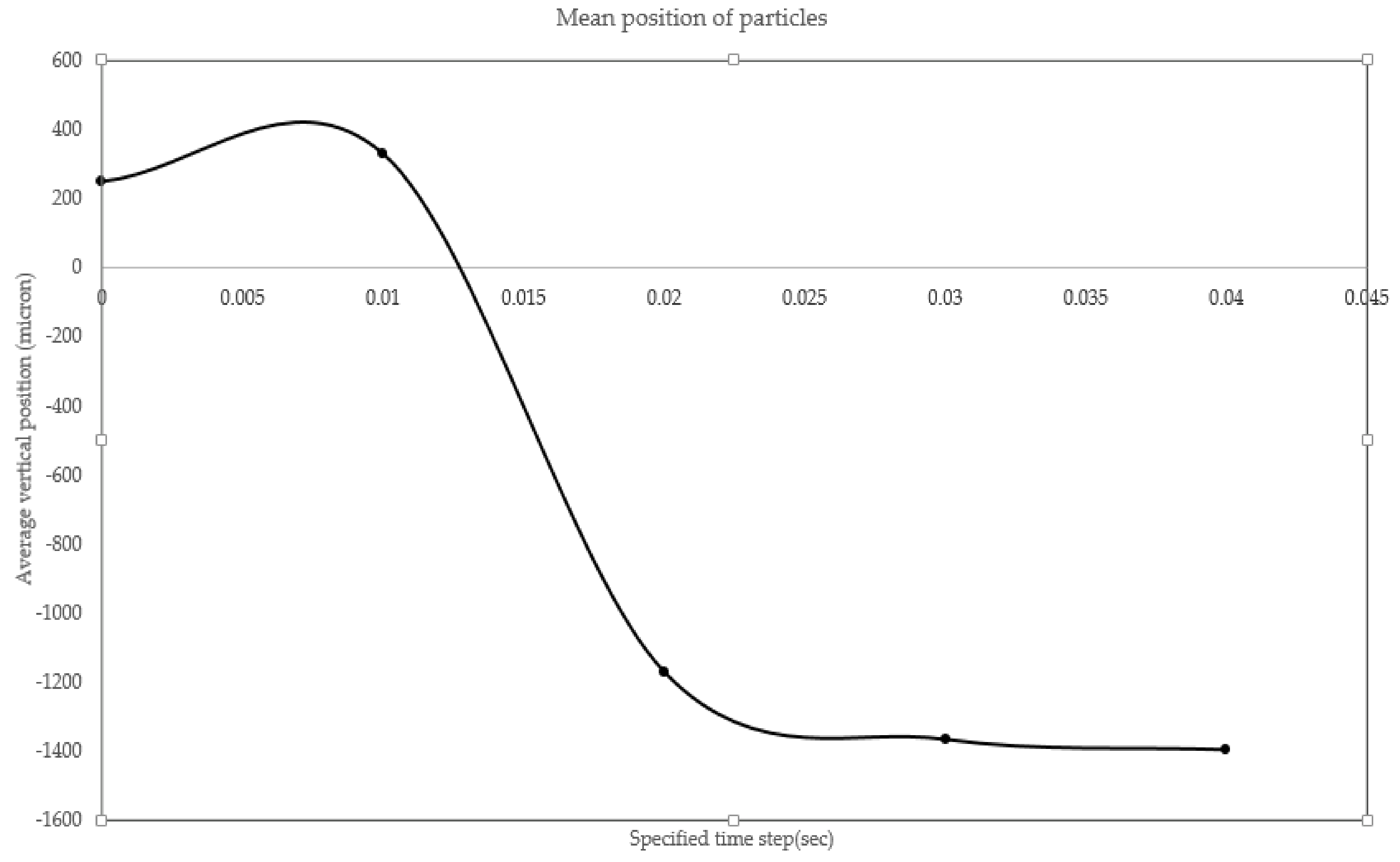
3.4. Quantification of Device as a Separation Unit
3.5. Order of Magnitude Analysis to Figure out Dominant Forces Exerting on the Particles
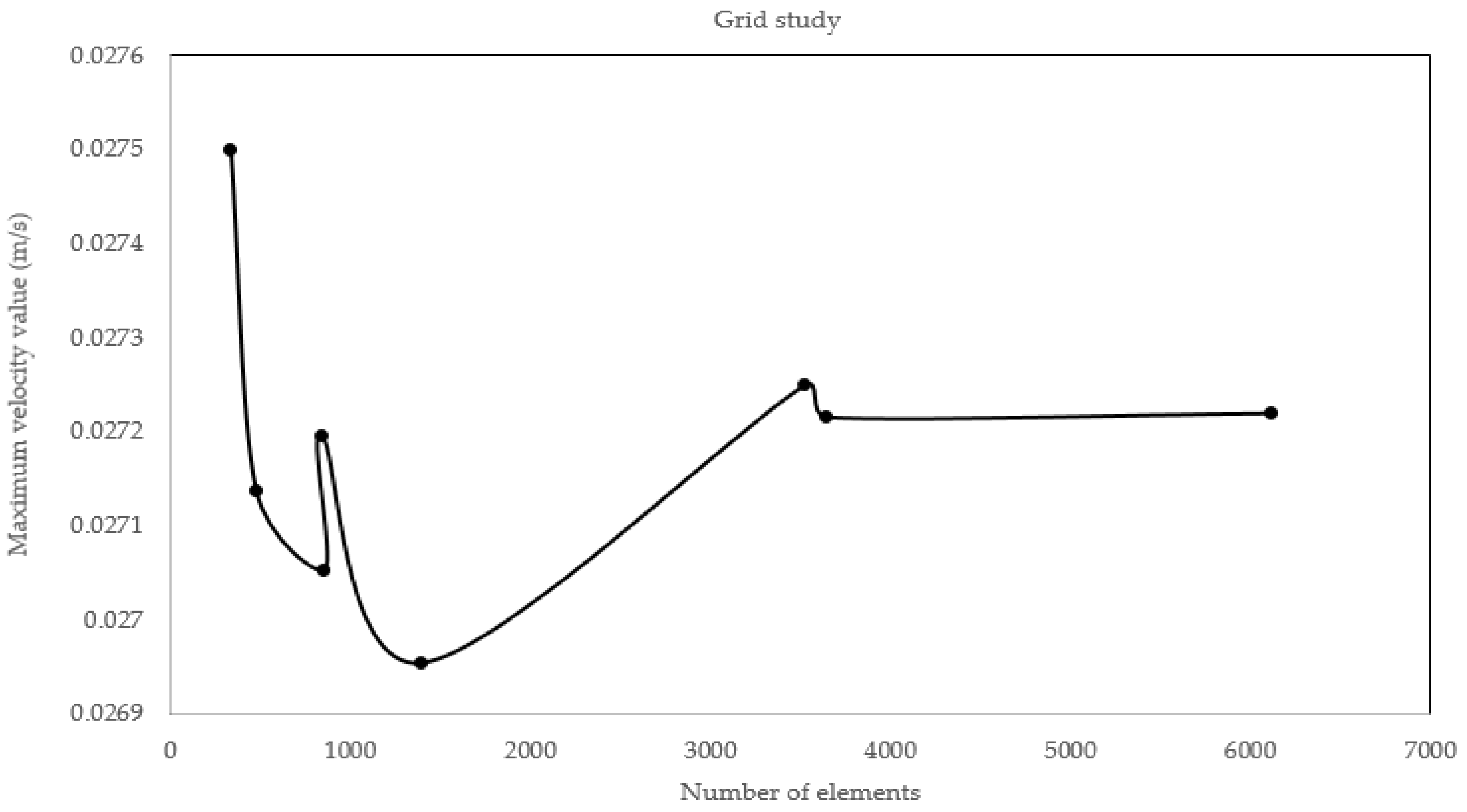
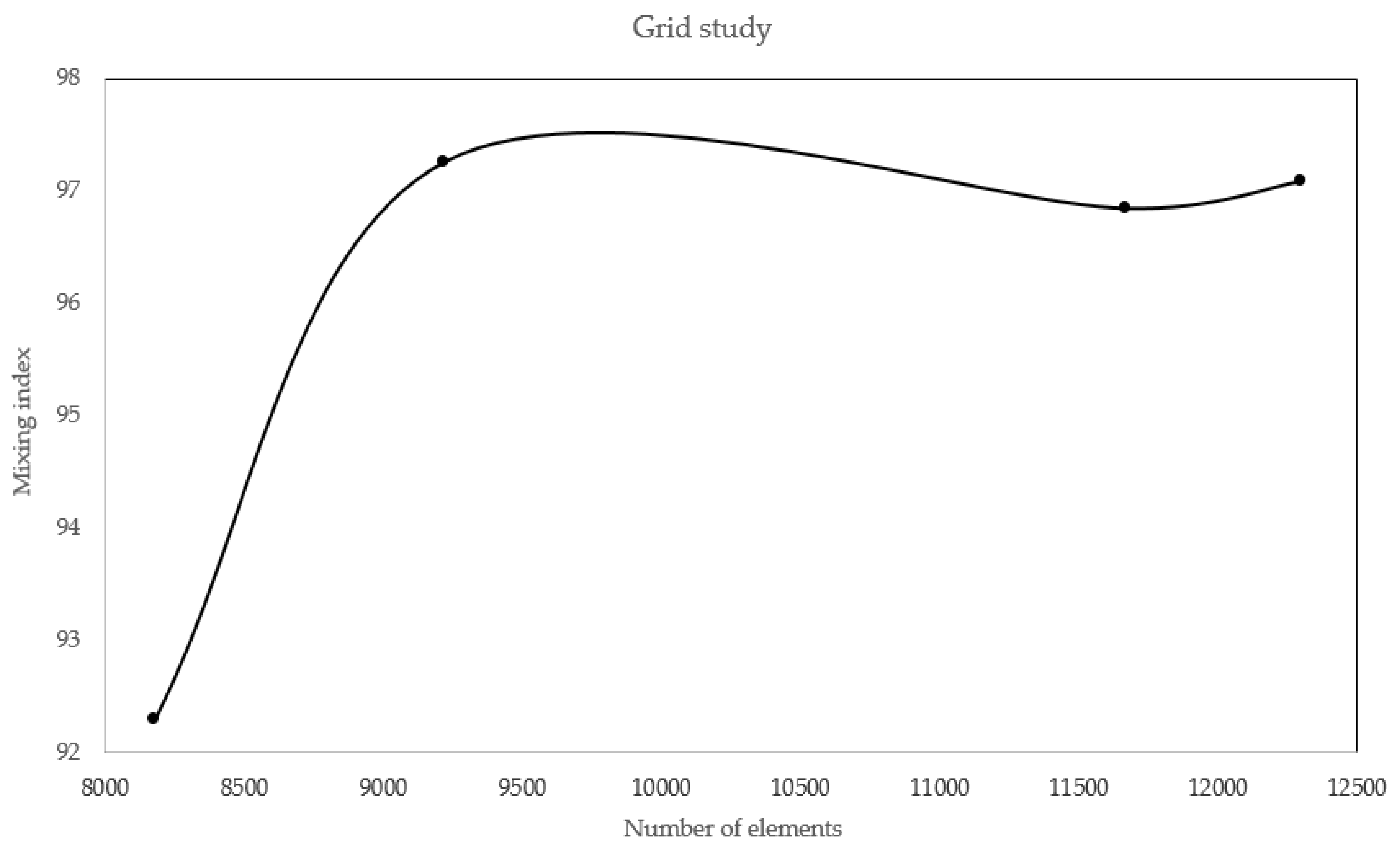
3.6. Grid Study for the Mixer
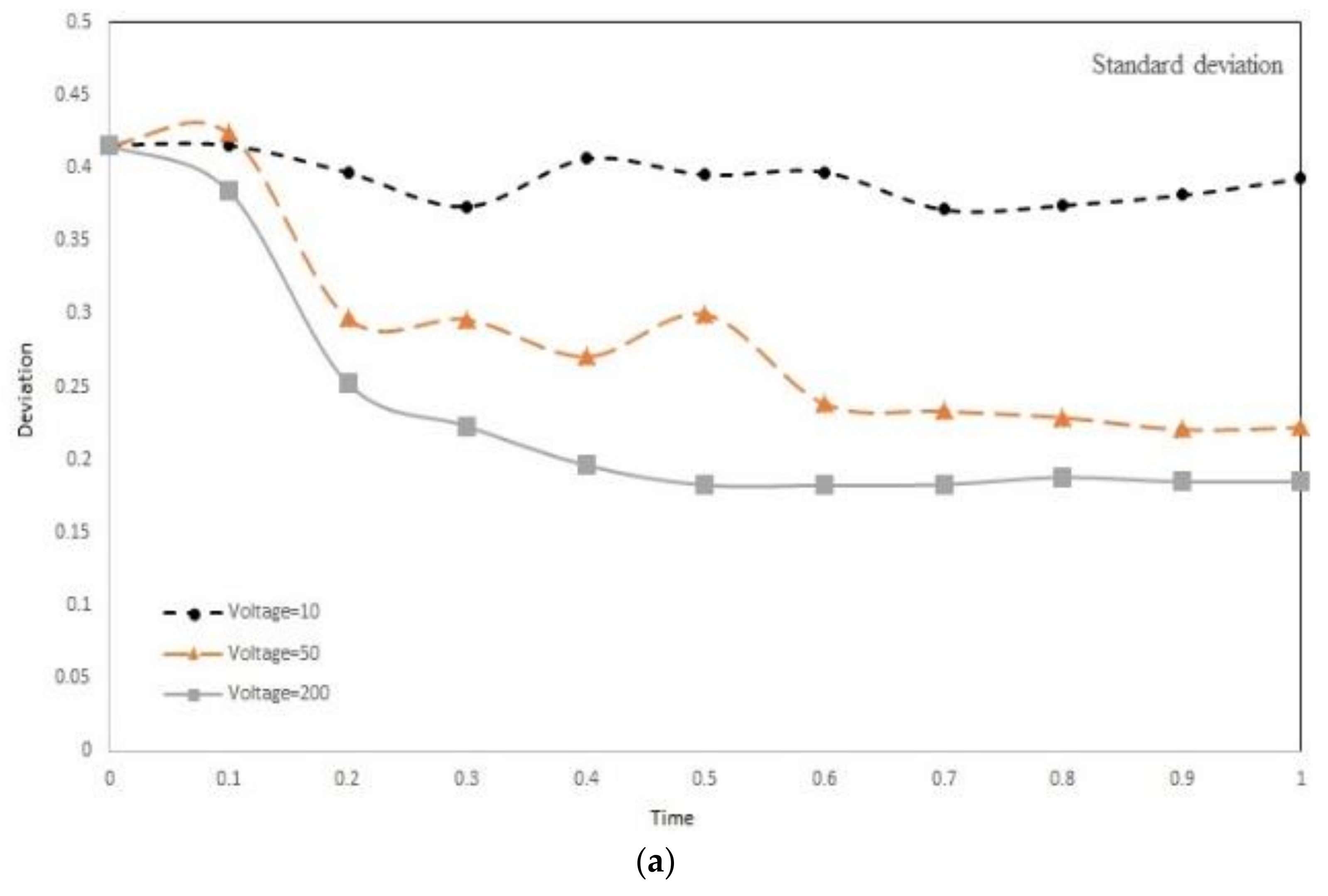
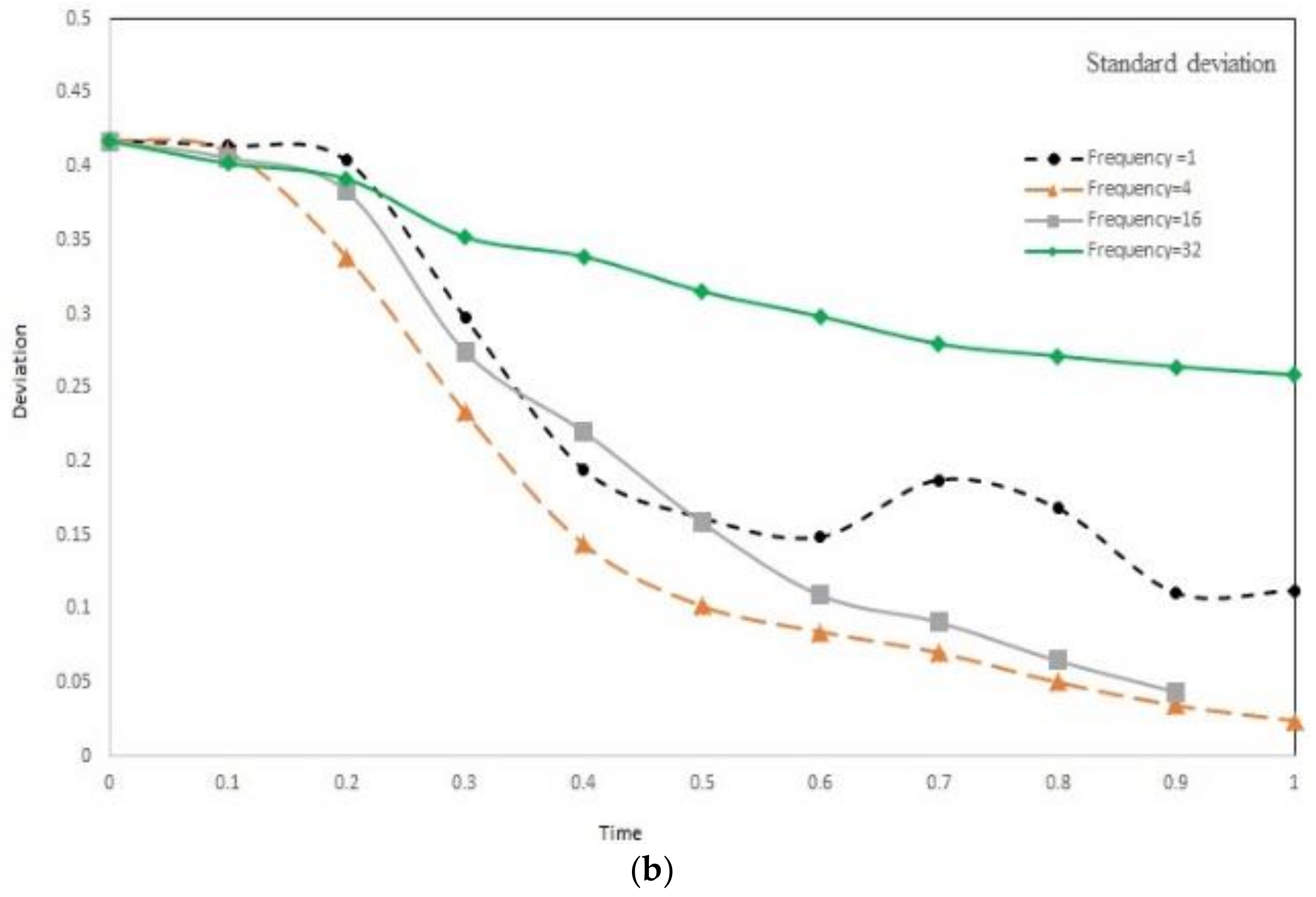
3.7. Effect of Voltage and Frequency on Mixing Index
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| CTC | Circulating Tumor Cells |
| FACS | Fluorescence-Activated Cell Sorting |
| MACS | Magnetic-Activated Cell Sorting |
| RBCs | Red Blood Cells |
References
- Torre, L.A.; Bray, F.; Siegel, R.L.; Ferlay, J.; Lortet-Tieulent, J.; Jemal, A. Global cancer statistics, 2012. CA Cancer J. Clin. 2015, 65, 87–108. [Google Scholar] [CrossRef] [PubMed]
- Au, S.H.; Edd, J.; Stoddard, A.E.; Wong, K.H.K.; Fachin, F.; Maheswaran, S.; Haber, D.A.; Stott, S.L.; Kapur, R.; Toner, M. Microfluidic isolation of circulating tumor cell clusters by size and asymmetry. Sci. Rep. 2017, 7, 24–33. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, M.M.; Ramani, V.C.; Jeffrey, S.S. Circulating tumor cell technologies. Mol. Oncol. 2016, 10, 374–394. [Google Scholar] [CrossRef] [PubMed]
- Williams, S.C. Circulating tumor cells. Proc. Natl. Acad. Sci. USA 2013, 110, 4861–4861. [Google Scholar] [CrossRef] [PubMed]
- Beebe, D.J.; Mensing, G.A.; Walker, G.M. Physics and applications of microfluidics in biology. Annu. Rev. Biomed. Eng. 2002, 4, 261–286. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, N.-T.; Wereley, S.T. Fundamentals and Applications of Microfluidics; Artech House: Norwood, MA, USA, 2002. [Google Scholar]
- Yamada, M.; Seki, M. Microfluidic particle sorter employing flow splitting and recombining. Anal. Chem. 2006, 78, 1357–1362. [Google Scholar] [CrossRef] [PubMed]
- Young, E.W.; Beebe, D.J. Fundamentals of microfluidic cell culture in controlled microenvironments. Chem. Soc. Rev. 2010, 39, 1036–1048. [Google Scholar] [CrossRef] [PubMed]
- Bhagat, A.A.; Bow, H.; Hou, H.W.; Tan, S.J.; Han, J.; Lim, C.T. Microfluidics for cell separation. Med. Biol. Eng. Comput. 2010, 48, 999–1014. [Google Scholar] [CrossRef] [PubMed]
- González, I.; Earl, J.; Fernández, L.J.; Sainz, B., Jr.; Pinto, A.; Monge, R.; Alcalá, S.; Castillejo, A.; Soto, J.L.; Carrato, A. A Label Free Disposable Device for Rapid Isolation of Rare Tumor Cells from Blood by Ultrasounds. Micromachines 2018, 9, 129. [Google Scholar]
- Zhang, C.; Khoshmanesh, K.; Mitchell, A.; Kalantar-zadeh, K. Dielectrophoresis for manipulation of micro/nano particles in microfluidic systems. Anal. Bioanal. Chem. 2010, 396, 401–420. [Google Scholar] [CrossRef] [PubMed]
- Furlani, E.P. Magnetophoretic separation of blood cells at the microscale. J. Phys. D Appl. Phys. 2007, 40, 1313–1319. [Google Scholar] [CrossRef]
- Huang, Y.-Y.; Hoshino, K.; Chen, P.; Wu, C.-H.; Lane, N.; Huebschman, M.; Liu, H.; Sokolov, K.; Uhr, J.W.; Frenkel, E.P. Immunomagnetic nanoscreening of circulating tumor cells with a motion controlled microfluidic system. Biomed. Microdevices 2013, 15, 673–681. [Google Scholar] [CrossRef] [PubMed]
- Chen, P.; Huang, Y.-Y.; Bhave, G.; Hoshino, K.; Zhang, X. Inkjet-print micromagnet array on glass slides for immunomagnetic enrichment of circulating tumor cells. Ann. Biomed. Eng. 2016, 44, 1710–1720. [Google Scholar] [CrossRef] [PubMed]
- Esmaeilsabzali, H.; Beischlag, T.V.; Cox, M.E.; Dechev, N.; Parameswaran, A.M.; Park, E.J. An integrated microfluidic chip for immunomagnetic detection and isolation of rare prostate cancer cells from blood. Biomed. Microdevices 2016, 18, 22. [Google Scholar] [CrossRef] [PubMed]
- Shamloo, A.; Selahi, A.; Madadelahi, M. Designing and modeling a centrifugal microfluidic device to separate target blood cells. J. Micromech. Microeng. 2016, 26, 035017. [Google Scholar] [CrossRef]
- Renier, C.; Pao, E.; Che, J.; Liu, H.E.; Lemaire, C.A.; Matsumoto, M.; Triboulet, M.; Srivinas, S.; Jeffrey, S.S.; Rettig, M. Label-free isolation of prostate circulating tumor cells using Vortex microfluidic technology. npj Precis. Oncol. 2017, 1, 15. [Google Scholar] [CrossRef] [PubMed]
- Bazant, M.Z.; Squires, T.M. Induced-charge electrokinetic phenomena: Theory and microfluidic applications. Phys. Rev. Lett. 2004, 92, 066101. [Google Scholar] [CrossRef] [PubMed]
- Shamloo, A.; Madadelahi, M.; Abdorahimzadeh, S. Three-dimensional numerical simulation of a novel electroosmotic micromixer. Chem. Eng. Process. Process Intensif. 2017, 119, 25–33. [Google Scholar] [CrossRef]
- Vatankhah, P.; Shamloo, A. Parametric study on mixing process in an in-plane spiral micromixer utilizing chaotic advection. Anal. Chim. Acta 2018, 1022, 96–105. [Google Scholar] [CrossRef] [PubMed]
- Shamloo, A.; Boodaghi, M. Design and simulation of a microfluidic device for acoustic cell separation. Ultrasonics 2018, 84, 234–243. [Google Scholar] [CrossRef] [PubMed]
- Shamloo, A.; Mashhadian, A. Inertial particle focusing in serpentine channels on a centrifugal platform. Phys. Fluids 2018, 30, 012002. [Google Scholar] [CrossRef]

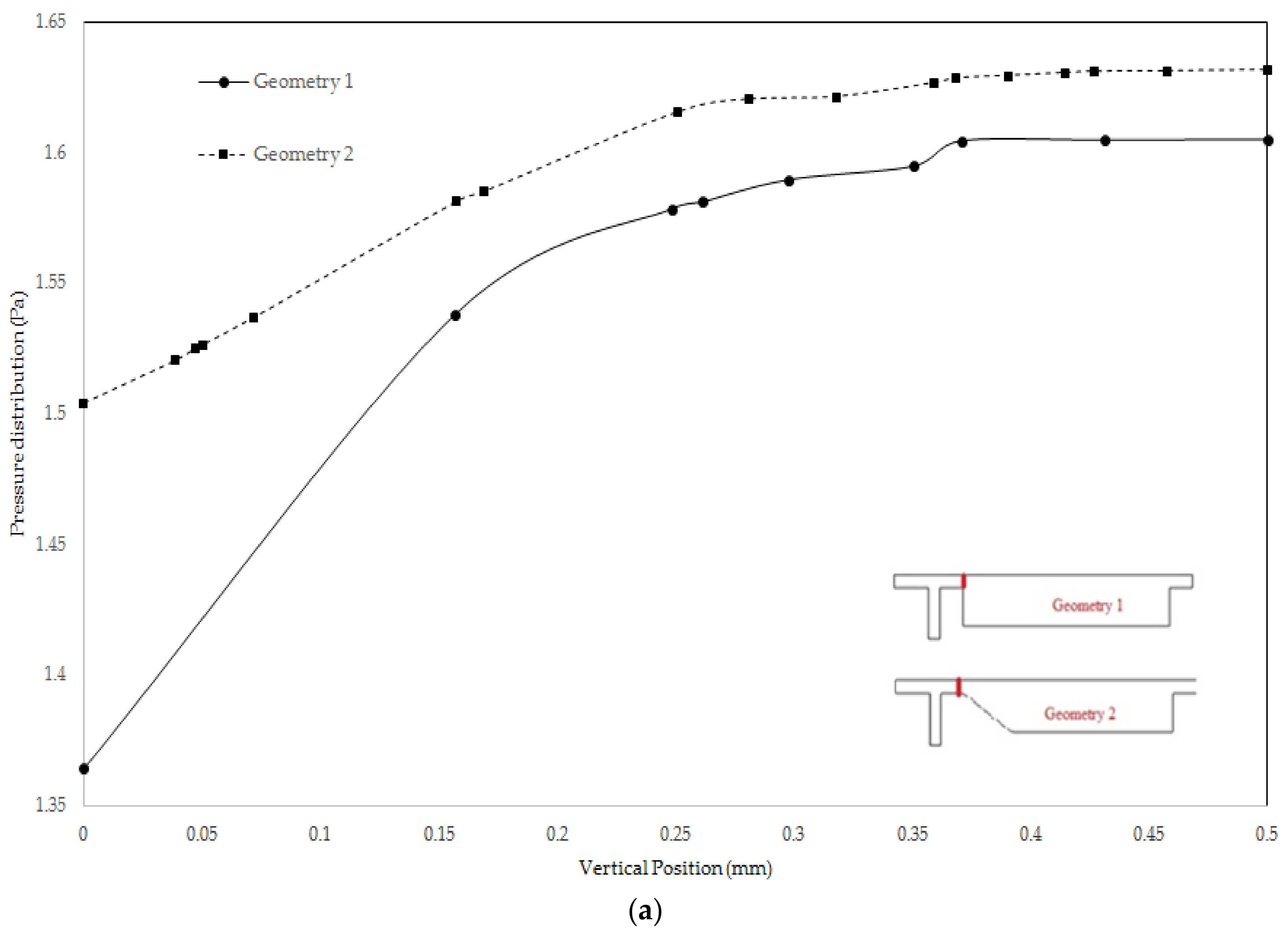
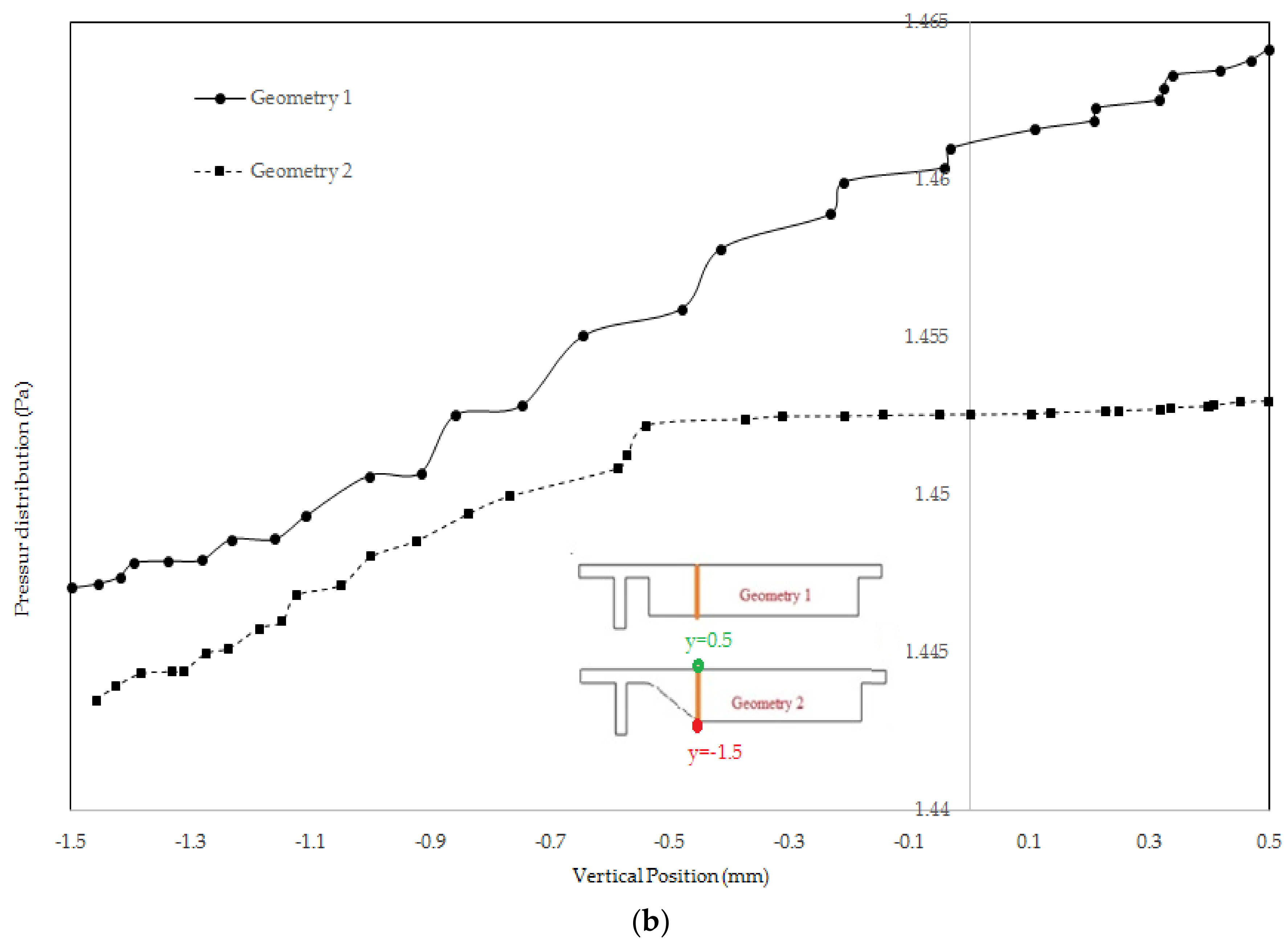
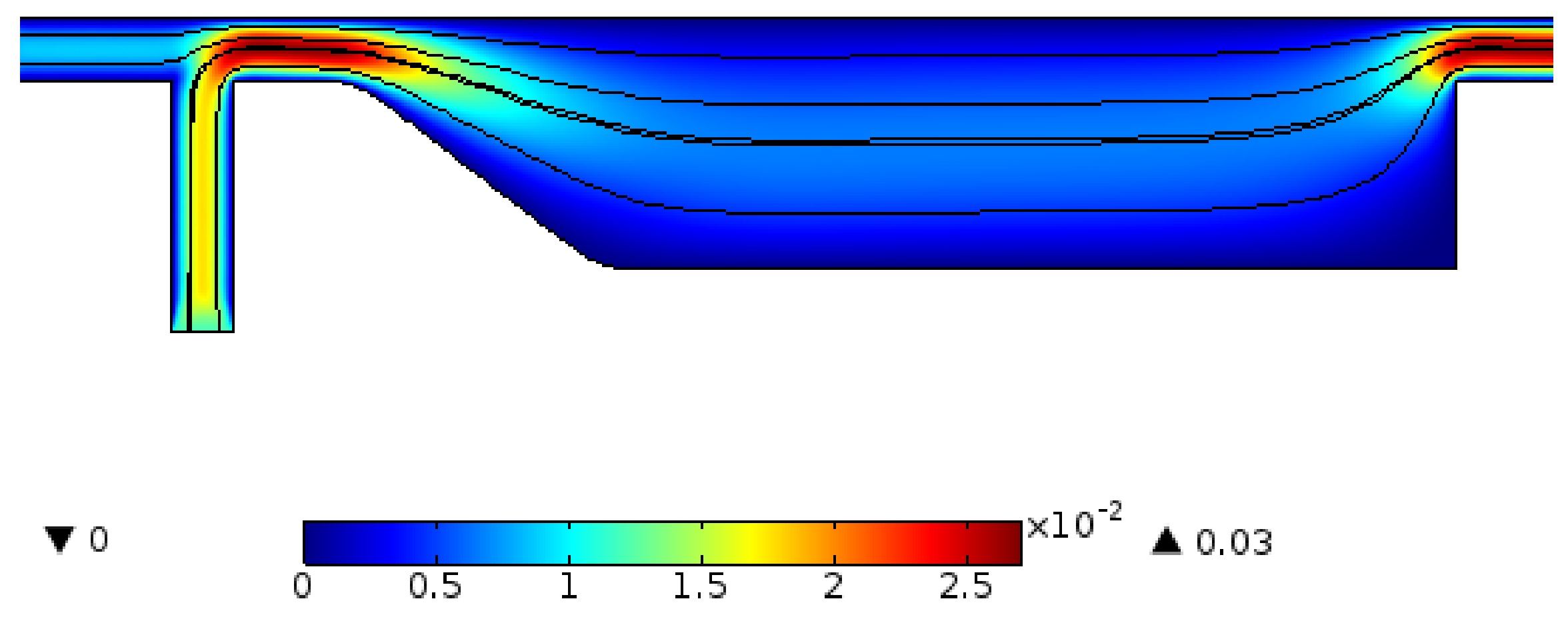
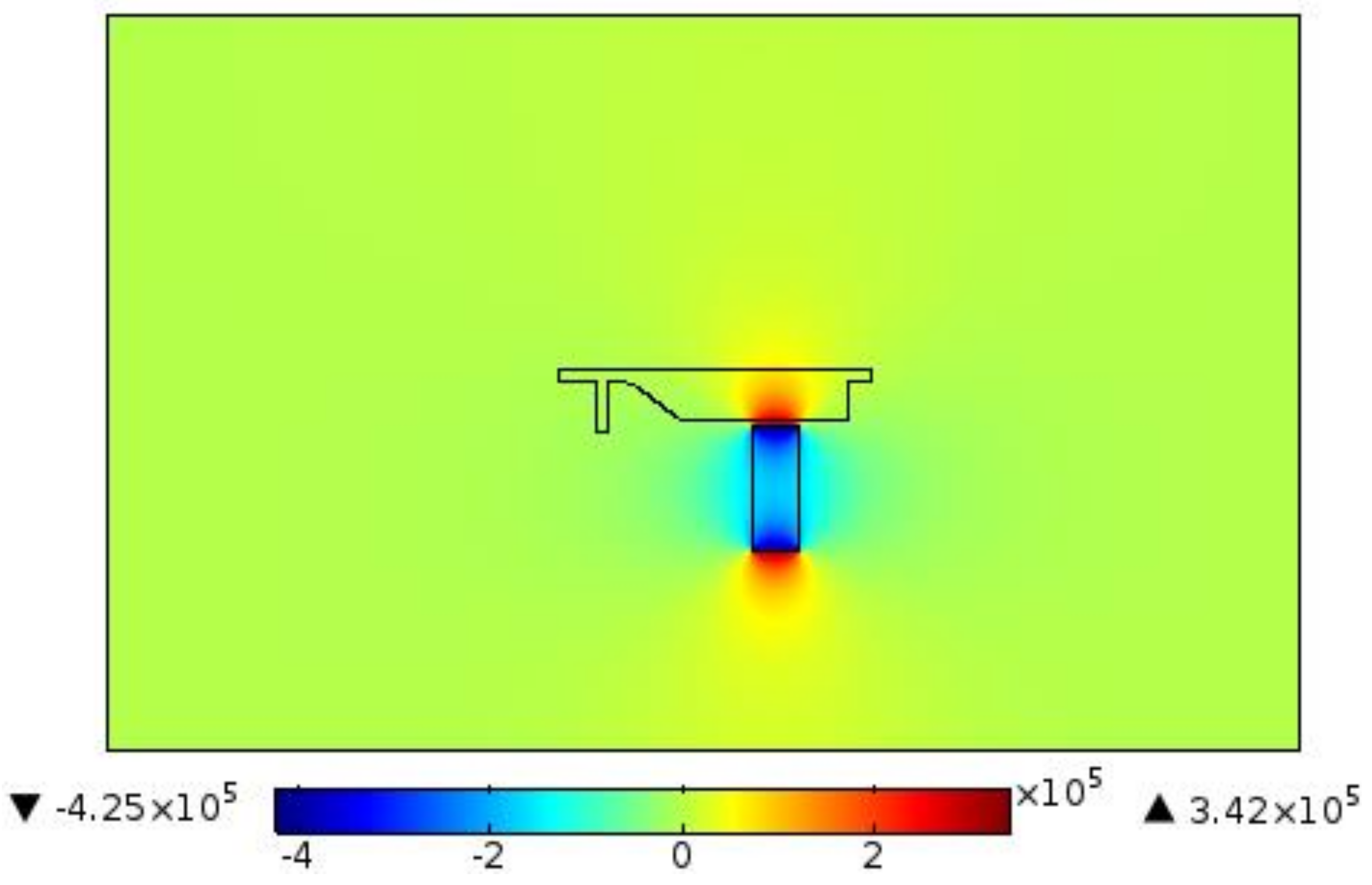

| Without Deflecting Channel | ||||
| Vertical Position of Particles (mm) | Min. | −0.98364 mm | ||
| Particle 1 | Particle 2 | Particle 3 | Max. | −0.00295 mm |
| −0.00295 | −0.4913 | 0.98364 | Diff. | 0.98069 mm |
| Without Deflecting Channel | ||||
| Vertical Position of Particles (mm) | Min. | −0.16094 mm | ||
| Particle 1 | Particle 2 | Particle 3 | Max. | 0.22983 mm |
| 0.22983 | 0.003208 | −0.16094 | Diff. | 0.39077 mm |
| Position of Magnet (mm) | Horizontal Position of Particle (mm) | Dispersion Distance (mm) | ||
|---|---|---|---|---|
| Particle 1 | Particle 2 | Particle 3 | ||
| X = 5 | 5.6101 | 5.8540 | 4.6818 | 1.1722 |
| X = 6 | 5.9842 | 6.4064 | 5.3900 | 1.0164 |
| X = 7 | 6.1083 | 7.0192 | 6.1233 | 0.9109 |
| X = 8 | 7.7192 | 6.8852 | 6.9711 | 0.8340 |
| X = 9 | 7.3598 | 8.040 | 7.8558 | 0.6802 |
| X = 10 | 8.1068 | 7.8119 | 8.7126 | 0.9007 |
| X = 11 | 8.3495 | 9.0202 | 9.5384 | 1.1889 |
| X = 12 | 9.1278 | 10.372 | 10.328 | 1.2442 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shamloo, A.; Ahmad, S.; Momeni, M. Design and Parameter Study of Integrated Microfluidic Platform for CTC Isolation and Enquiry; A Numerical Approach. Biosensors 2018, 8, 56. https://doi.org/10.3390/bios8020056
Shamloo A, Ahmad S, Momeni M. Design and Parameter Study of Integrated Microfluidic Platform for CTC Isolation and Enquiry; A Numerical Approach. Biosensors. 2018; 8(2):56. https://doi.org/10.3390/bios8020056
Chicago/Turabian StyleShamloo, Amir, Saba Ahmad, and Maede Momeni. 2018. "Design and Parameter Study of Integrated Microfluidic Platform for CTC Isolation and Enquiry; A Numerical Approach" Biosensors 8, no. 2: 56. https://doi.org/10.3390/bios8020056
APA StyleShamloo, A., Ahmad, S., & Momeni, M. (2018). Design and Parameter Study of Integrated Microfluidic Platform for CTC Isolation and Enquiry; A Numerical Approach. Biosensors, 8(2), 56. https://doi.org/10.3390/bios8020056





