Calibration of Minimally Invasive Continuous Glucose Monitoring Sensors: State-of-The-Art and Current Perspectives
Abstract
:1. Introduction
2. Calibration of Minimally-Invasive CGM Sensors
2.1. Problem Statement
2.2. Critical Aspects Affecting Calibration
3. State-of-the-Art Calibration Algorithms
4. Current Perspectives
5. Conclusions
Author Contributions
Conflicts of Interest
References
- World Health Organization (WHO). Definition, Diagnosis and Classification of Diabetes Mellitus and Its Complications; WHO: Geneva, Switzerland, 1999. [Google Scholar]
- Van Dijk, H.W.; Verbraak, F.D.; Fok, P.H.; Garvin, M.K.; Sonka, M.; Lee, K.; De Vries, J.H.; Michels, R.P.; Van Velthoven, M.E.; Schlingemann, R.O.; et al. Decreased retinal ganglion cell layer thickness in patients with type 1 diabetes. Investig. Ophthalmol. Vis. Sci. 2010, 51, 3660–3665. [Google Scholar] [CrossRef] [PubMed]
- Vriesendorp, T.M.; De Vries, J.H.; Van Santen, S.; Moeniralam, H.S.; De Jonge, E.; Roos, Y.B.; Schults, M.J.; Rosendaal, F.R.; Hoekstra, J.B. Evaluation of short-term consequences of hypoglycemia in an intensive care unit. Crit. Care Med. 2006, 34, 2714–2718. [Google Scholar] [CrossRef] [PubMed]
- Lemkes, B.A.; Hermanides, J.; De Vries, J.H.; Holleman, F.; Meijers, J.C.; Hoekstra, J.B. Hyperglycemia: A protrombotic factor? J. Thromb. Haemost. 2010, 8, 1663–1669. [Google Scholar] [CrossRef] [PubMed]
- You, W.P.; Henneberg, M. Type 1 diabetes prevalence increasing globally and regionally: The role of natural selection and life expectancy at birth. BMJ Open Diabetes Res. Care 2016, 4, e000161. [Google Scholar] [CrossRef] [PubMed]
- American Diabetes Association. Classification and diagnosis of diabetes: Standards of medical care in diabetes-2018. Diabetes Care 2018, 41, S13–S27. [Google Scholar]
- World Health Organization (WHO). Diabetes Facts Sheet. Available online: http://www.who.int/mediacentre/factsheets/fs312/en/ (accessed on 10 January 2017).
- Hayes, C.; Kriska, A. Role of physical activity in diabetes management and prevention. J. Am. Diet. Assoc. 2008, 108, S19–S23. [Google Scholar] [CrossRef] [PubMed]
- Ley, S.H.; Hamdy, O.; Mohan, V.; Hu, F.B. Prevention and management of type 2 diabetes: Dietary components and nutritional strategies. Lancet 2014, 383, 1999–2007. [Google Scholar] [CrossRef]
- Clarke, S.F.; Foster, J.R. A history of blood glucose meters and their role in self-monitoring of diabetes mellitus. Br. J. Biomed. Sci. 2012, 69, 83–93. [Google Scholar] [PubMed]
- Wang, J. Electrochemical glucose biosensors. Chem. Rev. 2008, 108, 814–825. [Google Scholar] [CrossRef] [PubMed]
- Sonksen, P.H.; Judd, S.L.; Lowy, C. Home monitoring of blood-glucose. Method for improving diabetic control. Lancet 1978, 1, 729–732. [Google Scholar] [CrossRef]
- Walford, S.; Gale, E.A.; Allison, S.P.; Tattersall, R.B. Self-monitoring of blood-glucose. Improvement of diabetic control. Lancet 1978, 1, 732–735. [Google Scholar] [CrossRef]
- Ikeda, Y.; Tajima, N.; Minami, N.; Ide, Y.; Yokoyama, J.; Abe, M. Pilot study of self-measurement of blood glucose using the Dextrostix-Eyetone system for juvenile-onset diabetes. Diabetologia 1978, 15, 91–93. [Google Scholar] [CrossRef] [PubMed]
- Christiansen, M.; Bailey, T.; Watkins, E.; Liljenquist, D.; Price, D.; Nakamura, K.; Boock, R.; Peyser, T. A new-generation continuous glucose monitoring system: Improved accuracy and reliability compared with a previous-generation system. Diabetes Technol. Ther. 2013, 15, 881–888. [Google Scholar] [CrossRef] [PubMed]
- Yoo, E.H.; Lee, S.Y. Glucose biosensors: An overview of use in clinical practice. Sensors 2010, 10, 4558–4576. [Google Scholar] [CrossRef] [PubMed]
- Cappon, G.; Acciaroli, G.; Vettoretti, M.; Facchinetti, A.; Sparacino, G. Wearable continuous glucose monitoring sensors: A revolution in diabetes treatment. Electronics 2017, 6, 65. [Google Scholar] [CrossRef]
- Lane, J.E.; Shivers, J.P.; Zisser, H. Continuous glucose monitors: Current status and future developments. Curr. Opin. Endocrinol. Diabetes Obes. 2013, 20, 106–111. [Google Scholar] [CrossRef] [PubMed]
- Pickup, J.C.; Holloway, M.F.; Samsi, K. Real-time continuous glucose monitoring in type 1 diabetes: A qualitative framework analysis of patient narratives. Diabetes Care 2015, 38, 544–550. [Google Scholar] [CrossRef] [PubMed]
- De Salvo, D.; Buckingham, B. Continuous glucose monitoring: Current use and future directions. Curr. Diabetes Rep. 2013, 13, 657–662. [Google Scholar] [CrossRef] [PubMed]
- Mauras, N.; Fox, L.; Englert, K.; Beck, R.W. Continuous glucose monitoring in type 1 diabetes. Endocrine 2013, 43, 41–50. [Google Scholar] [CrossRef] [PubMed]
- Haviland, N.; Walsh, J.; Roberts, R.; Bailey, T.S. Update on clinical utility of continuous glucose monitoring in type 1 diabetes. Curr. Diabetes Rep. 2016, 16, 115. [Google Scholar] [CrossRef] [PubMed]
- Parkin, C.G.; Graham, C.; Smolskis, J. Continuous glucose monitoring use in type 1 diabetes: Longitudinal analysis demonstrates meaningful improvements in HbA1c and reductions in health care utilization. J. Diabetes Sci. Technol. 2017, 11, 522–528. [Google Scholar] [CrossRef] [PubMed]
- Toschi, E.; Wolpert, H. Utility of continuous glucose monitoring in type 1 and type 2 diabetes. Endocrinol. Metab. Clin. 2016, 45, 895–904. [Google Scholar] [CrossRef] [PubMed]
- Polonsky, W.H.; Hessler, D.; Ruedy, K.J.; Beck, R.W.; DIAMOND Study Group. The impact of continuous glucose monitoring on markers of quality of life in adults with type 1 diabetes: Further findings from the DIAMOND randomized clinical trial. Diabetes Care 2017, 40, 736–741. [Google Scholar] [CrossRef] [PubMed]
- Litchman, M.L.; Allen, N.A. Real-time continuous glucose monitoring facilitates feelings of safety in older adults with type 1 diabetes: A qualitative study. J. Diabetes Sci. Technol. 2017, 11, 988–995. [Google Scholar] [CrossRef] [PubMed]
- Vaddiraju, S.; Burgess, D.J.; Tomazos, I.; Jain, F.C.; Papadimitrakopoulos, F. Technologies for continuous glucose monitoring: Current problems and future promises. J. Diabetes Sci. Technol. 2010, 4, 1540–1562. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.; Chowdhury, M.K.; Sharma, S.; Sharma, N. Blood glucose monitoring using non invasive optical method: Design limitations and challenges. Int. J. Adv. Res. Electr. Electron. Instrum. Eng. 2013, 2, 615–620. [Google Scholar]
- Wang, G.; He, X.; Wang, L.; Gu, A.; Huang, Y.; Fang, B.; Geng, B.; Zhang, X. Non-enzymatic electrochemical sensing of glucose. Microchim. Acta 2013, 180, 161–186. [Google Scholar] [CrossRef]
- Mohammadi, L.B.; Klotzbuecher, T.; Sigloch, S.; Welzel, K.; Göddel, M.; Pieber, T.R.; Schaupp, L. In vivo evaluation of a chip based near infrared sensor for continuous glucose monitoring. Biosens. Bioelectron. 2014, 15, 99–104. [Google Scholar] [CrossRef] [PubMed]
- Mortellaro, M.; DeHennis, A. Performance characterization of an abiotic and fluorescent-based continuous glucose monitoring system in patients with type 1 diabetes. Biosens. Bioelectron. 2014, 61, 227–231. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Guo, X.; Wang, Y.; Duan, X.; Qu, H.; Zhang, H.; Zhang, D.; Pang, W. Microchip based electrochemical-piezoelectric integrated multi-mode sensing system for continuous glucose monitoring. Sens. Actuators B 2016, 223, 83–88. [Google Scholar] [CrossRef]
- Salam, N.A.B.A.; bin Mohd Saad, W.H.; Manap, Z.B.; Salehuddin, F. The evolution of non-invasive blood glucose monitoring system for personal application. J. Telecommun. Electron. Comput. Eng. 2016, 8, 59–65. [Google Scholar]
- Rumpler, M.; Mader, J.K.; Fischer, J.P.; Thar, R.; Granger, J.M.; Deliane, F.; Klimant, I.; Aberer, F.; Sinner, F.; Pieber, T.R. First application of a transcutaneous optical single-port glucose monitoring device in patients with type 1 diabetes mellitus. Biosens. Bioelectron. 2017, 88, 240–248. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Zhao, X.L.; Li, Z.H.; Zhu, Z.G.; Qian, S.H.; Flewitt, A.J. Current and emerging technology for continuous glucose monitoring. Sensors 2017, 17, 182. [Google Scholar] [CrossRef] [PubMed]
- McGarraugh, G. The chemistry of commercial continuous glucose monitors. Diabetes Technol. Ther. 2009, 11, S17–S24. [Google Scholar] [CrossRef] [PubMed]
- Rossetti, P.; Bondia, J.; Vehi, J.; Fanelli, C.G. Estimating plasma glucose from interstitial glucose: The issue of calibration algorithms in commercial continuous glucose monitoring devices. Sensors 2010, 10, 10936–10952. [Google Scholar] [CrossRef] [PubMed]
- Bequette, B.W. Continuous glucose monitoring: Real-time algorithms for calibration, filtering, and alarms. J. Diabetes Sci. Technol. 2010, 4, 404–418. [Google Scholar] [CrossRef] [PubMed]
- Sparacino, G.; Facchinetti, A.; Cobelli, C. “Smart” continuous glucose monitoring sensors: On-line signal processing issues. Sensors 2010, 10, 6751–6772. [Google Scholar] [CrossRef] [PubMed]
- Lodwing, V.; Heinemann, L. Continuous glucose monitoring with glucose sensors: Calibration and assessment criteria. Diabetes Technol. Ther. 2003, 5, 572–586. [Google Scholar] [CrossRef] [PubMed]
- Dexcom G4 Platinum Continuous Glucose Monitoring System User’s Guide. Available online: https://s3-us-west-2.amazonaws.com/dexcompdf/LBL012528+Rev+004+User’s+Guide%2C+G4+PLATINUM+with+Share+US+Web+with+cover.pdf (accessed on 10 January 2018).
- Dexcom G5 Mobile Continuous Glucose Monitoring System User Guide. Available online: https://s3-us-west-2.amazonaws.com/dexcompdf/LBL013990-REV003-G5-Mobile-User-Guide-NA-Android-US.pdf (accessed on 10 January 2018).
- Medtronic Diabetes. Sensors & Transmitters. Calibrating Your Sensor. Available online: https://www.medtronicdiabetes.com/customer-support/sensors-and-transmitters-support/calibration-sensor (accessed on 10 January 2018).
- Panteleon, A.E.; Rebrin, K.; Steil, G.M. The role of the independent variable to glucose sensor calibration. Diabetes Technol. Ther. 2003, 5, 401–410. [Google Scholar] [CrossRef] [PubMed]
- Mastrototaro, J.J.; Gross, T.M.; Shin, J.J. Glucose Monitor Calibration Methods. U.S. Patent 6,424,847, 23 July 2002. [Google Scholar]
- Shin, J.J.; Holtzclaw, K.R.; Dangui, N.D.; Kanderian, S., Jr.; Mastrototaro, J.J.; Hong, P.I. Real Time Self-Adjusting Calibration Algorithm. U.S. Patent 6,895,263, 17 May 2005. [Google Scholar]
- Kamath, A.U.; Simpson, P.C.; Brauker, J.H.; Goode, P.V., Jr. Calibration Techniques for a Continuous Analyte Sensor. U.S. Patent 8,428,678, 23 April 2013. [Google Scholar]
- Budiman, E.S. Method and Device for Providing Offset Model Based Calibration for Analyte Sensor. U.S. Patent 8,532,935, 10 September 2013. [Google Scholar]
- Choleau, C.; Klein, J.C.; Reach, G.; Aussedat, B.; Demaria-Pesce, V.; Wilson, G.S.; Gifford, R.; Ward, W.K. Calibration of a subcutaneous amperometric glucose sensor implanted for 7 days in diabetic patients: Part 2. Superiority of the one-point calibration method. Biosens. Bioelectron. 2002, 17, 647–654. [Google Scholar] [CrossRef]
- Mahmoudi, Z.; Johansen, M.D.; Christiansen, J.S.; Hejlesen, O. Comparison between one-point calibration and two-point calibration approaches in a continuous glucose monitoring algorithm. J. Diabetes Sci. Technol. 2014, 8, 709–719. [Google Scholar] [CrossRef] [PubMed]
- Rebrin, K.; Steil, G.M.; Van Antwerp, W.P.; Mastrototaro, J.J. Subcutaneous glucose predicts plasma glucose independent of insulin: Implications for continuous monitoring. Am. J. Physiol. Endocrinol. Metab. 1999, 277, E561–E571. [Google Scholar] [CrossRef]
- Schiavon, M.; Dalla Man, C.; Dube, S.; Slama, M.; Kudva, Y.C.; Peyser, T.; Basu, A.; Basu, R.; Cobelli, C. Modelling plasma-to-interstitium glucose kinetics from multitracer plasma and microdialysis data. Diabetes Technol. Ther. 2015, 17, 825–831. [Google Scholar] [CrossRef] [PubMed]
- Keenan, D.B.; Mastrototaro, J.J.; Voskanyan, G.; Steil, G.M. Delays in minimally invasive continuous glucose monitoring devices: A review of current technology. J. Diabetes Sci. Technol. 2009, 3, 1207–1214. [Google Scholar] [CrossRef] [PubMed]
- Rebrin, K.; Sheppard, N.F., Jr.; Steil, G.M. Use of subcutaneous interstitial fluid glucose to estimate blood glucose: Revisiting delay and sensor offset. J. Diabetes Sci. Technol. 2010, 5, 1087–1098. [Google Scholar] [CrossRef] [PubMed]
- Facchinetti, A.; Sparacino, G.; Cobelli, C. Reconstruction of glucose in plasma from interstitial fluid continuous glucose monitoring data: Role of sensor calibration. J. Diabetes Sci. Technol. 2007, 1, 617–623. [Google Scholar] [CrossRef] [PubMed]
- Helton, K.L.; Ratner, B.D.; Wisniewski, N.A. Biomechanics of the sensor-tissue interface—Effects of motion, pressure, and design on sensor performance and the foreign body response—Part I: Theoretical framework. J. Diabetes Sci. Technol. 2011, 5, 632–646. [Google Scholar] [CrossRef] [PubMed]
- Klueh, U.; Liu, Z.; Feldman, B.; Henning, T.P.; Cho, B.; Ouyang, T.; Kreutzer, D. Metabolic biofouling of glucose sensors in vivo: Role of tissue microhemorrhages. J. Diabetes Sci. Technol. 2011, 5, 583–595. [Google Scholar] [CrossRef] [PubMed]
- Diabetes Research in Children Network (Direcnet) Study Group; Buckingham, B.A.; Kollman, C.; Beck, R.; Kalajian, A.; Fiallo-Scharer, R.; Tansey, M.J.; Fox, L.A.; Wilson, D.M.; Weinzimer, S.A.; et al. Evaluation of factors affecting CGMS calibration. Diabetes Technol. Ther. 2006, 8, 318–325. [Google Scholar]
- Aussedat, B.; Thomè-Duret, V.; Reach, G.; Lemmonier, F.; Klein, J.C.; Hu, Y.; Wilson, G.S. A user-friendly method for calibrating a subcutaneous glucose sensor-based hypoglycemic alarm. Biosens. Bioelectron. 1997, 12, 1061–1071. [Google Scholar] [CrossRef]
- Knobbe, E.J.; Lim, W.L.; Buckingham, B.A. Method and Apparatus for Real-Time Estimation of Physiological Parameters. U.S. Patent 6,575,905, 10 June 2003. [Google Scholar]
- Knobbe, E.J.; Buckingham, B. The extended Kalman filter for continuous glucose monitoring. Diabetes Technol. Ther. 2005, 7, 15–27. [Google Scholar] [CrossRef] [PubMed]
- Kuure-Kinsey, M.; Palerm, C.C.; Bequette, B.W. A dual-rate Kalman filter for continuous glucose monitoring. In Proceedings of the 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 31 August–3 September 2006. [Google Scholar]
- Facchinetti, A.; Sparacino, G.; Cobelli, C. Enhanced accuracy of continuous glucose monitoring by online extended Kalman filtering. Diabetes Technol. Ther. 2010, 12, 353–363. [Google Scholar] [CrossRef] [PubMed]
- Leal, Y.; Garcia-Gabin, W.; Bondia, J.; Esteve, E.; Ricart, W.; Fernàndez-Real, J.M.; Vehì, J. Real-time glucose estimation algorithm for continuous glucose monitoring using autoregressive models. J. Diabetes Sci. Technol. 2010, 4, 391–403. [Google Scholar] [CrossRef] [PubMed]
- Leal, Y.; Garcia-Gabin, W.; Bondia, J.; Esteve, E.; Ricart, W.; Fernàndez-Real, J.M.; Vehì, J. Enhanced algorithm for continuous estimation using the continuous glucose monitoring system. Med. Sci. Monit. 2010, 16, MT51–MT58. [Google Scholar] [PubMed]
- Barceló-Rico, F.; Bondia, J.; Díez, J.L.; Rossetti, P. A multiple local models approach to accuracy improvement in continuous glucose monitoring. Diabetes Technol. Ther. 2012, 14, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Barceló-Rico, F.; Díez, J.L.; Rossetti, P.; Vehi, J.; Bondia, J. Adaptive calibration algorithm for plasma glucose estimation in continuous glucose monitoring. IEEE J. Biomed. Health Inf. 2013, 17, 530–538. [Google Scholar]
- Mahmoudi, Z.; Dencker Johansen, M.; Christiansen, J.S.; Hejlesen, O.K. A multistep algorithm for processing and calibration of microdialysis continuous glucose monitoring data. Diabetes Technol. Ther. 2013, 15, 825–835. [Google Scholar] [CrossRef] [PubMed]
- Kirchsteiger, H.; Zaccarian, L.; Renard, E.; del Re, L. A novel online recalibration strategy for continuous glucose measurement sensors employing LMI techniques. In Proceedings of the 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Osaka, Japan, 3–7 July 2013. [Google Scholar]
- Kirchsteiger, H.; Zaccarian, L.; Renard, E.; del Re, L. LMI-based approaches for the calibration of continuous glucose measurement sensors. IEEE J. Biomed. Health Inf. 2015, 19, 1697–1706. [Google Scholar] [CrossRef] [PubMed]
- Choleau, C.; Klein, J.C.; Reach, G.; Aussedat, B.; Demaria-Pesce, V.; Wilson, G.S.; Gifford, R.; Ward, W.K. Calibration of a subcutaneous amperometric glucose sensor: Part 1. Effect of measurement uncertainties on the determination of sensor sensitivity and background current. Biosens. Bioelectron. 2002, 17, 641–646. [Google Scholar] [CrossRef]
- Guerra, S.; Facchinetti, A.; Sparacino, G.; De Nicolao, G.; Cobelli, C. Enhancing the accuracy of subcutaneous glucose sensors: A real-time deconvolution-based approach. IEEE Trans. Biomed. Eng. 2012, 59, 1658–1669. [Google Scholar] [CrossRef] [PubMed]
- De Nicolao, G.; Sparacino, G.; Cobelli, C. Nonparametric input estimation in physiological systems: Problems, methods and case studies. Automatica 1997, 33, 851–870. [Google Scholar] [CrossRef]
- Vettoretti, M.; Facchinetti, A.; Del Favero, S.; Sparacino, G.; Cobelli, C. Online calibration of glucose sensor from the measured current by a time-varying calibration function and Bayesian priors. IEEE Trans. Biomed. Eng. 2016, 63, 1631–1641. [Google Scholar] [CrossRef] [PubMed]
- Acciaroli, G.; Vettoretti, M.; Facchinetti, A.; Sparacino, G.; Cobelli, C. From two to one per day calibration of Dexcom G4 Platinum by a time-varying day-specific Bayesian prior. Diabetes Technol. Ther. 2016, 18, 472–479. [Google Scholar] [CrossRef] [PubMed]
- Acciaroli, G.; Vettoretti, M.; Facchinetti, A.; Sparacino, G.; Cobelli, C. Reduction of blood glucose measurements to calibrate subcutaneous glucose sensors: A Bayesian multi-day framework. IEEE Trans. Biomed. Eng. 2017. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.B.; Dassau, E.; Doyle, F.J. A run-to-run approach to enhance continuous glucose monitoring accuracy based on continuous wear. IFAC-PapersOnline 2015, 48, 237–242. [Google Scholar] [CrossRef]
- Zavitsanou, S.; Lee, J.B.; Pinsker, J.E.; Church, M.M.; Doyle, F.J.; Dassau, E. A personalized week-to-week updating algorithm to improve continuous glucose monitoring performance. J. Diabetes Sci. Technol. 2017, 11, 1070–1079. [Google Scholar] [CrossRef] [PubMed]
- Hovorka, R.; Nodale, M.; Haidar, A.; Wilinska, M. Assessing performance of closed-loop insulin delivery systems by continuous glucose monitoring: Drawbacks and way forward. Diabetes Technol. Ther. 2013, 15, 4–12. [Google Scholar] [CrossRef] [PubMed]
- Del Favero, S.; Facchinetti, A.; Sparacino, G.; Cobelli, C. Improving accuracy and precision of glucose sensor profiles: Retrospective fitting by constrained deconvolution. IEEE Trans. Biomed. Eng. 2014, 61, 1044–1053. [Google Scholar] [CrossRef] [PubMed]
- Del Favero, S.; Facchinetti, A.; Sparacino, G.; Cobelli, C.; AP@ home consortium. Retrofitting of continuous glucose monitoring traces allows more accurate assessment of glucose control in outpatient studies. Diabetes Technol. Ther. 2015, 17, 355–363. [Google Scholar] [PubMed]
- Del Favero, S.; Facchinetti, A.; Sparacino, G.; Cobelli, C. Retrofitting real-life Dexcom G5 data. Diabetes Technol. Ther. 2017, 19, 237–245. [Google Scholar] [CrossRef] [PubMed]
- Acciaroli, G.; Vettoretti, M.; Facchinetti, A.; Sparacino, G. Toward calibration-free continuous glucose moitoring sensors: Bayesian calibration approach applied to next-generation technology. Diabetes Technol. Ther. 2018, 20, 59–67. [Google Scholar] [CrossRef] [PubMed]
- Garcia, A.; Rack-Gomer, A.L.; Bhavaraju, N.C.; Hampapuram, H.; Kamath, A.; Peyser, T.; Facchinetti, A.; Zecchin, C.; Sparacino, G.; Cobelli, C. Dexcom G4AP: An advanced continuous glucose monitor for the artificial pancreas. J. Diabetes Sci. Technol. 2013, 7, 1436–1445. [Google Scholar] [CrossRef] [PubMed]
- Sparacino, G.; Facchinetti, A.; Maran, A.; Cobelli, C. Continuous glucose monitoring time series and hypo/hyperglycemia prevention: Requirements, methods, open problema. Curr. Diabetes Rev. 2008, 4, 181–192. [Google Scholar] [CrossRef] [PubMed]
- Bailey, T.; Bode, B.W.; Christiansen, M.P.; Klaff, L.J.; Alva, S. The performance and usability of a factory-calibrated flash glucose monitoring system. Diabetes Technol. Ther. 2015, 17, 787–794. [Google Scholar] [CrossRef] [PubMed]
- Edelman, S.V. Regulation catches up to reality: Nonadjunctive use of continuous glucose monitoring data. J. Diabetes Sci. Technol. 2017, 11, 160–164. [Google Scholar] [CrossRef] [PubMed]
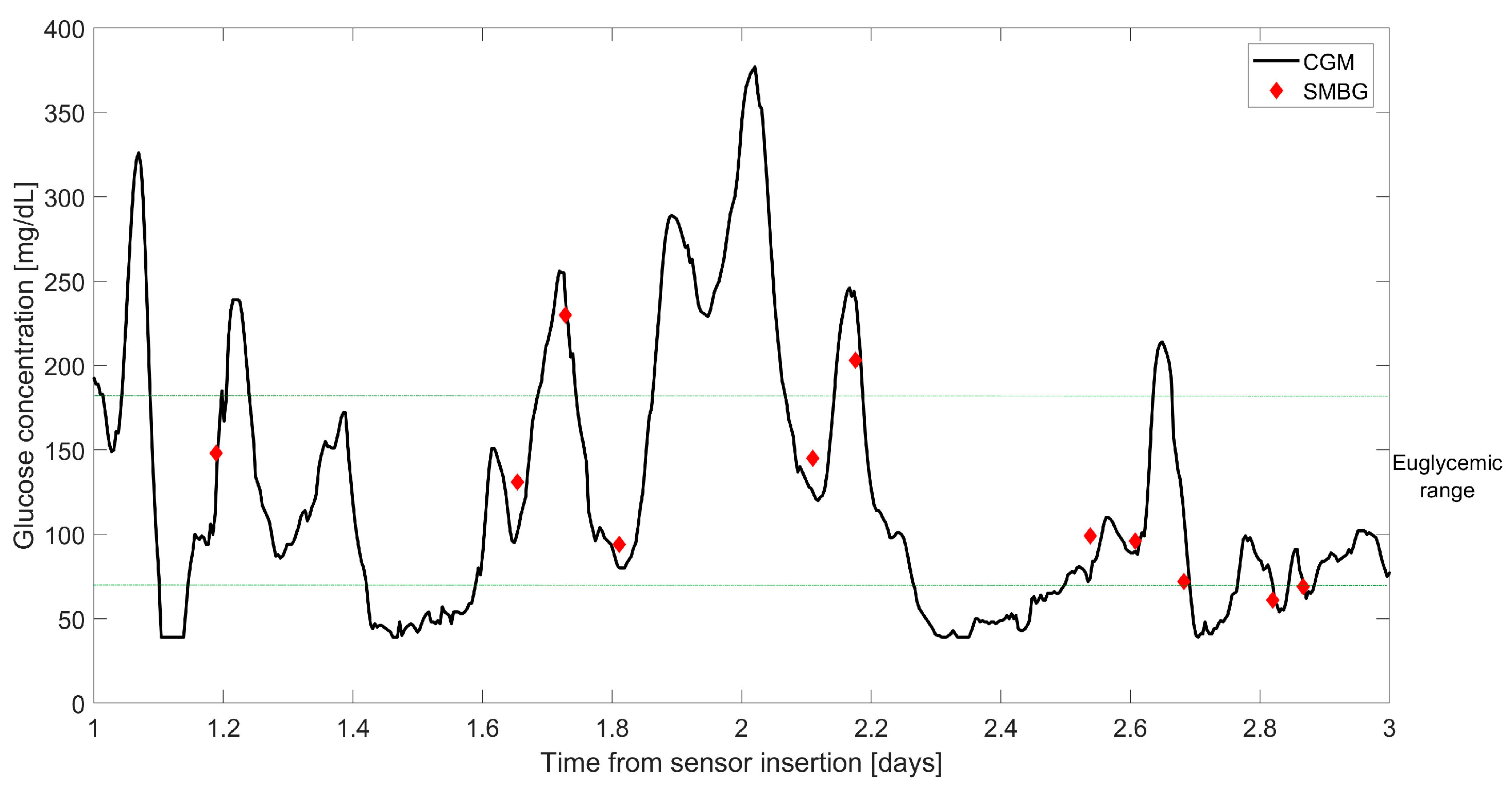
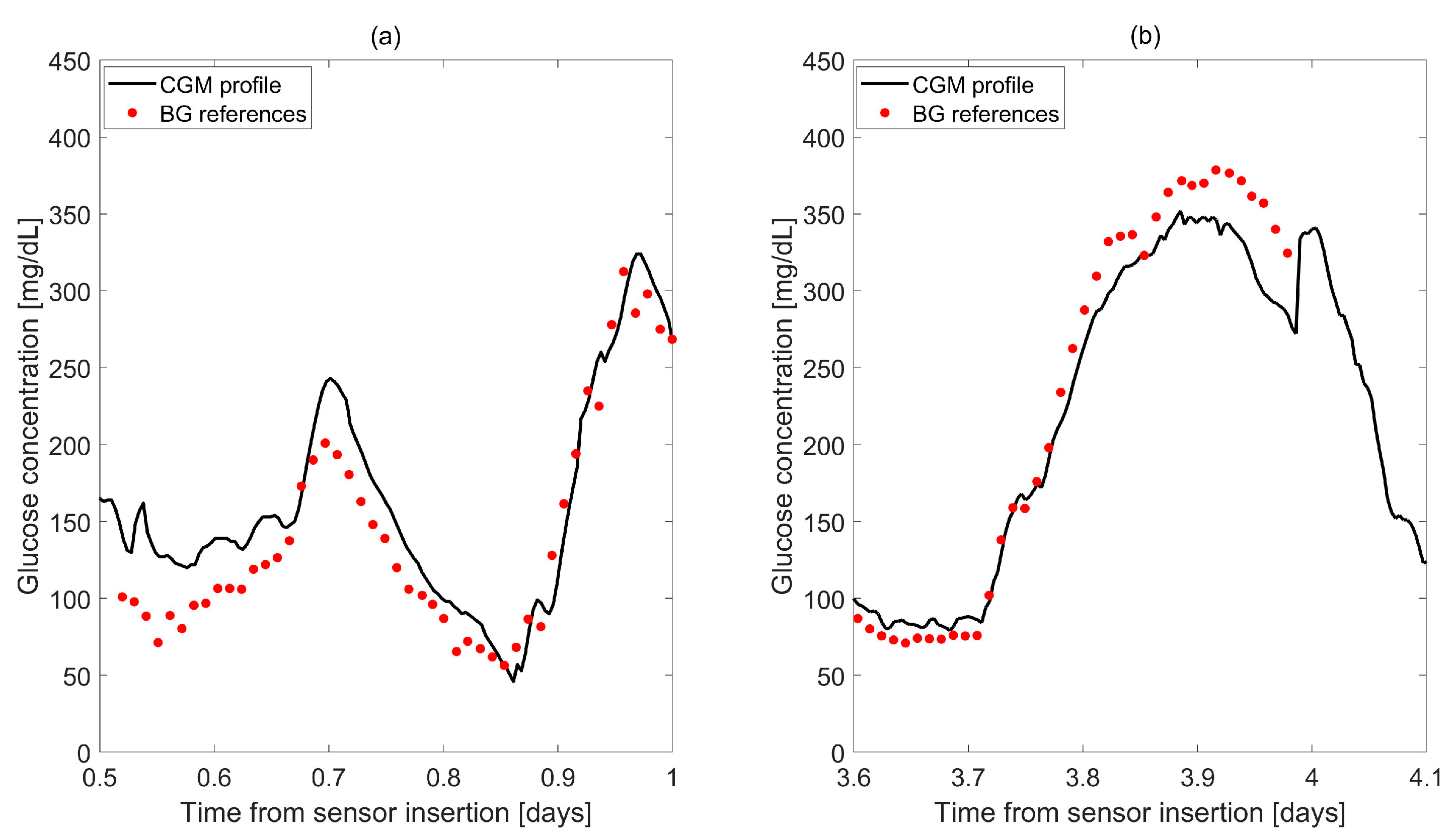
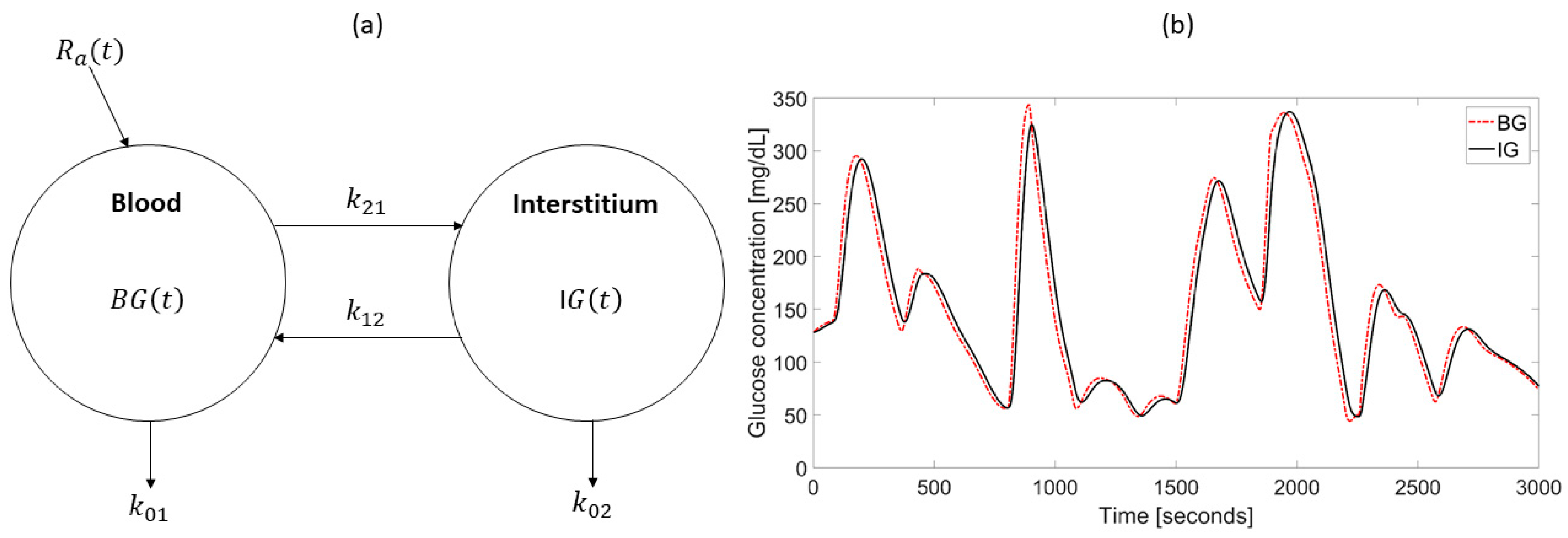
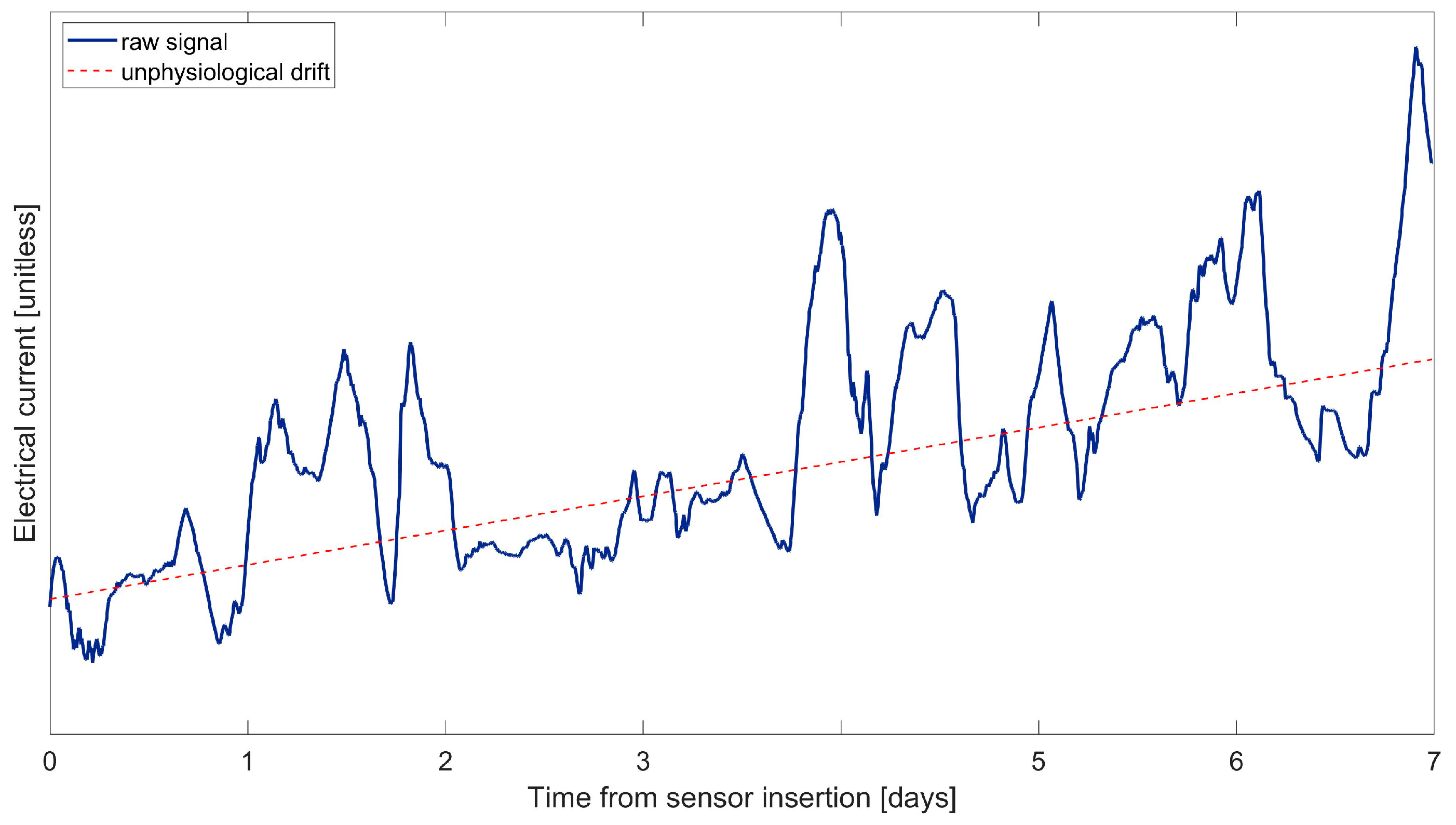
| Study | Calibration Technique | Model of BG-IG Dynamic | Real-Time Use in Wearable Devices | Calibrations per Day | Validation Data | Improvements Compared to Manufacturer (if Applicable) |
|---|---|---|---|---|---|---|
| Aussedat et al. [59] | Linear regression with feature to detect phases of steady state signal | No, but use of heuristic technique | Yes | Not specified | Real data from a miniaturized glucose sensor used in rats | / |
| Knobbe et al. [60,61] | Extended Kalman filter | Yes | Yes | Not specified | Real data from the Medronic (Northridge, CA, USA) MiniMed CGM system | / |
| Kuure-Kinsey et al. [62] | Dual rate Kalman filter | No | Yes | 3 | Synthetic data; data from an experimental glucose sensor used in rats | / |
| Facchinetti et al. [63] | Extended Kalman filter | Yes | Yes | 4 | Synthetic data | / |
| Leal et al. [64] | Auto-regressive models | No | Yes | At least 3 | Real data from the Medtronic (Northridge, CA, USA) MiniMed CGMS system gold | Median RAD 1 decreased of 4.6% |
| Leal et al. [65] | Linear regression | No | No | At least 3 | Real data from the Medtronic (Northridge, CA, USA) MiniMed CGMS system gold | Median RAD 1 decreased of 2% |
| Barceló-Rico [66,67] | Multiple local dynamic models [66] with adaptive parameters normalization [67] | Yes | Yes | 3–4 | Real data from the GlucoDay (Menarini, Florence, Italy) sensor [66]; synthetic data; real data from the Medtronic (Northridge, CA, USA) MiniMed CGMS system gold [67] | MARD 2 decreased of 3.9% in [66] and of 2.4% in [67] |
| Mahmoudi et al. [68] | Rate-limiting filtering, selective smoothing, and robust regression | No, but use of heuristic technique | Yes | Maximum 4 | Real data from SCGM 1 (Roche Diagnostic, Mannheim, Germany) system | / |
| Kirchsteiger et al. [69,70] | Linear matrix inequalities | Yes | Yes | Roughly 6 (more in day 1) | Real data from the FreeStyle Navigator (Abbott Diabetes Care, Alameda, CA, USA) system | MARD 2 decreased of about 4.7% [70] |
| Guerra et al. [72] | Linear regression and regularized deconvolution | Yes | Yes | 2 | Synthetic data; real data from the FreeStyle Navigator (Abbott Diabetes Care, Alameda, CA, USA) and DexCom Seven Plus (Dexcom Inc., San Diego, CA, USA) systems | RMSE 3 decreased of 7.2 mg/dL |
| Vettoretti et al. [74] | Linear regression and regularized deconvolution | Yes | Yes | 2 | Real data from the Dexcom G4 Platinum (Dexcom Inc., San Diego, CA, USA) system | MARD 2 decreased of 1.2% |
| Acciaroli et al. [75] | Linear regression and regularized deconvolution | Yes | Yes | 1 | Real data from the Dexcom G4 Platinum (Dexcom Inc., San Diego, CA, USA) system | MARD 2 decreased of 1.2%, calibrations reduced from 2 to 1 per day |
| Acciaroli et al. [76,83] | Multiple-day model and regularized deconvolution | Yes | Yes | 0.25 in [76]; zero in [83] | Real data from the Dexcom G4 Platinum (Dexcom Inc., San Diego, CA, USA) system [76] and a next-generation Dexcom prototype [83] | MARD 2 decreased of 1.2%, calibrations reduced from 2 to 0.25 per day [76] |
| Lee et al. [77] | Linear regression with run-to-run | No | Yes, after a few weeks of CGM use | 2 | Synthetic data | / |
| Zavitsanou et al. [78] | Linear regression with weakly updating feature | No | Yes, after a few weeks of CGM use | 2 | Real data from the Dexcom G4 Platinum (Dexcom Inc., San Diego, CA, USA) system | / |
| Del Favero et al. [80,81,82] | Linear regression and regularized constrained deconvolution | Yes | No | 13 in [80]; 10 in [82] | Real data from the DexCom Seven Plus [80,81] and Dexcom G5 Mobile [82] (Dexcom Inc., San Diego, CA, USA) systems | MARD 2 decreased of 6.9% in [80], of 2.6% and 4.1% in adults and pediatrics in [82] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Acciaroli, G.; Vettoretti, M.; Facchinetti, A.; Sparacino, G. Calibration of Minimally Invasive Continuous Glucose Monitoring Sensors: State-of-The-Art and Current Perspectives. Biosensors 2018, 8, 24. https://doi.org/10.3390/bios8010024
Acciaroli G, Vettoretti M, Facchinetti A, Sparacino G. Calibration of Minimally Invasive Continuous Glucose Monitoring Sensors: State-of-The-Art and Current Perspectives. Biosensors. 2018; 8(1):24. https://doi.org/10.3390/bios8010024
Chicago/Turabian StyleAcciaroli, Giada, Martina Vettoretti, Andrea Facchinetti, and Giovanni Sparacino. 2018. "Calibration of Minimally Invasive Continuous Glucose Monitoring Sensors: State-of-The-Art and Current Perspectives" Biosensors 8, no. 1: 24. https://doi.org/10.3390/bios8010024
APA StyleAcciaroli, G., Vettoretti, M., Facchinetti, A., & Sparacino, G. (2018). Calibration of Minimally Invasive Continuous Glucose Monitoring Sensors: State-of-The-Art and Current Perspectives. Biosensors, 8(1), 24. https://doi.org/10.3390/bios8010024







