A Radar-Based Smart Sensor for Unobtrusive Elderly Monitoring in Ambient Assisted Living Applications
Abstract
1. Introduction
2. Related Work
2.1. Wearable Solutions
2.2. Ambient Solutions
2.3. Radar-Based Fall Detection
2.4. Radar-Based Vital-Sign Measurement
3. Materials and Methods
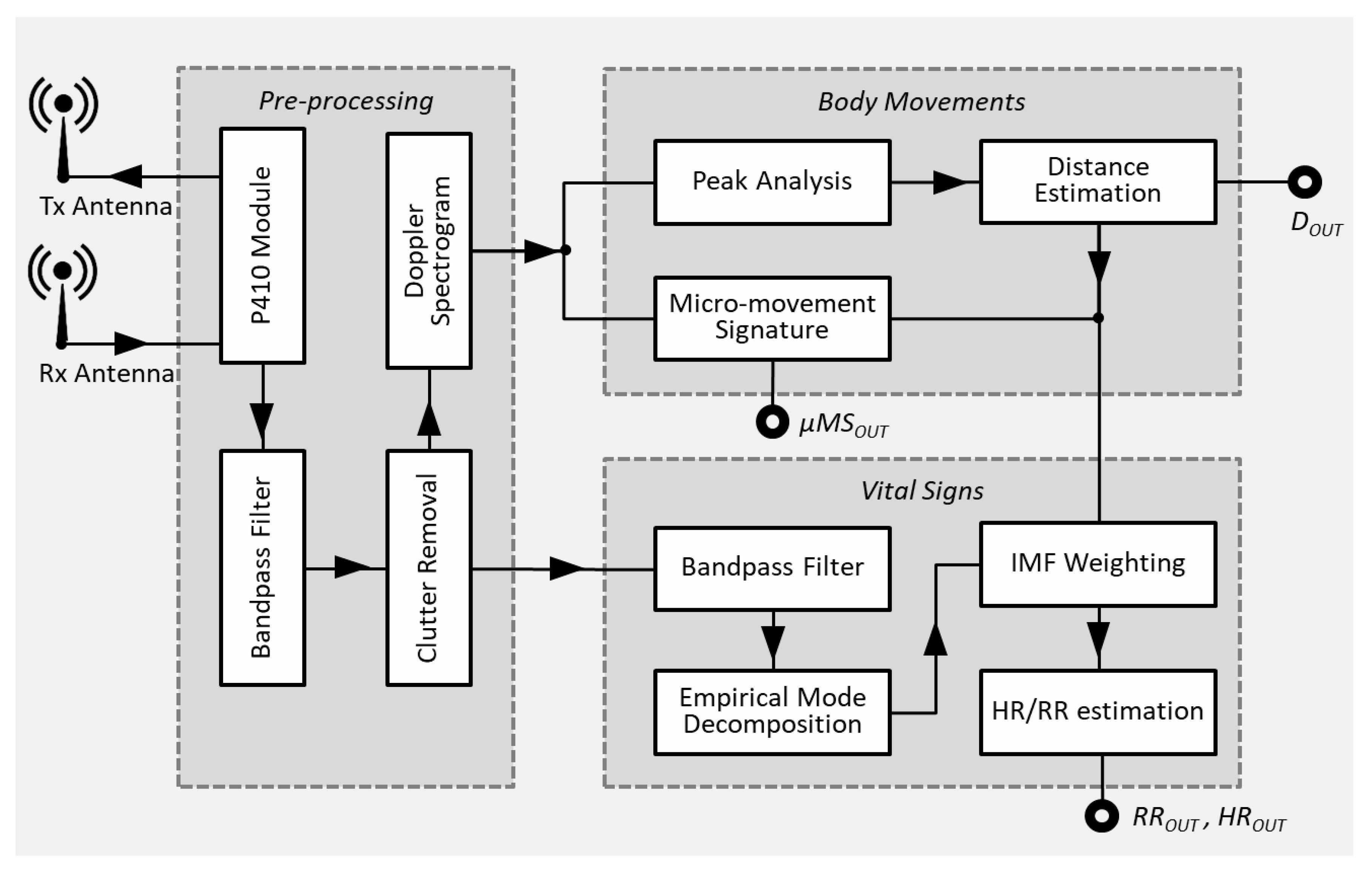
3.1. System Overview
3.2. Pre-Processing
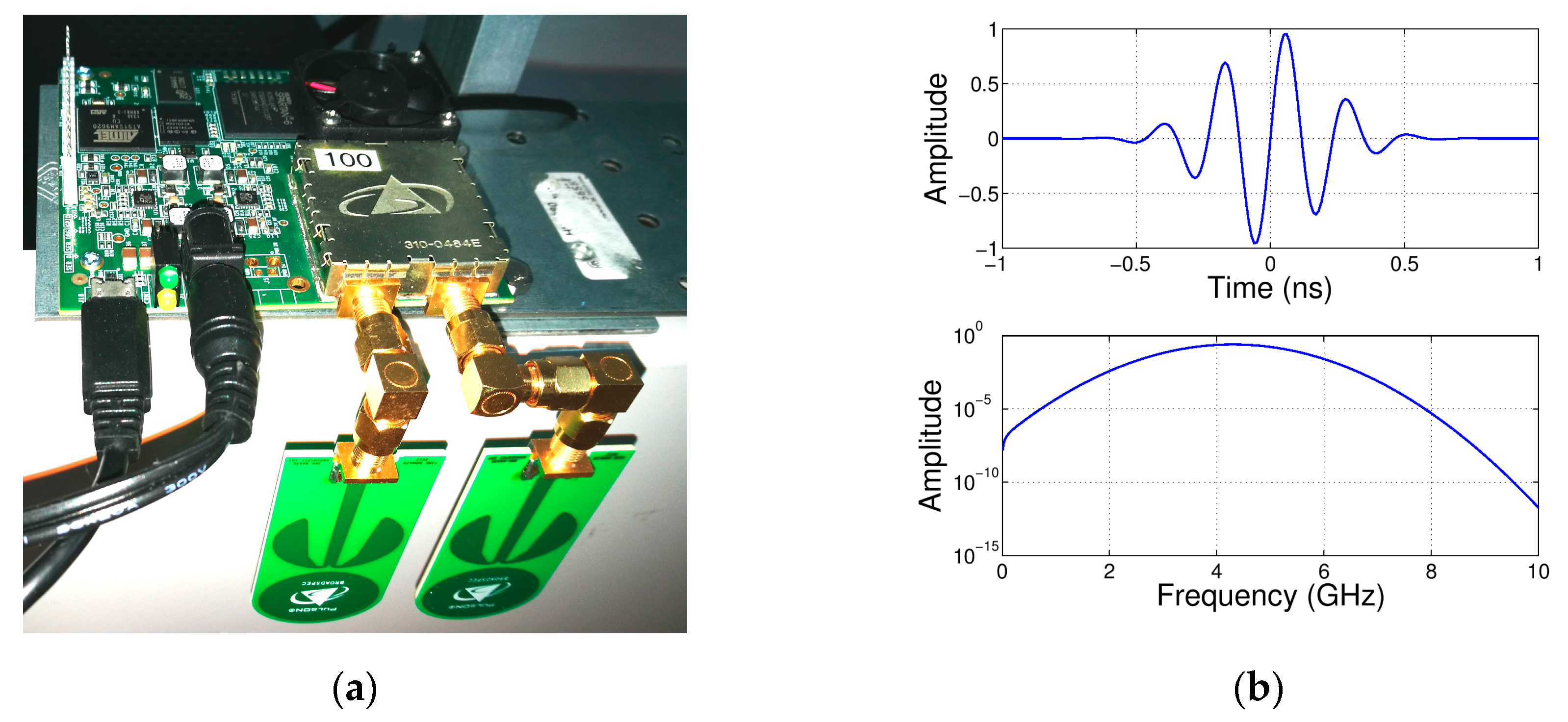
3.2.1. Radar Module
3.2.2. Bandpass Filtering
3.2.3. Clutter Removal
3.2.4. Micro-Doppler Spectrogram Processing
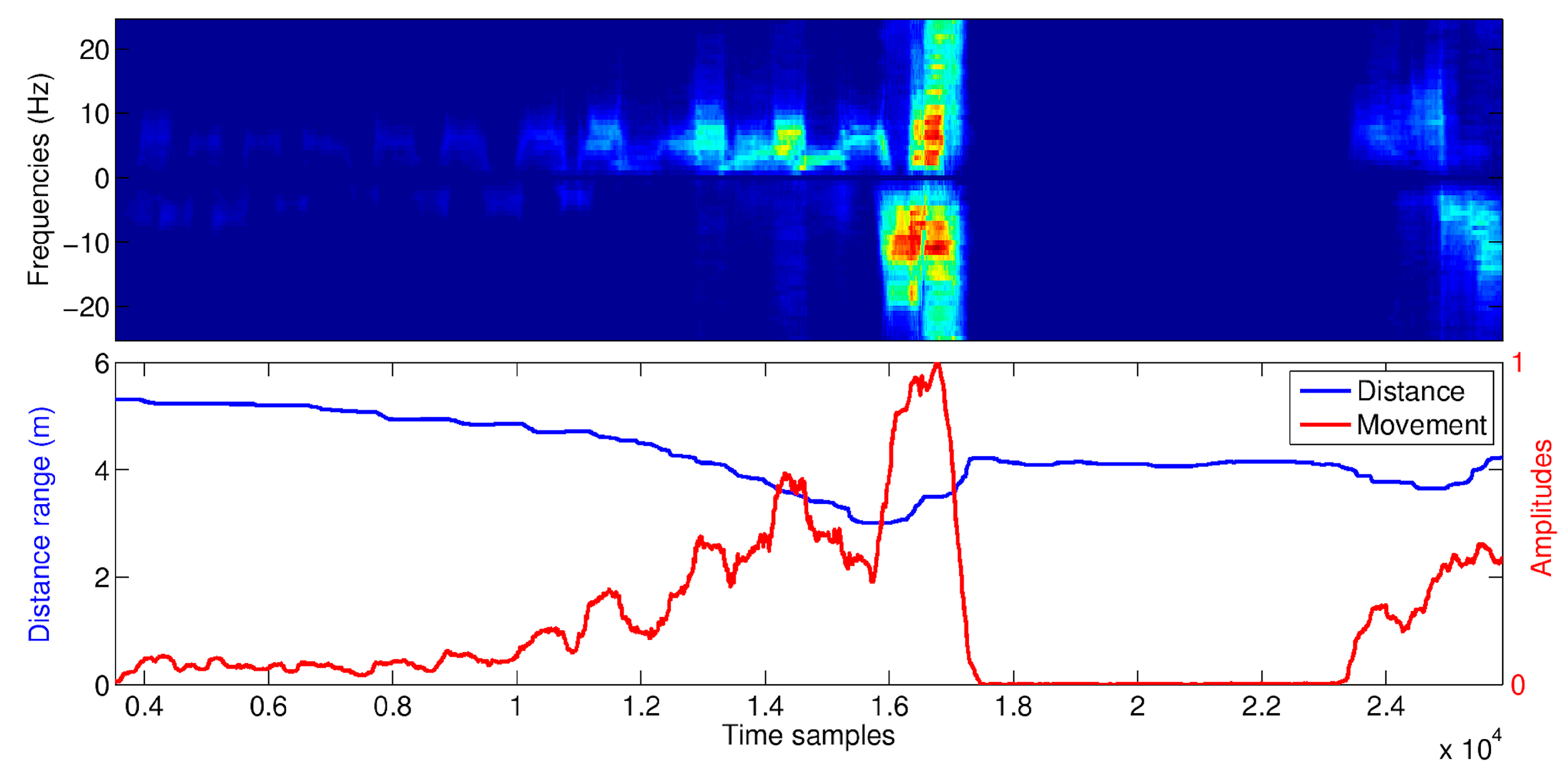
3.3. Body Movements
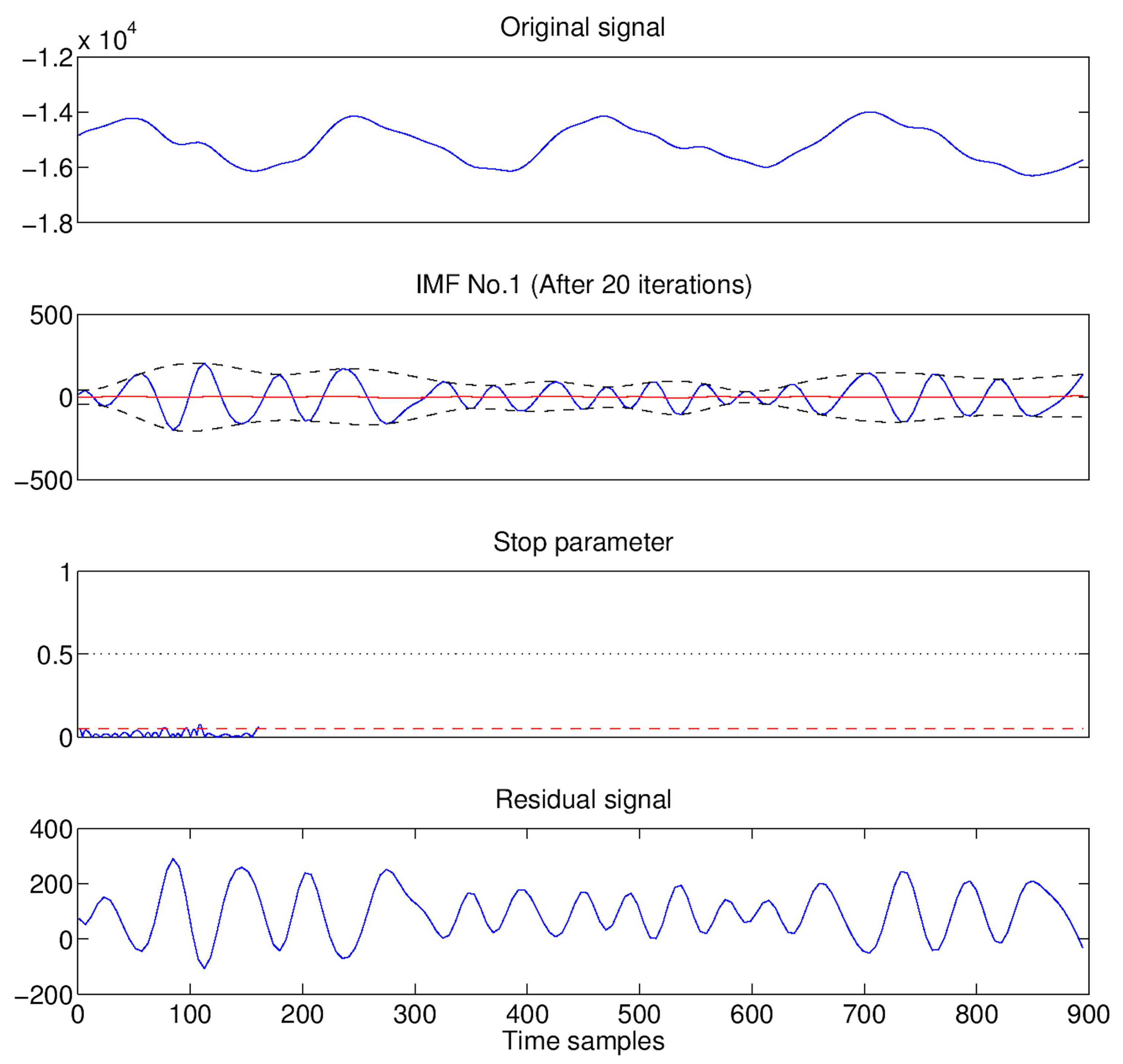
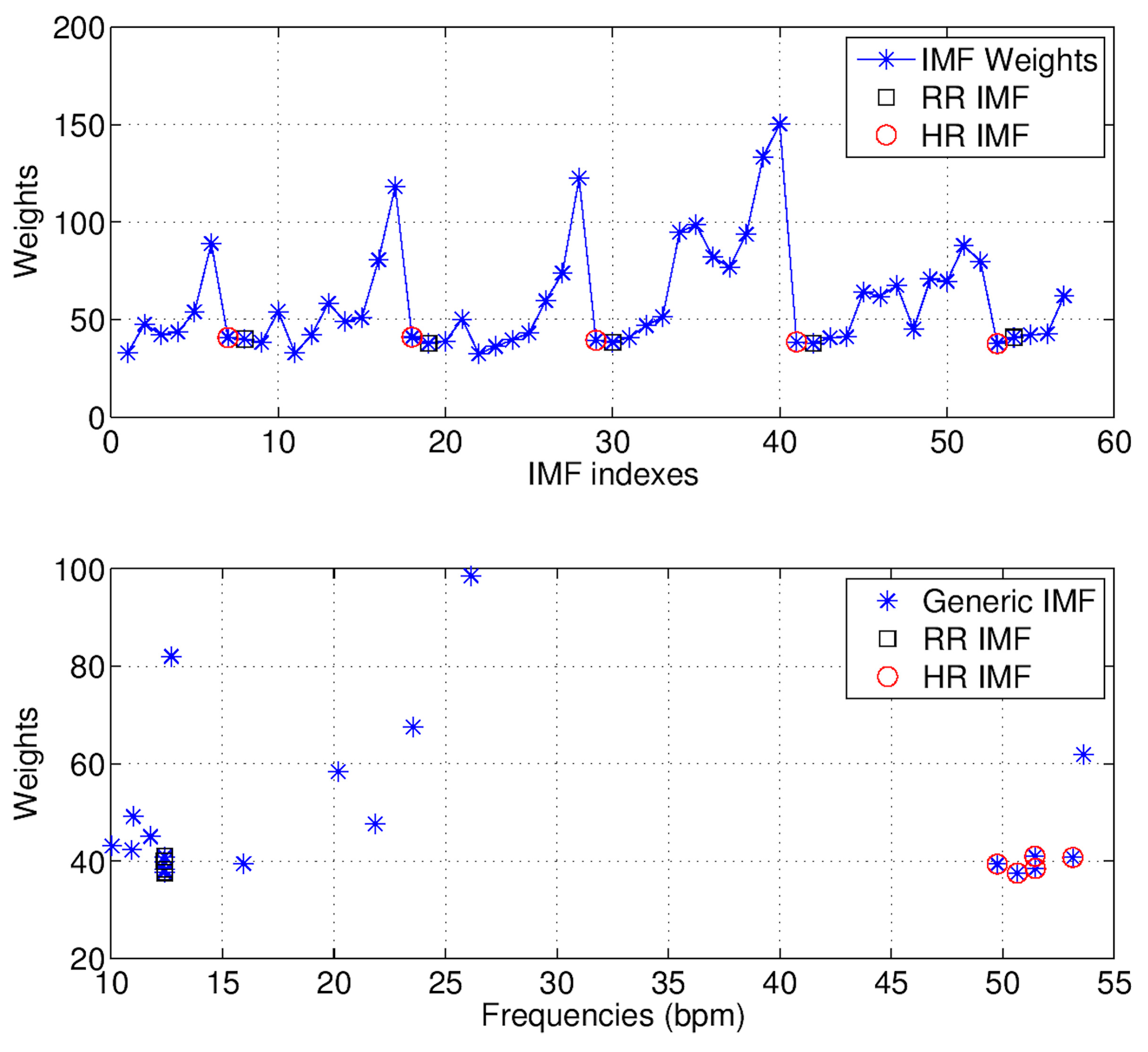
3.4. Vital Signs
- (1)
- The upper and lower envelopes of are estimated, by interpolating with cubic splines the local maxima (upper envelope) and local minima (lower envelope) of .
- (2)
- The mean of the two envelopes is calculated:
- (3)
- The local high-frequency signal is obtained as .
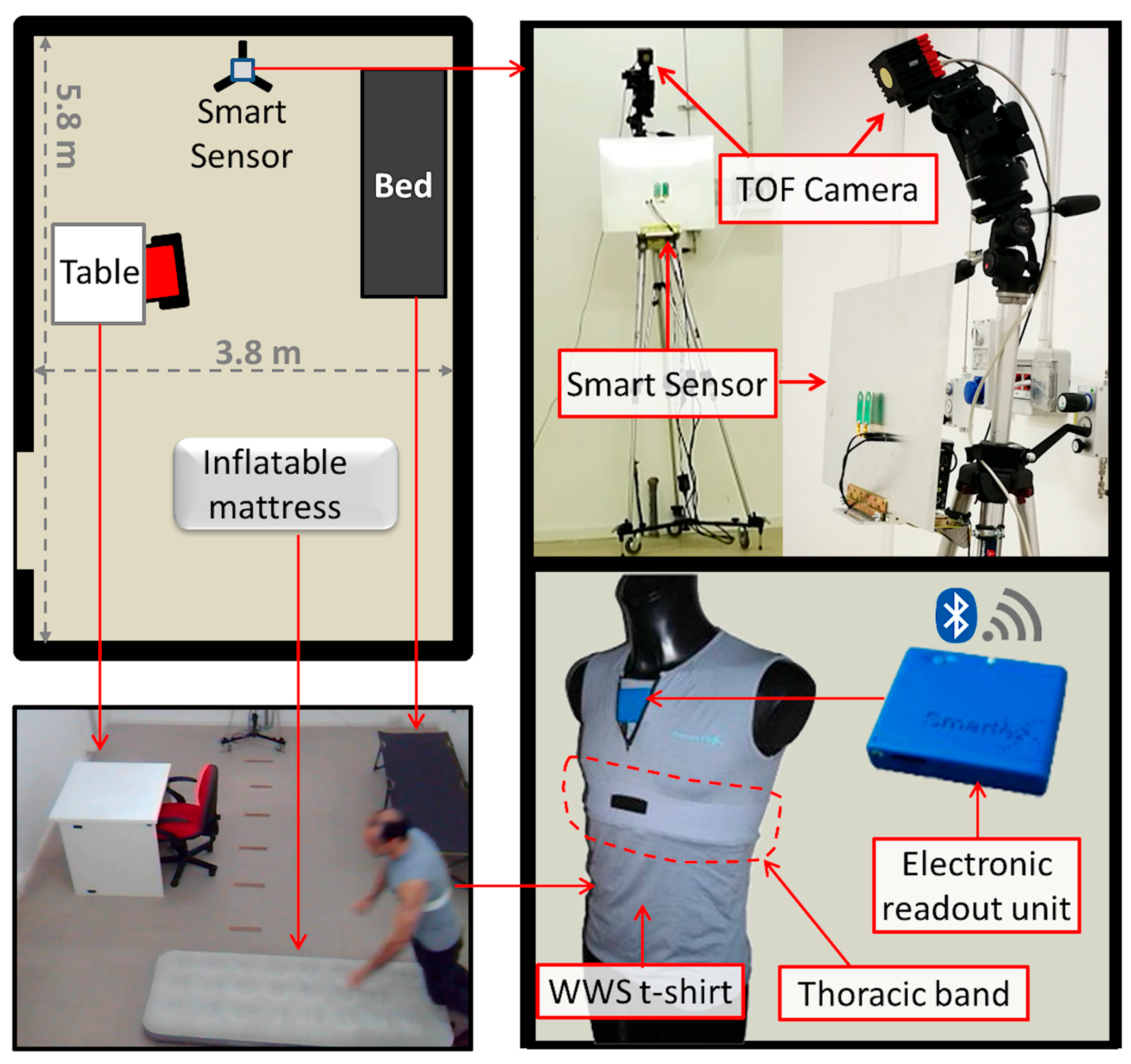
3.5. Experimental Setup
3.6. Validation
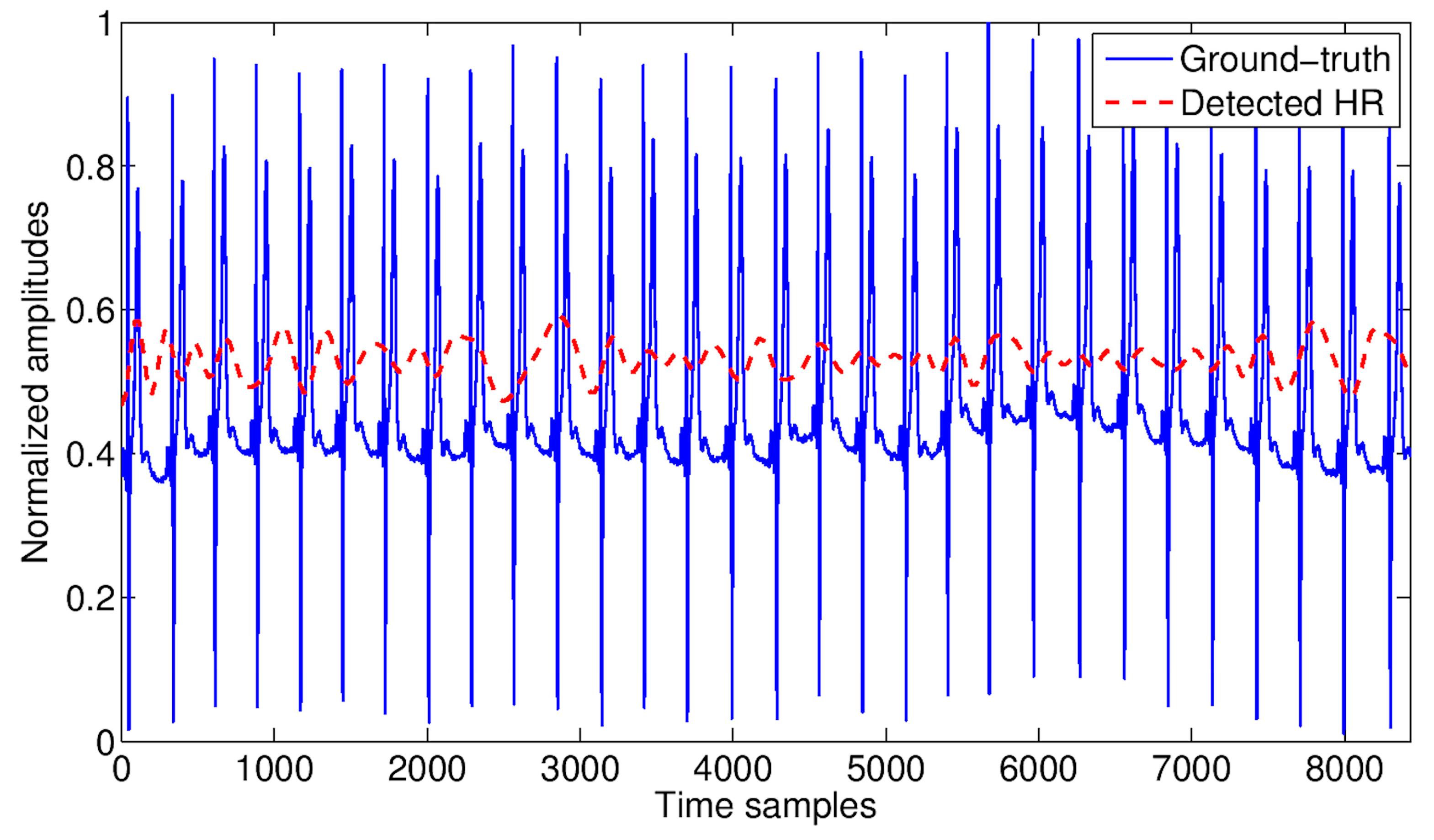
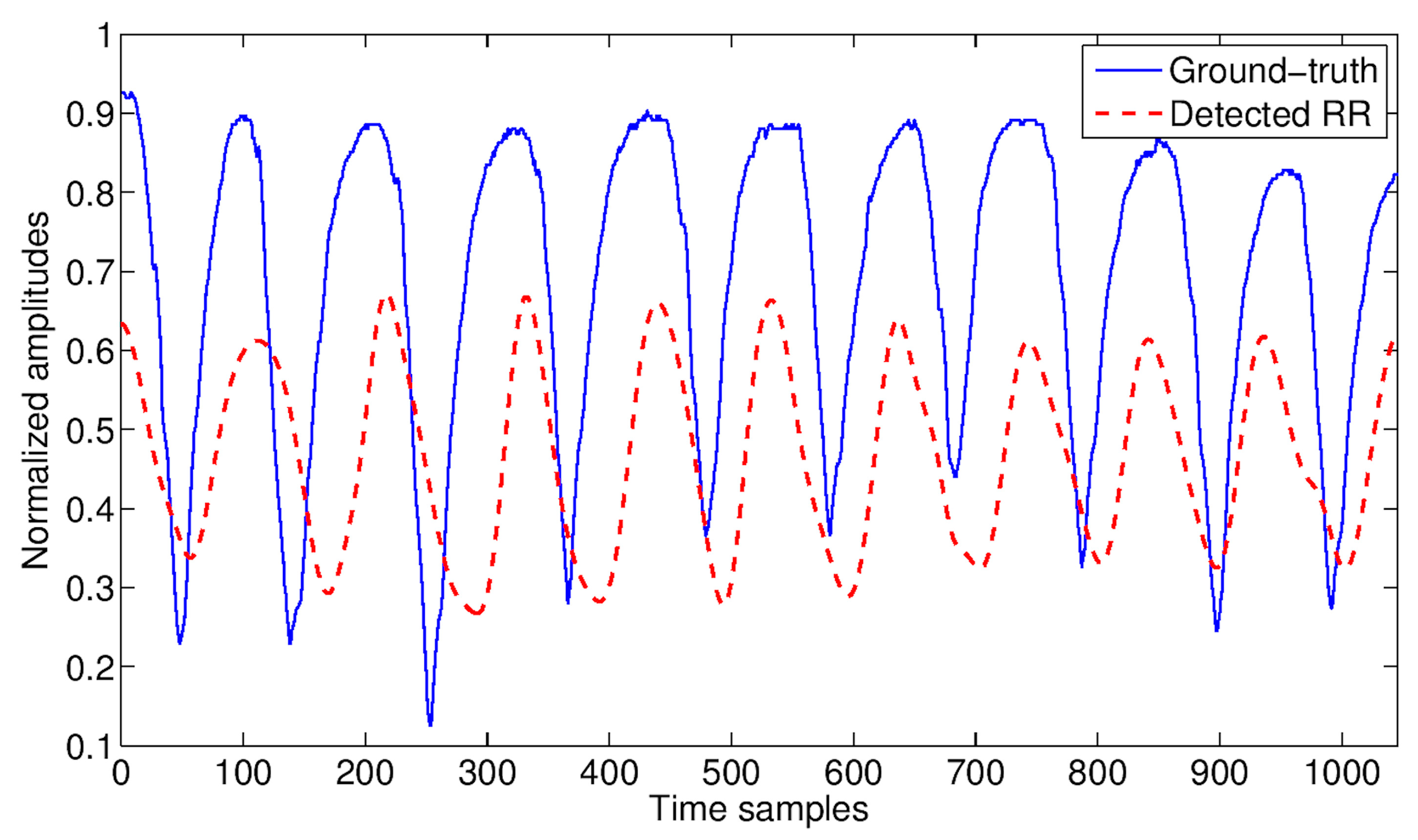
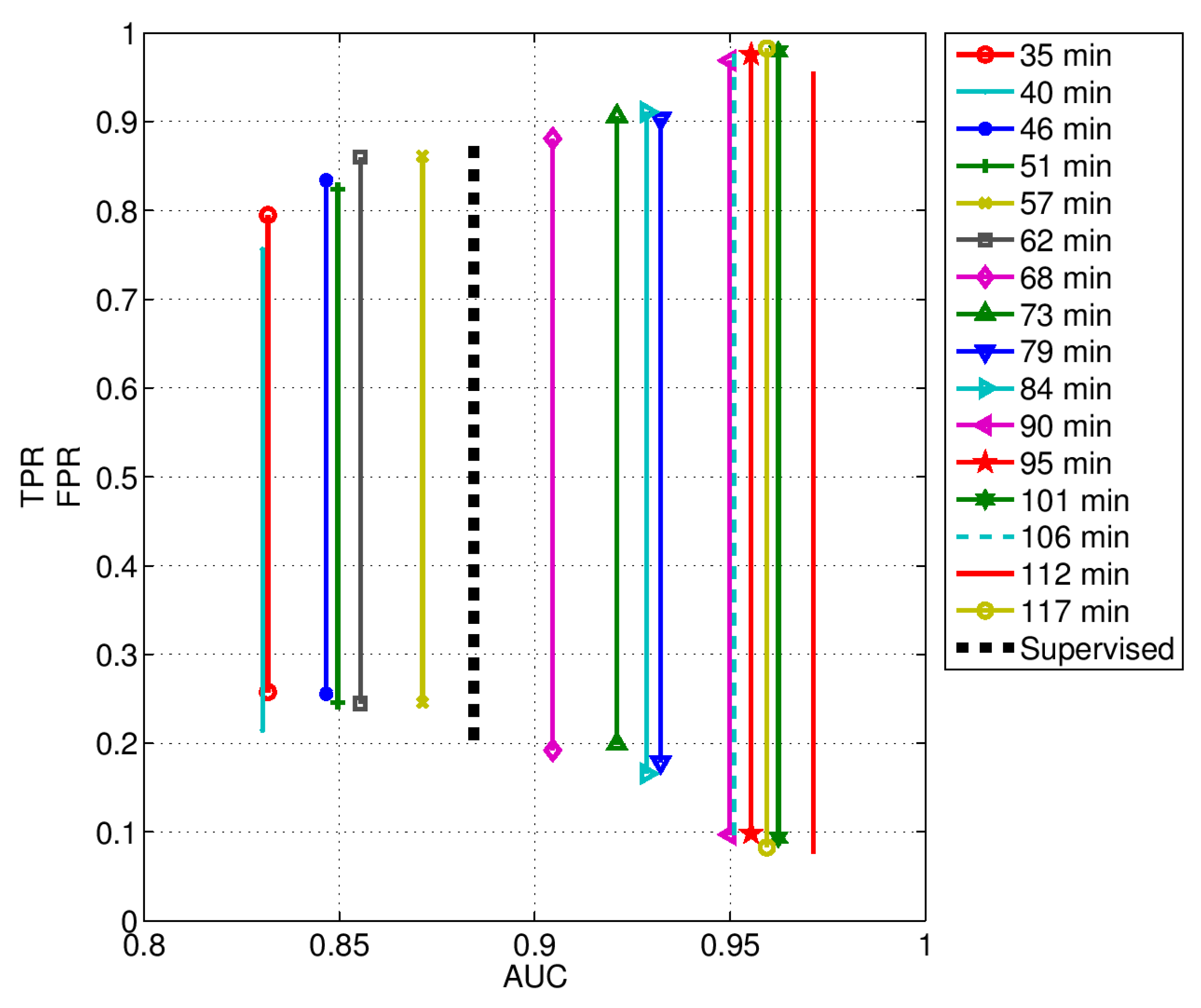
4. Results
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- United Nations, Department of Economic and Social Affairs, Population Division. World Population Prospects: The 2015 Revision, Volume II: Demographic Profiles. ST/ESA/SER.A/380. Available online: https://esa.un.org/unpd/wpp/Publications/Files/WPP2015_Volume-II-Demographic-Profiles.pdf (accessed on 29 October 2016).
- Rantz, M.J.; Skubic, M.; Miller, S.J. Using sensor technology to augment traditional healthcare. In Proceedings of the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society: Engineering the Future of Biomedicine, Minneapolis, MN, USA, 3–6 September 2009; pp. 6159–6162. [Google Scholar]
- World Health Organization, Media Centre. Falls—Fact Sheet. Reviewed September 2016. Available online: http://www.who.int/mediacentre/factsheets/fs344/en/ (accessed on 29 October 2016).
- Centers for Disease Control and Prevention. Injury Prevention & Control: Data & Statistics 2014. Available online: http://www.cdc.gov/injury/wisqars/ (accessed on 29 October 2016).
- Hossain, M.A.; Ahmed, D.T. Virtual caregiver: An ambient-aware elderly monitoring system. IEEE Trans. Inf. Technol. Biomed. 2012, 16, 1024–1031. [Google Scholar] [CrossRef] [PubMed]
- Pradeep Kumar, S.; Akash, D.; Murali, K.; Shriram, R. Call ambulance smart elderly monitoring system with nearest ambulance detection using Android and Bluetooth. In Proceedings of the 2nd International Conference on Science Technology Engineering and Management (ICONSTEM), Chennai, India, 30–31 March 2016; pp. 89–92. [Google Scholar]
- Lusardi, M.M.; Fritz, S.; Middleton, A.; Allison, L.; Wingood, M.; Phillips, E.; Criss, M.; Verma, S.; Osborne, J.; Chui, K. Determining Risk of falls in community dwelling older adults: A systematic review and meta-analysis using posttest probability. J. Geriatr. Phys. Ther. 2017, 40, 1–36. [Google Scholar] [CrossRef] [PubMed]
- Lord, S.; Sherrington, C.; Menz, H.; Close, J. Falls in Older People: Risk Factors and Strategies for Prevention, 2nd ed.; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Bergland, A.; Laake, K. Concurrent and predictive validity of “getting up from lying on the floor”. Aging Clin. Exp. Res. 2013, 17, 181–185. [Google Scholar] [CrossRef]
- Bloch, F. Critical falls: Why remaining on the ground after a fall can be dangerous, whatever the fall. J. Am. Geriatr. Soc. 2012, 60, 1375–1376. [Google Scholar] [CrossRef] [PubMed]
- Noury, N.; Fleury, A.; Rumeau, P.; Bourke, A.; Laighin, G.; Rialle, V.; Lundy, J.E. Fall detection-Principles and methods. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBS), Lyon, France, 22–26 August 2007; pp. 1663–1666. [Google Scholar]
- Janssens, J.P.; Pautex, S.; Hilleret, H.; Michel, J.P. Sleep disordered breathing in the elderly. Aging Clin. Exp. Res. 2000, 12, 417–429. [Google Scholar] [CrossRef]
- Casolo, G.; Balli, E.; Taddei, T.; Amuhasi, J.; Gori, C. Decreased spontaneous heart rate variability in congestive heart failure. Am. J. Cardiol. 1989, 64, 1162–1167. [Google Scholar] [CrossRef]
- Sajadieh, A.; Nielsen, O.W.; Rasmussen, V.; Hein, H.O.; Abedini, S.; Hansen, J.F. Increased heart rate and reduced heart-rate variability are associated with subclinical inflammation in middle-aged and elderly subjects with no apparent heart disease. Eur. Heart J. 2004, 25, 363–370. [Google Scholar] [CrossRef] [PubMed]
- Kooy, K.G.; Hout, H.P.J.; Marwijk, H.W.J.; Haan, M.; Stehouwer, C.D.A.; Beekman, A.T.F. Differences in heart rate variability between depressed and non-depressed elderly. Int. J. Geriatr. Psychiatry 2006, 21, 147–150. [Google Scholar] [CrossRef] [PubMed]
- Alonso, A.; Huang, X.; Mosley, T.H.; Heiss, G.; Chen, H. Heart rate variability and the risk of parkinson disease: The atherosclerosis risk in communities study. Ann. Neurol. 2015, 77, 877–883. [Google Scholar] [CrossRef] [PubMed]
- Ferini-Strambi, L.; Franceschi, M.; Pinto, P.; Zucconi, M.; Smirne, S. Respiration and heart rate variability during sleep in untreated Parkinson patients. Gerontology 1992, 38, 92–98. [Google Scholar] [CrossRef] [PubMed]
- Baig, M.M.; Gholamhosseini, H.; Connolly, M.J. Falls risk assessment for hospitalised older adults: A combination of motion data and vital signs. Aging Clin. Exp. Res. 2016, 28, 1159–1168. [Google Scholar] [CrossRef] [PubMed]
- Wild, K.; Boise, L.; Lundell, J.; Foucek, A. Unobtrusive in-home monitoring of cognitive and physical health: Reactions and perceptions of older adults. J. Appl. Gerontol. 2008, 27, 181–200. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, C.; Han, J. Time-Domain Ultra-Wideband Radar, Sensor and Components: Theory, Analysis and Design; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Federal Communications Commission (FCC). Document 00-163. Revision of Part 15 of the Commission’s Rules Regarding Ultra-Wideband Transmission Systems. No. 98–153; FCC: Washington, DC, USA, 2002. [Google Scholar]
- Khan, S.S.; Hoey, J. Review of fall detection techniques: A data availability perspective. Med. Eng. Phys. 2017, 39, 12–22. [Google Scholar] [CrossRef] [PubMed]
- Debes, C.; Merentitis, A.; Sukhanov, S.; Niessen, M.; Frangiadakis, N.; Bauer, A. Monitoring activities of daily living in smart homes: Understanding human behavior. IEEE Signal Process. Mag. 2016, 33, 81–94. [Google Scholar] [CrossRef]
- Igual, R.; Medrano, C.; Plaza, I. Challenges, issues and trends in fall detection systems. Biomed. Eng. Online 2013, 12. [Google Scholar] [CrossRef] [PubMed]
- Spasova, V.; Iliev, I. A survey on automatic fall Detection in the context of ambient assisted living systems. Int. J. Adv. Comput. Res. 2014, 4, 94–109. [Google Scholar]
- Malik, M. Heart rate variability: Standards of measurement, physiological interpretation, and clinical use. Circulation 1996, 93, 1043–1065. [Google Scholar] [CrossRef]
- Hafner, N.; Lubecke, V. Performance assessment techniques for Doppler radar physiological sensors. In Proceedings of the 31st Annual International Conference of the IEEE Engineering in Medicine and Biology Society: Engineering the Future of Biomedicine, Minneapolis, MN, USA, 3–6 September 2009; pp. 4848–4851. [Google Scholar]
- El-Amrawy, F.; Nounou, M.I. Are currently available wearable devices for activity tracking and heart rate monitoring accurate, precise, and medically beneficial? Healthc. Inform. Res. 2015, 21, 315–320. [Google Scholar] [CrossRef] [PubMed]
- Khan, Y.; Ostfeld, A.E.; Lochner, C.M.; Pierre, A.; Arias, A.C. Monitoring of vital signs with flexible and wearable medical devices. Adv. Mater. 2016, 28, 4373–4395. [Google Scholar] [CrossRef] [PubMed]
- Rashidi, P.; Mihailidis, A. A survey on ambient-assisted living tools for older adults. IEEE J. Biomed. Health Inform. 2013, 17, 579–590. [Google Scholar] [CrossRef] [PubMed]
- Min, C.; Kang, S.; Yoo, C.; Cha, J.; Choi, S.; Oh, Y.; Song, J. Exploring current practices for battery use and management of smartwatches. In Proceedings of the 2015 ACM International Symposium on Wearable Computers, Osaka, Japan, 7–11 September 2015; pp. 11–18. [Google Scholar]
- Rawassizadeh, R.; Momeni, E.; Dobbins, C.; Gharibshah, J.; Pazzani, M. Scalable daily human behavioral pattern mining from multivariate temporal data. IEEE Trans. Knowl. Data Eng. 2016, 28, 3098–3112. [Google Scholar] [CrossRef]
- Rawassizadeh, R.; Tomitsch, M.; Nourizadeh, M.; Momeni, E.; Peery, A.; Ulanova, L.; Pazzani, M. Energy-efficient integration of continuous context sensing and prediction into smartwatches. Sensors 2015, 15, 22616–22645. [Google Scholar] [CrossRef] [PubMed]
- Feng, G.; Mai, J.; Ban, Z.; Guo, X.; Wang, G. Floor pressure imaging for fall detection with fiber-optic sensors. IEEE Pervasive Comput. 2016, 15, 40–47. [Google Scholar] [CrossRef]
- Droghini, D.; Ferretti, D.; Principi, E.; Squartini, S.; Piazza, F. A combined one-class SVM and template-matching approach for user-aided human fall detection by means of floor acoustic features. Comput. Intell. Neurosci. 2017. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Ho, K.C.; Popescu, M. A microphone array system for automatic fall detection. IEEE Trans. Biomed. Eng. 2012, 59, 1291–1301. [Google Scholar] [PubMed]
- Rougier, C.; Meunier, J.; St-Arnaud, A.; Rousseau, J. Robust video surveillance for fall detection based on human shape deformation. IEEE Trans. Circuits Syst. Video Technol. 2011, 21, 611–622. [Google Scholar] [CrossRef]
- Kim, H.H.; Ha, K.N.; Lee, S.; Lee, K.C. Resident location-recognition algorithm using a Bayesian classifier in the PIR sensor-based indoor location-aware system. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2009, 39, 240–245. [Google Scholar]
- Popescu, M.; Hotrabhavananda, B.; Moore, M.; Skubic, M. VAMPIR—An automatic fall detection system using a vertical PIR sensor array. In Proceedings of the 6th International Conference on Pervasive Computing Technologies for Healthcare and Workshops (PervasiveHealth), San Diego, CA, USA, 21–24 May 2012; pp. 163–166. [Google Scholar]
- Lymberopoulos, D.; Bamis, A.; Savvides, A. Extracting spatiotemporal human activity patterns in assisted living using a home sensor network. Univers. Access Inf. Soc. 2011, 10, 125–138. [Google Scholar] [CrossRef]
- Dura-Bernal, S.; Garreau, G.; Georgiou, J.; Andreou, A.G.; Denham, S.L.; Wennekers, T. Multimodal integration of micro-doppler sonar and auditory signals for behavior classification with convolutional networks. Int. J. Neural Syst. 2013, 23. [Google Scholar] [CrossRef] [PubMed]
- Leone, A.; Diraco, G.; Siciliano, P. Detecting falls with 3D range camera in ambient assisted living applications: A preliminary study. Med. Eng. Phys. 2011, 33, 770–781. [Google Scholar] [CrossRef] [PubMed]
- Iarlori, S.; Ferracuti, F.; Giantomassi, A.; Longhi, S. RGB-D video monitoring system to assess the dementia disease state based on recurrent neural networks with parametric bias action recognition and DAFS index evaluation. In Proceedings of the Lecture Notes in Computer Science (LNCS-2), Paris, France, 9–11 July 2014; pp. 156–163. [Google Scholar]
- Amin, M.G.; Zhang, Y.D.; Ahmad, F.; Ho, K.D. Radar signal processing for elderly fall detection: The future for in-home monitoring. IEEE Signal Process. Mag. 2016, 33, 71–80. [Google Scholar] [CrossRef]
- Balaji, B.; Xu, J.; Nwokafor, A.; Gupta, R.; Agarwal, Y. Sentinel: Occupancy based HVAC actuation using existing WiFi infrastructure within commercial buildings. In Proceedings of the 11th ACM Conference on Embedded Networked Sensor Systems, Roma, Italy, 11–15 November 2013; p. 17. [Google Scholar]
- Laput, G.; Zhang, Y.; Harrison, C. Synthetic sensors: Towards general-purpose sensing. In Proceedings of the 2017 CHI Conference on Human Factors in Computing Systems, Denver, CO, USA, 6–11 May 2017; pp. 3986–3999. [Google Scholar]
- Droitcour, A.D.; Boric-Lubecke, O.; Lubecke, V.M.; Lin, J.; Kovacs, G.T.A. Range correlation and I/Q performance benefits in single-chip silicon Doppler radars for noncontact cardiopulmonary monitoring. IEEE Trans. Microw. Theory Tech. 2004, 52, 838–848. [Google Scholar] [CrossRef]
- Kolakowski, J.; Djaja-Josko, V.; Kolakowski, M. UWB monitoring system for AAL applications. Sensors 2017, 17. [Google Scholar] [CrossRef] [PubMed]
- Blumrosen, G.; Uziel, M.; Rubinsky, B.; Porrat, D. Non-contact UWB radar technology to assess tremor. In Proceedings of the XII Mediterranean Conference on Medical and Biological Engineering and Computing 2010, Chalkidiki, Greece, 27–30 May 2010; Volume 29, pp. 490–493. [Google Scholar]
- Rui, L.; Chen, S.; Ho, K.C.; Rantz, M.; Skubic, M. Estimation of human walking speed by Doppler radar for elderly care. J. Ambient Intell. Smart Environ. 2017, 9, 181–191. [Google Scholar] [CrossRef]
- Wang, F.; Skubic, M.; Rantz, M.; Cuddihy, P.E. Quantitative gait measurement with pulse-doppler radar for passive in-home gait assessment. IEEE Trans. Biomed. Eng. 2014, 61, 2434–2443. [Google Scholar] [CrossRef] [PubMed]
- Rahman, T.; Adams, A.T.; Ravichandran, R.V.; Zhang, M.; Patel, S.N.; Kientz, J.A.; Choudhury, T. Dopplesleep: A contactless unobtrusive sleep sensing system using short-range doppler radar. In Proceedings of the ACM International Joint Conference on Pervasive and Ubiquitous Computing, Osaka, Japan, 7–11 September 2015; pp. 39–50. [Google Scholar]
- Choi, J.W.; Yim, D.H.; Cho, S.H. People counting based on an IR-UWB radar sensor. IEEE Sens. J. 2017, 17, 5717–5727. [Google Scholar] [CrossRef]
- Su, B.Y.; Ho, K.C.; Rantz, M.J.; Skubic, M. Doppler radar fall activity detection using the wavelet transform. IEEE Trans. Biomed. Eng. 2015, 62, 865–875. [Google Scholar] [CrossRef] [PubMed]
- Wu, Q.; Zhang, Y.D.; Tao, W.; Amin, M.G. Radar-based fall detection based on doppler time-frequency signatures for assisted living. IET Radar Sonar Navig. 2015, 9, 164–172. [Google Scholar] [CrossRef]
- Jokanovic, B.; Amin, M.; Ahmad, F. Radar fall motion detection using deep learning. In Proceedings of the IEEE Radar Conference (RadarConf), Philadelphia, PA, USA, 2–6 May 2016; pp. 1–16. [Google Scholar]
- Erol, B.; Amin, M.G.; Boashash, B. Range-Doppler radar sensor fusion for fall detection. In Proceedings of the IEEE Radar Conference (RadarConf), Seattle, WA, USA, 8–12 May 2017; pp. 0819–0824. [Google Scholar]
- Caro, C.G.; Bloice, J.A. Contactless apnoea detector based on radar. Lancet 1971, 298, 959–961. [Google Scholar] [CrossRef]
- Franks, C.I.; Brown, B.H.; Johnston, D.M. Contactless respiration monitoring of infants. Med. Biol. Eng. 1976, 14, 306–312. [Google Scholar] [CrossRef] [PubMed]
- Lin, J.C. Noninvasive microwave measurement of respiration. Proc. IEEE 1975, 63, 1530. [Google Scholar] [CrossRef]
- Lin, J.C.; Kiernicki, J.; Kiernicki, M.; Wollschlaeger, P.B. Microwave apexcardiography. IEEE Trans. Microw. Theory Tech. 1979, 27, 618–620. [Google Scholar] [CrossRef]
- Lin, J.C. Microwave sensing of physiological movement and volume change: A review. Bioelectromagnetics 1992, 13, 557–565. [Google Scholar] [CrossRef] [PubMed]
- Greneker, E.F. Radar sensing of heartbeat and respiration at a distance with security applications. In Proceedings of the International Society for Optical Engineering (SPIE), Orlando, FL, USA, 21–25 April 1997; Volume 3066, pp. 22–27. [Google Scholar]
- Kim, K.-B.; Suh, J.-S.; Shin, D.-H.; Park, S.-O. High sensitivity doppler radar system for detecting respiration and heart rate using improved isolation technique. In Proceedings of the 31th URSI General Assembly and Scientific Symposium (GASS), Beijing, China, 16–23 August 2014. [Google Scholar]
- Petkie, D.T.; Benton, C.; Bryan, E. Millimeter-wave radar for vital signs sensing. In Proceedings of the International Society for Optical Engineering (SPIE), Orlando, FL, USA, 13–17 April 2009; Volume 7308. [Google Scholar]
- Vinci, G.; Lindner, S.; Barbon, F.; Hofmann, M.; Fischer, G.; Kissinger, D.; Koelpin, A. 24 GHz six-port medical radar for contactless respiration detection and heartbeat monitoring. In Proceedings of the 9th European Radar Conference (EuRAD), Amsterdam, The Netherlands, 31 October–2 November 2012; pp. 75–78. [Google Scholar]
- Li, C.; Lubecke, V.M.; Boric-Lubecke, O.; Lin, J. A review on recent advances in doppler radar sensors for noncontact healthcare monitoring. IEEE Trans. Microw. Theory Tech. 2013, 61, 2046–2060. [Google Scholar] [CrossRef]
- Schleicher, B.; Nasr, I.; Trasser, A.; Schumacher, H. IR-UWB radar demonstrator for ultra-fine movement detection and vital-sign monitoring. IEEE Trans. Microw. Theory Tech. 2013, 61, 2076–2085. [Google Scholar] [CrossRef]
- Li, C.; Lin, J. Random body movement cancellation in doppler radar vital sign detection. IEEE Trans. Microw. Theory Tech. 2008, 56, 3143–3152. [Google Scholar]
- Hu, X.; Jin, T. Short-range vital signs sensing based on EEMD and CWT using IR-UWB radar. Sensors 2016, 16. [Google Scholar] [CrossRef] [PubMed]
- Kumar, M.; Veeraraghavan, A.; Sabharwal, A. DistancePPG: Robust noncontact vital signs monitoring using a camera. Biomed. Opt. Express 2015, 6, 1565–1588. [Google Scholar] [CrossRef] [PubMed]
- Kranjec, J.; Beguš, S.; Geršak, G.; Drnovšek, J. Non-contact heart rate and heart rate variability measurements: A review. Biomed. Signal Process. Control 2014, 13, 102–112. [Google Scholar] [CrossRef]
- TIME DOMAIN. Pulson®p410 Radar Kit (27 May 2015). Available online: http://www.timedomain.com/ (accessed on 14 July 2016).
- The MathWorks. (November 2017) Signal Processing Toolbox User’s Guide. Available online: http://www.mathworks.com/access/helpdesk/help/toolbox/signal/ (accessed on 18 November 2017).
- Moulton, J.; Kassam, S.; Ahmad, F.; Amin, M.; Yemelyanov, K. Target and change detection in synthetic aperture radar sensing of urban structures. In Proceedings of the IEEE Radar Conference (RADAR), Rome, Italy, 26–30 May 2008; pp. 1–6. [Google Scholar]
- Yoon, Y.S.; Amin, M.G. Spatial filtering for wall-clutter mitigation in through-the-wall radar imaging. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3192–3208. [Google Scholar] [CrossRef]
- Dehmollaian, M.; Sarabandi, K. Refocusing through building walls using synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 2008, 46, 1589–1599. [Google Scholar] [CrossRef]
- Verma, P.K.; Gaikwad, A.N.; Singh, D.; Nigam, M.J. Analysis of clutter reduction techniques for through wall imaging in UWB range. Prog. Electromagn. Res. B 2009, 17, 29–48. [Google Scholar] [CrossRef]
- Vicen-Bueno, R.; Carrasco-lvarez, R.; Rosa-Zurera, M.; Nieto-Borge, J.C. Sea clutter reduction and target enhancement by neural networks in a marine radar system. Sensors 2009, 9, 1913–1936. [Google Scholar] [CrossRef] [PubMed]
- Mohsin Riaz, M.; Ghafoor, A. Through-wall image enhancement based on singular value decomposition. Int. J. Antennas Propag. 2012, 2012. [Google Scholar] [CrossRef]
- Li, J.; Liu, L.; Zeng, Z.; Liu, F. Advanced signal processing for vital sign extraction with applications in UWB radar detection of trapped victims in complex environments. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 783–791. [Google Scholar]
- Chen, V.C.; Li, F.; Ho, S.S.; Wechsler, H. Micro-Doppler effect in radar: Phenomenon, model, and simulation study. IEEE Trans. Aerosp. Electr. Syst. 2006, 42, 2–21. [Google Scholar] [CrossRef]
- Marple, S.L. Computing the discrete-time analytic signal via FFT. IEEE Trans. Signal Process. 1999, 47, 2600–2603. [Google Scholar] [CrossRef]
- Singh, M.; Ramachandran, G. Reconstruction of sequential cardiac in-plane displacement patterns on the chest wall by laser speckle interferometry. IEEE Trans. Biomed. Eng. 1991, 38, 483–489. [Google Scholar] [CrossRef] [PubMed]
- Tan, H.; Qiao, D.; Li, Y. Non-contact heart rate tracking using Doppler radar. In Proceedings of the IEEE International Conference on Systems and Informatics (ICSAI), Yantai, China, 19–20 May 2012; pp. 1711–1714. [Google Scholar]
- Portnoff, M.R. Time-frequency representation of digital signals and systems based on short-time Fourier analysis. IEEE Trans. Acoust. Speech Signal Process. 1980, 28, 55–69. [Google Scholar] [CrossRef]
- Lilly, J.M.; Olhede, S.C. On the analytic wavelet transform. IEEE Trans. Inf. Theory 2010, 56, 4135–4156. [Google Scholar] [CrossRef]
- Mann, S.; Haykin, S. The chirplet transform: Physical considerations. IEEE Trans. Signal Process. 1995, 43, 2745–2761. [Google Scholar] [CrossRef]
- Mandic, D.P.; ur Rehman, N.; Wu, Z.; Huang, N.E. Empirical mode decomposition-based time-frequency analysis of multivariate signals: The power of adaptive data analysis. IEEE Signal Process. Mag. 2013, 30, 74–86. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Hu, W.; Zhao, Z.; Wang, Y.; Zhang, H.; Lin, F. Noncontact accurate measurement of cardiopulmonary activity using a compact quadrature doppler radar sensor. IEEE Trans. Biomed. Eng. 2014, 61, 725–735. [Google Scholar] [CrossRef] [PubMed]
- Mostafanezhad, I.; Boric-Lubecke, O.; Lubecke, V.; Mandic, D.P. Application of empirical mode decomposition in removing fidgeting interference in doppler radar life signs monitoring devices. In Proceedings of the 31st IEEE Engineering in Medicine and Biology Society (EMBC), Minneapolis, MN, USA, 3–6 September 2009; pp. 340–343. [Google Scholar]
- Wang, H.; Narayanan, R.M.; Zhou, Z.-O.; Li, T.-J.; Kong, L.-J. Micro-Doppler character analysis of moving objects using through-wall radar based on improved EEMD. J. Electron. Inf. Technol. 2010, 32, 1355–1360. [Google Scholar]
- Mostafanezhad, I.; Yavari, E.; Boric-Lubecke, O.; Lubecke, V.M.; Mandic, D.P. Cancellation of unwanted doppler radar sensor motion using empirical mode decomposition. IEEE Sens. J. 2013, 13, 1897–1904. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R. A new view of nonlinear water waves: The Hilbert spectrum. Annu. Rev. Fluid Mech. 1999, 31, 417–457. [Google Scholar] [CrossRef]
- Komaty, A.; Boudraa, A.O.; Augier, B.; Dare-Emzivat, D. EMD-based filtering using similarity measure between probability density functions of IMFs. IEEE Trans. Instrum. Meas. 2014, 63, 27–34. [Google Scholar] [CrossRef]
- Axiomtek. eBOX530-820-FL Fanless Embedded System Datasheet. Available online: http://www.axiomtek.it (accessed on 15 February 2015).
- Noury, N.; Rumeau, P.; Bourke, A.; OLaighin, G.; Lundy, J. A proposal for the classification and evaluation of fall detectors. IRBM 2008, 29, 340–349. [Google Scholar] [CrossRef]
- Vlaeyen, E.; Deschodt, M.; Debard, G.; Dejaeger, E.; Boonen, S.; Goedemé, T.; Vanrumste, B.; Milisen, K. Fall incidents unraveled: A series of 26 video-based real-life fall events in three frail older persons. BMC Geriatr. 2013, 13. [Google Scholar] [CrossRef] [PubMed]
- Robinovitch, S.N.; Feldman, F.; Yang, Y.; Schonnop, R.; Leung, P.M.; Sarraf, T.; Sims-Gould, J.; Loughin, M. Video capture of the circumstances of falls in elderly people residing in long-term care: An observational study. Lancet 2013, 381, 47–54. [Google Scholar] [CrossRef]
- HEPTAGON. Available online: http://hptg.com/industrial (accessed on 28 September 2017).
- Diraco, G.; Leone, A.; Siciliano, P. People occupancy detection and profiling with 3D depth sensors for building energy management. Energy Build. 2015, 92, 246–266. [Google Scholar] [CrossRef]
- Diraco, G.; Leone, A.; Siciliano, P. In-home hierarchical posture classification with a time-of-flight 3D sensor. Gait Posture 2014, 39, 182–187. [Google Scholar] [CrossRef] [PubMed]
- Diraco, G.; Leone, A.; Siciliano, P. Geodesic-based human posture analysis by using a single 3D TOF camera. In Proceedings of the IEEE International Symposium on Industrial Electronics (ISIE), Gdansk, Poland, 27–30 June 2011. [Google Scholar]
- SMARTEX. Wearable Wellness System. Available online: http://www.smartex.it/en/our-products/232-wearable-wellness-systemwws/ (accessed on 1 March 2017).
- Yu, M.; Yu, Y.; Rhuma, A.; Naqvi, S.M.R.; Wang, L.; Chambers, J.A. An online one class support vector machine-based person-specific fall detection system for monitoring an elderly individual in a room environment. IEEE J. Biomed. Health Inform. 2013, 17, 1002–1014. [Google Scholar] [PubMed]
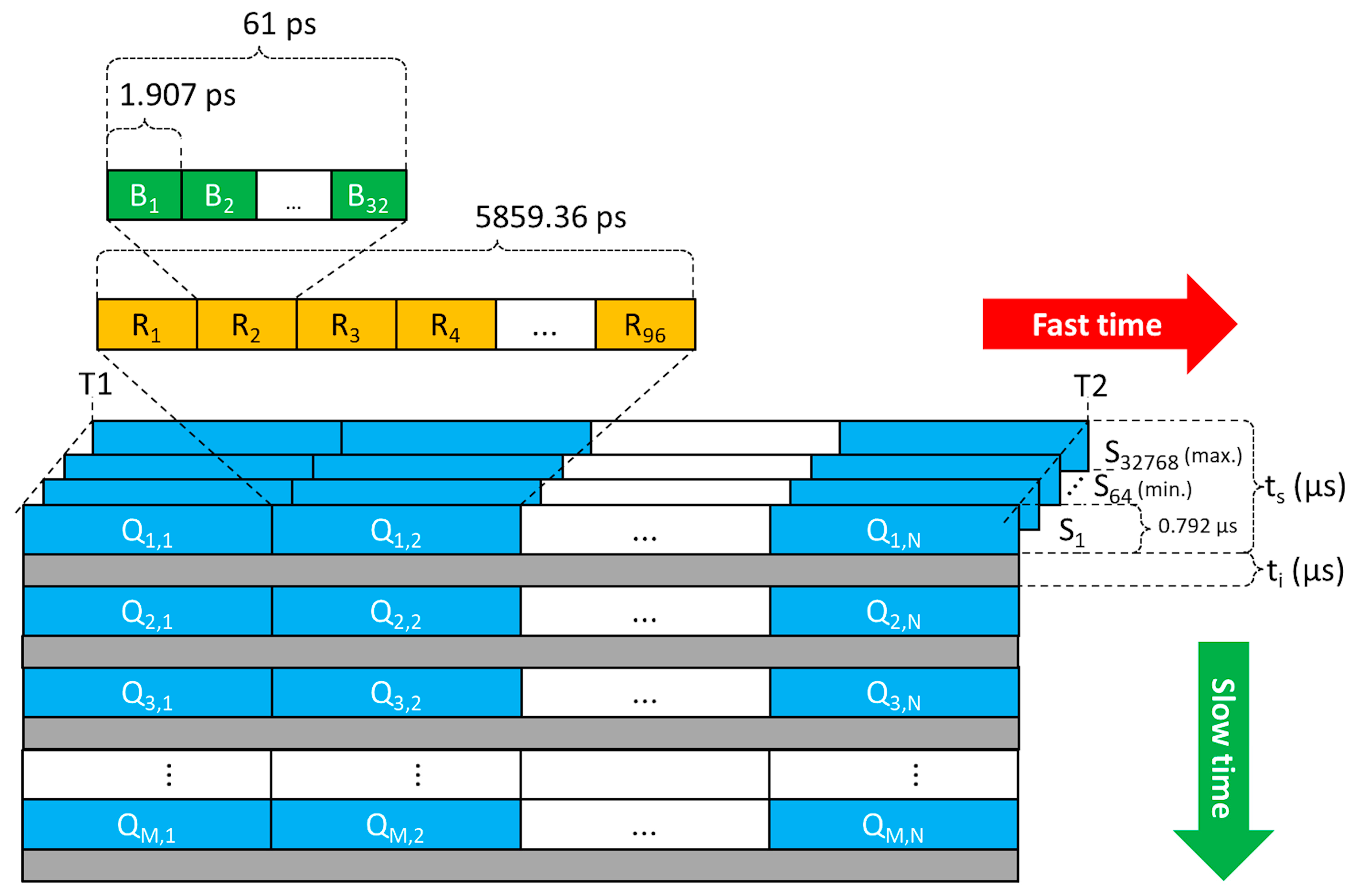


| (m) | (m) | R1 (m) | R2 (m) | T1 (ns) | T2 (ns) | N | (μs) | (μs) |
|---|---|---|---|---|---|---|---|---|
| 0.5 | 1.5 | 0.5 | 1.38 | 13.334 | 19.193 | 96 | 3244.03 | 16,755.97 |
| 0.5 | 1.5 | 0.5 | 2.26 | 13.334 | 25.053 | 192 | 6488.06 | 13,511.94 |
| 0.5 | 2.5 | 0.5 | 3.13 | 13.334 | 30.912 | 288 | 9732.10 | 10,267.90 |
| 0.5 | 3.5 | 0.5 | 4.01 | 13.334 | 36.771 | 384 | 12,976.13 | 7023.87 |
| 0.5 | 4.5 | 0.5 | 4.89 | 13.334 | 42.631 | 480 | 16,220.16 | 3779.84 |
| 0.5 | 5.5 | 0.5 | 5.77 | 13.334 | 48.490 | 576 | 19,464.19 | 535.81 |
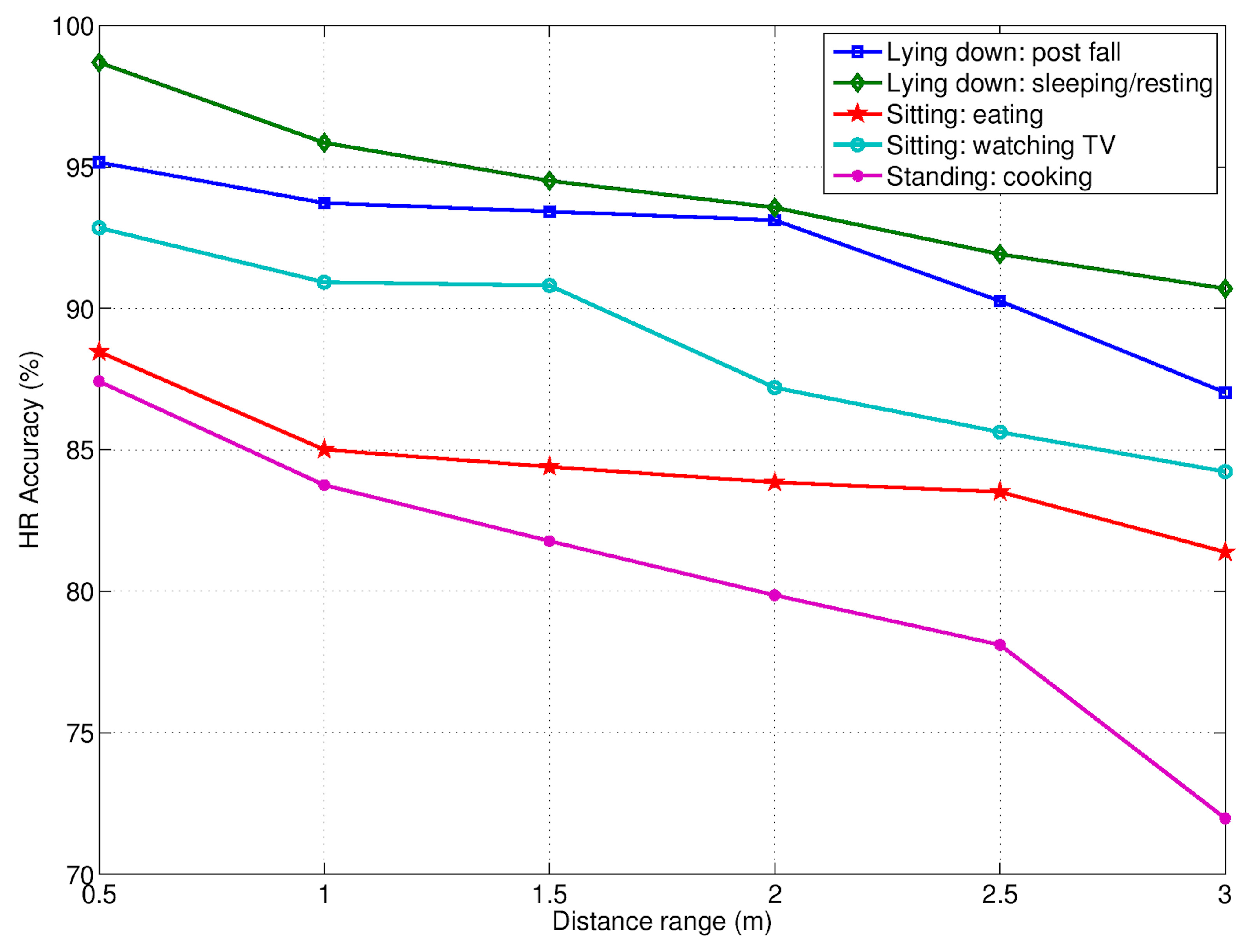
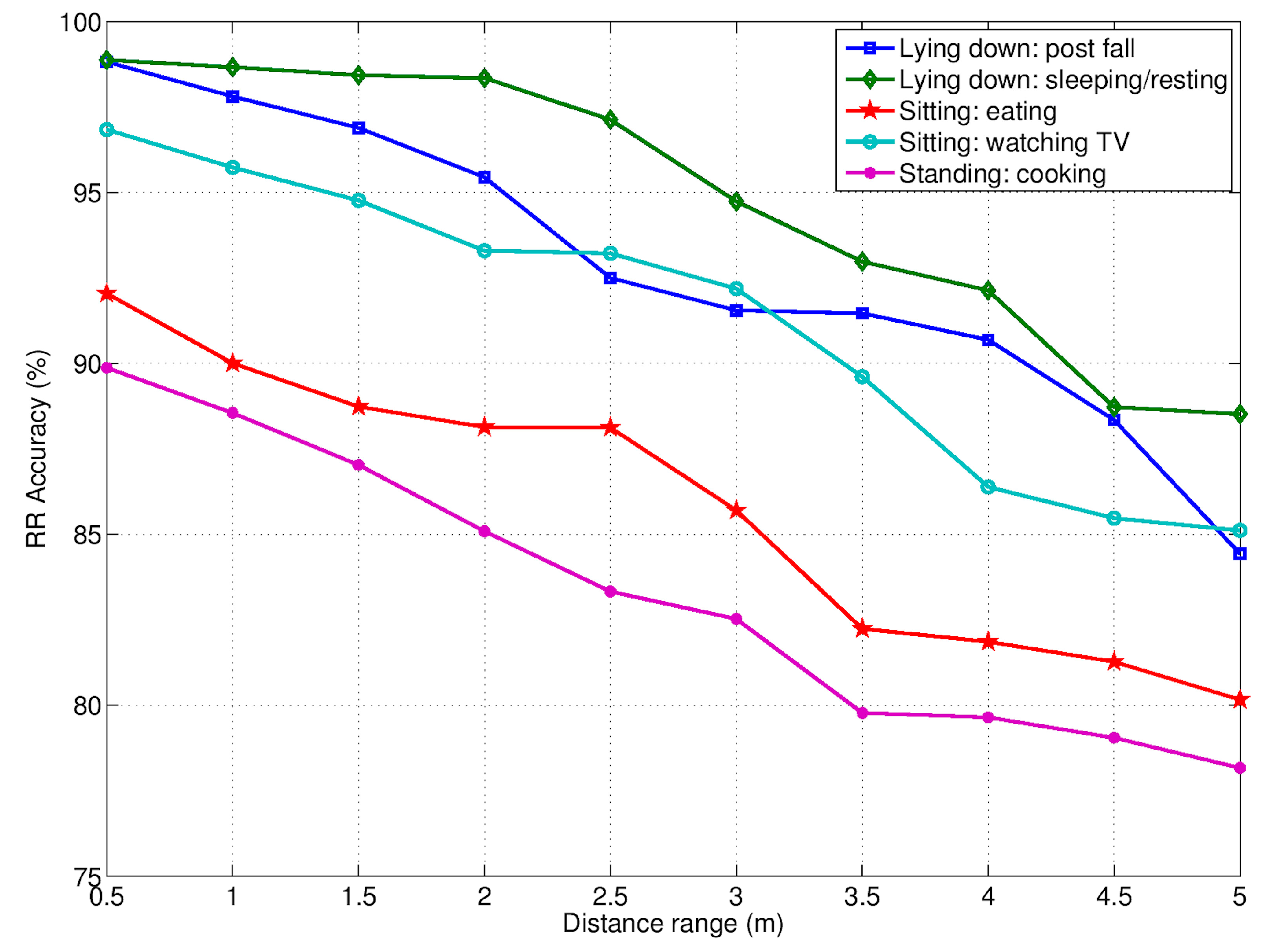
| Activity | HR Accuracy (%) | RR Accuracy (%) |
|---|---|---|
| Lying down: post fall | 89 | 93 |
| Lying down: sleeping/resting | 91 | 95 |
| Sitting: eating | 80 | 86 |
| Sitting: watching TV | 84 | 91 |
| Standing: cooking | 74 | 83 |
| Average value | 84 | 90 |
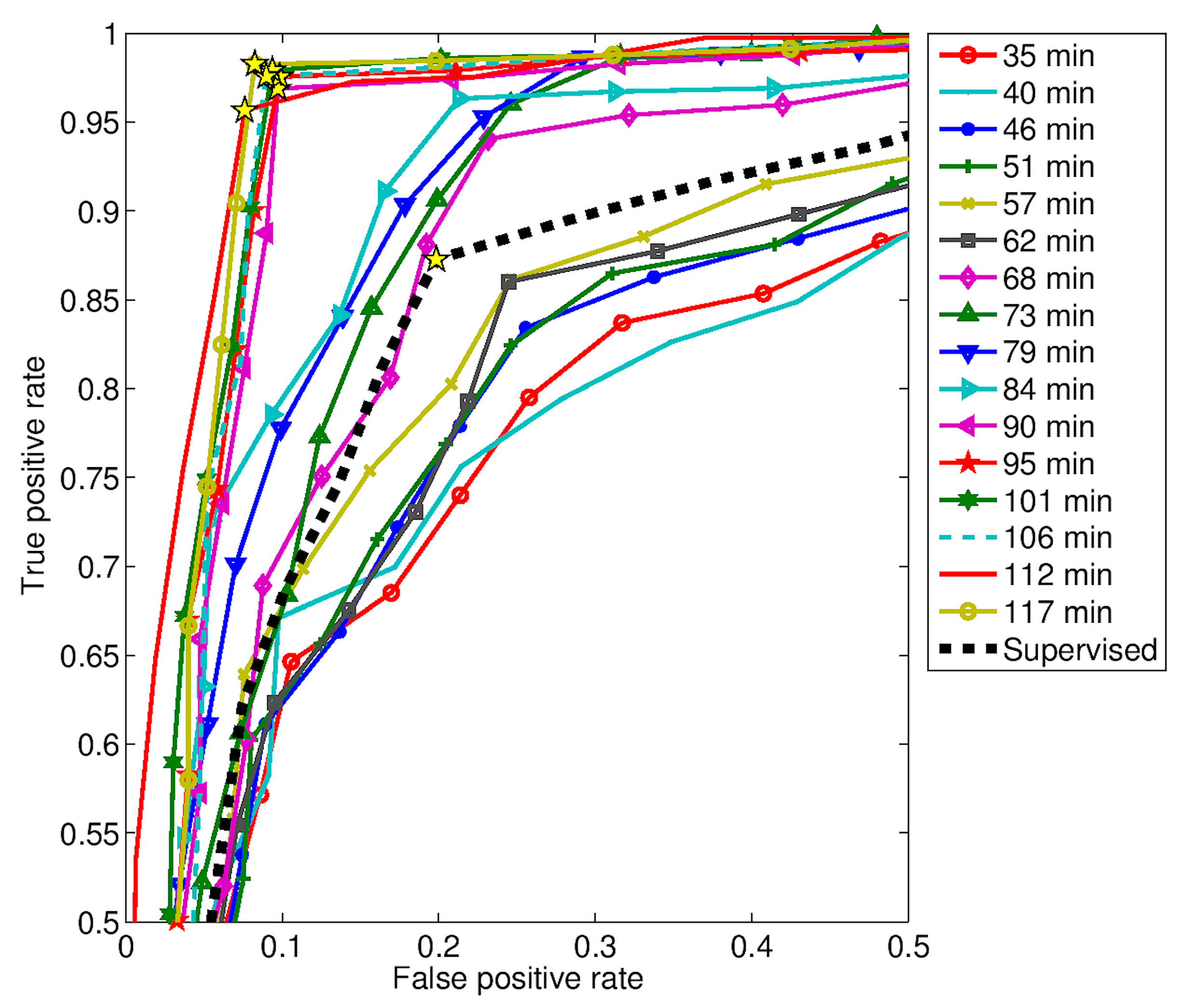
| Approach | Training (min.) | Sensitivity (%) | Specificity (%) |
|---|---|---|---|
| Unsupervised | 35 | 79.49 | 74.23 |
| 40 | 75.61 | 78.56 | |
| 46 | 83.42 | 74.44 | |
| 51 | 82.41 | 75.39 | |
| 57 | 86.14 | 75.41 | |
| 62 | 86.01 | 75.53 | |
| 68 | 88.10 | 80.79 | |
| 73 | 90.63 | 80.1 | |
| 79 | 90.34 | 82.16 | |
| 84 | 91.10 | 83.44 | |
| 90 | 96.89 | 90.28 | |
| 95 | 97.56 | 90.16 | |
| 101 | 97.91 | 90.63 | |
| 106 | 97.57 | 91.02 | |
| 112 | 95.66 | 92.39 | |
| 117 | 98.26 | 91.75 | |
| Supervised | N.A. | 87.27 | 80.15 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diraco, G.; Leone, A.; Siciliano, P. A Radar-Based Smart Sensor for Unobtrusive Elderly Monitoring in Ambient Assisted Living Applications. Biosensors 2017, 7, 55. https://doi.org/10.3390/bios7040055
Diraco G, Leone A, Siciliano P. A Radar-Based Smart Sensor for Unobtrusive Elderly Monitoring in Ambient Assisted Living Applications. Biosensors. 2017; 7(4):55. https://doi.org/10.3390/bios7040055
Chicago/Turabian StyleDiraco, Giovanni, Alessandro Leone, and Pietro Siciliano. 2017. "A Radar-Based Smart Sensor for Unobtrusive Elderly Monitoring in Ambient Assisted Living Applications" Biosensors 7, no. 4: 55. https://doi.org/10.3390/bios7040055
APA StyleDiraco, G., Leone, A., & Siciliano, P. (2017). A Radar-Based Smart Sensor for Unobtrusive Elderly Monitoring in Ambient Assisted Living Applications. Biosensors, 7(4), 55. https://doi.org/10.3390/bios7040055







