Silicon Integrated Dual-Mode Interferometer with Differential Outputs
Abstract
:1. Introduction
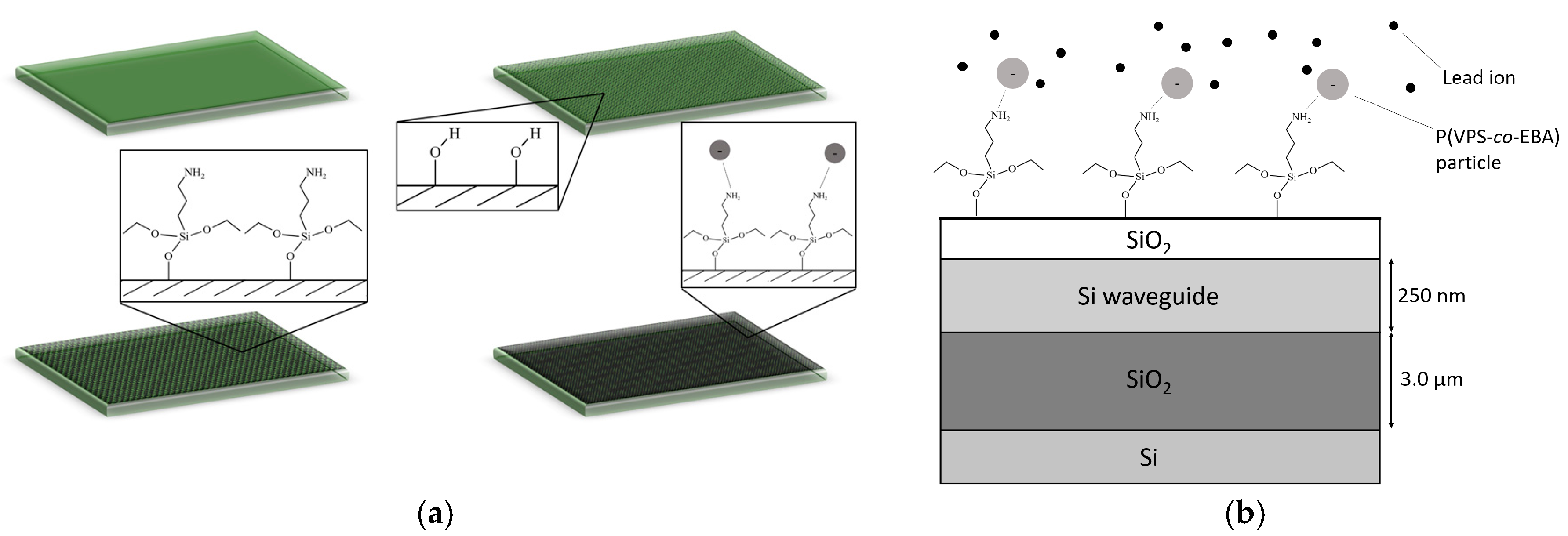
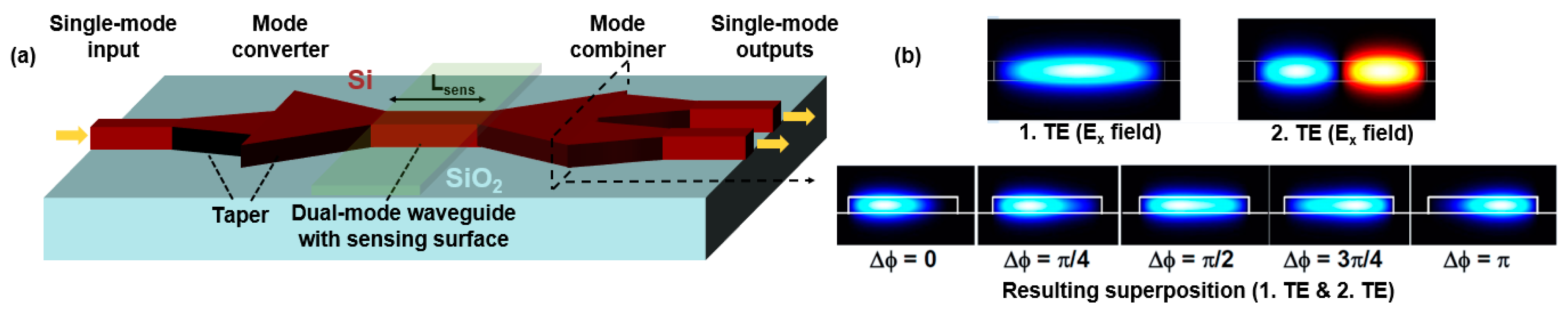
2. Designs of Dual-Mode Interferometers
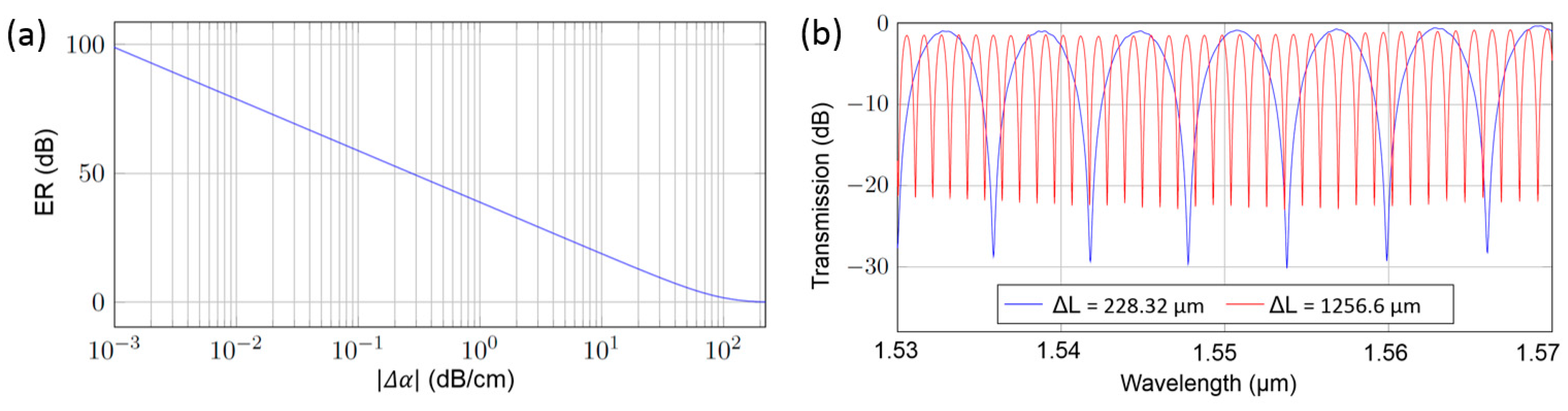
3. Operating Principle of the Dual-Mode Interferometer with Differential Outputs
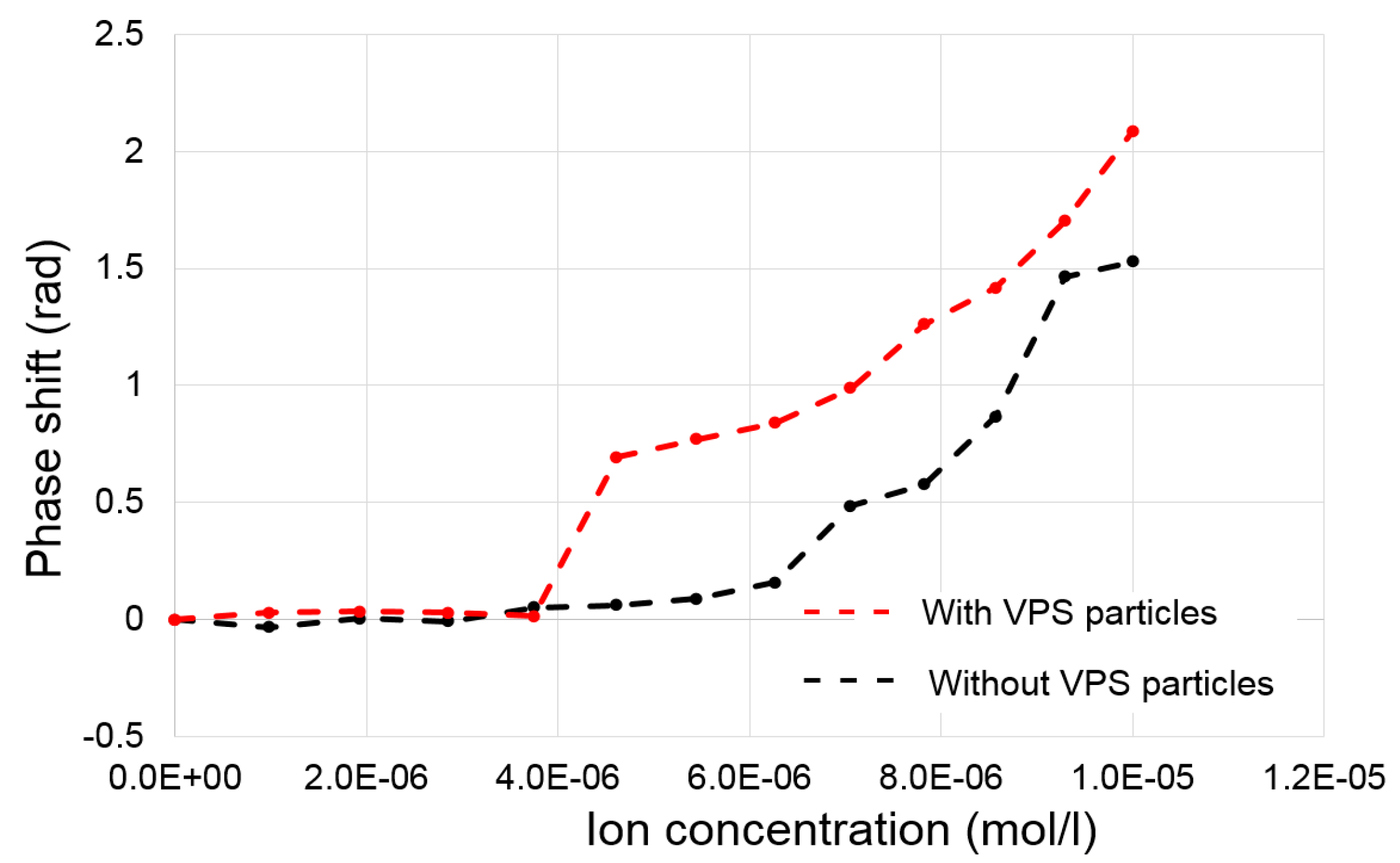
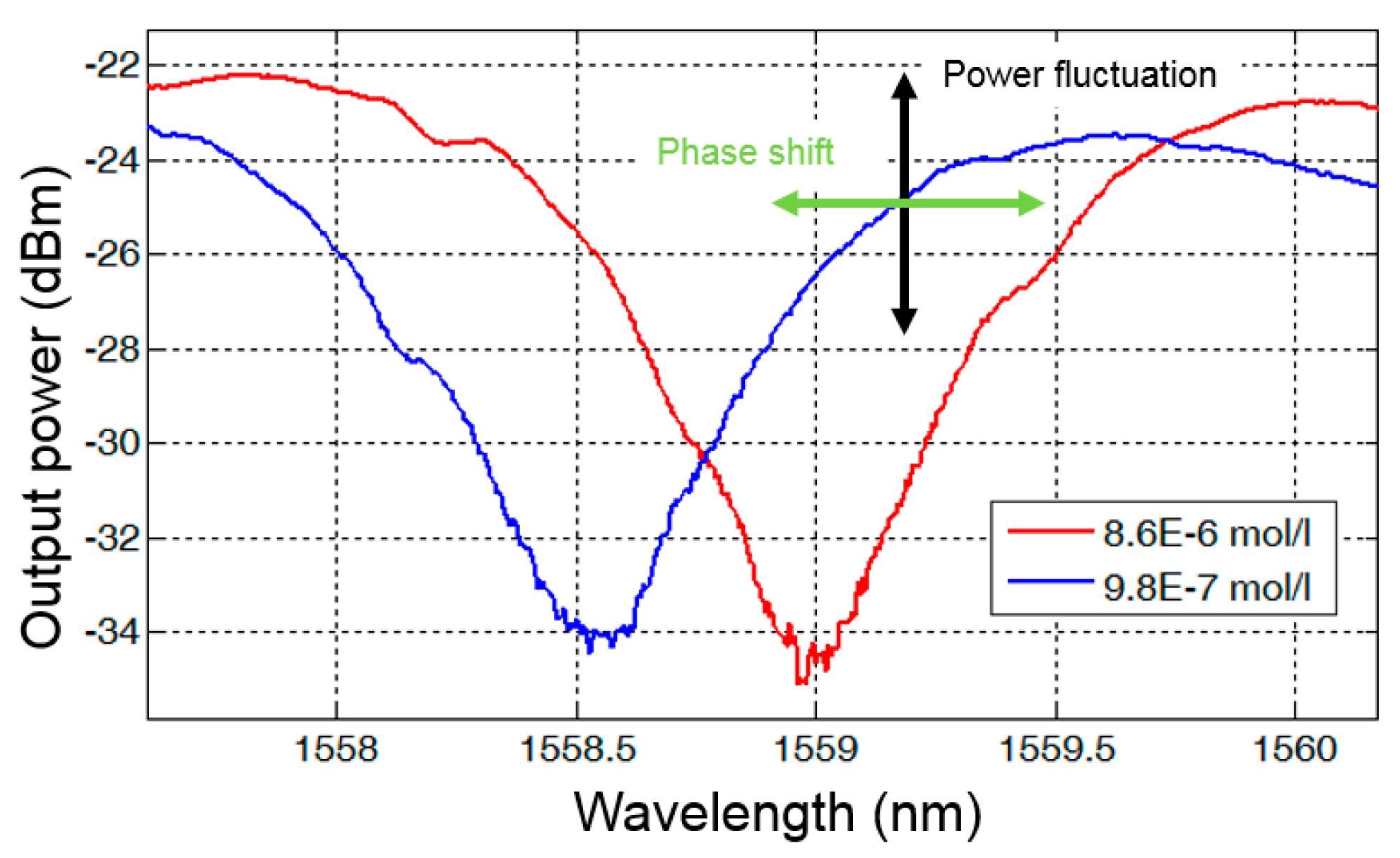
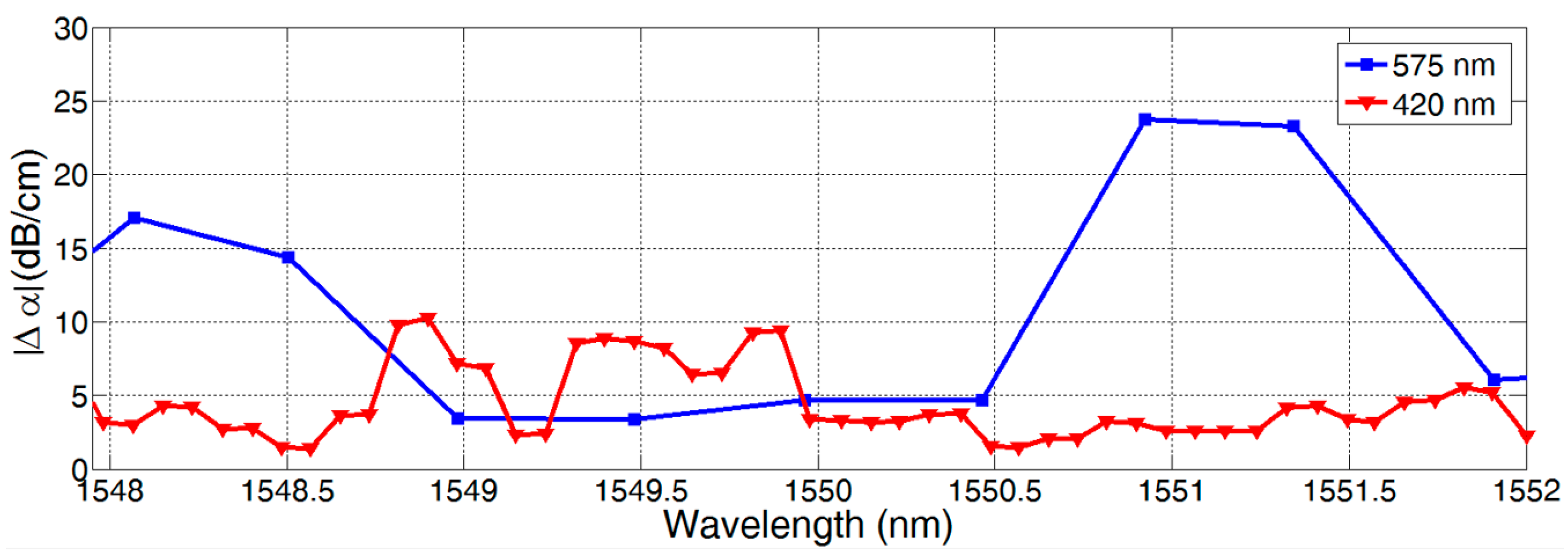
4. Performance of Type 7 Dual-Mode Interferometers
5. Comparison between DMI and MZI
6. Discussion and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A
References
- Dhakal, A.; Wuytens, P.; Peyskens, F.; Jans, K.; Le Thomas, N.; Baets, R. Nanophotonic Waveguide Enhanced Raman Spectroscopy of Biological Submonolayers. ACS Photonics 2016, 3, 2141–2149. [Google Scholar] [CrossRef]
- Makarona, E.; Petrou, P.; Kakabakos, S.; Misiakos, K.; Raptis, I. Point-of-Need bioanalytics based on planar optical interferometry. Biotechnol. Adv. 2016, 34, 209–233. [Google Scholar] [CrossRef] [PubMed]
- Duval, D.; González-Guerrero, A.; Dante, S.; Osmond, J.; Monge, R.; Fernández, L.; Zinoviev, K.; Domínguez, C.; Lechuga, M. Nanophotonic lab-on-a-chip platforms including novel bimodal interferometers, microfluidics and grating couplers. Lab Chip 2012, 12, 1987–1994. [Google Scholar] [CrossRef] [PubMed]
- Hoppe, N.; Diersing, P.; Föhn, T.; Kaschel, M.; Polder, T.; Vogel, W.; Rathgeber, L.; Félix Rosa, M.; Berroth, M. Integrated Dual-Mode Interferometer with Differential Single-Mode Outputs. In Proceedings of the European Conference on Integrated Optics (ECIO), Eindhoven, The Netherlands, 3–5 April 2017. [Google Scholar]
- Ramirez, J.; Lechuga, L.; Gabrielli, L.; Hernandez-Figueroa, H. Study of a low-cost trimodal polymer waveguide for interferometric optical biosensors. Opt. Express 2015, 23, 11985–11994. [Google Scholar] [CrossRef] [PubMed]
- Chao, T.; Davis, S.; Rommel, S.; Farca, G.; Luey, B.; Martin, A.; Anderson, M. Compact Liquid Crystal Waveguide Based Fourier Transform Spectrometer for In-Situ and Remote Gas and Chemical Sensing. Proc. SPIE 2008, 6977, 69770P. [Google Scholar] [CrossRef]
- Levy, R.; Ruschin, S. Design of a Single-Channel Modal Interferometer Waveguide Sensor. IEEE Sens. J. 2009, 9, 146–153. [Google Scholar] [CrossRef]
- Zinoviev, K.; González-Guerrero, A.; Domínguez, C.; Lechuga, M. Integrated Bimodal Waveguide Interferometric Biosensor for Label-Free Analysis. J. Light. Technol. 2011, 29, 1926–1930. [Google Scholar] [CrossRef]
- Liu, Q.; Kim, K.; Gu, Z.; Kee, J.; Park, M. Single-channel Mach-Zehnder interferometric biochemical sensor based on two-lateral-mode spiral waveguide. Opt. Express 2014, 22, 27910–27920. [Google Scholar] [CrossRef] [PubMed]
- Bruck, R.; Hainberger, R. Sensitivity and design of grating-assisted bimodal interferometers for integrated optical biosensing. Opt. Express 2014, 22, 32344–32352. [Google Scholar] [CrossRef] [PubMed]
- Hoppe, N.; Föhn, T.; Félix Rosa, M.P.; Vogel, W.; Sfar Zaoui, W.; Kaschel, M.; Butschke, J.; Letzkus, F.; Berroth, M. Integrated Dual-Mode Waveguide Interferometer. NUSOD 2015, 155–156. [Google Scholar] [CrossRef]
- Hoppe, N.; Föhn, T.; Diersing, P.; Scheck, P.; Vogel, W.; Félix Rosa, M.; Kaschel, M.; Bach, M.; Berroth, M. Design of an Integrated Dual-Mode Interferometer on 250 nm Silicon-on-Insulator. IEEE J. Sel. Top. Quantum Electron. 2017, 23, 444–451. [Google Scholar] [CrossRef]
- Dante, S.; Duval, D.; Sepúlveda, B.; González-Guerrero, A.; Sendra, J.; Lechuga, M. All-optical phase modulation for integrated interferometric biosensors. Opt. Express 2012, 20, 7195–7205. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Hu, X.; Wang, J. On-chip optical mode exchange using tapered directional coupler. Sci. Rep. 2015, 5, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Niedergall, K.; Kopp, D.; Besch, S.; Schiestel, T. Mixed-Matrix Membrane Adsorbers for the Selective Binding of Metal Ions from Diluted Solutions. Chem. Ing. Tech. 2016, 88, 437–446. [Google Scholar] [CrossRef]



| Reference/Year | DMI Array | Excess Loss of Mode Conversion | Single Wavelength Operation | ||
|---|---|---|---|---|---|
| Type 1 (side view) |  | [7]/2009 | ++ | 0.5 dB * | ✕ |
| Type 2 (side view) |  | [8]/2011 | + | unknown | ✓ |
| Type 3 (top view) |  | [9]/2014 | ++ | 0.5 dB * | ✕ |
| Type 4 (side view) |  | [10]/2014 | ++ | < 0.22 dB * | ✕ |
| Type 5 (top view) |  | [11]/2015 | 0 | < 4.2 dB | ✕ |
| Type 6 (top view) |  | [12]/2016 | ++ | 0.25 dB * < 0.5 dB | ✕ |
| Type 7 (top view) |  | [4]/2017 this work | ++ | 0.55 dB * < 2 dB | ✓ |
| Device | Waveguide Width | Sensor Region Length | Measured IL | Intrinsic Bulk Sensitivity | Measured ER | Bulk Sensitivity per Loss |
|---|---|---|---|---|---|---|
| MZI | 250 nm | 500 µm | 1 dB | 79% | >30 dB | 1441 dB−1 |
| 5000 µm | 11 dB | >25 dB | ||||
| DMI | 575 nm | 500 µm | 2.5 dB | 44% | ≈20 dB | 3237 dB−1 |
| 6400 µm | 5.2 dB | ≈10 dB |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hoppe, N.; Scheck, P.; Sweidan, R.; Diersing, P.; Rathgeber, L.; Vogel, W.; Riegger, B.; Southan, A.; Berroth, M. Silicon Integrated Dual-Mode Interferometer with Differential Outputs. Biosensors 2017, 7, 37. https://doi.org/10.3390/bios7030037
Hoppe N, Scheck P, Sweidan R, Diersing P, Rathgeber L, Vogel W, Riegger B, Southan A, Berroth M. Silicon Integrated Dual-Mode Interferometer with Differential Outputs. Biosensors. 2017; 7(3):37. https://doi.org/10.3390/bios7030037
Chicago/Turabian StyleHoppe, Niklas, Pascal Scheck, Rami Sweidan, Philipp Diersing, Lotte Rathgeber, Wolfgang Vogel, Benjamin Riegger, Alexander Southan, and Manfred Berroth. 2017. "Silicon Integrated Dual-Mode Interferometer with Differential Outputs" Biosensors 7, no. 3: 37. https://doi.org/10.3390/bios7030037
APA StyleHoppe, N., Scheck, P., Sweidan, R., Diersing, P., Rathgeber, L., Vogel, W., Riegger, B., Southan, A., & Berroth, M. (2017). Silicon Integrated Dual-Mode Interferometer with Differential Outputs. Biosensors, 7(3), 37. https://doi.org/10.3390/bios7030037





