TERMA Framework for Biomedical Signal Analysis: An Economic-Inspired Approach
Abstract
:1. Introduction and Motivation
2. Methods
2.1. Data Used
- For QRS detection in ECG signals: Eleven ECG databases are used to evaluate the robustness of the TERMA-based QRS detection algorithm. The 11 representative datasets are published on PhysioNet (https://physionet.org/) and represent different subject groups and recording conditions, such as sampling rates (between 128 Hz and 1 kHz) and interferences. Following is a brief description of the 11 datasets: the MIT-BIH Arrhythmia Database with 109,984 beats [7], the QT Database with 111,301 beats [8], the T Wave Alternans Database with 19,003 beats, selected for its wide range of pathological conditions [9], the Intracardiac Atrial Fibrillation Database with 6705 beats [10], the ST Change Database with 76,181 beats featuring stress ECGs [11], the Supraventricular Arrhythmia Database with 184,744 beats [12], the Atrial Fibrillation Termination Database with 7618 beats [13], the Fantasia Database with 278,996 beats from relaxed healthy subjects [14], the Noise Stress Test Database with 26,370 beats recorded under noise conditions typical of clinical environments [15], the St. Petersburg Institute of Cardiological Technics Arrhythmia Database with 175,918 beats [16] and the Normal Sinus Rhythm Database with 183,092 beats [16]. In the Fantasia Database, one record (‘f2y02’) was corrupted and was therefore excluded. Lead I of every record in these datasets was used without any exclusion. The R peaks in all of these publicly-available datasets were annotated. The training set was the MIT-BIH Arrhythmia Database, while the test set consisted of the other 10 databases.
- For systolic wave detection in PPG signals: One annotated Heat-Stress PPG Database [17] consists of 5071 beats of 40 healthy, heat-acclimatized emergency responders (30 males and 10 females). The PPG data were collected at a sampling rate of 367 Hz, and the duration of each recording was 20 s. The data used in the training set were the PPG signals measured at rest, while the data used in the test set were the PPG signals measured after three simulated heat stress exercises.
- For a, b, c, d and e waves detection in APG signals: One annotated Heat-Stress PPG Database [18] consists of 1469 beats of 27 healthy volunteers (males). The PPG data were collected at a sampling rate of 200 Hz, and the duration of each recording was 20 s. The data used in the training set were the APG signals after 1 h of exercise, while the data used in the test set consisted of the APG signals measured at rest and after 2 h of exercise.
- For S1 and S2 detection in heart sounds: One annotated Heart Sounds Database [19] was used that contains the heart sounds of 22 subjects with and without pulmonary artery hypertension (PAH). The heart sounds were recorded using a 3 M Littmann 3200 digital stethoscope over 20 s with sampling frequencies of 4000 Hz. Heart sounds were recorded sequentially at the second left intercostal space and the cardiac apex for 20 s. The data used in the training set were that of 11 subjects with mean pulmonary arterial pressure (PAP) mmHg collected from the apex site, while the data used in the test set were that of 11 subjects with mean PAP mmHg collected from the apex site, 11 subjects with mean PAP mmHg collected from the second left intercostal space (2 L) site and 11 subjects with mean PAP mmHg collected from the 2 L site.
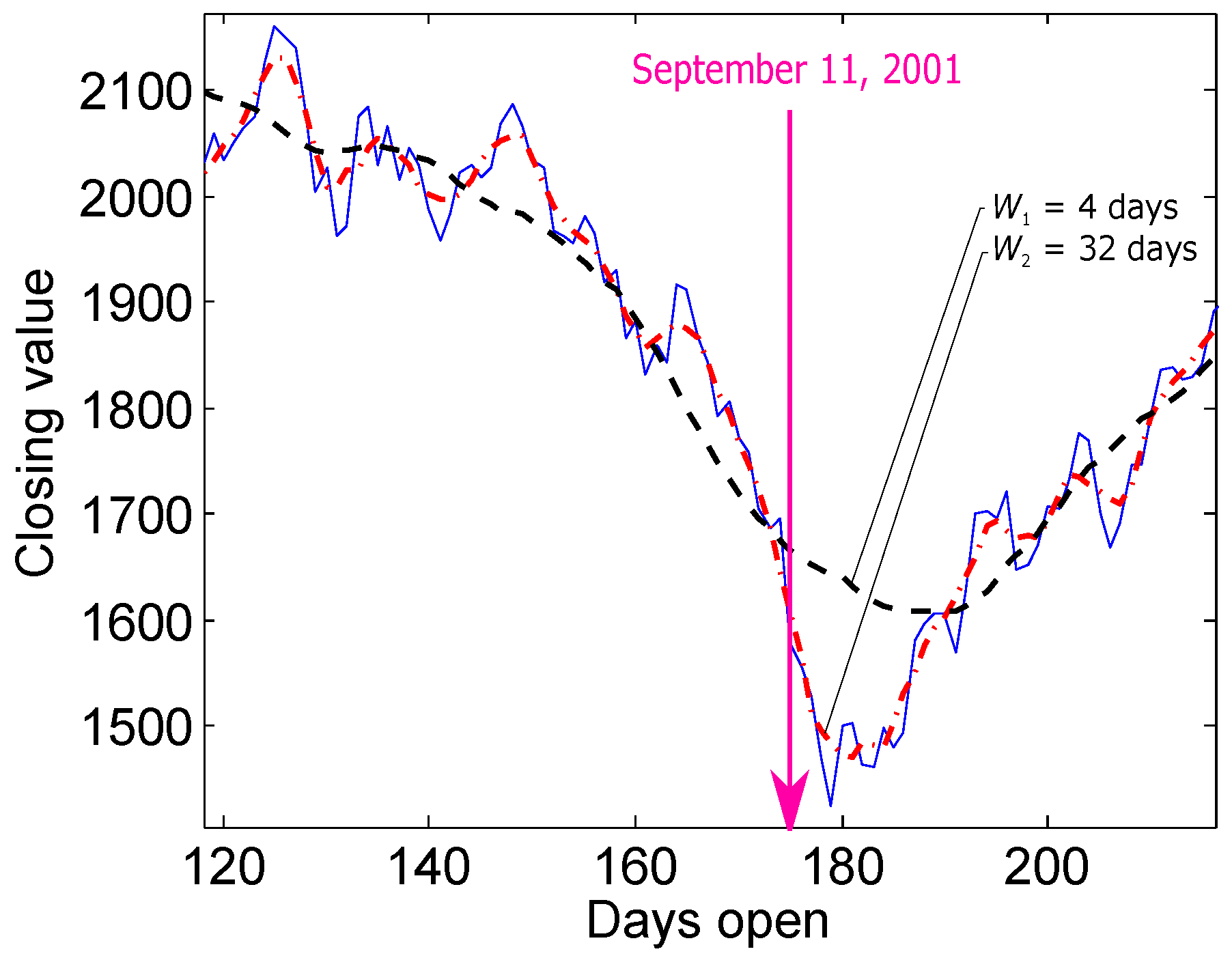
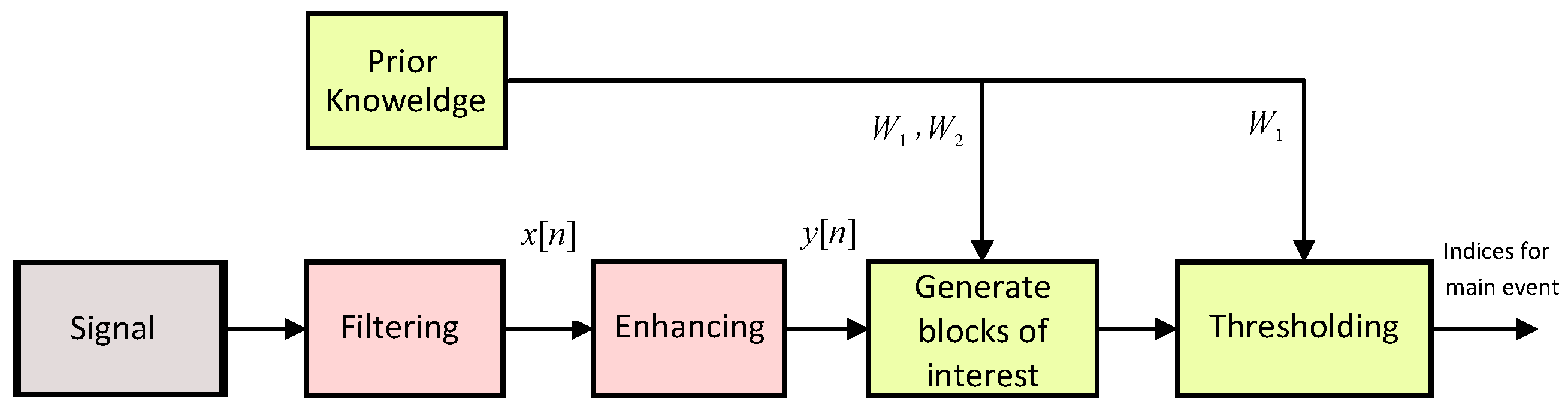
2.2. TERMA Framework
2.2.1. Prior Knowledge
2.2.2. Band-Pass Filter
2.2.3. Enhancing
2.2.4. Generating Blocks of Interest
2.2.5. Thresholding
2.2.6. Detecting Event Peak
3. Results
3.1. Training Results
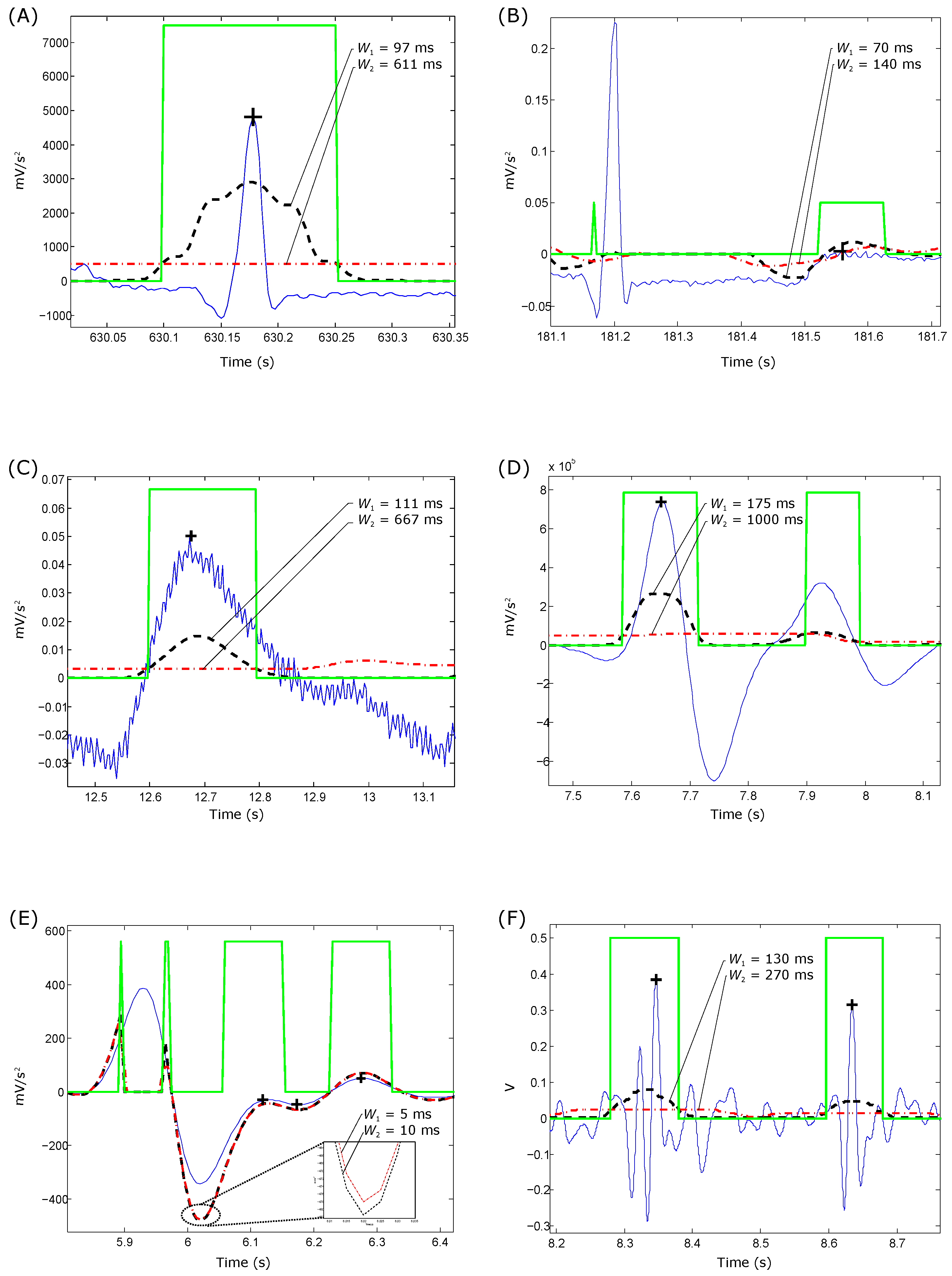
- For QRS detection in ECG signals: The optimization of the beat detector’s spectral window for lower frequency varied from Hz to Hz, with the higher frequency up to Hz. All combinations of the frequency band were 1–26 Hz. The window size of the ranged from ms to ms, whereas the window size of changed from ms to ms. However, the offset β was tested over the range to .
- For T wave detection in ECG signals: All combinations of the frequency band ranged from Hz to Hz. The window size of the ranged from ms to ms, whereas the window size of changed from ms to ms. However, the offset β was tested over the range to .
- For systolic wave detection in PPG signals: The lower frequency resulted in a value from Hz to Hz, while the higher frequency resulted in a value from Hz to Hz. The window size of varied from ms to ms, whereas the window size of varied from ms to ms. The offset β was tested over the range to .
- For a and b wave detection in APG signals: The lower frequency resulted in a value from Hz to Hz, while the higher frequency resulted in a value from Hz to Hz. The window size of varied from ms to ms, whereas the window size of varied from ms to ms. The offset β was tested over the range to .
- For c, d and e wave detection in APG signals: The lower frequency varied from Hz, while the higher frequency varied from Hz to Hz. The window size of varied from ms to ms, whereas the window size of varied from ms to ms, while the range of β varied from to .
- For S1 and S2 detection in heart sounds: The frequency band was optimized over from Hz to Hz; varied from ms to ms; varied from ms to ms; and β varied from to .
3.2. Testing Results
- For QRS detection in ECG signals: Interestingly, the TERMA-based QRS detector obtained an SE of 99.29% and a +P of 98.11% over the first lead of the validation databases (10 databases with a total of 1,179,812 beats). When applied to the well-known MIT-BIH Arrhythmia Database, an SE of 99.78% and a +P of 99.87% were attained [22]. The TERMA-based QRS detector outperformed most of the well-known QRS detector, such as Pan–Tompkins [4] (SE of 90.95% and +P of 99.56%) and Hamilton–Tompkins [28] (SE of 99.69% and +P of 99.77%).
- For T wave detection in ECG signals: Over the MIT-BIH Arrhythmia Database, the TERMA-based T wave detector achieved an SE of 99.86% and a +P of 99.65%, which are promising results for handling the non-stationary effects, low SNR, normal sinus rhythm (NSR), left bundle branch block (LBBB), right bundle branch block (RBBB), premature ventricular contraction (PVC) and premature atrial contraction (PAC) in ECG signals [25]. The TERMA-based T wave detector was not compared to other algorithms as the annotation of T-waves was published in 2015. However, the results are very promising, as the scored accuracy over arrhythmic ECG signals is .
- For systolic wave detection in PPG signals: The TERMA-based systolic wave detection algorithm was evaluated using 40 records after three heat stress simulations containing 5071 heartbeats, with an overall SE of 99.89% and +P of 99.84% [17]. The TERMA-based systolic detector slightly outperformed existing algorithms, such as Billauer’s [29] (SE of 99.88% and +P of 98.69%), Li’s [30] (SE of 97.9% and +P of 99.93%) and Zong’s [31] (SE of 99.69% and +P of 99.71%).
- For a and b wave detection in APG signals: The TERMA-based a wave detection algorithm demonstrated an overall SE of 99.78% and a +P of 100% over signals that suffer from: (1) non-stationary effects; (2) irregular heartbeats; and (3) low amplitude waves. In addition, the b detection algorithm (based on the detection of a waves) achieved an overall SE of 99.78% and +P of 99.95% [24]. The TERMA-based a and b waves detector was not compared to other algorithms, as it is a new area of investigation and is considered a pioneering concept in the field of PPG signal analysis. However, the results are very promising as the scored accuracy over heat-stressed PPG signals is >98%.
- For c, d and e wave detection in APG signals: The performance of the TERMA-based c, d and e wave detector was tested on 27 PPG records collected during rest and after 2 h of exercise, resulting in 97.39% SE and 99.82% +P [23]. The TERMA-based c, d and e waves detector was not compared to other algorithms, as it is a new area of investigation, and the work is a pioneering concept in the field of PPG signal analysis. However, the results are very promising, as the scored accuracy over heat-stressed PPG signals is >97%.
- For S1 and S2 detection in heart sounds: The SE and +P of the TERMA-based S1 and S2 detectors were 70% and 68%, respectively, for heart sounds collected from children with PAH [19]. The TERMA-based heart sounds detector outperformed existing algorithms, such as Liang’s [32] (SE of 59% and +P of 42%), Kumar’s [33] (SE of 19% and +P of 12%), Wang’s [34] (SE of 50% and +P of 45%) and Zhong [35] (SE of 43% and +P of 53%).
4. Discussion
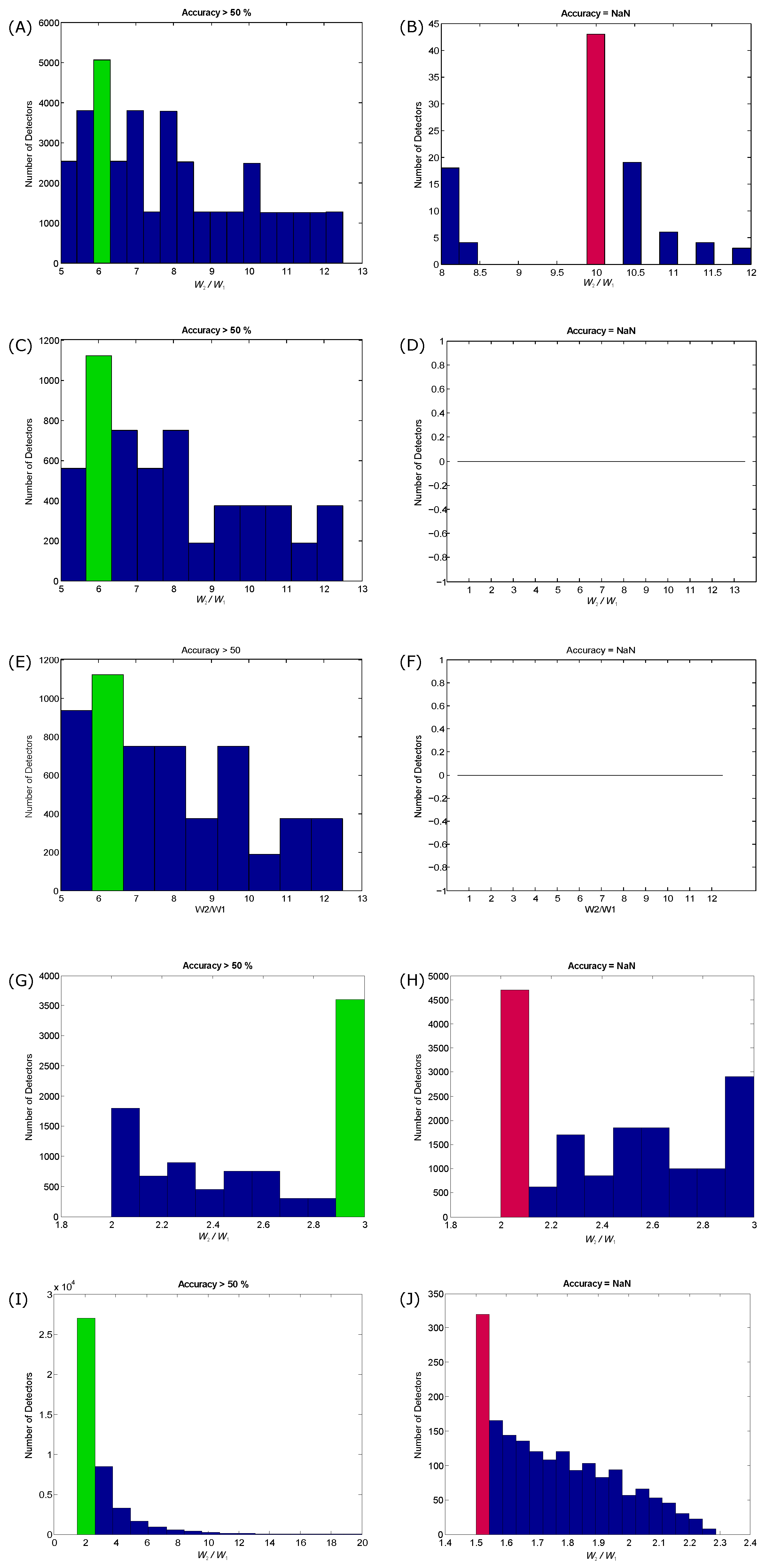
4.1. Frequency Band Choice
4.2. Window Size Choice
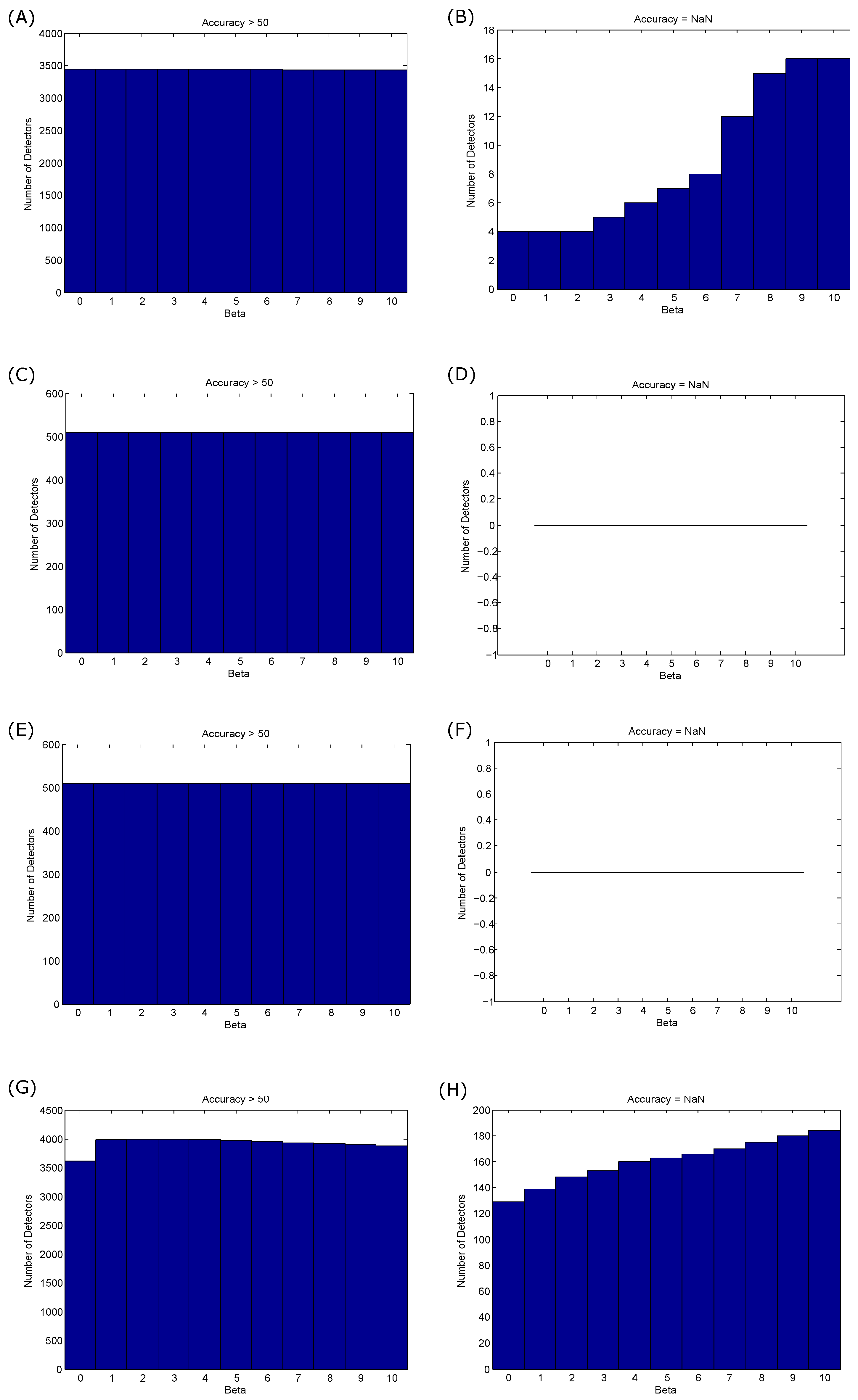
4.3. Offset β Choice
4.4. Battery-Driven Devices
4.5. Optimization Step
4.6. Significance of TERMA
5. Conclusions
Acknowledgments
Conflicts of Interest
References
- Dilaveris, P.E.; Gialafos, E.J.; Sideris, S.K.; Theopistou, A.M.; Andrikopoulos, G.K.; Kyriakidis, M.; Gialafos, J.E.; Toutouzas, P.K. Simple electrocardiographic markers for the prediction of paroxysmal idiopathic atrial fibrillation. Am. Heart J. 1998, 135, 733–738. [Google Scholar] [CrossRef]
- Lukac, L.P.; Brorsen, B.W.; Irwin, S.H. A test of futures market disequilibrium using twelve different technical trading systems. Appl. Econ. 1988, 20, 623–639. [Google Scholar] [CrossRef]
- Gençay, R.; Selçuk, F.; Whitcher, B.J. An Introduction to Wavelets and Other Filtering Methods in Finance and Economics; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Pan, J.; Tompkins, W. A real-time QRS detection algorithm. IEEE Trans. Biomed. Eng. 1985, 32, 230–236. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chen, S. A moving average based filtering system with its application to real-time QRS detection. In Proceedings of the IEEE Computers in Cardiology, Thessaloniki, Greece, 21–24 September 2003; pp. 585–588.
- Chen, S.W.; Chen, H.C.; Chan, H.L. A real-time QRS detection method based on moving-averaging incorporating with wavelet denoising. Comput. Methods Progr. Biomed. 2006, 82, 187–195. [Google Scholar] [CrossRef] [PubMed]
- Moody, G.B.; Mark, R.G. The impact of the MIT-BIH Arrhythmia Database. IEEE Eng. Med. Biol. Mag. 2001, 20, 45–50. [Google Scholar] [CrossRef] [PubMed]
- Laguna, P.; Mark, R.; Goldberg, A.; Moody, G. A database for evaluation of algorithms for measurement of QT and other waveform intervals in the ECG. In Proceedings of the IEEE Computers in Cardiology 1997, Lund, Sweden, 7–10 September 1997; pp. 673–676.
- Moody, G.B. The Physionet/Computers in Cardiology challenge 2008: T-wave alternans. In Proceedings of the IEEE Computers in Cardiology, Bologna, Italy, 14–17 September 2008; pp. 505–508.
- Goldberger, A.L.; Amaral, L.A.N.; Glass, L.; Hausdorff, J.M.; Ivanov, P.C.; Mark, R.G.; Mietus, J.E.; Moody, G.B.; Peng, C.K.; Stanley, H.E. PhysioBank, PhysioToolkit, and PhysioNet: Components of a New Research Resource for Complex Physiologic Signals. Circulation 2000, 101, e215–e220. [Google Scholar] [CrossRef] [PubMed]
- Albrecht, P. S-T Segment Characterization for Long-Term Automated ECG Analysis. Master’s Thesis, MIT Department of Electrical Engineering and Computer Science, Boston, MA, USA, 1983. [Google Scholar]
- Greenwald, S. Improved Detection and Classification of Arrhythmias in Noise-Corrupted Electrocardiograms Using Contextual Information. Ph.D. Thesis, Harvard-MIT Division of Health Sciences and Technology, Boston, MA, USA, 1990. [Google Scholar]
- Moody, G. Spontaneous termination of atrial fibrillation: A challenge from Physionet and Computers in Cardiology 2004. In Proceedings of the IEEE Computers in Cardiology, Chicago, IL, USA, 19–22 September 2004; pp. 101–104.
- Iyengar, N.; Peng, C.K.; Morin, R.; Goldberger, A.L.; Lipsitz, L.A. Age-related alterations in the fractal scaling of cardiac interbeat interval dynamics. Am. J. Physiol. Regulat. Integr. Comp. Physiol. 1996, 271, R1078–R1084. [Google Scholar]
- Moody, G.B.; Muldrow, W.; Mark, R. A noise stress test for arrhythmia detectors. In Proceedings of the IEEE Computers in Cardiology, Salt Lake City, UT, USA, 18–21 September 1984; pp. 381–384.
- Braunwald, E.; Zipes, D.; Libby, P.; Bonow, R. Braunwald’s Heart Disease: A Textbook of Cardiovascular Medicine, 7th ed.; Saunders: Philadelphia, PA, USA, 2004. [Google Scholar]
- Elgendi, M.; Norton, I.; Brearley, M.; Abbott, D.; Schuurmans, D. Systolic Peak Detection in Acceleration Photoplethysmograms Measured from Emergency Responders in Tropical Conditions. PLoS ONE 2013, 8, e76585. [Google Scholar] [CrossRef] [PubMed]
- Matsuyama, A. ECG and APG Signal Analysis during Exercise in a Hot Environment. Ph.D. Thesis, Charles Darwin University, Darwin, Australia, 2009. [Google Scholar]
- Elgendi, M.; Kumar, S.; Guo, L.; Rutledge, J.; Coe, J.Y.; Zemp, R.; Schuurmans, D.; Adatia, I. Detection of Heart Sounds in Children with and without Pulmonary Arterial Hypertension–Daubechies Wavelets Approach. PLoS ONE 2015, 10, e0143146. [Google Scholar] [CrossRef] [PubMed]
- Mattson, C.A.; Mullur, A.A.; Messac, A. Smart Pareto filter: Obtaining a minimal representation of multi-objective design space. Eng. Opt. 2004, 36, 721–740. [Google Scholar] [CrossRef]
- Oppenheim, A.; Shafer, R. Discrete-Time Signal Processing; Prentice Hall: Upper Saddle River, NJ, USA, 1989. [Google Scholar]
- Elgendi, M. Fast QRS Detection with an Optimized Knowledge-Based Method: Evaluation on 11 Standard ECG Databases. PLoS ONE 2013, 8, e73557. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M. Detection of c, d, and e waves in the acceleration photoplethysmogram. Comput. Methods Programs Biomed. 2014, 117, 125–136. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Norton, I.; Brearley, M.; Abbott, D.; Schuurmans, D. Detection of a and b waves in the acceleration photoplethysmogram. Biomed. Eng. Online 2014, 13, 139. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Eskofier, B.; Abbott, D. Fast T Wave Detection Calibrated by Clinical Knowledge with Annotation of P and T Waves. Sensors 2015, 15, 17693–17714. [Google Scholar] [PubMed]
- Firbank, M.; Coulthard, A.; Harrison, R.; Williams, E. A comparison of two methods for measuring the signal to noise ratio on MR images. Phys. Med. Biol. 1999, 44, 261–264. [Google Scholar] [CrossRef]
- Elgendi, M.; Eskofier, B.; Dokos, S.; Abbott, D. Revisiting QRS Detection Methodologies for Portable, Wearable, Battery-Operated, and Wireless ECG Systems. PLoS ONE 2014, 9, e84018. [Google Scholar] [CrossRef] [PubMed]
- Hamilton, P.S.; Tompkins, W.J. Adaptive matched filtering for QRS detection. In Proceedings of the IEEE Annual International Conference Engineering in Medicine and Biology Society, New Orleans, LA, USA, 4–7 November 1988; Volume 1, pp. 14–18.
- Billauer, E. Peakdet: Peak Detection Using MATLAB. Available online: http://billauer.co.il/peakdet.html (accessed on 28 October 2012).
- Li, B.N.; Dong, M.C.; Vai, M.I. On an automatic delineator for arterial blood pressure waveforms. Biomed. Signal Process. Control 2010, 5, 76–81. [Google Scholar] [CrossRef]
- Zong, W.; Heldt, T.; Moody, G.B.; Mark, R.G. An open-source algorithm to detect onset of arterial blood pressure pulses. In Proceedings of the IEEE Computers in Cardiology, Thessaloniki, Greece, 21–24 September 2003; pp. 259–262.
- Liang, H.; Lukkarinen, S.; Hartimo, I. Heart sound segmentation algorithm based on heart sound envelogram. In Proceedings of the IEEE Computers in Cardiology, Lund, Sweden, 7–10 September 1997; pp. 105–108.
- Kumar, D.; Carvalho, P.; Antunes, M.; Henriques, J.; Eugenio, L.; Schmidt, R.; Habetha, J. Detection of S1 and S2 heart sounds by high frequency signatures. In Proceedings of the 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 31 August–3 September 2006; pp. 1410–1416.
- Wang, X.; Li, Y.; Sun, C.; Liu, C. Detection of the first and second heart sound using heart sound energy. In Proceedings of the 2009 2nd International Conference on Biomedical Engineering and Informatics, Tianjin, China, 17–19 October 2009; pp. 1–4.
- Zhong, J.; Scalzo, F. Automatic heart sound signal analysis with reused multi-scale wavelet transform. Int. J. Eng. Sci. 2013, 2, 50–57. [Google Scholar]
- Thakor, N.V.; Webster, J.G.; Tompkins, W.J. Optimal QRS detector. Med. Biol. Eng. 1983, 21, 343–350. [Google Scholar] [CrossRef]
- Li, C.; Zheng, C.; Tai, C. Detection of ECG characteristic points using wavelet transforms. IEEE Trans. Biomed. Eng. 1995, 42, 21–28. [Google Scholar] [PubMed]
- Sahambi, J.S.; Tandon, S.; Bhatt, R.K.P. Using wavelet transforms for ECG characterization. An on-line digital signal processing system. IEEE Eng. Med. Biol. Mag. 1997, 16, 77–83. [Google Scholar] [CrossRef] [PubMed]
- Moraes, J.C.T.B.; Freitas, M.M.; Vilani, F.N.; Costa, E.V. A QRS complex detection algorithm using electrocardiogram leads. In Proceedings of the IEEE Computers in Cardiology, Memphis, USA, 22–25 September 2002; pp. 205–208.
- Mahmoodabadi, S.Z.; Ahmadian, A.; Abolhasani, M.D. ECG feature extraction using Daubechies wavelets. In Proceedings of the Fifth IASTED International Conference, Benindorm, Spain, 7–9 September 2005; pp. 343–348.
- Holsinger, W.; Kempner, K.; Miller, M. QRS preprocessor based on digital differentiation. IEEE Trans. Biomed. Eng. 1971, 18, 212–217. [Google Scholar] [CrossRef]
- Okada, M. A Digital Filter for the QRS Complex Detection. IEEE Trans. Biomed. Eng. 1979, 26, 700–703. [Google Scholar] [CrossRef] [PubMed]
- Morizet-Mahoudeaux, P.; Moreau, C.; Moreau, D.; Quarante, J.J. Simple microprocessor-based system for on-line e.c.g. arrhythmia analysis. Med. Biol. Eng. Comput. 1981, 19, 497–500. [Google Scholar] [CrossRef] [PubMed]
- Benitez, D.S.; Gaydecki, P.A.; Zaidi, A.; Fitzpatrick, A.P. A new QRS detection algorithm based on the Hilbert transform. In Proceedings of the IEEE Computers in Cardiology, Cambridge, MA, USA, 24–27 September 2000; pp. 379–382.
- Arzeno, N.; Poon, C.; Deng, Z. Quantitative Analysis of QRS Detection Algorithms Based on the First Derivative of the ECG. In Proceedings of the 28th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, New York, NY, USA, 31 August–3 September 2006; pp. 1788–1791.
- Zhang, F.; Lian, Y. Electrocardiogram QRS Detection Using Multiscale Filtering Based on Mathematical Morphology. In Proceedings of the 29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society, Lyon, France, 22–26 August 2007; pp. 3196–3199.
- Arzeno, N.; Deng, Z.; Poon, C. Analysis of First-Derivative Based QRS Detection Algorithms. IEEE Trans. Biomed. Eng. 2008, 55, 478–484. [Google Scholar] [CrossRef] [PubMed]
- Friesen, G.; Jannett, T.; Jadallah, M.; Yates, S.; Quint, S.; Nagle, H. A comparison of the noise sensitivity of nine QRS detection algorithms. IEEE Trans. Biomed. Eng. 1990, 37, 85–98. [Google Scholar] [CrossRef] [PubMed]
- Englese, W.A.H.; Zeelenberg, C. A single scan algorithm for QRS detection and feature extraction. In Proceedings of the IEEE Computers in Cardiology, Geneva, Switzerland, 26–28 September 1979; pp. 37–42.
- Fraden, J.; Neuman, M. QRS wave detection. Med. Biol. Eng. Comput. 1980, 18, 125–132. [Google Scholar] [CrossRef] [PubMed]
- Elgendi, M.; Howard, N.; Lovell, N.; Cichocki, A.; Brearley, M.; Abbott, D.; Adatia, I. A Six-Step Framework on Biomedical Signal Analysis for Tackling Noncommunicable Diseases: Current and Future Perspectives. JMIR Biomed. Eng. 2016, 1, e1. [Google Scholar]
- Elgendi, M. Optimal Signal Quality Index for Photoplethysmogram Signals. Bioengineering 2016, 3, 21. [Google Scholar] [CrossRef]
- Elgendi, M. Eventogram: A Visual Representation of Main Events in Biomedical Signals. Bioengineering 2016, 3, 22. [Google Scholar] [CrossRef]
- Christov, I.I. Real time electrocardiogram QRS detection using combined adaptive threshold. Biomed. Eng. Online 2004, 3, 28. [Google Scholar] [CrossRef] [PubMed]
- Chiarugi, F.; Sakkalis, V.; Emmanouilidou, D.; Krontiris, T.; Varanini, M.; Tollis, I. Adaptive threshold QRS detector with best channel selection based on a noise rating system. In Proceedings of the IEEE Computers in Cardiology, Durham, NC, USA, 30 September–3 October 2007; pp. 157–160.
- Mann, M.E.; Lees, J.M. Robust estimation of background noise and signal detection in climatic time series. Clim. Chang. 1996, 33, 409–445. [Google Scholar] [CrossRef]
- Chatterjee, S.K.; Das, S.; Maharatna, K.; Masi, E.; Santopolo, L.; Mancuso, S.; Vitaletti, A. Exploring strategies for classification of external stimuli using statistical features of the plant electrical response. J. R. Soc. Interface 2015, 12. [Google Scholar] [CrossRef] [PubMed]
- Koos, C.; Vorreau, P.; Vallaitis, T.; Dumon, P.; Bogaerts, W.; Baets, R.; Esembeson, B.; Biaggio, I.; Michinobu, T.; Diederich, F.; et al. All-optical high-speed signal processing with silicon–organic hybrid slot waveguides. Nat. Photon. 2009, 3, 216–219. [Google Scholar] [CrossRef]
- Furuya, M.; Hamano, Y.; Naito, I. Quasi-periodic wind signal as a possible excitation of Chandler wobble. J. Geophys. Res. Solid Earth 1996, 101, 25537–25546. [Google Scholar] [CrossRef]
- Stella, L.; Vietri, M. Lense-Thirring Precession and Quasi-periodic Oscillations in Low-Mass X-ray Binaries. Astrophys. J. Lett. 1998, 492, L59. [Google Scholar] [CrossRef]
- Jerolmack, D.J.; Paola, C. Shredding of environmental signals by sediment transport. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Tandon, N.; Choudhury, A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings. Tribol. Int. 1999, 32, 469–480. [Google Scholar] [CrossRef]

© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elgendi, M. TERMA Framework for Biomedical Signal Analysis: An Economic-Inspired Approach. Biosensors 2016, 6, 55. https://doi.org/10.3390/bios6040055
Elgendi M. TERMA Framework for Biomedical Signal Analysis: An Economic-Inspired Approach. Biosensors. 2016; 6(4):55. https://doi.org/10.3390/bios6040055
Chicago/Turabian StyleElgendi, Mohamed. 2016. "TERMA Framework for Biomedical Signal Analysis: An Economic-Inspired Approach" Biosensors 6, no. 4: 55. https://doi.org/10.3390/bios6040055
APA StyleElgendi, M. (2016). TERMA Framework for Biomedical Signal Analysis: An Economic-Inspired Approach. Biosensors, 6(4), 55. https://doi.org/10.3390/bios6040055





