Evaluating the Suitability of Perfusion-Based PD Probes for Use in Altered Gravity Environments
Abstract
1. Introduction
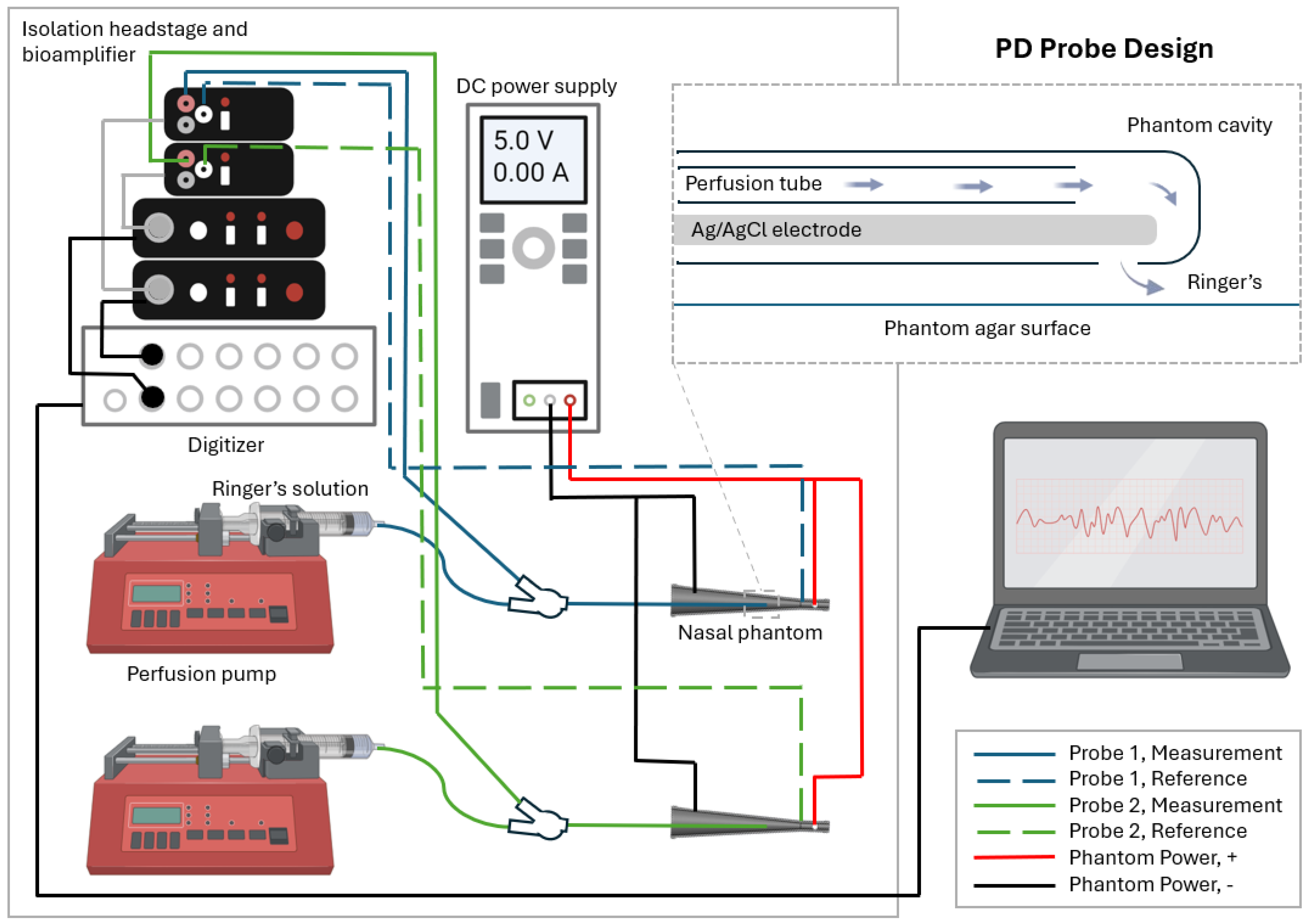
2. Materials and Methods
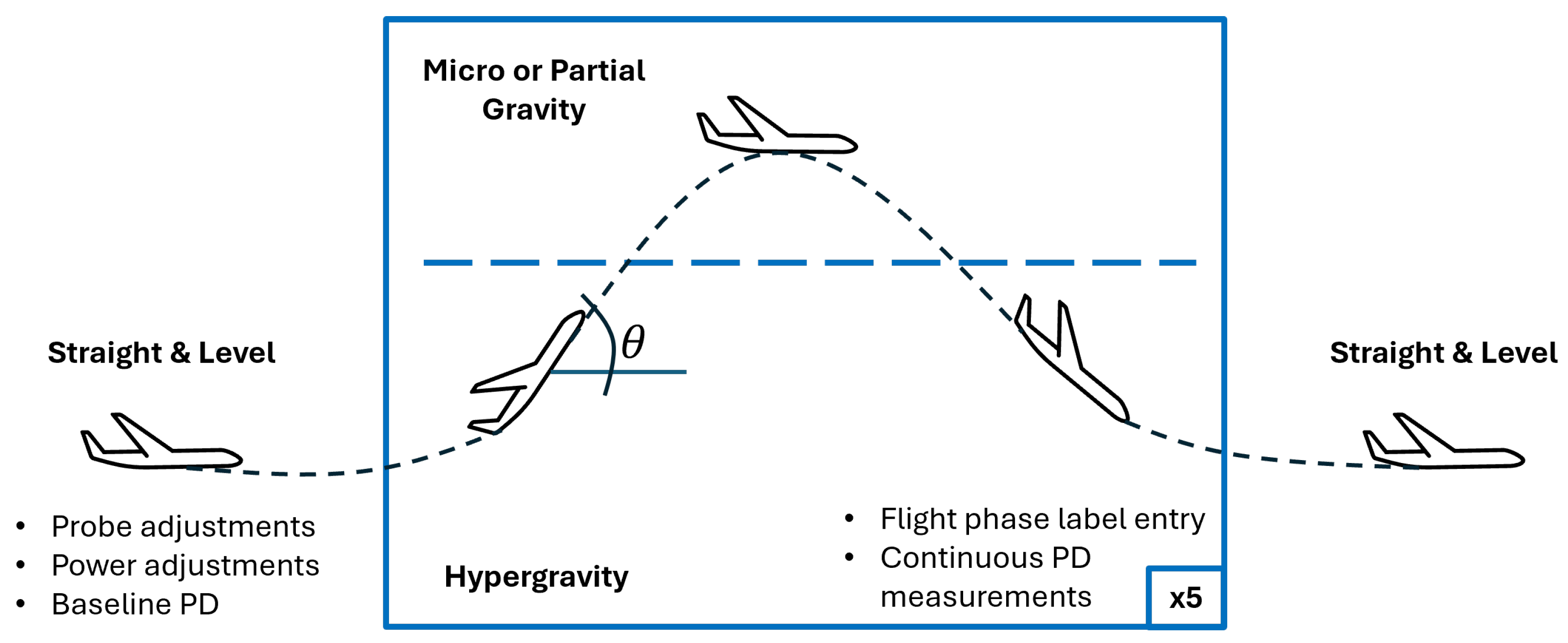
2.1. Parabolic Flight
2.2. Statistical Approach
2.3. Flight Procedures
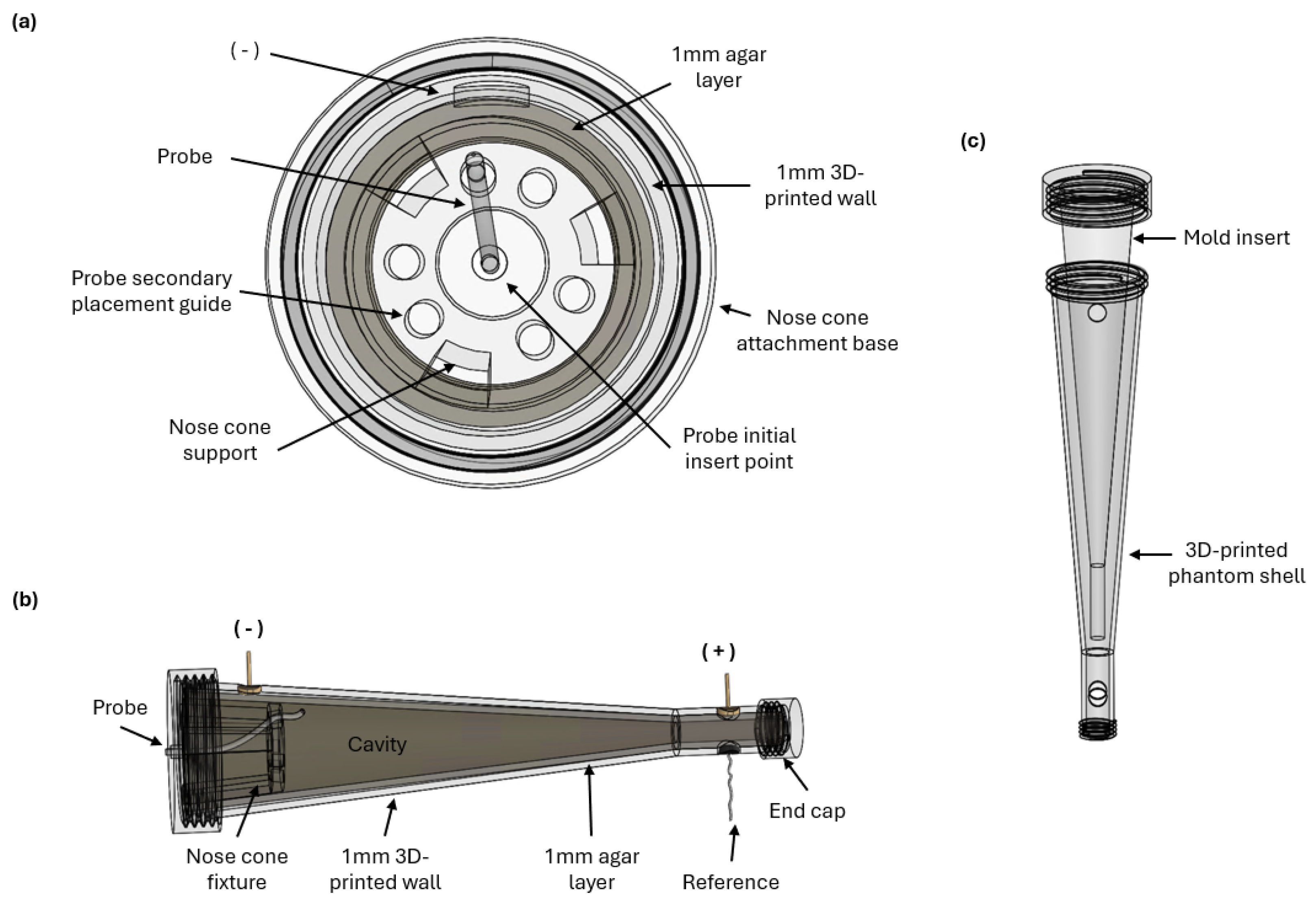
3. Nasal Phantom Design and Development
3.1. Phantom Geometry
3.2. Agar Layer
3.3. Power Supply and Reference Probe
3.4. Measurement Probe Insert Fixture
4. Results
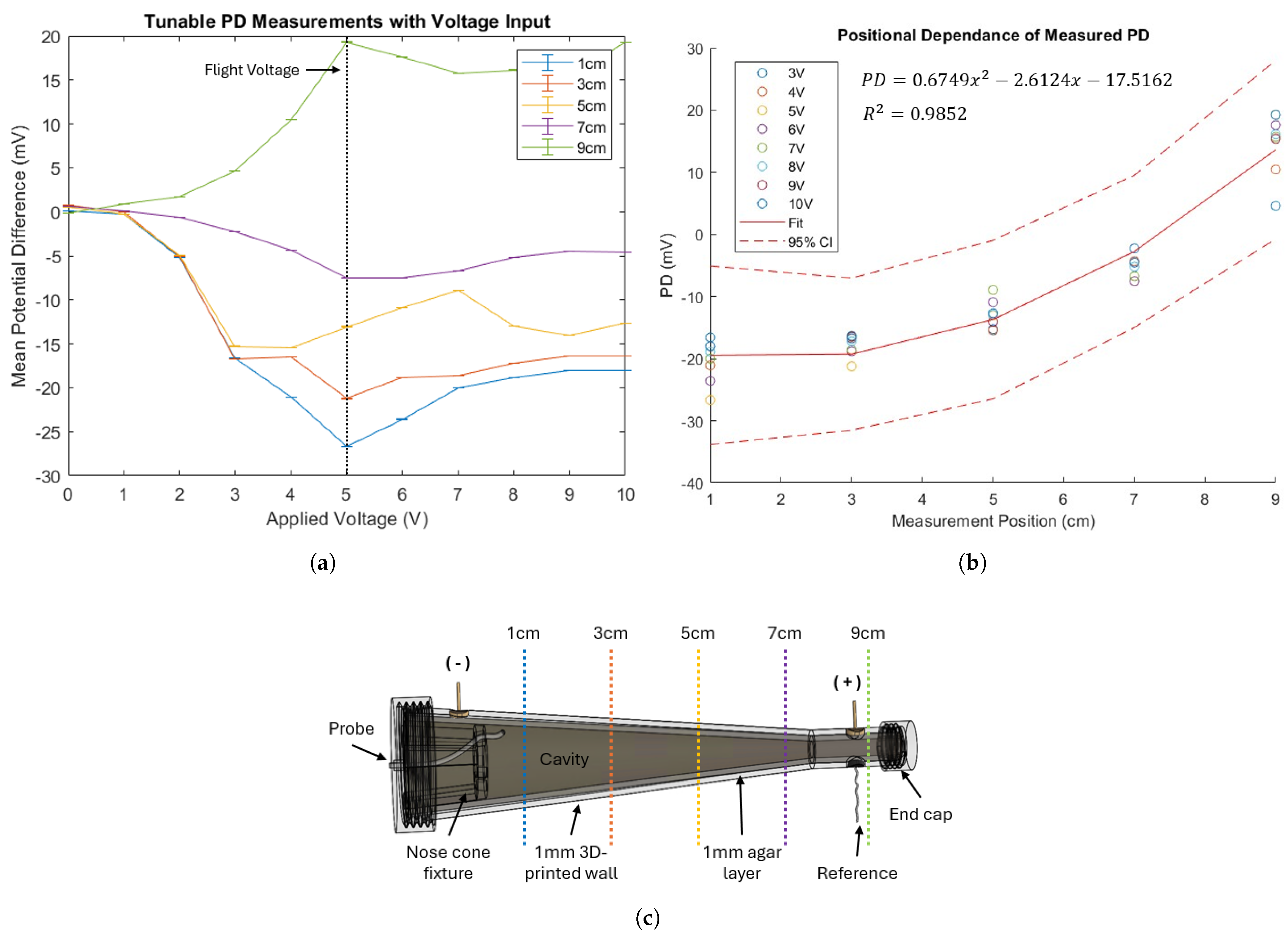
4.1. Ground Validation of Tunable PD
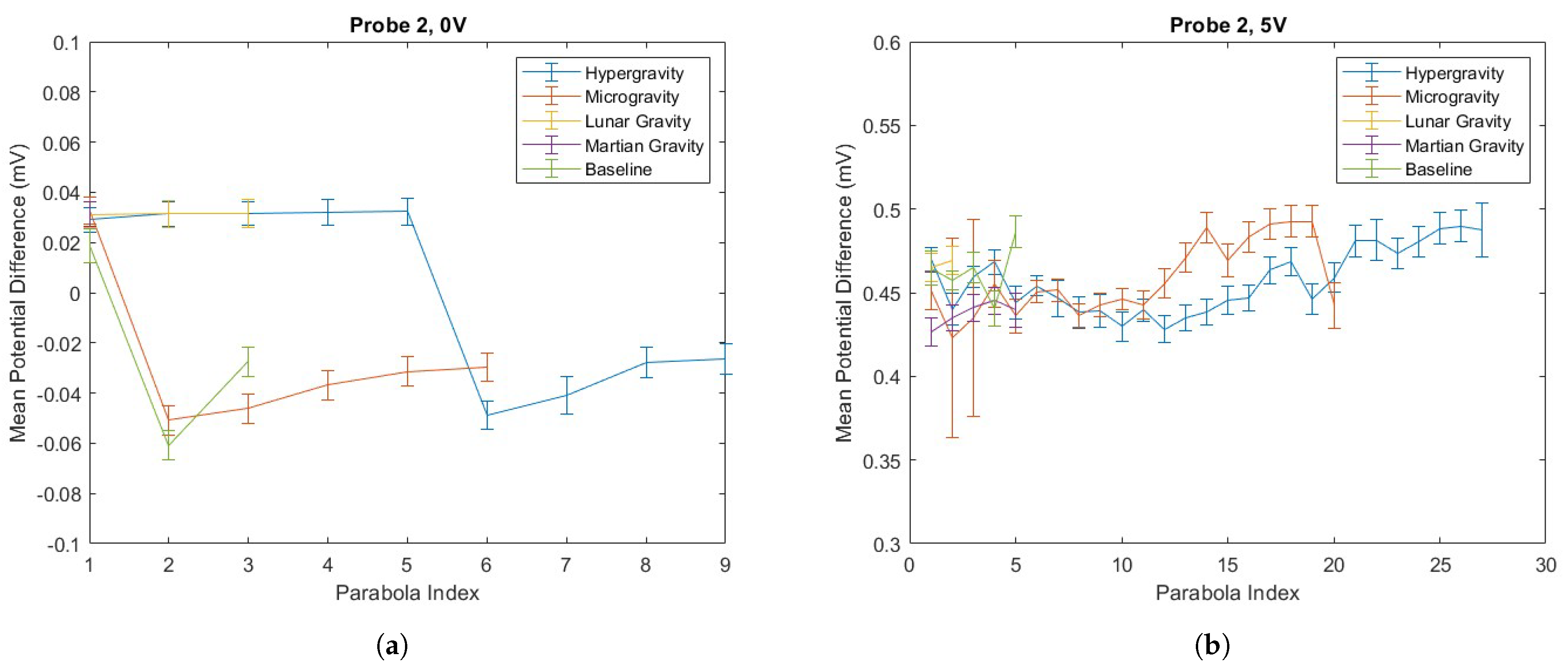
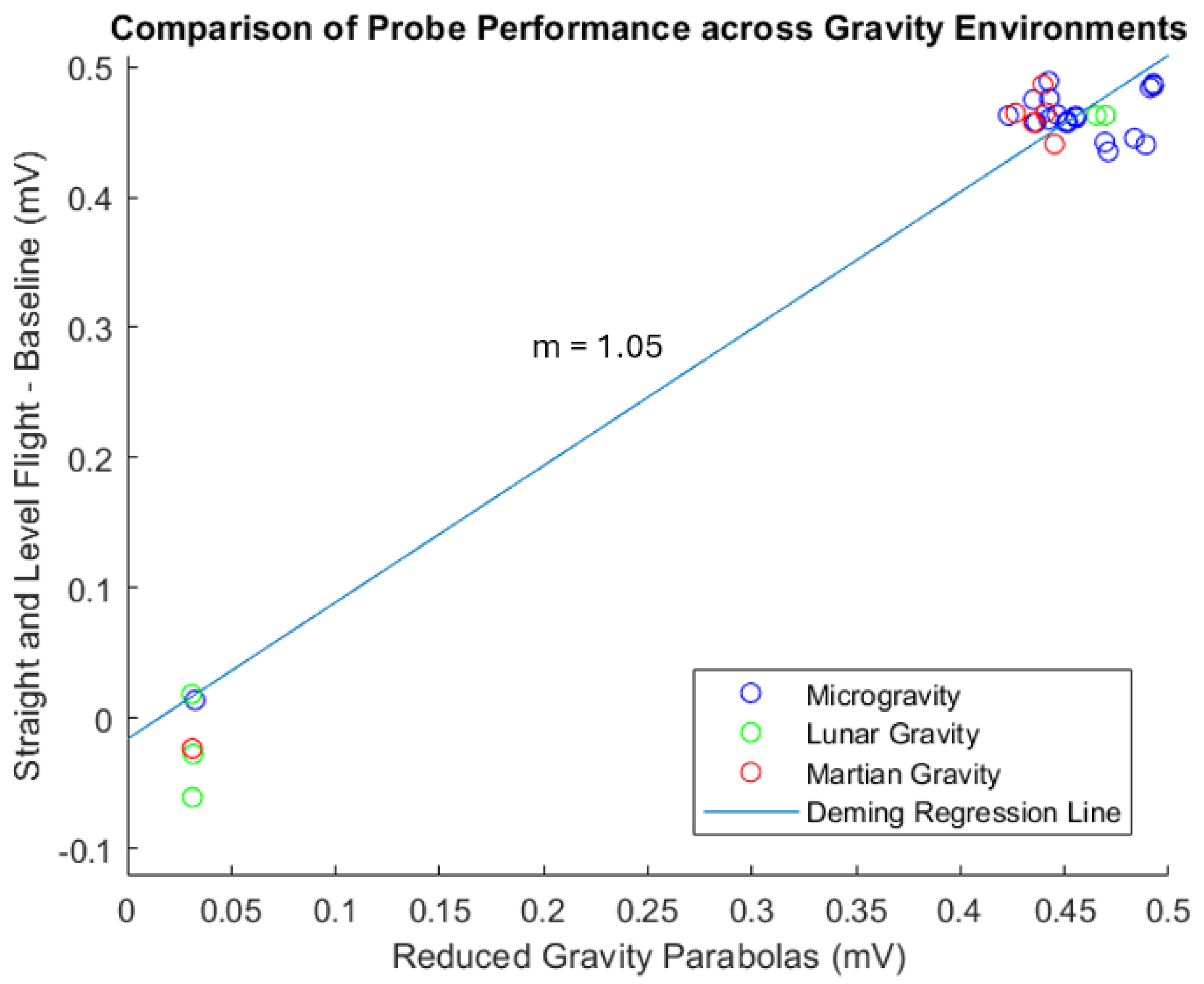
4.2. PD Probe Operation in Parabolic Flight
5. Discussion
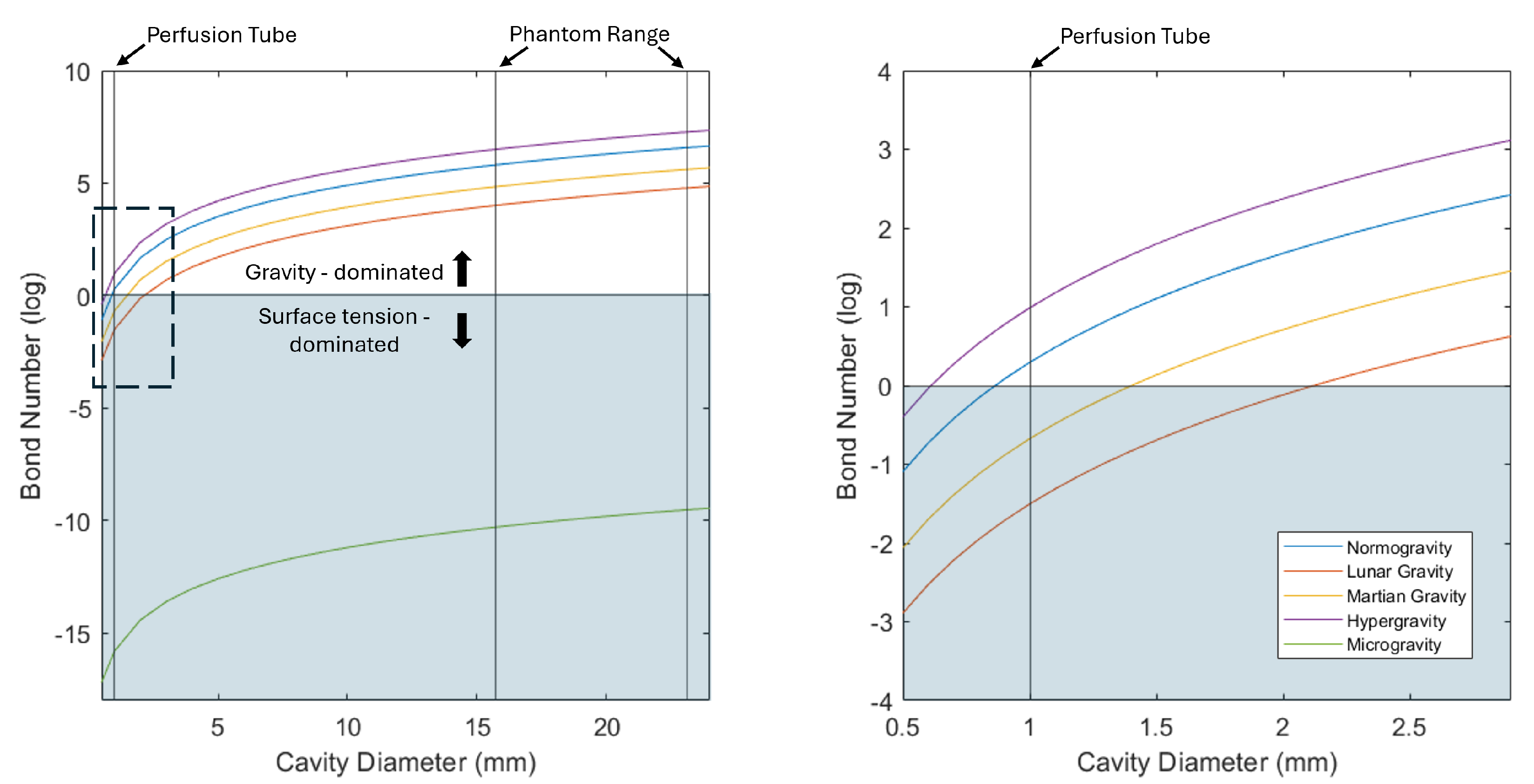
5.1. Perfusion Probes in Altered Gravity
5.2. Future Probe Design with Capillarity-Driven Perfusion
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Goodliff, K.E.; Merancy, N.F.; Bhakta, S.S.; Rucker, M.A.; Chai, P.R.P.; Ashurst, T.E.; Troutman, P.A.; Stromgren, C. Exploration Systems Development Mission Directorate (ESDMD) Moon-to-Mars Architecture Definition Document; National Aeronautics and Space Administration: Washington, DC, USA, 2023. [Google Scholar]
- Program, H.R. Risks; Technical Report; National Aeronautics and Space Administration: Washington, DC, USA, 2024. [Google Scholar]
- Wuest, S.L.; Gantenbein, B.; Ille, F.; Egli, M. Electrophysiological experiments in microgravity: Lessons learned and future challenges. NPJ Microgravity 2018, 4, 7. [Google Scholar] [CrossRef] [PubMed]
- Nday, C.M.; Frantzidis, C.; Jackson, G.; Bamidis, P.; Kourtidou-Papadeli, C. Neurophysiological changes in simulated microgravity: An animal model. Neurol. India 2019, 67, S221–S226. [Google Scholar] [CrossRef] [PubMed]
- Aubert, A.E.; Beckers, F.; Verheyden, B. Cardiovascular function and basics of physiology in microgravity. Acta Cardiol. 2005, 60, 129–151. [Google Scholar] [CrossRef] [PubMed]
- Clément, G.; Ngo-Anh, J.T. Space physiology II: Adaptation of the central nervous system to space flight—Past, current, and future studies. Eur. J. Appl. Physiol. 2013, 113, 1655–1672. [Google Scholar] [CrossRef] [PubMed]
- Otuya, D.O.; Gavgiotaki, E.; Carlson, C.J.; Shi, S.Q.; Lee, A.J.; Krall, A.A.; Chung, A.; Grant, C.G.; Bhat, N.M.; Choy, P.; et al. Minimally Invasive Image-Guided Gut Transport Function Measurement Probe. Front. Phys. 2021, 9, 735645. [Google Scholar] [CrossRef] [PubMed]
- Otuya, D.O.; Vijaykumar, K.; Anderson, J.; Dechene, N.; Zoghbi, S.; Hathore, H.; Baker, E.; Lignelli, T.C.; Chung, A.S.; Grant, C.N.; et al. Development of a Novel Potential Difference Probe with Bedside Validation Simulator for Potential Difference Testing. Am. J. Physiol.-Lung Cell. Mol. Physiol. 2024; in preparatin; under review. [Google Scholar]
- Baig, M. Effect of the gravitational field strength on the rate of chemical reactions. Open Phys. 2024, 22, 20240062. [Google Scholar] [CrossRef]
- Lecca, P. The effects of gravitational potential on chemical reaction rates. J. Phys. Conf. Ser. 2021, 2090, 012034. [Google Scholar] [CrossRef]
- Barmatz, M.; Hahn, I.; Lipa, J.; Duncan, R. Critical phenomena in microgravity: Past, present, and future. Rev. Mod. Phys. 2007, 79, 1–52. [Google Scholar] [CrossRef]
- Carruthers, J. Fluid behavior in a microgravity environment. Appl. Space Flight Mater. Sci. Technol. 1978, 1, 17. [Google Scholar]
- Lappa, M. Fluids, Materials and Microgravity: Numerical Techniques and Insights into Physics; Elsevier: Amsterdam, The Netherlands, 2004. [Google Scholar]
- Nijhuis, J.; Schmidt, S.; Tran, N.N.; Hessel, V. Microfluidics and Macrofluidics in Space: ISS-Proven Fluidic Transport and Handling Concepts. Front. Space Technol. 2022, 2, 779696. [Google Scholar] [CrossRef]
- Kimmel, W.M.; Beauchamp, P.M.; Frerking, M.A.; Kline, T.R.; Vassigh, K.K.; Willard, D.E.; Johnson, M.A.; Trenkle, T.G. Technology Readiness Assessment Best Practices Guide. 2020. Available online: https://ntrs.nasa.gov/citations/20205003605 (accessed on 13 July 2025).
- Karmali, F.; Shelhamer, M. The dynamics of parabolic flight: Flight characteristics and passenger percepts. Acta Astronaut. 2008, 63, 594–602. [Google Scholar] [CrossRef] [PubMed]
- Shelhamer, M. Parabolic flight as a spaceflight analog. J. Appl. Physiol. 2016, 120, 1442–1448. [Google Scholar] [CrossRef] [PubMed]
- Kang, H. Sample size determination and power analysis using the G* Power software. J. Educ. Eval. Health Prof. 2021, 18, 17. [Google Scholar] [CrossRef] [PubMed]
- Hommerich, C.; Riegel, A. Measuring of the piriform aperture in humans with 3D-SSD-CT-reconstructions. Ann. Anat.-Anat. Anz. 2002, 184, 455–459. [Google Scholar] [CrossRef] [PubMed]
- Carr, C.E.; Bryan, N.C.; Saboda, K.N.; Bhattaru, S.A.; Ruvkun, G.; Zuber, M.T. Acceleration profiles and processing methods for parabolic flight. NPJ Microgravity 2018, 4, 14. [Google Scholar] [CrossRef] [PubMed]
- Martin, R.F. General Deming regression for estimating systematic bias and its confidence interval in method-comparison studies. Clin. Chem. 2000, 46, 100–104. [Google Scholar] [CrossRef] [PubMed]
- Seber, G.A. Multivariate Observations; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Hirshorn, S.R.; Voss, L.D.; Bromley, L.K. NASA Systems Engineering Handbook; NASA: Washington, DC, USA, 2017. [Google Scholar]
- Washburn, E.W. The dynamics of capillary flow. Phys. Rev. 1921, 17, 273. [Google Scholar] [CrossRef]
- Ultra-Small Diameter Tubing. Available online: https://www.handytube.com/products/ultra-small-diameter-tubing (accessed on 13 July 2025).
- Hirata, Y.; Novotny, M. Techniques of capillary liquid chromatography. J. Chromatogr. A 1979, 186, 521–528. [Google Scholar] [CrossRef]
| Test Pairing | 5 V | 0 V | ||
|---|---|---|---|---|
| p-Value | Effect Size | p-Value | Effect Size | |
| Hypergravity vs. Baseline | 0.5334 | 0.0057 | 0.2818 | 0.0247 |
| Microgravity vs. Baseline | 0.5636 | 0.0049 | 0.9048 | 0.0038 |
| Lunar Gravity vs. Baseline | 0.3810 | 0.0046 | 0.1000 | 0.0546 |
| Martian Gravity vs. Baseline | 0.0317 | 0.0254 | 0.5000 | 0.0546 |
| Hypergravity vs. Microgravity | 0.8380 | 0.0008 | 0.2238 | 0.0285 |
| Hypergravity vs. Lunar Gravity | 0.4644 | 0.0103 | 0.6000 | 0.0299 |
| Hypergravity vs. Martian Gravity | 0.0333 | 0.0197 | 1 | 0.0299 |
| Microgravity vs. Lunar Gravity | 0.4579 | 0.0010 | 0.1667 | 0.0584 |
| Microgravity vs. Martian Gravity | 0.0324 | 0.0205 | 0.5714 | 0.0584 |
| Lunar Gravity vs. Martian Gravity | 0.0952 | 0.0300 | 1 | 0.0002 |
| Parabola Type and Index | Mean (m/s2) | Standard Deviation |
|---|---|---|
| Martian 1 | −3.1780 | 0.3181 |
| Lunar 1 | −1.2722 | 0.1658 |
| Lunar 2 | −1.0320 | 0.0897 |
| Lunar 3 | −1.0990 | 0.0956 |
| Microgravity 1 | 0.5166 | 0.1341 |
| Microgravity 2 | 0.4632 | 0.1694 |
| Microgravity 3 | 0.4627 | 0.1873 |
| Microgravity 4 | 0.5309 | 0.0642 |
| Microgravity 5 | 0.5154 | 0.0569 |
| Microgravity 6 | 0.4872 | 0.0967 |
| Microgravity 7 | 0.5540 | 0.0777 |
| Microgravity 8 | 0.5542 | 0.1108 |
| Microgravity 9 | 0.5981 | 0.1052 |
| Microgravity 10 | 0.5051 | 0.0893 |
| Microgravity 11 | 0.4800 | 0.1328 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
MacRobbie, M.; Chen, V.Z.; Paige, C.; Otuya, D.; Stankovic, A.; Tearney, G. Evaluating the Suitability of Perfusion-Based PD Probes for Use in Altered Gravity Environments. Biosensors 2025, 15, 478. https://doi.org/10.3390/bios15080478
MacRobbie M, Chen VZ, Paige C, Otuya D, Stankovic A, Tearney G. Evaluating the Suitability of Perfusion-Based PD Probes for Use in Altered Gravity Environments. Biosensors. 2025; 15(8):478. https://doi.org/10.3390/bios15080478
Chicago/Turabian StyleMacRobbie, Madelyn, Vanessa Z. Chen, Cody Paige, David Otuya, Aleksandra Stankovic, and Guillermo Tearney. 2025. "Evaluating the Suitability of Perfusion-Based PD Probes for Use in Altered Gravity Environments" Biosensors 15, no. 8: 478. https://doi.org/10.3390/bios15080478
APA StyleMacRobbie, M., Chen, V. Z., Paige, C., Otuya, D., Stankovic, A., & Tearney, G. (2025). Evaluating the Suitability of Perfusion-Based PD Probes for Use in Altered Gravity Environments. Biosensors, 15(8), 478. https://doi.org/10.3390/bios15080478





