Raman Spectroscopy for Urea Breath Test
Abstract
1. Introduction
2. Materials and Methods
2.1. Gas Analyzer
2.2. Samples
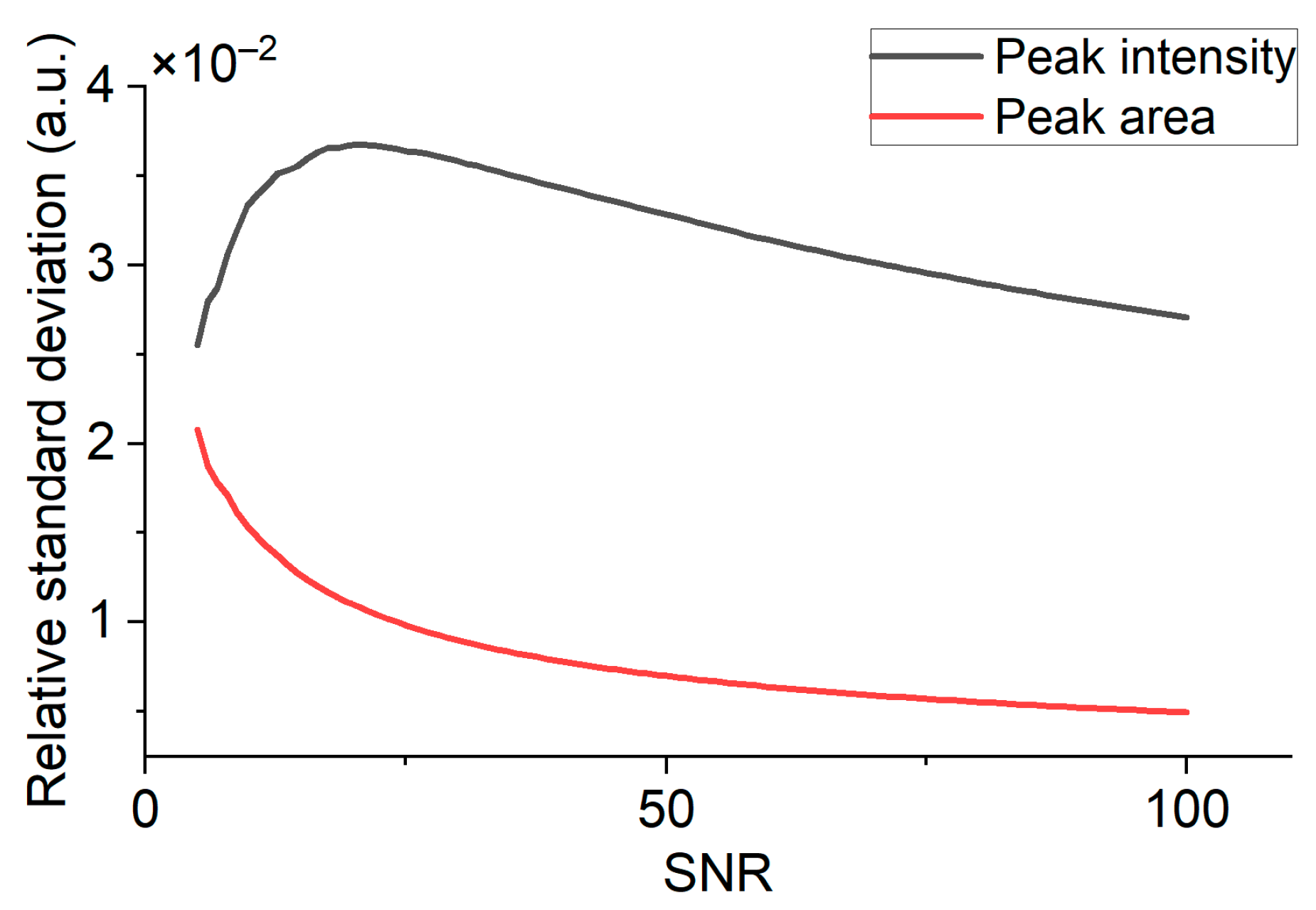
2.3. Signal Processing
X13C = k13·S13C·CΔw/(P·W·t)
2.4. Absolute Uncertainty of Measurement Requirements
3. Results
3.1. Influence of Temperature on SNR
3.2. Influence of Pressure on SNR
3.3. Exhaled Air Measurements
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Issitt, T.; Wiggins, L.; Veysey, M.; Sweeney, S.T.; Brackenbury, W.J.; Redeker, K. Volatile compounds in human breath: Critical review and meta-analysis. J. Breath Res. 2022, 16, 024001. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Zhang, Y.; Pan, F.; Liu, J.; Wang, K.; Zhang, C.; Gabriel, A.; Jesús, M.; Chen, D.; Cui, D. Breath analysis based on surface-enhanced Raman scattering sensors distinguishes early and advanced gastric cancer patients from healthy persons. ACS Nano 2016, 10, 8169–8179. [Google Scholar] [CrossRef] [PubMed]
- Ligor, T.; Szeliga, J.; Jackowski, M.; Buszewski, B. Preliminary study of volatile organic compounds from breath and stomach tissue by means of solid phase microextraction and gas chromatography–mass spectrometry. J. Breath Res. 2007, 1, 016001. [Google Scholar] [CrossRef] [PubMed]
- Jaimes, A.L.; Durán, C.M.; Gualdrón, O.E.; Ionescu, S.R. Stomach cancer detection through exhaled breath using biomarkers analysis. Chem. Eng. 2018, 68, 43–48. [Google Scholar]
- Kumar, S.; Huang, J.; Abbassi-Ghadi, N.; Španěl, P.; Smith, D.; Hanna, G.B. Selected ion flow tube mass spectrometry analysis of exhaled breath for volatile organic compound profiling of esophago-gastric cancer. Anal. Chem. 2013, 85, 6121–6128. [Google Scholar] [CrossRef]
- Kumar, S.; Huang, J.; Abbassi-Ghadi, N.; Mackenzie, H.A.; Veselkov, K.A.; Hoare, J.M.; Lovat, L.B.; Španěl, P.; Smith, D.; Hanna, G.B. Mass spectrometric analysis of exhaled breath for the identification of volatile organic compound biomarkers in esophageal and gastric adenocarcinoma. Ann. Surg. 2015, 262, 981–990. [Google Scholar] [CrossRef]
- Markar, S.R.; Wiggins, T.; Antonowicz, S.; Chin, S.T.; Romano, A.; Nikolic, K.; Benjamin, E.; David, C.; Muntzer, M.; Jesper, L.; et al. Assessment of a noninvasive exhaled breath test for the diagnosis of oesophagogastric cancer. JAMA Oncol. 2018, 4, 970–976. [Google Scholar] [CrossRef]
- Shehada, N.; Cancilla, J.C.; Torrecilla, J.S.; Pariente, E.S.; Brönstrup, G.; Christiansen, S.; Douglas, W.; Johnson Marcis, L.; Davies, M.P.A.; Liran, O.; et al. Silicon nanowire sensors enable diagnosis of patients via exhaled breath. ACS Nano 2016, 10, 7047–7057. [Google Scholar] [CrossRef]
- Gharra, A.; Broza, Y.Y.; Yu, G.; Mao, W.; Shen, D.; Deng, L.; Wu, C.; Wang, Q.; Sun, X.; Huang, J.; et al. Exhaled breath diagnostics of lung and gastric cancers in China using nanosensors. Cancer Commun. 2020, 40, 273. [Google Scholar] [CrossRef]
- Haddad, G.; Schouwenburg, S.; Altesha, A.; Xu, W.; Liu, G. Using breath analysis as a screening tool to detect gastric cancer: A systematic review. J. Breath Res. 2021, 15, 016013. [Google Scholar] [CrossRef]
- Franceschi, F.; Gasbarrini, A. Helicobacter pylori and extragastric diseases. Best Pract. Res. Clin. Gastroenterol. 2007, 21, 325–334. [Google Scholar] [CrossRef]
- Bordin, D.S.; Voynovan, I.N.; Andreev, D.N.; Maev, I.V. Current Helicobacter pylori diagnostics. Diagnostics 2021, 11, 1458. [Google Scholar] [CrossRef]
- Logan, R. Urea breath tests in the management of Helicobacter pylori infection. Gut 1998, 43, S47. [Google Scholar] [CrossRef]
- Metsälä, M. Optical techniques for breath analysis: From single to multi-species detection. J. Breath Res. 2018, 12, 027104. [Google Scholar] [CrossRef]
- Gisbert, J.P.; Pajares, J.M. 13C-urea breath test in the diagnosis of Helicobacter pylori infection—A critical review. Aliment. Pharmacol. Ther. 2004, 20, 1001–1017. [Google Scholar] [CrossRef]
- Barth, E.; Tugtekin, I.; Weidenbach, H.; Wachter, U.; Vogt, J.; Radermacher, P.; Adler, G.; Georgieff, M. Determination of 13CO2/12CO2 ratio by IRMS and NDIRS. Isot. Environ. Health Stud. 1998, 34, 209–213. [Google Scholar] [CrossRef]
- Kwon, Y.H.; Kim, N.; Lee, J.Y.; Choi, Y.J.; Yoon, K.; Hwang, J.J.; Hyun, J.L.; AeRa, L.; Yeon, S.J.; Sooyeon, O.; et al. The Diagnostic Validity of Citric Acid-Free, High Dose 13C-Urea Breath Test after Helicobacter pylori Eradication in Korea. Helicobacter 2015, 20, 159–168. [Google Scholar] [CrossRef]
- Kawai, S.; Arai, K.; Li, Y.; Nishiyama, T.; Sasakabe, T.; Wan, C.; Hiroto, M.; Kikuchi, S. Comparison of the detection of Helicobacter pylori infection by commercially available serological testing kits and the 13C-urea breath test. J. Infect. Chemother. 2019, 25, 769–773. [Google Scholar] [CrossRef]
- Machado, R.S.; Reber, M.; Patrício, F.R. 13C-urea breath test with infrared spectroscopy for diagnosing Helicobacter pylori infection in children and adolescents. J. Pediatr. Gastroenterol. Nutr. 2002, 35, 39–43. [Google Scholar]
- Плавник, Р.Г.; Невмержицкий, В.И.; Бутoрoва, Л.И.; Плавник, Т. Сравнительная oценка масс-спектрoметрии и инфракраснoй спектрoметрии при прoведении 13С-уреазнoгo дыхательнoгo теста на Helicobacter pylori. Клиническая медицина 2015, 93, 42–45. [Google Scholar]
- Pichon, M.; Pichard, B.; Barrioz, T.; Plouzeau, C.; Croquet, V.; Fotsin, G.; Chéron, A.; Vuillemin, É.; Wangermez, M.; Haineaux, P.A. Diagnostic Accuracy of a Noninvasive Test for Detection of Helicobacter pylori and Resistance to Clarithromycin in Stool by the Amplidiag H. pylori + ClariR Real-Time PCR Assay. J. Clin. Microbiol. 2020, 58, e01787-19. [Google Scholar] [CrossRef] [PubMed]
- Ferwana, M.; Abdulmajeed, I.; Alhajiahmed, A.; Madani, W.; Firwana, B.; Hasan, R.; Altayar, O.; Limburg, P.J.; Murad, M.H.; Knawy, B. Accuracy of urea breath test in Helicobacter pylori infection: Meta-analysis. World J. Gastroenterol. 2015, 21, 1305–1314. [Google Scholar] [CrossRef] [PubMed]
- Leal, Y.A.; Flores, L.L.; Fuentes-Pananá, E.M.; Cedillo-Rivera, R.; Torres, J. 13C-urea breath test for the diagnosis of Helicobacter pylori infection in children: A systematic review and meta-analysis. Helicobacter 2011, 16, 327–337. [Google Scholar] [CrossRef] [PubMed]
- Peng, N.J.; Lai, K.H.; Liu, R.S.; Lee, S.C.; Tsay, D.G.; Lo, C.C. Clinical significance of oral urease in diagnosis of Helicobacter pylori infection by [13C] urea breath test. Dig. Dis. Sci. 2001, 46, 1772–1778. [Google Scholar] [CrossRef]
- Vitkin, V.; Polishchuk, A.; Chubchenko, I.; Popov, E.; Grigorenko, K.; Kharitonov, A.; Davtian, A.; Kovalev, A.; Kurikova, V.; Camy, P.; et al. Raman laser spectrometer: Application to 12C/13C isotope identification in CH4 and CO2 greenhouse gases. Appl. Sci. 2020, 10, 7473. [Google Scholar] [CrossRef]
- Petrov, D.V.; Matrosov, I.I. Raman gas analyzer (RGA): Natural gas measurements. Appl. Spectrosc. 2016, 70, 1770–1776. [Google Scholar] [CrossRef]
- Petrov, D.V.; Matrosov, I.I.; Zaripov, A.R.; Tanichev, A.S. Raman Natural Gas Analyzer: Effects of Composition on Measurement Precision. Sensors 2022, 22, 3492. [Google Scholar] [CrossRef]
- Petrov, D.V.; Matrosov, I.I.; Kostenko, M.A. Possibilities of measuring the exhaled air composition using Raman spectroscopy. Quantum Electron. 2021, 51, 389. [Google Scholar] [CrossRef]
- Popov, E.E.; Polischuk, A.V.; Vitkin, V.V. Exhaled air Raman spectroscopy for Helicobacter pylori diagnostics. J. Phys. Conf. Ser. 2022, 2388, 012015. [Google Scholar] [CrossRef]
- Polishchuk, A.; Kenzhebayeva, Y.; Grigorenko, K.; Popov, E.; Vitkin, V. Raman-based high-resolution detection of 13CO2 isotopes in human breath Biomedical. Spectrosc. Microsc. Imaging 2020, 11359, 269–273. [Google Scholar]
- Velez, J.S.G.; Muller, A. Spontaneous Raman scattering at trace gas concentrations with a pressurized external multipass cavity. Meas. Sci. Technol. 2021, 32, 045501. [Google Scholar] [CrossRef]
- Popov, E.; Polishchuk, A.; Grigorenko, K.; Chubchenko, I.; Vitkin, V. Raman detector of carbon isotopes. Opt. Sens. Detect. VI 2020, 11354, 385–389. [Google Scholar]
- Richard, L. Chemical Analysis: A Series of Monographs on Analytical Chemistry and Its Applications; John Wiley & Sons: Hoboken, NJ, USA, 2000. [Google Scholar]
- Slater, C.; Preston, T.; Weaver, L.T. Stable isotopes and the international system of units. Rapid Commun. Mass Spectrom. 2001, 15, 1270–1273. [Google Scholar] [CrossRef]
- Pleil, J.D.; Wallace, M.A.G.; Davis, M.D.; Matty, C.M. The physics of human breathing: Flow, timing, volume, and pressure parameters for normal, on-demand, and ventilator respiration. J. Breath Res. 2021, 15, 042002. [Google Scholar] [CrossRef]
- Tsoukias Nikolaos, M.; Wilson, A.F.; George, S.C. Single-exhalation profiles of NO and CO2 in humans: Effect of dynamically changing flow rate. J. Appl. Physiol. 1998, 85, 642–652. [Google Scholar] [CrossRef]
- Eggleston, S.; Schmitt, J.; Bereiter, B.; Schneider, R.; Fischer, H. Evolution of the stable carbon isotope composition of atmospheric CO2 over the last glacial cycle. Paleoceanography 2016, 31, 434–452. [Google Scholar] [CrossRef]
- De Laeter, J.R.; Böhlke, J.K.; De Bievre, P.; Hidaka, H.; Peise, H.S.; Rosman, K.J.R.; Taylor, P.D.P. Atomic weights of the elements. Review 2000 (IUPAC Technical Report). Pure Appl. Chem. 2003, 75, 683–800. [Google Scholar] [CrossRef]
- Berglund, M.; Wieser, M.E. Isotopic compositions of the elements 2009 (IUPAC Technical Report). Pure Appl. Chem. 2011, 83, 397–410. [Google Scholar] [CrossRef]
- Widenhorn, R.; Blouke, M.M.; Weber, A.; Rest, A.; Bodegom, E. Temperature dependence of dark current in a CCD Sensors and Camera Systems for Scientific, Industrial, and Digital Photography. Appl. III 2002, 4669, 193–201. [Google Scholar]
- Jammu, K.S.; John GE, S.; Welsh, H.L. Pressure broadening of the rotational Raman lines of some simple gases. Can. J. Phys. 1966, 44, 797–814. [Google Scholar] [CrossRef]
- Polishchuk, A.V.; Kurikova, V.V.; Grigorenko, K.M.; Vitkin, V.V. High Resolution Raman Detection of 12CO2 and 13CO2 Isotopes in Human Breath. In Proceedings of the 2020 International Conference Laser Optics (ICLO), St. Petersburg, Russia, 2–6 November 2020; p. 1. [Google Scholar]
- Popov, E.E.; Kurikova, V.V. Human breath Raman analysis. In Proceedings of the 2020 International Conference Laser Optics (ICLO), St. Petersburg, Russia, 2–6 November 2020; p. 1. [Google Scholar]








| Sample | 12CO2 Volume Fraction | 13CO2 Volume Fraction | δ13C |
|---|---|---|---|
| Sample 1 | 5.78% ± 0.08% | 0.0647% ± 0.0008% | |
| Sample 2 | 4.89% ± 0.03% | 0.0526% ± 0.0003% | |
| Sample 3 | 4.89% ± 0.03% | 0.0548% ± 0.0003% | |
| Sample 4 | 3.9% ± 0.03% | 0.0426% ± 0.0003% |
| Participant | Volume Fraction of 12CO2, % | Volume Fraction of 13CO2 in Base Sample, % | Volume Fraction of 13CO2 in Diagnostic Sample, % |
|---|---|---|---|
| Participant 1 | 4.7 ± 0.2 | 0.037 ± 0.007 | 0.038 ± 0.007 |
| Participant 2 | 6.2 ± 0.3 | 0.045 ± 0.008 | 0.046 ± 0.008 |
| Participant 3 | 4.3 ± 0.2 | 0.030 ± 0.007 | 0.041 ± 0.008 |
| Participant 4 | 4.6 ± 0.2 | 0.034 ± 0.007 | 0.056 ± 0.008 |
| Participant 5 | 4.4 ± 0.2 | 0.035 ± 0.008 | 0.036 ± 0.007 |
| Participant 6 | 5.7 ± 0.3 | 0.041 ± 0.008 | 0.046 ± 0.008 |
| Participant 7 | 5.2 ± 0.2 | 0.038 ± 0.007 | 0.057 ± 0.008 |
| Participant 8 | 3.8 ± 0.1 | 0.025 ± 0.006 | 0.032 ± 0.007 |
| Participant 9 | 5.0 ± 0.2 | 0.039 ± 0.007 | 0.055 ± 0.008 |
| Participant 10 | 5.1 ± 0.2 | 0.031 ± 0.007 | 0.050 ± 0.008 |
| Participant 11 | 6.3 ± 0.3 | 0.045 ± 0.008 | 0.060 ± 0.009 |
| Participant 12 | 5.4 ± 0.3 | 0.038 ± 0.007 | 0.046 ± 0.008 |
| Participant 13 | 4.6 ± 0.2 | 0.032 ± 0.007 | 0.041 ± 0.008 |
| Participant 14 | 6.1 ± 0.3 | 0.048 ± 0.008 | 0.050 ± 0.008 |
| Participant 15 | 6.3 ± 0.3 | 0.044 ± 0.008 | 0.055 ± 0.009 |
| Participant | δ13C Difference, ‰ | Participant | δ13C Difference, ‰ |
|---|---|---|---|
| Participant 1 | 0.26 ± 0.02 | Participant 9 | 5.0 ± 0.2 |
| Participant 2 | 0.76 ± 0.02 | Participant 10 | 5.6 ± 0.3 |
| Participant 3 | 3.8 ± 0.2 | Participant 11 | 2.4 ± 0.05 |
| Participant 4 | 7.4 ± 0.2 | Participant 12 | 2.3 ± 0.05 |
| Participant 5 | 0.57 ± 0.02 | Participant 13 | 3.2 ± 0.05 |
| Participant 6 | 1.3 ± 0.05 | Participant 14 | 0.6 ± 0.03 |
| Participant 7 | 5.6 ± 0.3 | Participant 15 | 2.5 ± 0.05 |
| Participant 8 | 2.6 ± 0.1 |
| Participant | IgG Result | UBT Result |
|---|---|---|
| Participant 1 | negative | negative |
| Participant 2 | uncertain | negative |
| Participant 3 | uncertain | uncertain |
| Participant 4 | positive | positive |
| Participant 5 | negative | negative |
| Participant 6 | uncertain | negative |
| Participant 7 | positive | positive |
| Participant 8 | uncertain | negative |
| Participant 9 | positive | positive |
| Participant 10 | negative | positive |
| Participant 11 | negative | negative |
| Participant 12 | uncertain | negative |
| Participant 13 | uncertain | uncertain |
| Participant 14 | negative | negative |
| Participant 15 | positive | negative |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popov, E.; Polishchuk, A.; Kovalev, A.; Vitkin, V. Raman Spectroscopy for Urea Breath Test. Biosensors 2023, 13, 609. https://doi.org/10.3390/bios13060609
Popov E, Polishchuk A, Kovalev A, Vitkin V. Raman Spectroscopy for Urea Breath Test. Biosensors. 2023; 13(6):609. https://doi.org/10.3390/bios13060609
Chicago/Turabian StylePopov, Evgeniy, Anton Polishchuk, Anton Kovalev, and Vladimir Vitkin. 2023. "Raman Spectroscopy for Urea Breath Test" Biosensors 13, no. 6: 609. https://doi.org/10.3390/bios13060609
APA StylePopov, E., Polishchuk, A., Kovalev, A., & Vitkin, V. (2023). Raman Spectroscopy for Urea Breath Test. Biosensors, 13(6), 609. https://doi.org/10.3390/bios13060609





