Biosensor Design for the Detection of Circulating Tumor Cells Using the Quartz Crystal Resonator Technique
Abstract
1. Introduction
2. Materials and Methods
2.1. Mathematical Modeling of QCR Mass Sensitivity
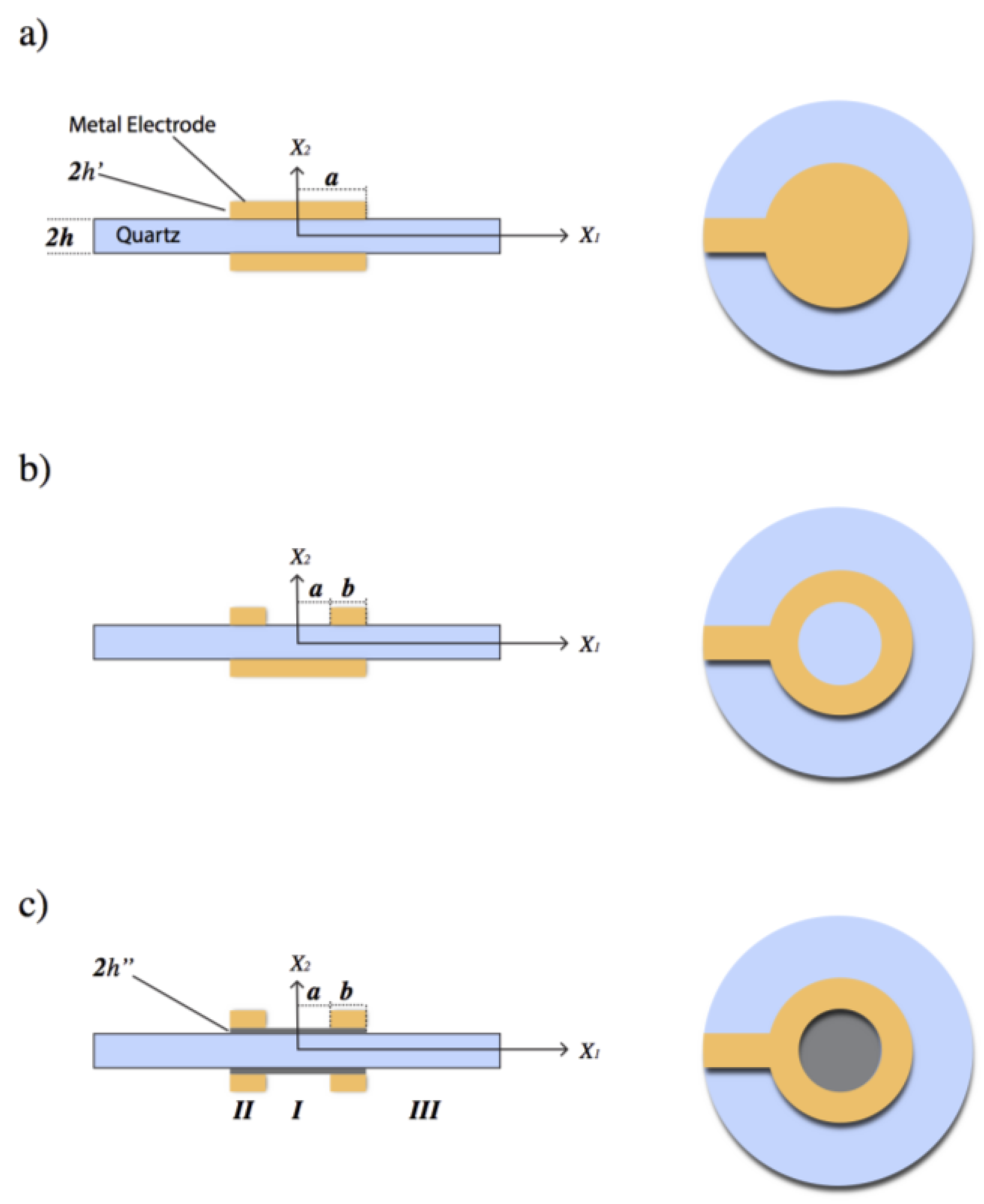
2.2. Quartz Crystal Design for Mass Sensitivity Measurements
2.3. Mass Sensitivity Distribution Measurements
2.4. Circulating Tumor Cell Detection
2.4.1. Surface Modification of the Ring Electrode
2.4.2. Surface Characterization and Cell Counting
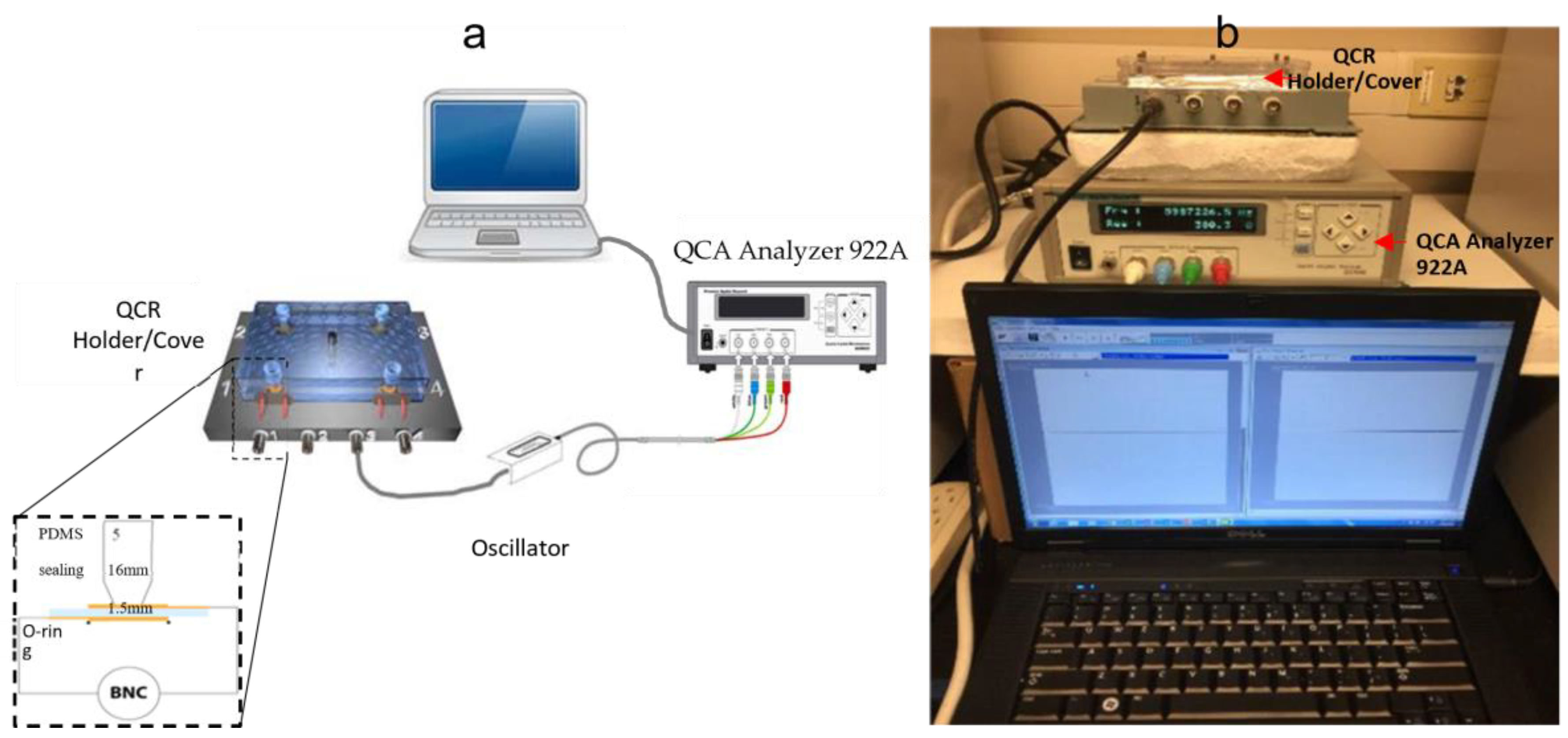
2.4.3. Quartz Crystal Holder Design and Fabrication
2.4.4. Biosensor Measurements
2.4.5. Origin of Cancer Cell Lines
3. Results and Discussion
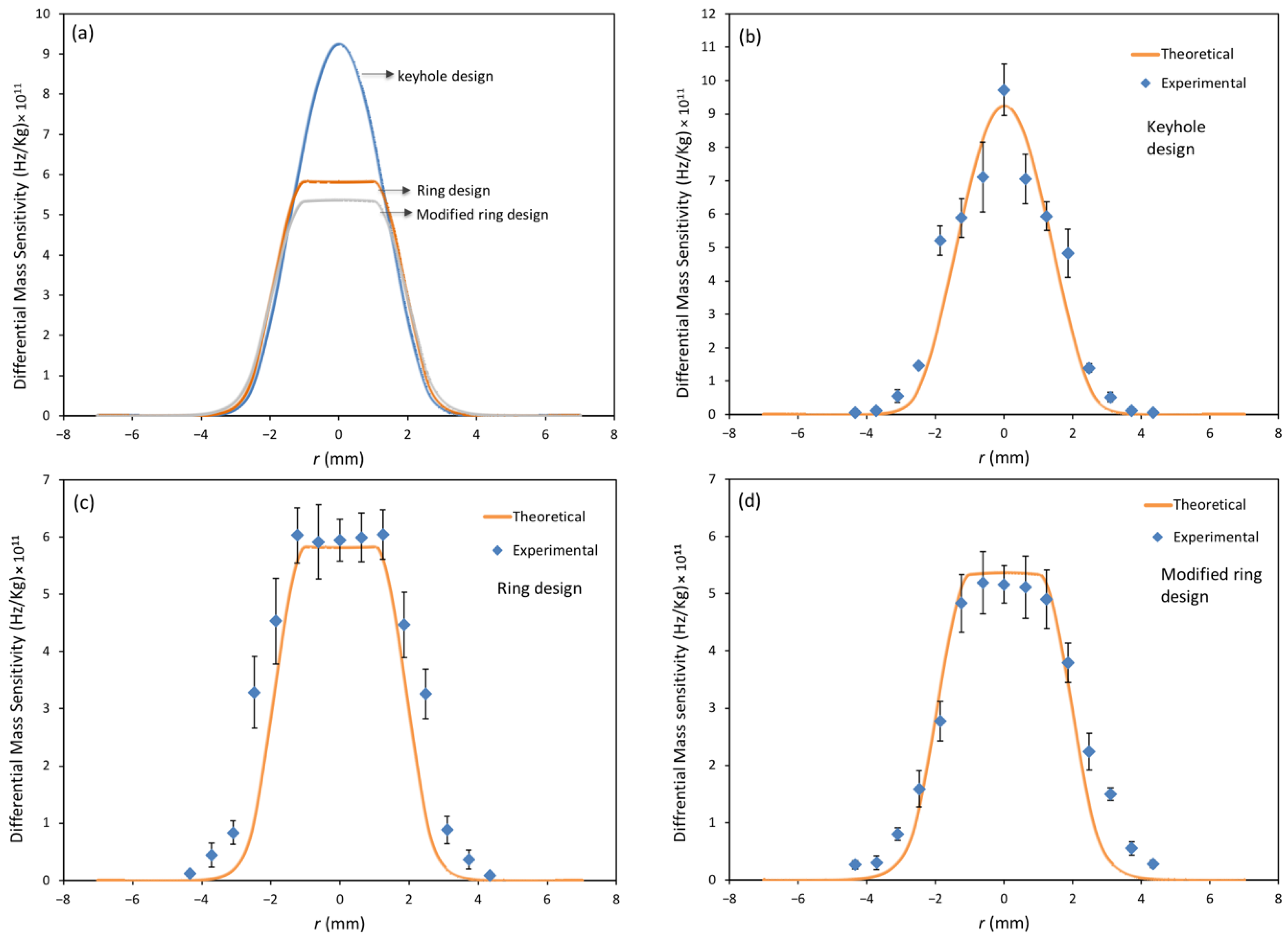
3.1. Mass Sensitivity Distribution Measurements
3.2. Analysis of Surface Modification
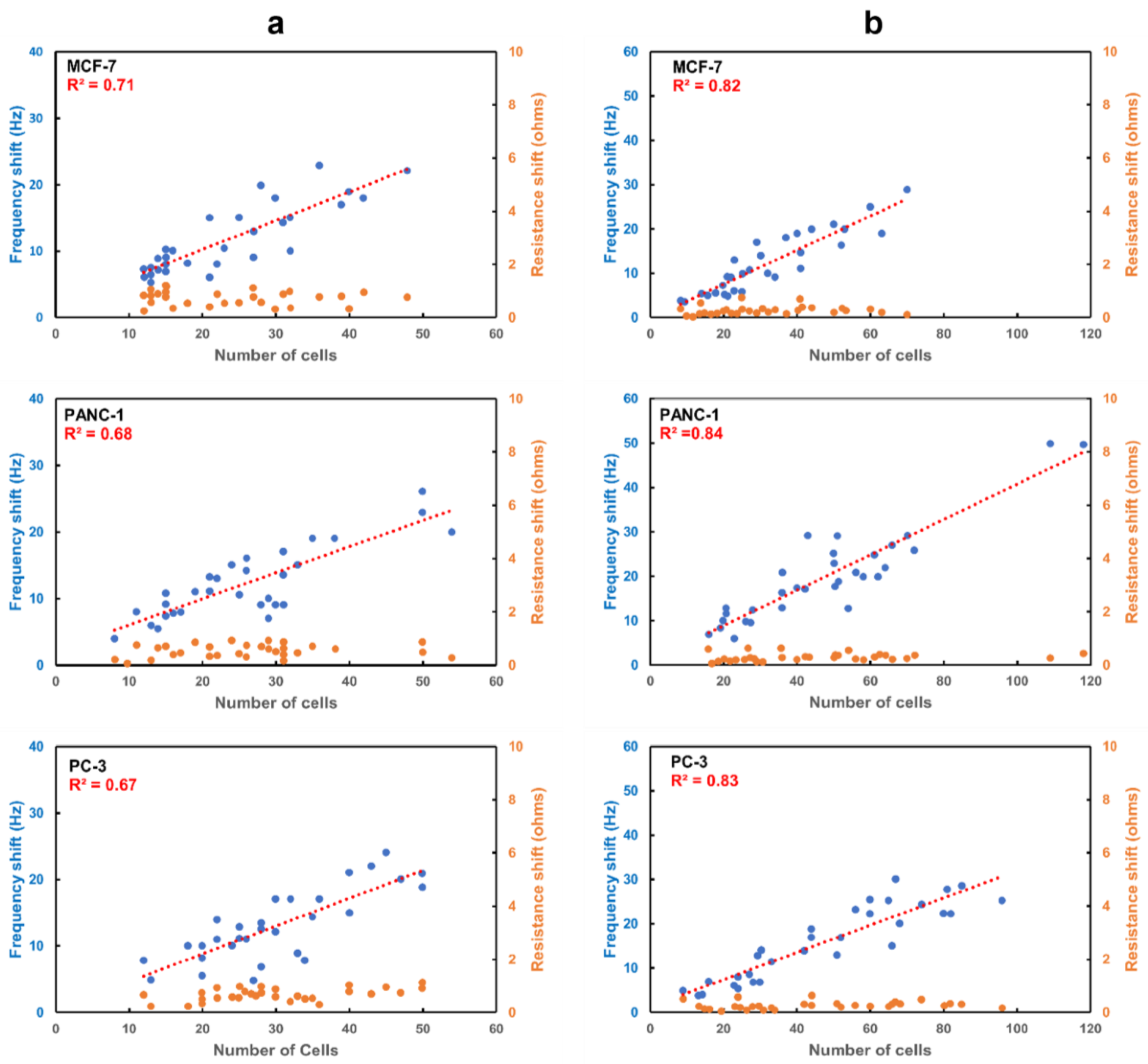
3.3. Cancer Cell Detection
3.3.1. Capture Efficiency of Anti-EpCAM Immobilized APTES Decorated Ring Electrode QCR
3.3.2. Spatial Sensitivity Measurements
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Keyhole Electrode QCR
Appendix A.2. Ring Electrode QCR
Appendix A.3. Modified Ring Electrode QCR
References
- Vashist, S.K. Point-of-Care Diagnostics: Recent Advances and Trends. Biosensors 2017, 7, 62. [Google Scholar] [CrossRef] [PubMed]
- Iliescu, F.S.; Ionescu, A.M.; Gogianu, L.; Simion, M.; Dediu, V.; Chifiriuc, M.C.; Pircalabioru, G.G.; Iliescu, C. Point-of-Care Testing & mdash; The Key in the Battle against SARS-CoV-2 Pandemic. Micromachines 2021, 12, 1464. [Google Scholar] [CrossRef] [PubMed]
- Bhaskar, S.; Singh, A.K.; Das, P.; Jana, P.; Kanvah, S.; Bhaktha, B.N.S.; Ramamurthy, S.S. Superior Resonant Nanocavities Engineering on the Photonic Crystal-Coupled Emission Platform for the Detection of Femtomolar Iodide and Zeptomolar Cortisol. ACS Appl. Mater. Interfaces 2020, 12, 34323–34336. [Google Scholar] [CrossRef]
- Choi, S.; Goryll, M.; Sin, L.Y.M.; Wong, P.K.; Chae, J. Microfluidic-Based Biosensors toward Point-of-Care Detection of Nucleic Acids and Proteins. Microfluid. Nanofluidics 2010, 10, 231–247. [Google Scholar] [CrossRef]
- Choudhary, S.; Altintas, Z. Development of a Point-of-Care SPR Sensor for the Diagnosis of Acute Myocardial Infarction. Biosensors 2023, 13, 229. [Google Scholar] [CrossRef]
- Hwang, C.; Lee, W.J.; Kim, S.D.; Park, S.; Kim, J.H. Recent Advances in Biosensor Technologies for Point-of-Care Urinalysis. Biosensors 2022, 12, 1020. [Google Scholar] [CrossRef] [PubMed]
- Kaur, J.; Srivastava, R.; Borse, V. Recent Advances in Point-of-Care Diagnostics for Oral Cancer. Biosens. Bioelectron. 2021, 178, 112995. [Google Scholar] [CrossRef]
- Bacon, A.; Wang, W.; Lee, H.; Umrao, S.; Sinawang, P.D.; Akin, D.; Khemtonglang, K.; Tan, A.; Hirshfield, S.; Demirci, U.; et al. Review of HIV Self Testing Technologies and Promising Approaches for the Next Generation. Biosensors 2023, 13, 298. [Google Scholar] [CrossRef]
- Plaks, V.; Koopman, C.D.; Werb, Z. Circulating Tumor Cells. Science 2013, 341, 1186–1188. [Google Scholar] [CrossRef]
- Paterlini-Brechot, P.; Benali, N.L. Circulating Tumor Cells (CTC) Detection: Clinical Impact and Future Directions. Cancer Lett. 2007, 253, 180–204. [Google Scholar] [CrossRef]
- Krebs, M.G.; Hou, J.M.; Ward, T.H.; Blackhall, F.H.; Dive, C. Circulating Tumour Cells: Their Utility in Cancer Management and Predicting Outcomes. SAGE J. 2010, 2, 351–365. [Google Scholar] [CrossRef] [PubMed]
- Nima, Z.A.; Mahmood, M.; Xu, Y.; Mustafa, T.; Watanabe, F.; Nedosekin, D.A.; Juratli, M.A.; Fahmi, T.; Galanzha, E.I.; Nolan, J.P.; et al. Circulating Tumor Cell Identification by Functionalized Silver-Gold Nanorods with Multicolor, Super-Enhanced SERS and Photothermal Resonances. Sci. Rep. 2014, 4, 04752. [Google Scholar] [CrossRef]
- Galanzha, E.I.; Shashkov, E.V.; Kelly, T.; Kim, J.W.; Yang, L.; Zharov, V.P. In Vivo Magnetic Enrichment and Multiplex Photoacoustic Detection of Circulating Tumour Cells. Nat. Nanotechnol. 2009, 4, 855–860. [Google Scholar] [CrossRef]
- Nagrath, S.; Sequist, L.V.; Maheswaran, S.; Bell, D.W.; Irimia, D.; Ulkus, L.; Smith, M.R.; Kwak, E.L.; Digumarthy, S.; Muzikansky, A.; et al. Isolation of Rare Circulating Tumour Cells in Cancer Patients by Microchip Technology. Nature 2007, 450, 1235–1239. [Google Scholar] [CrossRef] [PubMed]
- Kuo, A.H.; Clarke, M.F. Identifying the Metastatic Seeds of Breast Cancer. Nat. Biotechnol. 2013, 31, 504–505. [Google Scholar] [CrossRef]
- Stott, S.L.; Hsu, C.H.; Tsukrov, D.I.; Yu, M.; Miyamoto, D.T.; Waltman, B.A.; Michael Rothenberg, S.; Shah, A.M.; Smas, M.E.; Korir, G.K.; et al. Isolation of Circulating Tumor Cells Using a Microvortex-Generating Herringbone-Chip. Proc. Natl. Acad. Sci. USA 2010, 107, 18392–18397. [Google Scholar] [CrossRef]
- Hao, S.J.; Wan, Y.; Xia, Y.Q.; Zou, X.; Zheng, S.Y. Size-Based Separation Methods of Circulating Tumor Cells. Adv. Drug Deliv. Rev. 2018, 125, 3–20. [Google Scholar] [CrossRef]
- Dao, M.; Suresh, S.; Huang, T.J.; Li, P.; Mao, Z.; Peng, Z.; Zhou, L.; Chen, Y.; Huang, P.H.; Truica, C.I.; et al. Acoustic Separation of Circulating Tumor Cells. Proc. Natl. Acad. Sci. USA 2015, 112, 4970–4975. [Google Scholar] [CrossRef]
- Unser, S.; Bruzas, I.; He, J.; Sagle, L. Localized Surface Plasmon Resonance Biosensing: Current Challenges and Approaches. Sensors 2015, 15, 15684–15716. [Google Scholar] [CrossRef] [PubMed]
- Medley, C.D.; Smith, J.E.; Tang, Z.; Wu, Y.; Bamrungsap, S.; Tan, W. Gold Nanoparticle-Based Colorimetric Assay for the Direct Detection of Cancerous Cells. Anal. Chem. 2008, 80, 1067–1072. [Google Scholar] [CrossRef]
- Yang, J.; Wang, X.; Sun, Y.; Chen, B.; Hu, F.; Guo, C.; Yang, T. Recent Advances in Colorimetric Sensors Based on Gold Nanoparticles for Pathogen Detection. Biosensors 2022, 13, 29. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.M.; Park, J.S.; Jung, S.W.; Yeom, J.; Yoo, S.M. Biosensing Applications Using Nanostructure-Based Localized Surface Plasmon Resonance Sensors. Sensors 2021, 21, 3191. [Google Scholar] [CrossRef] [PubMed]
- Zhu, S.; Xie, Z.; Chen, Y.; Liu, S.; Kwan, Y.W.; Zeng, S.; Yuan, W.; Ho, H.P. Real-Time Detection of Circulating Tumor Cells in Bloodstream Using Plasmonic Fiber Sensors. Biosensors 2022, 12, 968. [Google Scholar] [CrossRef]
- Lu, C.; Czanderna, A.W. Applications of Piezoelectric Quartz Crystal Microbalances; Elsevier: Amsterdam, The Netherlands, 1984; p. 408. [Google Scholar]
- Redepenning, J.; Schlesinger, T.K.; Mechalke, E.J.; Puleo, D.A.; Bizios, R. Osteoblast Attachment Monitored with a Quartz Crystal Microbalance. Anal. Chem. 1993, 65, 3378–3381. [Google Scholar] [CrossRef] [PubMed]
- Gryte, D.M.; Ward, M.D.; Hu, W.-S. Real-Time Measurement of Anchorage-Dependent Cell Adhesion Using a Quartz Crystal Microbalance. Biotechnol. Prog. 1993, 9, 105–108. [Google Scholar] [CrossRef] [PubMed]
- Fredriksson, C.; Kihlman, S.; Rodahl, M.; Kasemo, B. The Piezoelectric Quartz Crystal Mass and Dissipation Sensor: A Means of Studying Cell Adhesion. Biology 1998, 14, 248–251. [Google Scholar] [CrossRef]
- Fredriksson, C.; Khilman, S.; Kasemo, B.; Steel, D.M. In Vitro Real-Time Characterization of Cell Attachment and Spreading. J Mater. Sci. Mater. Med. 1998, 9, 785–788. [Google Scholar] [CrossRef]
- Atay, S.; Pişkin, K.; Yilmaz, F.; Çakir, C.; Yavuz, H.; Denizli, A. Quartz Crystal Microbalance Based Biosensors for Detecting Highly Metastatic Breast Cancer Cells via Their Transferrin Receptors. Anal. Methods 2016, 8, 153–161. [Google Scholar] [CrossRef]
- Zhang, S.; Bai, H.; Luo, J.; Yang, P.; Cai, J. A Recyclable Chitosan-Based QCM Biosensor for Sensitive and Selective Detection of Breast Cancer Cells in Real Time. Analyst 2014, 139, 6259–6265. [Google Scholar] [CrossRef]
- Sauerbrey, G. Verwendung von Schwingquarzen Zur Wägung Dünner Schichten Und Zur Mikrowägung. Z. Für Phys. 1959, 155, 206–222. [Google Scholar] [CrossRef]
- Cumpson, P.J.; Seah, M.P. The Quartz Crystal Microbalance; Radial/Polar Dependence of Mass Sensitivity Both on and off the Electrodes. Meas. Sci. Technol. 1990, 1, 544. [Google Scholar] [CrossRef]
- Josse, F.; Lee, Y.; Martin, S.J.; Cernosek, R.W. Analysis of the Radial Dependence of Mass Sensitivity for Modified-Electrode Quartz Crystal Resonators. Anal. Chem. 1998, 70, 237–247. [Google Scholar] [CrossRef]
- Lee, Y.; Josse, F. Radial Dependence of Mass Sensitivity for Modified-Electrode Quartz Crystal Resonators. Proc. IEEE Ultrason. Symp. 1996, 1, 321–325. [Google Scholar] [CrossRef]
- Richardson, A.; Bhethanabotla, V.R.; Smith, A.L.; Josse, F. Patterned Electrodes for Thickness Shear Mode Quartz Resonators to Achieve Uniform Mass Sensitivity Distribution. Proc. IEEE Sens. 2008, 1206–1209. [Google Scholar] [CrossRef]
- Gao, J.; Huang, X.; Wang, Y. The Modified Design of Ring Electrode Quartz Crystal Resonator for Uniform Mass Sensitivity Distribution. IEEE Trans. Ultrason. 2013, 60, 2031–2034. [Google Scholar] [CrossRef]
- Tiersten, H.F. Linear Piezoelectric Plate Vibrations; Springer: Berlin/Heidelberg, Germany, 1969. [Google Scholar] [CrossRef]
- Mindlin, R.D. Thickness-Twist Vibrations of an Infinite, Monoclinic, Crystal Plate. Int. J. Solids Struct. 1965, 1, 141–145. [Google Scholar] [CrossRef]
- Mclachlan, N.W. Bessel Functions for Engineers; Clarendon Press: London, UK, 1955. [Google Scholar]
- Hafner, E.I. Crystal Resonators. IEEE Trans. Sonics Ultrason. 1974, 21, 220–237. [Google Scholar] [CrossRef]
- Martin, B.A.; Hager, H.E. Velocity Profile on Quartz Crystals Oscillating in Liquids. J. Appl. Phys. 1998, 65, 2630. [Google Scholar] [CrossRef]
- Cumpson, P.J. Quartz Crystal Microbalance: A New Design Eliminates Sensitivity Outside the Electrodes, Often Wrongly Attributed to the Electric Fringing Field. J. Vac. Sci. Technol. A Vac. Surf. Film. 1998, 15, 2407. [Google Scholar] [CrossRef]
- Went, P.T.; Lugli, A.; Meier, S.; Bundi, M.; Mirlacher, M.; Sauter, G.; Dirnhofer, S. Frequent EpCam Protein Expression in Human Carcinomas. Hum. Pathol. 2004, 35, 122–128. [Google Scholar] [CrossRef]
- Coen, M.C.; Lehmann, R.; Gröning, P.; Bielmann, M.; Galli, C.; Schlapbach, L. Adsorption and Bioactivity of Protein A on Silicon Surfaces Studied by AFM and XPS. J. Colloid. Interface Sci. 2001, 233, 180–189. [Google Scholar] [CrossRef] [PubMed]
- Farris, L.R.; McDonald, M.J. AFM Imaging of ALYGNSA Polymer-Protein Surfaces: Evidence of Antibody Orientation. Anal. Bioanal. Chem. 2011, 401, 2821–2829. [Google Scholar] [CrossRef]
- Purification and Some Properties of Streptococcal Protein G, a Novel IgG-Binding Reagent—PubMed. Available online: https://pubmed.ncbi.nlm.nih.gov/6234364/ (accessed on 19 March 2023).
- Protein A of Staphylococcus Aureus and Related Immunoglobulin Receptors Produced by Streptococci and Pneumonococci—PubMed. Available online: https://pubmed.ncbi.nlm.nih.gov/7051784/ (accessed on 19 March 2023).
- O’Kennedy, R.; Fitzgerald, S.; Murphy, C. Don’t Blame It All on Antibodies—The Need for Exhaustive Characterisation, Appropriate Handling, and Addressing the Issues That Affect Specificity. Trends Anal. Chem. 2017, 89, 53–59. [Google Scholar] [CrossRef]
- Ma, Z.; Wu, J.; Zhou, T.; Chen, Z.; Dong, Y.; Tang, J.; Sui, S. Detection of Human Lung Carcinoma Cell Using Quartz Crystal Microbalance Amplified by Enlarging Au Nanoparticles in Vitro. New J. Chem. 2002, 26, 1795–1798. [Google Scholar] [CrossRef]
- Lu, W.; Arumugam, S.R.; Senapati, D.; Singh, A.K.; Arbneshi, T.; Khan, S.A.; Yu, H.; Ray, P.C. Multifunctional Oval-Shaped Gold-Nanoparticle-Based Selective Detection of Breast Cancer Cells Using Simple Colorimetric and Highly Sensitive Two-Photon Scattering Assay. ACS Nano 2010, 4, 1739–1749. [Google Scholar] [CrossRef] [PubMed]
- Bakhshpour, M.; Piskin, A.K.; Yavuz, H.; Denizli, A. Quartz Crystal Microbalance Biosensor for Label-Free MDA MB 231 Cancer Cell Detection via Notch-4 Receptor. Talanta 2019, 204, 840–845. [Google Scholar] [CrossRef]
- Shen, H.; Yang, J.; Chen, Z.; Chen, X.; Wang, L.; Hu, J.; Ji, F.; Xie, G.; Feng, W. A Novel Label-Free and Reusable Electrochemical Cytosensor for Highly Sensitive Detection and Specific Collection of CTCs. Biosens. Bioelectron. 2016, 81, 495–502. [Google Scholar] [CrossRef]
- Mclachlan, N.W. Theory of Vibration; Dover Publications: New York, NY, USA, 1951. [Google Scholar]




| Electrode Design | Inner Radius a (mm) | Outer Radius b (mm) | Gold Electrode Thickness (nm) | Titanium Electrode Thickness (nm) | Mass Loading | Amplitude Constants | |||
|---|---|---|---|---|---|---|---|---|---|
| C1 | C2 | C3 | C4 | ||||||
| 6 MHz-ring | 1 | 2.5 | 110 | 15 | 0.0060 | −0.069 | −0.085 | −0.038 | −0.993 |
| 6 MHz-modified ring | 1 | 2.5 | 50 | 50 | 0.0046 | −0.124 | −0.152 | −0.060 | −0.978 |
| 9 MHz-ring | 1 | 2.5 | 35 | 15 | 0.0031 | −0.027 | −0.033 | −0.017 | −0.998 |
| Elemental Composition (Atomic %) | ||||
|---|---|---|---|---|
| QCRs | Si | O | C | N |
| APTES | 30.05 ± 0.3 | 55.48 ± 0.63 | 12.19 ± 0.83 | 2.28 ± 0.14 |
| Anti-EpCAM | 20.89 ± 0.82 | 39.91 ± 1.23 | 31.67 ± 1.68 | 7.52 ± 0.43 |
| Protein A/G | 14.65 ± 0.79 | 30.96 ± 1.36 | 44.86 ± 2.05 | 9.54 ± 0.29 |
| Technique | Recognition Element | Sensitivity of Detection | Targeted Cells | Reference |
|---|---|---|---|---|
| Quartz crystal microbalance biosensor | transferrin | 500 cells | MDA-MB 231, MCF-7 | [29] |
| Quartz crystal microbalance biosensor | Folic acid (FA) | 430 cells | MCF-7 | [30] |
| Quartz crystal microbalance biosensor | ALT04 antibody | 100 cells | LCC | [49] |
| Au nanoparticle-based colorimetric method | HER2 | 100 cells | SK-BR-3 | [50] |
| Quartz crystal microbalance biosensor | Notch-4 receptor antibody | 42 cells * | MDA MB 231 | [51] |
| Electrochemical impedance spectroscopy | Anti-EpCAM antibody | 10 cells | MCF-7 | [52] |
| Ring electrode QCR biosensor | Anti-EpCAM antibody | 10 cells | MCF-7, PANC-1, and PC-3 | this study |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alawajji, R.A.; Alsudani, Z.A.N.; Biris, A.S.; Kannarpady, G.K. Biosensor Design for the Detection of Circulating Tumor Cells Using the Quartz Crystal Resonator Technique. Biosensors 2023, 13, 433. https://doi.org/10.3390/bios13040433
Alawajji RA, Alsudani ZAN, Biris AS, Kannarpady GK. Biosensor Design for the Detection of Circulating Tumor Cells Using the Quartz Crystal Resonator Technique. Biosensors. 2023; 13(4):433. https://doi.org/10.3390/bios13040433
Chicago/Turabian StyleAlawajji, Raad A., Zeid A. Nima Alsudani, Alexandrus S. Biris, and Ganesh K. Kannarpady. 2023. "Biosensor Design for the Detection of Circulating Tumor Cells Using the Quartz Crystal Resonator Technique" Biosensors 13, no. 4: 433. https://doi.org/10.3390/bios13040433
APA StyleAlawajji, R. A., Alsudani, Z. A. N., Biris, A. S., & Kannarpady, G. K. (2023). Biosensor Design for the Detection of Circulating Tumor Cells Using the Quartz Crystal Resonator Technique. Biosensors, 13(4), 433. https://doi.org/10.3390/bios13040433





