1. Introduction
In the last decade, the properties of Majorana zero-energy modes (MZMs) hosted in topological superconductors have gathered considerable interest. Indeed, their non-abelian statistics has been proposed as the working principle of a fault-tolerant topological quantum computation [
1]. However, a crucial challenge towards the topological quantum computer is to implement quantum operations of nearly degenerate quantum states by a dynamical process involving Majorana fermions; the main one is the braiding dynamics in superconducting nanowires. From the theoretical side, the simplest model for realizing MZMs is the one-dimensional spinless
p-wave chain proposed by Kitaev [
2]. A realistic implementation of the Kitaev model has been proposed lately in the pioneering work by Fu and Kane [
3] who have predicted the presence of MZMs as a result of the proximity effect between an s-wave superconductor and the surface states of a strong topological insulator.
Many experimental works have been performed to realize the theoretical predictions of the Kitaev model and, in particular, Mourik and coworkers [
4] have shown evidence of MZMs in the tunnel conductance of an
nanowire proximized by an s-wave superconductor. Two years later, by implementing a previous theoretical proposal [
5], Nadj-Perge et al. [
6] exhibited a scanning tunneling microscopy measurement of a long chain of iron atoms deposited on a lead substrate, in which local density of states (LDOS) highlighted the presence of MZMs localized at the system edges.
Despite the existence of a rich literature on the topological phases of closed systems, or on different probes of MZMs in nanostructures (see, e.g., [
7,
8,
9]), it remains relevant to understand how the topological phases are modified by the measurement procedure which is realized, e.g., by coupling the system to the normal tip of a scanning tunneling microscope (STM). To this aim, we study the charge transport through a Kitaev chain (KC) and a Kitaev ladder (KL) coupled to a normal and a
p-wave superconducting electrode acting, respectively, as source and drain of the topological nanodevice. Using a scattering matrix approach, we analyse to what extent the topological edge states are perturbed by the passage of a current, also varying the distance and the position of the tip (i.e., the normal electrode). To test the robustness of the topological phase, we also consider the effect of disorder on transport properties and show the persistence of a quantized zero-bias peak in the conductance. Beyond a robust zero-bias conductance peak, the existence of quasi-zero energy peaks is shown, revealing the presence of hybridized MZMs or quasi-Majorana modes, i.e., quantum states strongly coupled to the external leads which present a spatial distribution peaked at the edges and extended over the entire system. Our results can be useful for the interpretation of future experimental works involving STM characterization of topological superconductors. From the methodological viewpoint, the presented analysis can be relevant to characterize the transport properties of nanodevices based on innovative materials whose minimal model can be mapped into an effective multi-orbital Kitaev chain theory (e.g., the one-dimensional heterostructures exploiting the emergent properties of the LaAlO
/SrTiO
interfaces [
10]). Going beyond the context of condensed matter, our findings could be relevant for the emergent field of
atomtronics [
11] aiming at the high-precision control of atomic matter waves. Atomtronics experiments can be implemented with bosonic or fermionic atoms under extremely controllable conditions and are the ideal playground to implement concepts borrowed by quantum electronics, both in equilibrium and in non-equilibrium conditions.
The paper is thus organized as follows. In
Section 2 and
Section 3, we summarize the main properties of the isolated Kitaev chain and ladder and discuss the topological phases. The tight-binding model for the normal/Kitaev-chain/superconductor (N-KC-SC) device is introduced and analyzed in
Section 4, where we also report the results for the conductance and study the evolution of the zero-bias peak as a function of the parameters driving the topological phase transition. The charge transport through a normal/Kitaev-ladder/superconductor (N-KL-SC) device is analyzed in
Section 5, also discussing the effect of disorder on the zero-bias peak (
Section 6). The conclusions are given in
Section 7. Technical details on the analytical calculations and the tight binding Bogoliubov–de Gennes (BdG) equations are given in the
Appendix A. Conductance lowering effects in branched quantum devices and the analogies with the Blonder–Tinkham–Klapwijk (BTK) theory of transport in N-SC junction are discussed in the
Appendix B. Charge neutrality of hybridized Majorana modes is analyzed in
Appendix C.
2. Majorana Fermions in the Kitaev Chain
In this section, we briefly discuss the main topological properties of the Kitaev chain. This discussion provides the appropriate starting point before treating the open quantum systems and serves to fix the notation. Following the Kitaev seminal work [
2], we consider a system of spinless fermions confined to a one-dimensional lattice and subject to a
p-wave superconducting coupling described by the Hamiltonian:
where
(
) is the fermionic annihilation (creation) operator for a site
j (
),
is the amplitude of nearest-neighbor hopping,
is the amplitude of the superconducting pairing, while
represents the chemical potential. For the Kitaev special case (
,
), using the Majorana basis
and
, the Hamiltonian in Equation (
1) becomes:
where the hermitian Majorana operators fulfill the anticommutation relation
. In this case, the Hamiltonian has two zero-energy Majorana modes, namely
and
, which are located at the end of the wire and combine to form a zero-energy non-local fermion
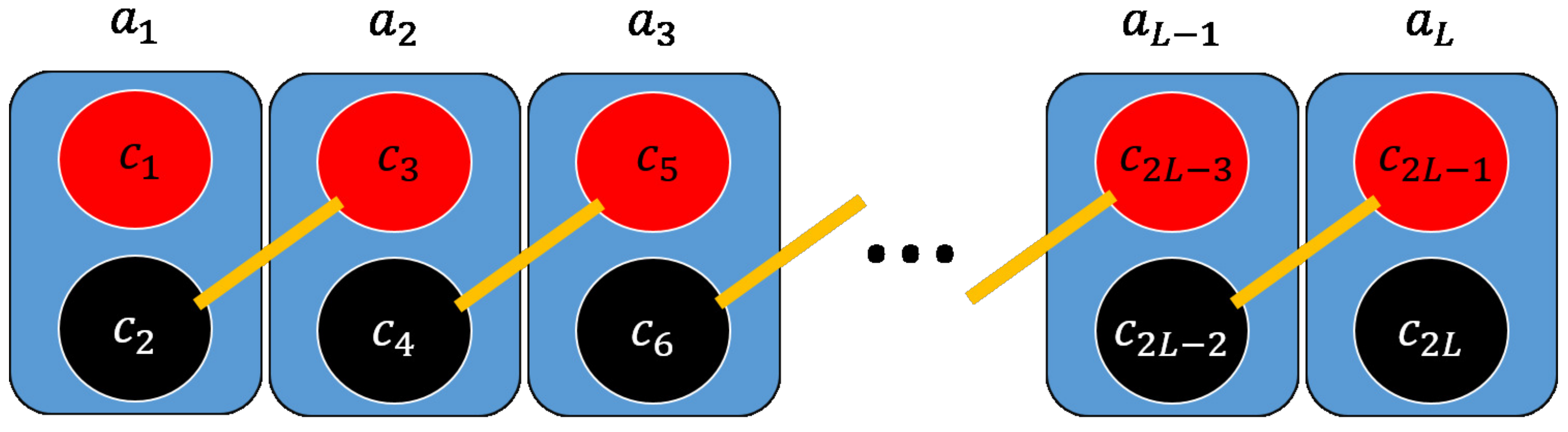
. The other
fermionic modes (Bogoliubov modes)
,
, are degenerate with energy
and connect the neighbouring sites in the bulk as depicted in
Figure 1.
For arbitrary values of
,
t,
, the Kitaev Hamiltonian
can be diagonalized by the Bogoliubov transformation
, where the quasiparticle fermionic annihilation and creation operators
and
obey canonical anticommutation relations. The Bogoliubov amplitudes
and
satisfy the Bogoliubov–de Gennes (BdG) equations:
with excitation energy
. The diagonal form of
reads:
where
is the energy of ground state
of Bogoliubov modes so that
for all
.
This model admits a topological phase for
(see
Figure 2) with a robust zero-energy edge mode, which is here labeled by setting
. The energy
of this mode is not exactly zero, as expected in thermodynamic limit, and presents an exponential decay with the system size
L (i.e.,
, where
represents a characteristic decay length). The remaining non-topological modes of the spectrum are gapped and form a band.
The zero-energy Majorana modes are localised at the left/right edge of the wire and decay inside the bulk; the annihilation operators of such modes are given by:
where the real valued eigenfunctions
and
are obtained by the explicit solution of the BdG Equation (
2). Following Ref. [
12], it is possible to show that
and
, where
and
.
In the thermodynamic limit (), the presence of such edge modes results in an exact degeneration of the ground state that corresponds to the presence or absence of the non-local fermion . In fact, in this limit, the two ground states (zero-energy states) , have different parity and thus and .
3. Ladder of Two Kitaev Chains
Various generalizations of the single Kitaev chain have recently appeared [
13,
14,
15,
16,
17,
18], the simplest one being obtained by coupling two single Kitaev chains with transversal hopping and pairing terms to form a Kitaev ladder (KL) [
19]. The Hamiltonian of the system is given by:
where
and
are the Hamiltonians of the isolated Kitaev chains given in Equation (
1), while
describes the interchain coupling whose expression is given by:
The labels
in Equation (
5) denote the two chains,
j is the site index,
represents the transversal hopping amplitude and
is the transversal pairing term. All the model parameters, namely
t,
,
and
, are taken as real numbers. In the momentum representation, the Hamiltonian (
4) can be written as
where
represents the Nambu spinor. The Hamiltonian is given by
with
and
. By construction, the Hamiltonian (
8) satisfies the particle-hole symmetry (
)
implemented by the operator
which is defined in terms of the complex conjugation operator
and of the Pauli matrix
, while
represents the identity operator. The Hamiltonian satisfies also the time-reversal symmetry (
)
and the chiral symmetry (
)
According to the mentioned symmetry properties enjoyed by
, the Hamiltonian model belongs to the BDI symmetry class with Z topological index [
20]. The spectrum of the Hamiltonian can be easily obtained and is given by
The topological phase diagram can be obtained by the calculation of the winding number [
18,
21]. Using the chiral basis, the Hamiltonian (
8) assumes the following off-diagonal form [
21]
where
U is the basis change matrix and
is the
matrix
Following Zhou et al. [
18], we calculate the winding number as
and compute the topological phase diagram, which is systematically analyzed in the following discussion. To provide evidence of the richness of the topological phases of the model, in the following, we present our results using an extended parameters range, which in principle could be completely explored in cold atoms experiments rather than in condensed matter systems. In
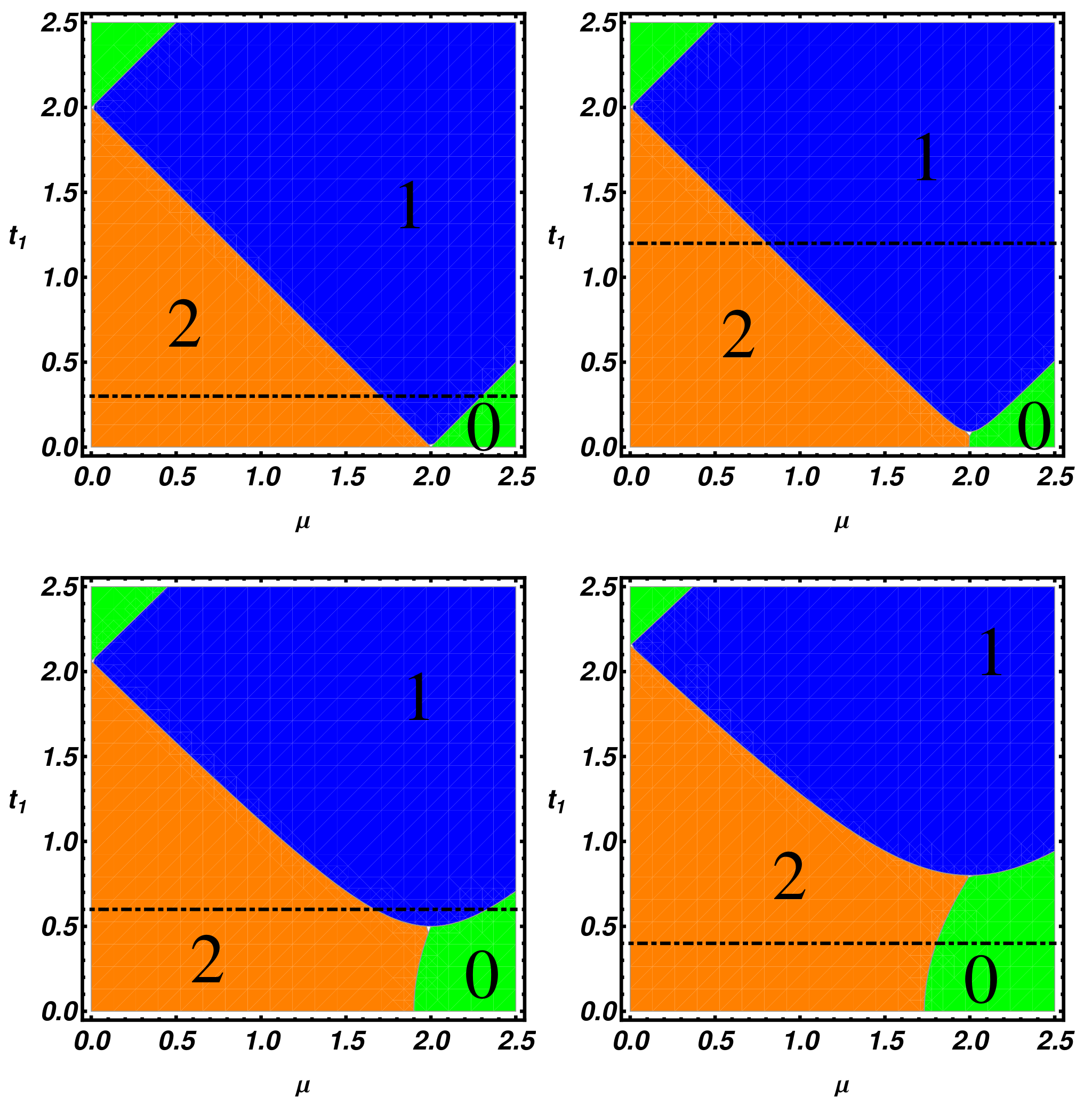
Figure 3, we present the topological phase diagram in the (
,
) plane by fixing
and setting different values of
(
,
0.5,
, respectively), while taking
t as an energy unit.
The integers in the figures correspond to the winding number and are related to the number of MZMs at every edge of the ladder. By direct inspection of
Figure 3, we notice that an increase of the pairing term
produces an enlargement of the trivial region, labeled by 0. The expansion of the trivial region changes the phase boundaries and induces a modification of the linear phase boundaries, which are peculiar to the
case. A further consequence of the enlargement of trivial region is the possibility, changing the chemical potential and setting appropriate
values, to have a direct transition from the two MZMs region to the trivial phase without crossing the one MZM phase. Interestingly, an additional consequence of the interchain coupling is that the critical value of the chemical potential,
, defining 2–0 phase boundary is progressively lowered as
increases. As a consequence,
becomes smaller than the one established by Kitaev for the 1–0 phase boundary of a single chain, i.e.,
.
In
Figure 4, we present the topological phase diagrams in the (
,
) plane. The different panels are realized by setting two values of
, namely
(left panel) and
(right panel), while retaining the remaining parameters as in
Figure 3. Direct observation of
Figure 4 shows that, for a weak interchain hopping parameter (
), a phase with two MZMs is favored compared to the one MZM phase. On the other hand, when the transverse hopping is increased (
Figure 4, right panel), the phase with one Majorana mode per edge is favored and the system behaves like an effective two-orbital single Kitaev chain.
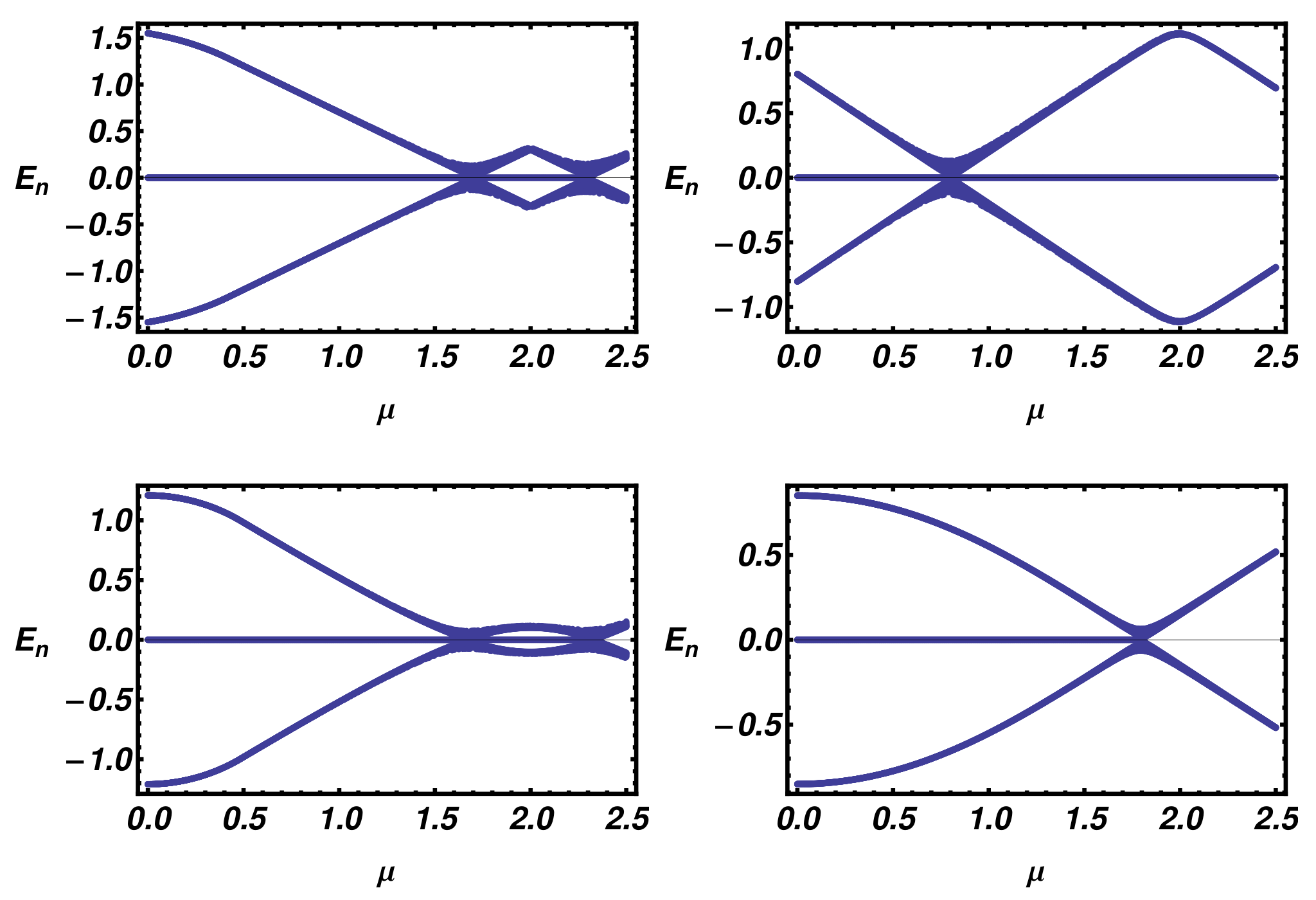
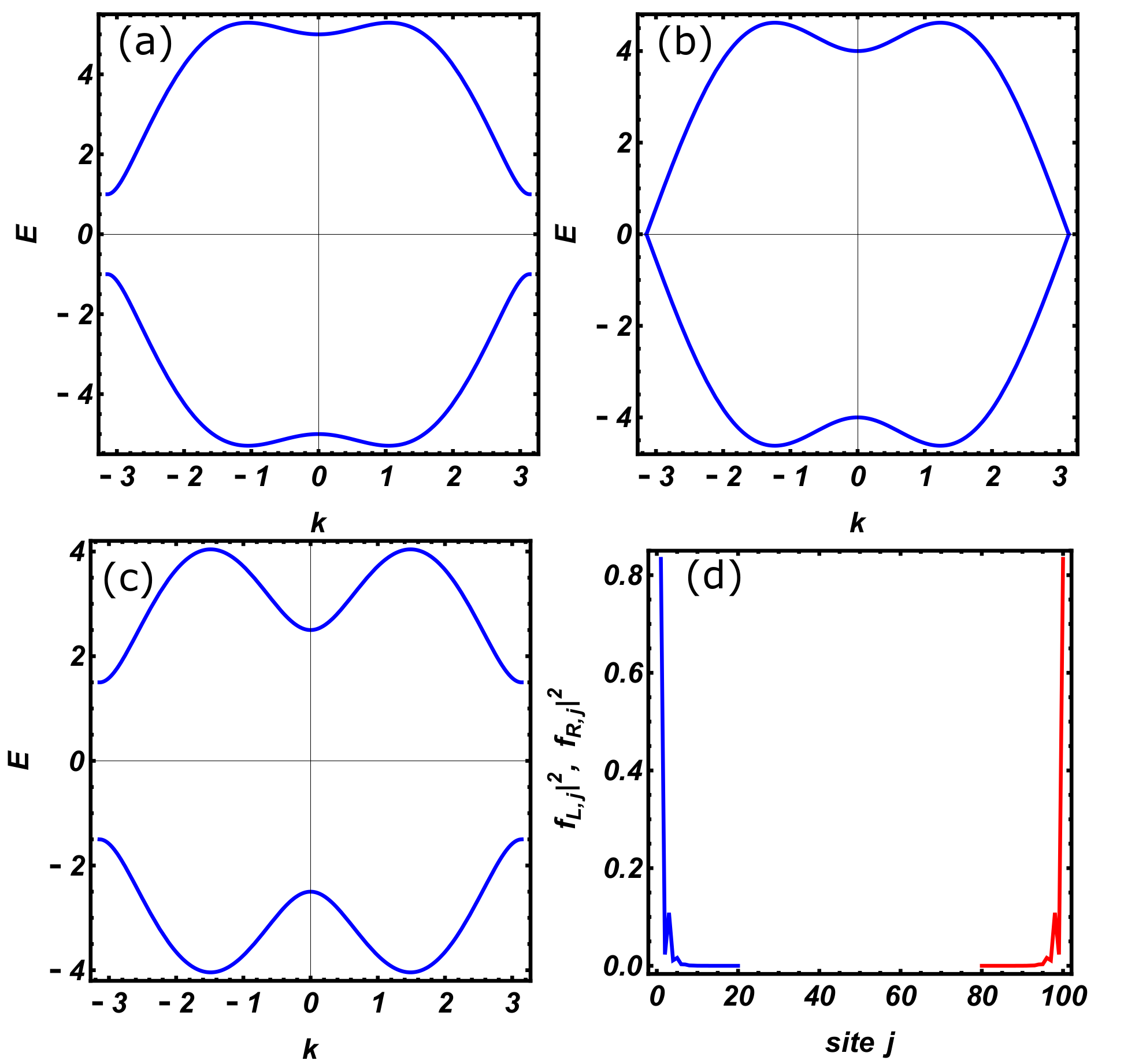
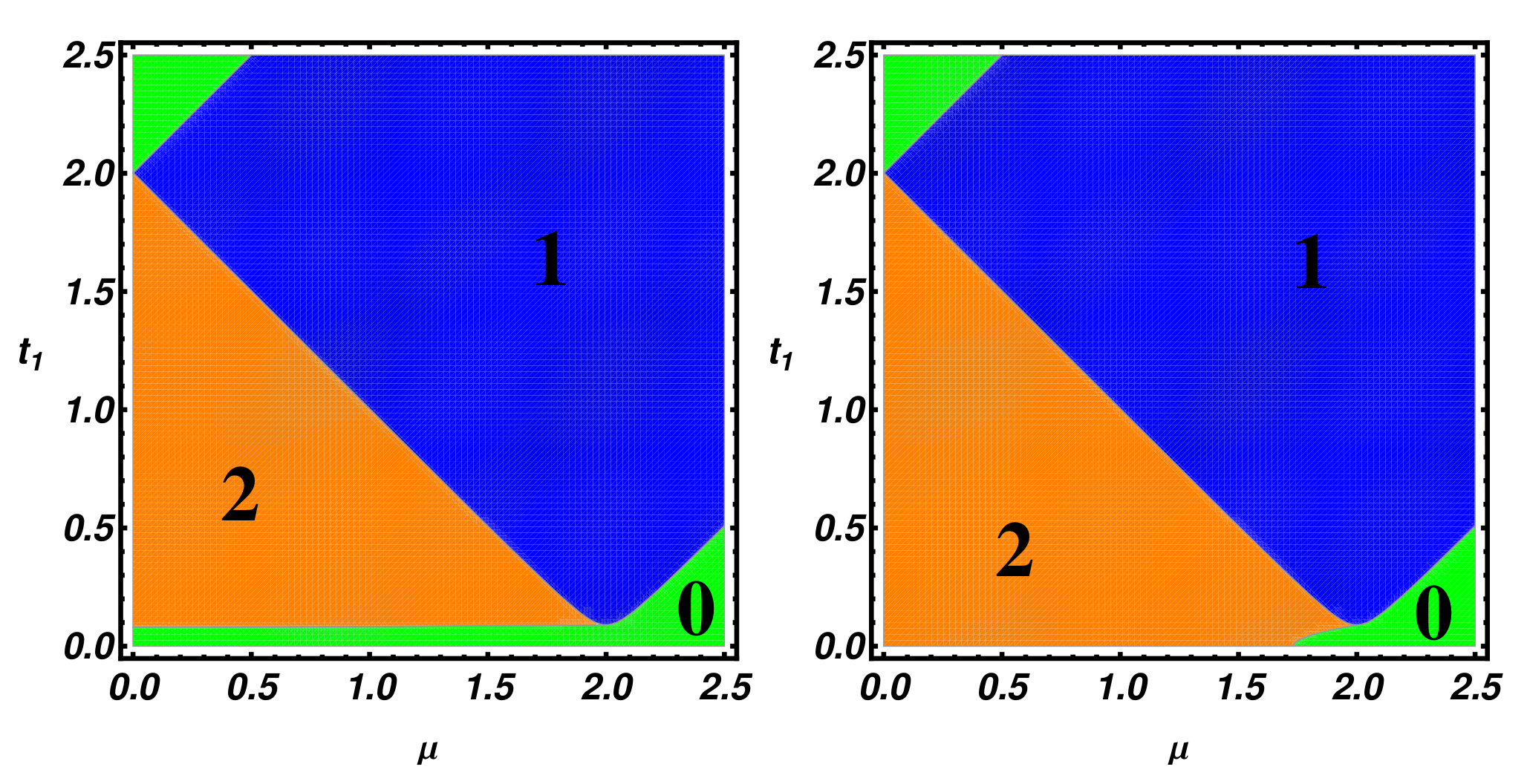
In order to verify the bulk-edge correspondence, in
Figure 5, we present the low-energy part of the energy spectra of a ladder of
lattice sites as a function of the chemical potential
. The analysis of the finite-size system confirms the presence and the multiplicity of zero-energy modes as prescribed by the winding number analysis.
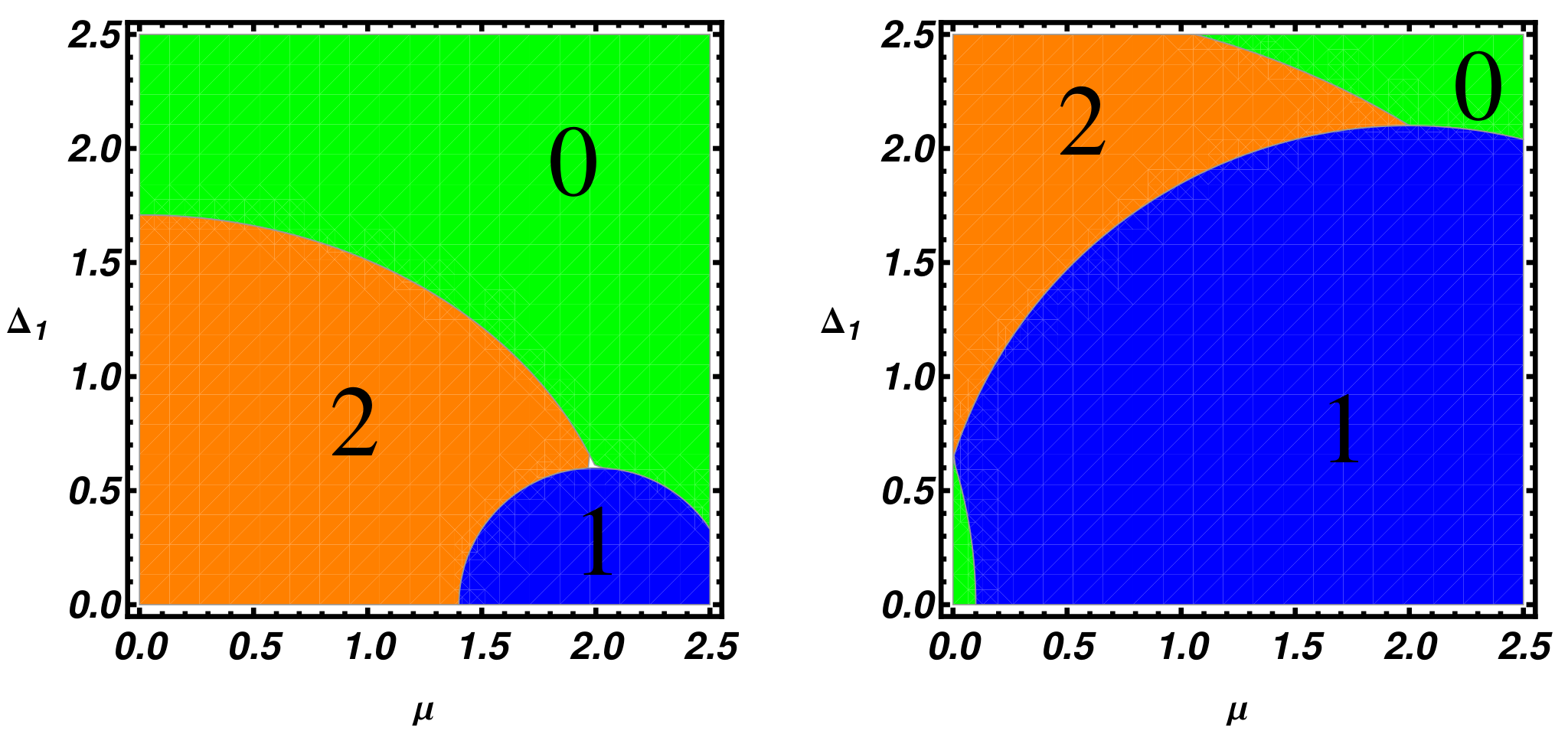
Up to now, we have explored an extended topological phase diagram in order to emphasize the richness of the topological phase plane of a ladder model. Hereafter, in
Figure 6, we specialize to the case of a condensed matter system and present phase diagrams showing a parameters region containing the device working point considered in the transport properties simulations (see
Section 5). In particular, in
Figure 6 (left panel), the asymmetric pairing case (i.e.,
and
) is analyzed, while the equal pairing case (
) is presented in the right panel. In the asymmetric situation (
), a trivial region is found for
and arbitrary
values, the latter region being reduced in the symmetric case (right panel). Let us finally note that the situation
, considered here, is realizable in multiorbital materials where the magnitude of different order parameters may well be different.
Figure 5.
Low energy part of the ladder energy spectra as a function of , evaluated for different values of and . From the left to the right and from the top to the bottom, the parameters are: .
Figure 5.
Low energy part of the ladder energy spectra as a function of , evaluated for different values of and . From the left to the right and from the top to the bottom, the parameters are: .
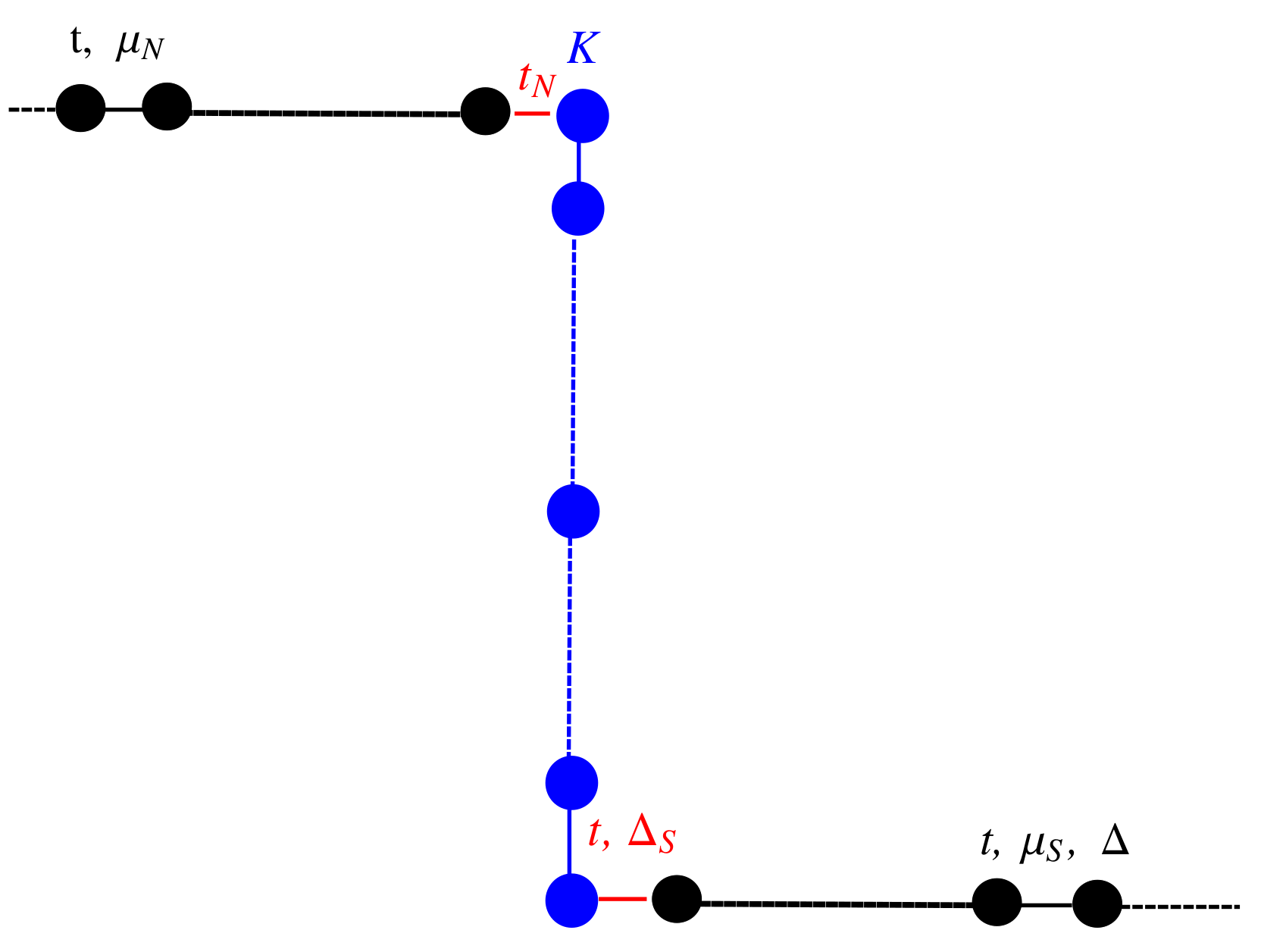
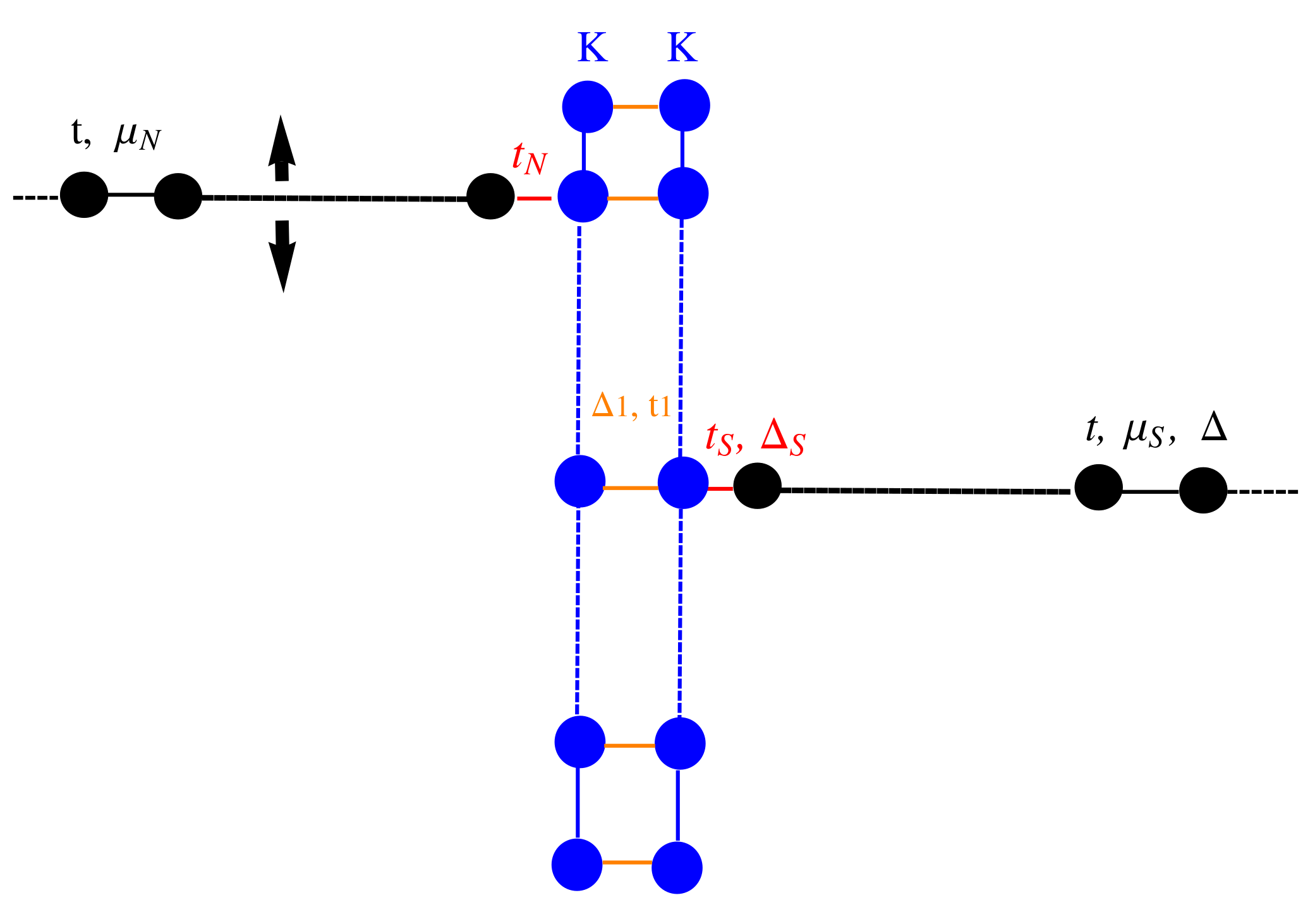
4. Quantum Transport through a Normal/Kitaev Chain/Superconductor Device
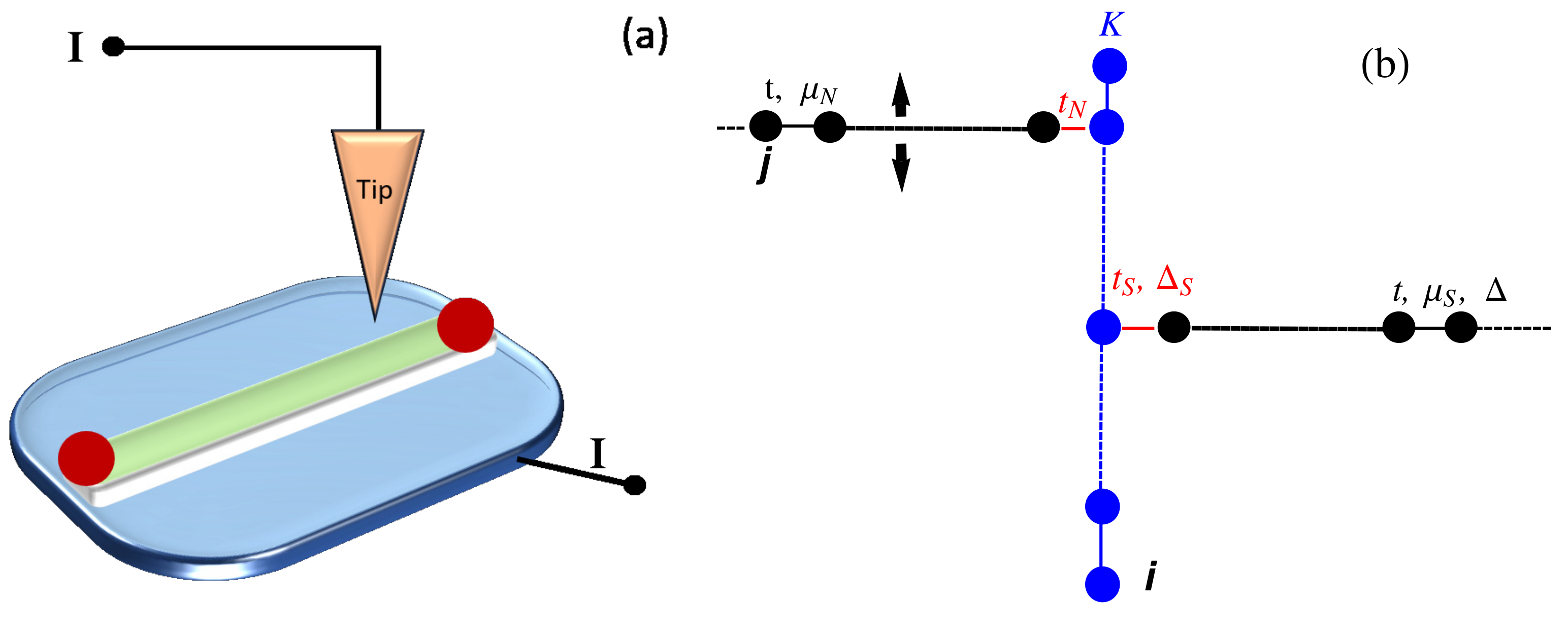
Using the scattering matrix approach, we study the transport properties of a Kitaev chain coupled to a normal and a superconducting
p-wave lead (
Figure 7). The Kitaev chain and the superconducting lead define a T-stub configuration (i.e., a waveguide with a closed sidearm [
22]) with the junction point located in the middle of the Kitaev chain, while the normal electrode position can be changed to simulate an STM measurement configuration. The
parameter defines the hopping between the normal and the KC, while
represents the hopping between the KC and the superconducting lead, while
defines the pairing amplitude. In the following, we study the topological signatures on the transport properties of the system considering a finite Kitaev chain of
sites.
The scattering state of the normal electrode is given by (see
Appendix A.1 for details)
which represents an electron coming from the normal bulk having an ordinary reflection probability
and an Andreev reflection probability given by
. The wave vectors
are obtained by the solution of the BdG equations:
where
E is the energy of the scattering process,
the chemical potential and
t the hopping amplitude of the normal lead. Inside the superconducting electrode, the propagating state is given by (see
Appendix A.2 for details):
where
and
are transmission coefficients of an
e-like and
h-like quasiparticle. The BCS coherence factors
,
for a
p-wave superconductor are given by:
where
is the momentum-dependent superconducting gap.
Resorting to a numerical solution of the scattering problem, we obtain the transmission and reflection coefficients and the wave functions of the resonant modes along the Kitaev chain (we call these modes Kitaev modes by analogy with the Majorana zero-energy modes introduced by Kitaev [
2]). The wave functions of modes belonging to the Kitaev chain, being a byproduct of the solution of the scattering problem, are not normalized with respect to the position since scattering states are normalized with respect to the particle flux.
The conservation of probability of all scattering processes can be written in terms of the scattering coefficients implying the following relation:
written under Andreev approximation
which has been adopted in numerical evaluations. Once the scattering coefficients are known, the conduction properties of the system can be computed adopting a BTK-like approach. Accordingly, the zero-temperature differential conductance can be written as:
where
and
represent the Andreev reflection and the normal reflection probability, respectively [
23].
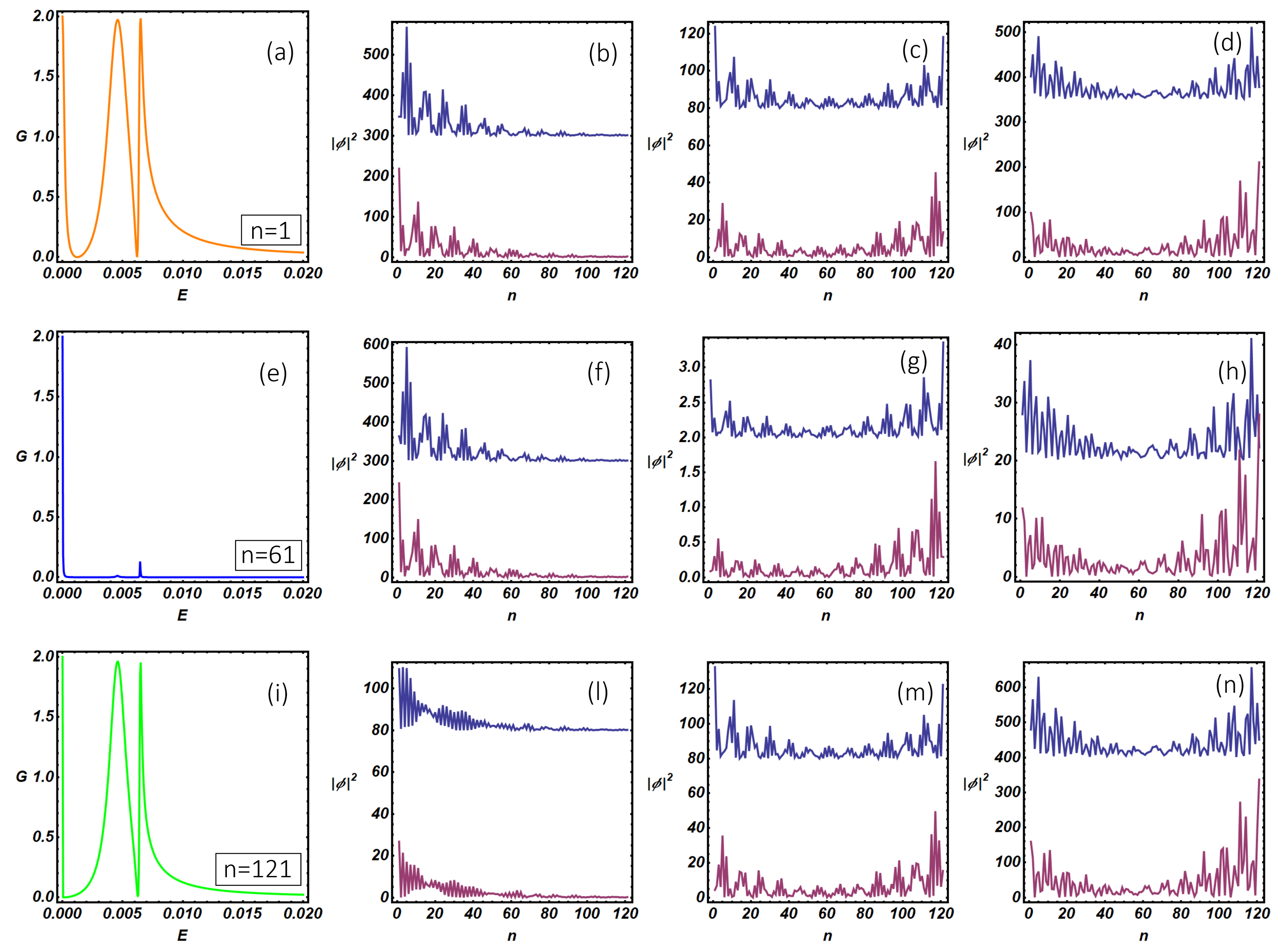
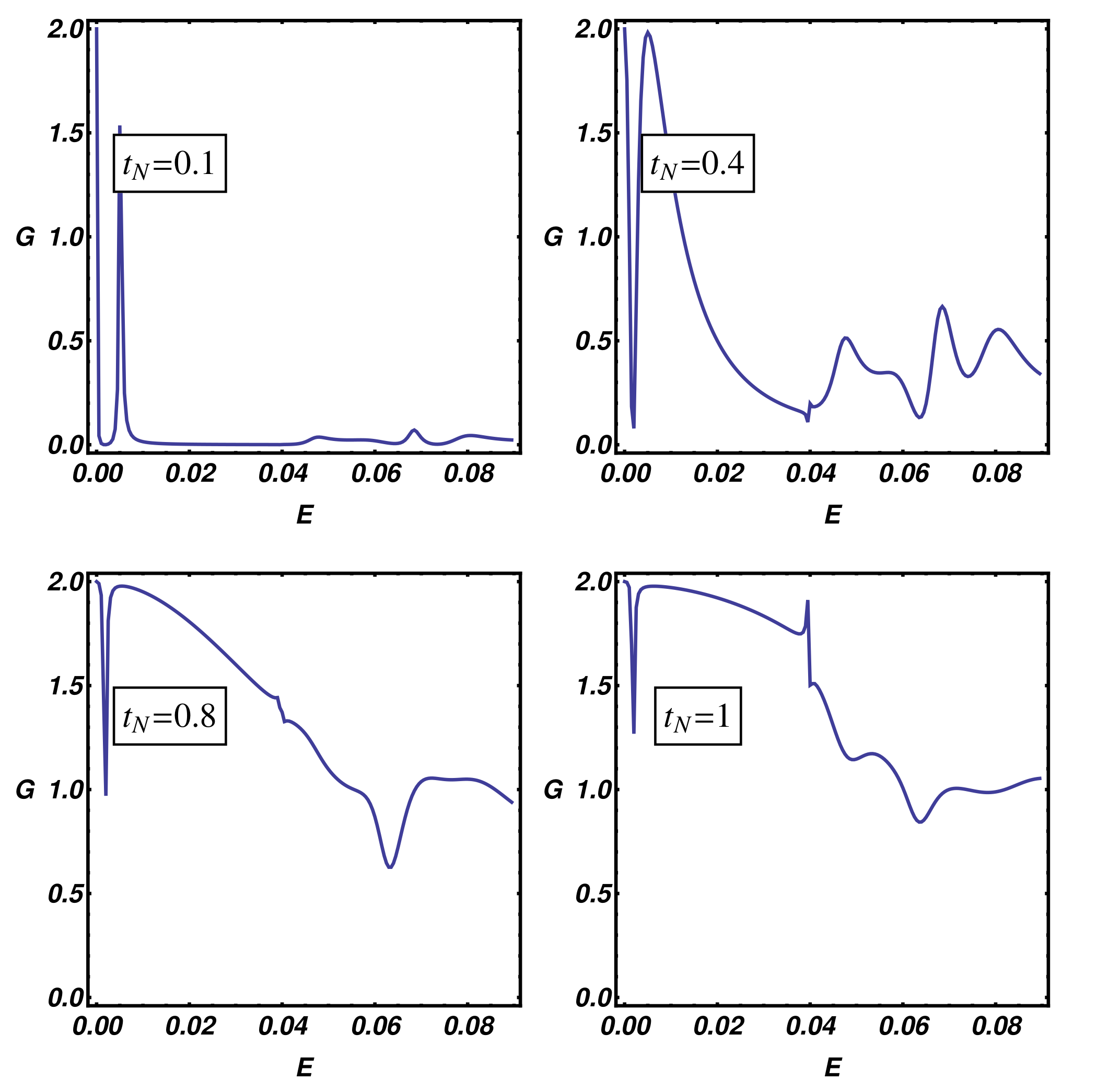
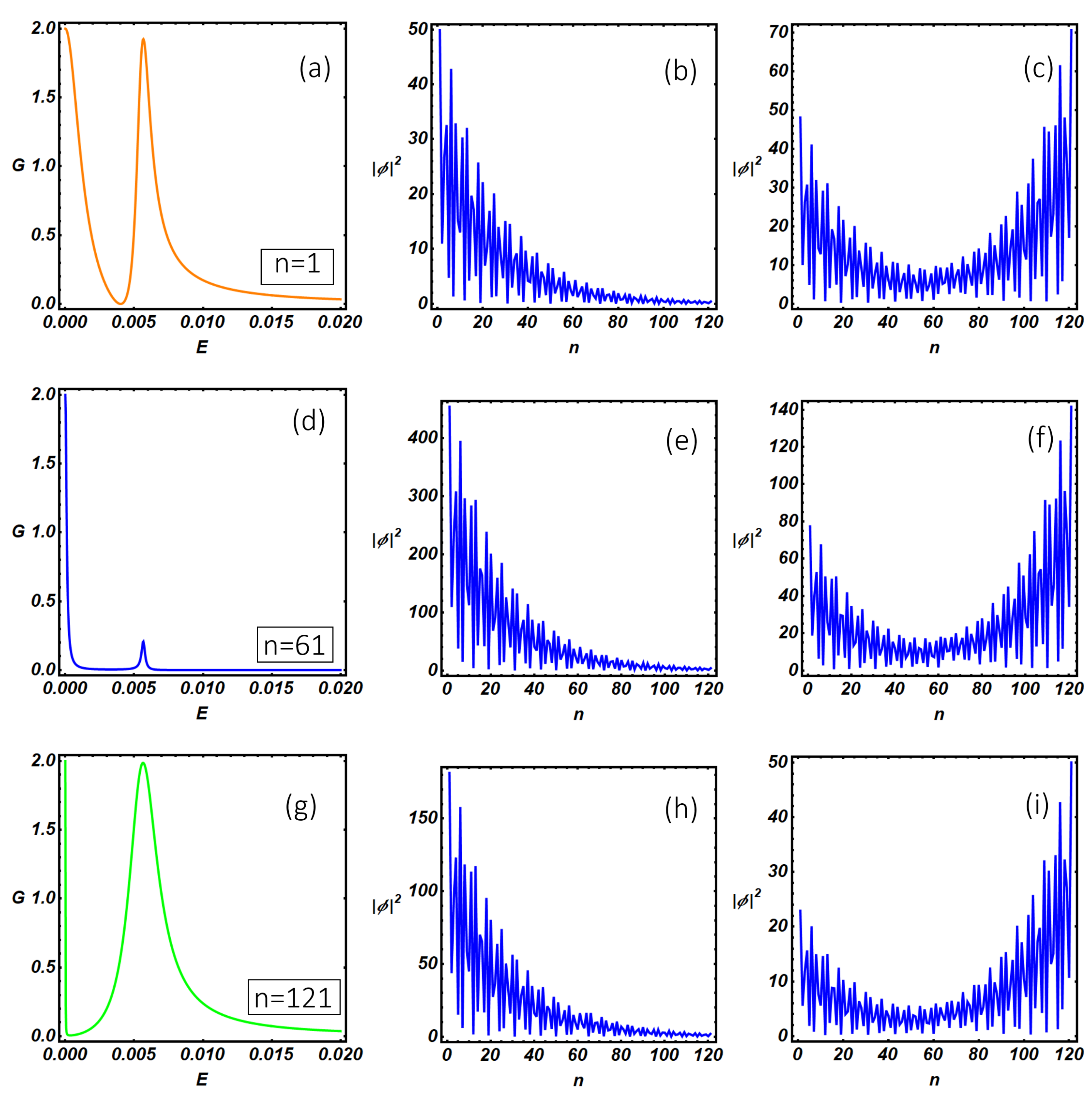
Using the quantum transport theory presented above, we have studied the differential conductance and the internal resonant modes of the N-KC-SC topological device. In particular, in
Figure 8, we study the differential conductance of the N-KC-SC device as a function of the N-KC link position and setting the model parameters inside the topological non-trivial region, where Majorana modes are expected to be relevant. Panels (a), (d), (g) show the conductance curves at selected N-KC link positions (specified within the figures inset) corresponding to the left end (
), the middle (
) and the right end (
) of the nanowire. In
Figure 8a, two peaks are clearly visible: a quantized zero-bias peak (
) and its satellite at higher energy (
). The analysis of the internal modes makes it evident that the quantized zero-bias peak, which is expected when the system undergoes a topological phase transition (the so-called zero-bias anomaly (ZBA)), corresponds to a MZM peaked at the left end of the wire (b). On the other hand, the peak at higher energy (
) corresponds to hybridized Majorana modes which originate a U-shaped wave function peaked at the two ends of the wire (panel (c)) and extended along the whole length of the Kitaev chain. The width of the resonant conductance peaks depends on the amplitude of the internal mode wave function at the N-KC linking point, the latter quantity being relevant in defining the overlap between the scattering states of the normal electrode and the internal modes of the Kitaev chain. The overlap increases with the wave function amplitude and depends on the normal electrode position and on the conductance peak considered. As a consequence, a narrow (broaden) peak is observed when the normal lead is weakly (strongly) coupled with the Kitaev chain internal modes, the latter situation corresponding to poor (strong) overlap between the normal electrode and the nanowire quantum states. These overlap effects are clearly visible in
Figure 8a–c in which the two broadened conductance peaks originate from the non-vanishing values of the wave function amplitudes at the
position, i.e., the N-KC linking point.
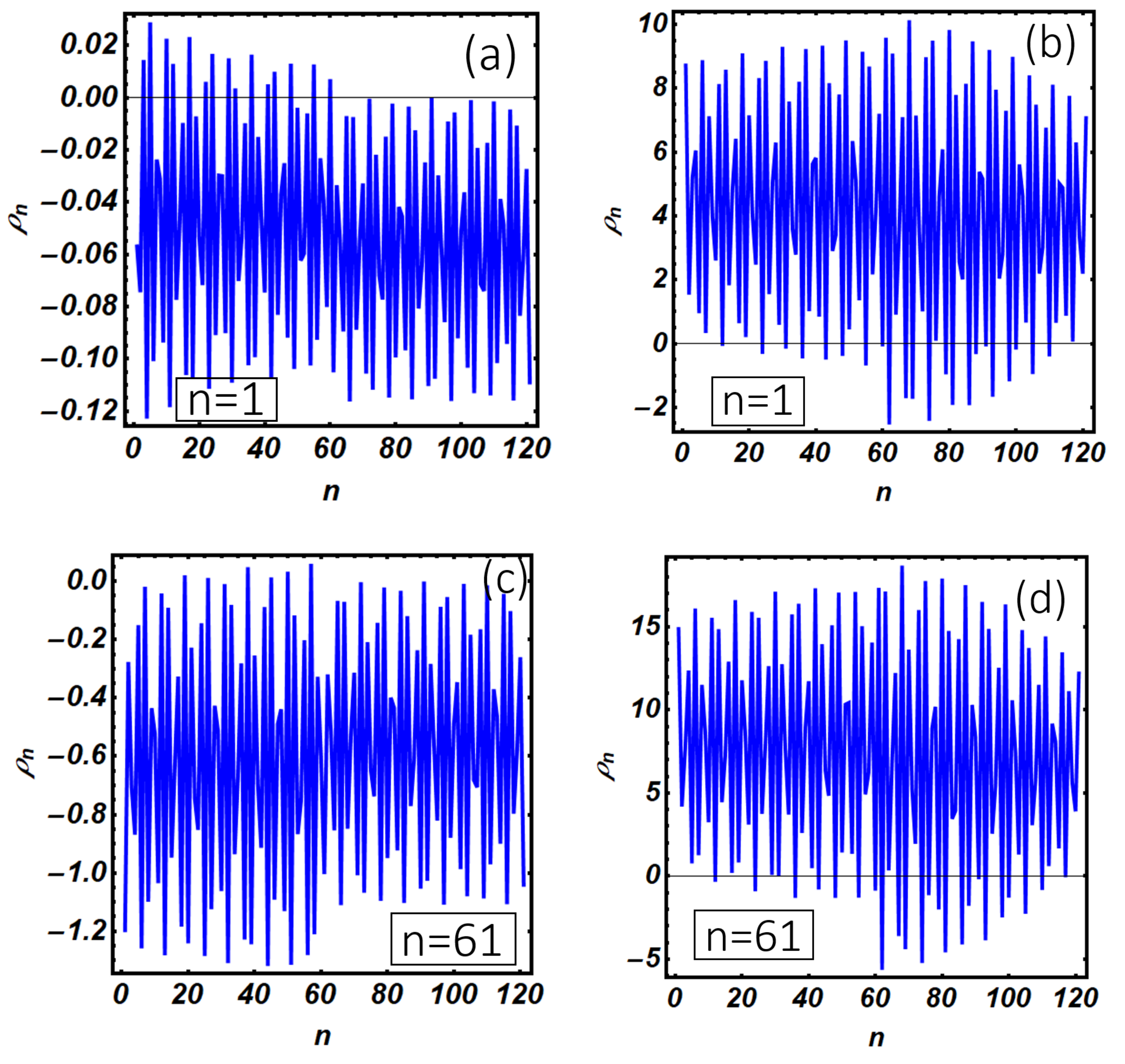
It is worth mentioning here that changing the linking point does not produce a qualitative change of the internal modes amplitude along the system. As a consequence, in (d) and (g), we observe the progressive and monotonic width reduction of the zero-bias peak, which follows the lowering of the wave function amplitude as the normal electrode is moved towards the right end of the Kitaev chain (panels (e) and (h)). The broadening of the satellite of the zero-bias peak is not monotonic as a function of the N-KC link position and follows the U-shaped behavior characteristic of the wave function amplitude (see (c), (f), (i)) of the internal Kitaev modes. From the experimental side, these observations suggest the possibility to reconstruct the wave function amplitude profile of the internal modes of the Kitaev chain by measuring the conductance peak broadening as the normal tip of an STM is moved along the system, the latter method being an interesting tool in characterizing the survival of topological properties under non-equilibrium conditions. It is worth mentioning here that pure Majorana modes are neutral excitations and thus they are not able to sustain a charge current. For this reason, a certain degree of hybridization of these topological modes is a necessary condition to have a finite charge current flowing through the system. The degree of hybridization of the Majorana modes inside the Kitaev chain can be quantified by studying the site-dependent charge density
associated with the internal modes profile presented in
Figure 8b, c, e, f, h, i. The complete analysis, which is reported in
Appendix C, shows that the average charge density
corresponding to the internal modes presented in (b), (e), (h) is much lower than the corresponding quantity computed for panels (c), (f), (i). This circumstance suggests that zero-bias conductance peak originates from a genuine Majorana mode presenting a weak hybridization with a hole-like non-topological mode, the latter conclusion being supported by the negative sign of
. On the other hand, satellite conductance peaks at higher energy are associated with internal states, presented in (c), (f) and (i), with a strong electron-like character (i.e.,
).
As a final comment, we notice that, despite the wave guide spatial configurations corresponding to the (a) and (g) panels are one the mirror reflected of the other with respect to a reflection line coincident with the superconducting electrode, the Hamiltonian of the entire system does not satisfy this symmetry and thus the conductance curves pertaining to these cases are not coincident. This statement can be easily proven. Reflection transformation of the isolated Kitaev chain Hamiltonian (Equation (
1)) can be implemented by the change of indices
. The reflection does not modify the structure of the Hamiltonian but transforms the initial pairing term
into
. The transformed Kitaev Hamiltonian is equivalent to the initial one via a
gauge transformation of the fermionic operators (
). For the above reasons, physical properties of the isolated Kitaev chain are invariant under reflection. When the KC is connected to external reservoirs, the above procedure is still applicable with a different outcome. Indeed, the electrodes’ Hamiltonians are invariant under reflection transformation, which is only implemented on the Hamiltonian of the Kitaev chain. On the other hand, the N-KC junction position is altered by the transformation (i.e.,
), while the position of the KC-SC link (
) remains unaffected since it is a fixed point. Thus, the described reflection transformation not only provides a reflected spatial configuration of the initial system but also determines a phase difference between the superconducting pairing terms of the Kitaev chain and the superconducting electrode. Implementing a gauge transformation as the one used for the isolated Kitaev chain does not eliminate the phase gradient (which is now transferred to the N-KC and KC-SC hopping amplitudes), the latter producing observable effects. We have verified that conductance curve of the system described by the transformed Hamiltonian is coincident with the curve shown in
Figure 8a, obtained for the initial Hamiltonian. Moreover, the transformed Hamiltonian does not correspond to the Hamiltonian used in
Figure 8g, where the mentioned phase gradient is absent. These arguments prove our conclusions and can be equally applicable to the ladder case discussed in
Section 5 (see
Figure 11a–i).
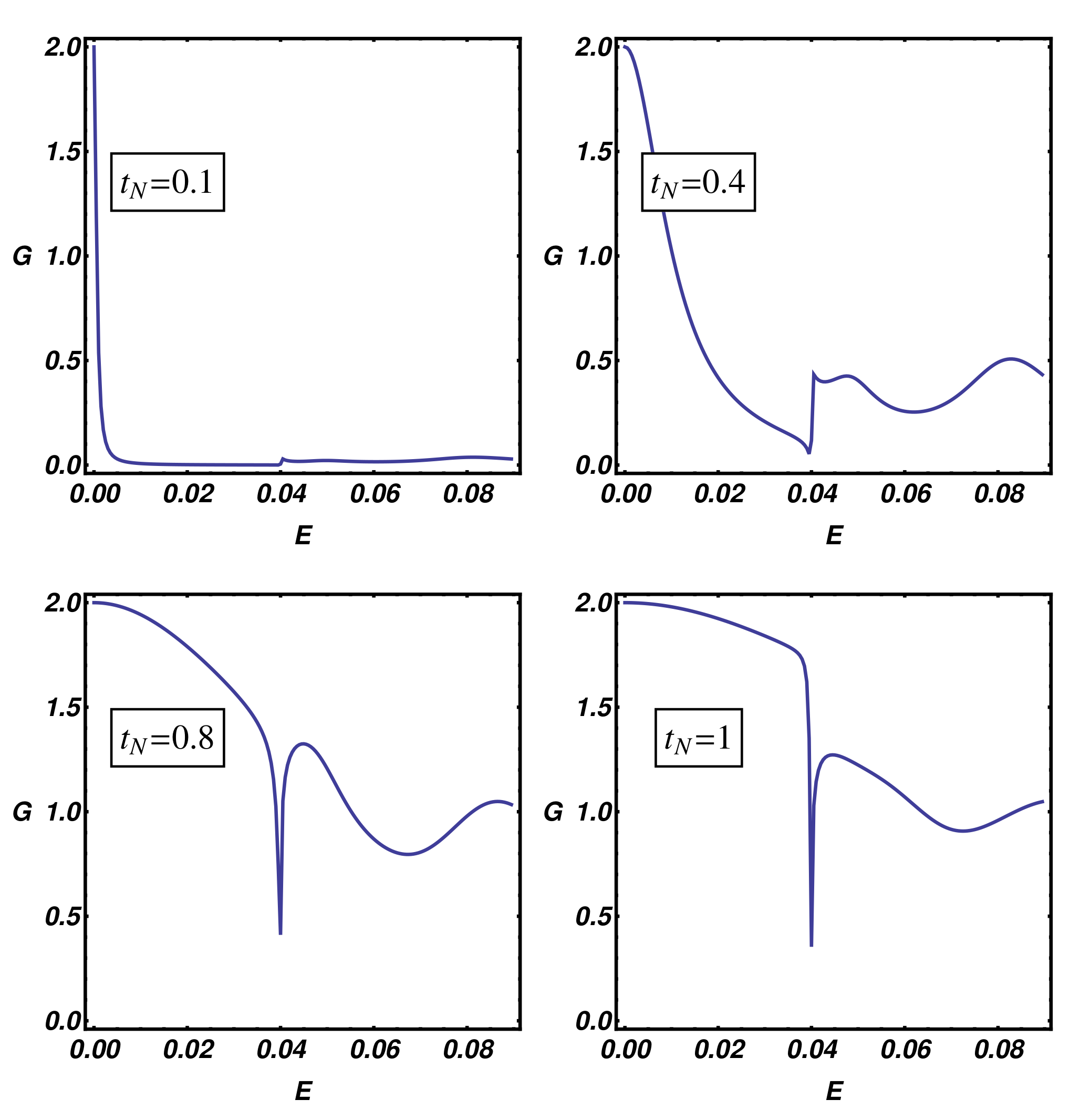
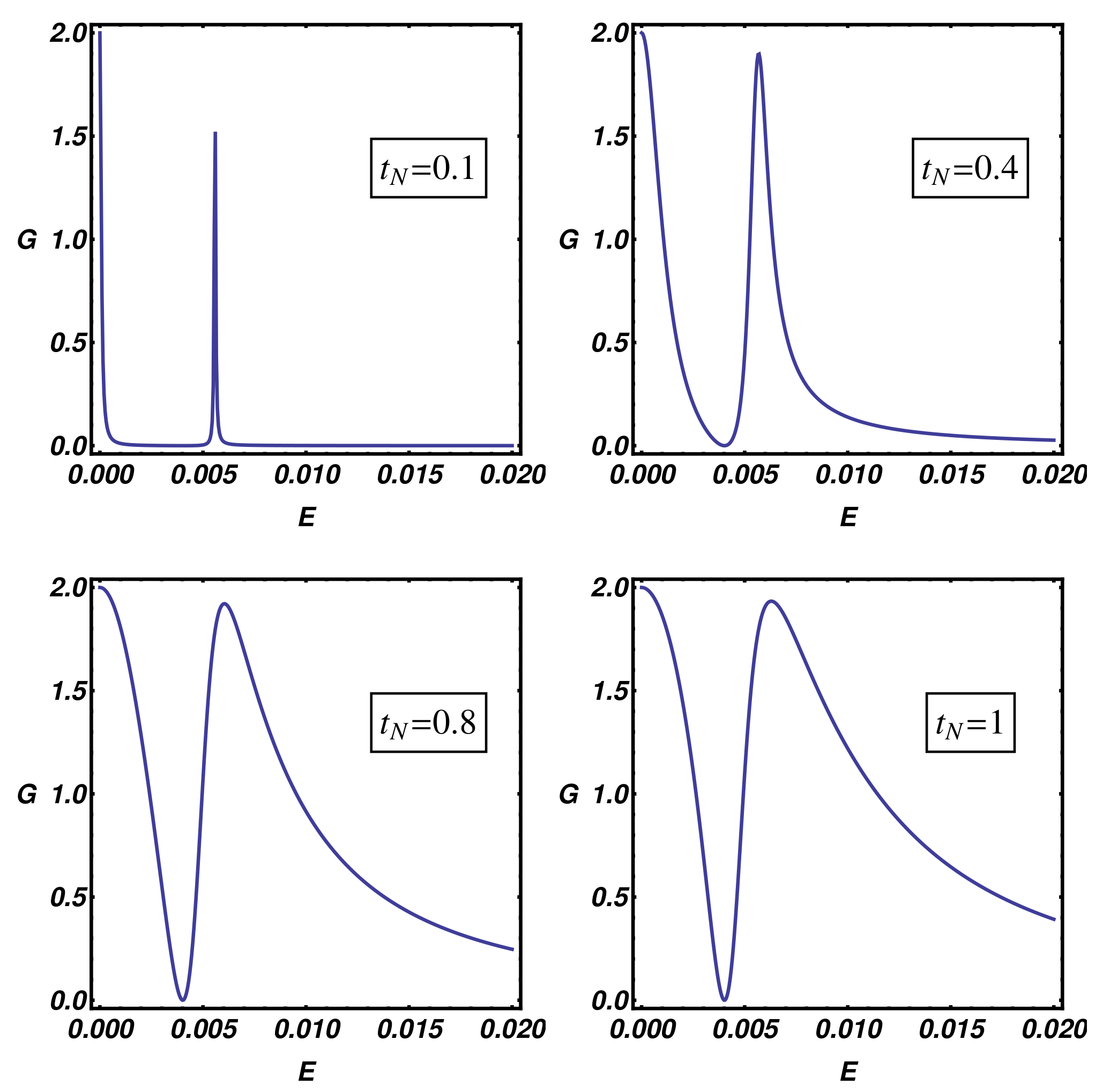
Up to now, we have shown that the overlap between quantum states of the normal electrode and the internal modes of the Kitaev chain can be changed by varying the normal electrode position along the nanowire. From the experimental viewpoint, an alternative way to modify this coupling consists in changing the N-KC distance, e.g., by modifying the distance of an STM normal tip (normal electrode) from the topological nanowire to be measured. In this way, the transmission at the N-KC interface becomes exponentially suppressed at increasing distance due to the vacuum tunneling phenomenon and the same effect is induced on the overlap between quantum states belonging to the normal electrode and the Kitaev chain. Within the considered transport model, the above-mentioned effects can be considered by acting on the hopping amplitude
, which is related to the transparency of the N-KC interface. In order to perform this analysis, in
Figure 9, we present the differential conductance curves of the topological device for selected values of
going from tunneling (
) to the metallic (
) regime. Direct observation of
Figure 9 shows that the resonance broadening of the conductance peaks increases when
increases, the latter condition being related to a reduced N-KC distance. On the other hand, a smaller hopping amplitude induces a resonance shrinking which reflects a reduced overlap between the tip and system modes, this condition being appropriate to describe an increased N-KC spatial gap. The analysis of
Figure 9 also suggests that the transparent limit of the BTK theory, characterized by a constant subgap conductance plateau sustained by the Andreev reflection, is not accessible within the considered T-stub geometry in which additional scattering events are originated at the waveguide junctions. The BTK transparent limit can be approached using the geometry described in
Appendix B, which, in general, does not correspond to the experimental conditions of an STM measurement and thus presents a limited relevance in our discussion.
To complete our analysis, let us note that the emergence of topological phases in closed systems is commonly discussed in terms of properties of the Hamiltonian spectrum. For the open system considered here, the mentioned classification can be done by studying the scattering matrix properties. Indeed, following the work by Beenakker et al. [
24], we consider the reflection submatrix
r of the scattering matrix
S:
and introduce the topological number
. We have verified that a numerical estimate of
Q gives the same topological phase boundary in the
plane as the one of an isolated Kitaev chain, confirming that one can characterize the non-trivial phase of the system under study via the scattering matrix properties.
5. Quantum Transport through a Normal/Kitaev Ladder/Superconductor Device
In this section, we consider the transport properties of the N-KL-SC device depicted in
Figure 10. Proceeding as was done for the N-KC-SC device, we have determined the scattering matrix elements by imposing appropriate matching conditions on the incident and transmitted scattering states and we have evaluated the differential conductance in terms of Andreev and normal reflection probability.
The results of this analysis are shown in
Figure 11 where the conductance curves and the internal modes of the Kitaev ladder are shown. The model parameters used in the computations are those that determine the emergence of a topological phase with two Majorana fermions per edge for the closed system [
19] discussed in
Section 3 (
Figure 6). The conductance curves ((a), (e), and (i)) show a multiple peaks structure containing a zero-bias conductance peak accompanied by two satellite peaks at higher energy (
and
). The zero-bias conductance peak is related to a Majorana mode peaked at the left end of the ladder, while satellite peaks are related with U-shaped internal modes peaked at the ladder edges (see (c), (d), (g), (h), (m), and (n)). Internal modes pertaining to the satellite peaks can be associated with quantum states coming from hybridization processes of genuine Majorana modes. The hybridization of such states, which is favored by the opening of the system, produces a degradation of the initial topological properties and gives rise to quasi-Majorana states [
25]. As discussed before, the degree of hybridization of the ladder internal states can be deduced by measuring the resonance width of the conductance peaks. In close analogy with the discussion reported for the N-KC-SC device, we do observe a clear correspondence between the internal modes wave function at the N-KL interface and the resonance broadening of the conductance peaks. In the next section, we describe disorder effects on quasi-Majorana states.
Figure 11.
N-KL-SC device: zero-temperature differential conductance (in the unit of ) as a function of the energy. Different panels, namely (a,e,i), are obtained by changing the linking position, given by n, between the normal lead and the nearest Kitaev wire of the ladder. The blue and purple modes in panels (b–d,f–h,l–n) represent the modulus squared of the resonant modes on the upper and lower chain of the ladder (shifted by a convenient vertical offset) evaluated at energy values corresponding to the sub-gap conductance peaks. From the left to the right and from the top to the bottom, we have set the following parameters: (b): , . (c): , . (d): , . (f): , . (g): , . (h): , . (l): , . (m): , . (n): , . The remaining model parameters have been fixed as: , , , , , , .
Figure 11.
N-KL-SC device: zero-temperature differential conductance (in the unit of ) as a function of the energy. Different panels, namely (a,e,i), are obtained by changing the linking position, given by n, between the normal lead and the nearest Kitaev wire of the ladder. The blue and purple modes in panels (b–d,f–h,l–n) represent the modulus squared of the resonant modes on the upper and lower chain of the ladder (shifted by a convenient vertical offset) evaluated at energy values corresponding to the sub-gap conductance peaks. From the left to the right and from the top to the bottom, we have set the following parameters: (b): , . (c): , . (d): , . (f): , . (g): , . (h): , . (l): , . (m): , . (n): , . The remaining model parameters have been fixed as: , , , , , , .
![Nanomaterials 09 00894 g011 Nanomaterials 09 00894 g011]()
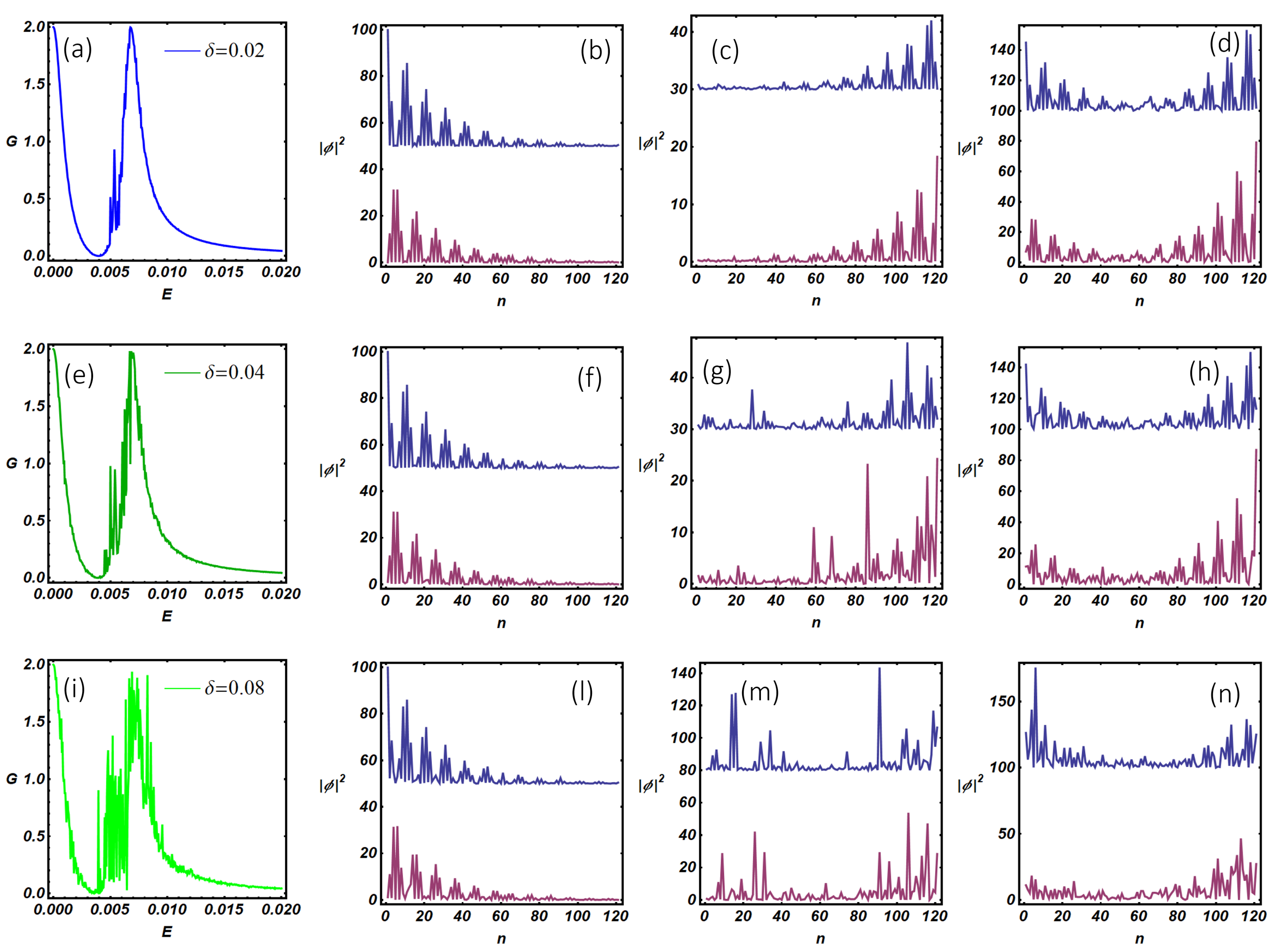
6. Disorder Effects in a Normal/Kitaev Ladder/Superconductor Device
In order to test the robustness of the topological phase in the N-KL-SC device, we include a random potential in the ladder model which emulates, for instance, the intrinsic effect of impurities and inhomogeneities in semiconducting nanowires. On the other hand, when Majorana quasiparticles are realized using ordered assemblies of magnetic atoms on the surface of conventional superconductors [
26,
27], extrinsic disorder effects can be induced by the random strength of the atom-surface coupling. We model these effects assigning random values of the on-site potential
at any system site; the random realizations have been obtained generating random numbers
with uniform distribution in the interval
, with
fixed as
,
,
(
Figure 12). Accordingly, the statistical average of the on-site potential is zero, while its variance is given by
. The remaining model parameters have been fixed as in panel (a) of
Figure 11. When the conductance of a single disordered realization is analyzed (panels (a), (e), (i)), we observe the progressive degradation of the three-peaks structure observed in
Figure 11a, which has been obtained in the absence of disorder. Disorder has a different impact depending on the peak considered. In particular, the zero-bias peak, which corresponds to a robust Majorana mode, remains quantized and disorder only produces a broadening effect on the resonant peak. The above result reflects the fact that disorder introduces a finite mean free path (related to the variance of the random on-site potential) which renormalizes the quasi-particles lifetime and induces a resonance broadening. The two satellite peaks at quasi-zero energy (see
Figure 11a) are fragile against disorder effects. Indeed, in the presence of disorder, one peak is completely suppressed, while the one at higher energy appears broadened and no more quantized (at high disorder). The presented phenomenology suggests that quasi-zero energy modes are related to the hybridization of genuine Majorana states. Such states, being distributed along the whole system, are quite fragile to disorder effects. The suppression of the intermediate resonant peak in the presence of disorder is easily explained looking at panel (c) of
Figure 11 and (c), (g) and (m) of
Figure 12. Indeed, the internal mode in
Figure 11c (in the absence of disorder) is peaked at the system edges. Accordingly, the latter state is well coupled with the scattering states of the normal electrode. When the disorder is included, the overlap of this state with the normal electrode states goes to zero, producing the disappearance of the conductance peak. This effect originates from the disorder-assisted localization of the ladder resonant mode at a system edge which is not connected with the normal electrode (see (c), (g), and (m)). The latter effect is not observed for quasi-zero energy mode at higher energy, which starts to be severely degraded only at high disorder (
). This is confirmed by the internal modes analysis which has been shown in panels (d), (h), and (n). In this case, the analysis provides evidence that internal modes are peaked at both the system edges and thus are well coupled with the normal electrode states, the latter being a requisite to observe a finite conductance.
The above findings suggest that topological protection of quantum states can be lost as an effect of the opening of the isolated quantum system. Indeed, the connection of a topological system with external reservoirs produces hybridization of the internal modes, which is the prerequisite to manifest fragility against the detrimental effects of disorder.