Thermoelectric Inversion in a Resonant Quantum Dot-Cavity System in the Steady-State Regime
Abstract
1. Introduction
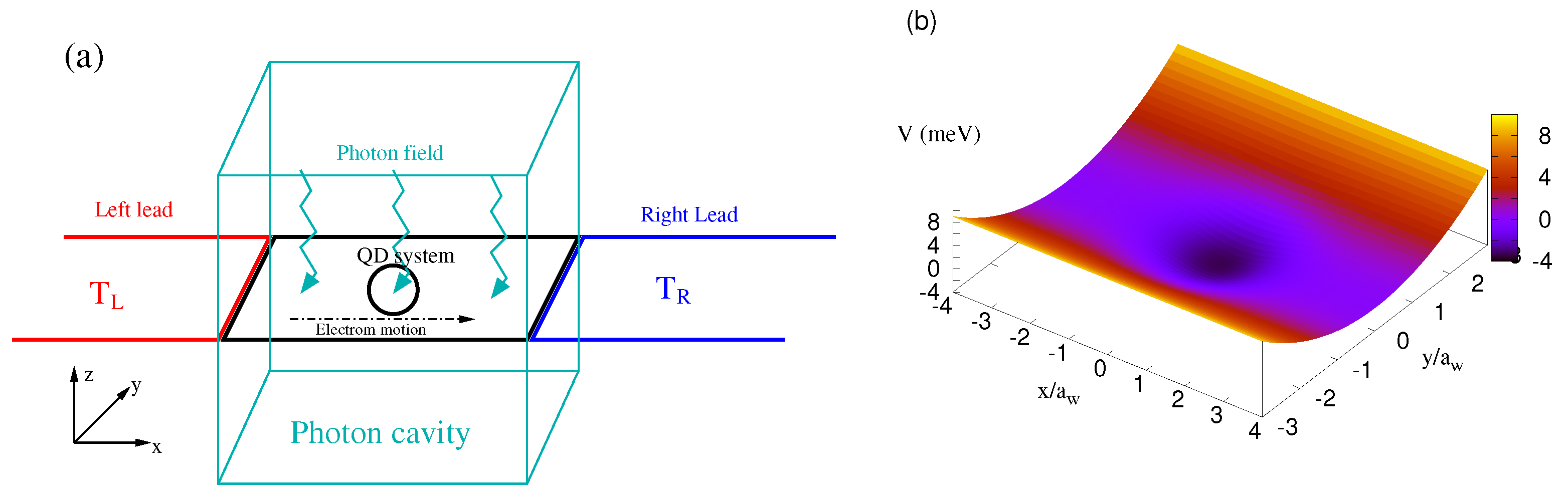
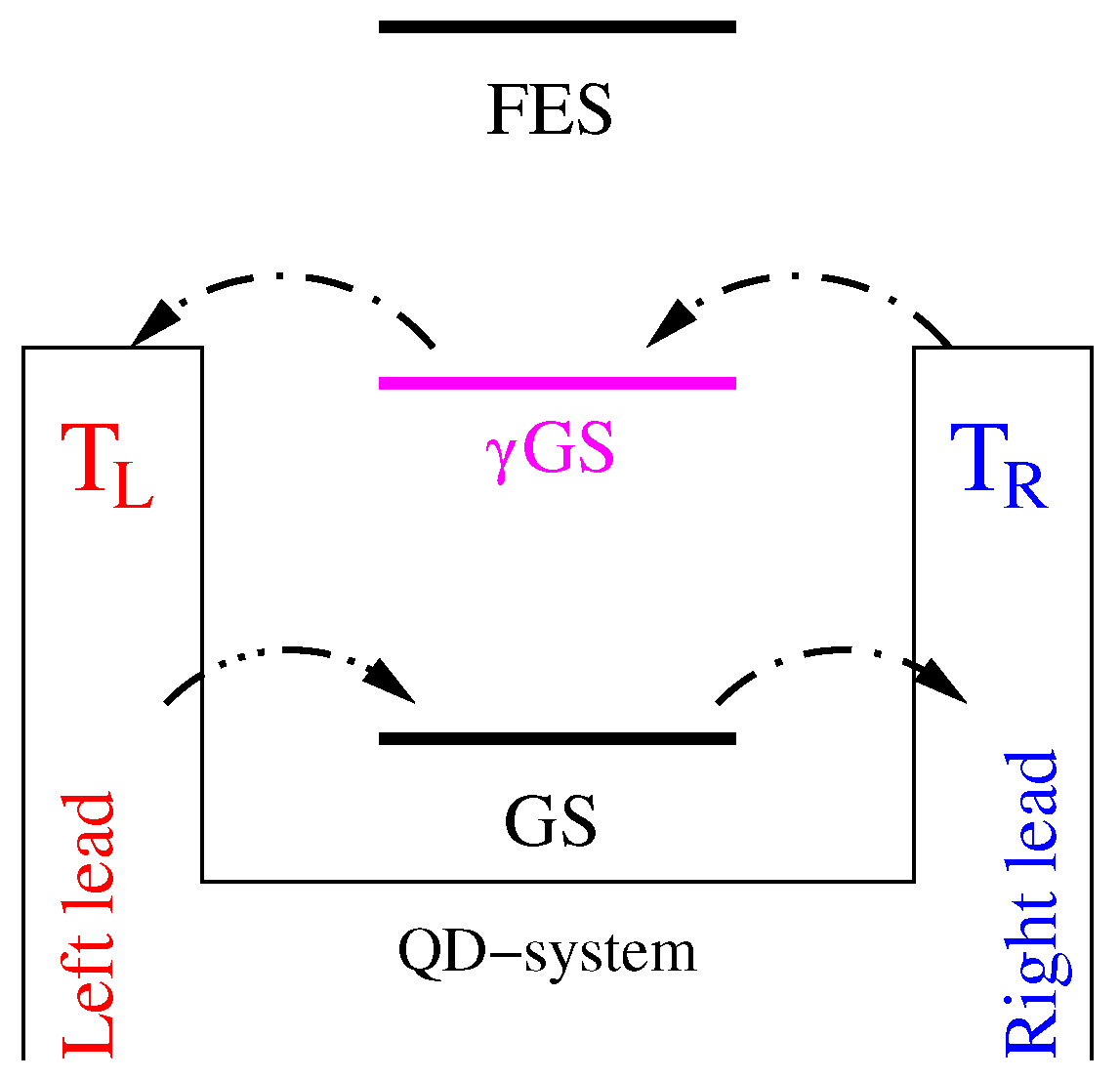
2. Modeling and Formalism
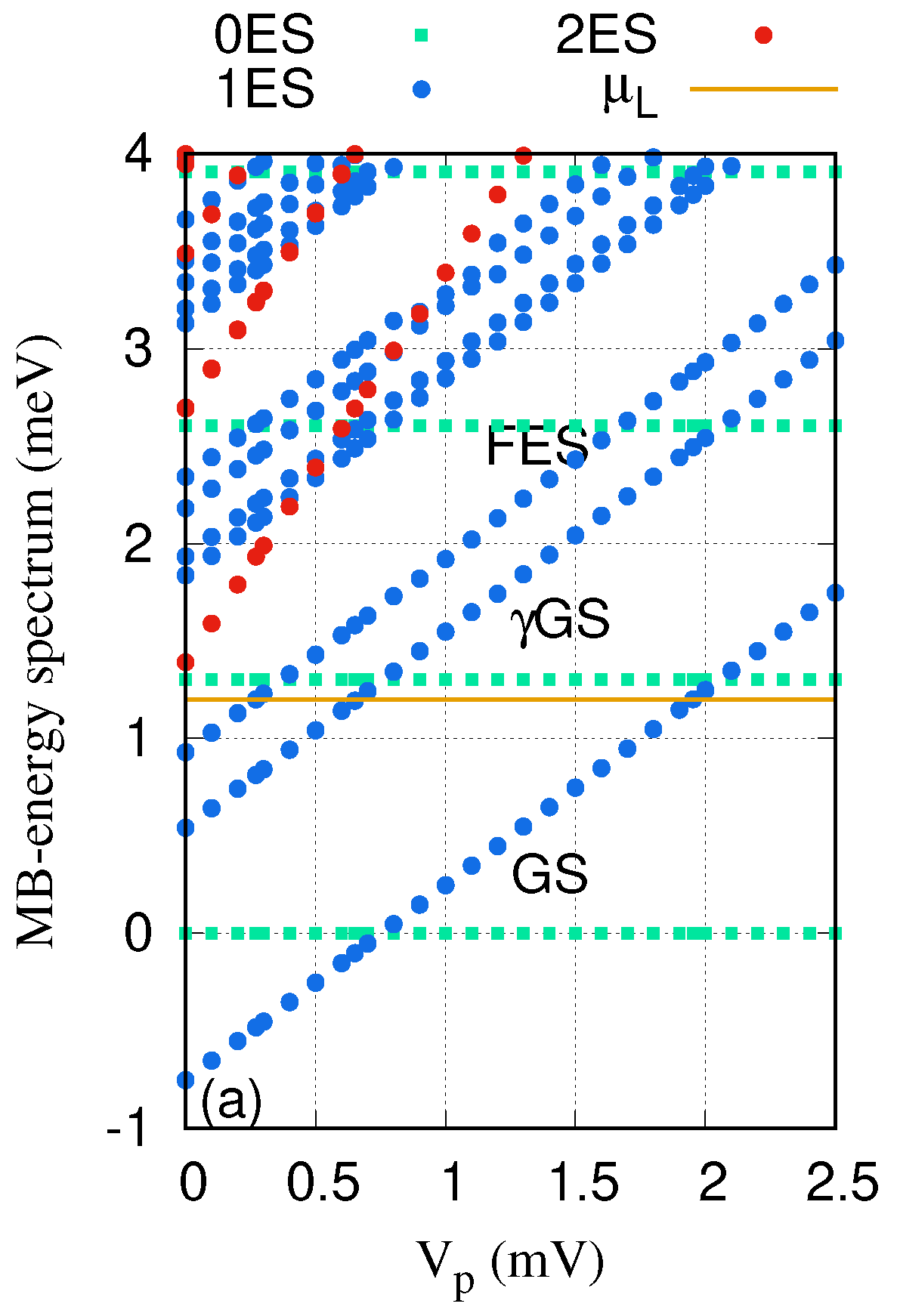
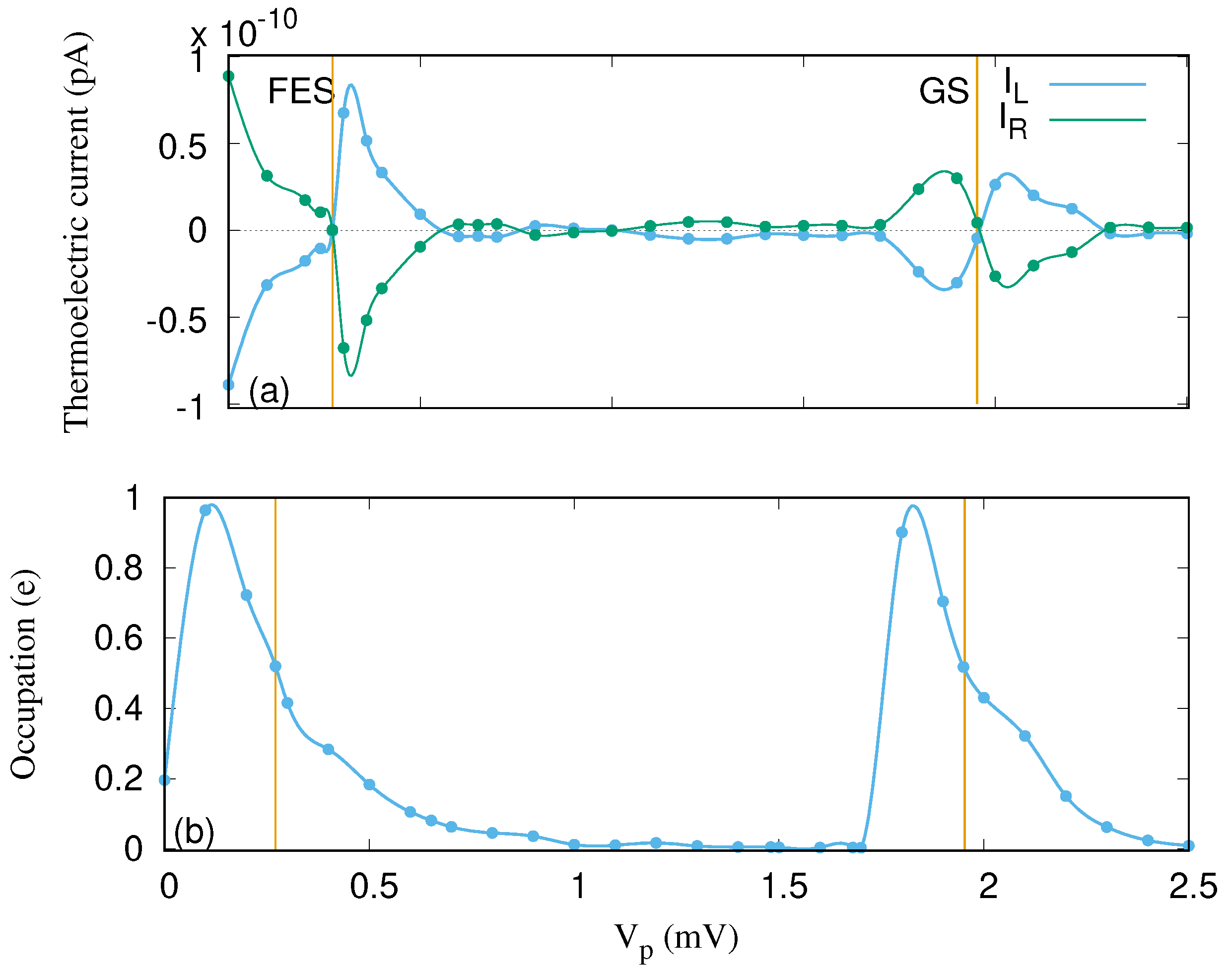
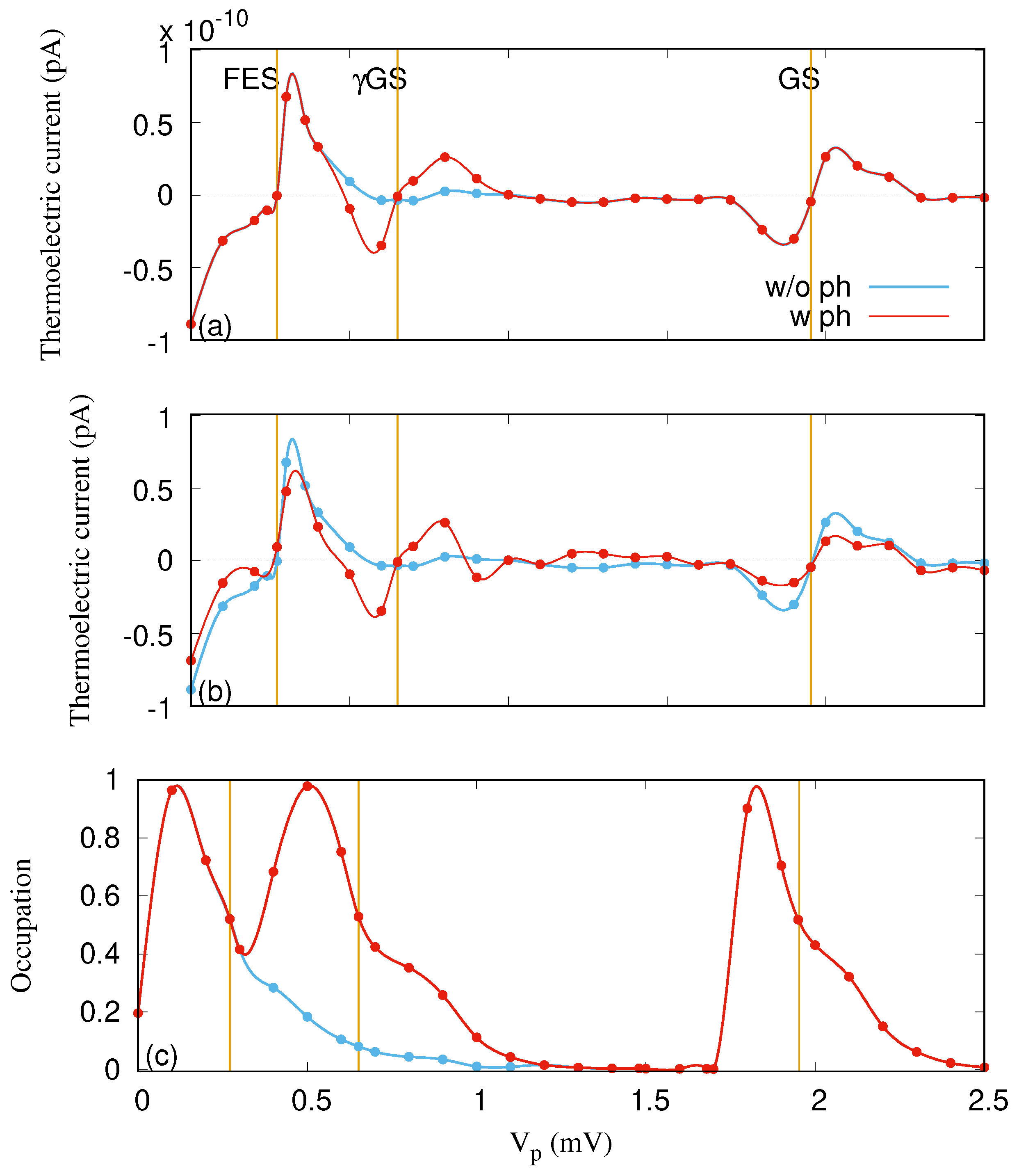
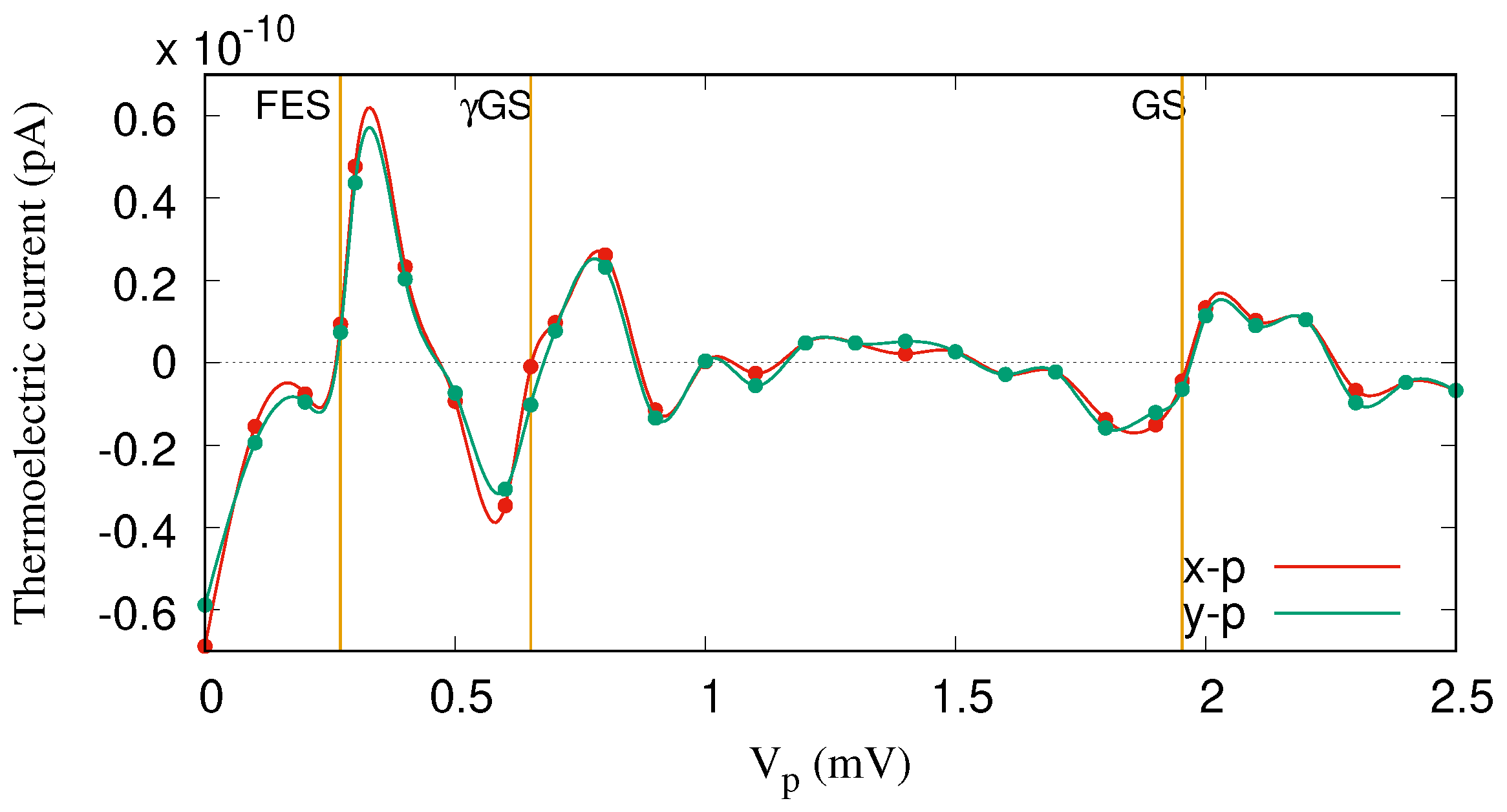
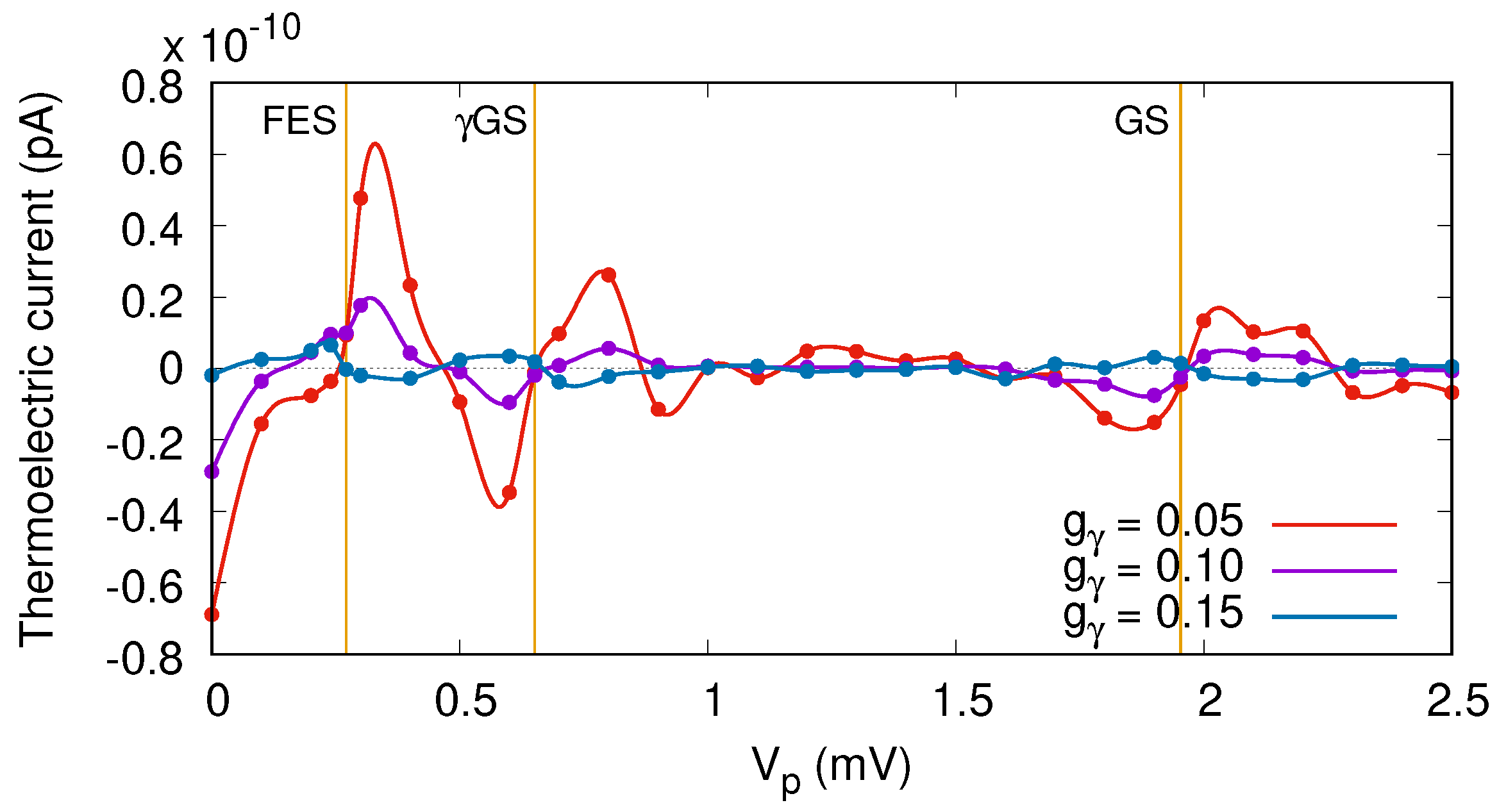
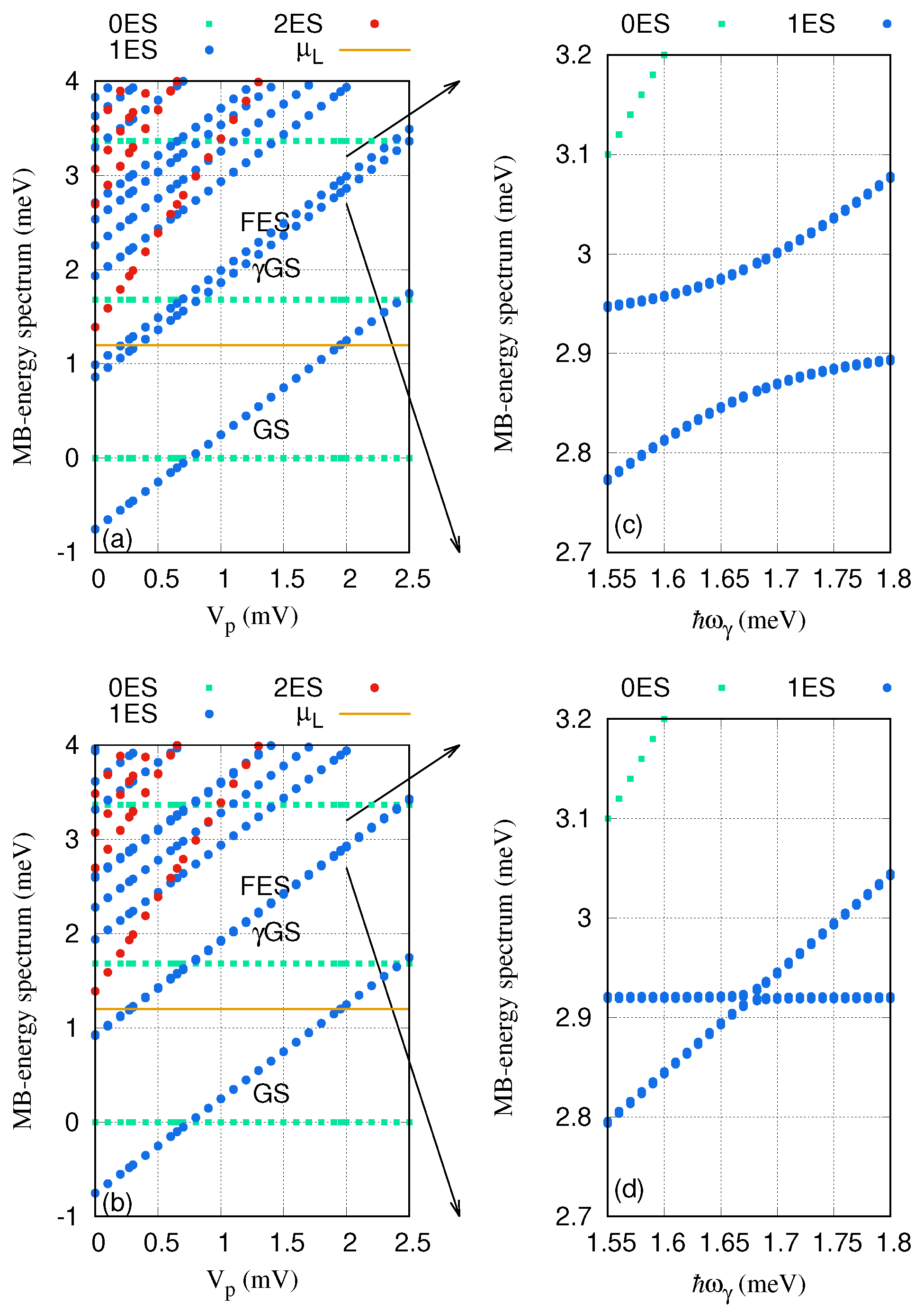
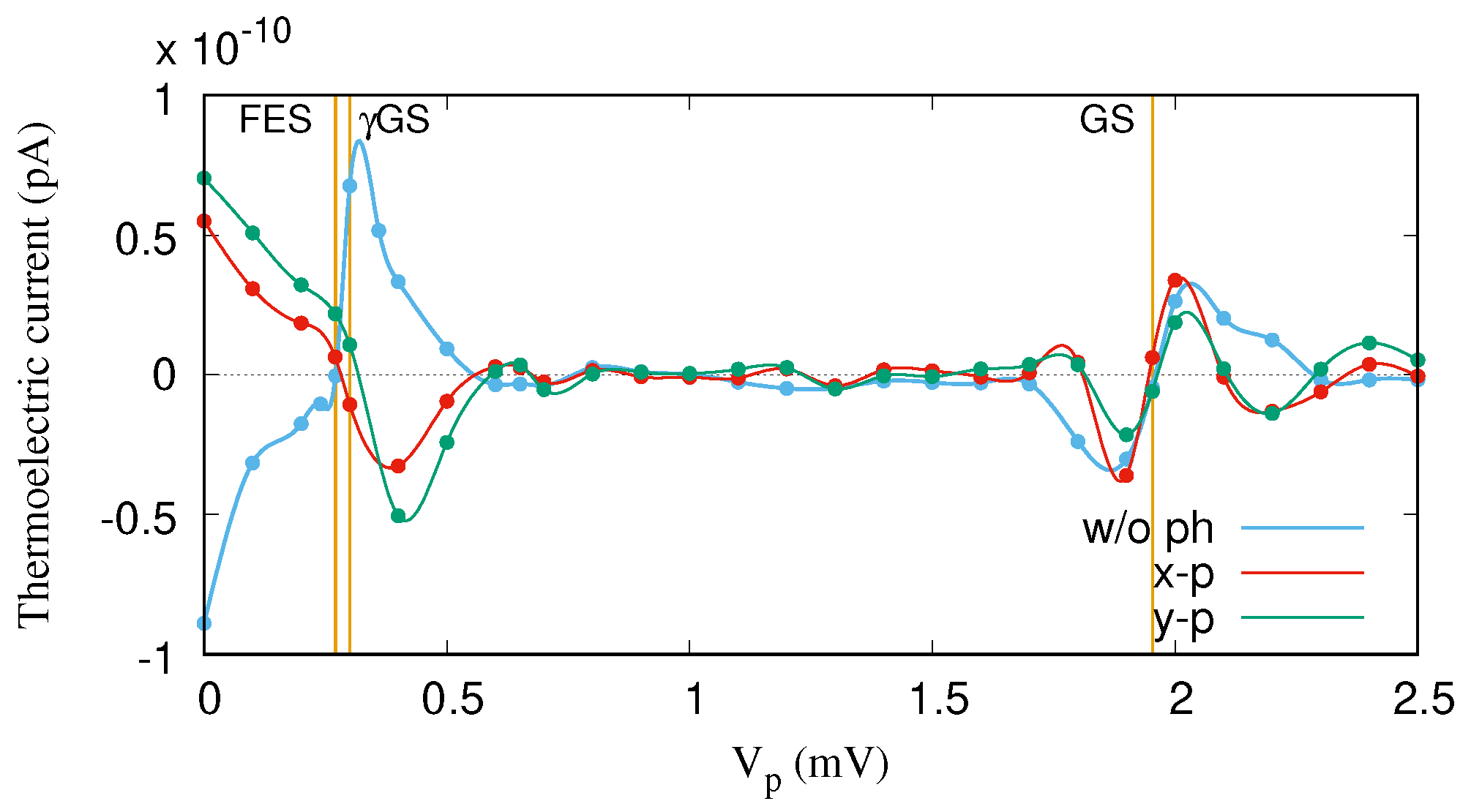
Results
3. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| QD | Quantum dot |
| NEGF | Non-equilibrium Green’s function |
| Temperature of the left lead | |
| Temperature of the right lead | |
| MB | Many-body states |
| GS | Ground-state energy |
| GS | One-photon replica of the ground-state |
| FES | First-excited state energy |
References
- Sothmann, B.; Sánchez, R.; Jordan, A.N. Thermoelectric energy harvesting with quantum dots. Nanotechnology 2015, 26, 032001. [Google Scholar] [CrossRef]
- Scheibner, R.; Buhmann, H.; Reuter, D.; Kiselev, M.N.; Molenkamp, L.W. Thermopower of a Kondo Spin-Correlated Quantum Dot. Phys. Rev. Lett. 2005, 95, 176602. [Google Scholar] [CrossRef] [PubMed]
- Boese, D.; Fazio, R. Thermoelectric effects in Kondo-correlated quantum dots. Europhys. Lett. 2001, 56, 576–582. [Google Scholar] [CrossRef][Green Version]
- Turek, M.; Matveev, K.A. Cotunneling thermopower of single electron transistors. Phys. Rev. B 2002, 65, 115332. [Google Scholar] [CrossRef]
- Pichard, J.L.; Whitney, R.S. Mesoscopic thermoelectric phenomena/Phénomènes thermoélectriques mésoscopiques. C. R. Phys. 2016, 17, 1039–1046. [Google Scholar] [CrossRef]
- Andreev, A.V.; Matveev, K.A. Coulomb Blockade Oscillations in the Thermopower of Open Quantum Dots. Phys. Rev. Lett. 2001, 86, 280–283. [Google Scholar] [CrossRef]
- Beenakker, C.W.J.; Staring, A.A.M. Theory of the thermopower of a quantum dot. Phys. Rev. B 1992, 46, 9667–9676. [Google Scholar] [CrossRef]
- Sierra, M.A.; Sánchez, D. Strongly nonlinear thermovoltage and heat dissipation in interacting quantum dots. Phys. Rev. B 2014, 90, 115313. [Google Scholar] [CrossRef]
- Liu, J.; Sun, Q.f.; Xie, X.C. Enhancement of the thermoelectric figure of merit in a quantum dot due to the Coulomb blockade effect. Phys. Rev. B 2010, 81, 245323. [Google Scholar] [CrossRef]
- Tsaousidou, M.; Triberis, G.P. Thermoelectric properties of a weakly coupled quantum dot: enhanced thermoelectric efficiency. J. Phys. Condens. Matter 2010, 22, 355304. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Liu, J.; Song, J.; Sun, Q.f.; Xie, X.C. Electric-current-induced heat generation in a strongly interacting quantum dot in the Coulomb blockade regime. Phys. Rev. B 2009, 79, 161309. [Google Scholar] [CrossRef]
- Trocha, P.; Barnaś, J. Spin-dependent thermoelectric phenomena in a quantum dot attached to ferromagnetic and superconducting electrodes. Phys. Rev. B 2017, 95, 165439. [Google Scholar] [CrossRef]
- Hauptmann, J.R.; Paaske, J.; Lindelof, P.E. Electric-field-controlled spin reversal in a quantum dot with ferromagnetic contacts. Nat. Phys. 2008, 4, 373–376. [Google Scholar] [CrossRef]
- Bathen, M.E.; Linder, J. Spin Seebeck effect and thermoelectric phenomena in superconducting hybrids with magnetic textures or spin-orbit coupling. Sci. Rep. 2017, 7, 41409. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Spin-dependent heat and thermoelectric currents in a Rashba ring coupled to a photon cavity. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 95, 102–107. [Google Scholar] [CrossRef]
- Ojanen, T.; Jauho, A.P. Mesoscopic Photon Heat Transistor. Phys. Rev. Lett. 2008, 100, 155902. [Google Scholar] [CrossRef]
- Joulain, K.; Drevillon, J.; Ezzahri, Y.; Ordonez-Miranda, J. Quantum Thermal Transistor. Phys. Rev. Lett. 2016, 116, 200601. [Google Scholar] [CrossRef]
- Meschke, M.; Guichard, W.; Pekola, J.P. Single-mode heat conduction by photons. Nature 2006, 444, 187–190. [Google Scholar] [CrossRef]
- Chi, F.; Dubi, Y. Microwave-mediated heat transport in a quantum dot attached to leads. J. Phys. Condens. Matter 2012, 24, 145301. [Google Scholar] [CrossRef]
- Nakajima, S. On quantum theory of transport phenomena steady diffusion. Prog. Theor. Phys. 1958, 20, 948. [Google Scholar] [CrossRef]
- Zwanzig, R. Ensemble Method in the Theory of Irreversibility. J. Chem. Phys. 1960, 33, 1338–1341. [Google Scholar] [CrossRef]
- Jonsson, T.H.; Manolescu, A.; Goan, H.S.; Abdullah, N.R.; Sitek, A.; Tang, C.S.; Gudmundsson, V. Efficient determination of the Markovian time-evolution towards a steady-state of a complex open quantum system. Comput. Phys. Commun. 2017, 220, 81–90. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Cavity-Photon Controlled Thermoelectric Transport through a Quantum Wire. ACS Photonics 2016, 3, 249–254. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Effects of photon field on heat transport through a quantum wire attached to leads. Phys. Lett. A 2018, 382, 199–204. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Marif, R.B.; Rashid, H.O. Photon-Mediated Thermoelectric and Heat Currents through a Resonant Quantum Wire-Cavity System. Energies 2019, 12, 1082. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Gudmundsson, V. Single-photon controlled thermospin transport in a resonant ring-cavity system. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 104, 223–228. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Arnold, T.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Photon-induced tunability of the thermospin current in a Rashba ring. J. Phys. Condens. Matter 2018, 30, 145303. [Google Scholar] [CrossRef]
- Abdullah, N.R. Optical control of spin-dependent thermal transport in a quantum ring. Phys. Lett. A 2018. [Google Scholar] [CrossRef]
- Arnold, T.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Excitation spectra of a quantum ring embedded in a photon cavity. J. Opt. 2015, 17, 015201. [Google Scholar] [CrossRef]
- Jonasson, O.; Tang, C.S.; Goan, H.S.; Manolescu, A.; Gudmundsson, V. Nonperturbative approach to circuit quantum electrodynamics. Phys. Rev. E 2012, 86, 046701. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Competition of static magnetic and dynamic photon forces in electronic transport through a quantum dot. J. Phys. Condens. Matter 2016, 28, 375301. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Electron transport through a quantum dot assisted by cavity photons. J. Phys. Condens. Matter 2013, 25, 465302. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Jonasson, O.; Arnold, T.; Tang, C.S.; Goan, H.S.; Manolescu, A. Stepwise introduction of model complexity in a general master equation approach to time-dependent transport. Fortschr. Phys. 2013, 61, 305. [Google Scholar] [CrossRef]
- Gudmundsson, V.; Abdullah, N.R.; Sitek, A.; Goan, H.S.; Tang, C.S.; Manolescu, A. Current correlations for the transport of interacting electrons through parallel quantum dots in a photon cavity. Phys. Lett. A 2018, 382, 1672–1678. [Google Scholar] [CrossRef]
- Lax, M. Formal Theory of Quantum Fluctuations from a Driven State. Phys. Rev. 1963, 129, 2342–2348. [Google Scholar] [CrossRef]
- Gardiner, C.W.; Collett, M.J. Input and output in damped quantum systems: Quantum stochastic differential equations and the master equation. Phys. Rev. A 1985, 31, 3761–3774. [Google Scholar] [CrossRef]
- Beaudoin, F.; Gambetta, J.M.; Blais, A. Dissipation and ultrastrong coupling in circuit QED. Phys. Rev. A 2011, 84, 043832. [Google Scholar] [CrossRef]
- Tan, S.G.; Jalil, M.B. 2—Nanoscale physics and electronics. In Introduction to the Physics of Nanoelectronics; Tan, S.G., Jalil, M.B., Eds.; Woodhead Publishing Series in Electronic and Optical Materials; Woodhead Publishing: Sawston, UK, 2012; pp. 23–77. [Google Scholar] [CrossRef]
- Smakula, A.; Skribanowitz, N.; Szorc, A. Dielectric Properties of Semiconductors at Low Temperatures. J. Appl. Phys. 1972, 43, 508–515. [Google Scholar] [CrossRef]
- Tagani, M.B.; Soleimani, H.R. Photon-phonon -assisted thermoelectric effects in the molecular devices. Physica E 2013, 48, 36–41. [Google Scholar] [CrossRef]
- Torfason, K.; Manolescu, A.; Erlingsson, S.I.; Gudmundsson, V. Thermoelectric current and Coulomb-blockade plateaus in a quantum dot. Physica E 2013, 53, 178–185. [Google Scholar] [CrossRef][Green Version]
- Gudmundsson, V.; Gainar, C.; Tang, C.S.; Moldoveanu, V.; Manolecu, A. Time-dependent transport via the generalized master equation through a finit quantum wire with an embedded subsystem. New J. Phys. 2009, 11, 113007. [Google Scholar] [CrossRef]
- Chen, X.; Liu, D.; Duan, W.; Guo, H. Photon-assisted thermoelectric properties of noncollinear spin valves. Phys. Rev. B 2013, 87, 085427. [Google Scholar] [CrossRef]
- Tagani, M.B.; Soleimani, H.R. Phonon-assisted thermoelectric effects in a two-level molecule. Phys. B Condens. Matter 2013, 413, 86–91. [Google Scholar] [CrossRef]
- Abdullah, N.R.; Tang, C.S.; Manolescu, A.; Gudmundsson, V. Delocalization of electrons by cavity photons in transport through a quantum dot molecule. Physica E 2014, 64, 254–262. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Abdullah, N.R.; Tang, C.-S.; Manolescu, A.; Gudmundsson, V. Thermoelectric Inversion in a Resonant Quantum Dot-Cavity System in the Steady-State Regime. Nanomaterials 2019, 9, 741. https://doi.org/10.3390/nano9050741
Abdullah NR, Tang C-S, Manolescu A, Gudmundsson V. Thermoelectric Inversion in a Resonant Quantum Dot-Cavity System in the Steady-State Regime. Nanomaterials. 2019; 9(5):741. https://doi.org/10.3390/nano9050741
Chicago/Turabian StyleAbdullah, Nzar Rauf, Chi-Shung Tang, Andrei Manolescu, and Vidar Gudmundsson. 2019. "Thermoelectric Inversion in a Resonant Quantum Dot-Cavity System in the Steady-State Regime" Nanomaterials 9, no. 5: 741. https://doi.org/10.3390/nano9050741
APA StyleAbdullah, N. R., Tang, C.-S., Manolescu, A., & Gudmundsson, V. (2019). Thermoelectric Inversion in a Resonant Quantum Dot-Cavity System in the Steady-State Regime. Nanomaterials, 9(5), 741. https://doi.org/10.3390/nano9050741




