Morphology and Kinetics Evolution of Nanoscale Phase in Fe–Cr Alloys under External Strain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Elastic Strain Energy
2.2. Phase-Field Model
2.3. Numerical Calculation
3. Results and Discussions
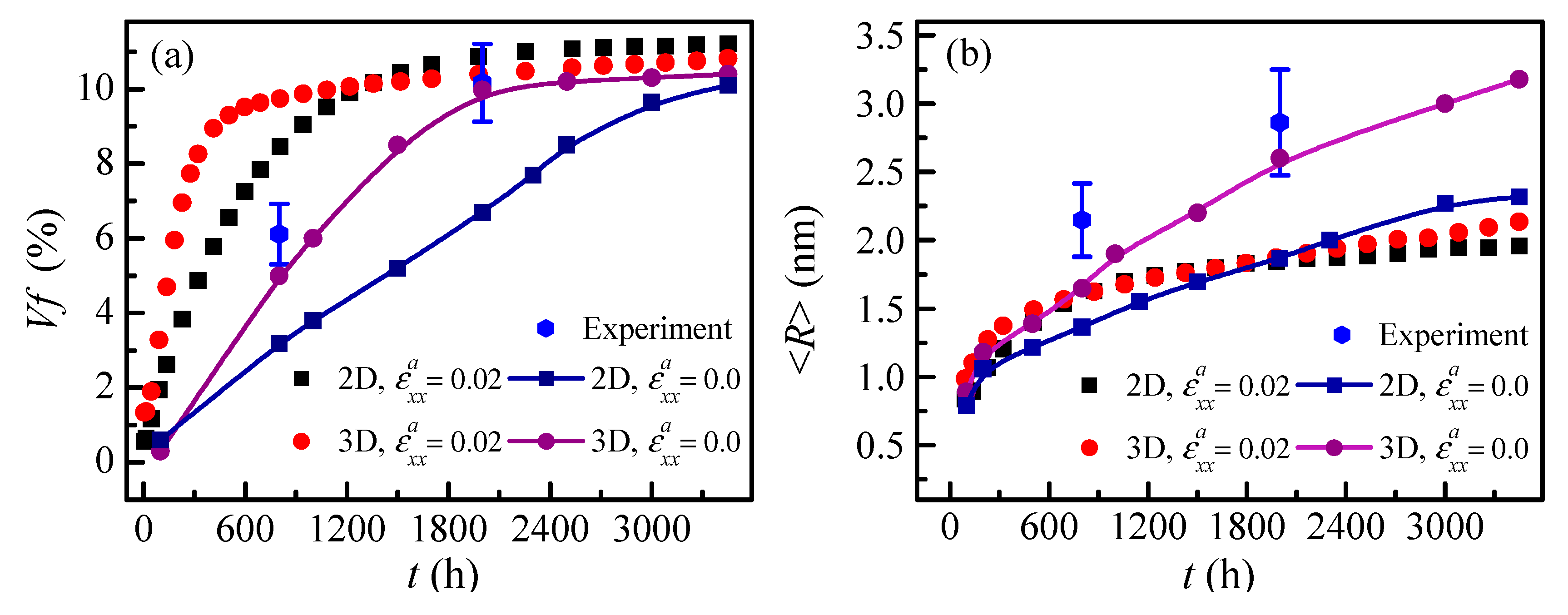
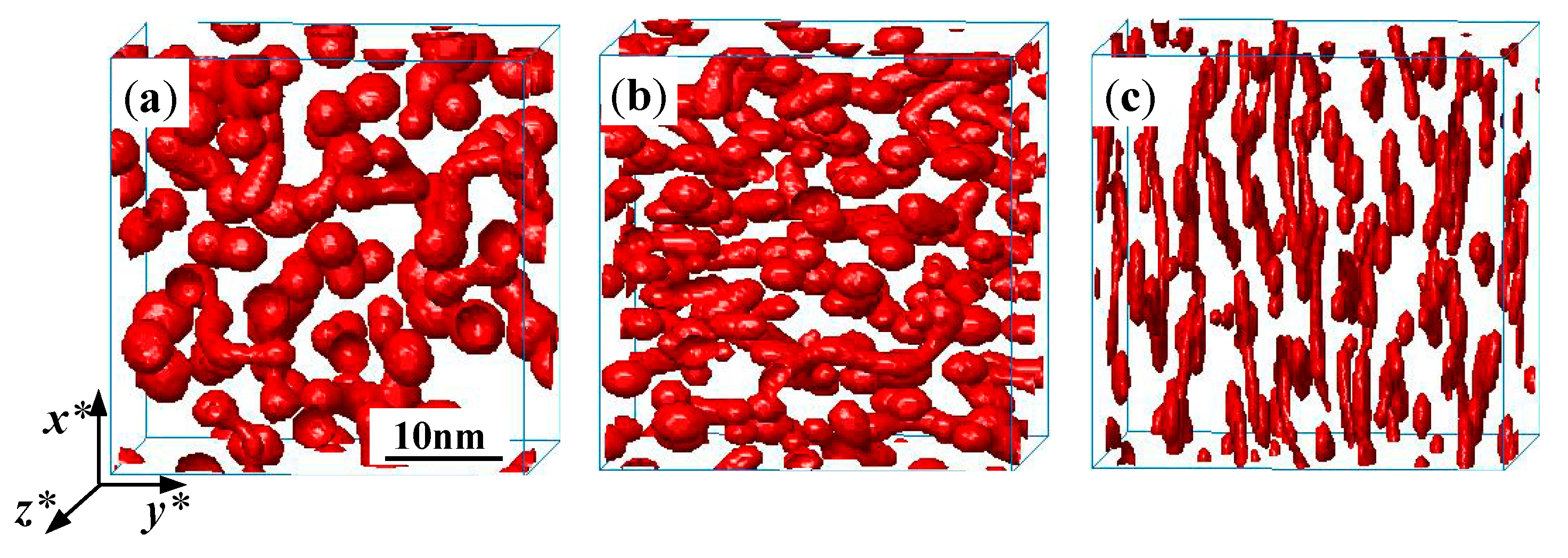
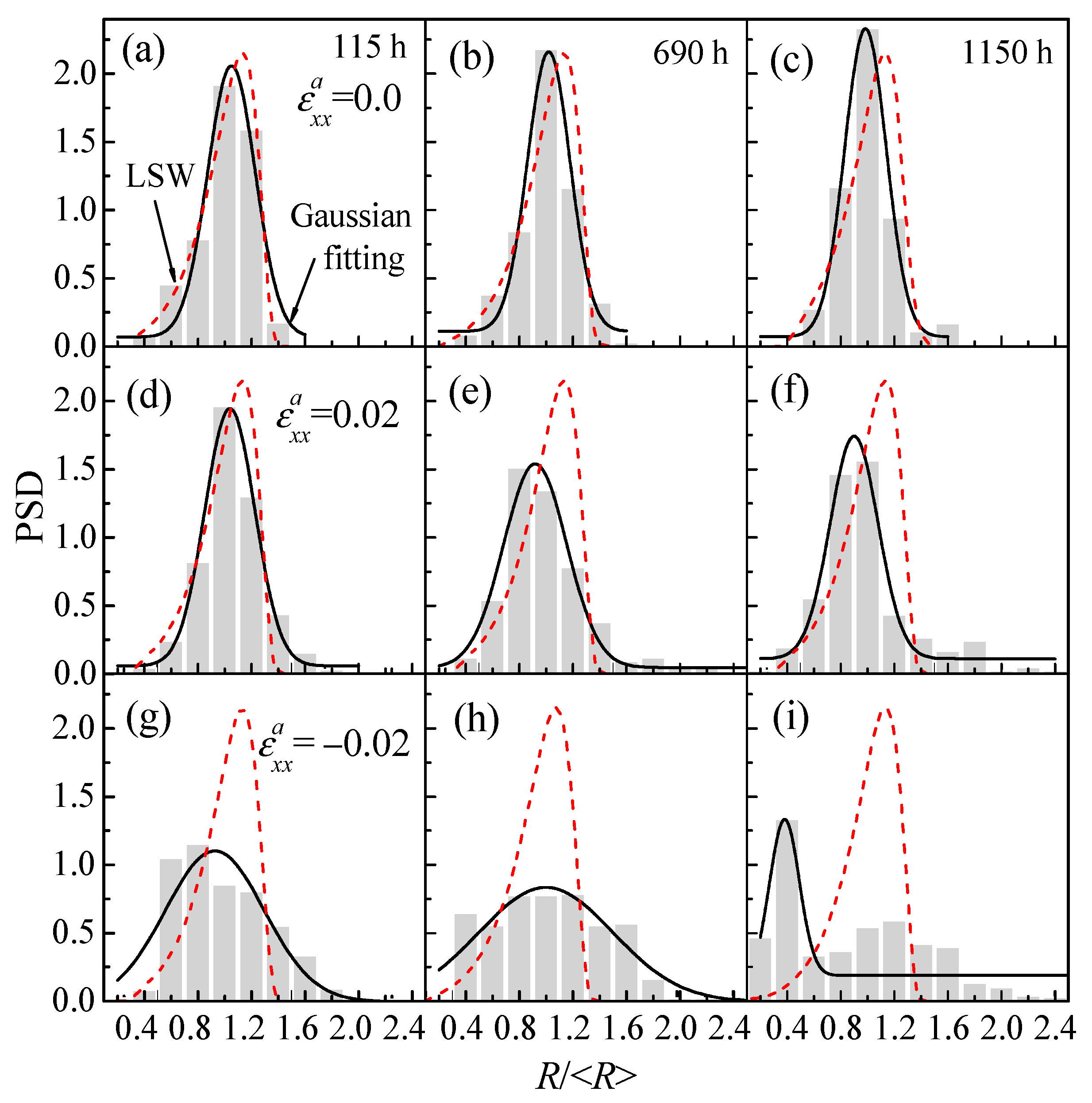
3.1. Morphological Evolution of the α′ Phase
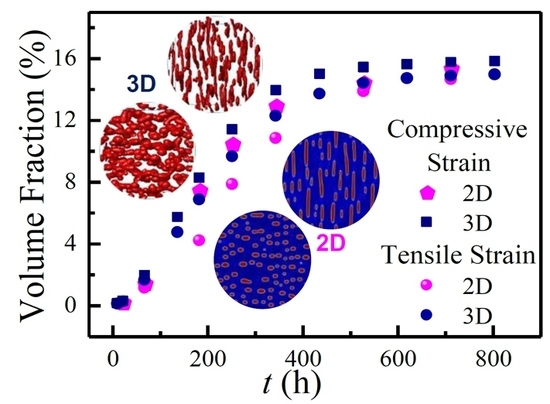
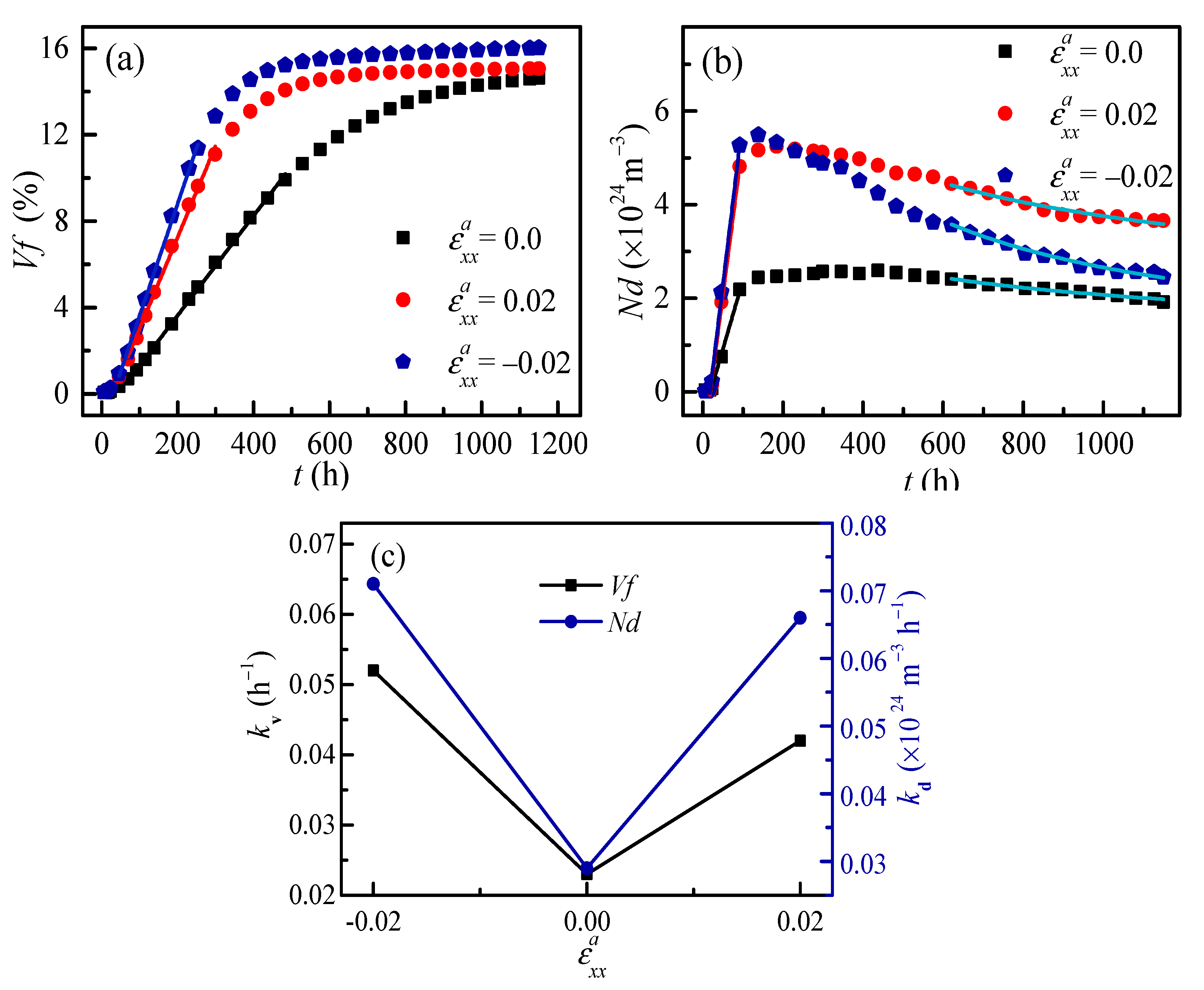
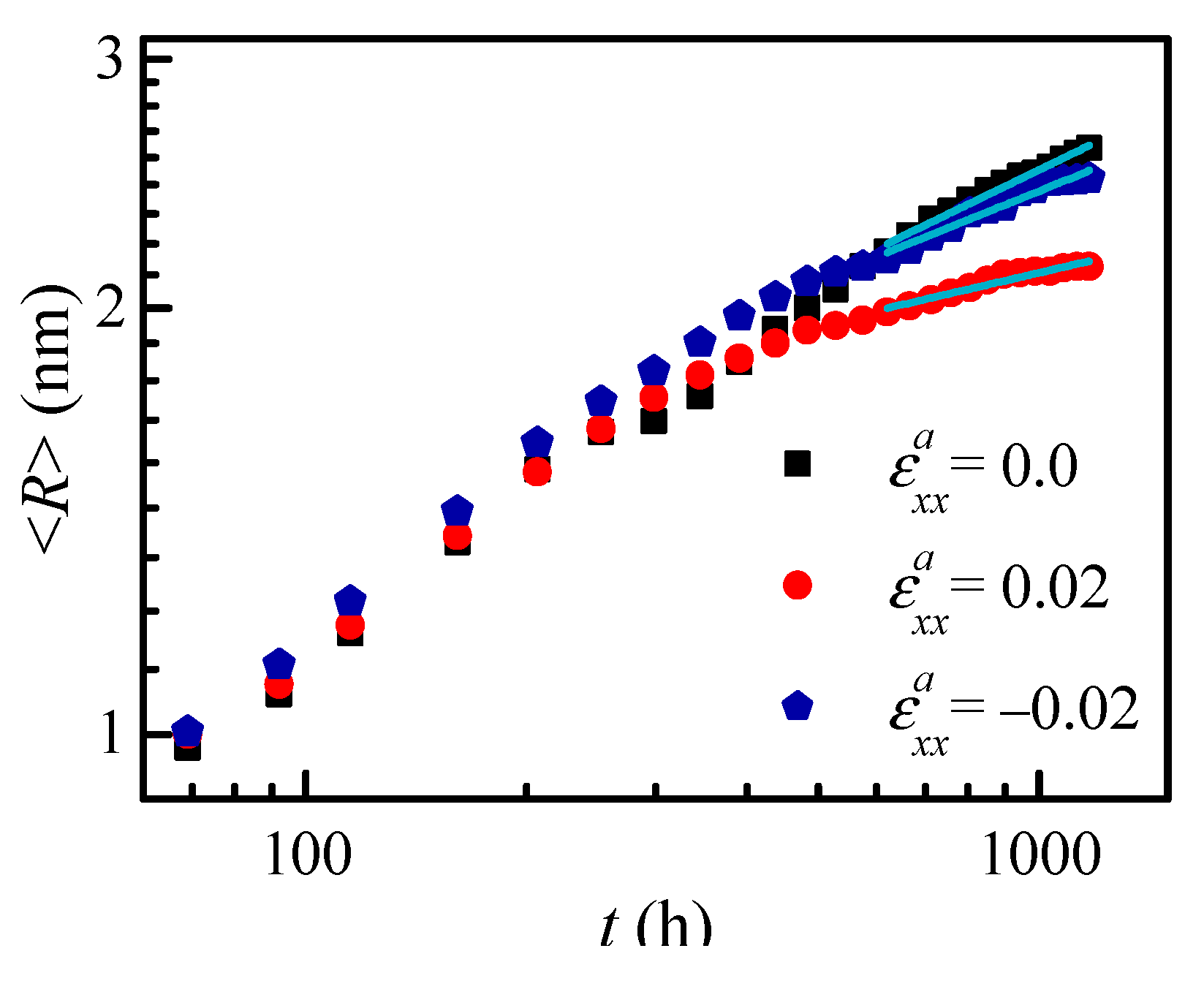
3.2. Effect of Applied Strain on Separation Kinetics
3.2.1. Composition Boundary Change under Applied Strain
3.2.2. Orientation Morphology of the α′ Phase under Applied Strain
3.2.3. Separation Kinetics of the α′ Phase under Applied Strain
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhou, J.; Odqvist, J.; Ruban, A.; Thuvander, M.; Xiong, W.; Ågren, J.; Olson, G.B.; Hedström, P. Effect of solution treatment on spinodal decomposition during aging of an Fe-46.5 at.% Cr alloy. J. Mater. Sci. 2017, 52, 326–335. [Google Scholar] [CrossRef]
- Barkar, T.; Höglund, L.; Odqvist, J.; Ågren, J. Effect of concentration dependent gradient energy coefficient on spinodal decomposition in the Fe–Cr system. Comput. Mater. Sci. 2018, 143, 446–453. [Google Scholar] [CrossRef]
- Tissot, O.; Pareige, C.; Meslin, E.; Decamps, B.; Henry, J. Kinetics of α′ precipitation in an electron-irradiated Fe15Cr alloy. Scr. Mater. 2016, 122, 31–35. [Google Scholar] [CrossRef]
- Reese, E.R.; Bachhav, M.; Wells, P.; Yamamoto, T.; Odette, G.R.; Marquis, E.A. On α′ precipitate composition in thermally annealed and neutron-irradiated Fe-9-18Cr alloys. J. Nucl. Mater. 2018, 500, 192–198. [Google Scholar] [CrossRef]
- Zhou, J.; Odqvist, J.; Höglund, L.; Thuvander, M.; Barkar, T.; Hedström, P. Initial clustering–a key factor for phase separation kinetics in Fe–Cr based alloys. Scr. Mater. 2014, 75, 62–65. [Google Scholar] [CrossRef]
- Zhou, J.; Odqvist, J.; Ågren, J.; Ruban, A.; Thuvander, M.; Xiong, W.; Olson, G.B.; Hedström, P. Direct atom probe tomography observations of concentration fluctuations in Fe–Cr solid solution. Scr. Mater. 2015, 98, 13–15. [Google Scholar] [CrossRef]
- Li, Y.S.; Li, S.X.; Zhang, T.Y. Effect of dislocations on spinodal decomposition in Fe–Cr alloys. J. Nucl. Mater. 2009, 395, 120–130. [Google Scholar] [CrossRef]
- Dahlström, A.; Danoix, F.; Hedström, P.; Odqvist, J.; Zapolsky, H. An experimental assessment of the α+α’ miscibility gap in Fe–Cr. In TMS 2017 146th Annual Meeting & Exhibition Supplemental Proceedings; The Minerals, Metals & Materials Series; TMS, Ed.; Springer: Cham, Switzerland, 2017; pp. 711–718. [Google Scholar]
- Li, Y.S.; Zhu, H.; Zhang, L.; Cheng, X.L. Phase decomposition and morphology characteristic in thermal aging Fe–Cr alloys under applied strain: A phase-field simulation. J. Nucl. Mater. 2012, 429, 13–18. [Google Scholar] [CrossRef]
- Rogozhkin, S.V.; Korchuganova, O.A.; Aleev, A.A. Kinetics of α′ phase nucleation during thermal aging of Fe-22% Cr alloy. Inorg. Mater. Appl. Res. 2016, 7, 210–213. [Google Scholar] [CrossRef]
- Yan, Z.L.; Li, Y.S.; Zhou, X.R.; Zhang, Y.D.; Hu, R. Evolution of nanoscale Cr-rich phase in a Fe-35 at.% Cr alloy during isothermal aging. J. Alloys Compd. 2017, 725, 1035–1043. [Google Scholar] [CrossRef]
- Novy, S.; Pareige, P.; Pareige, C. Atomic scale analysis and phase separation understanding in a thermally aged Fe-20 at.% Cr alloy. J. Nucl. Mater. 2009, 384, 96–102. [Google Scholar] [CrossRef]
- Sahu, J.K.; Krupp, U.; Ghosh, R.N.; Christ, H.J. Effect of 475 °C embrittlement on the mechanical properties of duplex stainless steel. Mater. Sci. Eng. A 2009, 508, 1–14. [Google Scholar] [CrossRef]
- Eshelby, J.D. The determination of the elastic field of an ellipsoidal inclusion and related problems. Proc. R. Soc. A 1957, 241, 376–396. [Google Scholar]
- Eshelby, J.D. The elastic field outside an ellipsoidal inclusion. Proc. R. Soc. A 1959, 252, 561–566. [Google Scholar]
- Eshelby, J.D. Elastic inclusions and inhomogeneities. In Sneddon IN; Hill, R., Ed.; Progress in Solid Mechanics: Amsterdam, The Netherlands, 1961; pp. 87–140. [Google Scholar]
- Walpole, L.J. The elastic field of an inclusion in an anisotropic medium. Proc. R. Soc. A 1967, 300, 270–289. [Google Scholar]
- Kinoshita, N.; Mura, T. Elastic fields of inclusion in anisotropic media. Phys. Status Solidi 1971, 5, 759–768. [Google Scholar] [CrossRef]
- Khachaturyan, A.G. Theory of Structural Transformation in Solids; John Wiley and Sons: New York, NY, USA, 1983. [Google Scholar]
- Lee, J.K. Elastic stress and microstructural evolution. Mater. Trans. JIM 1998, 39, 114–132. [Google Scholar] [CrossRef]
- Fratzl, P.; Penrose, O.; Lebowitz, J.L. Modeling of phase separation in alloys with coherent elastic misfit. J. Stat. Phys. 1999, 95, 1429–1503. [Google Scholar] [CrossRef]
- Tien, J.K.; Gamble, R.P. Effects of stress coarsening on coherent particle strengthening. Metall. Trans. 1972, 3, 2157–2162. [Google Scholar] [CrossRef]
- Tien, J.K.; Copley, S.M. The effect of uniaxial stress on the periodic morphology of coherent gamma prime precipitates in nickel-base superalloy crystals. Metall. Trans. 1971, 2, 215–219. [Google Scholar] [CrossRef]
- Tien, J.K.; Copley, S.M. The effect of orientation and sense of applied uniaxial stress on the morphology of coherent gamma prime precipitates in stress annealed nickel-base superalloy crystals. Metall. Trans. 1971, 2, 543–553. [Google Scholar] [CrossRef]
- Zhu, L.H.; Li, Y.S.; Liu, C.W.; Chen, S.; Shi, S.J.; Jin, S.S. Effect of applied strain on phase separation of Fe-28 at.% Cr alloy: 3D phase-field simulation. Model. Simul. Mater. Sci. Eng. 2018, 26, 035015. [Google Scholar] [CrossRef]
- Prikhodko, S.V.; Ardell, A.J. Coarsening of γ′ in Ni–Al alloys aged under uniaxial compression: I. Early-stage kinetics. Acta Mater. 2003, 51, 5001–5012. [Google Scholar] [CrossRef]
- Ardell, A.J.; Prikhodko, S.V. Coarsening of γ′ in Ni–Al alloys aged under uniaxial compression: II. Diffusion under stress and retardation of coarsening kinetics. Acta Mater. 2003, 51, 5013–5019. [Google Scholar] [CrossRef]
- Prikhodko, S.V.; Ardell, A.J. Coarsening of γ′ in Ni–Al alloys aged under uniaxial compression: III. Characterization of the morphology. Acta Mater. 2003, 51, 5021–5036. [Google Scholar] [CrossRef]
- Li, D.Y.; Chen, L.Q. Computer simulation of morphological evolution and rafting of γ′ particles in Ni-based superalloys under applied stresses. Scr. Mater. 1997, 37, 1271–1277. [Google Scholar] [CrossRef]
- Khachaturyan, A.G.; Semenovskaya, S.; Tsakalakos, T. Elastic strain energy of inhomogeneous solids. Phys. Rev. B 1995, 52, 15909–15919. [Google Scholar] [CrossRef]
- Cahn, J.W. On spinodal decomposition. Acta Metall. 1961, 9, 795–801. [Google Scholar] [CrossRef]
- Andersson, J.O.; Ågren, J. Models for numerical treatment of multicomponent diffusion in simple phases. J. Appl. Phys. 1992, 72, 1350–1355. [Google Scholar] [CrossRef]
- Mohanty, R.R.; Guyer, J.E.; Sohn, Y.H. Diffusion under temperature gradient: A phase-field model study. J. Appl. Phys. 2009, 106, 034912. [Google Scholar] [CrossRef]
- Cahn, J.W. Phase separation by spinodal decomposition in isotropic system. J. Chem. Phys. 1965, 42, 93–99. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a non-uniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Xiong, W.; Selleby, M.; Chen, Q.; Odqvist, J.; Du, Y. Phase equilibria and thermodynamic properties in the Fe–Cr system. Crtic. Rev. Solid State 2010, 35, 125–152. [Google Scholar] [CrossRef]
- Dever, D.J. Temperature dependence of the elastic constants in α-iron single crystals: Relationship to spinorder and diffusion anomalies. J. Appl. Phys. 1972, 43, 3293–3301. [Google Scholar] [CrossRef]
- Katahara, K.W.; Nimalendran, M.; Manghnani, M.H.; Fisher, E.S. Elastic moduli of paramagnetic chromium and Ti-V-Cr alloys. J. Phys. F Metal. Phys. 2001, 9, 2167–2176. [Google Scholar] [CrossRef]
- Gururajan, M.P.; Abinandanan, T.A. Phase field study of precipitate rafting under a uniaxial stress. Acta Mater. 2007, 55, 5015–5026. [Google Scholar] [CrossRef]
- Li, Y.S.; Shi, S.J.; Zhu, L.H.; Yan, Z.L.; Huang, M.; Maqbool, S. Continuum separation of nanoscale phase in thermal aging Fe–Cr alloys: Phase-field simulation and experiment. JOM 2019. [Google Scholar] [CrossRef]
- Vaithyanathan, V.; Chen, L.Q. Coarsening kinetics of δ′-Al3Li precipitates: Phase-field simulation in 2D and 3D. Scr. Mater. 2000, 42, 967–973. [Google Scholar] [CrossRef]
- Andersson, J.O.; Sundman, B. Thermodynamic properties of the Cr–Fe system. Calphad 1987, 11, 83–92. [Google Scholar] [CrossRef]
- Binder, K. Nucleation barriers, spinodals, and the Ginzburg criterion. Phys. Rev. A 1984, 29, 341–349. [Google Scholar] [CrossRef]
- Wang, J.C.; Osawa, M.; Yokokaw, T.; Harada, H.; Enomoto, M. Modeling the microstructural evolution of Ni-base superalloys by phase field method combined with CALPHAD and CVM. Comput. Mater. Sci. 2007, 39, 871–879. [Google Scholar] [CrossRef]
- Schmidt, I.; Gross, D. Directional coarsening in Ni-base superalloys: Analytical results for an elasticity based model. Proc. R. Soc. A 1999, 455, 3085–3106. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, L.Q.; Khachaturyan, A.G. Shape evolution of a precipitate during strain-induced coarsening. A computer simulation. Scr. Metall. Mater. 1991, 25, 1387–1392. [Google Scholar] [CrossRef]
- Kim, K.; Voorhees, P.W. Ostwald ripening of spheroidal particles in multicomponent alloys. Acta Mater. 2018, 152, 327–337. [Google Scholar] [CrossRef]
- Lifshitz, I.M.; Slyozov, V.V. The kinetics of precipitation from supersaturated solid solutions. J. Phys. Chem. Solids 1961, 19, 35–50. [Google Scholar] [CrossRef]

| Strain | α (at. % Cr) | α′ (at. % Cr) |
|---|---|---|
| 16.9 | 84.2 | |
| 17.5 | 82.3 | |
| 18.1 | 82.0 |
| Time Exponent | |||
|---|---|---|---|
| m (Nd ~ tm) | −0.62 | −0.32 | −0.34 |
| n (<R> ~ tn) | 0.21 | 0.25 | 0.12 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, L.; Li, Y.; Shi, S.; Yan, Z.; Chen, J.; Maqbool, S. Morphology and Kinetics Evolution of Nanoscale Phase in Fe–Cr Alloys under External Strain. Nanomaterials 2019, 9, 294. https://doi.org/10.3390/nano9020294
Zhu L, Li Y, Shi S, Yan Z, Chen J, Maqbool S. Morphology and Kinetics Evolution of Nanoscale Phase in Fe–Cr Alloys under External Strain. Nanomaterials. 2019; 9(2):294. https://doi.org/10.3390/nano9020294
Chicago/Turabian StyleZhu, Lihui, Yongsheng Li, Shujing Shi, Zhengwei Yan, Jing Chen, and Shahid Maqbool. 2019. "Morphology and Kinetics Evolution of Nanoscale Phase in Fe–Cr Alloys under External Strain" Nanomaterials 9, no. 2: 294. https://doi.org/10.3390/nano9020294
APA StyleZhu, L., Li, Y., Shi, S., Yan, Z., Chen, J., & Maqbool, S. (2019). Morphology and Kinetics Evolution of Nanoscale Phase in Fe–Cr Alloys under External Strain. Nanomaterials, 9(2), 294. https://doi.org/10.3390/nano9020294