DC Self-Field Critical Current in Superconductor/Dirac-Cone Material/Superconductor Junctions
Abstract
1. Introduction
2. Models Description
3. Results
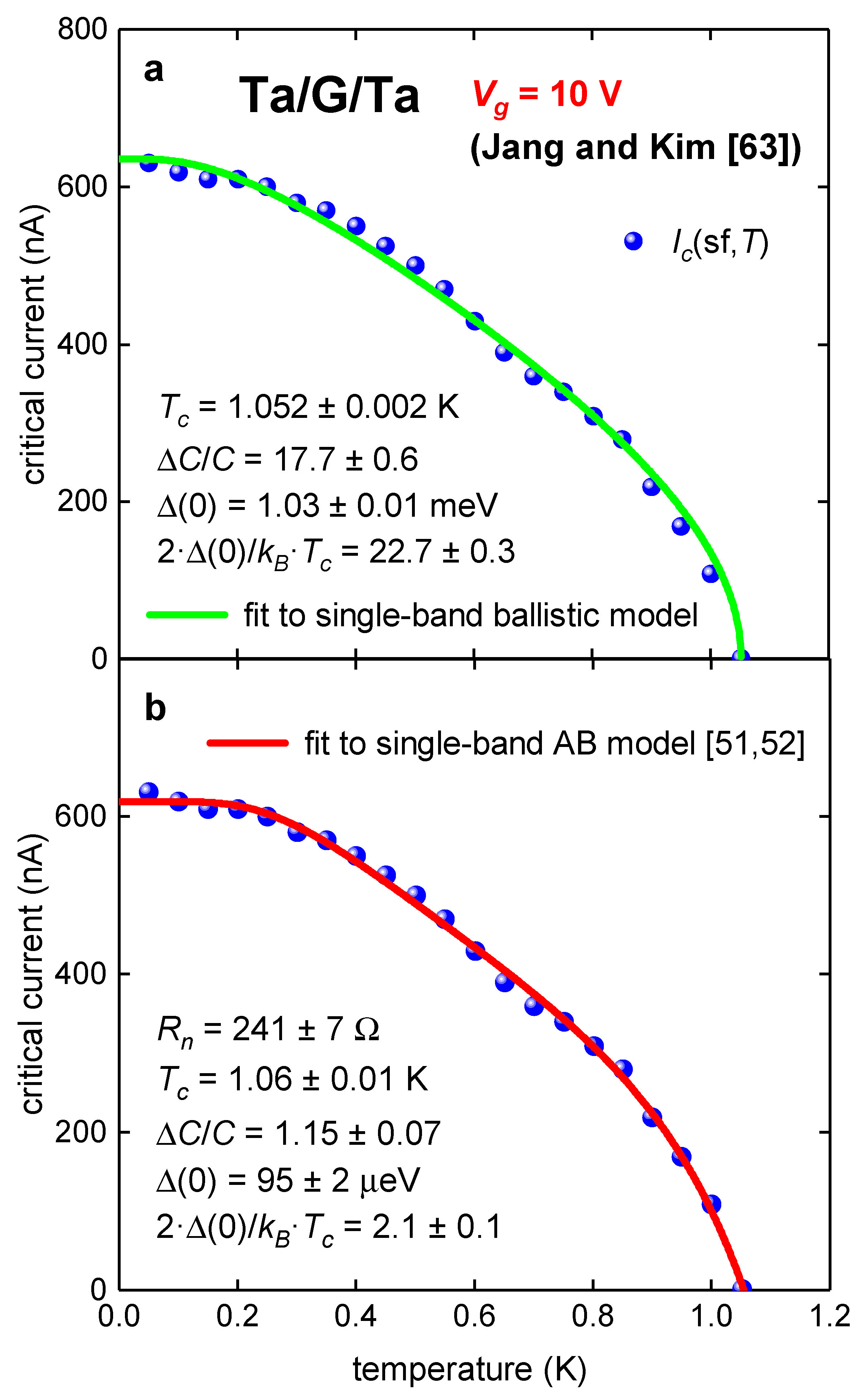
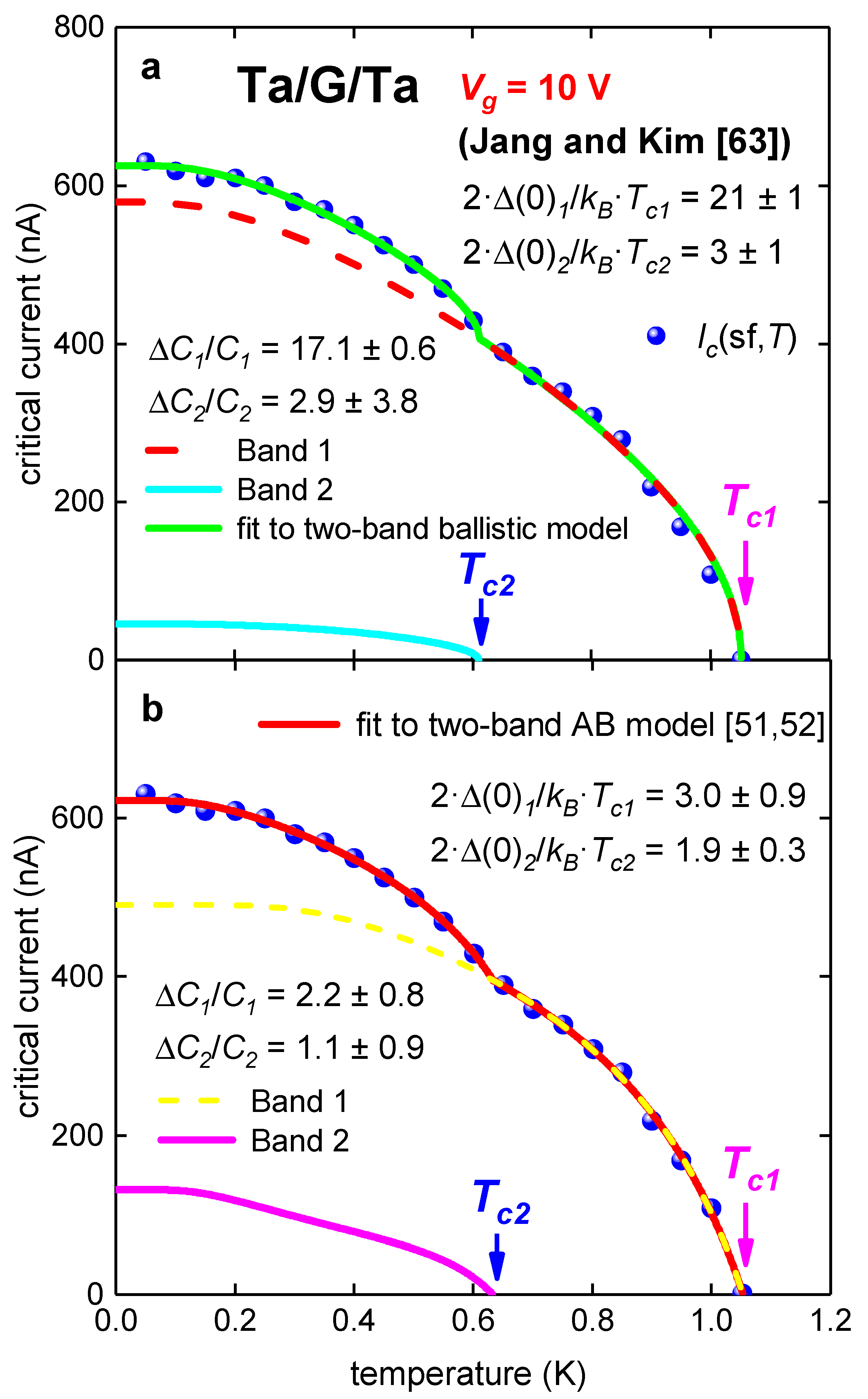
3.1. Micrometer-Long Tantalum/Graphene/Tantalum (Ta/G/Ta) Junction
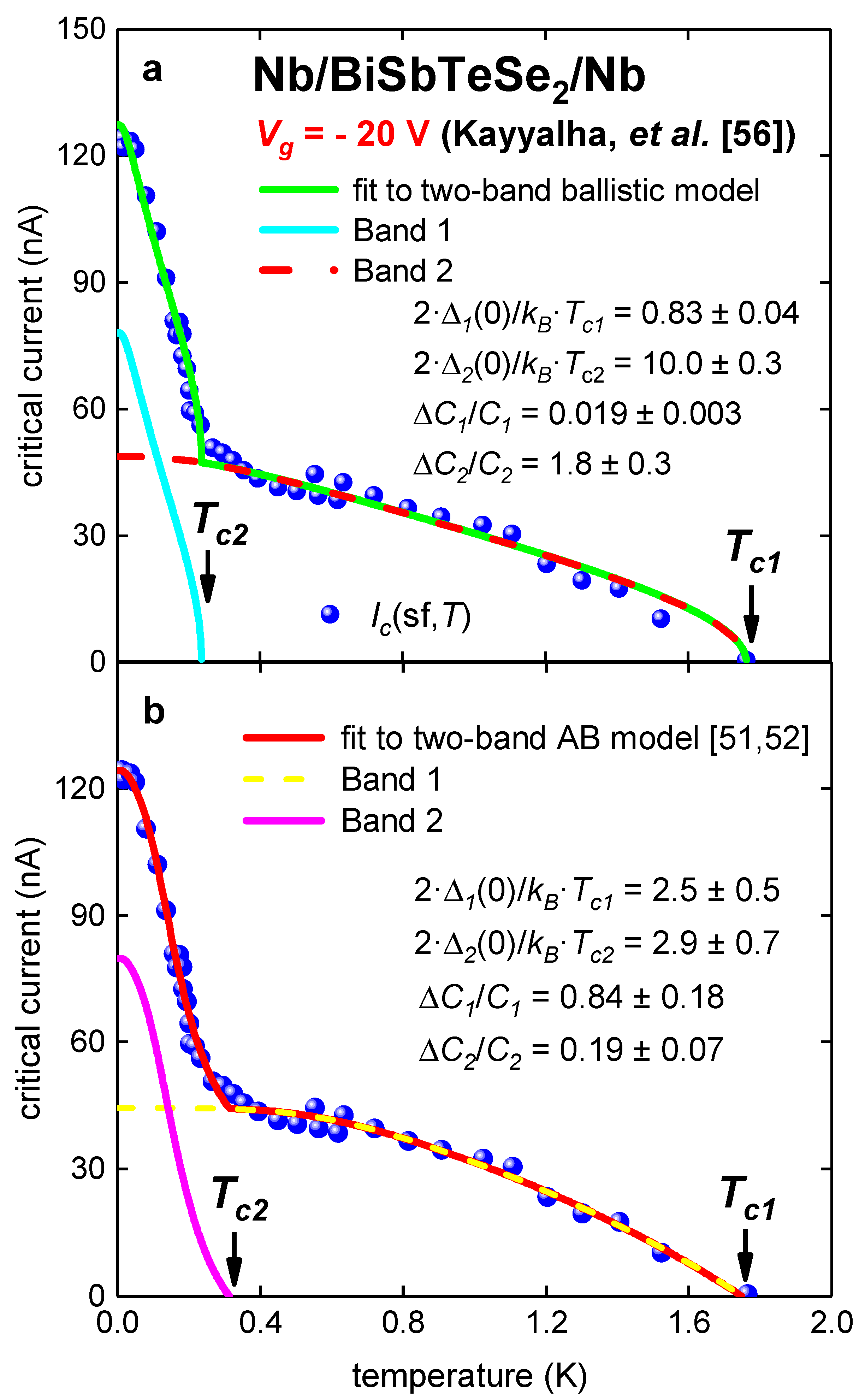
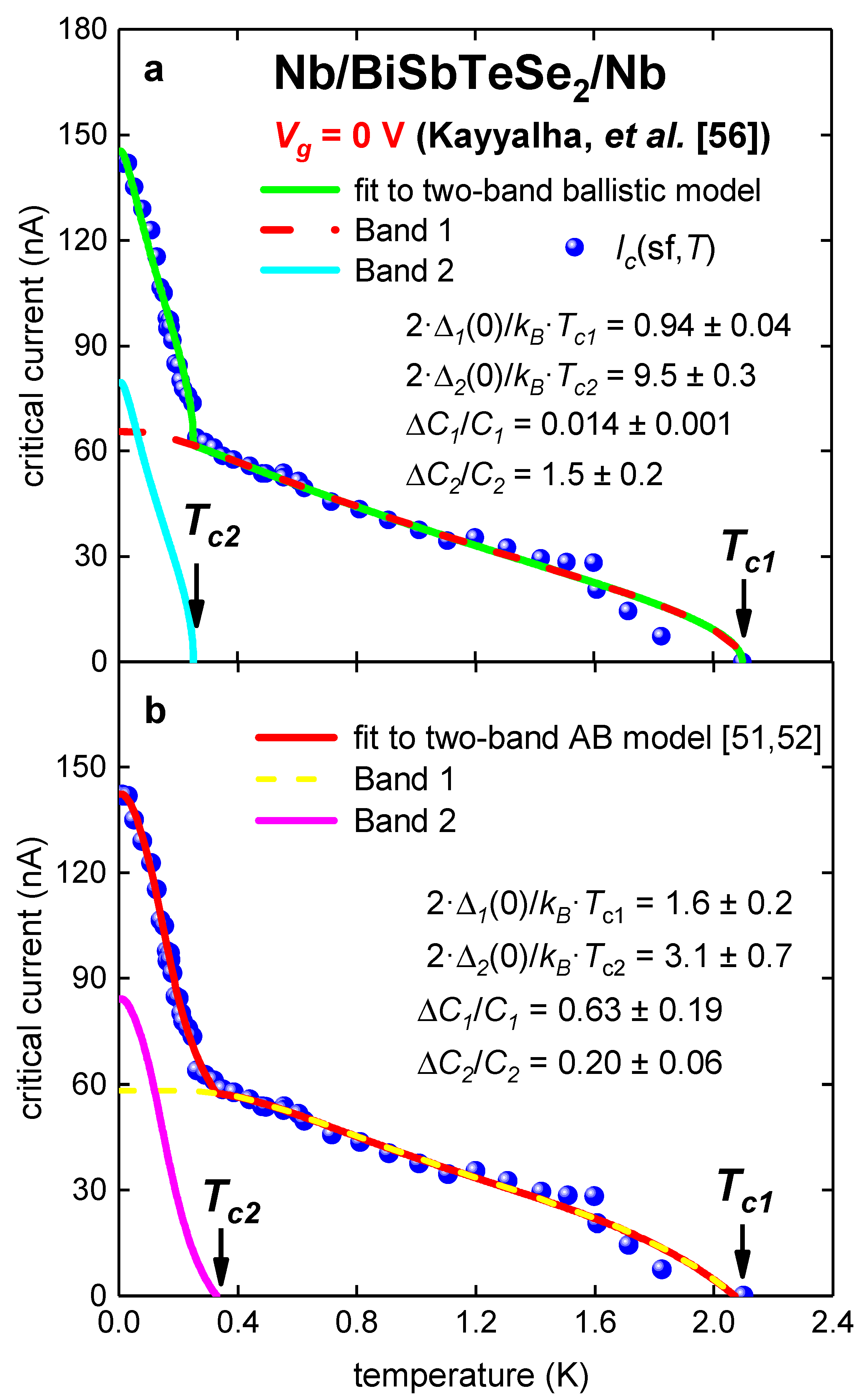
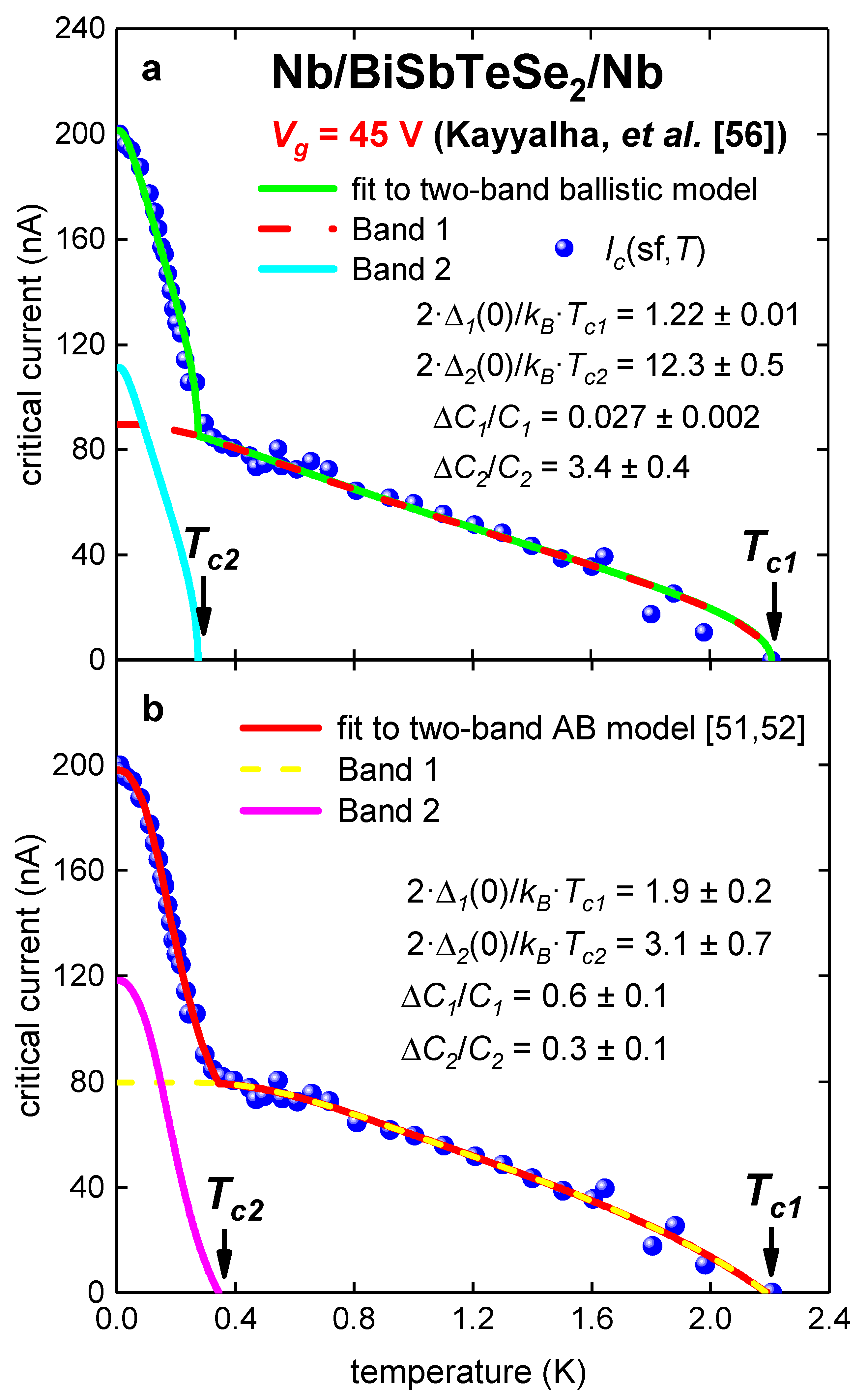
3.2. Planar Nb/BiSbTeSe2-Nanoribbon/Nb Junctions
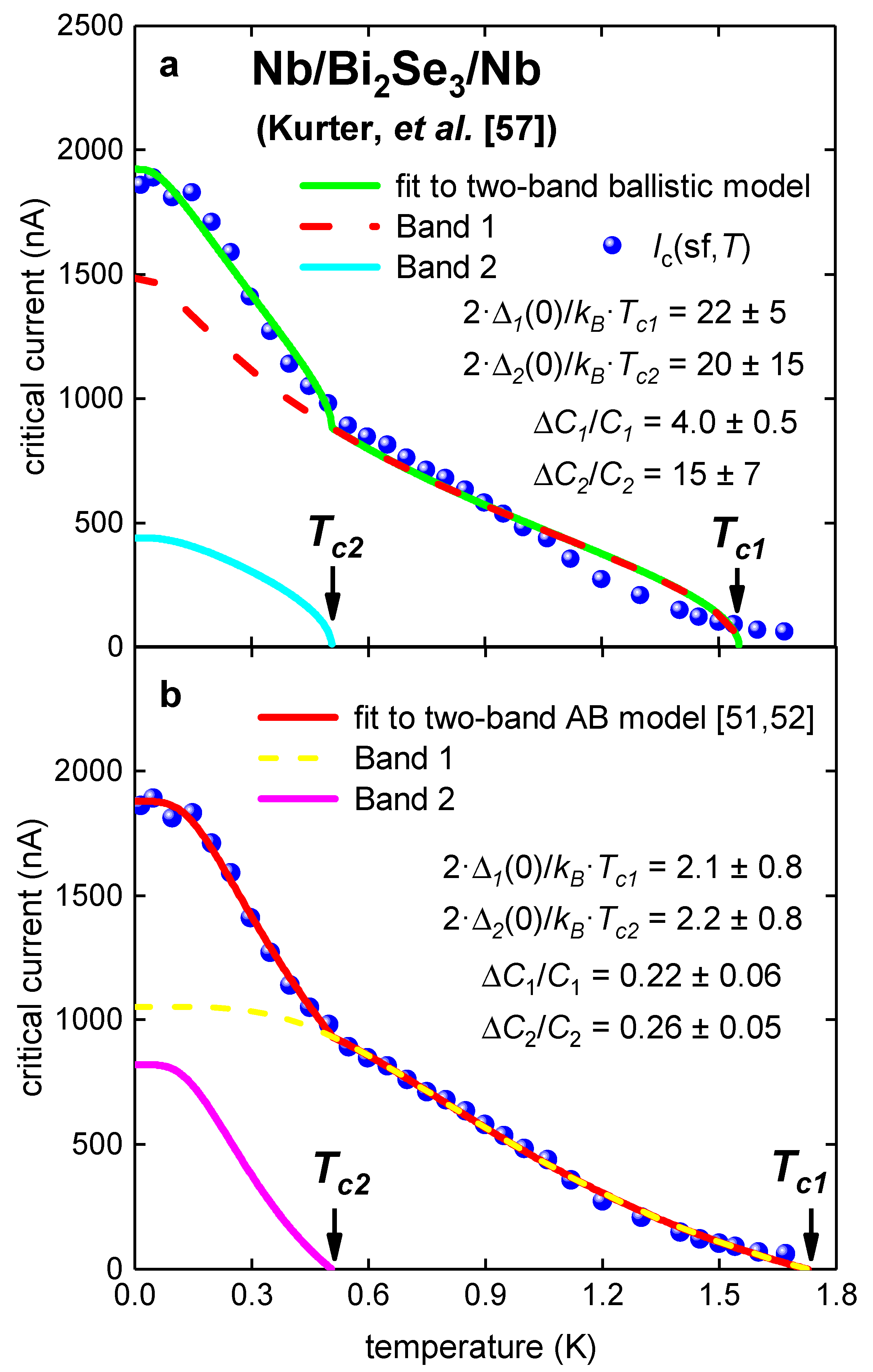
3.3. Planar Nb/Bi2Se3/Nb Junction [56]
4. Discussion
5. Conclusions
Funding
Conflicts of Interest
References
- Hirsch, J.E.; Maple, M.B.; Marsiglio, F. Superconducting materials classes: Introduction and overview. Physica C 2015, 514, 1–8. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Tallon, J.L. Universal self-field critical currents for thin-film superconductors. Nat. Commun. 2015, 6, 7820. [Google Scholar] [CrossRef] [PubMed]
- Talantsev, E.F.; Crump, W.P.; Tallon, J.L. Thermodynamic parameters of single-or multi-band superconductors derived from self-field critical currents. Ann. Phys. 2017, 529, 1700197. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Crump, W.P. Weak-link criterion for pnictide and cuprate superconductors. Supercond. Sci. Technol. 2018, 31, 124001. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Crump, W.P.; Tallon, J.L. Universal scaling of the self-field critical current in superconductors: From sub-nanometre to millimetre size. Sci. Rep. 2018, 7, 10010. [Google Scholar] [CrossRef] [PubMed]
- Holm, R.; Meissner, W. Messungen mit Hilfe von flüssigem Helium. XIII. Kontaktwiderstand zwischen Supraleitern und Nichtsupraleitern (Measurements using liquid helium. XIII. Contact resistance between superconductors and non-superconductors). Zeitschrift für Physik 1932, 74, 715–735. [Google Scholar] [CrossRef]
- Ambegaokar, V.; Baratoff, A. Tunneling between superconductors. Phys. Rev. Lett. 1963, 10, 486–489. [Google Scholar] [CrossRef]
- Ambegaokar, V.; Baratoff, A. Errata: Tunneling between superconductors. Phys. Rev. Lett. 1963, 11, 104. [Google Scholar] [CrossRef]
- Josephson, B.D. Possible new effects in superconductive tunneling. Phys. Lett. 1962, 1, 251–253. [Google Scholar] [CrossRef]
- Kulik, I.O.; Omel’yanchuk, A.N. Contribution to the microscopic theory of the Josephson effect in superconducting bridges. JETP Lett. 1975, 21, 96–97. [Google Scholar]
- Kulik, I.O.; Omel’yanchuk, A.N. Properties of superconducting microbridges in the pure limit. Sov. J. Low Temp. Phys. 1977, 3, 459–462. [Google Scholar]
- Kulik, I.; Omelyanchouk, A. The Josephson effect in superconducting constructions: Microscopic theory. J. Phys. Colloq. 1978, 39. [Google Scholar] [CrossRef]
- Lee, G.H.; Lee, H.J. Proximity coupling in superconductor-graphene heterostructures. Rep. Prog. Phys. 2018, 81, 056502. [Google Scholar] [CrossRef] [PubMed]
- Park, J.; Lee, J.H.; Lee, G.-H.; Takane, Y.; Imura, K.-I.; Taniguchi, T.; Watanabe, K.; Lee, H.-J. Short ballistic Josephson coupling in planar graphene junctions with inhomogeneous carrier doping. Phys. Rev. Lett. 2018, 120, 077701. [Google Scholar] [CrossRef]
- Takane, Y.; Imura, K.-I. Quasiclassical theory of the Josephson effect in ballistic graphene junctions. J. Phys. Soc. Jpn. 2012, 81, 094707. [Google Scholar] [CrossRef]
- Strickland, N.M.; Long, N.J.; Talantsev, E.F.; Hoefakker, P.; Xia, J.A.; Rupich, M.W.; Zhang, W.; Li, X.; Kodenkandath, T.; Huang, Y. Nanoparticle additions for enhanced flux pinning in YBCO HTS films. Curr. Appl. Phys. 2008, 8, 372–375. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Strickland, N.M.; Hoefakker, P.; Xia, J.A.; Long, N.J. Critical current anisotropy for second generation HTS wires. Curr. Appl. Phys. 2008, 8, 388–390. [Google Scholar] [CrossRef]
- Chepikov, V.; Mineev, N.; Degtyarenko, P.; Lee, S.; Petrykin, V.; Ovcharov, A.; Vasiliev, A.; Kaul, A.; Amelichev, V.; Kamenev, A.; et al. Introduction of BaSnO3 and BaZrO3 artificial pinning centres into 2G HTS wires based on PLD-GdBCO films. Phase I of the industrial R&D programme at SuperOx. Supercond. Sci. Technol. 2017, 30, 124001. [Google Scholar]
- Paturi, P.; Malmivirta, M.; Hynninen, T.; Huhtinen, H. Angle dependent molecular dynamics simulation of flux pinning in YBCO superconductors with artificial pinning sites. J. Phys. Condens. Matter 2018, 30, 315902. [Google Scholar] [CrossRef]
- Hänisch, J.; Iida, K.; Hühne, R.; Tarantini, C. Fe-based superconducting thin films—Preparation and tuning of superconducting properties. Supercond. Sci. Technol. 2019, 32, 093001. [Google Scholar] [CrossRef]
- Qu, D.-X.; Teslich, N.E.; Dai, Z.; Chapline, G.F.; Schenkel, T.; Durham, S.R.; Dubois, J. Onset of a two-dimensional superconducting phase in a topological-insulator—Normal-metal Bi1−xSbx/Pt junction fabricated by ion-beam techniques. Phys. Rev. Lett. 2018, 121, 037001. [Google Scholar] [CrossRef] [PubMed]
- Li, C.-Z.; Li, C.; Wang, L.-X.; Wang, S.; Liao, Z.-M.; Brinkman, A.; Yu, D.-P. Bulk and surface states carried supercurrent in ballistic Nb-Dirac semimetal Cd3As2 nanowire-Nb junctions. Phys. Rev. B 2018, 97, 115446. [Google Scholar] [CrossRef]
- Reyren, N.; Thiel, S.; Caviglia, A.D.; Kourkoutis, L.F.; Hammerl, G.; Richter, C.; Schneider, C.W.; Kopp, T.; Rüetschi, A.-S.; Jaccard, D.; et al. Superconducting interfaces between insulating oxides. Science 2007, 317, 1196–1199. [Google Scholar] [CrossRef] [PubMed]
- Gozar, A.; Logvenov, G.; Fitting Kourkoutis, L.; Bollinger, A.T.; Giannuzzi, L.A.; Muller, D.A.; Bozovic, I. High-temperature interface superconductivity between metallic and insulating copper oxides. Nature 2008, 455, 782–785. [Google Scholar] [CrossRef] [PubMed]
- Di Castro, D.; Balestrino, G. Superconductivity in interacting interfaces of cuprate-based heterostructures. Supercond. Sci. Technol. 2018, 31, 073001. [Google Scholar]
- Wang, Q.-Y.; Li, Z.; Zhang, W.-H.; Zhang, Z.-C.; Zhang, J.-S.; Li, W.; Ding, H.; OU, Y.-B.; Deng, P.; Chang, K.; et al. Interface-induced high-temperature superconductivity in single unit-cell FeSe films on SrTiO3. Chin. Phys. Lett. 2012, 29, 037402. [Google Scholar] [CrossRef]
- Zhang, W.H.; Sun, Y.; Zhang, J.; Li, F.; Guo, M.; Zhao, Y.; Zhang, H.; Peng, J.; Xing, Y.; Wang, H.; et al. Direct observation of high-temperature superconductivity in one-unit-cell FeSe films. Chin. Phys. Lett. 2014, 31, 017401. [Google Scholar] [CrossRef]
- Ge, J.F.; Liu, Z.L.; Liu, C.; Gao, C.L.; Qian, D.; Xue, Q.K.; Liu, Y.; Jia, J.F. Superconductivity above 100 K in single-layer FeSe films on doped SrTiO3. Nat. Mater. 2015, 14, 285–289. [Google Scholar] [CrossRef]
- Zhang, H.M.; Sun, Y.; Li, W.; Peng, J.P.; Song, C.L.; Xing, Y.; Zhang, Q.; Guan, J.; Li, Z.; Zhao, Y.; et al. Detection of a superconducting phase in a two-atom layer of hexagonal Ga film grown on semiconducting GaN(0001). Phys. Rev. Lett. 2015, 114, 107003. [Google Scholar] [CrossRef]
- Xing, Y.; Zhang, H.M.; Fu, H.L.; Liu, H.; Sun, Y.; Peng, J.P.; Wang, F.; Lin, X.; Ma, X.C.; Xue, Q.K.; et al. Quantum Griffiths singularity of superconductor-metal transition in Ga thin films. Science 2015, 350, 542–545. [Google Scholar] [CrossRef]
- Navarro-Moratalla, E.; Island, J.O.; Mañas-Valero, S.; Pinilla-Cienfuegos, E.; Castellanos-Gomez, A.; Quereda, J.; Rubio-Bollinger, G.; Chirolli, L.; Silva-Guillén, J.A.; Agraït, N.; et al. Enhanced superconductivity in atomically thin TaS2. Nat. Commun. 2016, 7, 11043. [Google Scholar] [CrossRef] [PubMed]
- Yankowitz, M.; Chen, S.; Polshyn, H.; Watanabe, K.; Taniguchi, T.; Graf, D.; Young, A.F.; Dean, C.R. Tuning superconductivity in twisted bilayer graphene. Science 2019, 363, 1059–1064. [Google Scholar] [CrossRef] [PubMed]
- Lucignano, P.; Alfè, D.; Cataudella, V.; Ninno, D.; Cantele, G. The crucial role of atomic corrugation on the flat bands and energy gaps of twisted bilayer graphene at the “magic angle” θ ∼ 1.08°. Phys. Rev. B 2019, 99, 195419. [Google Scholar] [CrossRef]
- Fête, A.; Rossi, L.; Augieri, A.; Senatore, C. Ionic liquid gating of ultra-thin YBa2Cu3O7-x films. Appl. Phys. Lett. 2016, 109, 192601. [Google Scholar] [CrossRef]
- Fête, A.; Senatore, C. Strong improvement of the transport characteristics of YBa2Cu3O7−x grain boundaries using ionic liquid gating. Sci. Rep. 2017, 8, 17703. [Google Scholar] [CrossRef]
- Paradiso, N.; Nguyen, A.-T.; Kloss, K.E.; Strunk, C. Phase slip lines in superconducting few-layer NbSe2 crystals. 2D Mater. 2019, 6, 025039. [Google Scholar] [CrossRef]
- Guo, J.G.; Chen, X.; Jia, X.Y.; Zhang, Q.H.; Liu, N.; Lei, H.C.; Li, S.Y.; Gu, L.; Jin, S.F.; Chen, X.L.; et al. Quasi-two-dimensional superconductivity from dimerization of atomically ordered AuTe2Se4/3 cubes. Nat. Commun. 2017, 8, 871. [Google Scholar] [CrossRef]
- Pan, J.; Guo, C.; Song, C.; Lai, X.; Li, H.; Zhao, W.; Zhang, H.; Mu, G.; Bu, K.; Lin, T.; et al. Enhanced superconductivity in restacked TaS2 nanosheets. J. Am. Chem. Soc. 2017, 139, 4623. [Google Scholar] [CrossRef]
- Ma, Y.; Pan, J.; Guo, C.; Zhang, X.; Wang, L.; Hu, T.; Mu, G.; Huang, F.; Xie, X. Unusual evolution of Bc2 and Tc with inclined fields in restacked TaS2 nanosheets. NPJ Quantum Mater. 2018, 3, 34. [Google Scholar] [CrossRef]
- Desrat, W.; Moret, M.; Briot, O.; Ngo, T.-H.; Piot, B.A.; Jabakhanji, B.; Gil, B. Superconducting Ga/GaSe layers grown by van der Waals epitaxy. Mater. Res. Express 2018, 5, 045901. [Google Scholar] [CrossRef]
- Liu, C.; Lian, C.-S.; Liao, M.-H.; Wang, Y.; Zhong, Y.; Ding, C.; Li, W.; Song, C.-L.; He, K.; Ma, X.-C.; et al. Two-dimensional superconductivity and topological states in PdTe2 thin films. Phys. Rev. Mater. 2018, 2, 094001. [Google Scholar] [CrossRef]
- Peng, J.; Yu, Z.; Wu, J.; Zhou, Y.; Guo, Y.; Li, Z.; Zhao, J.; Wu, C.; Xie, Y. Disorder enhanced superconductivity toward TaS2 monolayer. ACS Nano 2018, 12, 9461–9466. [Google Scholar] [CrossRef] [PubMed]
- De La Barrera, S.C.; Sinko, M.R.; Gopalan, D.P.; Sivadas, N.; Seyler, K.L.; Watanabe, K.; Taniguchi, T.; Tsen, A.W.; Xu, X.; Xiao, D.; et al. Tuning Ising superconductivity with layer and spin-orbit coupling in two-dimensional transition-metal dichalcogenides. Nat. Commun. 2018, 9, 1427. [Google Scholar] [CrossRef] [PubMed]
- Liao, M.; Zang, Y.; Guan, Z.; Li, H.; Gong, Y.; Zhu, K.; Hu, X.-P.; Zhang, D.; Xu, Y.; Wang, Y.-Y.; et al. Superconductivity in few-layer stanene. Nat. Phys. 2018, 14, 344–348. [Google Scholar] [CrossRef]
- Wu, Y.; He, J.; Liu, J.; Xing, H.; Mao, Z.; Liu, Y. Dimensional reduction and ionic gating induced enhancement of superconductivity in atomically thin crystals of 2H-TaSe2. Nanotechnology 2019, 30, 035702. [Google Scholar] [CrossRef]
- Alidoust, M.; Willatzen, M.; Jauho, A.-P. Symmetry of superconducting correlations in displaced bilayers of graphene. Phys. Rev. B 2019, 99, 155413. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Mataira, R.C.; Crump, W.P. Classifying superconductivity in Moiré graphene superlattices. arXiv 2019, arXiv:1902.07410v2. [Google Scholar]
- Rhodes, D.; Yuan, N.F.; Jung, Y.; Antony, A.; Wang, H.; Kim, B.; Chiu, Y.; Taniguchi, T.; Watanabe, K.; Barmak, K.; et al. Enhanced superconductivity in monolayer Td-MoTe2 with tilted Ising spin texture. arXiv 2019, arXiv:1905.06508. [Google Scholar]
- Yang, H.; Gao, Z.-Q.; Wang, F. Effect of defects in superconducting phase of twisted bilayer graphene. arXiv 2019, arXiv:1908.09555v2. [Google Scholar]
- Talantsev, E.F.; Crump, W.P.; Island, J.O.; Xing, Y.; Sun, Y.; Wang, J.; Tallon, J.L. On the origin of critical temperature enhancement in atomically thin superconductors. 2D Mater. 2017, 4, 025072. [Google Scholar] [CrossRef]
- Talantsev, E.F.; Crump, W.P.; Tallon, J.L. Two-band induced superconductivity in single-layer graphene and topological insulator bismuth selenide. Supercond. Sci. Technol. 2018, 31, 015011. [Google Scholar] [CrossRef]
- Talantsev, E.F. Classifying induced superconductivity in atomically thin Dirac-cone materials. Condensed Matter 2019, 4, 83. [Google Scholar] [CrossRef]
- Titov, M.; Beenakker, C.W.J. Josephson effect in ballistic graphene. Phys. Rev. B 2006, 74, 041401. [Google Scholar] [CrossRef]
- Calado, V.E.; Goswami, S.; Nanda, G.; Diez, M.; Akhmerov, A.R.; Watanabe, K.; Taniguchi, T.; Klapwijk, T.M.; Vandersypen, L.M.K. Ballistic Josephson junctions in edge-contacted graphene. Nat. Nanotechnol. 2015, 10, 761–764. [Google Scholar] [CrossRef] [PubMed]
- Borzenets, I.V.; Amet, F.; Ke, C.T.; Draelos, A.W.; Wei, M.T.; Seredinski, A.; Watanabe, K.; Taniguchi, T.; Bomze, Y.; Yamamoto, M.; et al. Ballistic graphene Josephson junctions from the short to the long junction regimes. Phys. Rev. Lett. 2016, 117, 237002. [Google Scholar] [CrossRef]
- Kayyalha, M.; Kargarian, M.; Kazakov, A.; Miotkowski, I.; Galitski, V.M.; Yakovenko, V.M.; Rokhinson, L.P.; Chen, Y.P. Anomalous low-temperature enhancement of supercurrent in topological-insulator nanoribbon Josephson junctions: Evidence for low-energy Andreev bound states. Phys. Rev. Lett. 2019, 122, 047003. [Google Scholar] [CrossRef]
- Kurter, C.; Finck, A.D.K.; Hor, Y.S.; Van Harlingen, D.J. Evidence for an anomalous current–phase relation in topological insulator Josephson junctions. Nat. Commun. 2015, 6, 7130. [Google Scholar] [CrossRef]
- Gross, F.; Chandrasekhar, B.S.; Einzel, D.; Andres, K.; Hirschfeld, P.J.; Ott, H.R.; Beuers, J.; Fisk, Z.; Smith, J.L. Anomalous temperature dependence of the magnetic field penetration depth in superconducting UBe13. Zeitschrift für Physik B Condensed Matter 1986, 64, 175–188. [Google Scholar] [CrossRef]
- Natterer, F.D.; Ha, J.; Baek, H.; Zhang, D.; Cullen, W.G.; Zhitenev, N.B.; Kuk, Y.; Stroscio, J.A. Scanning tunneling spectroscopy of proximity superconductivity in epitaxial multilayer graphene. Phys. Rev. B 2016, 93, 045406. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieffer, J.R. Theory of Superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Dyson, F. A meeting with Enrico Fermi. Nature 2004, 427, 297. [Google Scholar] [CrossRef] [PubMed]
- Piantadosi, S.T. One parameter is always enough. AIP Adv. 2018, 8, 095118. [Google Scholar] [CrossRef]
- Jang, S.; Kim, E. Short ballistic Josephson coupling in micrometer-long tantalum/graphene/tantalum junction. Curr. Appl. Phys. 2019, 19, 436–439. [Google Scholar] [CrossRef]
- Carbotte, J.P. Properties of boson-exchange superconductors. Rev. Mod. Phys. 1990, 62, 1027–1157. [Google Scholar] [CrossRef]
- Nicol, E.J.; Carbotte, J.P. Properties of the superconducting state in a two-band model. Phys. Rev. B 2005, 71, 054501. [Google Scholar] [CrossRef]
- Talantsev, E.F. Evaluation of a practical level of critical current densities in pnictides and recently discovered superconductors. Supercond. Sci. Technol. 2019, 32, 084007. [Google Scholar] [CrossRef]
- Mackinnon, I.D.R.; Talbot, P.C.; Alarco, J.A. Phonon dispersion anomalies and superconductivity in metal substituted MgB2. Comput. Mater. Sci. 2017, 130, 191–203. [Google Scholar] [CrossRef]
- Alarco, J.A.; Talbot, P.C.; Mackinnon, I.D.R. Identification of superconductivity mechanisms and prediction of new materials using Density Functional Theory (DFT) calculations. J. Phys. Conf. Ser. 2018, 1143, 012028. [Google Scholar] [CrossRef]
| Parameter | TB Model | AB Model |
|---|---|---|
| Tc (K) | 1.052 ± 0.002 | 1.06 ± 0.01 |
| ΔC/C | 17.7 ± 0.6 | 1.15 ± 0.07 |
| Δ(0) (meV) | 1.03 ± 0.01 | 0.095 ± 0.002 |
| 2·Δ(0)/kB·Tc | 22.7 ± 0.3 | 2.1 ± 0.1 |
| Parameter | TB Model | AB Model |
|---|---|---|
| Tc1 (K) | 1.052 ± 0.001 | 1.053 ± 0.003 |
| Tc2 (K) | 0.61 ± 0.02 | 0.63 ± 0.03 |
| ΔC1/C1 | 17.1 ± 0.6 | 2.2 ± 0.8 |
| ΔC2/C2 | 2.9 ± 3.8 | 1.1 ± 0.9 |
| 2·Δ1(0)/kB·Tc1 | 21 ± 1 | 3.0 ± 0.9 |
| 2·Δ2(0)/kB·Tc2 | 3 ± 1 | 1.9 ± 0.3 |
| Parameter | TB Model | AB Model |
|---|---|---|
| Tc1 (K) | 1.76 ± 0.01 | 1.74 ± 0.04 |
| Tc2 (K) | 0.236 ± 0.003 | 0.31 ± 0.02 |
| ΔC1/C1 | 0.019 ± 0.03 | 0.84 ± 0.18 |
| ΔC2/C2 | 1.8 ± 0.3 | 0.19 ± 0.07 |
| 2·Δ1(0)/kB·Tc1 | 0.83 ± 0.04 | 2.5 ± 0.5 |
| 2·Δ2(0)/kB·Tc2 | 10.0 ± 0.3 | 2.85 ± 0.70 |
| Parameter | TB Model | AB Model |
|---|---|---|
| Tc1 (K) | 2.10 ± 0.01 | 2.07 ± 0.03 |
| Tc2 (K) | 0.252 ± 0.005 | 0.33 ± 0.02 |
| ΔC1/C1 | 0.014 ± 0.001 | 0.6 ± 0.2 |
| ΔC2/C2 | 1.5 ± 0.2 | 0.20 ± 0.06 |
| 2·Δ1(0)/kB·Tc1 | 0.94 ± 0.04 | 1.6 ± 0.2 |
| 2·Δ2(0)/kB·Tc2 | 9.5 ± 0.3 | 3.1 ± 0.7 |
| Parameter | TB Model | AB Model |
|---|---|---|
| Tc1 (K) | 2.21 ± 0.01 | 2.19 ± 0.03 |
| Tc2 (K) | 0.274 ± 0.006 | 0.34 ± 0.01 |
| ΔC1/C1 | 0.027 ± 0.002 | 0.6 ± 0.1 |
| ΔC2/C2 | 3.4 ± 0.4 | 0.30 ± 0.08 |
| 2·Δ1(0)/kB·Tc1 | 1.22 ± 0.01 | 1.9 ± 0.2 |
| 2·Δ2(0)/kB·Tc2 | 12.3 ± 0.5 | 3.1 ± 0.7 |
| Parameter | TB Model | AB Model |
| Tc1 (K) | 1.55 ± 0.02 | 1.73 ± 0.05 |
| Tc2 (K) | 0.51 ± 0.03 | 0.51 ± 0.03 |
| ΔC1/C1 | 4.0 ± 0.5 | 0.22 ± 0.06 |
| ΔC2/C2 | 15 ± 7 | 0.26 ± 0.05 |
| 2·Δ1(0)/kB·Tc1 | 22 ± 5 | 2.1 ± 0.8 |
| 2·Δ2(0)/kB·Tc2 | 15 ± 7 | 2.2 ± 0.8 |
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talantsev, E.F. DC Self-Field Critical Current in Superconductor/Dirac-Cone Material/Superconductor Junctions. Nanomaterials 2019, 9, 1554. https://doi.org/10.3390/nano9111554
Talantsev EF. DC Self-Field Critical Current in Superconductor/Dirac-Cone Material/Superconductor Junctions. Nanomaterials. 2019; 9(11):1554. https://doi.org/10.3390/nano9111554
Chicago/Turabian StyleTalantsev, Evgueni F. 2019. "DC Self-Field Critical Current in Superconductor/Dirac-Cone Material/Superconductor Junctions" Nanomaterials 9, no. 11: 1554. https://doi.org/10.3390/nano9111554
APA StyleTalantsev, E. F. (2019). DC Self-Field Critical Current in Superconductor/Dirac-Cone Material/Superconductor Junctions. Nanomaterials, 9(11), 1554. https://doi.org/10.3390/nano9111554





