Readable High-Speed Racetrack Memory Based on an Antiferromagnetically Coupled Soft/Hard Magnetic Bilayer
Abstract
:1. Introduction
2. Model
3. Results and Discussion
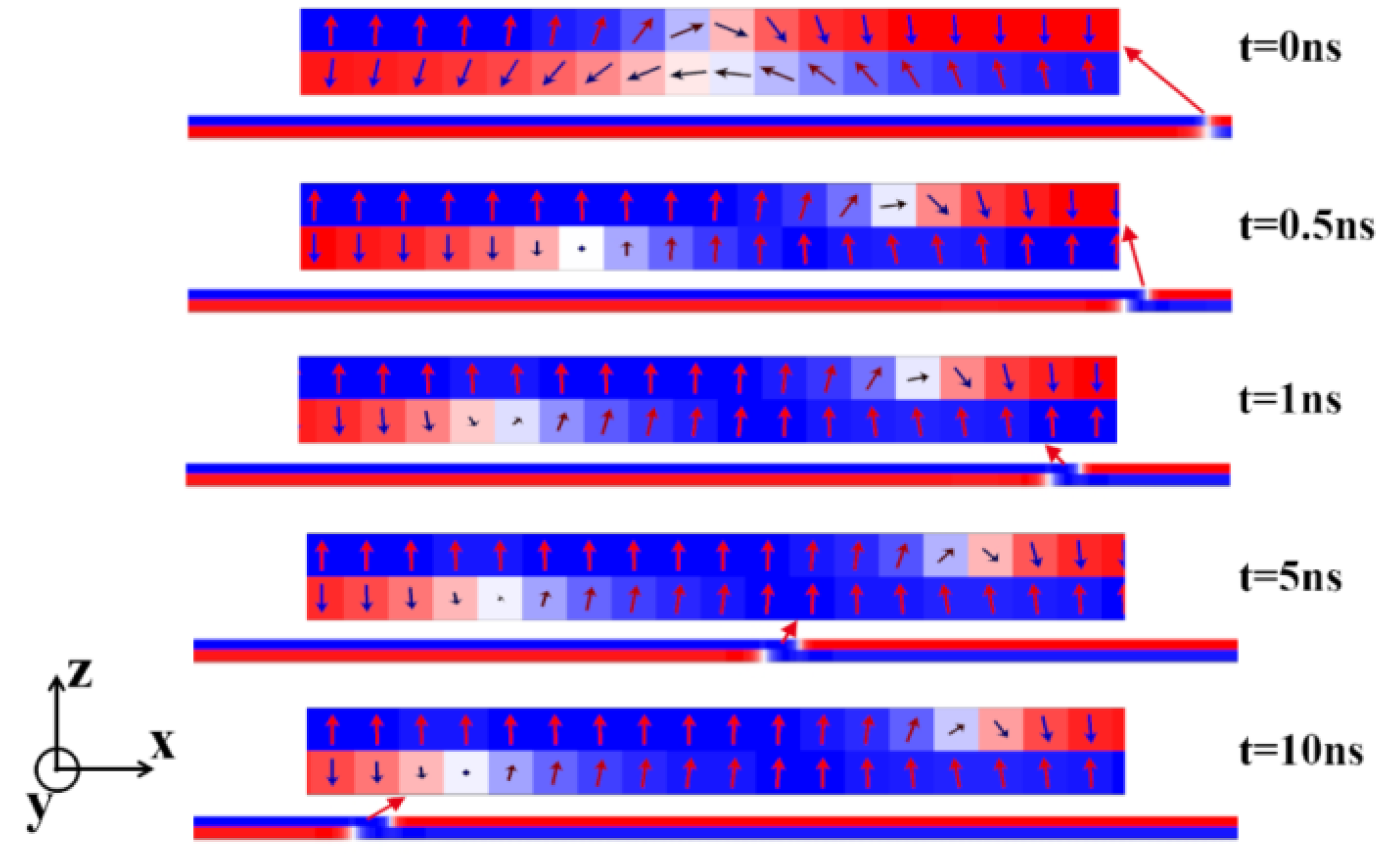
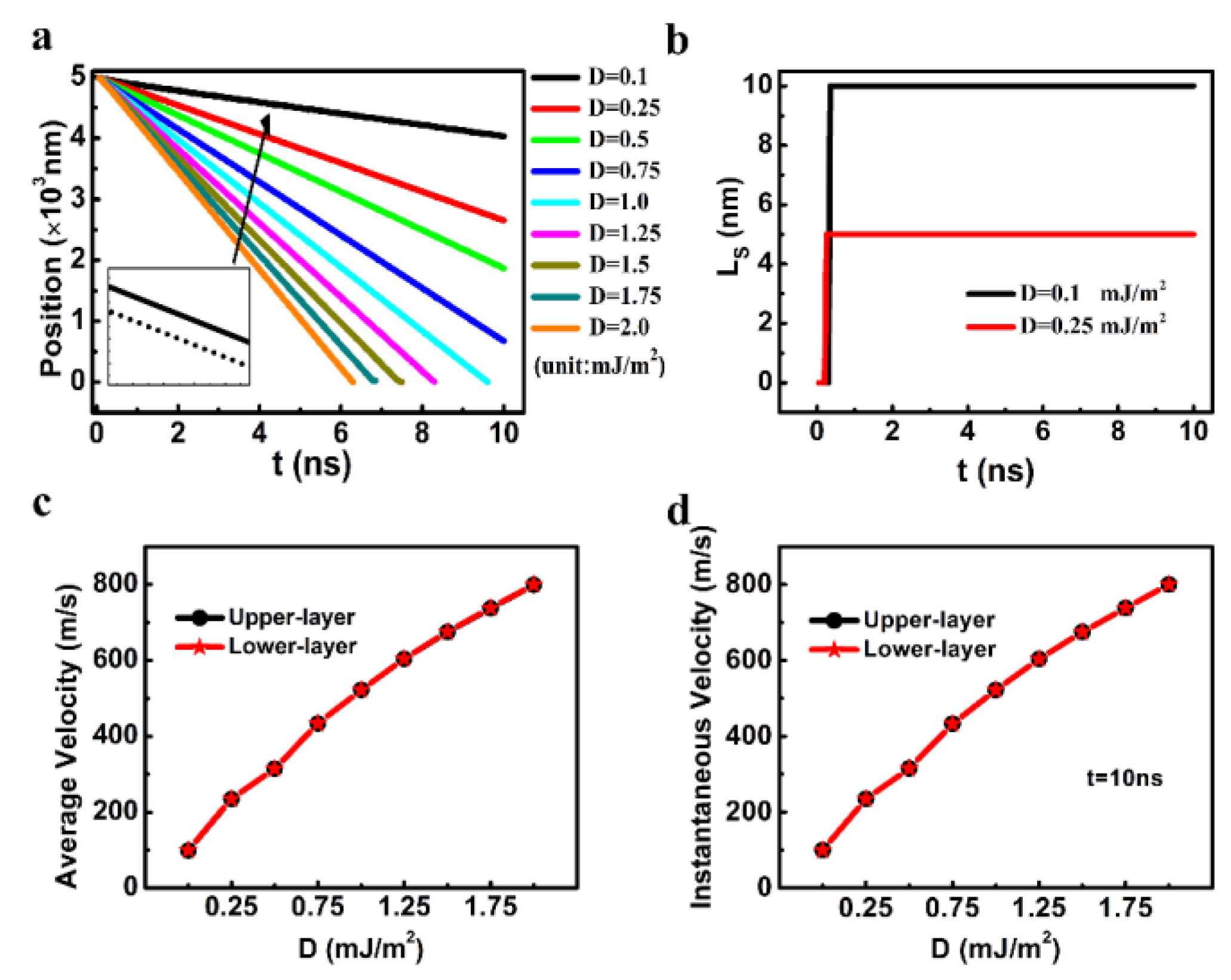
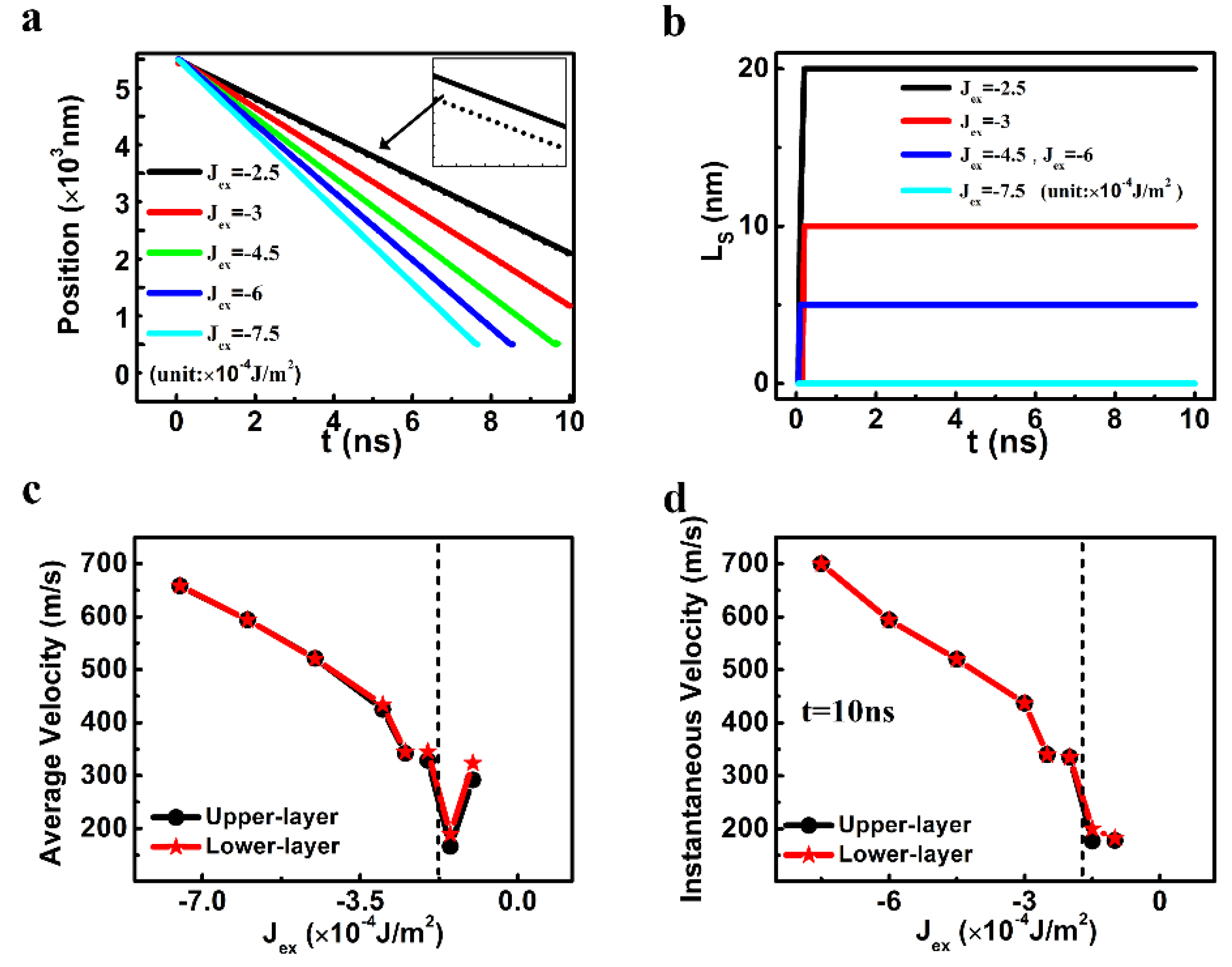
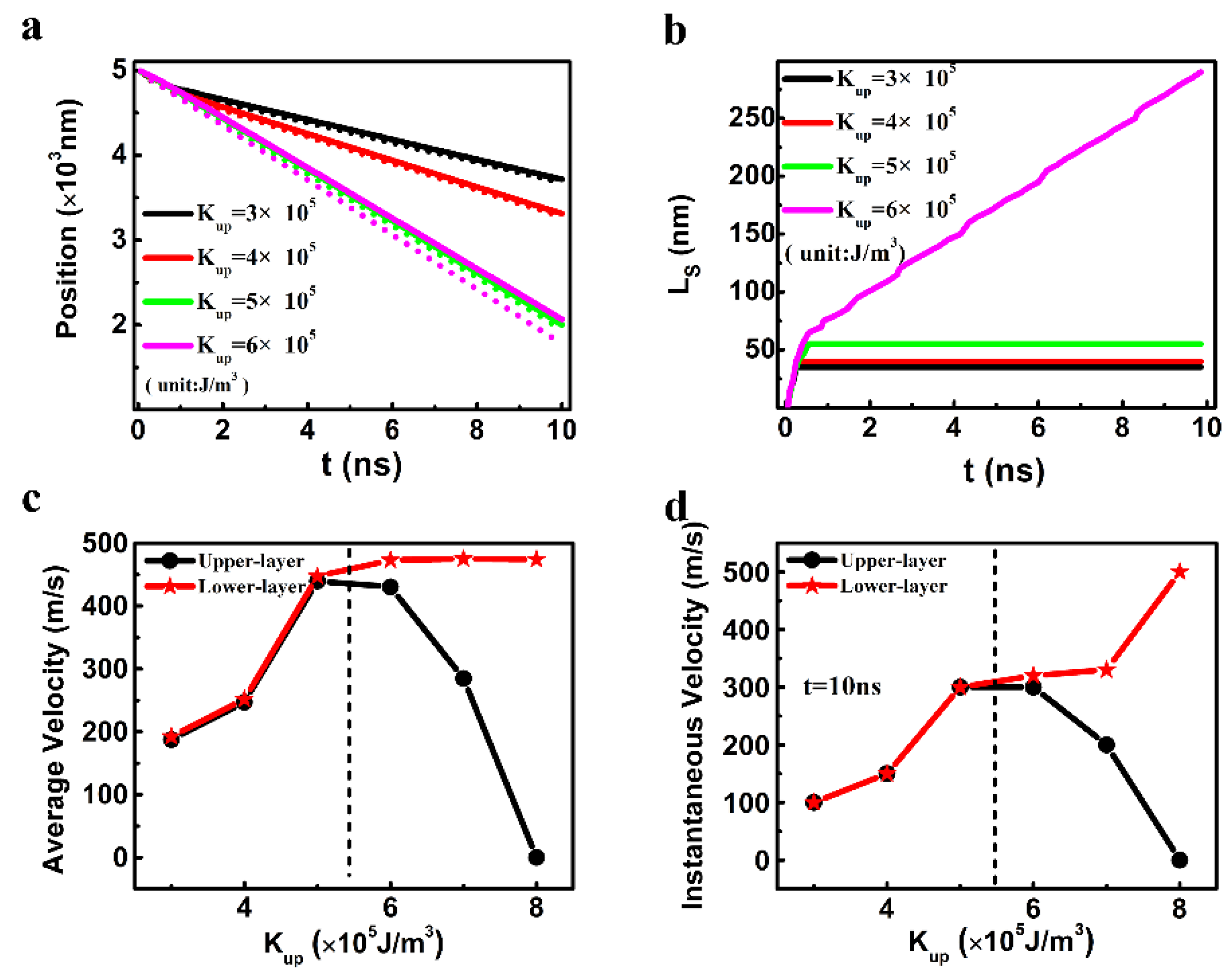
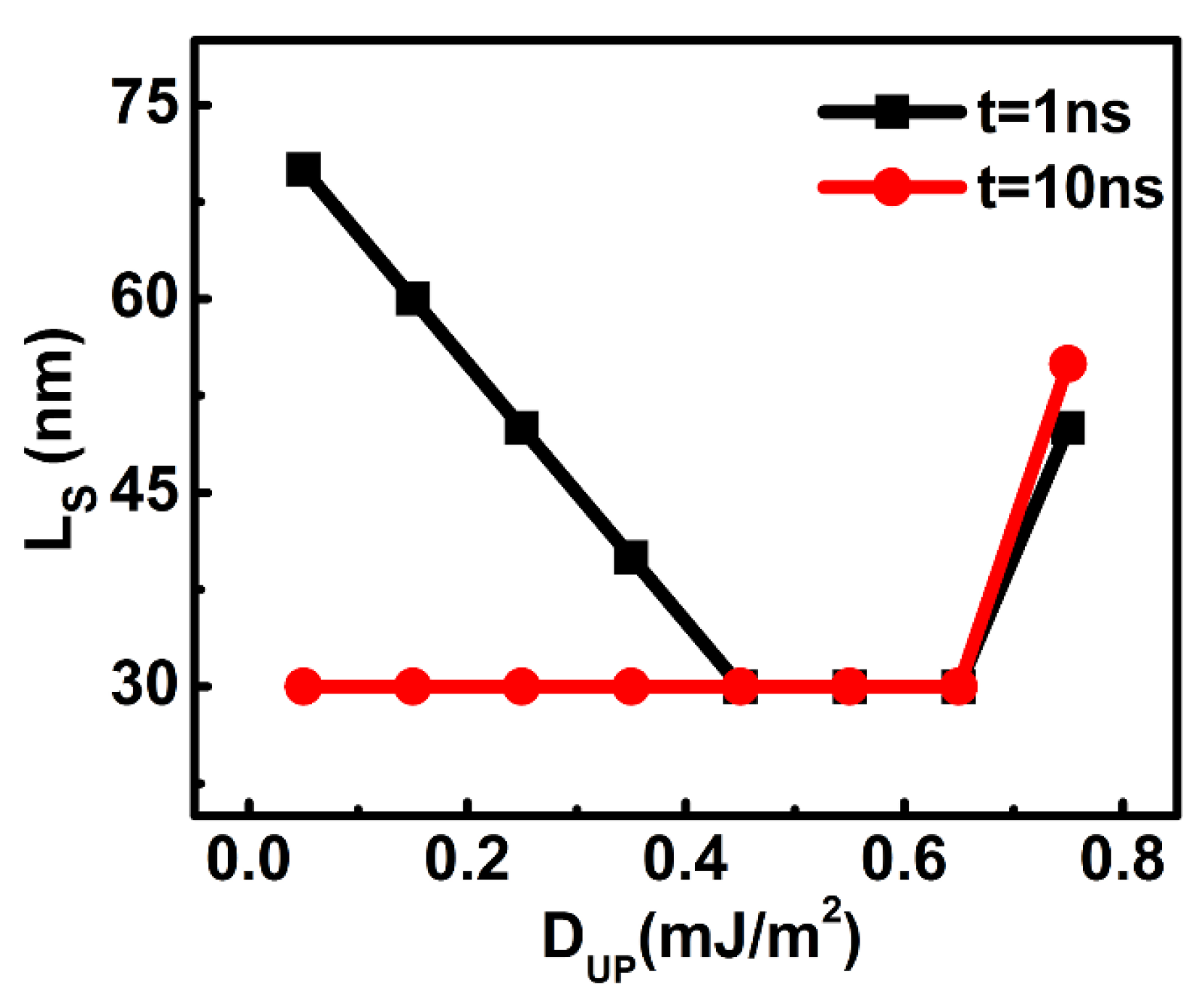
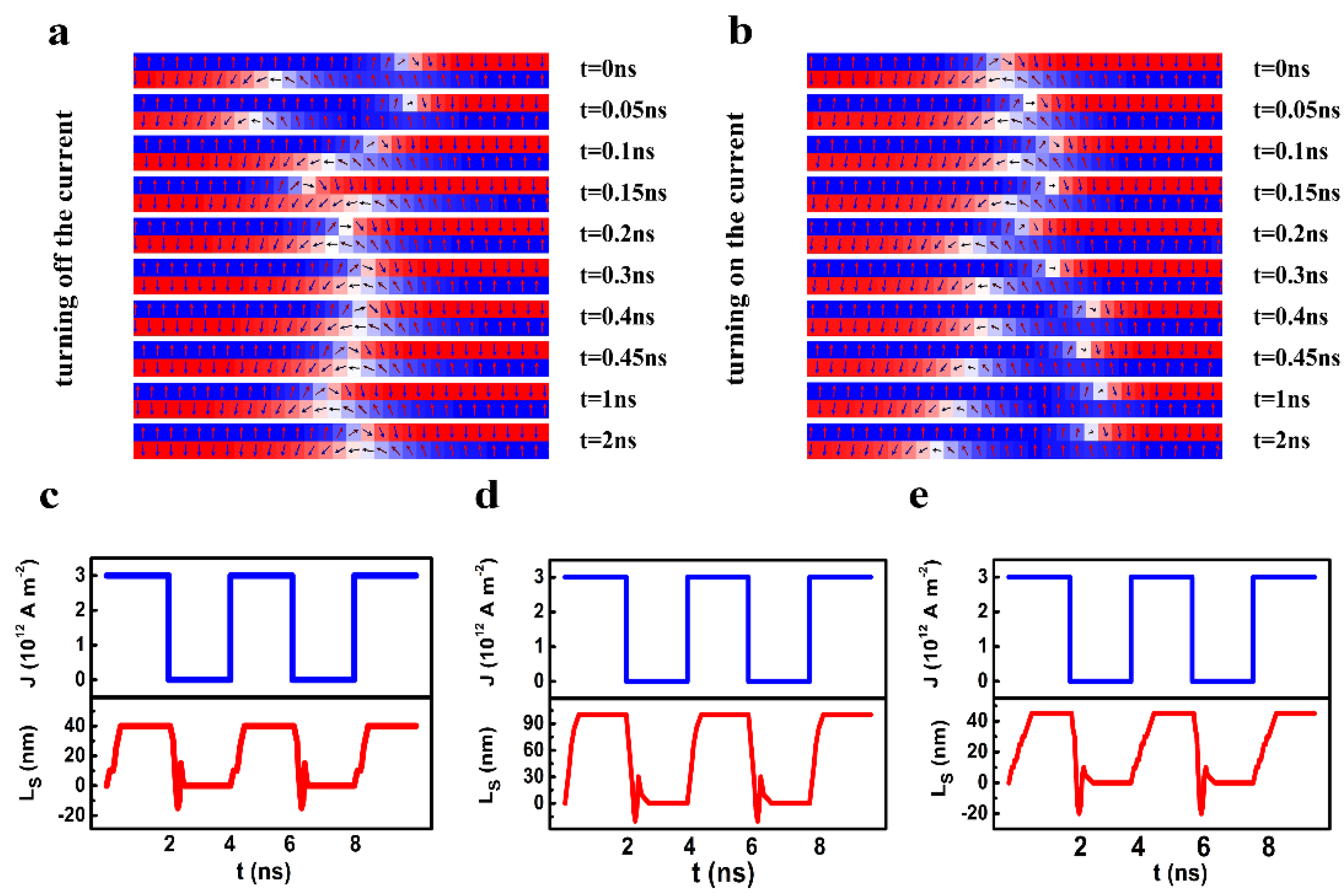
3.1. The Results of the Micromagnetic Simulation
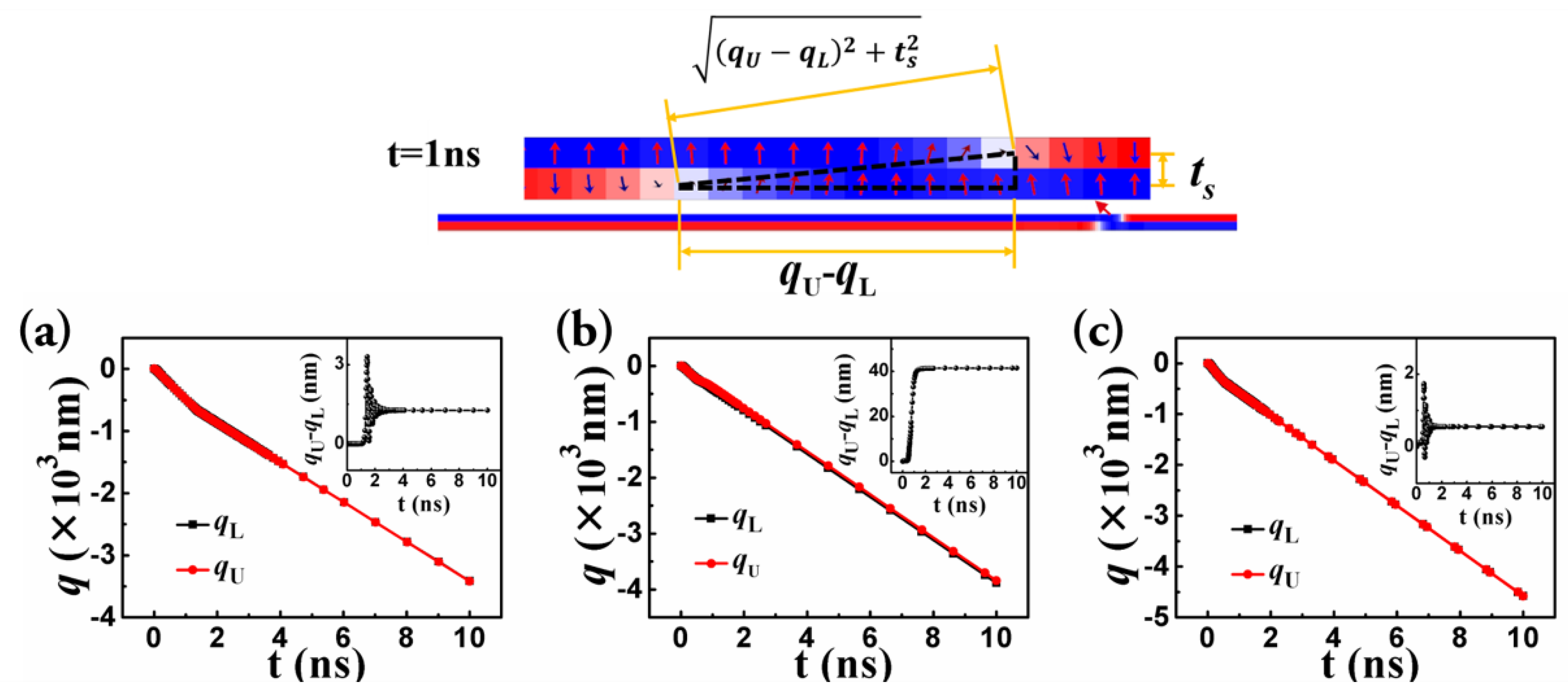
3.2. Theoretical Analysis Based on the Cooperative Coordinate Method
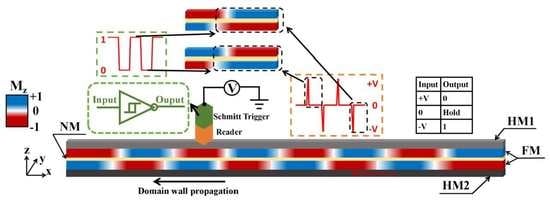
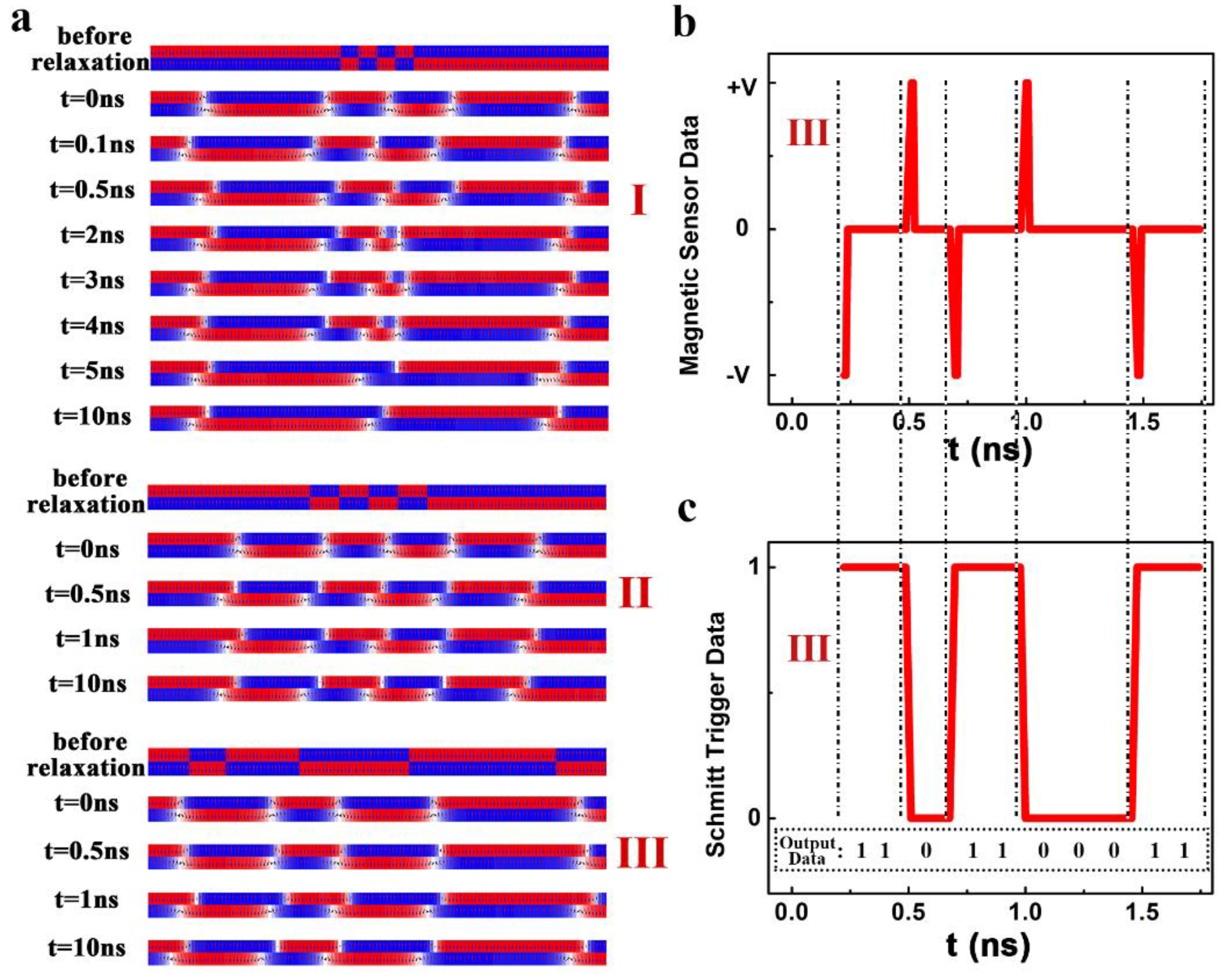
3.3. The Application of the Staggered Domain Region in the SAF Racetrack Memory
4. Summary
5. Method
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Parkin, S.S.; Hayashi, M.; Thomas, L. Magnetic domain-wall racetrack memory. Science 2008, 320, 190–194. [Google Scholar] [CrossRef] [PubMed]
- Yang, S.H.; Parkin, S. Novel domain wall dynamics in synthetic antiferromagnets. J. Phys. Condens. Matter 2017, 29, 303001. [Google Scholar] [CrossRef] [PubMed]
- Boulle, O.; Kimling, J.; Warnicke, P.; Kläui, M.; Rüdiger, U.; Malinowski, G.; Swagten, H.J.M.; Koopmans, B.; Ulysse, C.; Faini, G. Non-Adiabatic spin transfer torque in high anisotropic magnetic nanowires with narrow domain walls. Phys. Rev. Lett. 2008, 101, 216601. [Google Scholar] [CrossRef] [PubMed]
- Eiji, S.; Hideki, M.; Takehiro, Y.; Gen, T. Current-induced resonance and mass determination of a single magnetic domain wall. Nature 2004, 432, 203–206. [Google Scholar]
- Rushforth, A.W. Domain wall motion driven by spin Hall effect-Tuning with in-plane magnetic anisotropy. Appl. Phys. Lett. 2014, 104, 162408. [Google Scholar] [CrossRef]
- Claudiogonzalez, D.; Thiaville, A.; Miltat, J. Domain wall dynamics under nonlocal spin-transfer torque. Phys. Rev. Lett. 2012, 108, 227208. [Google Scholar] [CrossRef]
- Hayashi, M.; Thomas, L.; Moriya, R.; Rettner, C.; Parkin, S.S. Current-controlled magnetic domain-wall nanowire shift register. Science 2008, 320, 209. [Google Scholar] [CrossRef]
- Moriya, R.; Thomas, L.; Hayashi, M.; Bazaliy, Y.B.; Rettner, C.; Parkin, S.S.P. Probing vortex-core dynamics using current-induced resonant excitation of a trapped domain wall. Nat. Phys. 2008, 4, 368–372. [Google Scholar] [CrossRef]
- Emori, S.; Bauer, U.; Ahn, S.M.; Martinez, E.; Beach, G.S. Current-driven dynamics of chiral ferromagnetic domain walls. Nat. Mater. 2013, 12, 611–616. [Google Scholar] [CrossRef] [Green Version]
- Ryu, K.S.; Thomas, L.; Yang, S.H.; Parkin, S. Chiral spin torque at magnetic domain walls. Nat. Nanotechnol. 2013, 8, 527–533. [Google Scholar] [CrossRef]
- Franken, J.H.; Herps, M.; Swagten, H.J.M.; Koopmans, B. Tunable chiral spin texture in magnetic domain-walls. Sci. Rep. 2014, 4, 5248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Emori, S.; Martinez, E.; Lee, K.J.; Lee, H.W.; Bauer, U.; Ahn, S.M.; Agrawal, P.; Bono, D.C.; Beach, G.S.D. Spin Hall torque magnetometry of Dzyaloshinskii domain walls. Phys. Rev. B 2013, 90, 178–185. [Google Scholar] [CrossRef]
- Haazen, P.P.; Murè, E.; Franken, J.H.; Lavrijsen, R.; Swagten, H.J.; Koopmans, B. Domain wall depinning governed by the spin Hall effect. Nat. Mater. 2012, 12, 299–303. [Google Scholar] [CrossRef] [PubMed]
- Martinez, E.; Emori, S.; Beach, G.S.D. Current-driven domain wall motion along high perpendicular anisotropy multilayers: The role of the Rashba field, the spin Hall effect, and the Dzyaloshinskii-Moriya interaction. Appl. Phys. Lett. 2013, 103, 072406. [Google Scholar] [CrossRef]
- Yue, Z.; Luo, S.; Yang, X.; Chang, Y. Spin-orbit-torque-induced magnetic domain wall motion in Ta/CoFe nanowires with sloped perpendicular magnetic anisotropy. Sci. Rep. 2017, 7, 2047. [Google Scholar]
- Ryu, K.S.; Thomas, L.; Yang, S.H.; Parkin, S.S.P. Current Induced Tilting of Domain Walls in High Velocity Motion along Perpendicularly Magnetized Micron-Sized Co/Ni/Co Racetracks. Appl. Phys. Express 2012, 5, 3006. [Google Scholar] [CrossRef]
- Boulle, O.; Rohart, S.; Budaprejbeanu, L.D.; Jué, E.; Miron, I.M.; Pizzini, S.; Vogel, J.; Gaudin, G.; Thiaville, A. Domain wall tilting in the presence of the Dzyaloshinskii-Moriya interaction in out-of-plane magnetized magnetic nanotracks. Phys. Rev. Lett. 2013, 111, 1352–1355. [Google Scholar] [CrossRef]
- Yang, S.H.; Ryu, K.S.; Parkin, S. Domain-wall velocities of up to 750 m s−1 driven by exchange-coupling torque in synthetic antiferromagnets. Nat. Nanotechnol. 2015, 10, 221–226. [Google Scholar] [CrossRef]
- Sinova, J.; Jungwirth, T.; Gomonay, O. Antiferromagnetic spintronics. Nat. Nanotechnol. 2016, 11, 231. [Google Scholar] [CrossRef]
- Gomonay, O.; Baltz, V.; Brataas, A.; Tserkovnyak, Y. Antiferromagnetic spin textures and dynamics. Nat. Phys. 2018, 14, 213–216. [Google Scholar] [CrossRef]
- Loth, S.; Baumann, S.; Lutz, C.P.; Eigler, D.M.; Heinrich, A.J. Bistability in atomic-scale antiferromagnets. Science 2012, 335, 196–199. [Google Scholar] [CrossRef] [PubMed]
- Marti, X.; Fina, I.; Frontera, C.; Liu, J.; Wadley, P.; He, Q.; Paull, R.J.; Clarkson, J.D.; Kudrnovský, J.; Turek, I. Room-temperature antiferromagnetic memory resistor. Nat. Mater. 2014, 13, 367–374. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wadley, P.; Howells, B.; Železný, J.; Andrews, C.; Hills, V.; Campion, R.P.; Novák, V.; Olejník, K.; Maccherozzi, F.; Dhesi, S.S. Electrical switching of an antiferromagnet. Science 2016, 351, 587–590. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, S.H.; Garg, C.; Parkin, S.S.P. Chiral exchange drag and chirality oscillations in synthetic antiferromagnets. Nat. Phys. 2019, 15, 543. [Google Scholar] [CrossRef]
- Samardak, A.; Kolesnikov, A.; Stebliy, M.; Chebotkevich, L.; Sadovnikov, A.; Nikitov, S.; Talapatra, A.; Mohanty, J.; Ognev, A. Enhanced interfacial Dzyaloshinskii-Moriya interaction and isolated skyrmions in the inversion-symmetry-broken Ru/Co/W/Ru films. Appl. Phys. Lett. 2018, 112, 192406. [Google Scholar] [CrossRef]
- Hrabec, A.; Porter, N.A.; Wells, A.; Benitez, M.J.; Burnell, G.; McVitie, S.; McGrouther, D.; Moore, T.A.; Marrows, C.H. Measuring and tailoring the Dzyaloshinskii-Moriya interaction in perpendicularly magnetized thin films. Phys. Rev. B 2014, 90, 020402. [Google Scholar] [CrossRef]
- Koyama, T.; Chiba, D.; Ueda, K.; Kondou, K.; Tanigawa, H.; Fukami, S.; Suzuki, T.; Ohshima, N.; Ishiwata, N.; Nakatani, Y.; et al. Observation of the intrinsic pinning of a magnetic domain wall in a ferromagnetic nanowire. Nat. Mater. 2011, 10, 194–197. [Google Scholar] [CrossRef]
- Alejos, O.; Raposo, V.; Sanchez-Tejerina, L.; Tomasello, R.; Finocchio, G.; Martinez, E. Current-driven domain wall dynamics in ferromagnetic layers synthetically exchange-coupled by a spacer: A micromagnetic study. J. Appl. Phys. 2018, 123, 013901. [Google Scholar] [CrossRef] [Green Version]
- Thiele, A.A. Steady-State Motion of Magnetic Domains. Phys. Rev. Lett. 1973, 30, 230–233. [Google Scholar] [CrossRef]
- Donahue, M.J.; Porter, D.J. OOMMF User’s Guide; Version 1; NIST: Gaithersburg, MD, USA, 2002. [Google Scholar]
- Emori, S.; Beach, G.S. Roles of the magnetic field and electric current in thermally activated domain wall motion in a submicrometer magnetic strip with perpendicular magnetic anisotropy. J. Phys. Condens. Matter 2012, 24, 024214. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, Z.; Wei, C.; Yi, F.; Xiong, R. Readable High-Speed Racetrack Memory Based on an Antiferromagnetically Coupled Soft/Hard Magnetic Bilayer. Nanomaterials 2019, 9, 1538. https://doi.org/10.3390/nano9111538
Yu Z, Wei C, Yi F, Xiong R. Readable High-Speed Racetrack Memory Based on an Antiferromagnetically Coupled Soft/Hard Magnetic Bilayer. Nanomaterials. 2019; 9(11):1538. https://doi.org/10.3390/nano9111538
Chicago/Turabian StyleYu, Ziyang, Chenhuinan Wei, Fan Yi, and Rui Xiong. 2019. "Readable High-Speed Racetrack Memory Based on an Antiferromagnetically Coupled Soft/Hard Magnetic Bilayer" Nanomaterials 9, no. 11: 1538. https://doi.org/10.3390/nano9111538
APA StyleYu, Z., Wei, C., Yi, F., & Xiong, R. (2019). Readable High-Speed Racetrack Memory Based on an Antiferromagnetically Coupled Soft/Hard Magnetic Bilayer. Nanomaterials, 9(11), 1538. https://doi.org/10.3390/nano9111538