Wave Propagation of Porous Nanoshells
Abstract
1. Introduction
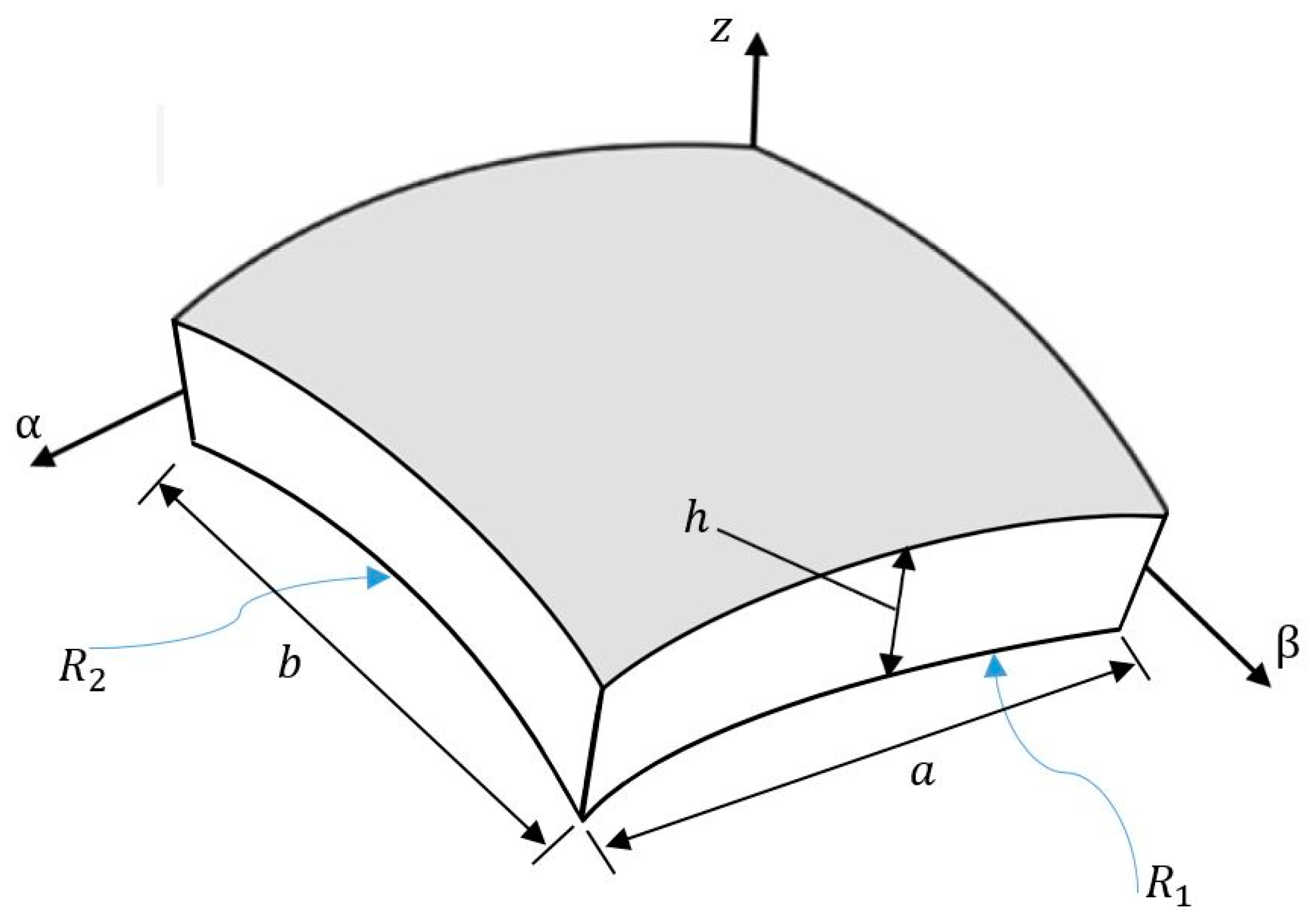
2. Theory and Formulation
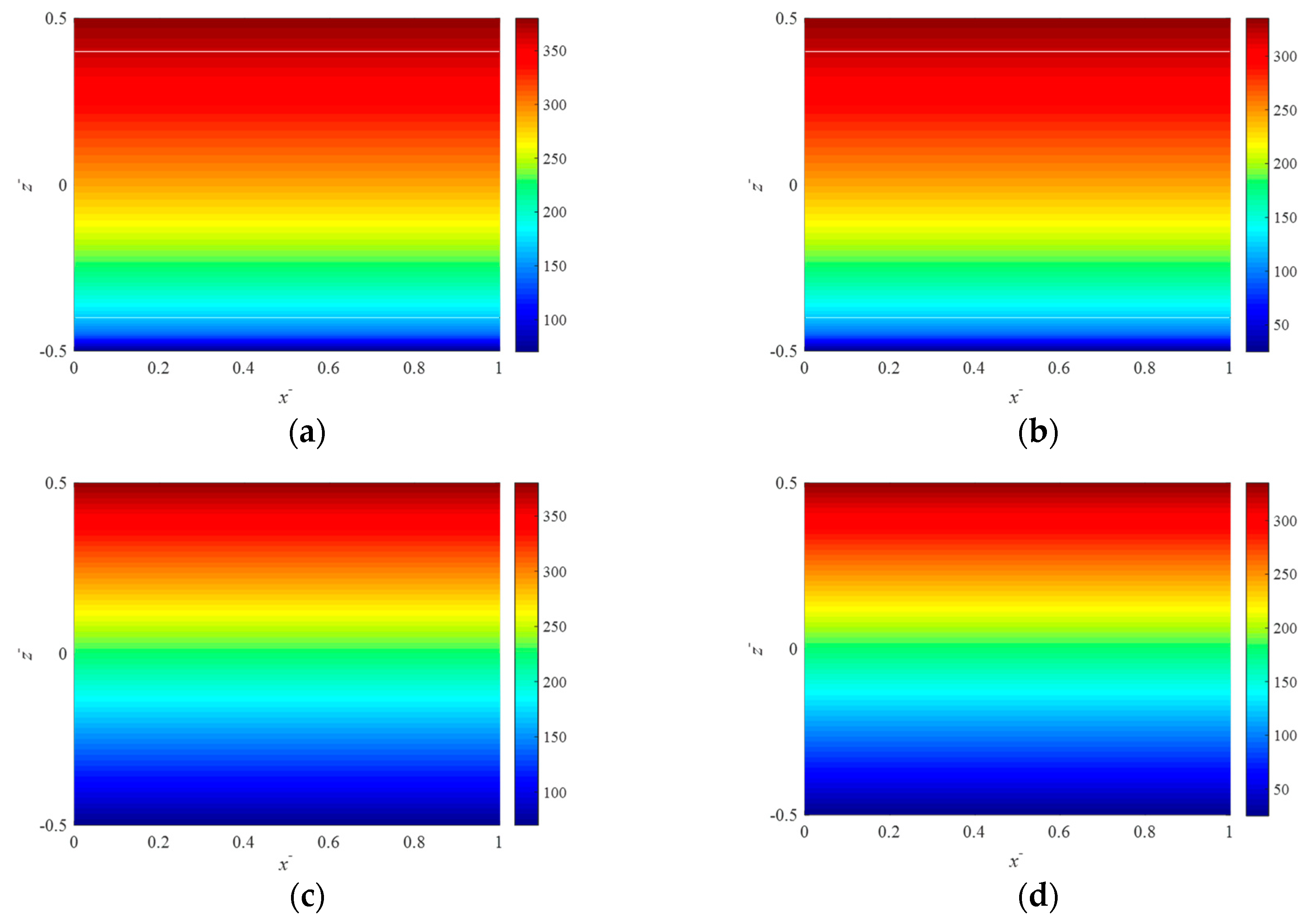
2.1. Porosity-Dependent Functionally Graded Materials
2.2. The General Non Local-Strain Gradient Elasticity Theory
2.3. Kinematic Relations
3. Analytical Wave Propagation Solution
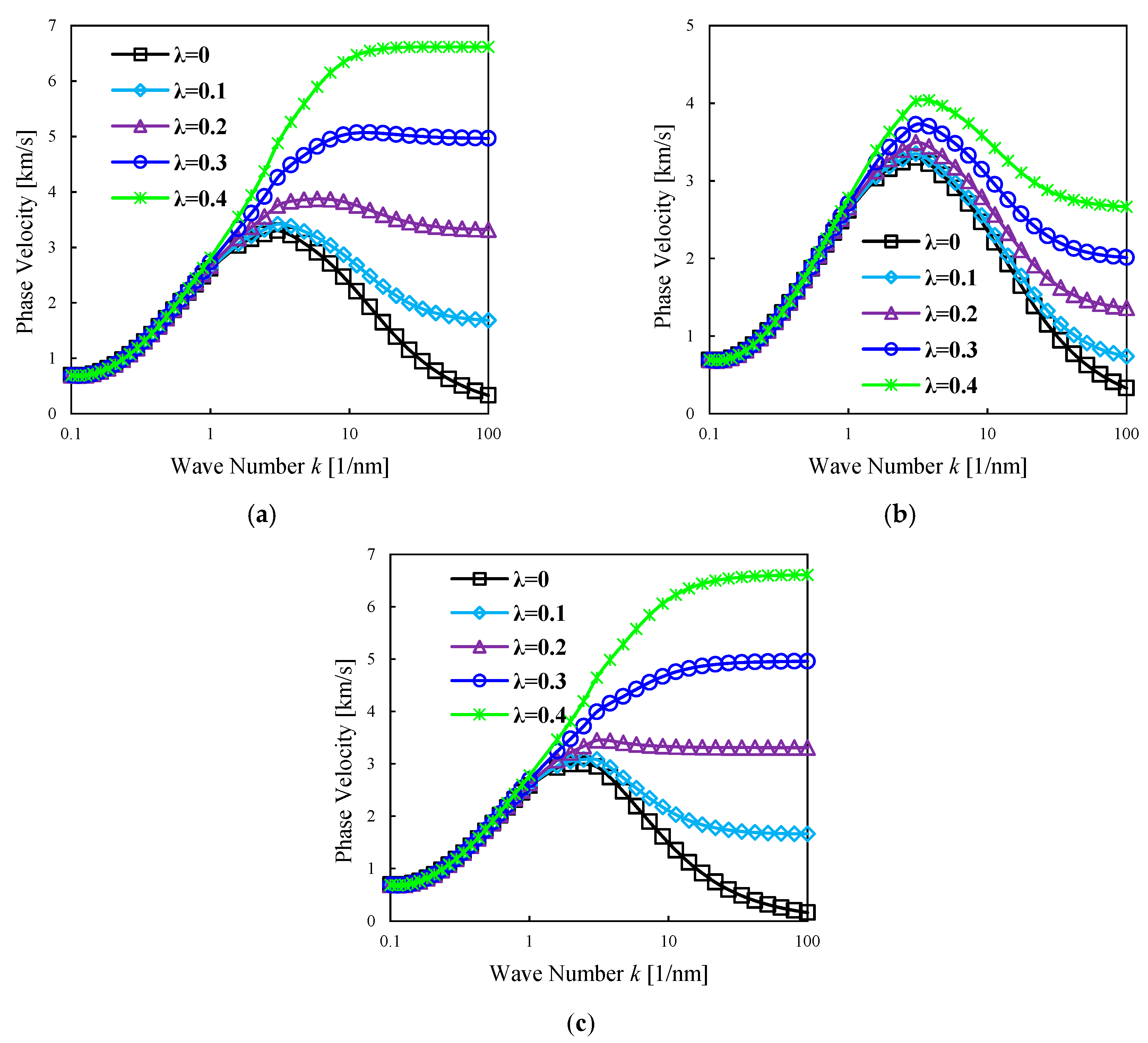
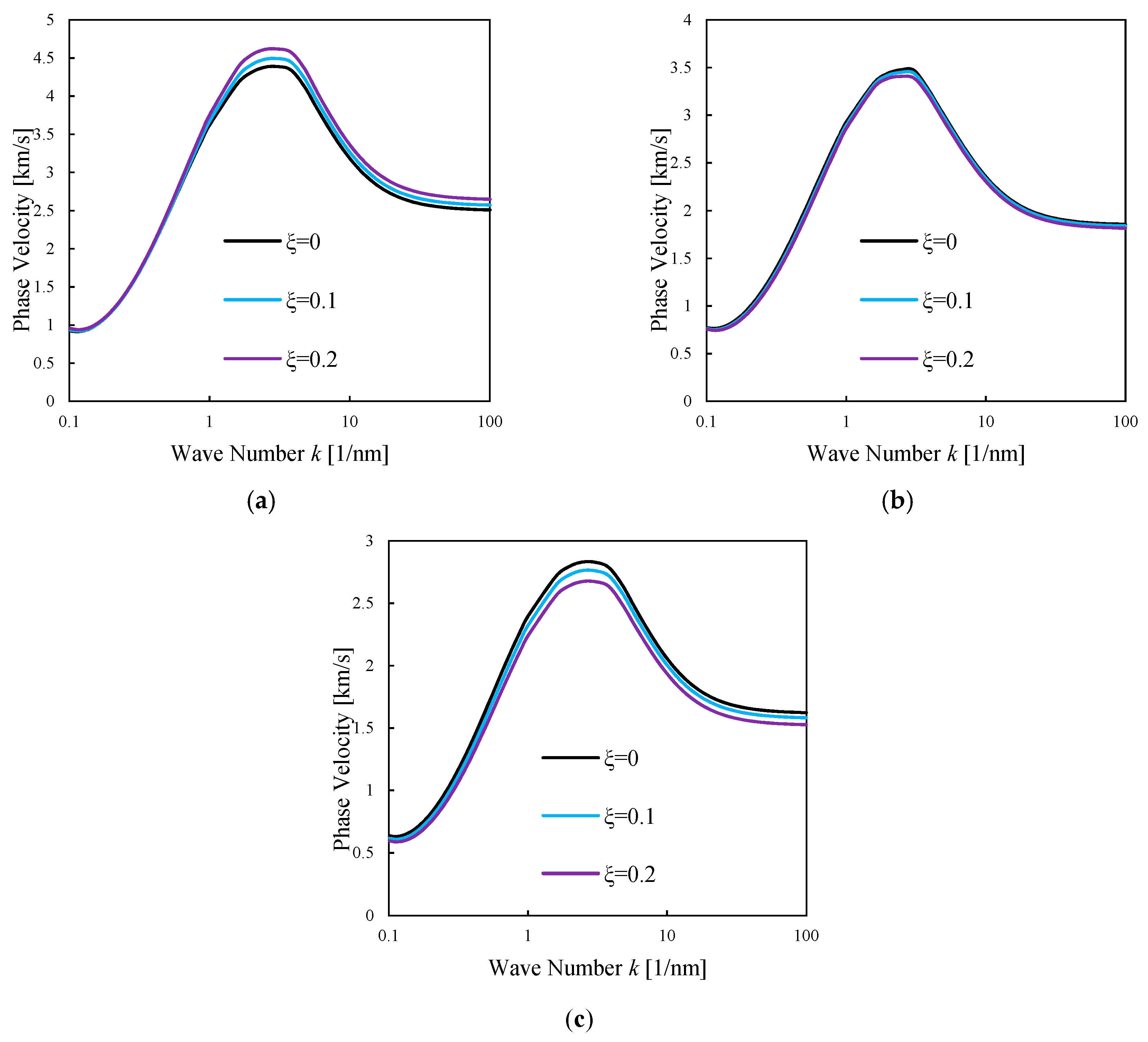
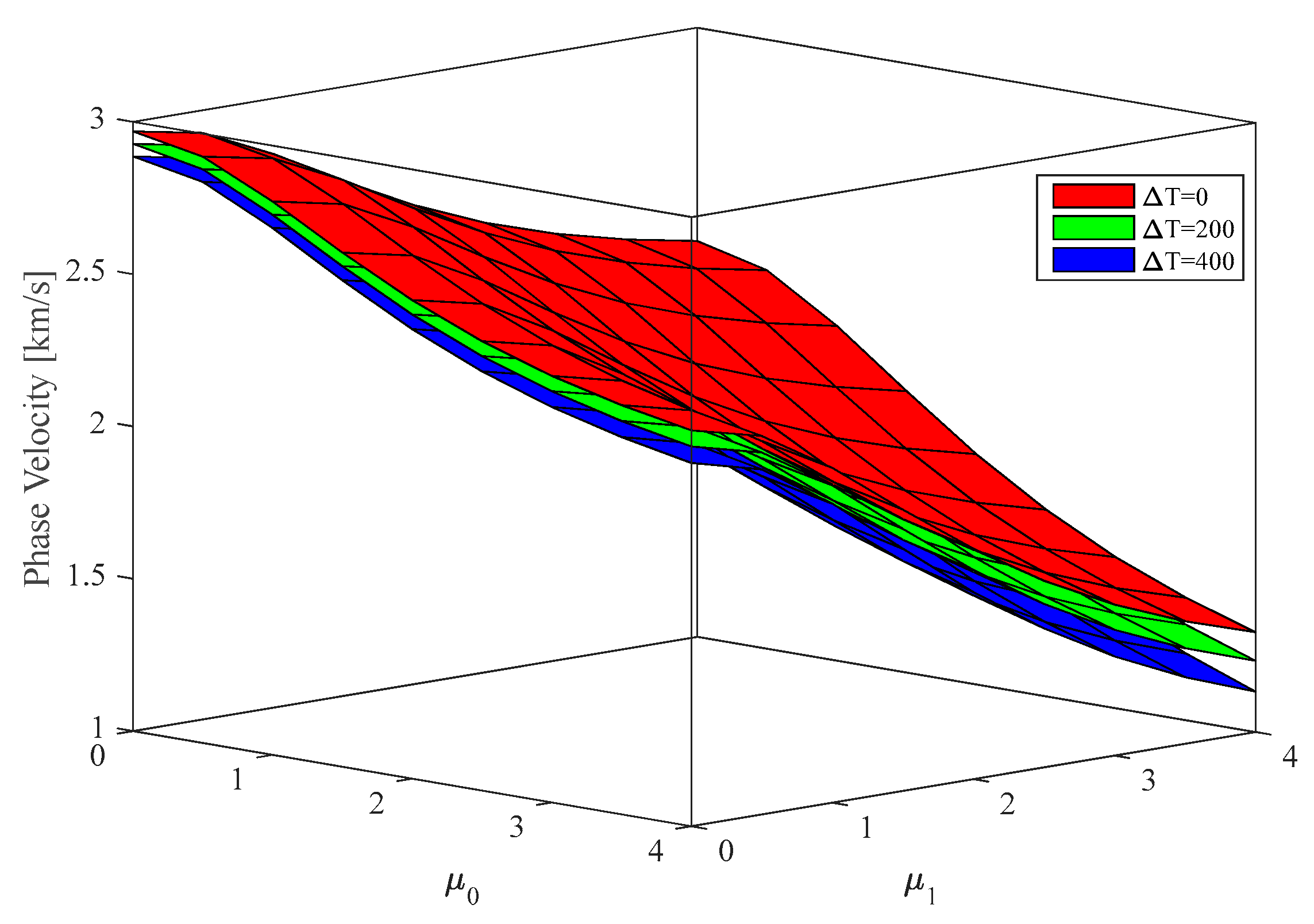
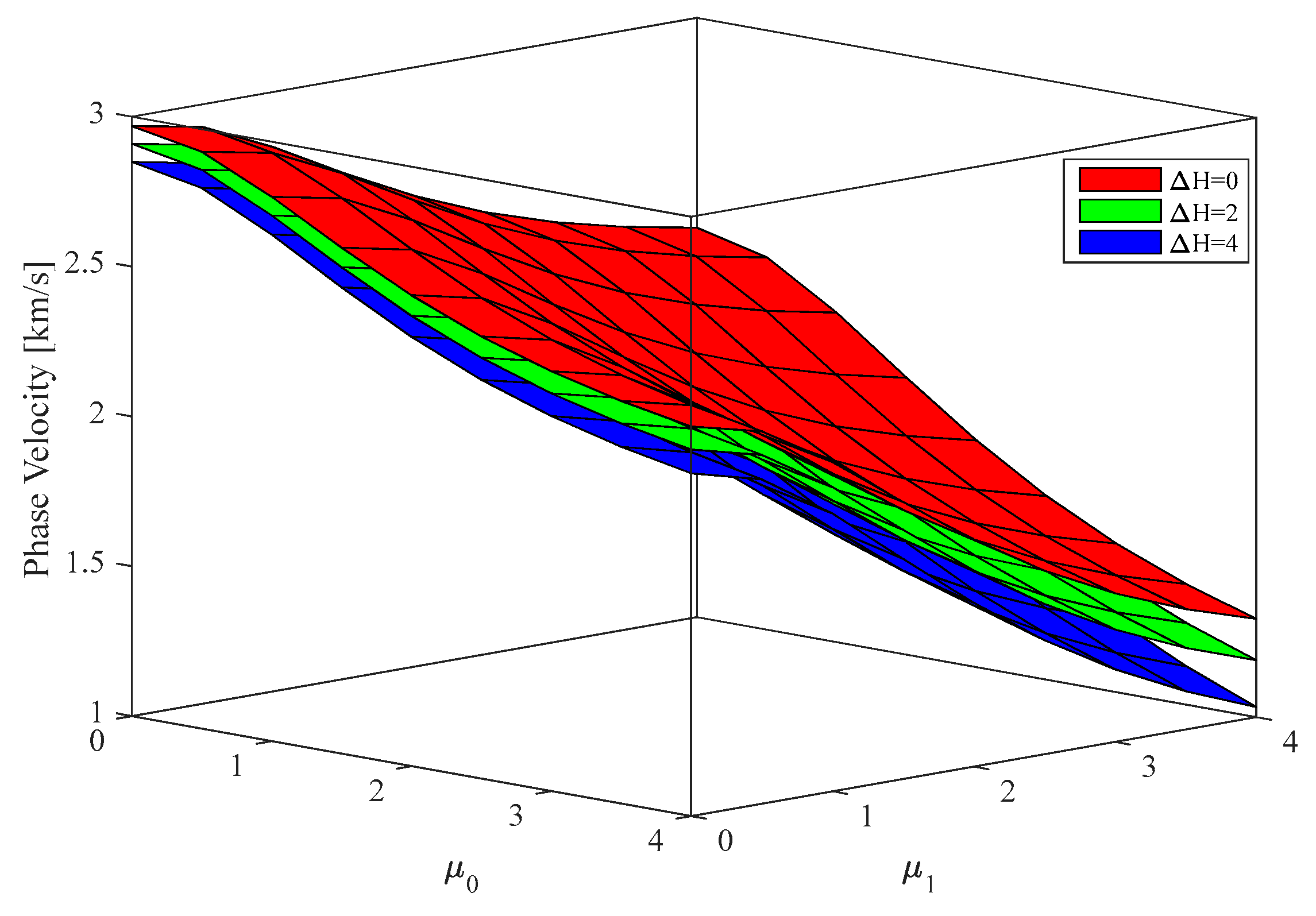
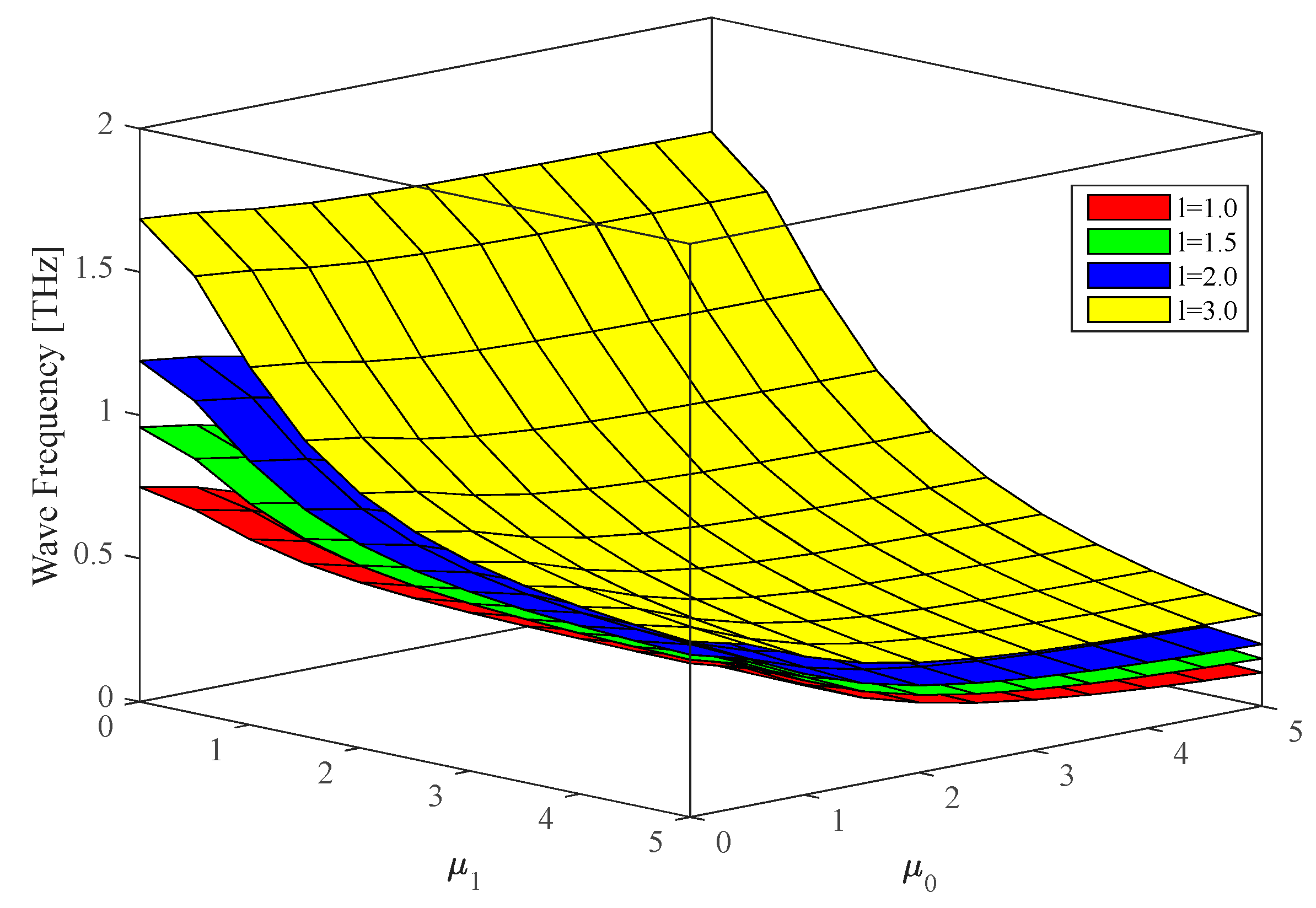
4. Numerical Results and Discussion
5. Conclusions
- (1)
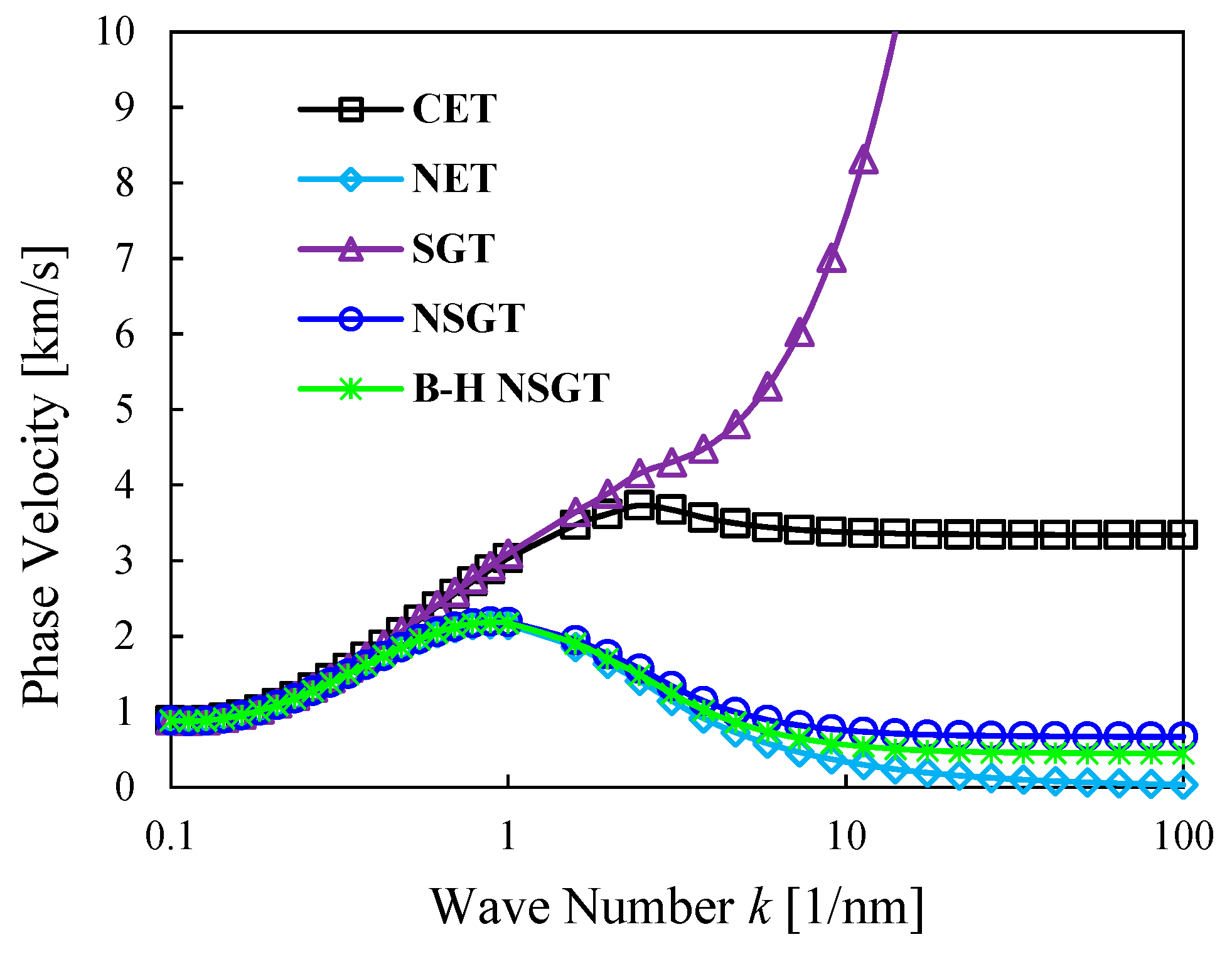
- The non-local strain gradient model (NSGT), applied here for porous nanoshells, provides the same results as those ones obtained for porous nanoplates, nanobeams and nanotubes.
- (2)
- The hygrothermal environment has a decreasing effect on the variation of the phase velocity at all small-scale parameters.
- (3)
- The porosity has varying effect on the results of nanoshells depending on the selected value of the power-lax index parameter. This conclusion is perfectly in line with similar findings from the literature obtained for nanobeams and nanotubes.
- (4)
- The effect of small-scale parameters on the structural response of nanostructures depends on the wave number value and the nature of the selected material.
- (5)
- The geometry does not affect significantly the final trend of results. Thus, it is suggested to use the most simplified structures such as the beam and tube, instead of plates and shells, when the main focus of the analysis is just related to the size-dependent behavior of a nanostructure system. In this way, the study of possible size-dependent effects could disregard any kind of complex equations.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Feng, L.; Liu, Z. Graphene in biomedicine: Opportunities and challenges. Nanomedicine 2011, 6, 317–324. [Google Scholar] [CrossRef] [PubMed]
- Delcea, M.; Möhwald, H.; Skirtach, A.G. Stimuli-responsive lbl capsules and nanoshells for drug delivery. Adv. Drug Deliv. Rev. 2011, 63, 730–747. [Google Scholar] [CrossRef] [PubMed]
- Cabrera, C.R.; Miranda, F. Advanced Nanomaterials for Aerospace Applications; Pan Stanford: Singapore, 2014. [Google Scholar]
- Du, B.G.; Zhang, J.X.; Zhu, H.T.; Zhou, L.S. The application of nano-material in automobile. Commun. Stand. 2005, 4, 018. [Google Scholar]
- Tiginyanu, I.; Braniste, T.; Smazna, D.; Deng, M.; Schütt, F.; Schuchardt, A.; Stevens-Kalceff, M.A.; Raevschi, S.; Schürmann, U.; Kienle, L. Self-organized and self-propelled aero-gan with dual hydrophilic-hydrophobic behavior. Nano Energy 2018. [Google Scholar] [CrossRef]
- Abbasi, A.; Park, K.; Bose, A.; Bothun, G.D. Near-infrared responsive gold–layersome nanoshells. Langmuir 2017, 33, 5321–5327. [Google Scholar] [CrossRef] [PubMed]
- Villaverde, A. Nanoparticles in Translational Science and Medicine; Academic Press: Cambridge, MA, USA, 2011; Volume 104. [Google Scholar]
- Timoshenko, S.P.; Woinowsky-Krieger, S. Theory of Plates and Shells; McGraw-hill: New York, NY, USA, 1959. [Google Scholar]
- Vlasov, V.Z. General Theory of Shells And Its Application in Engineering; NASA TT F-99; National Aeronautics and Space Administration: Washington, DC, USA, 1964.
- Niordson, F.I. Shell Theory; Elsevier: New York, NY, USA, 2012; Volume 29. [Google Scholar]
- Ciarlet, P.G. Theory of Shells; Elsevier: New York, NY, USA, 2000; Volume 3. [Google Scholar]
- Tornabene, F.; Fantuzzi, N. Mechanics of Laminated Composite Doubly-Curvel Shell Structures: The Generalized Differential Quadrature Method and The Strong Formulation Finite Element Method; Società Editrice Esculapio: Bologna, Italy, 2014. [Google Scholar]
- Fuller, C.; Fahy, F.J. Characteristics of wave propagation and energy distributions in cylindrical elastic shells filled with fluid. J. Sound Vib. 1982, 81, 501–518. [Google Scholar] [CrossRef]
- Mead, D. Wave propagation in continuous periodic structures: Research contributions from southampton, 1964–1995. J. Sound Vib. 1996, 190, 495–524. [Google Scholar] [CrossRef]
- Yuan, F.; Hsieh, C. Three-dimensional wave propagation in composite cylindrical shells. Compos. Struct. 1998, 42, 153–167. [Google Scholar] [CrossRef]
- Solaroli, G.; Gu, Z.; Baz, A.; Ruzzene, M. Wave propagation in periodic stiffened shells: Spectral finite element modeling and experiments. Modal Anal. 2003, 9, 1057–1081. [Google Scholar] [CrossRef]
- Wang, X.; Lu, G.; Guillow, S. Stress wave propagation in orthotropic laminated thick-walled spherical shells. Int. J. Solids Struct. 2002, 39, 4027–4037. [Google Scholar] [CrossRef]
- Golbahar Haghighi, M.; Malekzadeh, P.; Rahideh, H.; Vaghefi, M. Inverse transient heat conduction problems of a multilayered functionally graded cylinder. Numer. Heat Transf. Part A Appl. 2012, 61, 717–733. [Google Scholar] [CrossRef]
- Graff, K.F. Wave Motion in Elastic Solids; Courier Corporation: Chelmsford, MA, USA, 2012. [Google Scholar]
- Thai, H.-T.; Kim, S.-E. A review of theories for the modeling and analysis of functionally graded plates and shells. Compos. Struct. 2015, 128, 70–86. [Google Scholar] [CrossRef]
- Alijani, F.; Amabili, M. Non-linear vibrations of shells: A literature review from 2003 to 2013. Int. J. Non-Linear Mech. 2014, 58, 233–257. [Google Scholar] [CrossRef]
- Tornabene, F.; Fantuzzi, N.; Viola, E.; Batra, R.C. Stress and strain recovery for functionally graded free-form and doubly-curved sandwich shells using higher-order equivalent single layer theory. Compos. Struct. 2015, 119, 67–89. [Google Scholar] [CrossRef]
- Reddy, J.N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis; CRC Press: Bocaton, FL, USA, 2004. [Google Scholar]
- Shimpi, R.; Patel, H. A two variable refined plate theory for orthotropic plate analysis. Int. J. Solids Struct. 2006, 43, 6783–6799. [Google Scholar] [CrossRef]
- Thai, H.-T.; Vo, T.P.; Nguyen, T.-K.; Kim, S.-E. A review of continuum mechanics models for size-dependent analysis of beams and plates. Compos. Struct. 2017, 177, 196–219. [Google Scholar] [CrossRef]
- Reddy, J.; Phan, N. Stability and vibration of isotropic, orthotropic and laminated plates according to a higher-order shear deformation theory. J. Sound Vib. 1985, 98, 157–170. [Google Scholar] [CrossRef]
- Amabili, M. Non-linearities in rotation and thickness deformation in a new third-order thickness deformation theory for static and dynamic analysis of isotropic and laminated doubly curved shells. Int. J. Non-Linear Mech. 2015, 69, 109–128. [Google Scholar] [CrossRef]
- Amabili, M. A new third-order shear deformation theory with non-linearities in shear for static and dynamic analysis of laminated doubly curved shells. Compos. Struct. 2015, 128, 260–273. [Google Scholar] [CrossRef]
- Carrera, E.; Brischetto, S.; Cinefra, M.; Soave, M. Effects of thickness stretching in functionally graded plates and shells. Compos. Part B Eng. 2011, 42, 123–133. [Google Scholar] [CrossRef]
- Neves, A.; Ferreira, A.; Carrera, E.; Cinefra, M.; Roque, C.; Jorge, R.; Soares, C.M. Static, free vibration and buckling analysis of isotropic and sandwich functionally graded plates using a quasi-3d higher-order shear deformation theory and a meshless technique. Compos. Part B Eng. 2013, 44, 657–674. [Google Scholar] [CrossRef]
- Thai, H.-T.; Kim, S.-E. A simple quasi-3d sinusoidal shear deformation theory for functionally graded plates. Compos. Struct. 2013, 99, 172–180. [Google Scholar] [CrossRef]
- She, G.-L.; Yuan, F.-G.; Karami, B.; Ren, Y.-R.; Xiao, W.-S. On nonlinear bending behavior of fg porous curved nanotubes. Int. J. Eng. Sci. 2019, 135, 58–74. [Google Scholar] [CrossRef]
- She, G.-L.; Yuan, F.-G.; Ren, Y.-R.; Liu, H.-B.; Xiao, W.-S. Nonlinear bending and vibration analysis of functionally graded porous tubes via a nonlocal strain gradient theory. Compos. Struct. 2018, 203, 614–623. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Janghorban, M. Wave propagation analysis in functionally graded (fg) nanoplates under in-plane magnetic field based on nonlocal strain gradient theory and four variable refined plate theory. Mech. Adv. Mater. Struct. 2018, 25, 1047–1057. [Google Scholar] [CrossRef]
- Shahsavari, D.; Karami, B.; Li, L. A high-order gradient model for wave propagation analysis of porous fg nanoplates. Steel Compos. Struct. 2018, 29, 53–66. [Google Scholar]
- Karami, B.; Shahsavari, D.; Li, L.; Karami, M.; Janghorban, M. Thermal buckling of embedded sandwich piezoelectric nanoplates with functionally graded core by a nonlocal second-order shear deformation theory. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018. [Google Scholar] [CrossRef]
- Heshmati, M.; Amini, Y. A comprehensive study on the functionally graded piezoelectric energy harvesting from vibrations of a graded beam under travelling multi-oscillators. Appl. Math. Model. 2019, 66, 344–361. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Janghorban, M. A comprehensive analytical study on functionally graded carbon nanotube-reinforced composite plates. Aerosp. Sci. Technol. 2018, 82, 499–512. [Google Scholar] [CrossRef]
- Yee, D.W.; Schulz, M.D.; Grubbs, R.H.; Greer, J.R. Functionalized 3d architected materials via thiol-michael addition and two-photon lithography. Adv. Mater. 2017, 29, 1605293. [Google Scholar] [CrossRef]
- Liontas, R.; Jafary-Zadeh, M.; Zeng, Q.; Zhang, Y.-W.; Mao, W.L.; Greer, J.R. Substantial tensile ductility in sputtered zr-ni-al nano-sized metallic glass. Acta Mater. 2016, 118, 270–285. [Google Scholar] [CrossRef]
- Shahsavari, D.; Shahsavari, M.; Li, L.; Karami, B. A novel quasi-3d hyperbolic theory for free vibration of fg plates with porosities resting on winkler/pasternak/kerr foundation. Aerosp. Sci. Technol. 2018, 72, 134–149. [Google Scholar] [CrossRef]
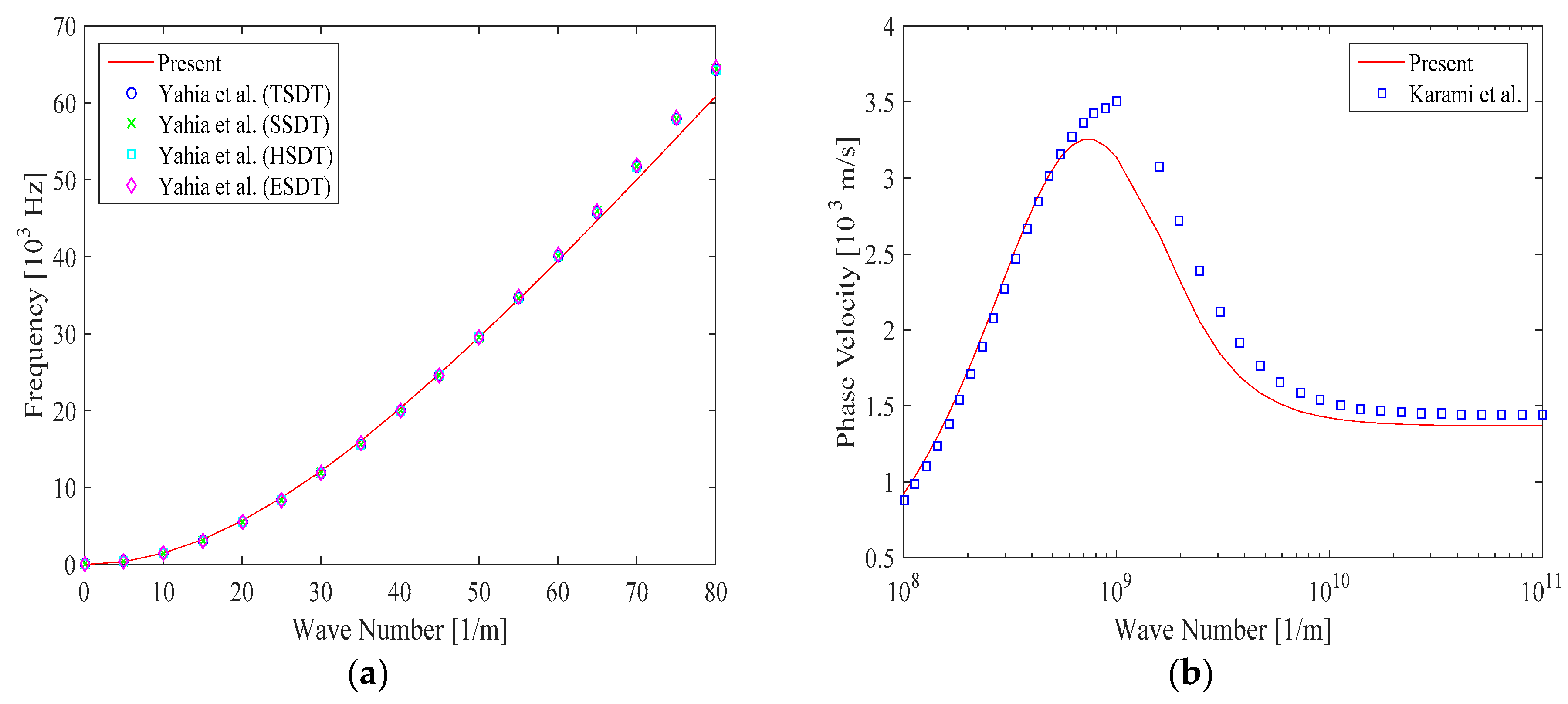
- Yahia, S.A.; Atmane, H.A.; Houari, M.S.A.; Tounsi, A. Wave propagation in functionally graded plates with porosities using various higher-order shear deformation plate theories. Struct. Eng. Mech. 2015, 53, 1143–1165. [Google Scholar] [CrossRef]
- Lellep, J.; Majak, J. Nonlinear constitutive behavior of orthotropic materials. Mech. Compos. Mater. 2000, 36, 261–266. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Tounsi, A. Variational approach for wave dispersion in anisotropic doubly-curved nanoshells based on a new nonlocal strain gradient higher order shell theory. Thin-Walled Struct. 2018, 129, 251–264. [Google Scholar] [CrossRef]
- Dai, H.; Wang, X. Stress wave propagation in laminated piezoelectric spherical shells under thermal shock and electric excitation. Eur. J. Mech. A/Solids 2005, 24, 263–276. [Google Scholar] [CrossRef]
- Wattanasakulpong, N.; Ungbhakorn, V. Linear and nonlinear vibration analysis of elastically restrained ends fgm beams with porosities. Aerosp. Sci. Technol. 2014, 32, 111–120. [Google Scholar] [CrossRef]
- Magnucki, K.; Malinowski, M.; Kasprzak, J. Bending and buckling of a rectangular porous plate. Steel Compos. Struct. 2006, 6, 319–333. [Google Scholar] [CrossRef]
- Şimşek, M.; Aydın, M. Size-dependent forced vibration of an imperfect functionally graded (fg) microplate with porosities subjected to a moving load using the modified couple stress theory. Compos. Struct. 2017, 160, 408–421. [Google Scholar] [CrossRef]
- Shahsavari, D.; Karami, B.; Fahham, H.R.; Li, L. On the shear buckling of porous nanoplates using a new size-dependent quasi-3d shear deformation theory. Acta Mech. 2018, 1–25. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Shahsavari, D.; Tounsi, A. A size-dependent quasi-3d model for wave dispersion analysis of fg nanoplates. Steel Compos. Struct. 2018, 28, 99–110. [Google Scholar]
- Arash, B.; Ansari, R. Evaluation of nonlocal parameter in the vibrations of single-walled carbon nanotubes with initial strain. Phys. E Low-Dimens. Syst. Nanostruct. 2010, 42, 2058–2064. [Google Scholar] [CrossRef]
- Ghavanloo, E.; Fazelzadeh, S.A. Radial vibration of free anisotropic nanoparticles based on nonlocal continuum mechanics. Nanotechnology 2013, 24, 075702. [Google Scholar] [CrossRef]
- Giwa, A.M.; Aitken, Z.H.; Jafary-Zadeh, M.; Liaw, P.K.; Zhang, Y.-W.; Greer, J.R. Temperature effect on Small-Scale Deformation of Individual on the phases of Al0.7CoCrFeNi High Entropy Alloy HEA. Available online: https://mse.utk.edu (accessed on 18 May 2018).
- Ni, X.; Papanikolaou, S.; Vajente, G.; Adhikari, R.X.; Greer, J.R. Probing microplasticity in small-scale fcc crystals via dynamic mechanical analysis. Phys. Rev. Lett. 2017, 118, 155501. [Google Scholar] [CrossRef]
- Eringen, A.C.; Edelen, D. On nonlocal elasticity. Int. J. Eng. Sci. 1972, 10, 233–248. [Google Scholar] [CrossRef]
- Lam, D.C.; Yang, F.; Chong, A.; Wang, J.; Tong, P. Experiments and theory in strain gradient elasticity. J. Mech. Phys. Solids 2003, 51, 1477–1508. [Google Scholar] [CrossRef]
- Aifantis, E.C. Update on a class of gradient theories. Mech. Mater. 2003, 35, 259–280. [Google Scholar] [CrossRef]
- Ebrahimi, F.; Barati, M.R.; Dabbagh, A. A nonlocal strain gradient theory for wave propagation analysis in temperature-dependent inhomogeneous nanoplates. Int. J. Eng. Sci. 2016, 107, 169–182. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Tounsi, A. Effects of triaxial magnetic field on the anisotropic nanoplates. Steel Compos. Struct. 2017, 25, 361–374. [Google Scholar]
- Karami, B.; Janghorban, M.; Tounsi, A. Nonlocal strain gradient 3d elasticity theory for anisotropic spherical nanoparticles. Steel Compos. Struct. 2018, 27, 201–216. [Google Scholar]
- Khaniki, H.B.; Hosseini-Hashemi, S. Buckling analysis of tapered nanobeams using nonlocal strain gradient theory and a generalized differential quadrature method. Mater. Res. Express 2017, 4, 065003. [Google Scholar] [CrossRef]
- Nami, M.R.; Janghorban, M. Resonance behavior of fg rectangular micro/nano plate based on nonlocal elasticity theory and strain gradient theory with one gradient constant. Compos. Struct. 2014, 111, 349–353. [Google Scholar] [CrossRef]
- She, G.-L.; Yan, K.-M.; Zhang, Y.-L.; Liu, H.-B.; Ren, Y.-R. Wave propagation of functionally graded porous nanobeams based on non-local strain gradient theory. Eur. Phys. J. Plus 2018, 133, 368. [Google Scholar] [CrossRef]
- She, G.-L.; Ren, Y.-R.; Yuan, F.-G.; Xiao, W.-S. On vibrations of porous nanotubes. Int. J. Eng. Sci. 2018, 125, 23–35. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Tounsi, A. Galerkin’s approach for buckling analysis of functionally graded anisotropic nanoplates/different boundary conditions. Eng. Comput. 2018. [Google Scholar] [CrossRef]
- Shahsavari, D.; Karami, B.; Mansouri, S. Shear buckling of single layer graphene sheets in hygrothermal environment resting on elastic foundation based on different nonlocal strain gradient theories. Eur. J. Mech. A/Solids 2018, 67, 200–214. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Ling, L. Wave propagation in viscoelastic single-walled carbon nanotubes with surface effect under magnetic field based on nonlocal strain gradient theory. Phys. E Low-Dimens. Syst. Nanostruct. 2016, 75, 118–124. [Google Scholar] [CrossRef]
- Xiao, W.; Li, L.; Wang, M. Propagation of in-plane wave in viscoelastic monolayer graphene via nonlocal strain gradient theory. Appl. Phys. A 2017, 123, 388. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Janghorban, M.; Li, L. Wave dispersion of mounted graphene with initial stress. Thin-Walled Struct. 2018, 122, 102–111. [Google Scholar] [CrossRef]
- Mehralian, F.; Beni, Y.T.; Zeverdejani, M.K. Nonlocal strain gradient theory calibration using molecular dynamics simulation based on small scale vibration of nanotubes. Phys. B Condens. Matter 2017, 514, 61–69. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Li, L. Temperature-dependent flexural wave propagation in nanoplate-type porous heterogenous material subjected to in-plane magnetic field. J. Therm. Stresses 2018, 41, 483–499. [Google Scholar] [CrossRef]
- Barati, M.R. On wave propagation in nanoporous materials. Int. J. Eng. Sci. 2017, 116, 1–11. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Li, L. Hygrothermal wave propagation in viscoelastic graphene under in-plane magnetic field based on nonlocal strain gradient theory. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 97, 317–327. [Google Scholar] [CrossRef]
- Shahsavari, D.; Karami, B.; Li, L. Damped vibration of a graphene sheet using a higher-order nonlocal strain-gradient kirchhoff plate model. Comptes Rendus Mécanique 2018, 346, 1216–1232. [Google Scholar] [CrossRef]
- She, G.-L.; Yuan, F.-G.; Ren, Y.-R. On wave propagation of porous nanotubes. Int. J. Eng. Sci. 2018, 130, 62–74. [Google Scholar] [CrossRef]
- Karami, B.; Janghorban, M.; Li, L. On guided wave propagation in fully clamped porous functionally graded nanoplates. Acta Astronaut. 2018, 143, 380–390. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Nazemosadat, S.M.R.; Li, L.; Ebrahimi, A. Thermal buckling of smart porous functionally graded nanobeam rested on kerr foundation. Steel Compos. Struct. 2018, 29, 349–362. [Google Scholar]
- Askes, H.; Aifantis, E.C. Gradient elasticity and flexural wave dispersion in carbon nanotubes. Phys. Rev. B 2009, 80, 195412. [Google Scholar] [CrossRef]
- Lim, C.; Zhang, G.; Reddy, J. A higher-order nonlocal elasticity and strain gradient theory and its applications in wave propagation. J. Mech. Phys. Solids 2015, 78, 298–313. [Google Scholar] [CrossRef]
- Chen, H.; Wang, A.; Hao, Y.; Zhang, W. Free vibration of fgm sandwich doubly-curved shallow shell based on a new shear deformation theory with stretching effects. Compos. Struct. 2017. [Google Scholar] [CrossRef]
- Amabili, M. Nonlinear Mechanics of Shells and Plates in Composite, Soft and Biological Materials; Cambridge University Press: Cambridge, UK, 2018. [Google Scholar]
- Ebrahimi, F.; Barati, M.R. Wave propagation analysis of quasi-3d fg nanobeams in thermal environment based on nonlocal strain gradient theory. Appl. Phys. A 2016, 122, 843. [Google Scholar] [CrossRef]
- Shahsavari, D.; Karami, B.; Janghorban, M.; Li, L. Dynamic characteristics of viscoelastic nanoplates under moving load embedded within visco-pasternak substrate and hygrothermal environment. Mater. Res. Express 2017, 4, 085013. [Google Scholar] [CrossRef]
- Karami, B.; Shahsavari, D.; Karami, M.; Li, L. Hygrothermal wave characteristic of nanobeam-type inhomogeneous materials with porosity under magnetic field. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2018. [Google Scholar] [CrossRef]
- Pandey, A.; Patel, A.K.; Kumar, V.; Sharma, R.K.; Kanhed, S.; Nigam, V.K.; Keshri, A.; Agarwal, A.; Balani, K. Enhanced tribological and bacterial resistance of carbon nanotube with ceria-and silver-incorporated hydroxyapatite biocoating. Nanomaterials 2018, 8, 363. [Google Scholar] [CrossRef]
- Pei, Y.; Zhong, H.; Wang, M.; Zhang, P.; Zhao, Y. Effect of contact pressure on the performance of carbon nanotube arrays thermal interface material. Nanomaterials 2018, 8, 732. [Google Scholar] [CrossRef]
- Pan, J.; Liu, S.; Yang, Y.; Lu, J. A highly sensitive resistive pressure sensor based on a carbon nanotube-liquid crystal-pdms composite. Nanomaterials 2018, 8, 413. [Google Scholar] [CrossRef]
- Song, M.; Yang, J.; Kitipornchai, S. Bending and buckling analyses of functionally graded polymer composite plates reinforced with graphene nanoplatelets. Compos. Part B Eng. 2018, 134, 106–113. [Google Scholar] [CrossRef]
- Huang, J.; Her, S.-C.; Yang, X.; Zhi, M. Synthesis and characterization of multi-walled carbon nanotube/graphene nanoplatelet hybrid film for flexible strain sensors. Nanomaterials 2018, 8, 786. [Google Scholar] [CrossRef]
- Slattery, A.; Shearer, C.; Shapter, J.; Blanch, A.; Quinton, J.; Gibson, C. Improved application of carbon nanotube atomic force microscopy probes using peakforce tapping mode. Nanomaterials 2018, 8, 807. [Google Scholar] [CrossRef]
- Giwa, A.M.; Liaw, P.K.; Dahmen, K.A.; Greer, J.R. Microstructure and small-scale size effects in plasticity of individual phases of al 0.7 cocrfeni high entropy alloy. Extreme Mech. Lett. 2016, 8, 220–228. [Google Scholar] [CrossRef]
- Rosenkrantz, E.; Bottero, A.; Komatitsch, D.; Monteiller, V. A flexible numerical approach for non-destructive ultrasonic testing based on a time-domain spectral-element method: Ultrasonic modeling of lamb waves in immersed defective structures and of bulk waves in damaged anisotropic materials. NDT E Int. 2019, 101, 72–86. [Google Scholar] [CrossRef]
- Wu, J.; Li, X.; Cao, W. Flexural waves in multi-walled carbon nanotubes using gradient elasticity beam theory. Comput. Mater. Sci. 2013, 67, 188–195. [Google Scholar] [CrossRef]
- Papargyri-Beskou, S.; Polyzos, D.; Beskos, D. Wave dispersion in gradient elastic solids and structures: A unified treatment. Int. J. Solids Struct. 2009, 46, 3751–3759. [Google Scholar] [CrossRef]
- Li, L.; Hu, Y.; Ling, L. Flexural wave propagation in small-scaled functionally graded beams via a nonlocal strain gradient theory. Compos. Struct. 2015, 133, 1079–1092. [Google Scholar]
| Material | E (GPa) | ||||
|---|---|---|---|---|---|
| Aluminum (Al) | 70 | 2702 | 0.3 | 0.44 | |
| 380 | 3800 | 0.3 | 0.001 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karami, B.; Shahsavari, D.; Janghorban, M.; Dimitri, R.; Tornabene, F. Wave Propagation of Porous Nanoshells. Nanomaterials 2019, 9, 22. https://doi.org/10.3390/nano9010022
Karami B, Shahsavari D, Janghorban M, Dimitri R, Tornabene F. Wave Propagation of Porous Nanoshells. Nanomaterials. 2019; 9(1):22. https://doi.org/10.3390/nano9010022
Chicago/Turabian StyleKarami, Behrouz, Davood Shahsavari, Maziar Janghorban, Rossana Dimitri, and Francesco Tornabene. 2019. "Wave Propagation of Porous Nanoshells" Nanomaterials 9, no. 1: 22. https://doi.org/10.3390/nano9010022
APA StyleKarami, B., Shahsavari, D., Janghorban, M., Dimitri, R., & Tornabene, F. (2019). Wave Propagation of Porous Nanoshells. Nanomaterials, 9(1), 22. https://doi.org/10.3390/nano9010022







