Numerical Comparison of Prediction Models for Aerosol Filtration Efficiency Applied on a Hollow-Fiber Membrane Pore Structure
Abstract
1. Introduction
2. Prediction Models for Air Filtration Efficiency
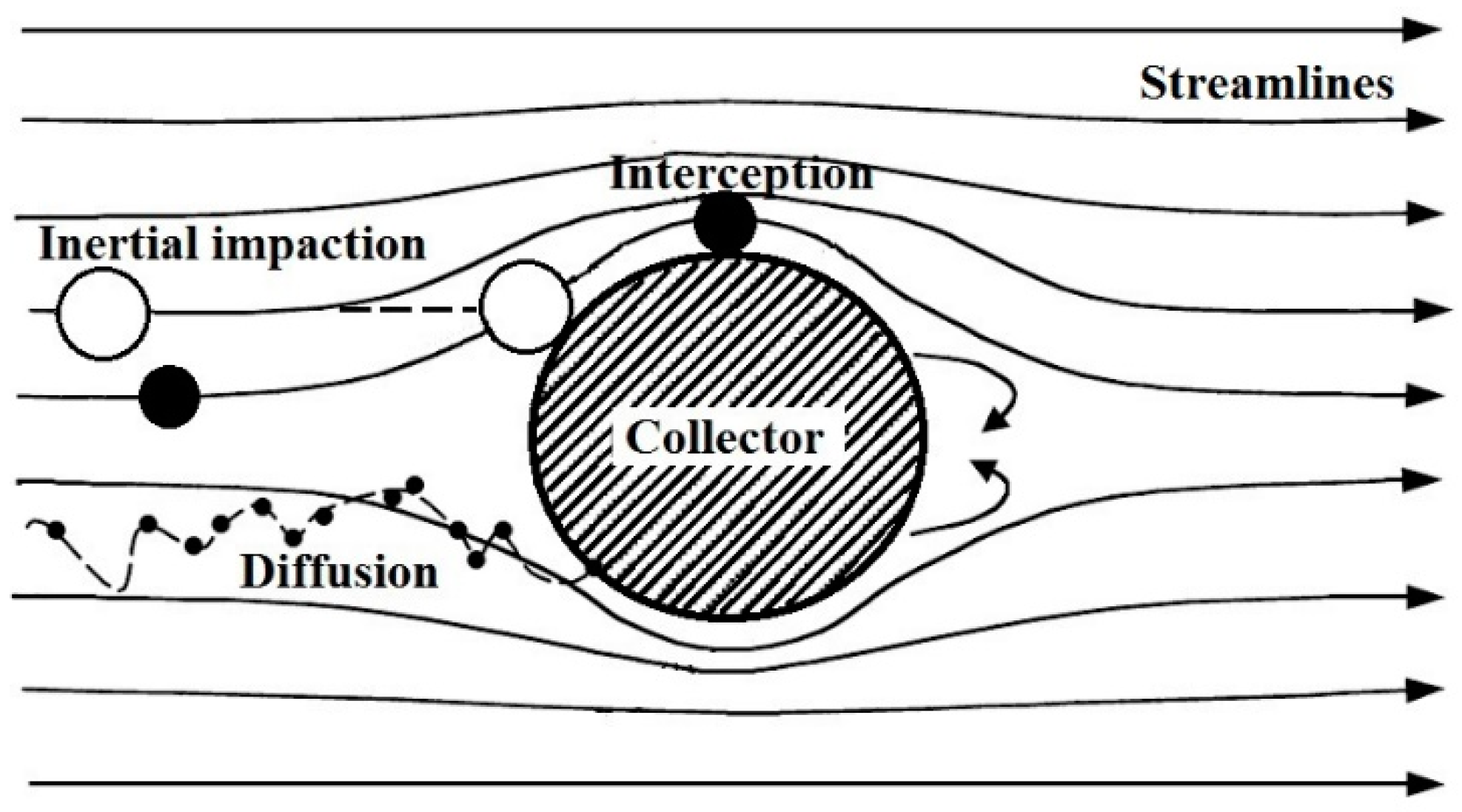
2.1. Efficiency Prediction of Fibrous Filters
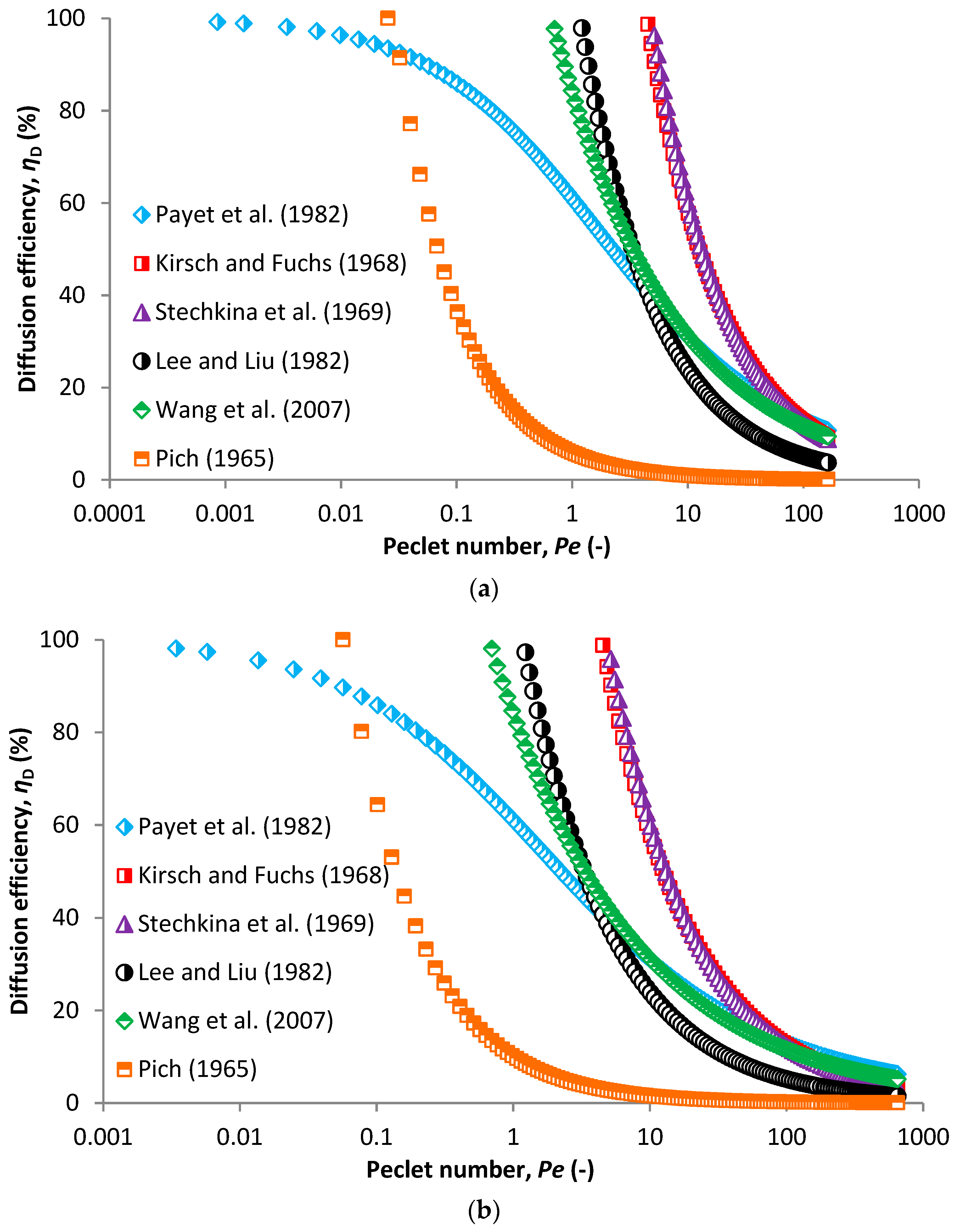
2.1.1. SCE Due to Brownian Motion
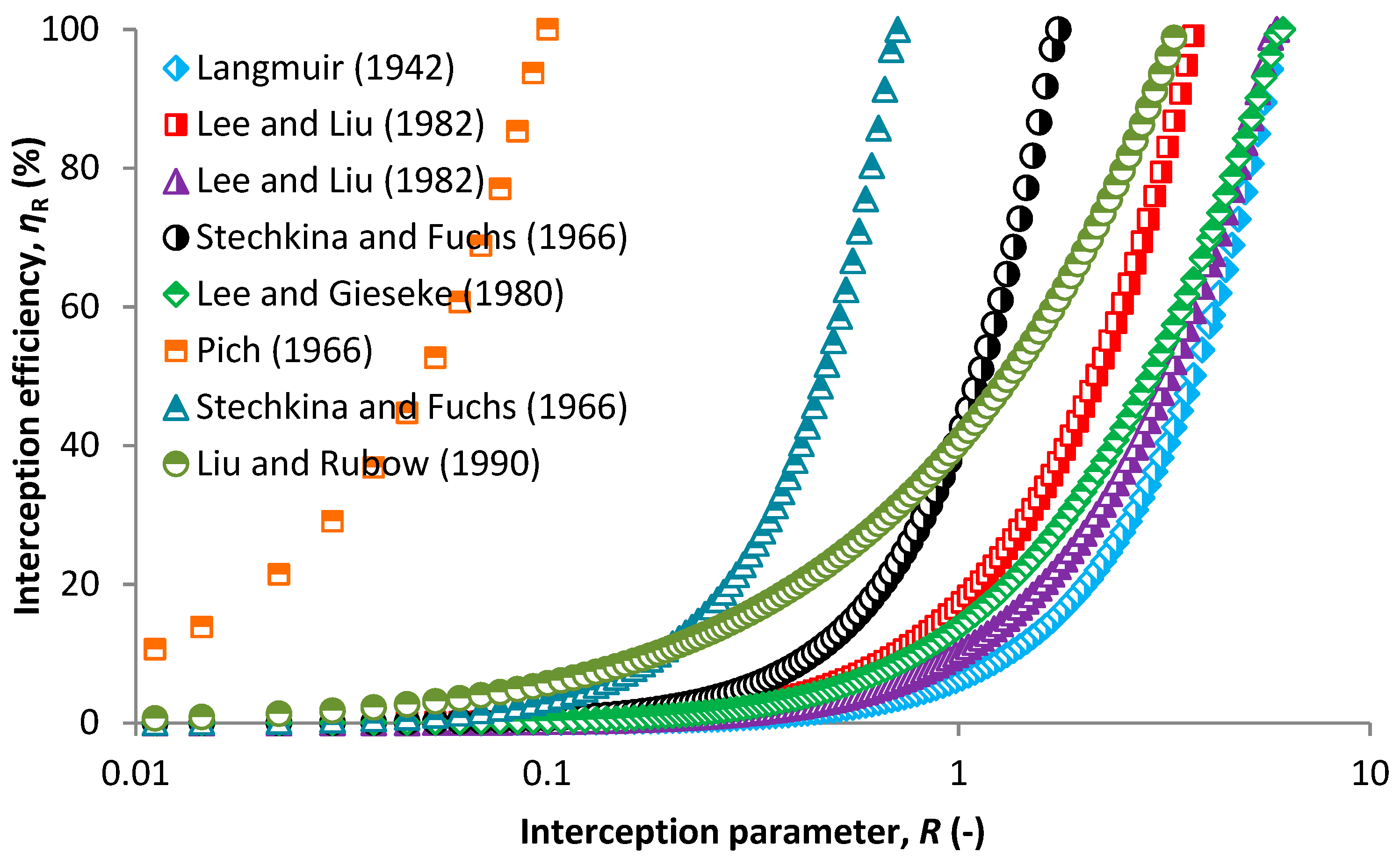
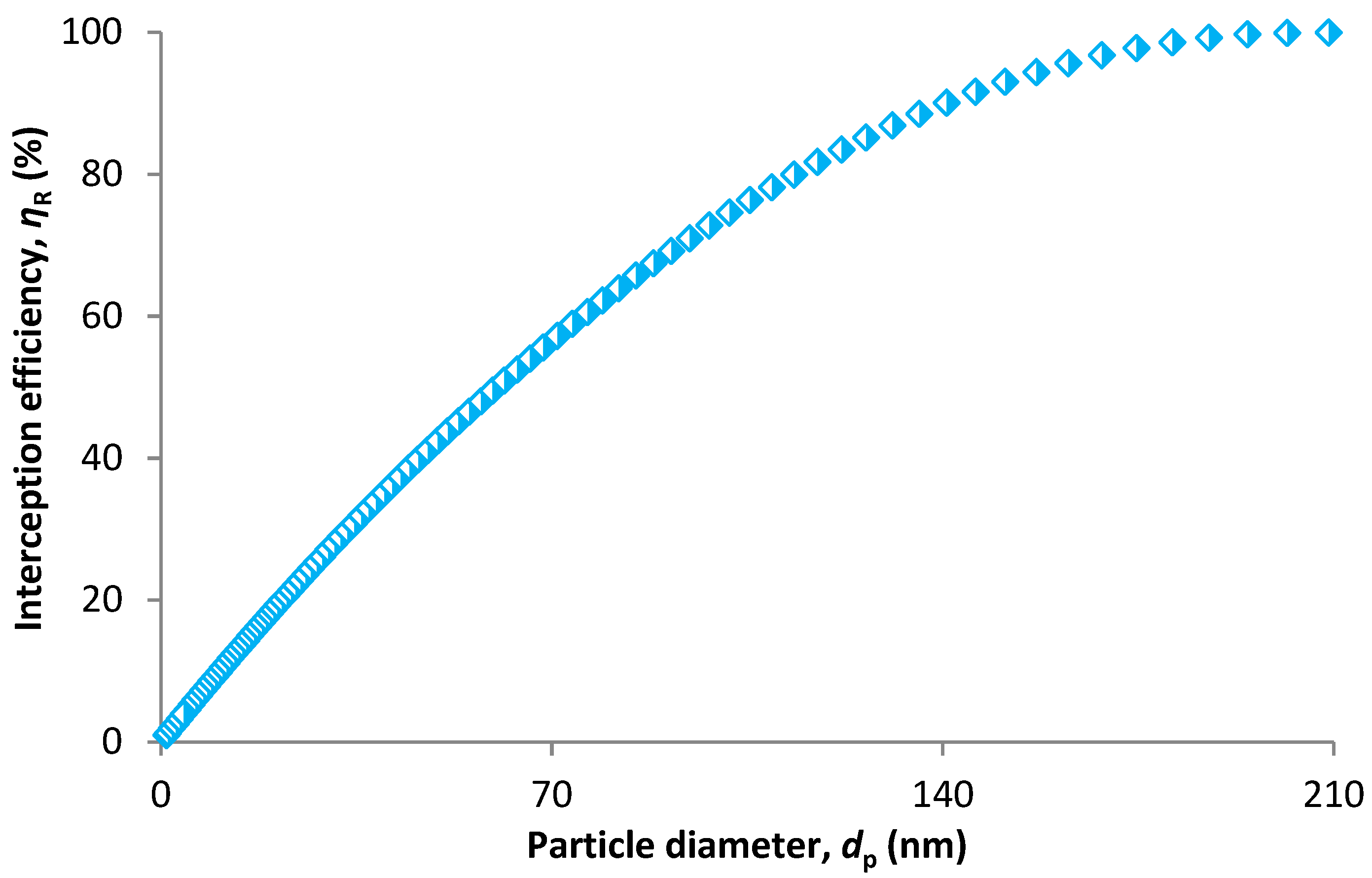
2.1.2. SCE Due to Interception
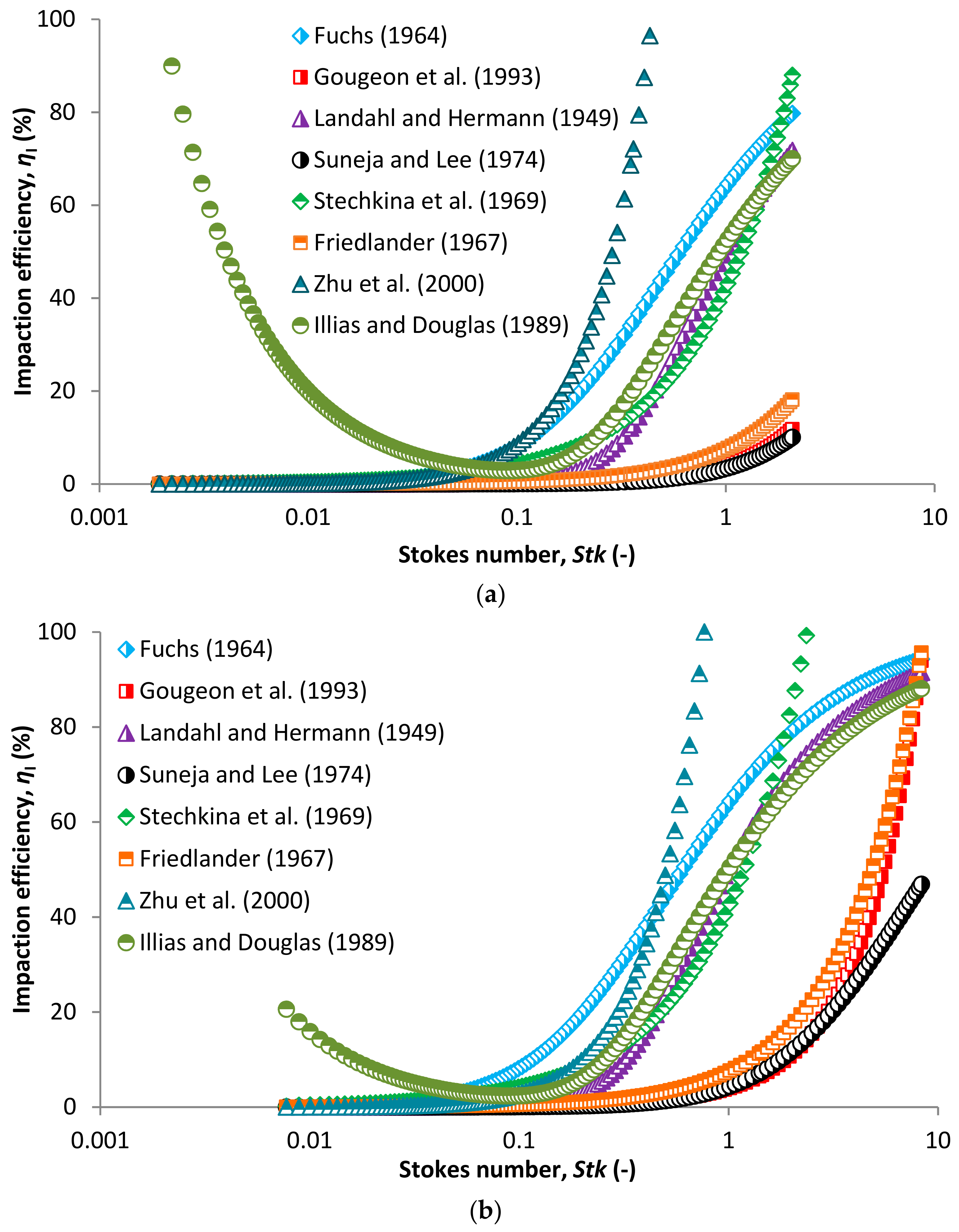
2.1.3. SCE Due to Inertial Impaction
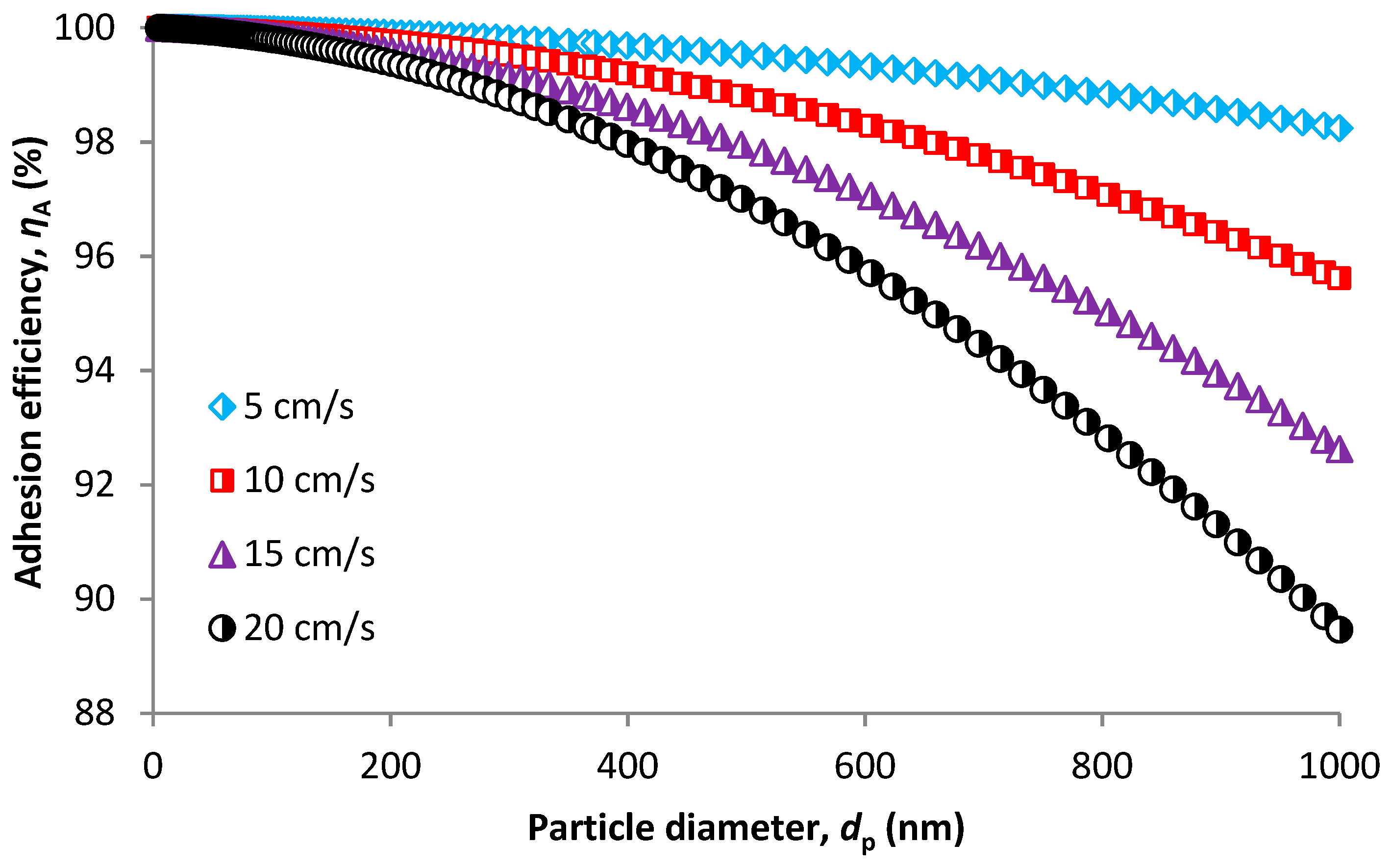
2.1.4. SCE Due to Adhesion
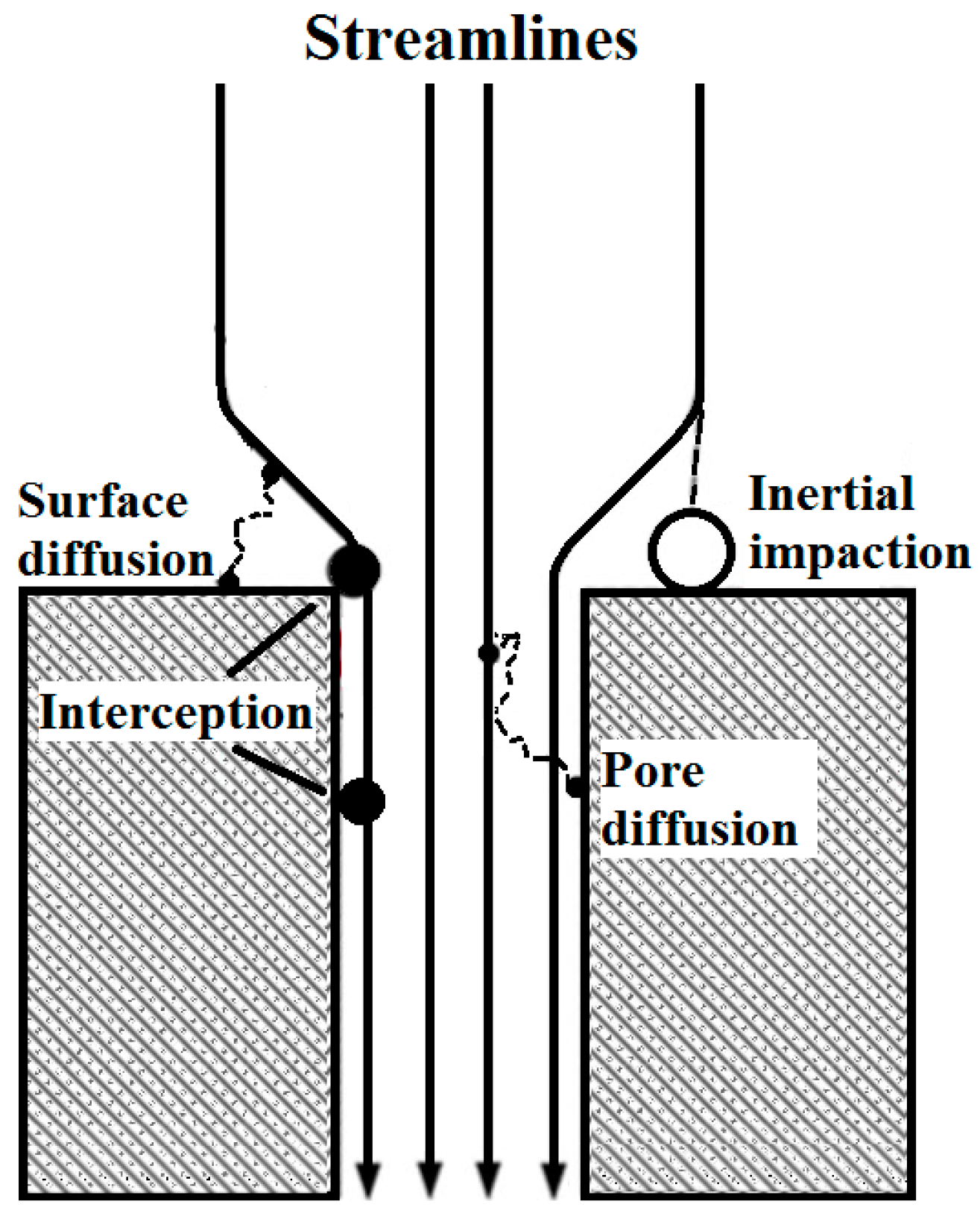
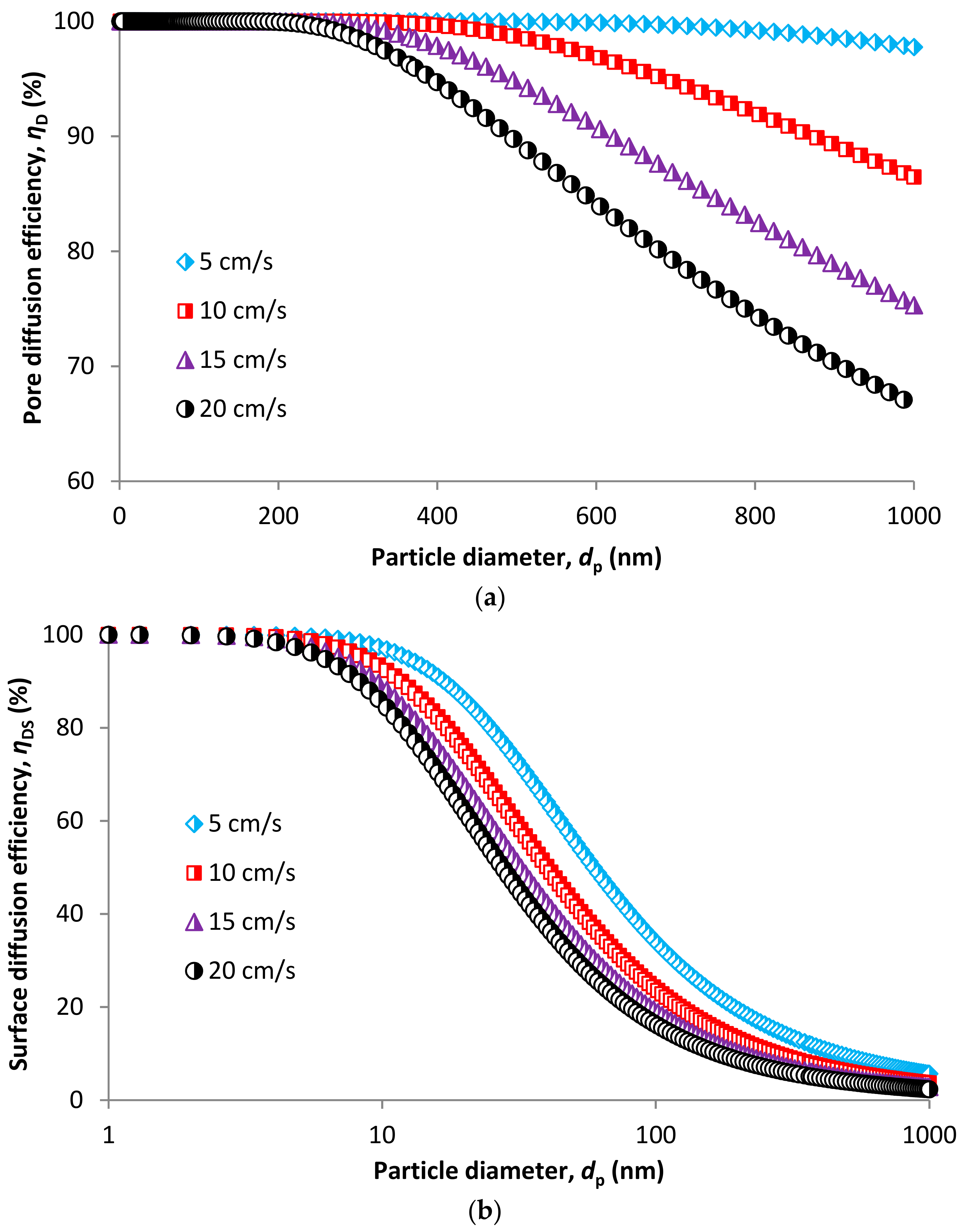
2.2. Efficiency Prediction of CPM
3. Materials and Methods
Hollow-Fiber Membranes
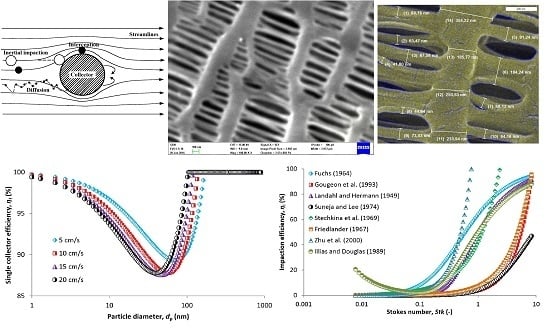
4. Results and Discussion
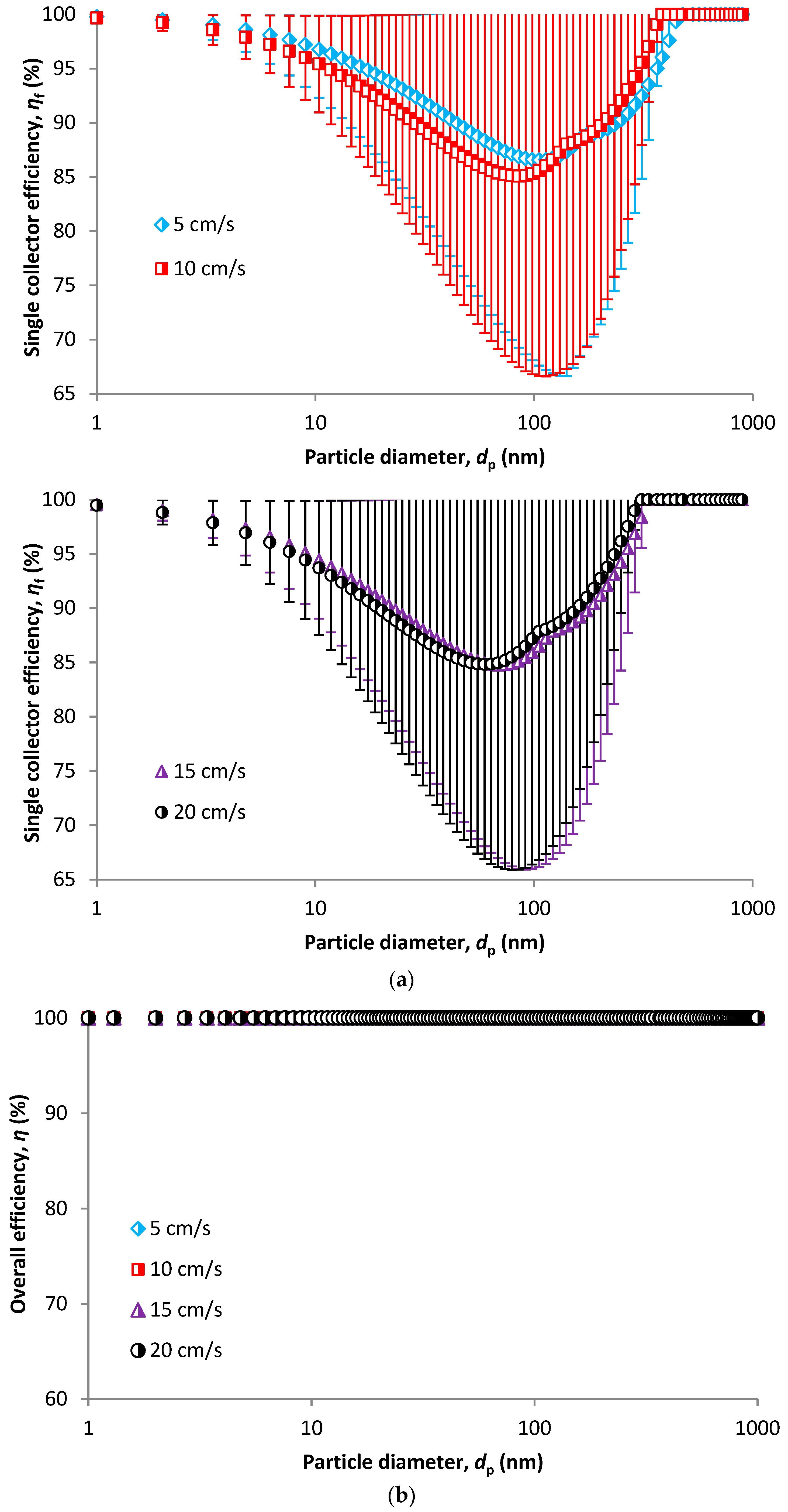
4.1. Fibrous Filters
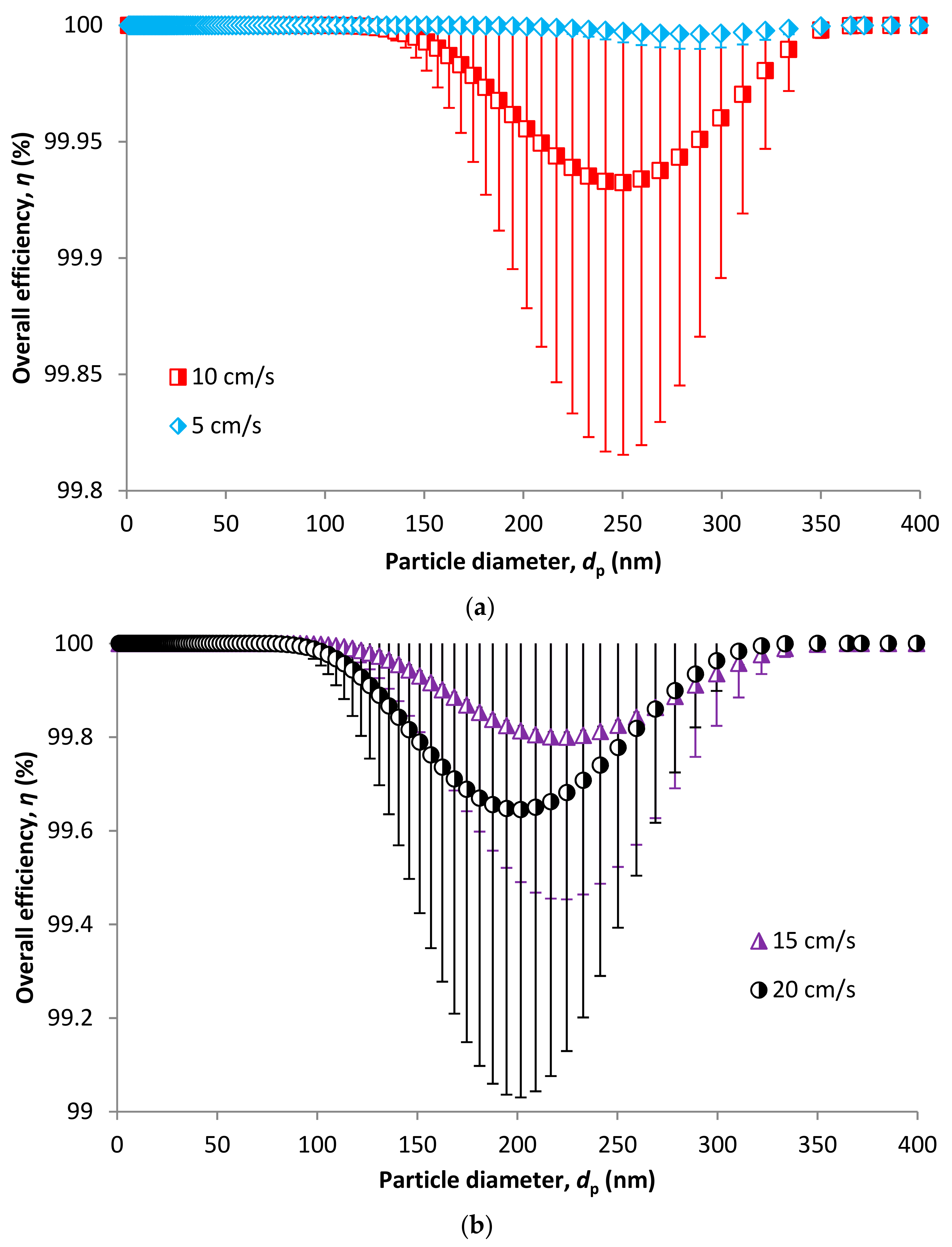
Overall SCE and overall Filtration Efficiency
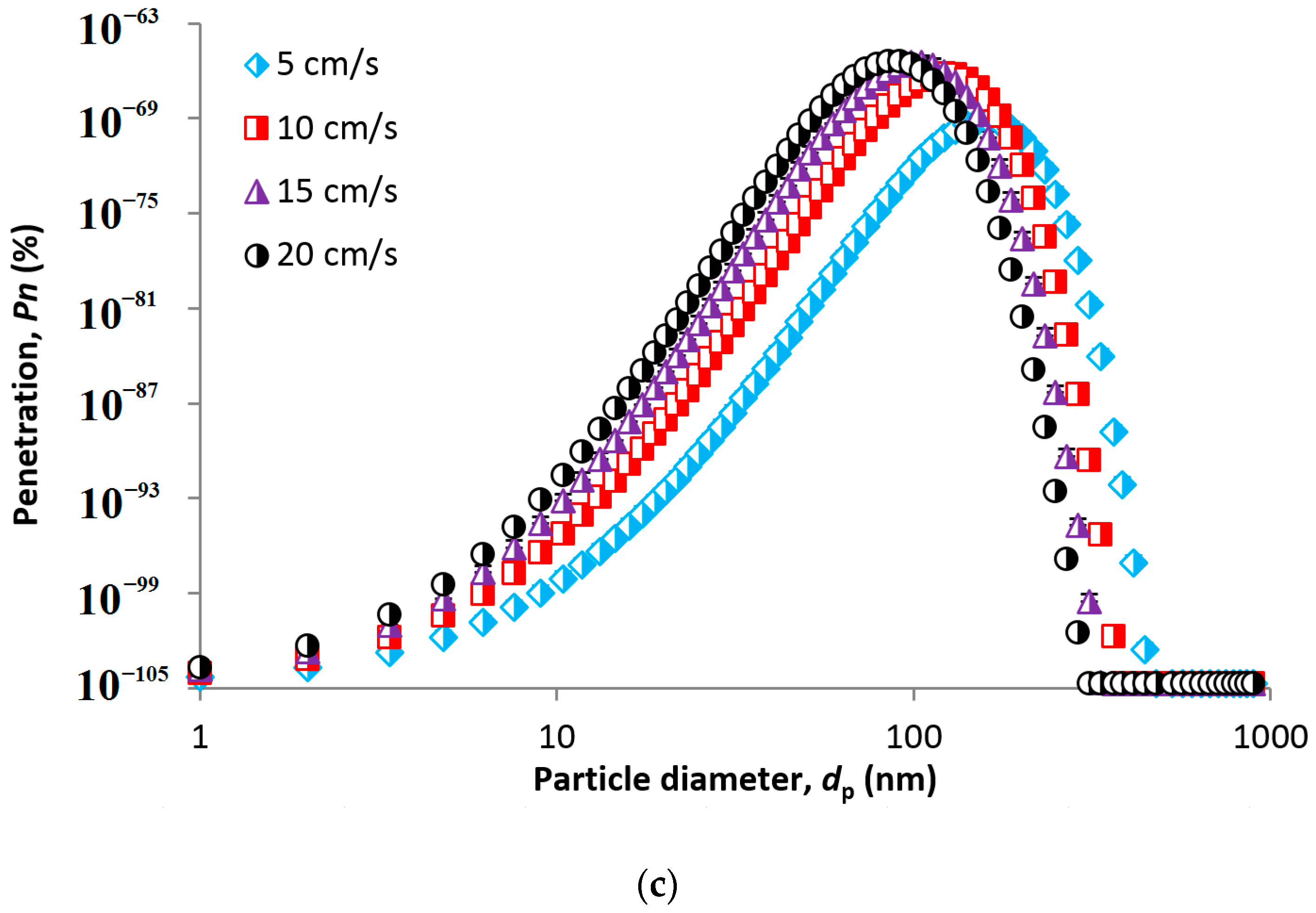
4.2. CPM
5. Conclusions
Supplementary Materials
Funding
Conflicts of Interest
References
- Givehchi, R.; Tan, Z. An Overview of Airborne Nanoparticle Filtration and Thermal Rebound Theory. Aerosol Air Qual. Res. 2014, 14, 45–63. [Google Scholar] [CrossRef]
- Givehchi, R.; Tan, Z. The effect of capillary force on airborne nanoparticle filtration. J. Aerosol Sci. 2015, 83, 12–24. [Google Scholar] [CrossRef]
- Darçın, M. Association between air quality and quality of life. Environ. Sci. Pollut. Res. 2014, 21, 1954–1959. [Google Scholar] [CrossRef] [PubMed]
- Luo, C.; Zhu, X.; Yao, C.; Hou, L.; Zhang, J.; Cao, J.; Wang, A. Short-term exposure to particulate air pollution and risk of myocardial infarction: a systematic review and meta-analysis. Environ. Sci. Pollut. Res. 2015, 22, 14651–14662. [Google Scholar] [CrossRef] [PubMed]
- Landlová, L.; Čupr, P.; Franců, J.; Klánová, J.; Lammel, G. Composition and effects of inhalable size fractions of atmospheric aerosols in the polluted atmosphere. Environ. Sci. Pollut. Res. 2014, 21, 6188–6204. [Google Scholar] [CrossRef] [PubMed]
- Bulejko, P.; Adamec, V.; Schüllerová, B.; Skeřil, R. Levels, sources, and health risk assessment of polycyclic aromatic hydrocarbons in Brno, Czech Republic: A 5-year study. Environ. Sci. Pollut. Res. 2016, 23, 20462–20473. [Google Scholar] [CrossRef] [PubMed]
- Jung, K.H.; Yan, B.; Chillrud, S.N.; Perera, F.P.; Whyatt, R.; Camann, D.; Kinney, P.L.; Miller, R.L. Assessment of Benzo(a)pyrene-equivalent Carcinogenicity and Mutagenicity of Residential Indoor versus Outdoor Polycyclic Aromatic Hydrocarbons Exposing Young Children in New York City. Int. J. Environ. Res. Public Health 2010, 7, 1889–1900. [Google Scholar] [CrossRef] [PubMed]
- Murr, L.E.; Soto, K.F.; Garza, K.M.; Guerrero, P.A.; Martinez, F.; Esquivel, E.V.; Ramirez, D.A.; Shi, Y.; Bang, J.J.; Venzor, J., 3rd. Combustion-Generated Nanoparticulates in the El Paso, TX, USA/Juarez, Mexico Metroplex: Their Comparative Characterization and Potential for Adverse Health Effects. Int. J. Environ. Res. Public Health 2006, 3, 48–66. [Google Scholar] [CrossRef] [PubMed]
- Pini, M.; Cedillo González, E.I.; Neri, P.; Siligardi, C.; Ferrari, A.M. Assessment of Environmental Performance of TiO2 Nanoparticles Coated Self-Cleaning Float Glass. Coatings 2017, 7, 8. [Google Scholar] [CrossRef]
- Kumar, P.; Fennell, P.; Robins, A. Comparison of the behaviour of manufactured and other airborne nanoparticles and the consequences for prioritising research and regulation activities. J. Nanopart. Res. 2010, 12, 1523–1530. [Google Scholar] [CrossRef] [PubMed]
- Shaffer, R.E.; Rengasamy, S. Respiratory protection against airborne nanoparticles: A review. J. Nanopart. Res. 2009, 11, 1661. [Google Scholar] [CrossRef]
- Vinh, N.; Kim, H.-M. Electrospinning Fabrication and Performance Evaluation of Polyacrylonitrile Nanofiber for Air Filter Applications. Appl. Sci. 2016, 6, 235. [Google Scholar] [CrossRef]
- Wu, C.-M.; Chou, M.-H.; Zeng, W.-Y. Piezoelectric Response of Aligned Electrospun Polyvinylidene Fluoride/Carbon Nanotube Nanofibrous Membranes. Nanomaterials 2018, 8, 420. [Google Scholar] [CrossRef] [PubMed]
- Ge, J.C.; Choi, N.J. Fabrication of Functional Polyurethane/Rare Earth Nanocomposite Membranes by Electrospinning and Its VOCs Absorption Capacity from Air. Nanomaterials 2017, 7, 60. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, H.; Tanioka, A. Functionality in Electrospun Nanofibrous Membranes Based on Fiber’s Size, Surface Area, and Molecular Orientation. Membranes 2011, 1, 249–264. [Google Scholar] [CrossRef] [PubMed]
- Ling, T.Y.; Wang, J.; Pui, D.Y.H. Measurement of filtration efficiency of Nuclepore filters challenged with polystyrene latex nanoparticles: Experiments and modeling. J. Nanopart. Res. 2011, 13, 5415–5424. [Google Scholar] [CrossRef]
- Chen, S.-C.; Wang, J.; Fissan, H.; Pui, D.Y.H. Use of Nuclepore filters for ambient and workplace nanoparticle exposure assessment—Spherical particles. Atmos. Environ. 2013, 77, 385–393. [Google Scholar] [CrossRef]
- Chen, S.-C.; Wang, J.; Fissan, H.; Pui, D.Y.H. Exposure assessment of nanosized engineered agglomerates and aggregates using Nuclepore filter. J. Nanopart. Res. 2013, 15, 1955. [Google Scholar] [CrossRef]
- Homaeigohar, S.; Elbahri, M. Nanocomposite Electrospun Nanofiber Membranes for Environmental Remediation. Materials 2014, 7, 1017–1045. [Google Scholar] [CrossRef] [PubMed]
- Lin, P.-H.; Horng, R.-Y.; Hsu, S.-F.; Chen, S.-S.; Ho, C.-H. A Feasibility Study of Ammonia Recovery from Coking Wastewater by Coupled Operation of a Membrane Contactor and Membrane Distillation. Int. J. Environ. Res. Public Health 2018, 15, 441. [Google Scholar] [CrossRef] [PubMed]
- Akhondi, E.; Zamani, F.; Tng, K.H.; Leslie, G.; Krantz, W.B.; Fane, A.G.; Chew, J.W. The Performance and Fouling Control of Submerged Hollow Fiber (HF) Systems: A Review. Appl. Sci. 2017, 7, 765. [Google Scholar] [CrossRef]
- Simone, S.; Galiano, F.; Faccini, M.; Boerrigter, M.E.; Chaumette, C.; Drioli, E.; Figoli, A. Preparation and Characterization of Polymeric-Hybrid PES/TiO2 Hollow Fiber Membranes for Potential Applications in Water Treatment. Fibers 2017, 5, 14. [Google Scholar] [CrossRef]
- Aluwi Shakir, N.A.; Wong, K.Y.; Noordin, M.Y.; Sudin, I. Development of a High Performance PES Ultrafiltration Hollow Fiber Membrane for Oily Wastewater Treatment Using Response Surface Methodology. Sustainability 2015, 7, 16465–16482. [Google Scholar] [CrossRef]
- Chong, K.C.; Lai, S.O.; Lau, W.J.; Thiam, H.S.; Ismail, A.F.; Roslan, R.A. Preparation, Characterization, and Performance Evaluation of Polysulfone Hollow Fiber Membrane with PEBAX or PDMS Coating for Oxygen Enhancement Process. Polymers 2018, 10, 126. [Google Scholar] [CrossRef]
- Brozova, T.; Raudensky, M. Determination of surface wettability of polymeric hollow fibres. J. Elastom. Plast. 2018. [Google Scholar] [CrossRef]
- Weiß, K.; Astrouski, I.; Reppich, M.; Raudenský, M. Polymeric Hollow Fiber Bundles as Immersed Heat Exchangers. Chem. Eng. Technol. 2018. [Google Scholar] [CrossRef]
- Bulejko, P.; Dohnal, M.; Pospíšil, J.; Svěrák, T. Air filtration performance of symmetric polypropylene hollow-fibre membranes for nanoparticle removal. Sep. Purif. Technol. 2018, 197, 122–128. [Google Scholar] [CrossRef]
- Feng, Y.; Wang, K.; Davies, C.; Wang, H. Carbon Nanotube/Alumina/Polyethersulfone Hybrid Hollow Fiber Membranes with Enhanced Mechanical and Anti-Fouling Properties. Nanomaterials 2015, 5, 1366–1378. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Wu, A.; Ciacchi, L.C.; Wei, G. Recent Advances in Nanoporous Membranes for Water Purification. Nanomaterials 2018, 8, 65. [Google Scholar] [CrossRef] [PubMed]
- Experton, J.; Wu, X.; Martin, C.R. From Ion Current to Electroosmotic Flow Rectification in Asymmetric Nanopore Membranes. Nanomaterials 2017, 7, 445. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.-Y.; Yong, W.F.; Yu, L.E.; Chung, T.-S. Design of high efficiency PVDF-PEG hollow fibers for air filtration of ultrafine particles. J. Membr. Sci. 2017, 535, 342–349. [Google Scholar] [CrossRef]
- Li, M.; Feng, Y.; Wang, K.; Yong, W.F.; Yu, L.; Chung, T.-S. Novel Hollow Fiber Air Filters for the Removal of Ultrafine Particles in PM2.5 with Repetitive Usage Capability. Environ. Sci. Technol. 2017, 51, 10041–10049. [Google Scholar] [CrossRef] [PubMed]
- Zena Membranes s.r.o. Brno, Czech Republic. Available online: www.zena-membranes.cz/ (accessed on 19 June 2018).
- Asmatulu, R.; Muppalla, H.; Veisi, Z.; Khan, W.; Asaduzzaman, A.; Nuraje, N. Study of Hydrophilic Electrospun Nanofiber Membranes for Filtration of Micro and Nanosize Suspended Particles. Membranes 2013, 3, 375–388. [Google Scholar] [CrossRef] [PubMed]
- Zander, N.; Gillan, M.; Sweetser, D. Recycled PET Nanofibers for Water Filtration Applications. Materials 2016, 9, 247. [Google Scholar] [CrossRef] [PubMed]
- Beatriz, S.-P.; Luis, N.; Leonor, C.; Laura, M.; Elena, M.; Yolanda, F.-N. Imaging Techniques and Scanning Electron Microscopy as Tools for Characterizing a Si-Based Material Used in Air Monitoring Applications. Materials 2016, 9, 109. [Google Scholar] [CrossRef] [PubMed]
- Balamurugan, R.; Sundarrajan, S.; Ramakrishna, S. Recent Trends in Nanofibrous Membranes and Their Suitability for Air and Water Filtrations. Membranes 2011, 1, 232–248. [Google Scholar] [CrossRef] [PubMed]
- Galka, N.; Saxena, A. High efficiency air filtration: The growing impact of membranes. Filtration 2009, 46, 22–25. [Google Scholar] [CrossRef]
- Cyrs, W.D.; Boysen, D.A.; Casuccio, G.; Lersch, T.; Peters, T.M. Nanoparticle collection efficiency of capillary pore membrane filters. J. Aerosol Sci. 2010, 41, 655–664. [Google Scholar] [CrossRef]
- Spurny, K.R.; Gentry, J.W. Aerosol fractionization by graded nuclepore filters. A review. Powder Technol. 1979, 24, 129–142. [Google Scholar] [CrossRef]
- Shaw, G.E. Nuclepore filters as diffusion screens: Effect of barrel-shaped pore distortions. J. Aerosol Sci. 1985, 16, 307–313. [Google Scholar] [CrossRef]
- Gentry, J.W.; Spurny, K.R. Measurements of collection efficiency of nuclepore filters for asbestos fibers. J. Colloid Interface Sci. 1978, 65, 174–180. [Google Scholar] [CrossRef]
- Romo-Kröger, C.M. A qualitative study of atmospheric aerosols and particles deposited on flat membrane surfaces by microscopy and other techniques. Powder Technol. 2006, 161, 235–241. [Google Scholar] [CrossRef]
- Wang, C.; Otani, Y. Removal of Nanoparticles from Gas Streams by Fibrous Filters: A Review. Ind. Eng. Chem. Res. 2012, 52, 5–17. [Google Scholar] [CrossRef]
- Brown, R.C. Air Filtration: An Integrated Approach to the Theory and Applications of Fibrous Filters; Elsevier Science & Technology Books: New York, NY, USA, 1993; ISBN 978-0-08-041274-0. [Google Scholar]
- Maddineni, A.K.; Das, D.; Damodaran, R.M. Air-borne particle capture by fibrous filter media under collision effect: A CFD-based approach. Sep. Purif. Technol. 2018, 193, 1–10. [Google Scholar] [CrossRef]
- Kasper, G.; Schollmeier, S.; Meyer, J.; Hoferer, J. The collection efficiency of a particle-loaded single filter fiber. J. Aerosol Sci. 2009, 40, 993–1009. [Google Scholar] [CrossRef]
- Wang, J.; Chen, D.R.; Pui, D.Y.H. Modeling of filtration efficiency of nanoparticles in standard filter media. J. Nanopart. Res. 2007, 9, 109–115. [Google Scholar] [CrossRef]
- Kirsch, A.A.; Fuchs, N.A. Studies on Fibrous Aerosol Filters—III Diffusional Deposition of Aerosols in Fibrous Filters. Ann. Occup. Hyg. 1968, 299–304. [Google Scholar] [CrossRef]
- Stechkina, I.; Kirsch, A.; Fuchs, N. Studies on Fibrous Aerosol Filters—IV Calculation of Aerosol Deposition in Model Filters in the Range of Maximum Penetration. Ann. Occup. Hyg. 1969, 12, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Pich, J. The filtration theory of highly dispersed aerosols. Staub Reinhalt. Luft 1965, 5, 16–23. [Google Scholar] [CrossRef]
- Lee, K.W.; Liu, B.Y.H. Theoretical Study of Aerosol Filtration by Fibrous Filters. Aerosol Sci. Technol. 1982, 1, 147–161. [Google Scholar] [CrossRef]
- Kirsch, A.A.; Stechkina, I.B. The Theory of Aerosol Filtration with Fibrous Filters. In Fundamentals of Aerosol Science; Shaw, D.T., Ed.; Wiley: New York, NY, USA, 1978. [Google Scholar]
- Liu, B.Y.H.; Rubow, K.L. Efficiency, pressure drop and figure of merit of high efficiency fibrous and membrane filter media. In Proceedings of the 5th World Filtration Congress, Nice, France, 5–8 June 1990; p. 112. [Google Scholar]
- Payet, S.; Boulaud, D.; Madelaine, G.; Renoux, A. Penetration and pressure drop of a HEPA filter during loading with submicron liquid particles. J. Aerosol Sci. 1992, 23, 723–735. [Google Scholar] [CrossRef]
- Kuwabara, S. The Forces experienced by Randomly Distributed Parallel Circular Cylinders or Spheres in a Viscous Flow at Small Reynolds Numbers. J. Phys. Soc. Jpn. 1959, 14, 527–532. [Google Scholar] [CrossRef]
- Bałazy, A.; Podgórski, A. Deposition efficiency of fractal-like aggregates in fibrous filters calculated using Brownian dynamics method. J. Colloid Interface Sci. 2007, 311, 323–337. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y. Indoor Air Quality Engineering, 1st ed.; CRC Press: Boca Raton, FL, USA, 2005; ISBN 978-1-56670-674-2. [Google Scholar]
- Lamb, H. Hydrodynamics; University Press: Oxford, UK, 1916. [Google Scholar]
- Langmuir, I. OSRD Report No. 865; Office of Scientific Research and Development: Washington, DC, USA, 1942.
- Stechkina, I.B.; Fuchs, N.A.F. Studies on Fibrous Aerosol Filters—I. Calculation of Diffusional Deposition of Aerosols in Fibrous Filters. Ann. Occup. Hyg. 1966, 59–64. [Google Scholar] [CrossRef]
- Lee, K.W.; Gieseke, J.A. Note on the approximation of interceptional collection efficiencies. J. Aerosol Sci. 1980, 11, 335–341. [Google Scholar] [CrossRef]
- Pich, J. The effectiveness of the barrier effect in fiber filters at small Knudsen numbers. Staub Reinhalt. Luft 1966, 26, 1–4. [Google Scholar]
- Landahl, H.D.; Herrmann, R.G. Sampling of liquid aerosols by wires, cylinders, and slides, and the efficiency of impaction of the droplets. J. Colloid Sci. 1949, 4, 103–136. [Google Scholar] [CrossRef]
- Saleh, A.M.; Hosseini, S.A.; Tafreshi, H.V.; Pourdeyhimi, B. 3-D microscale simulation of dust-loading in thin flat-sheet filters: A comparison with 1-D macroscale simulations. Chem. Eng. Sci. 2013, 99, 284–291. [Google Scholar] [CrossRef]
- Fuchs, N.A. The Mechanics of Aerosols, 1st ed.; Pergamon Press: London, UK, 1964; ISBN 978-0-486-66055-4. [Google Scholar]
- Gougeon, R.; Boulaud, D.; Renoux, A. Comparison of theory and experiment in stationary filtration. J. Aerosol Sci. 1993, 24, S273–S274. [Google Scholar] [CrossRef]
- Friedlander, S.K. Aerosol Filtration by Fibrous Filters. In Biochemical and Biological Engineering Science; Academic Press: London, UK, 1967; pp. 49–67. ISBN 978-0-12-103601-0. [Google Scholar]
- Zhu, C.; Lin, C.-H.; Cheung, C.S. Inertial impaction-dominated fibrous filtration with rectangular or cylindrical fibers. Powder Technol. 2000, 112, 149–162. [Google Scholar] [CrossRef]
- Suneja, S.K.; Lee, C.H. Aerosol filtration by fibrous filters at intermediate Reynolds numbers (≤ 100). Atmos. Environ. 1974, 8, 1081–1094. [Google Scholar] [CrossRef]
- Ilias, S.; Douglas, P.L. Inertial impaction of aerosol particles on cylinders at intermediate and high reynolds numbers. Chem. Eng. Sci. 1989, 44, 81–99. [Google Scholar] [CrossRef]
- Ptak, T.; Jaroszczyk, T. Theoretical-Experimental Aerosol Filtration Model for Fibrous Filters at Intermediate Reynolds Numbers. In Proceedings of the 5th World Filtration Congress, Nice, France, 5–8 June 1990; pp. 566–572. [Google Scholar]
- Chambers, F.W.; Al-Sarkhi, A.; Yao, S. Velocity distribution effects in air filter testing. Part. Sci. Technol. 2001, 19, 1–21. [Google Scholar] [CrossRef]
- Pich, J. Impaction of aerosol particles in the neighbourhood of a circular hole. Collect. Czechoslov. Chem. Commun. 1964, 29, 2223–2227. [Google Scholar] [CrossRef]
- Spurny, K.; Lodge, J.P.; Frank, E.R.; Sheesley, D.C. Aerosol filtration by means of Nuclepore filters: Structural and filtration properties. Environ. Sci. Technol. 1969, 3, 453–464. [Google Scholar] [CrossRef]
- Manton, M.J. Brownian diffusion of aerosols to the face of a nuclepore filter. Atmos. Environ. 1979, 13, 525–531. [Google Scholar] [CrossRef]
- Lu, Y.; Shah, K.; Xu, J. Synthesis, Morphologies and Building Applications of Nanostructured Polymers. Polymers 2017, 9, 506. [Google Scholar] [CrossRef]
- Leung, W.W.-F.; Hung, C.-H.; Yuen, P.-T. Effect of face velocity, nanofiber packing density and thickness on filtration performance of filters with nanofibers coated on a substrate. Sep. Purif. Technol. 2010, 71, 30–37. [Google Scholar] [CrossRef]
- Wang, Q.; Bai, Y.; Xie, J.; Jiang, Q.; Qiu, Y. Synthesis and filtration properties of polyimide nanofiber membrane/carbon woven fabric sandwiched hot gas filters for removal of PM 2.5 particles. Powder Technol. 2016, 292, 54–63. [Google Scholar] [CrossRef]
- Wang, J.; Tronville, P. Toward standardized test methods to determine the effectiveness of filtration media against airborne nanoparticles. J. Nanopart. Res. 2014, 16. [Google Scholar] [CrossRef]
- Rajagopalan, R.; Tien, C. Trajectory analysis of deep-bed filtration with the sphere-in-cell porous media model. AIChE J. 1976, 22, 523–533. [Google Scholar] [CrossRef]
- Zhong, W.; Pan, N. Aerosol Filtration by Fibrous Filters: A Statistical Mechanics Approach. Text. Res. J. 2007, 77, 284–289. [Google Scholar] [CrossRef]
- Israelachvili, J.N. Intermolecular and Surface Forces, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2011; ISBN 978-0-12-375182-9. [Google Scholar]

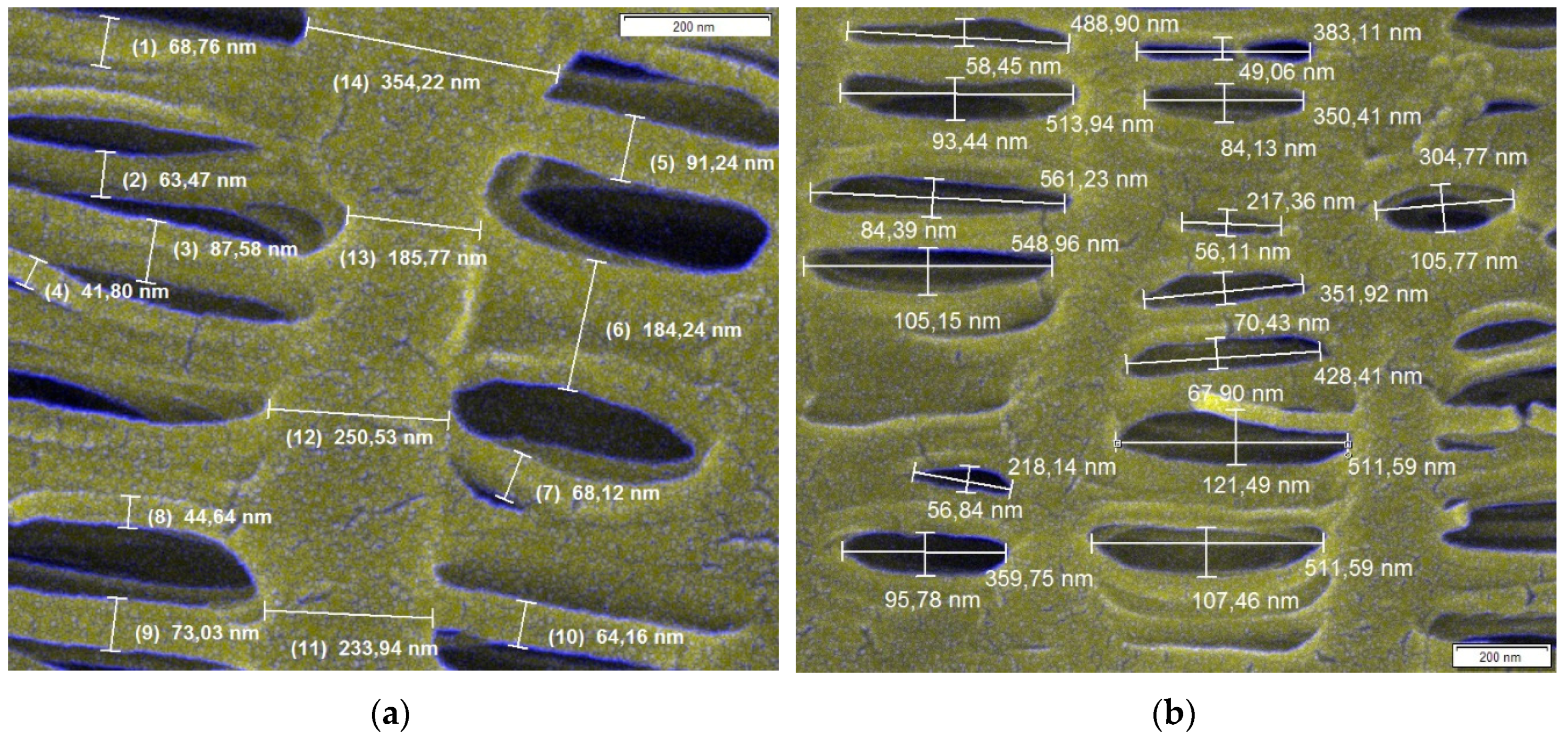

| Fiber wall thickness, Z (µm) | 36 |
| Average pore size, do (nm) | 205 ± 157 |
| Average collector diameter, df (nm) | 90 ± 83 |
| Solidity, α (%) | 48 |
| Porosity, ε (%) | 52 |
| Temperature, T (K) | 296.15 |
| Air density, ρ (kg m−3) | 1.21 |
| Air dynamic viscosity, µ (Pa s) | 1.83 × 10−5 |
| Particle density, ρp (kg m−3) | 1060 |
| Mean free path of air molecules, λ (nm) | 67.3 |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bulejko, P. Numerical Comparison of Prediction Models for Aerosol Filtration Efficiency Applied on a Hollow-Fiber Membrane Pore Structure. Nanomaterials 2018, 8, 447. https://doi.org/10.3390/nano8060447
Bulejko P. Numerical Comparison of Prediction Models for Aerosol Filtration Efficiency Applied on a Hollow-Fiber Membrane Pore Structure. Nanomaterials. 2018; 8(6):447. https://doi.org/10.3390/nano8060447
Chicago/Turabian StyleBulejko, Pavel. 2018. "Numerical Comparison of Prediction Models for Aerosol Filtration Efficiency Applied on a Hollow-Fiber Membrane Pore Structure" Nanomaterials 8, no. 6: 447. https://doi.org/10.3390/nano8060447
APA StyleBulejko, P. (2018). Numerical Comparison of Prediction Models for Aerosol Filtration Efficiency Applied on a Hollow-Fiber Membrane Pore Structure. Nanomaterials, 8(6), 447. https://doi.org/10.3390/nano8060447