Enhanced Conductivity of Composite Membranes Based on Sulfonated Poly(Ether Ether Ketone) (SPEEK) with Zeolitic Imidazolate Frameworks (ZIFs)
Abstract
1. Introduction
2. Materials and Methods
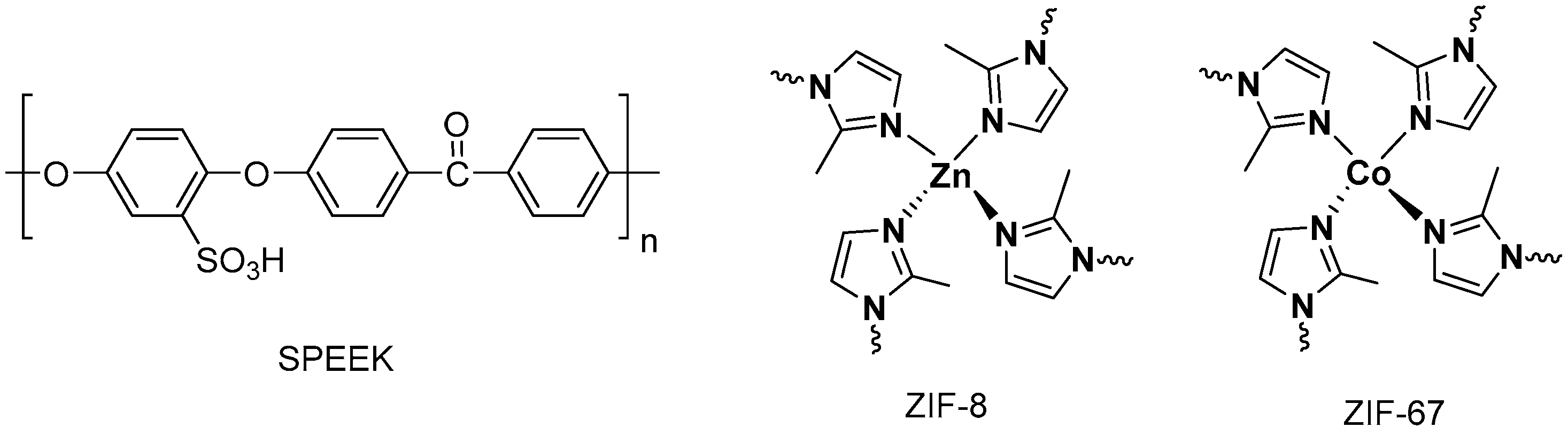
2.1. Materials
2.2. Experimental Procedures
2.2.1. Synthesis of ZIF-8
2.2.2. Synthesis of ZIF-67
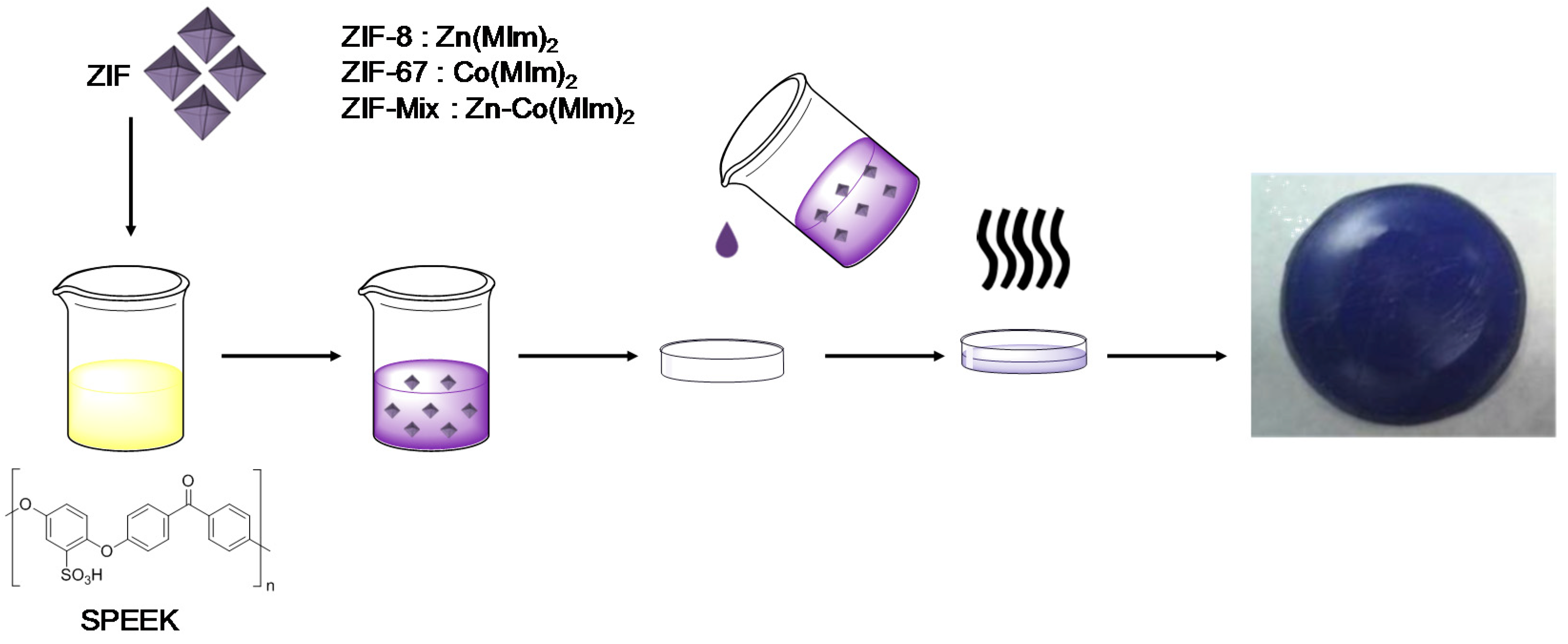
2.2.3. Membrane Preparation
2.3. Characterization
3. Results and Discussion
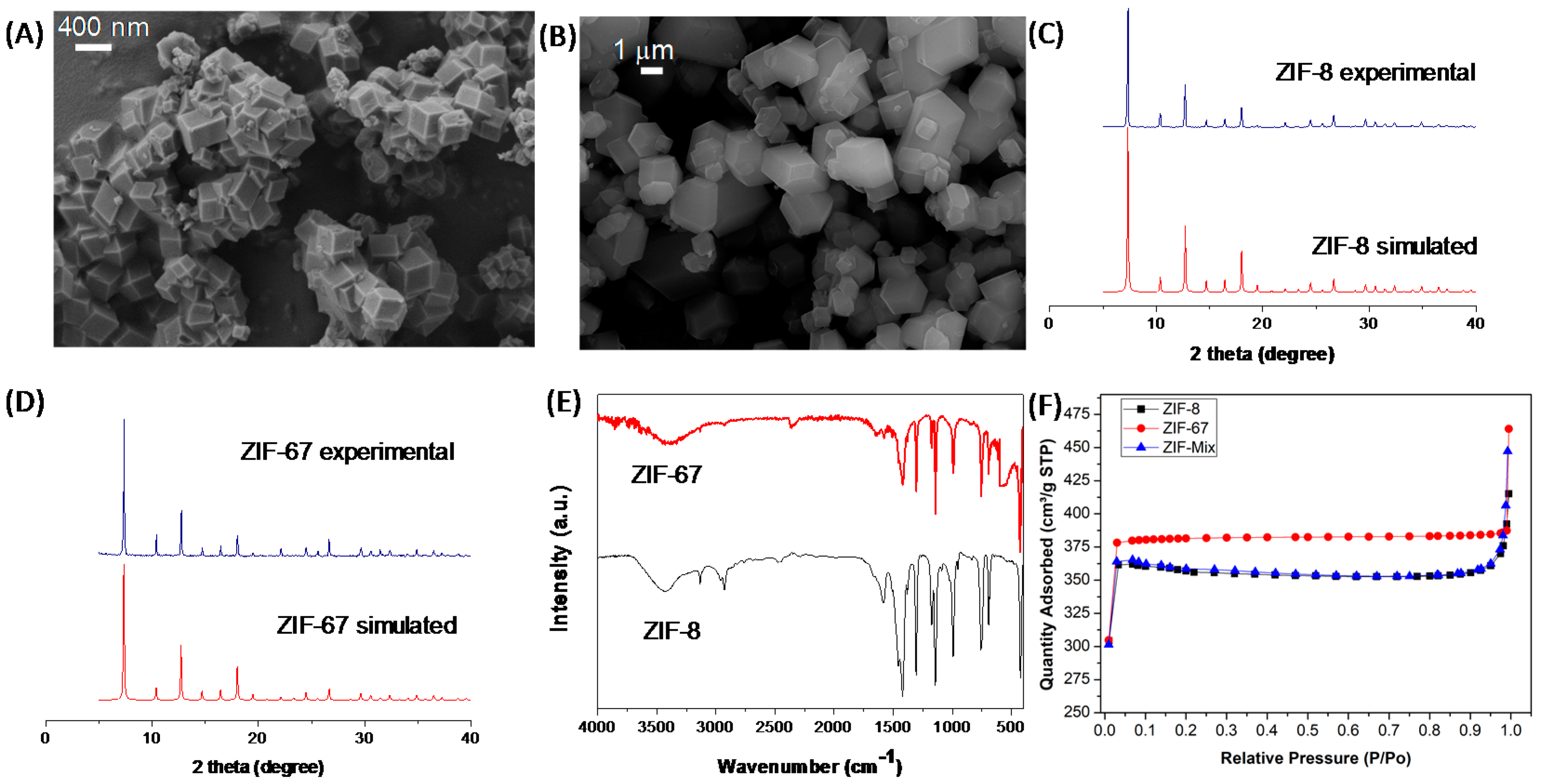
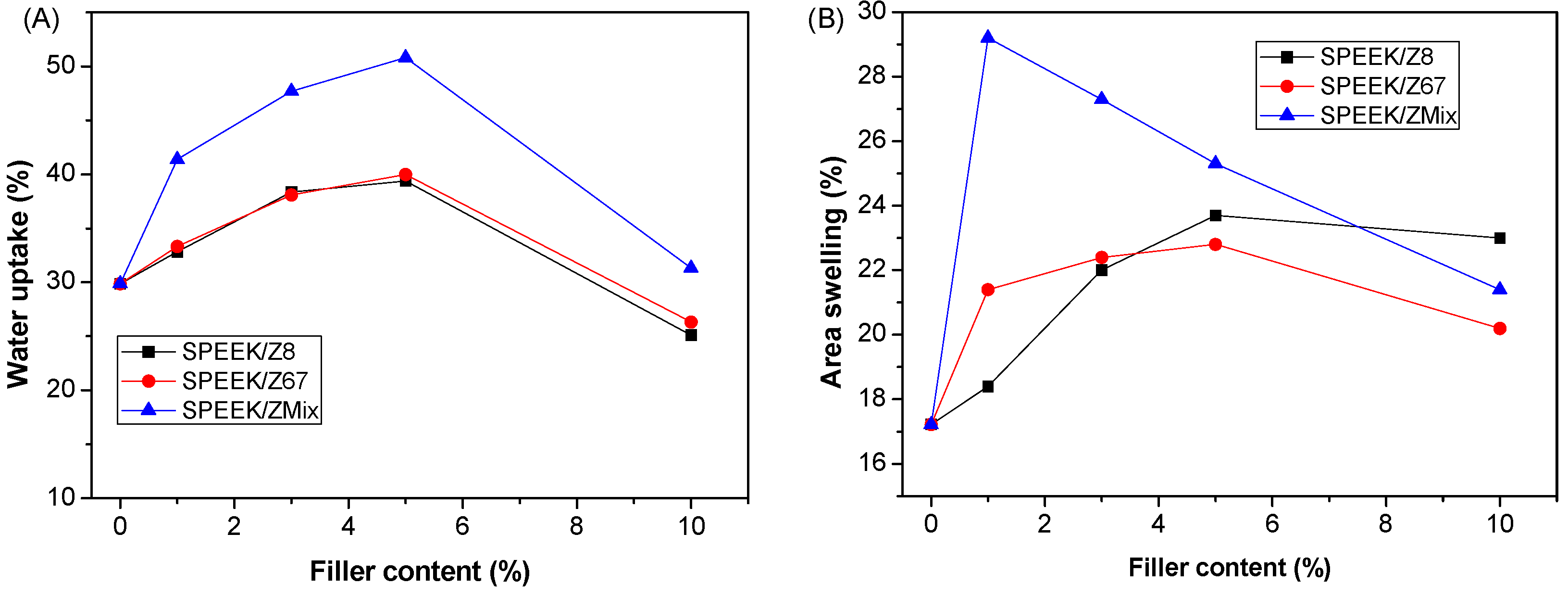
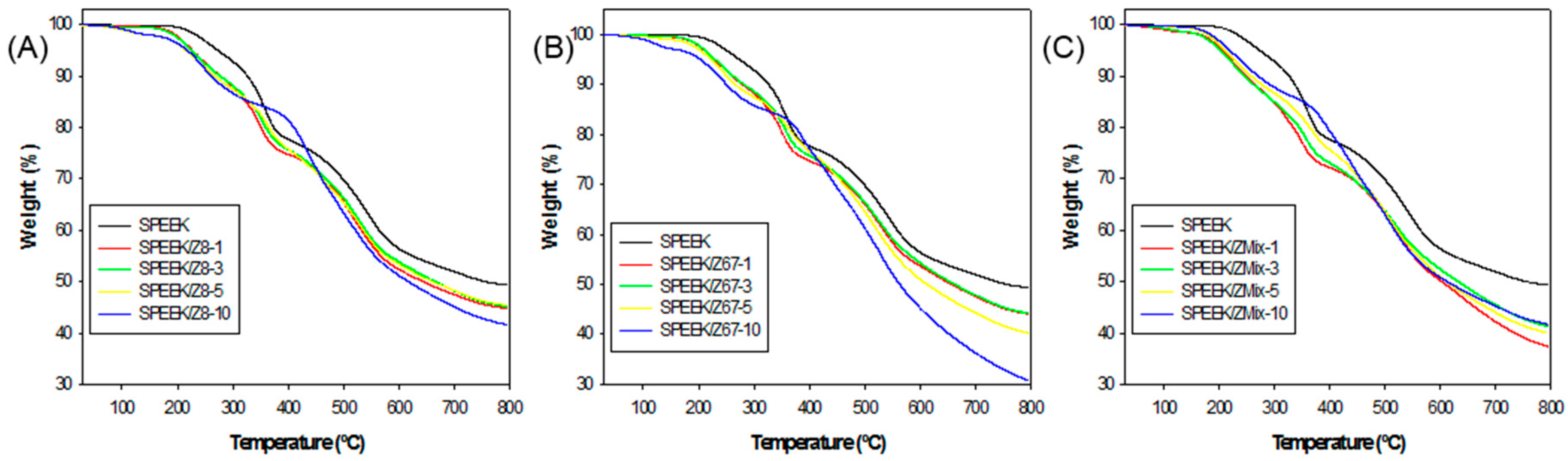
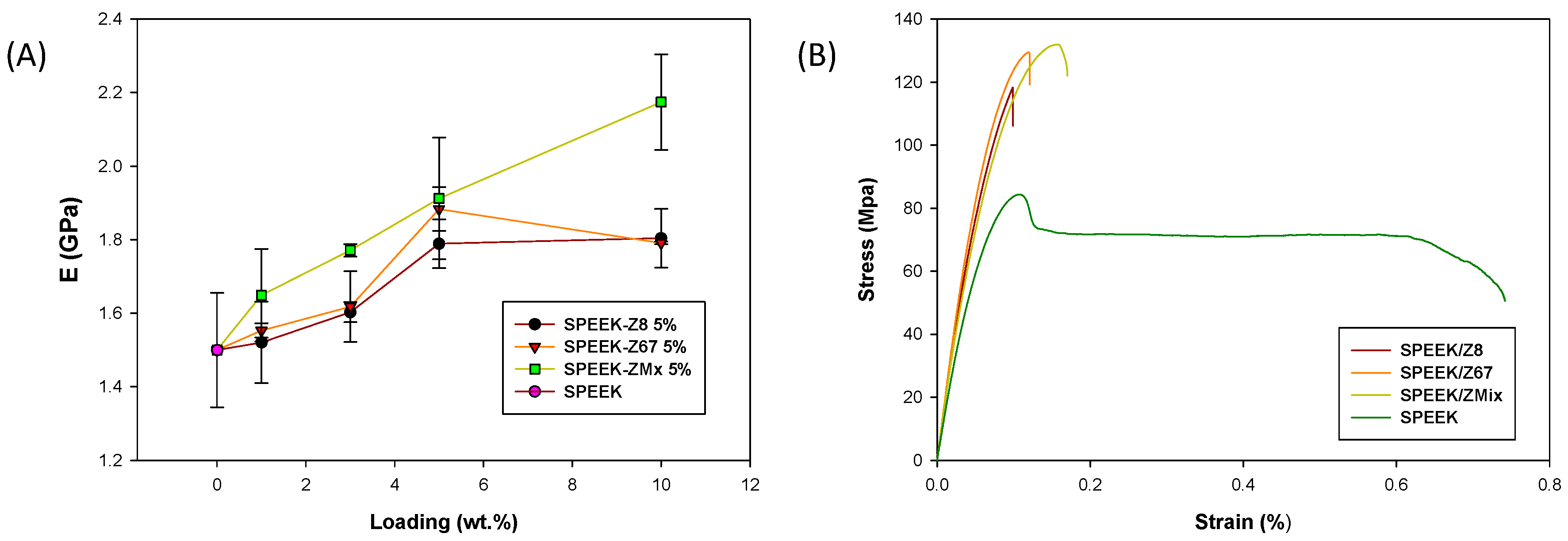
3.1. Characterization of Mixed Matrix Membranes
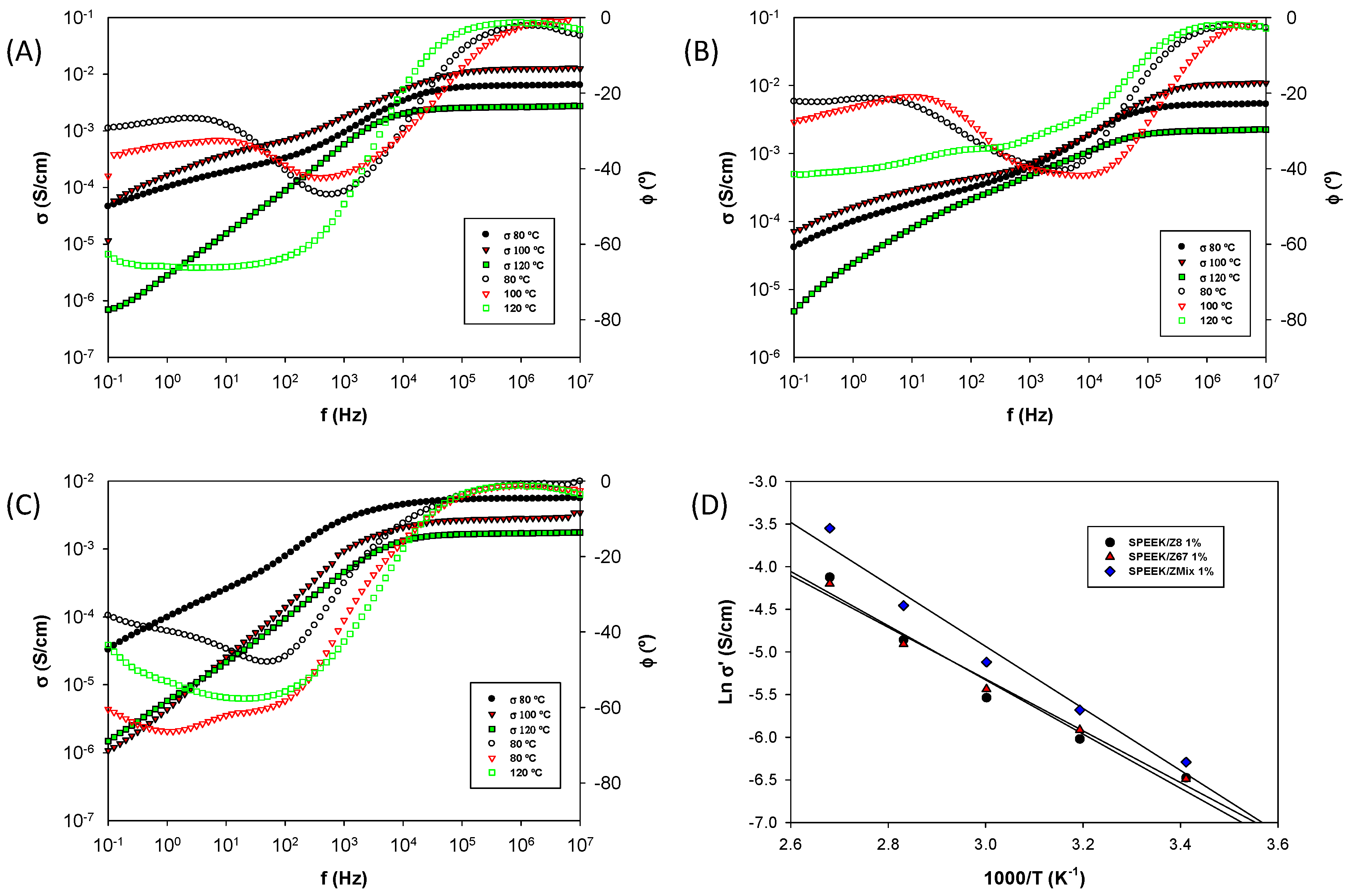
3.2. Proton Conduction of Mixed Matrix Membranes
3.3. Determination of Diffusion Coefficient and Ion Concentration
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Veziroglu, A.; Macario, R. Fuel cell vehicles: State of the art with economic and environmental concerns. Int. J. Hydrogen Energy 2011, 36, 25–43. [Google Scholar] [CrossRef]
- Granovskii, M.; Dincer, I.; Rosen, M.A. Environmental and economic aspects of hydrogen production and utilization in fuel cell vehicles. J. Power Sources 2006, 157, 411–421. [Google Scholar] [CrossRef]
- Kraytsberg, A.; Ein-Eli, Y. Review of advanced materials for proton exchange membrane fuel cells. Energy Fuels 2014, 28, 7303–7330. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, K.S.; Mishler, J.; Cho, S.C.; Adroher, X.C. A review of polymer electrolyte membrane fuel cells: Technology, applications, and needs on fundamental research. Appl. Energy 2011, 88, 981–1007. [Google Scholar] [CrossRef]
- Álvarez, G.; Alcaide, F.; Cabot, P.L.; Lázaro, M.J.; Pastor, E.; Solla-Gullóne, J. Electrochemical performance of low temperature PEMFC with surface tailored carbon nanofibers as catalyst support. Int. J. Hydrogen Energy 2012, 37, 393–404. [Google Scholar] [CrossRef]
- Li, Q.F.; He, R.H.; Jensen, J.O.; Bjerrum, N.J. Approaches and recent development of polymer electrolyte membranes for fuel cells operating above 100 °C. Chem. Mater. 2003, 15, 4896–4915. [Google Scholar] [CrossRef]
- Rasheed, R.K.A.; Liao, Q.; Zhang, C.; Chan, S.H. A review on modelling of high temperature proton exchange membrane fuel cells (HT-PEIVIFCs). Int. J. Hydrogen Energy 2017, 42, 3142–3165. [Google Scholar] [CrossRef]
- Quartarone, E.; Angioni, S.; Mustarelli, P. Polymer and composite membranes for proton-conducting, high-temperature fuel cells: A critical review. Materials 2017, 10, 687. [Google Scholar] [CrossRef]
- Steele, B.C.; Heinzel, A. Materials for fuel-cell technologies. Nature 2001, 414, 345–352. [Google Scholar] [CrossRef]
- Mauritz, K.A.; Moore, R.B. State of understanding of Nafion. Chem. Rev. 2004, 104, 4535–4585. [Google Scholar] [CrossRef]
- Casciola, M.; Alberti, G.; Sganappa, M.; Narducci, R. On the decay of Nafion proton conductivity at high temperature and relative humidity. J. Power Sources 2006, 162, 141–145. [Google Scholar] [CrossRef]
- Dupuis, A.-C. Proton exchange membranes for fuel cells operated at medium temperatures: Materials and experimental techniques. Prog. Mater. Sci. 2011, 56, 289–327. [Google Scholar] [CrossRef]
- Li, Q.; He, R.; Gao, J.-A.; Jensen, J.O.; Bjerrum, N.J. The CO poisoning effect in PEMFCs operational at temperatures up to 200 °C. J. Electrochem. Soc. 2003, 150, A1599–A1605. [Google Scholar] [CrossRef]
- Sun, B.; Song, H.; Qiu, X.; Zhu, W. New anhydrous proton exchange membrane for intermediate temperature proton exchange membrane fuel cells. ChemPhysChem 2011, 12, 1196–1201. [Google Scholar] [CrossRef] [PubMed]
- Zaidi, S.M.J.; Mikhailenko, S.D.; Robertson, G.P.; Guiver, M.D.; Kaliaguine, S. Proton conducting composite membranes from polyether ether ketone and heteropolyacids for fuel cell applications. J. Membr. Sci. 2000, 173, 17–34. [Google Scholar] [CrossRef]
- Iulianelli, A.; Basile, A. Sulfonated PEEK-based polymers in PEMFC and DMFC applications: A review. Int. J. Hydrogen Energy 2012, 37, 15241–15255. [Google Scholar] [CrossRef]
- Nag, S.; Castro, M.; Choudhary, V.; Feller, J.F. Sulfonated poly(ether ether ketone) [SPEEK] nanocomposites based on hybrid nanocarbons for the detection and discrimination of some lung cancer VOC biomarkers. J. Mater. Chem. B 2017, 5, 348–359. [Google Scholar] [CrossRef]
- Neburchilov, V.; Martin, J.; Wang, H.; Zhang, J. A review of polymer electrolyte membranes for direct methanol fuel cells. J. Power Sources 2007, 169, 221–238. [Google Scholar] [CrossRef]
- Paddison, S.J. Proton conduction mechanisms at low degrees of hydration in sulfonic acid–based polymer electrolyte membranes. Annu. Rev. Mater. Res. 2003, 33, 289–319. [Google Scholar] [CrossRef]
- Dechnik, J.; Gascon, J.; Doonan, C.J.; Janiak, C.; Sumby, C.J. Mixed-matrix membranes. Angew. Chem. Int. Ed. 2017, 56, 9292–9310. [Google Scholar] [CrossRef]
- Reyes-Rodriguez, J.L.; Escorihuela, J.; García-Bernabé, A.; Giménez, E.; Solorza-Feria, O.; Compañ, V. Proton conducting electrospun sulfonated polyether ether ketone graphene oxide composite membranes. RSC Adv. 2017, 7, 53481–53491. [Google Scholar] [CrossRef]
- Zhang, Z.; Han, S.; Wang, C.; Li, J.; Xu, G. Single-Walled Carbon Nanohorns for Energy Applications. Nanomaterials 2015, 5, 1732–1755. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Wei, H.; Lu, Y.; Wei, S.; Wujcik, E.K.; Guo, Z. Multifunctional carbon nanostructures for advanced energy storage applications. Nanomaterials 2015, 5, 755–777. [Google Scholar] [CrossRef] [PubMed]
- Du, L.; Yan, G.; He, G.; Wu, X.; Hu, Z.; Wang, Y. SPEEK proton exchange membranes modified with silica sulfuric acid nanoparticles. Int. J. Hydrogen Energy 2012, 37, 11853–11861. [Google Scholar] [CrossRef]
- Venkatesana, P.N.; Dharmalingam, S. Effect of zeolite on SPEEK/zeolite hybrid membrane as electrolyte for microbial fuel cell applications. RSC Adv. 2015, 5, 84004–84013. [Google Scholar] [CrossRef]
- Fuentes, I.; Andrio, A.; García-Bernabé, A.; Escorihuela, J.; Viñas, C.; Teixidor, F.; Compañ, V. Structural and dielectric properties of cobaltacarborane composite polybenzimidazole membranes as solid polymer electrolytes at high temperature. Phys. Chem. Chem. Phys. 2018, 20, 10173–10184. [Google Scholar] [CrossRef] [PubMed]
- Phang, W.J.; Jo, H.; Lee, W.R.; Song, J.H.; Yoo, K.; Kim, B.; Hong, C.S. Superprotonic conductivity of a UiO-66 framework functionalized with sulfonic acid groups by facile postsynthetic oxidation. Angew. Chem. Int. Ed. 2015, 54, 5142–5146. [Google Scholar] [CrossRef]
- Ramaswamy, P.; Wong, N.E.; Gelfand, B.S.; Shimizu, G.K.H. A water stable magnesium MOF that conducts protons over 10−2 S cm−1. J. Am. Chem. Soc. 2015, 137, 7640–7643. [Google Scholar] [CrossRef]
- Escorihuela, J.; Narducci, R.; Compañ, V.; Costantino, F. Proton conductivity of mixed membranes with metal-organic frameworks in proton exchange membranes for fuel cell applications. Adv. Mater. Interfaces 2019, 6. [Google Scholar] [CrossRef]
- Furukawa, H.; Cordova, K.E.; O’Keeffe, M.; Yaghi, O.M. The chemistry and applications of metal-organic frameworks. Science 2013, 341, 974. [Google Scholar] [CrossRef]
- James, S.L. Metal-organic frameworks. Chem. Soc. Rev. 2003, 32, 276–288. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Xie, L.-H.; Wang, X.; Liu, X.-M.; Li, J.; Li, J.-R. Applications of metal-organic frameworks for green energy and environment: New advances in adsorptive gas separation, storage and removal. Green Energy Environ. 2018, 3, 191–228. [Google Scholar] [CrossRef]
- Sumida, K.; Rogow, D.L.; Mason, J.A.; McDonald, T.M.; Bloch, E.D.; Herm, Z.R.; Bae, T.-H.; Long, J.R. Carbon dioxide capture in metal-organic frameworks. Chem. Rev. 2012, 112, 724–781. [Google Scholar] [CrossRef] [PubMed]
- Yoon, M.; Srirambalaji, R.; Kim, K. Homochiral metal-organic frameworks for asymmetric heterogeneous catalysis. Chem. Rev. 2012, 112, 1196–1231. [Google Scholar] [CrossRef] [PubMed]
- Liu, J.; Chen, L.; Cui, H.; Zhang, J.; Zhang, L.; Su, C.-Y. Applications of metal-organic frameworks in heterogeneous supramolecular catalysis. Chem. Soc. Rev. 2014, 43, 6011–6061. [Google Scholar] [CrossRef] [PubMed]
- Kreno, L.E.; Leong, K.; Farha, O.K.; Allendorf, M.; Van Duyne, R.P.; Hupp, J.T. Metal-organic framework materials as chemical sensors. Chem. Rev. 2012, 112, 1105–1125. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Deibert, B.K.; Li, J. Luminescent metal-organic frameworks for chemical sensing and explosive detection. Chem. Soc. Rev. 2014, 43, 5815–5840. [Google Scholar] [CrossRef]
- Horcajada, P.; Gref, R.; Baati, T.; Allan, P.K.; Maurin, G.; Couvreur, P.; Férey, G.; Morris, R.E.; Serre, C. Metal–organic frameworks in biomedicine. Chem. Rev. 2012, 112, 1232–1268. [Google Scholar] [CrossRef]
- Wang, L.; Zheng, M.; Xie, Z. Nanoscale metal-organic frameworks for drug delivery: A conventional platform with new promise. J. Mater. Chem. B 2018, 6, 707–717. [Google Scholar] [CrossRef]
- Xu, M.; Yuan, S.; Chen, X.-Y.; Chang, Y.-J.; Day, G.; Gu, Z.-Y.; Zhou, H.-C. Two-dimensional metal-organic framework nanosheets as an enzyme inhibitor: Modulation of the α-Chymotrypsin activity. J. Am. Chem. Soc. 2017, 139, 8312–8319. [Google Scholar] [CrossRef]
- Sun, H.; Tang, B.; Wu, P. Rational design of S-UiO-66@GO hybrid nanosheets for proton exchange membranes with significantly enhanced transport performance. ACS Appl. Mater. Interfaces 2017, 9, 26077–26087. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; He, G.; Zhao, Y.; Cao, Y.; Wu, H.; Li, Y.; Jiang, Z. Enhanced proton conductivity of proton exchange membranes by incorporating sulfonated metal-organic frameworks. J. Power Sources 2014, 262, 372–379. [Google Scholar] [CrossRef]
- Zhang, B.; Cao, Y.; Li, Z.; Wu, H.; Yin, Y.; Cao, L.; He, X.; Jiang, Z. Proton exchange nanohybrid membranes with high phosphotungstic acid loading within metal-organic frameworks for PEMFC applications. Electrochim. Acta 2017, 240, 186–194. [Google Scholar] [CrossRef]
- Park, K.S.; Ni, Z.; Cote, A.P.; Choi, J.Y.; Huang, R.; Uribe-Romo, F.J.; Chae, H.K.; O’Keeffe, M.; Yaghi, O.M. Exceptional chemical and thermal stability of zeolitic imidazolate frameworks. Proc. Natl. Acad. Sci. USA 2006, 103, 10186–10191. [Google Scholar] [CrossRef] [PubMed]
- Phan, A.; Doonan, C.J.; Uribe-Romo, F.J.; Knobler, C.B.; O’Keeffe, M.; Yagh, O.M. Synthesis, structure, and carbon dioxide capture properties of zeolitic imidazolate frameworks. Acc. Chem. Res. 2010, 43, 58–67. [Google Scholar] [CrossRef] [PubMed]
- Sun, H.; Tang, B.; Wu, P. Two-Dimensional zeolitic imidazolate framework/carbon nanotube hybrid networks modified proton exchange membranes for improving transport properties. ACS Appl. Mater. Interfaces 2017, 9, 35075–35085. [Google Scholar] [CrossRef] [PubMed]
- McCarthy, M.C.; Varela-Guerrero, V.; Barnett, G.V.; Jeong, H.-K. Synthesis of zeolitic imidazolate framework films and membranes with controlled microstructures. Langmuir 2010, 26, 14636–14641. [Google Scholar] [CrossRef]
- Qian, J.; Sun, F.; Qin, L. Hydrothermal synthesis of zeolitic imidazolate framework-67 (ZIF-67) nanocrystals. Mater. Lett. 2012, 82, 220–223. [Google Scholar] [CrossRef]
- Wu, B.; Pan, J.F.; Ge, L.; Wu, L.; Wang, H.T.; Xu, T.W. Oriented MOF-polymer composite nanofiber membranes for high proton conductivity at high temperature and anhydrous condition. Sci. Rep. 2014, 4, 4334. [Google Scholar] [CrossRef]
- Panchariya, D.K.; Rai, R.K.; Kumar, E.A.; Singh, S.K. Core–shell zeolitic imidazolate frameworks for enhanced hydrogen storage. ACS Omega 2018, 3, 167–175. [Google Scholar] [CrossRef]
- Rangel-Cárdenas, A.L.; Koper, G.J.M. Transport in Proton Exchange Membranes for Fuel Cell Applications—A Systematic Non-Equilibrium Approach. Materials 2017, 10, 576. [Google Scholar] [CrossRef]
- Escorihuela, J.; Sahuquillo, O.; García-Bernabé, A.; Giménez, E.; Compañ, V. phosphoric acid doped polybenzimidazole (PBI)/zeolitic imidazolate framework composite membranes with significantly enhanced proton conductivity under low humidity conditions. Nanomaterials 2018, 8, 775. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Shen, X.H.; Cao, Y.; Li, Z.; Jiang, Z.Y. Composite proton conductive membranes composed of sulfonated poly(ether ether ketone) and phosphotungstic acid-loaded imidazole microcapsules as acid reservoirs. J. Membr. Sci. 2014, 451, 74–84. [Google Scholar] [CrossRef]
- Nie, L.L.; Wang, J.T.; Xu, T.; Dong, H.; Wu, H.; Jiang, Z.Y. Enhancing proton conduction under low humidity by incorporating core-shell polymeric phosphonic acid submicrospheres into sulfonated poly(ether ether ketone) membrane. J. Power Sources 2012, 213, 1–9. [Google Scholar] [CrossRef]
- Xing, P.; Robertson, G.P.; Guiver, M.D.; Mikhailenko, S.D.; Wang, K.; Kaliaguine, S. Synthesis and characterization of sulfonated poly(ether ether ketone) for proton exchange membranes. J. Membr. Sci. 2004, 229, 95–106. [Google Scholar] [CrossRef]
- Ru, C.; Li, Z.; Zhao, C.; Duan, Y.; Zhuang, Z.; Bu, F.; Na, H. Enhanced proton conductivity of sulfonated hybrid poly(aryleneether ketone) membranes by incorporating an amino–sulfobifunctionalized metal−organic framework for direct methanol fuel cells. ACS Appl. Mater. Interfaces 2018, 10, 7963–7973. [Google Scholar] [CrossRef]
- Lee, C.H.; Park, H.B.; Lee, Y.M.; Lee, R.D. Importance of proton conductivity measurement in polymer electrolyte membrane for fuel cell application. Ind. Eng. Chem. Res. 2005, 44, 7617–7626. [Google Scholar] [CrossRef]
- Lânyi, Š. Polarization in ionic crystals with incompletely blocking electrodes. J. Phys. Chem. Solids 1975, 36, 775–781. [Google Scholar] [CrossRef]
- Ogihara, N.; Itou, Y.; Sasaki, T.; Takeuchi, Y. Impedance spectroscopy characterization of porous electrodes under different electrode thickness using a symmetric cell for high-performance lithium-ion batteries. J. Phys. Chem. C 2015, 119, 4612–4619. [Google Scholar] [CrossRef]
- Vega, J.; Andrio, A.; Lemus, A.A.; del Castillo, L.F.; Compañ, V. Conductivity study of zeolitic imidazolate frameworks, tetrabutylammonium hydroxide doped with zeolitic imidazolate frameworks, and mixed matrix membranes of polyetherimide/tetrabutylammonium hydroxide doped with zeolitic imidazolate frameworks for proton conducting applications. Electrochim. Acta 2017, 258, 153–166. [Google Scholar]
- Zhang, J.; Bai, H.-J.; Ren, Q.; Luo, H.-B.; Ren, X.-M.; Tian, Z.-F.; Lu, S. Extra water- and acid-stable MOF-801 with high proton conductivity and its composite membrane for proton-exchange membrane. ACS Appl. Mater. Interfaces 2018, 10, 28656–28663. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Zheng, S.; Xue, H.; Pang, H. Metal-organic frameworks/graphene-based materials: Preparations and applications. Adv. Funct. Mater. 2018, 28, 1804950. [Google Scholar] [CrossRef]
- Lux, F.J. Models proposed to explain the electrical conductivity of mixtures made of conductive and insulating materials. Mater. Sci. 1993, 28, 285–301. [Google Scholar] [CrossRef]
- Nan, C.W.; Smith, D.M. Ac electrical properties of composite solid electrolytes. Mater. Sci. Eng. B 1991, 10, 99–106. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, C.N.; Fan, F.; Sangoro, J.R.; Berman, M.B.; Greenbaum, S.G.; Zawodzinski, T.A.; Sokolov, A.P. Examination of methods to determine free-ion diffusivity and number density from analysis of electrode polarization. Phys. Rev. E 2013, 87, 042308. [Google Scholar] [CrossRef] [PubMed]
- Klein, R.J.; Zhang, S.; Dou, S.; Jones, B.H.; Colby, R.H.; Runt, J. Modeling electrode polarization in dielectric spectroscopy: Ion mobility and mobile ion concentration of single-ion polymer electrolytes. J. Chem. Phys. 2006, 124, 144903. [Google Scholar] [CrossRef] [PubMed]
- MacDonald, J.R. Theory of AC space-charge polarization effects in photoconductors, semiconductors, and electrolytes. Phys. Rev. 1953, 92, 4–17. [Google Scholar] [CrossRef]
- Sørensen, T.S.; Compañ, V.; Diaz-Calleja, R. Complex permittivity of a film of poly [4-(acryloxy)phenyl-(4-chlorophenyl)methanone] containing free ion impurities and the separation of the contributions from interfacial polarization, Maxwell-Wagner-Sillars effects and dielectric relaxations of the polymer chains. J. Chem. Soc. Faraday Trans. 1996, 92, 1947–1957. [Google Scholar]
- Sørensen, T.S.; Compañ, V. Complex permittivity of a conducting, dielectric layer containing arbitrary binary Nernst–Planck electrolytes with applications to polymer films and cellulose acetate membranes. J. Chem. Soc. Faraday Trans. 1995, 91, 4235–4250. [Google Scholar] [CrossRef]
- Serghei, A.; Tress, M.; Sangoro, J.R.; Kremer, F. Electrode polarization and charge transport at solid interfaces. Phys. Rev. 2009, 80, 184301. [Google Scholar] [CrossRef]
- Bandara, T.M.W.J.; Dissanayake, M.A.K.L.; Albinsson, I.; Mellander, B.-E. Mobile charge carrier concentration and mobility of a polymer electrolyte containing PEO and Pr4N+ I− using electrical and dielectric measurements. Solid State Ionics 2011, 189, 63–68. [Google Scholar] [CrossRef]
- Coelho, R. Sur la relaxation d’une charge d’espace. Revue Phys. Appl. 1983, 18, 137. [Google Scholar] [CrossRef]
- Schütt, H.J.; Gerdes, E. Space-charge relaxation in ionicly conducting oxide glasses. I. Model and frequency response. J. Non-Cryst. Solids 1992, 144, 1–13. [Google Scholar] [CrossRef]
- Altava, B.; Compañ, V.; Andrio, A.; del Castillo, L.F.; Mollá, S.; Burguete, M.I.; García-Verdugo, E.; Luis, S.V. Conductive films based on composite polymers containing ionic liquids absorbed on crosslinked polymeric ionic-like liquids (SILLPs). Polymer 2015, 72, 69–81. [Google Scholar] [CrossRef]
- García-Bernabé, A.; Rivera, A.; Granados, A.; Luis, S.V.; Compañ, V. Ionic transport on composite polymers containing covalently attached and absorbed ionic liquid fragments. Electrochim. Acta 2016, 213, 887–897. [Google Scholar] [CrossRef]
- Cole, K.S.; Cole, R.H. Dispersion and Absorption in Dielectrics I. Alternating Current Characteristics. J. Chem. Phys. 1941, 9, 341–351. [Google Scholar]
- Sangoro, J.R.; Iacob, C.; Agapov, A.L.; Wang, Y.; Berdzinski, S.; Rexhausen, H.; Strehmel, V.; Friedrich, C.; Sokolov, A.P.; Kremer, P. Decoupling of ionic conductivity from structural dynamics in polymerized ionic liquids. Soft Matter 2014, 10, 3536–3540. [Google Scholar] [CrossRef] [PubMed]
- Krause, C.; Sangoro, J.R.; Iacob, C.; Kremer, F. Charge transport and dipolar relaxations in imidazolium-based ionic liquids. J. Phys. Chem. B 2010, 114, 382–386. [Google Scholar] [CrossRef]
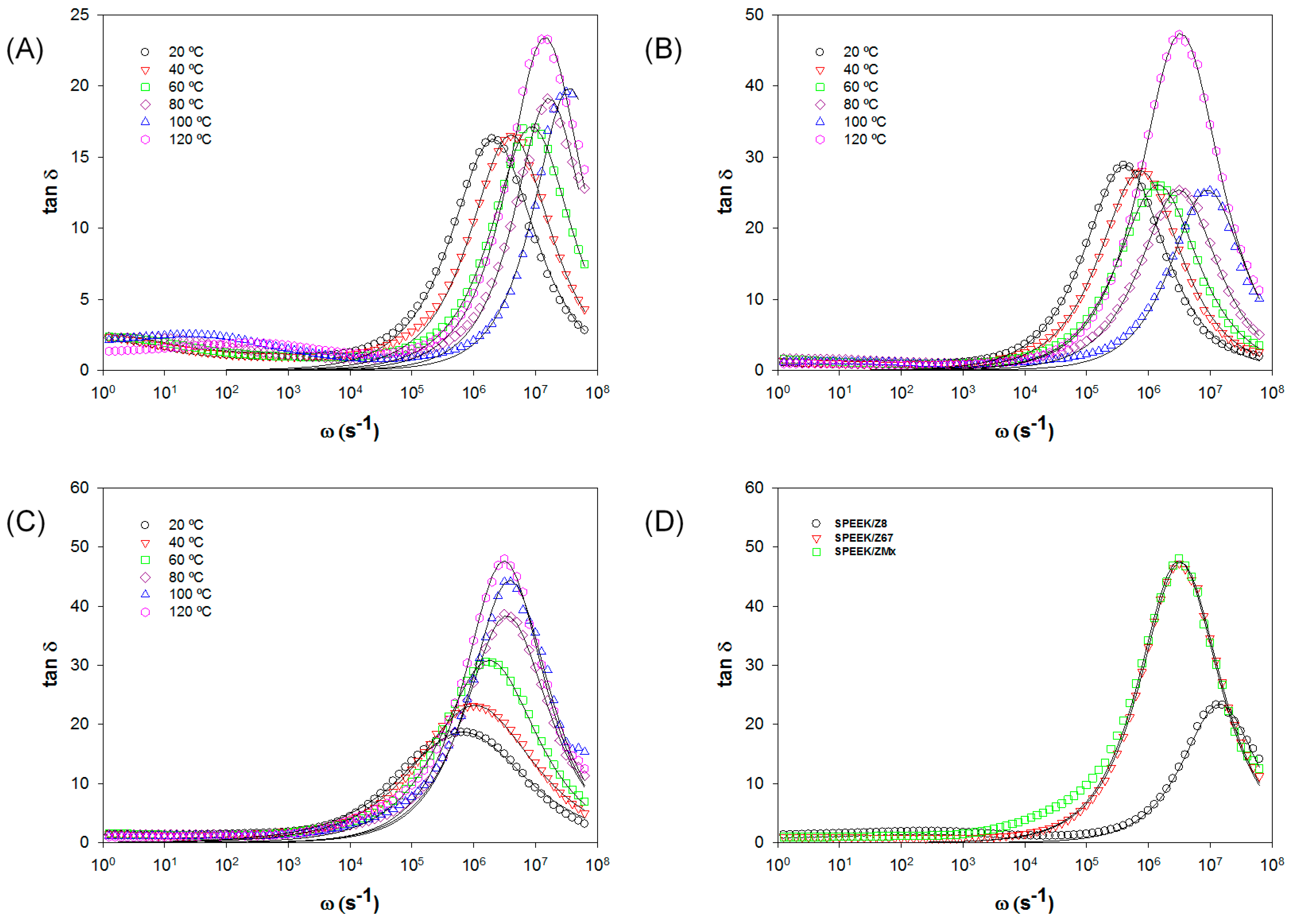
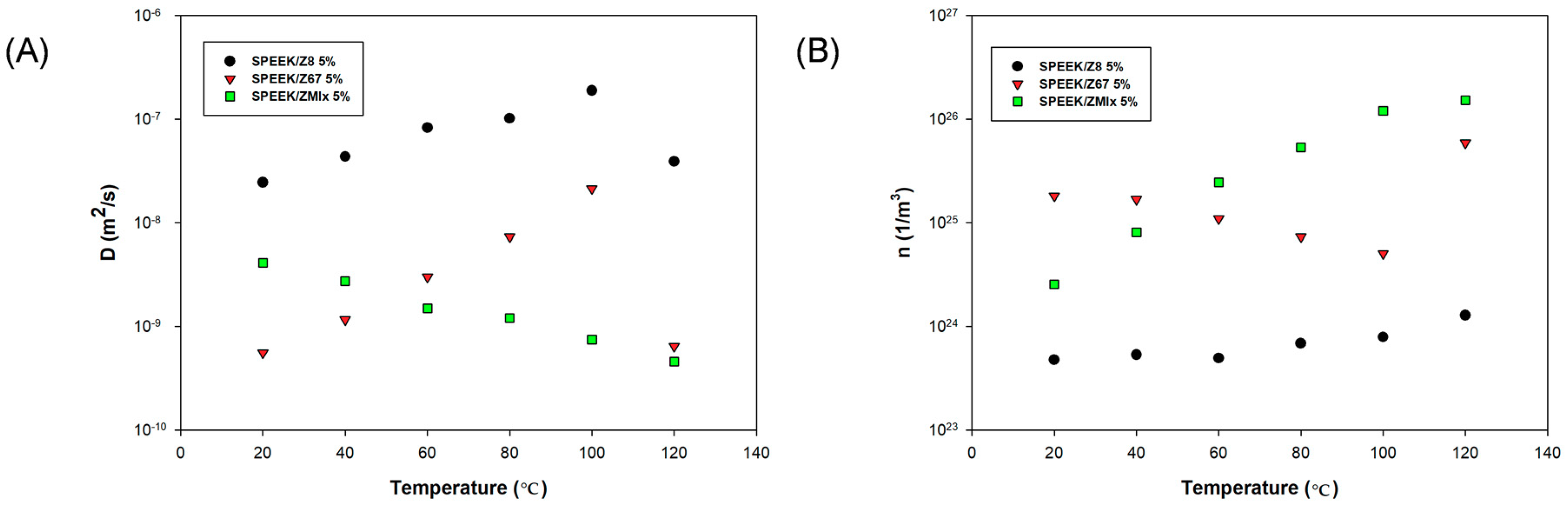
| Membrane | T = 40 °C | T = 80 °C | T = 120 °C | ||||||
|---|---|---|---|---|---|---|---|---|---|
| M | τm × 107 (s) | D × 107 (cm2/s) | M | τm × 107 (s) | D × 107 (cm2/s) | M | τm × 107 (s) | D × 107 (cm2/s) | |
| SPEEK/Z8 | 790 | 2.00 | 80.1 | 12,580 | 0.35 | 1.81 | 19,000 | 1.30 | 0.21 |
| SPEEK/Z67 | 990 | 3.0 | 76.5 | 3420 | 1.00 | 19.2 | 5200 | 2.50 | 3.33 |
| SPEEK/ZMix | 1580 | 7.00 | 5.16 | 11,460 | 0.8 | 0.6 | 18,800 | 1.18 | 0.22 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barjola, A.; Escorihuela, J.; Andrio, A.; Giménez, E.; Compañ, V. Enhanced Conductivity of Composite Membranes Based on Sulfonated Poly(Ether Ether Ketone) (SPEEK) with Zeolitic Imidazolate Frameworks (ZIFs). Nanomaterials 2018, 8, 1042. https://doi.org/10.3390/nano8121042
Barjola A, Escorihuela J, Andrio A, Giménez E, Compañ V. Enhanced Conductivity of Composite Membranes Based on Sulfonated Poly(Ether Ether Ketone) (SPEEK) with Zeolitic Imidazolate Frameworks (ZIFs). Nanomaterials. 2018; 8(12):1042. https://doi.org/10.3390/nano8121042
Chicago/Turabian StyleBarjola, Arturo, Jorge Escorihuela, Andreu Andrio, Enrique Giménez, and Vicente Compañ. 2018. "Enhanced Conductivity of Composite Membranes Based on Sulfonated Poly(Ether Ether Ketone) (SPEEK) with Zeolitic Imidazolate Frameworks (ZIFs)" Nanomaterials 8, no. 12: 1042. https://doi.org/10.3390/nano8121042
APA StyleBarjola, A., Escorihuela, J., Andrio, A., Giménez, E., & Compañ, V. (2018). Enhanced Conductivity of Composite Membranes Based on Sulfonated Poly(Ether Ether Ketone) (SPEEK) with Zeolitic Imidazolate Frameworks (ZIFs). Nanomaterials, 8(12), 1042. https://doi.org/10.3390/nano8121042