Refractory Ultra-Broadband Perfect Absorber from Visible to Near-Infrared
Abstract
1. Introduction
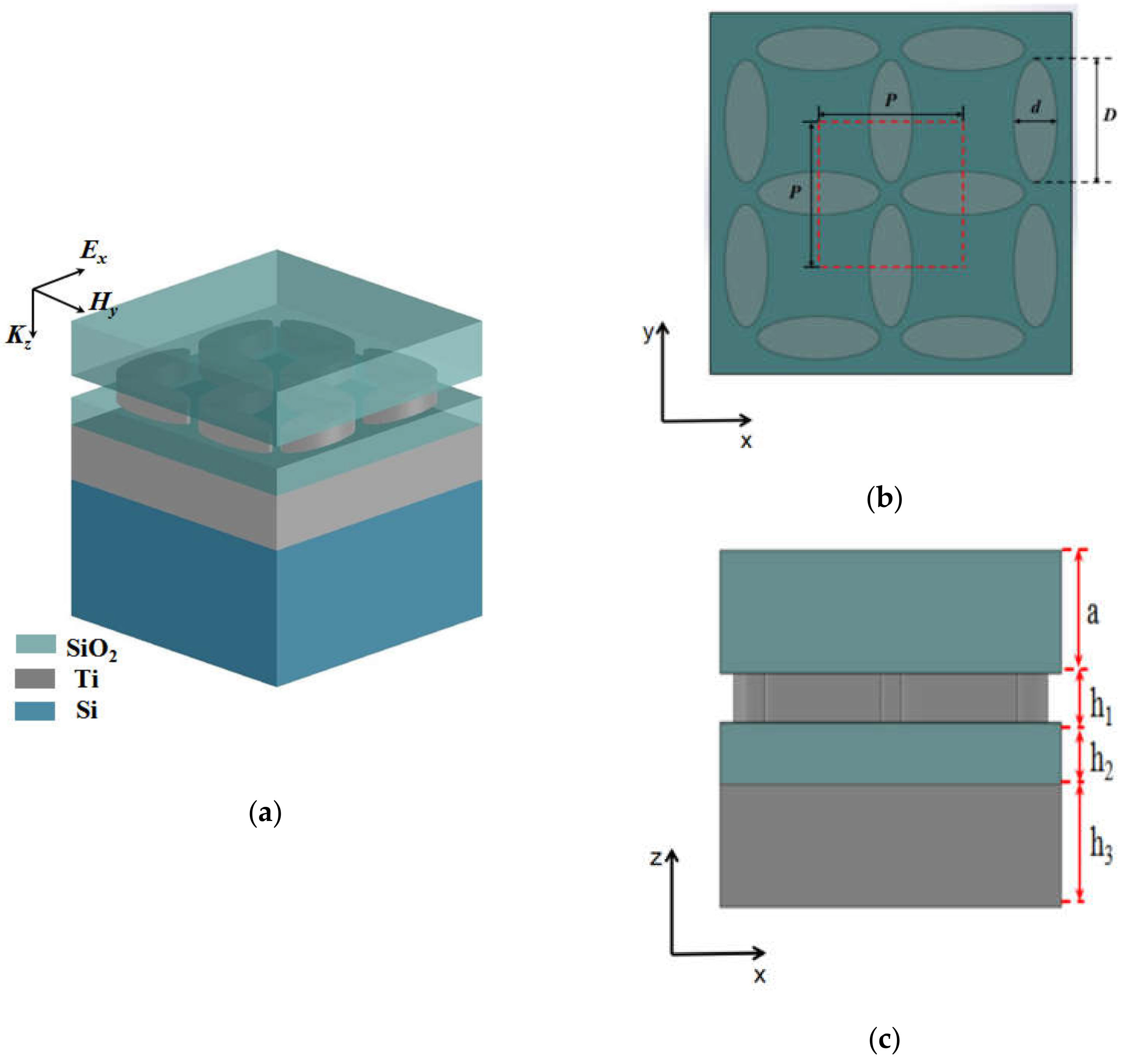
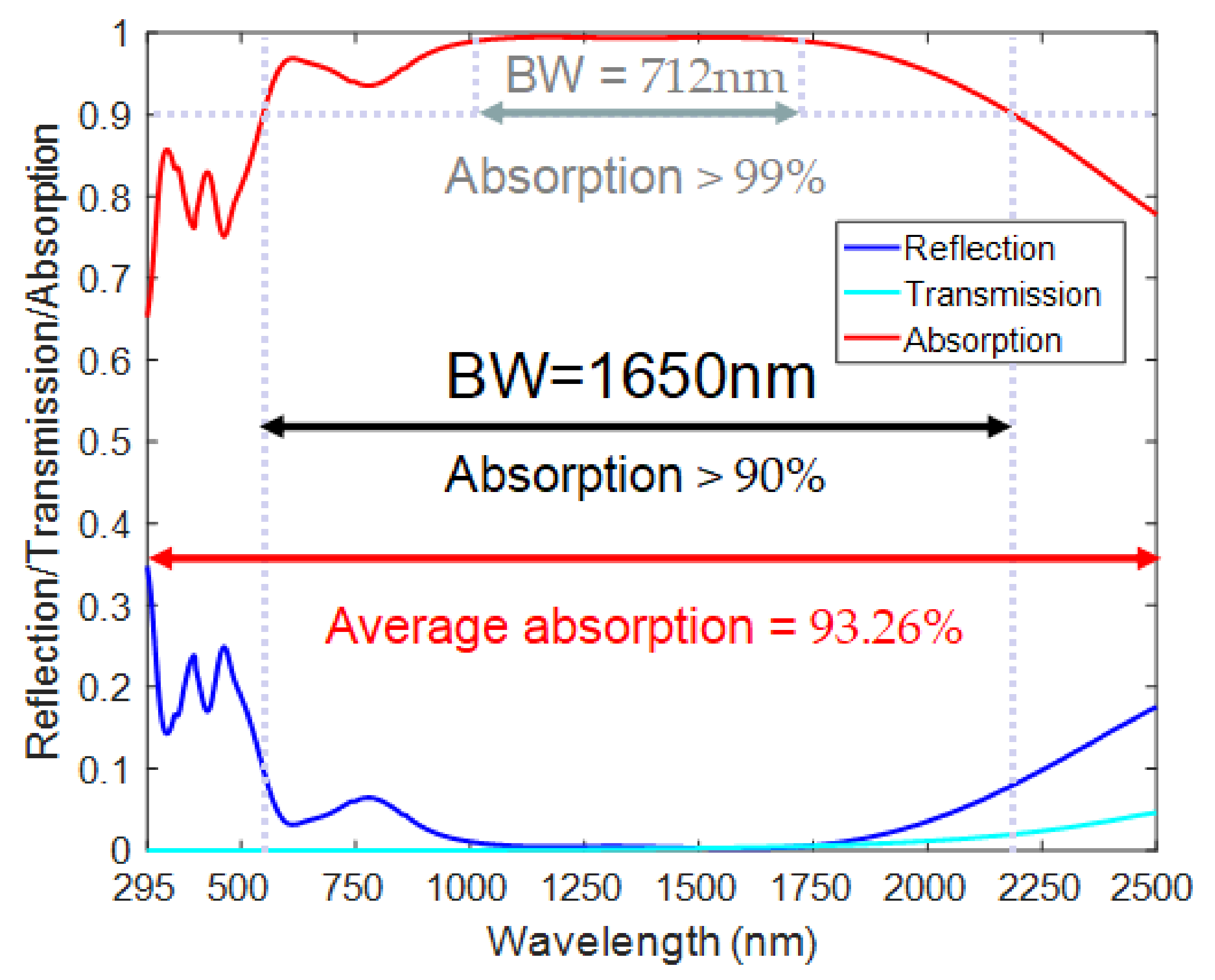
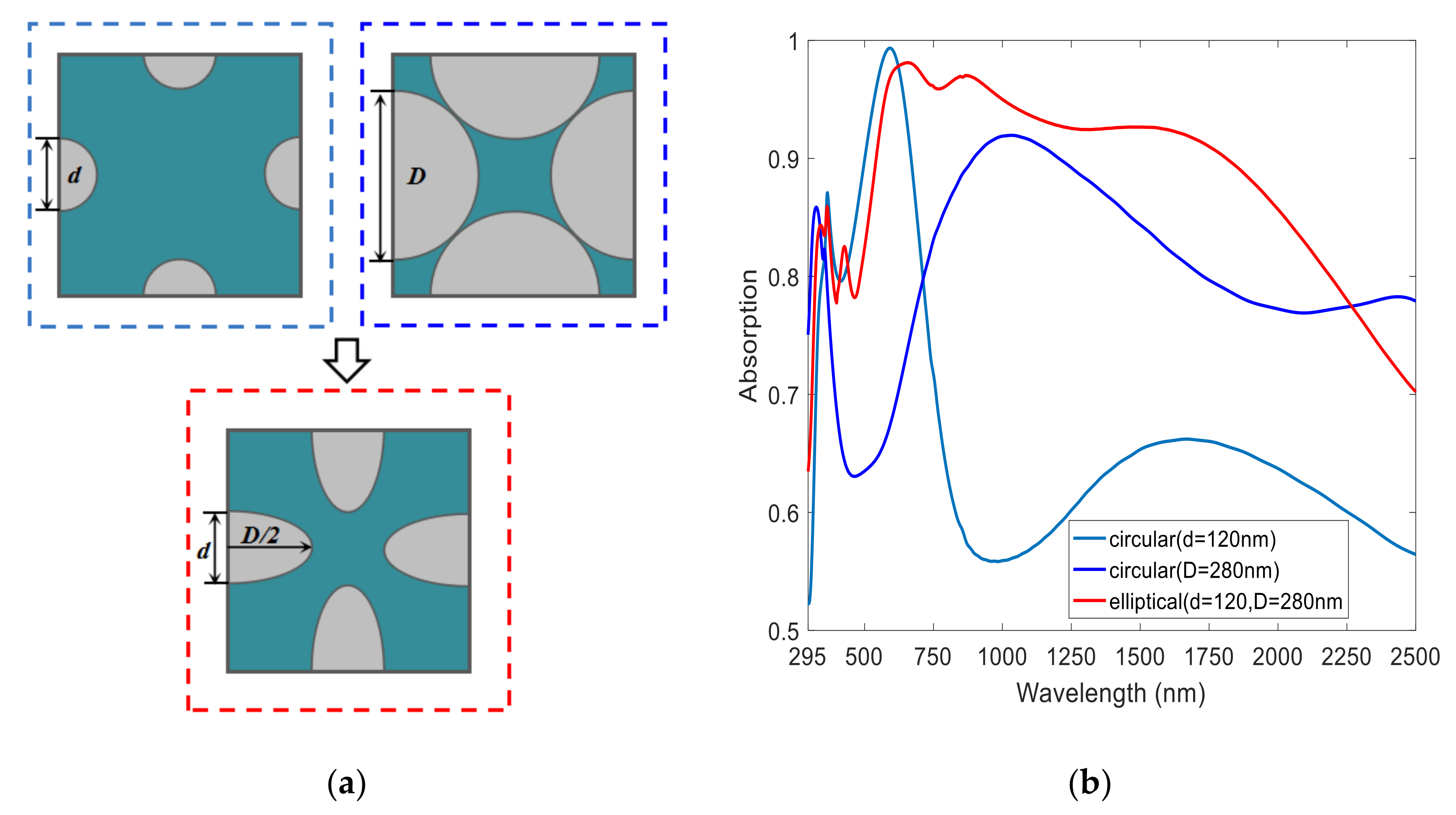
2. Physical Modeling and Ultra-Broadband Absorption
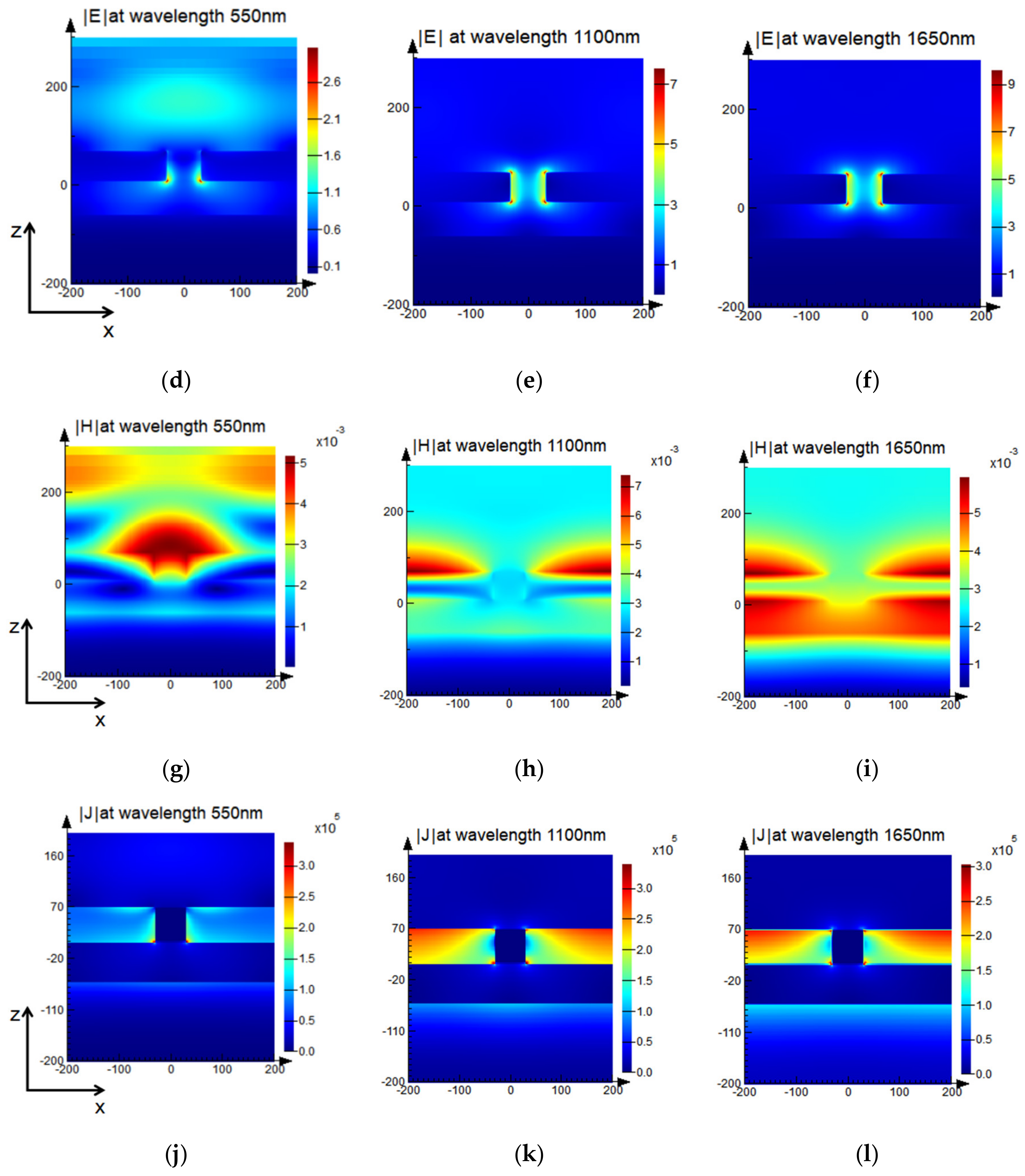
3. Extraordinary Optical Phenomena of Ultra-Broadband Perfect Absorber
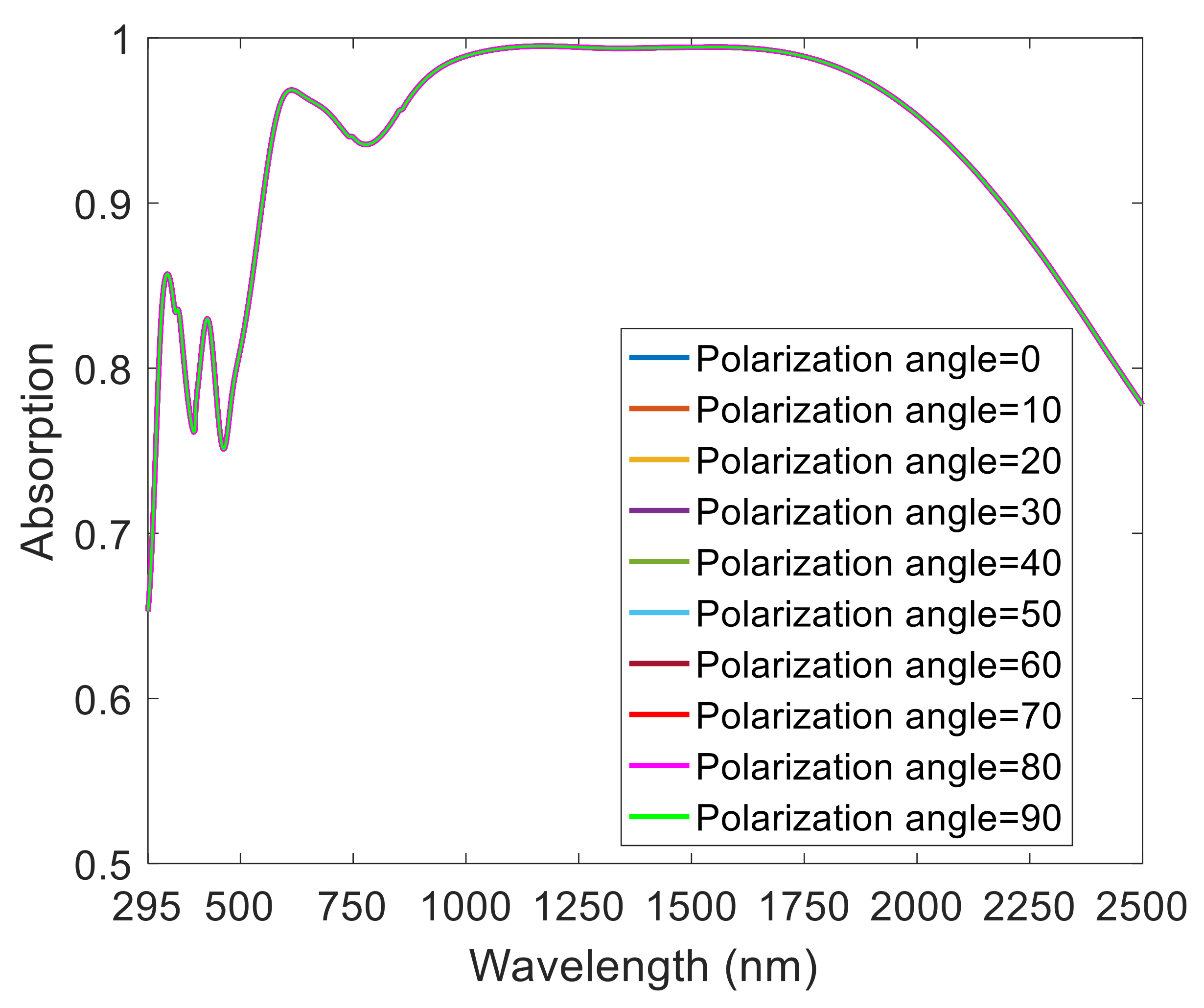
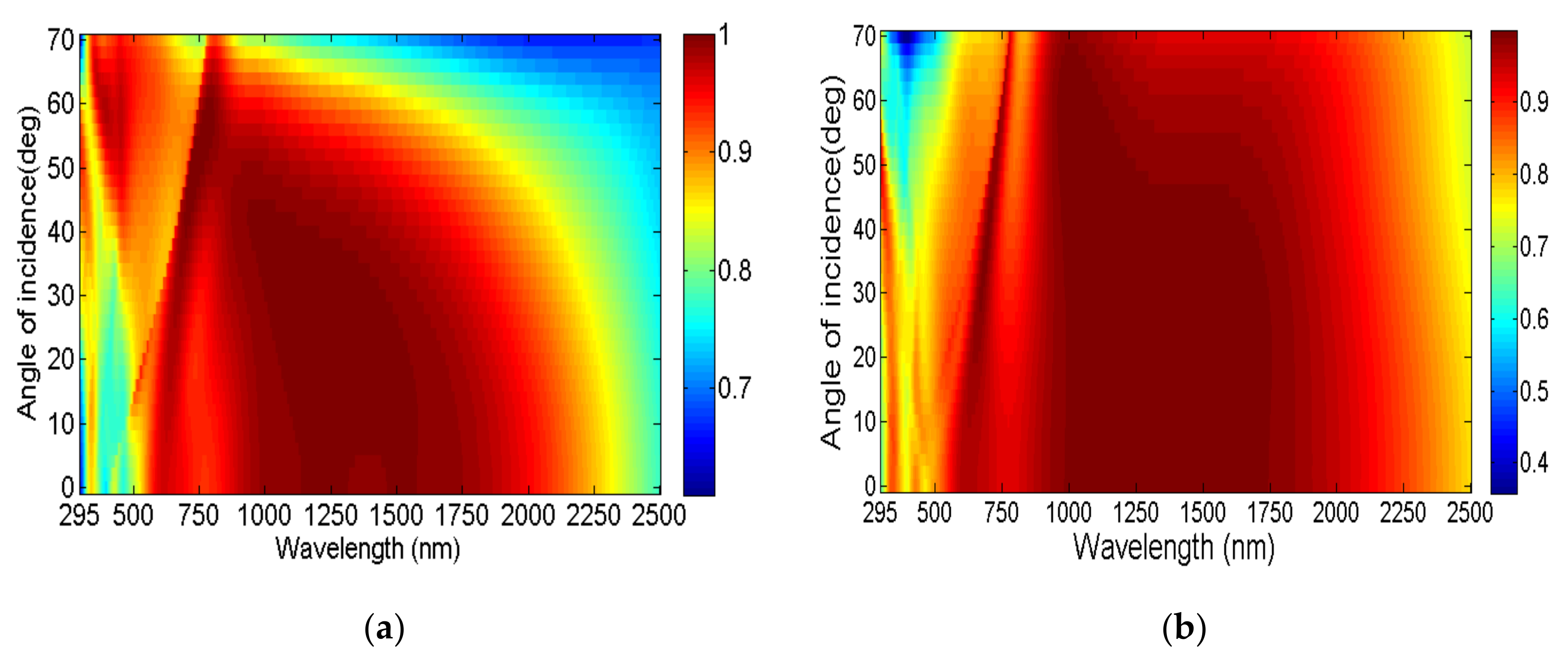
3.1. Polarization Independence and Large Incident-Angle Insensitivity
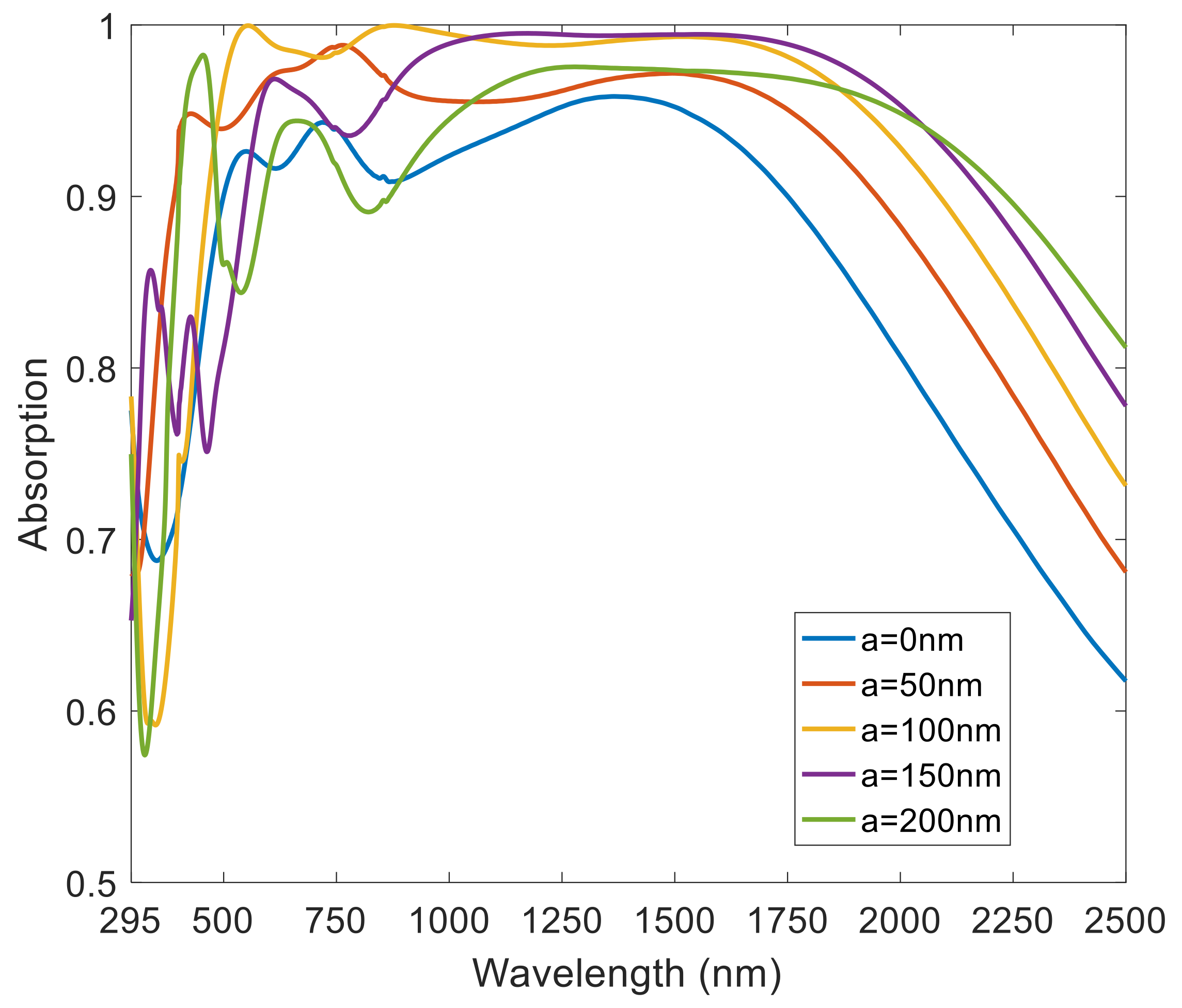
3.2. Influence of Structural Parameters on Absorber Performance
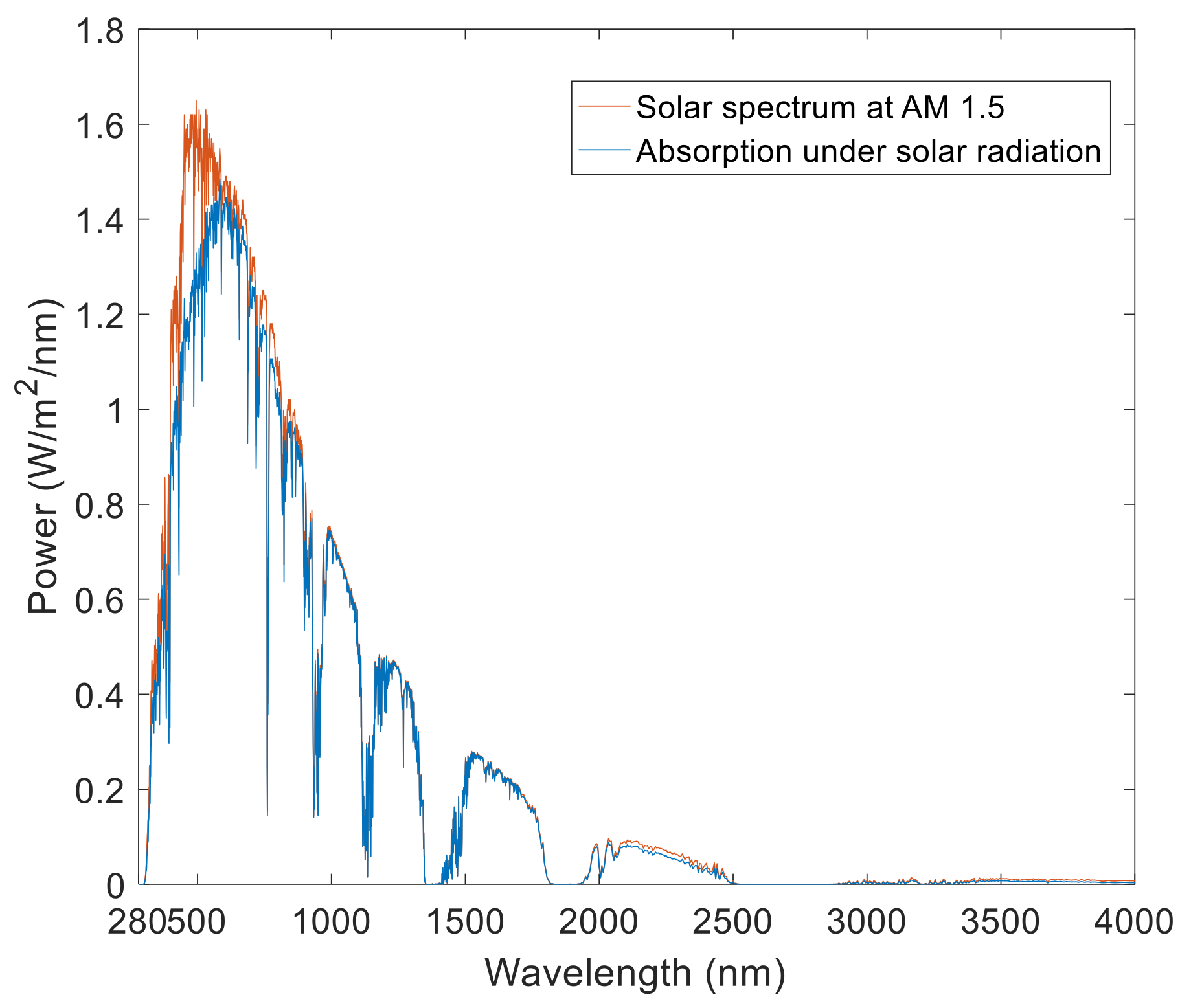
3.3. Super Capture Capability under Air Mass (AM) 1.5 Solar Spectrum
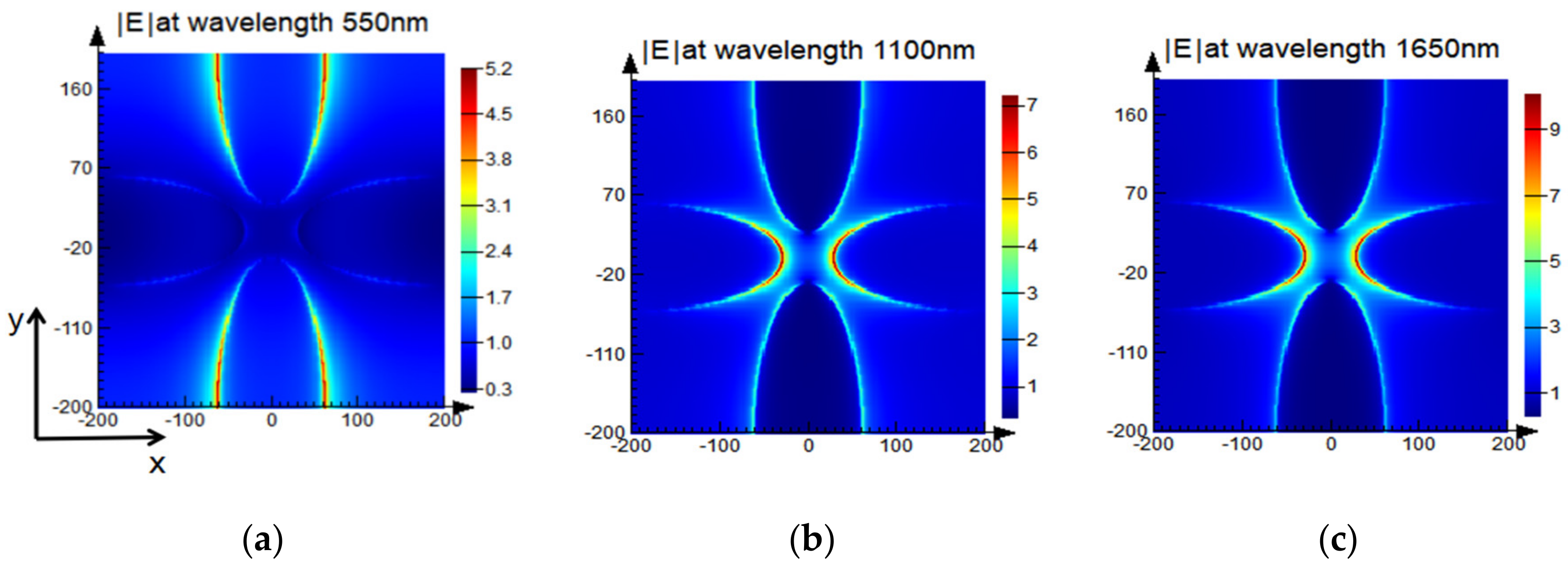
4. The Physical Origin and Simple Fabrication Method of the Ultra-Broadband Absorber
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J. A Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef] [PubMed]
- Liu, N.; Mesch, M.; Weiss, T. Infrared Perfect Absorber and Its Application as Plasmonic Sensor. Nano Lett. 2010, 10, 2342–2348. [Google Scholar] [CrossRef]
- Tao, H.; Bingham, C.M.; Strikwerda, A.C. Highly flexible wide angle of incidence terahertz metamaterial absorber: Design, fabrication, and characterization. Phys. Rev. B 2008, 78, 241103. [Google Scholar] [CrossRef]
- Zhang, B.X.; Zhao, Y.H.; Hao, Q.Z. Polarization-independent dual-band infrared perfect absorber based on a metal-dielectric-metal elliptical nanodisk array. Opt. Express 2011, 19, 15221–15228. [Google Scholar] [CrossRef] [PubMed]
- Shen, X.P.; Cui, T.J.; Zhao, J.M. Polarization-independent wide-angle triple-band metamaterial absorber. Opt. Express 2011, 19, 9401–9407. [Google Scholar] [CrossRef] [PubMed]
- Zhao, L.; Liu, H.; He, Z.H. Design of multi-narrowband metamaterial perfect absorbers in near-infrared band based on resonators asymmetric method and modified resonators stacked method. Opt. Commun. 2018, 420, 95–103. [Google Scholar] [CrossRef]
- Watts, C.M.; Liu, X.L.; Padilla, W.J. Metamaterial Electromagnetic Wave Absorbers. Adv. Mater. 2012, 24, OP98–OP120. [Google Scholar] [CrossRef]
- Diem, M.; Koschny, T.; Soukoulis, C.M. Wide-angle perfect absorber/thermal emitter in the terahertz regime. Phys. Rev. B 2009, 79, 033101. [Google Scholar] [CrossRef]
- Park, H.; Lee, S.Y.; Kim, J. Near-infrared coherent perfect absorption in plasmonic metal-insulator-metal waveguide. Opt. Express 2015, 23, 24464–24474. [Google Scholar] [CrossRef] [PubMed]
- Li, W.; Guler, U.; Kinsey, N. Refractory Plasmonics with Titanium Nitride: Broadband Metamaterial Absorber. Adv. Mater. 2014, 26, 7959–7965. [Google Scholar] [CrossRef] [PubMed]
- Hedayati, M.K.; Javaherirahim, M.; Mozooni, B. Design of a Perfect Black Absorber at Visible Frequencies Using Plasmonic Metamaterials. Adv. Mater. 2011, 23, 5410–5414. [Google Scholar] [CrossRef] [PubMed]
- Zhou, J.Y.; Yan, S.; Li, C.W. Perfect ultraviolet absorption in graphene using the magnetic resonance of an all-dielectric nanostructure. Opt. Express 2018, 26, 18155–18163. [Google Scholar] [CrossRef] [PubMed]
- Baqir, M.A.; Choudhury, P.K. Hyperbolic Metamaterial-Based UV Absorber. IEEE Photonics Technol. Lett. 2017, 29, 1548–1551. [Google Scholar] [CrossRef]
- Cheng, F.; Yang, X.D.; Gao, J. Enhancing intensity and refractive index sensing capability with infrared plasmonic perfect absorbers. Opt. Lett. 2014, 39, 3185–3188. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.Q.; Yu, M.D.; Huang, S. Enhancing refractive index sensing capability with hybrid plasmonic-photonic absorbers. J. Mater. Chem. C 2015, 3, 4222–4226. [Google Scholar] [CrossRef]
- Deng, H.X.; Li, Z.G.; Stan, L. Broadband perfect absorber based on one ultrathin layer of refractory metal. Opt. Lett. 2015, 40, 2592–2595. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.Q.; Liu, G.Q.; Huang, Z.P. Ultra-broadband perfect solar absorber by an ultra-thin refractory titanium nitride meta-surface. Sol. Energy Mater. Sol. Cells 2018, 179, 346–352. [Google Scholar] [CrossRef]
- Cui, Y.X.; Fung, K.H.; Xu, J. Ultrabroadband Light Absorption by a Sawtooth Anisotropic Metamaterial Slab. Nano Lett. 2012, 12, 1443–1447. [Google Scholar] [CrossRef] [PubMed]
- Ding, F.; Cui, Y.X.; Ge, X.C. Ultra-broadband microwave metamaterial absorber. Appl. Phys. Lett. 2012, 100, 103506. [Google Scholar] [CrossRef]
- Cui, Y.X.; Xu, J.; Fung, K.H. A thin film broadband absorber based on multi-sized nanoantennas. Appl. Phys. Lett. 2011, 99, 253101. [Google Scholar] [CrossRef]
- Ye, L.F.; Chen, X.; Zhuo, J.L. Actively tunable broadband terahertz absorption using periodically square-patterned graphene. Appl. Phys. Express 2018, 11, 102201. [Google Scholar] [CrossRef]
- Chen, M.J.; He, Y.R. Plasmonic nanostructures for broadband solar absorption based on the intrinsic absorption of metals. Sol. Energy Mater. Sol. Cells 2018, 188, 156–163. [Google Scholar] [CrossRef]
- Lei, L.; Li, S.; Huang, H.X. Ultra-broadband absorber from visible to near-infrared using plasmonic metamaterial. Opt. Express 2018, 26, 5686–5693. [Google Scholar] [CrossRef] [PubMed]
- Huang, Y.J.; Liu, L.; Pu, M.B. A refractory metamaterial absorber for ultra-broadband, omnidirectional and polarization-independent absorption in the UV-NIR spectrum. Nanoscale 2018, 10, 8298–8303. [Google Scholar] [CrossRef] [PubMed]
- Huo, D.W.; Zhang, J.W.; Wang, Y.C. Broadband Perfect Absorber Based on TiN-Nanocone Metasurface. Nanomaterials 2018, 8, 485. [Google Scholar] [CrossRef] [PubMed]
- Wu, S.L.; Gu, Y.; Ye, Y. Omnidirectional broadband metasurface absorber operating in visible to near-infrared regime. Opt. Express 2018, 26, 21479–21489. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Orlando, FL, USA, 1985. [Google Scholar]


© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, H.; Peng, W.; Chu, S.; Cui, W.; Liu, Z.; Yu, L.; Jing, Z. Refractory Ultra-Broadband Perfect Absorber from Visible to Near-Infrared. Nanomaterials 2018, 8, 1038. https://doi.org/10.3390/nano8121038
Gao H, Peng W, Chu S, Cui W, Liu Z, Yu L, Jing Z. Refractory Ultra-Broadband Perfect Absorber from Visible to Near-Infrared. Nanomaterials. 2018; 8(12):1038. https://doi.org/10.3390/nano8121038
Chicago/Turabian StyleGao, Huixuan, Wei Peng, Shuwen Chu, Wenli Cui, Zhi Liu, Li Yu, and Zhenguo Jing. 2018. "Refractory Ultra-Broadband Perfect Absorber from Visible to Near-Infrared" Nanomaterials 8, no. 12: 1038. https://doi.org/10.3390/nano8121038
APA StyleGao, H., Peng, W., Chu, S., Cui, W., Liu, Z., Yu, L., & Jing, Z. (2018). Refractory Ultra-Broadband Perfect Absorber from Visible to Near-Infrared. Nanomaterials, 8(12), 1038. https://doi.org/10.3390/nano8121038



