Piezoelectric Potential in Single-Crystalline ZnO Nanohelices Based on Finite Element Analysis
Abstract
:1. Introduction
2. Model and Method
2.1. Model Configuration
2.2. FEM Modeling of Nanowires and Nanohelices
3. Simulation Results and Discussion
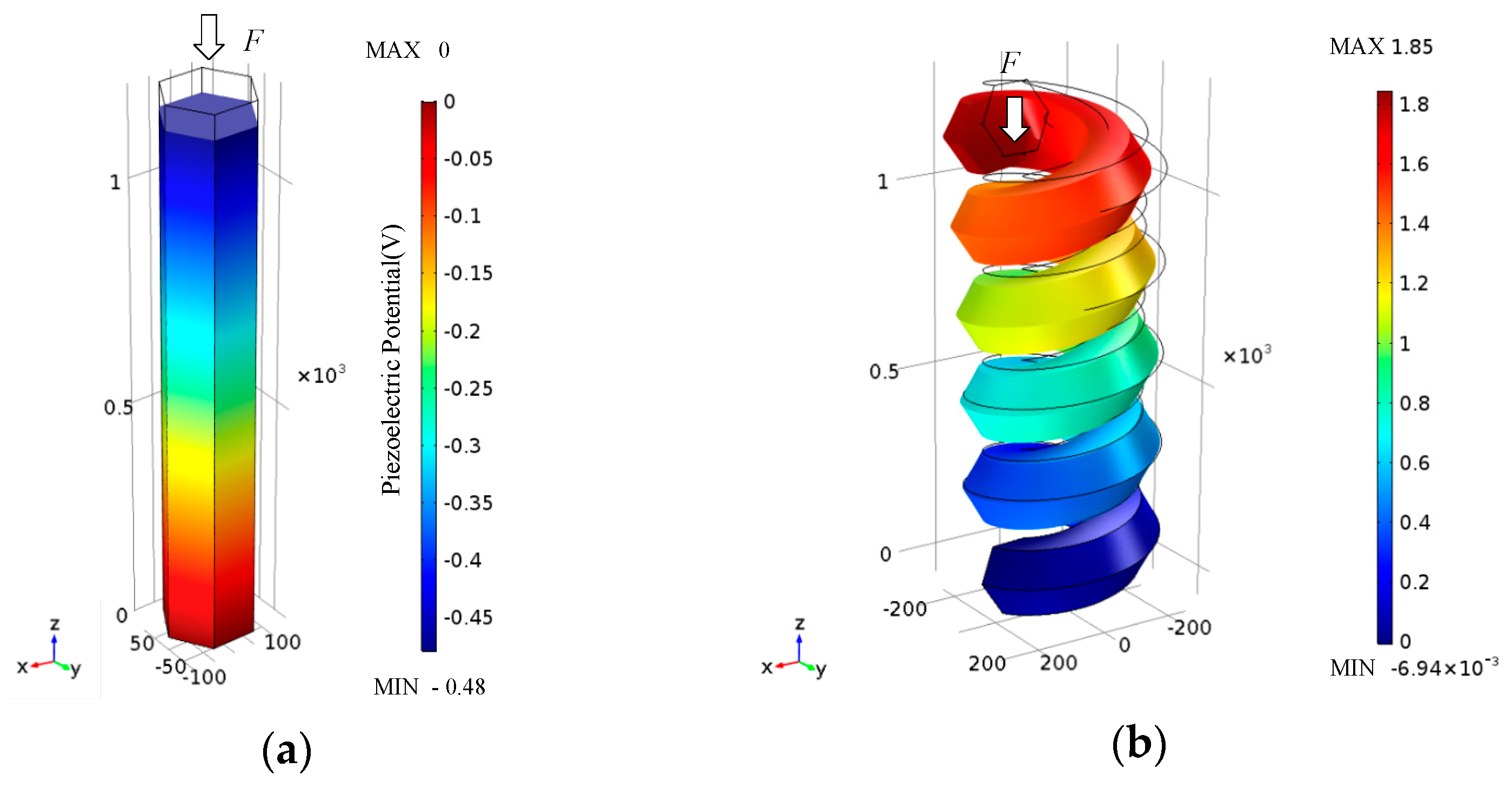
3.1. Pizeoelectric Potential and Displacement of the ZnO Nanohelix and Nanowire
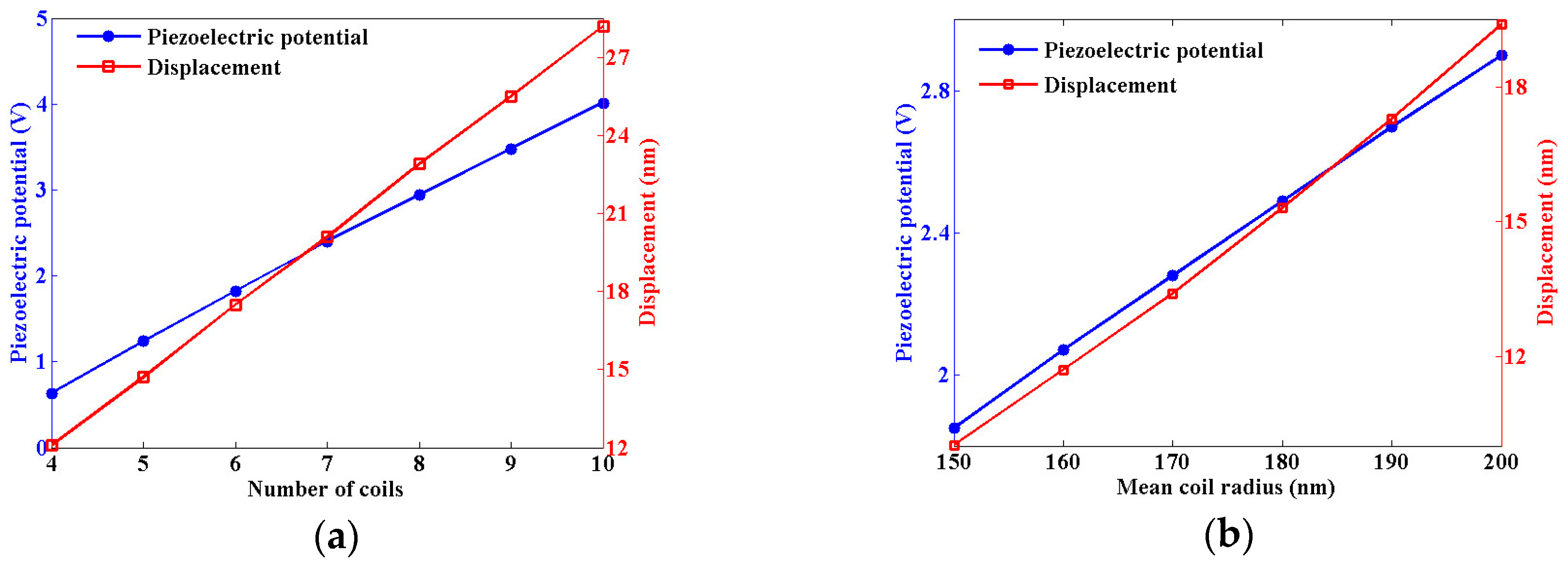
3.2. Effect of the Number of Coils and the Mean Radius of the Coil on the Pizeoelectric Potential of a Nanohelix
3.3. Effect of Acting Forces on the Pizeoelectric Potential and Displacement
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Yang, R.S.; Ding, Y.; Wang, Z.L. Deformation-free single-crystal nanohelixes of polar nanowires. Nano Lett. 2004, 4, 1309–1312. [Google Scholar] [CrossRef]
- Gao, P.X.; Mai, W.; Wang, Z.L. Superelasticity and nanofracture mechanics of zno nanohelices. Nano Lett. 2006, 6, 2536–2543. [Google Scholar] [CrossRef] [PubMed]
- Gao, H.; Zhang, X.T.; Zhou, M.Y.; Zhang, Z.G.; Wang, X.Z. Growth of novel zno nanohelices modified by sio 2-sheathed zno discs. Nanotechnology 2007, 18, 065601. [Google Scholar] [CrossRef]
- Kong, X.Y.; Ding, Y.; Yang, R.; Wang, Z.L. Single-crystal nanorings formed by epitaxial self-coiling of polar nanobelts. Science 2004, 303, 1348–1351. [Google Scholar] [CrossRef] [PubMed]
- Kong, X.Y.; Wang, Z.L. Spontaneous polarization-induced nanohelixes, nanosprings, and nanorings of piezoelectric nanobelts. Nano Lett. 2003, 3, 1625–1631. [Google Scholar] [CrossRef]
- Gao, P.X.; Wang, Z.L. High-yield synthesis of single-crystal nanosprings of zno. Small 2005, 1, 945–949. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Wang, Z.L. Springs, rings, and spirals of rutile-structured tin oxide nanobelts. J. Am. Chem. Soc. 2006, 128, 1466–1467. [Google Scholar] [CrossRef] [PubMed]
- Huang, T.; Liu, Z.; Huang, G.; Liu, R.; Mei, Y. Grating-structured metallic microsprings. Nanoscale 2014, 6, 9428–9435. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L.; Song, J.H. Piezoelectric nanogenerators based on zinc oxide nanowire arrays. Science 2006, 312, 242–246. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.D.; Song, J.H.; Liu, J.; Wang, Z.L. Direct-current nanogenerator driven by ultrasonic waves. Science 2007, 316, 102–105. [Google Scholar] [CrossRef] [PubMed]
- Yang, R.; Qin, Y.; Dai, L.; Wang, Z.L. Power generation with laterally packaged piezoelectric fine wires. Nat. Nanotechnol. 2009, 4, 34–39. [Google Scholar] [CrossRef] [PubMed]
- Zhu, R.; Zhang, W.G.; Yang, R.S. High output piezoelectric nanogenerator: Development and application. Sci. Adv. Mater. 2012, 4, 798–804. [Google Scholar] [CrossRef]
- Wang, X.D.; Zhou, J.; Song, J.H.; Liu, J.; Xu, N.S.; Wang, Z.L. Piezoelectric field effect transistor and nanoforce sensor based on a single zno nanowire. Nano Lett. 2006, 6, 2768–2772. [Google Scholar] [CrossRef] [PubMed]
- Kory, J.; Rusen, Y. Mechanical transfer of zno nanowires for a flexible and conformal piezotronic strain sensor. Semicond. Sci. Technol. 2017, 32, 074004. [Google Scholar]
- Zhou, J.; Gu, Y.; Fei, P.; Mai, W.; Gao, Y.; Yang, R.; Bao, G.; Wang, Z.L. Flexible piezotronic strain sensor. Nano Lett. 2008, 8, 3035–3040. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.Z.; Wang, Z.L. Piezotronic nanowire-based resistive switches as programmable electromechanical memories. Nano Lett. 2011, 11, 2779–2785. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.Z.; Wei, Y.G.; Wang, Z.L. Strain-gated piezotronic logic nanodevices. Adv. Mater. 2010, 22, 4711–4715. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Wang, Z.L. Electrostatic potential in a bent piezoelectric nanowire. The fundamental theory of nanogenerator and nanopiezotronics. Nano Lett. 2007, 7, 2499–2505. [Google Scholar] [CrossRef] [PubMed]
- Gao, Z.; Zhou, J.; Gu, Y.; Fei, P.; Hao, Y.; Bao, G.; Wang, Z.L. Effects of piezoelectric potential on the transport characteristics of metal-zno nanowire-metal field effect transistor. J. Appl. Phys. 2009, 105, 113707. [Google Scholar] [CrossRef] [PubMed]
- Sun, C.L.; Shi, J.A.; Wang, X.D. Fundamental study of mechanical energy harvesting using piezoelectric nanostructures. J. Appl. Phys. 2010, 108, 034309. [Google Scholar] [CrossRef]
- Chen, X.Q.; Zhang, S.L.; Dikin, D.A.; Ding, W.Q.; Ruoff, R.S.; Pan, L.J.; Nakayama, Y. Mechanics of a carbon nanocoil. Nano Lett. 2003, 3, 1299–1304. [Google Scholar] [CrossRef]
- Wang, J.-S.; Feng, X.-Q.; Wang, G.-F.; Yu, S.-W. Twisting of nanowires induced by anisotropic surface stresses. Appl. Phys. Lett. 2008, 92, 191901. [Google Scholar] [CrossRef]
- Da Fonseca, A.F.; Galvão, D.S. Mechanical properties of nanosprings. Phys. Rev. Lett. 2004, 92, 175502. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.; Mailhiot, C. Theory of semiconductor superlattice electronic structure. Rev. Modern Phys. 1990, 62, 173. [Google Scholar] [CrossRef]
- Clarke, D.R. Varistor ceramics. J. Am. Ceram. Soc. 1999, 82, 485–502. [Google Scholar] [CrossRef]
- Hwang, G.; Hashimoto, H.; Bell, D.J.; Dong, L.; Nelson, B.J.; Schön, S. Piezoresistive ingaas/gaas nanosprings with metal connectors. Nano Lett. 2009, 9, 554–561. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.-Y.; Zhao, Y.-P. Optical properties of helical Ag nanostructures calculated by discrete dipole approximation method. Appl. Phys. Lett. 2007, 90, 221501. [Google Scholar] [CrossRef]
- Zhang, Z.-Y.; Zhao, Y.-P. Optical properties of helical and multiring Ag nanostructures: The effect of pitch height. J. Appl. Phys. 2008, 104, 013517. [Google Scholar] [CrossRef]
- Kamata, K.; Suzuki, S.; Ohtsuka, M.; Nakagawa, M.; Iyoda, T.; Yamada, A. Fabrication of left-handed metal microcoil from spiral vessel of vascular plant. Adv. Mater. 2011, 23, 5509–5513. [Google Scholar] [CrossRef] [PubMed]
- Gao, Y.; Wang, Z.L. Equilibrium potential of free charge carriers in a bent piezoelectric semiconductive nanowire. Nano Lett. 2009, 9, 1103–1110. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L. Progress in piezotronics and piezo-phototronics. Adv. Mater. 2012, 24, 4632–4646. [Google Scholar] [CrossRef] [PubMed]
- Granet, I. Strength of Materials for Engineering Technology, 2nd ed.; Reston Pub. Co.: Reston, VA, USA, 1980. [Google Scholar]
- Wahl, A. Mechanical Springs; McGraw-Hill: New York, NY, USA, 1963; p. 119. [Google Scholar]
- Nguyen, V.; Zhu, R.; Jenkins, K.; Yang, R. Self-assembly of diphenylalanine peptide with controlled polarization for power generation. Nat. Commun. 2016, 7, 13566. [Google Scholar] [CrossRef] [PubMed]
- Wu, W.Z.; Wen, X.N.; Wang, Z.L. Taxel-addressable matrix of vertical-nanowire piezotronic transistors for active and adaptive tactile imaging. Science 2013, 340, 952–957. [Google Scholar] [CrossRef] [PubMed]
- Jenkins, K.; Nguyen, V.; Zhu, R.; Yang, R. Piezotronic effect: An emerging mechanism for sensing applications. Sensors 2015, 15, 22914–22940. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.L.; Wu, W.Z. Piezotronics and piezo-phototronics: Fundamentals and applications. Natl. Sci. Rev. 2014, 1, 62–90. [Google Scholar] [CrossRef]

| Parameters | Value |
|---|---|
| Density (kg/m3) | 5680 |
| Elastic constants | |
| c11 (GPa) | 209.7 |
| c12 (GPa) | 121.1 |
| c13 (GPa) | 105.1 |
| c33 (GPa) | 211.3 |
| c44 (GPa) | 42.3 |
| c55 (GPa) | 43.6 |
| Piezoelectric constants | |
| e31 (C/m2) | −0.57 |
| e33 (C/m2) | 1.32 |
| e15 (C/m2) | −0.48 |
| Relative dielectric constants | |
| 8.54 | |
| 10.20 | |
| Applied Force Components (nN) | Piezoelectric Potential (V) | Displacement (nm) | ||
|---|---|---|---|---|
| x-Axis | y-Axis | z-Axis | ||
| 0 | 0 | 100 | 1.85 | 10.2 |
| 0 | 100 | 0 | 0.35 | 48.3 |
| 100 | 0 | 0 | 0.29 | 47.3 |
| 100 | 100 | 0 | 0.48 | 67.8 |
| 100 | 0 | 100 | 1.85 | 37.6 |
| 0 | 100 | 100 | 1.60 | 49.4 |
| 100 | 100 | 100 | 1.60 | 61.6 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, H.; Jenkins, K.; Huang, X.; Xu, Y.; Huang, J.; Yang, R. Piezoelectric Potential in Single-Crystalline ZnO Nanohelices Based on Finite Element Analysis. Nanomaterials 2017, 7, 430. https://doi.org/10.3390/nano7120430
Hao H, Jenkins K, Huang X, Xu Y, Huang J, Yang R. Piezoelectric Potential in Single-Crystalline ZnO Nanohelices Based on Finite Element Analysis. Nanomaterials. 2017; 7(12):430. https://doi.org/10.3390/nano7120430
Chicago/Turabian StyleHao, Huimin, Kory Jenkins, Xiaowen Huang, Yiqian Xu, Jiahai Huang, and Rusen Yang. 2017. "Piezoelectric Potential in Single-Crystalline ZnO Nanohelices Based on Finite Element Analysis" Nanomaterials 7, no. 12: 430. https://doi.org/10.3390/nano7120430
APA StyleHao, H., Jenkins, K., Huang, X., Xu, Y., Huang, J., & Yang, R. (2017). Piezoelectric Potential in Single-Crystalline ZnO Nanohelices Based on Finite Element Analysis. Nanomaterials, 7(12), 430. https://doi.org/10.3390/nano7120430







