The UV Plasmonic Behavior of Distorted Rhodium Nanocubes
Abstract
:1. Introduction
2. Theoretical Methods
3. Results and Discussion
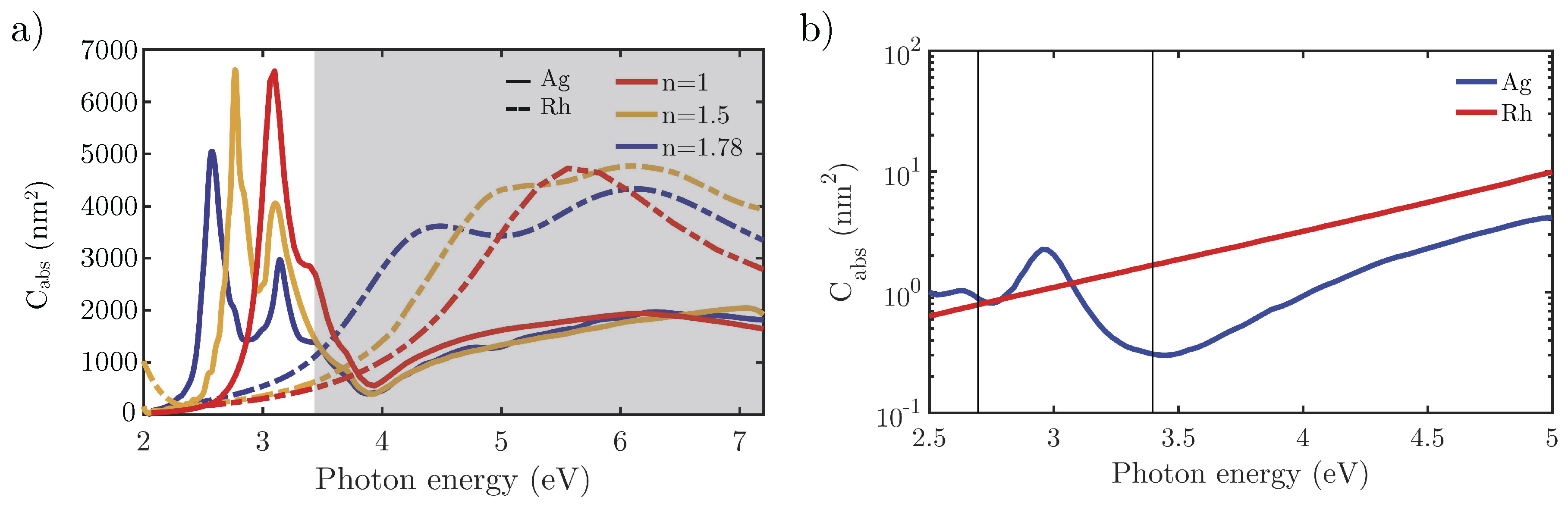
3.1. Comparison of Ag and Rh in Simple Geometries
3.2. Rh Nanocubes
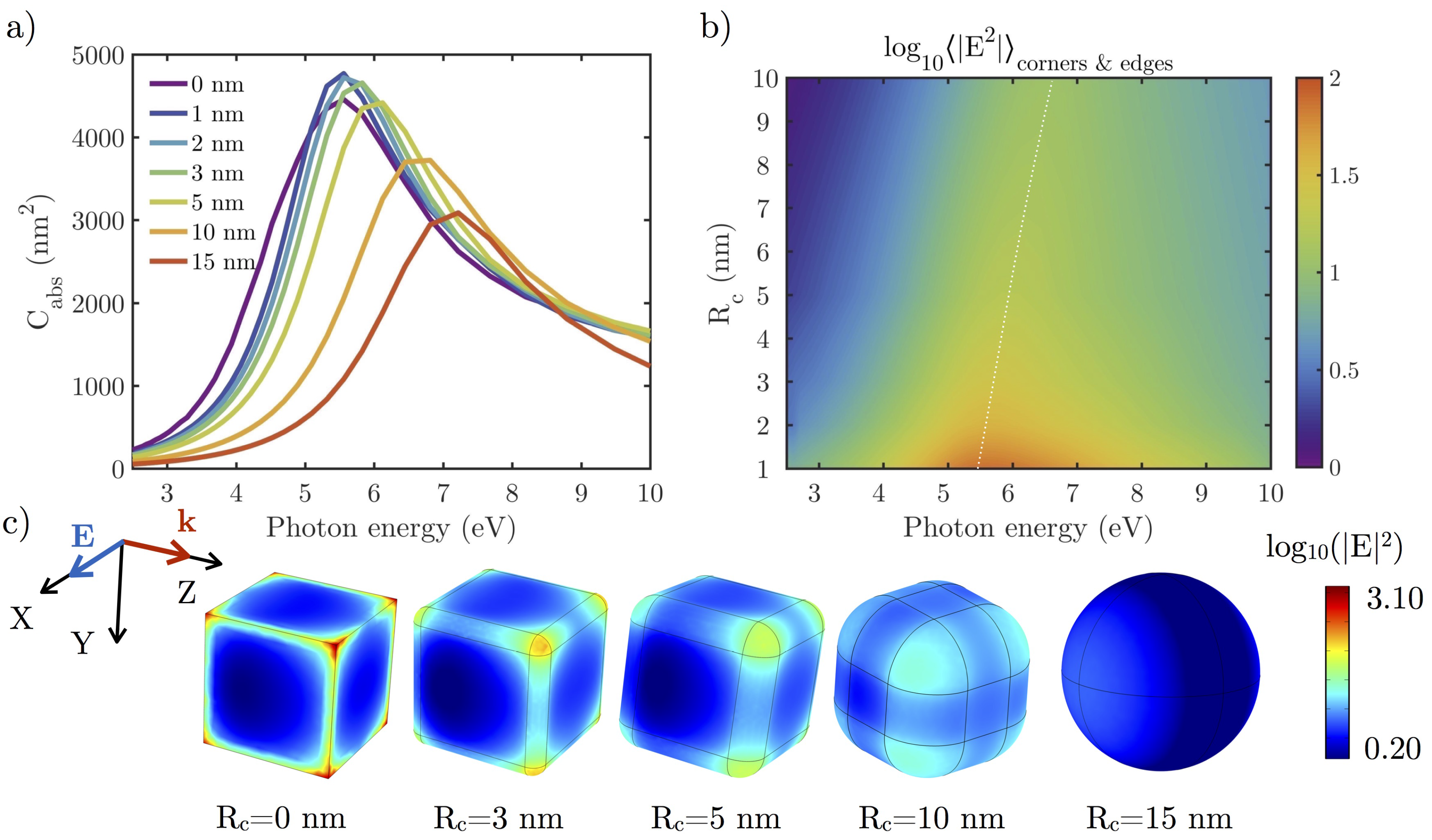
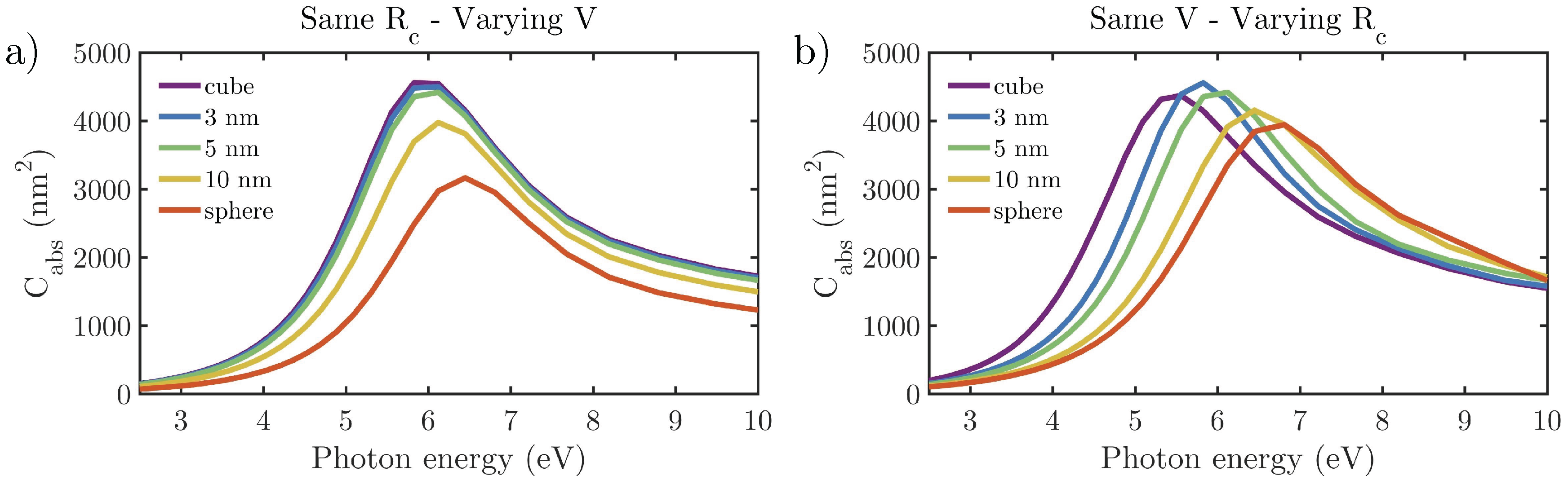
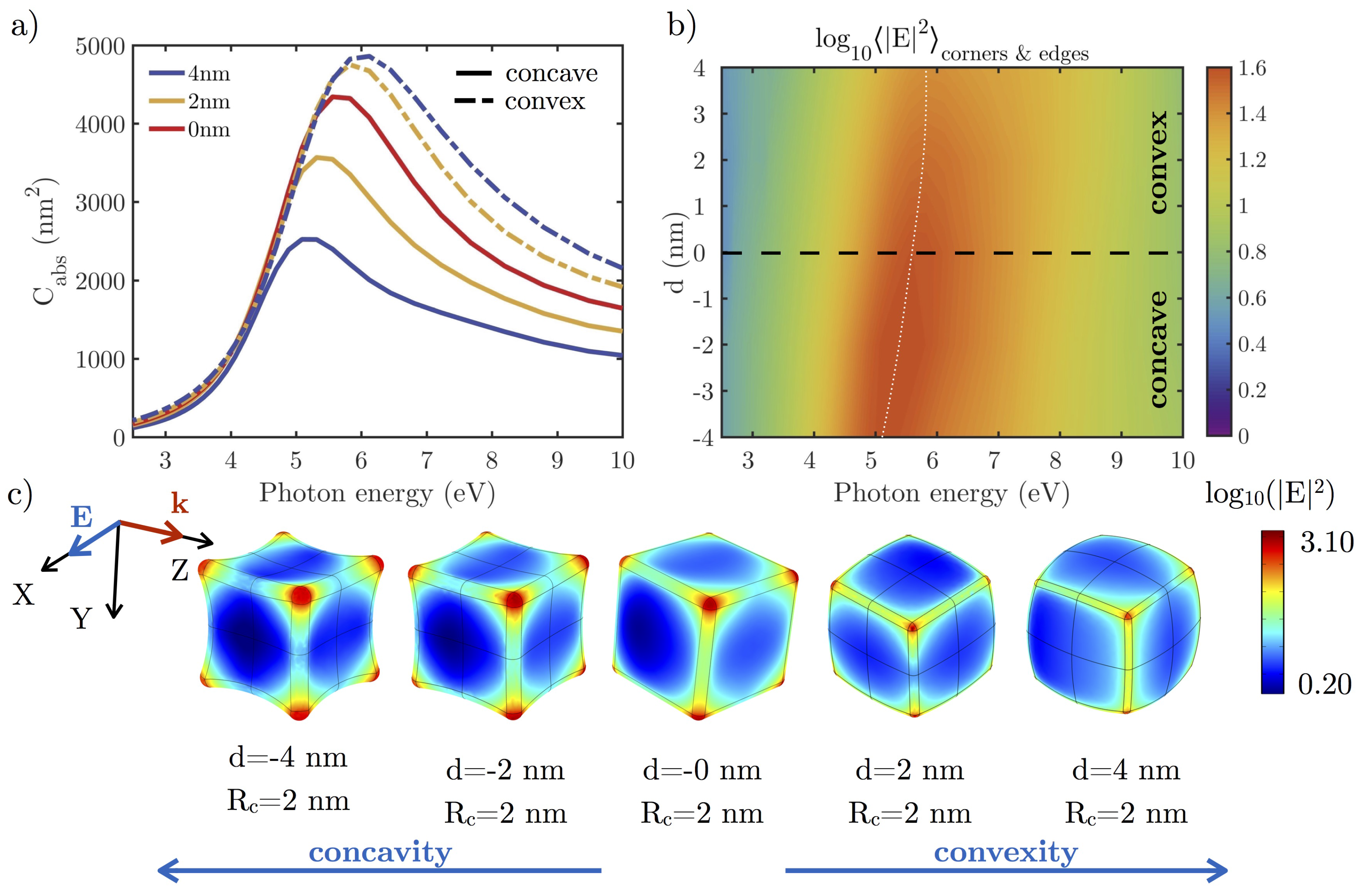
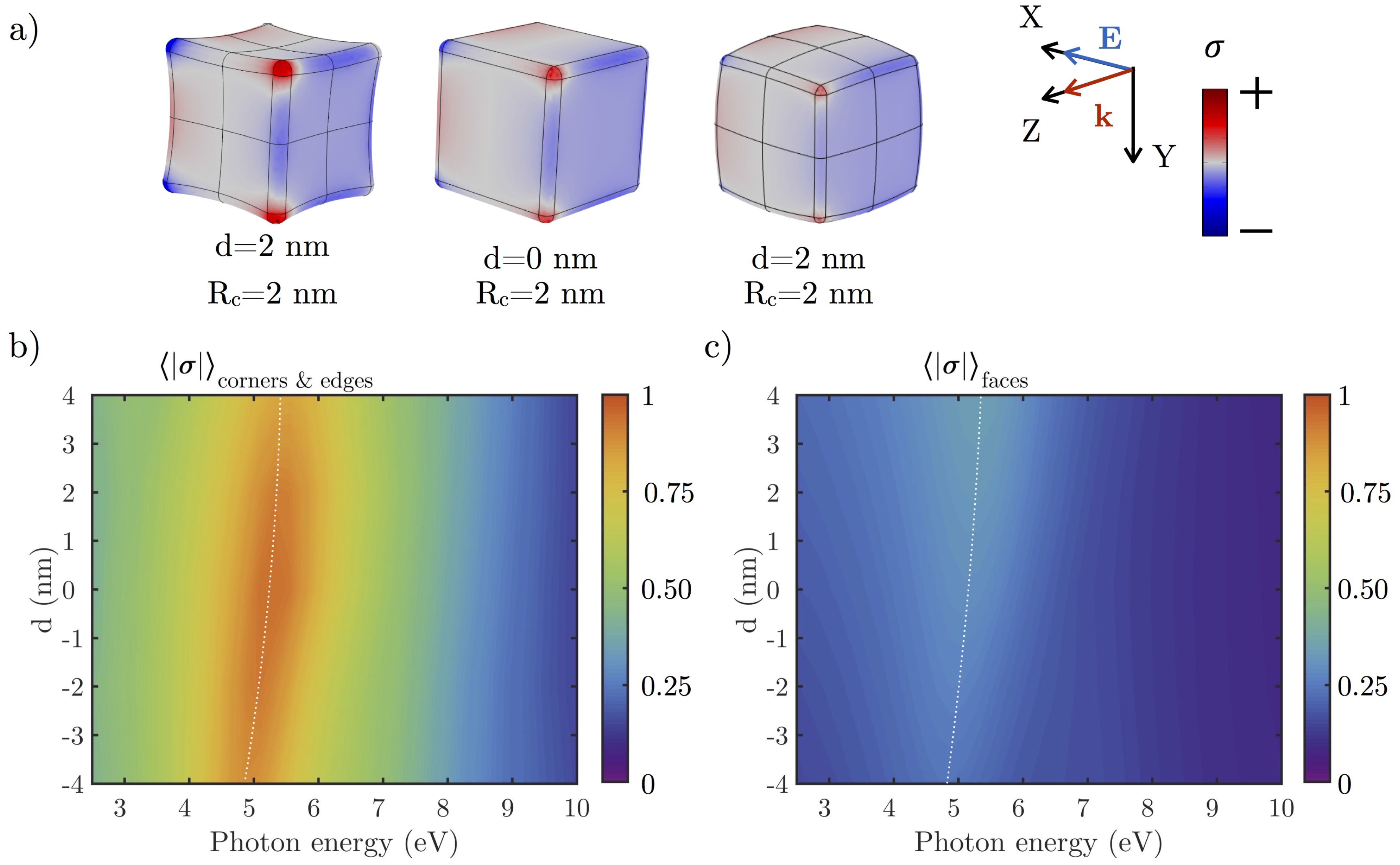
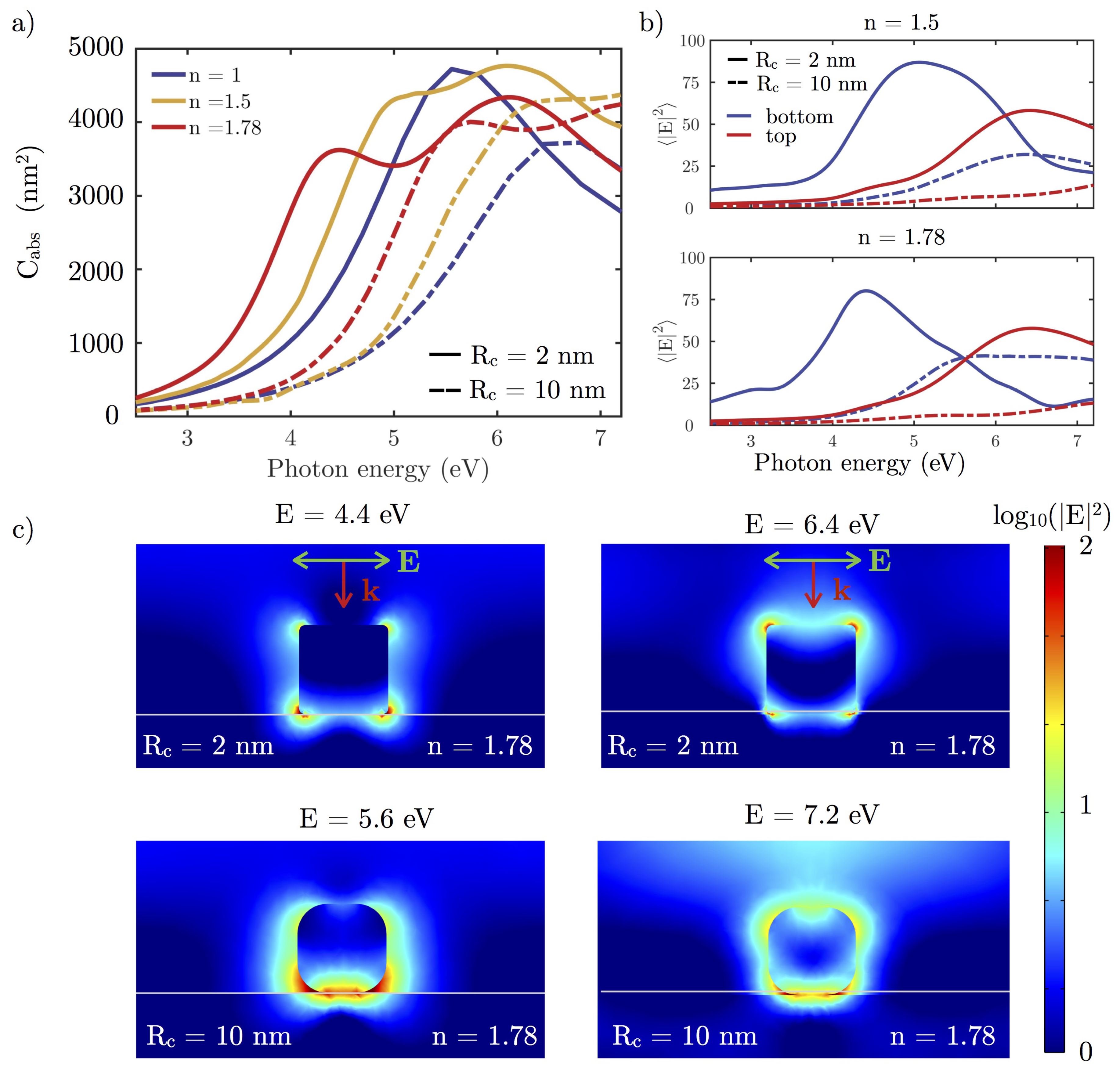
3.2.1. Effect of the Shape
3.2.2. Dielectric Substrate
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Prasad, P.N. Nanophotonics; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Maier, S.A. Plasmonics: Fundamentals and Applications; Springer: Boston, MA, USA, 2007. [Google Scholar]
- Pelton, M.; Aizpurua, J.; Bryant, G. Metal nanoparticle plasmonics. Laser Photonics Rev. 2008, 2, 136–159. [Google Scholar] [CrossRef]
- Aroca, R.F.; Teo, G.Y.; Mohan, H.; Guerrero, A.R.; Albella, P.; Moreno, F. Plasmon-enhanced fluorescence and spectral modification in SHINEF. J. Phys. Chem. C 2011, 115, 20419–20424. [Google Scholar] [CrossRef]
- Mishra, Y.K.; Chakravadhanula, V.S.K.; Hrkac, V.; Jebril, S.; Agarwal, D.C.; Mohapatra, S.; Avasthi, D.K.; Kienle, L.; Adelung, R. Crystal growth behaviour in Au–ZnO nanocomposite under different annealing environments and photoswitchability. J. Appl. Phys. 2012, 112, 064308. [Google Scholar] [CrossRef]
- Chakravadhanula, V.S.K.; Mishra, Y.K.; Kotnur, V.G.; Avasthi, D.K.; Strunskus, T.; Zaporotchenko, V.; Fink, D.; Kienle, L.; Faupel, F. Microstructural and plasmonic modifications in Ag-TiO2 and Au-TiO2 nanocomposites through ion beam irradiation. Beilstein J. Nanotechnol. 2014, 5, 1419–1431. [Google Scholar] [CrossRef] [PubMed]
- Sharma, B.; Frontiera, R.R.; Henry, A.I.; Ringe, E.; Van Duyne, R.P. SERS: Materials, applications, and the future. Mater. Today 2012, 15, 16–25. [Google Scholar] [CrossRef]
- Yang, Y.; Callahan, J.M.; Kim, T.H.; Brown, A.S.; Everitt, H.O. Ultraviolet nanoplasmonics: A demonstration of surface-enhanced raman spectroscopy, fluorescence, and photodegradation using gallium nanoparticles. Nano Lett. 2013, 13, 2837–2841. [Google Scholar] [CrossRef] [PubMed]
- Watson, A.M.; Zhang, X.; Alcaraz de la Osa, R.; Marcos Sanz, J.; González, F.; Moreno, F.; Finkelstein, G.; Liu, J.; Everitt, H.O. Rhodium nanoparticles for ultraviolet plasmonics. Nano Lett. 2015, 15, 1095–1100. [Google Scholar] [CrossRef] [PubMed]
- Lin, X.F.; Ren, B.; Yang, Z.L.; Liu, G.K.; Tian, Z.Q. Surface-enhanced Raman spectroscopy with ultraviolet excitation. J. Raman Spectrosc. 2005, 36, 606–612. [Google Scholar] [CrossRef]
- Linic, S.; Christopher, P.; Ingram, D.B. Plasmonic-metal nanostructures for efficient conversion of solar to chemical energy. Nat. Mater. 2011, 10, 911–921. [Google Scholar] [CrossRef] [PubMed]
- McClain, M.J.; Schlather, A.E.; Ringe, E.; King, N.S.; Liu, L.; Manjavacas, A.; Knight, M.W.; Kumar, I.; Whitmire, K.H.; Everitt, H.O.; et al. Aluminum Nanocrystals. Nano Lett. 2015, 15, 2751–2755. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhao, H.; Zhou, L.; Schlather, A.E.; Dong, L.; McClain, M.J.; Swearer, D.F.; Nordlander, P.; Halas, N.J. Al–Pd Nanodisk Heterodimers as Antenna–Reactor Photocatalysts. Nano Lett. 2016, 16, 6677–6682. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Tan, Y.; Wang, J.; Xu, W.; Yuan, Y.; Cai, W.; Zhu, S.; Zhu, J. 3D self-assembly of aluminium nanoparticles for plasmon-enhanced solar desalination. Nat. Photonics 2016, 10, 393–398. [Google Scholar] [CrossRef]
- Aslan, K.; Lakowicz, J.R.; Geddes, C.D. Plasmon light scattering in biology and medicine: New sensing approaches, visions and perspectives. Curr. Opin. Chem. Biol. 2005, 9, 538–544. [Google Scholar] [CrossRef] [PubMed]
- Anker, J.N.; Hall, W.P.; Lyandres, O.; Shah, N.C.; Zhao, J.; Van Duyne, R.P. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef] [PubMed]
- Knight, M.W.; Liu, L.; Wang, Y.; Brown, L.; Mukherjee, S.; King, N.S.; Everitt, H.O.; Nordlander, P.; Halas, N.J. Aluminum plasmonic nanoantennas. Nano Lett. 2012, 12, 6000–6004. [Google Scholar] [CrossRef] [PubMed]
- Knight, M.W.; King, N.S.; Liu, L.; Everitt, H.O.; Nordlander, P.; Halas, N.J. Aluminum for plasmonics. ACS Nano 2014, 8, 834–840. [Google Scholar] [CrossRef] [PubMed]
- Sanz, J.M.; Ortiz, D.; Alcaraz de la Osa, R.; Saiz, J.M.; González, F.; Brown, A.S.; Losurdo, M.; Everitt, H.O.; Moreno, F. UV plasmonic behavior of various metal nanoparticles in the near- and far-field regimes: Geometry and substrate effects. J. Phys. Chem. C 2013, 117, 19606–19615. [Google Scholar] [CrossRef]
- DeSantis, C.J.; McClain, M.J.; Halas, N.J. Walking the Walk: A giant step toward sustainable plasmonics. ACS Nano 2016, 10, 9772–9775. [Google Scholar] [CrossRef] [PubMed]
- Rai, A.; Park, K.; Zhou, L.; Zachariah, M.R. Understanding the mechanism of aluminium nanoparticle oxidation. Combust. Theory Model. 2006, 10, 843–859. [Google Scholar] [CrossRef]
- Gutierrez, Y.; Ortiz, D.; Sanz, J.M.; Saiz, J.M.; Gonzalez, F.; Everitt, H.O.; Moreno, F. How an oxide shell affects the ultraviolet plasmonic behavior of Ga, Mg, and Al nanostructures. Opt. Express 2016, 24, 20621. [Google Scholar] [CrossRef] [PubMed]
- Sterl, F.; Strohfeldt, N.; Walter, R.; Griessen, R.; Tittl, A.; Giessen, H. Magnesium as novel material for active plasmonics in the visible wavelength range. Nano Lett. 2015, 15, 7949–7955. [Google Scholar] [CrossRef] [PubMed]
- Fournier, V.; Marcus, P.; Olefjord, I. Oxidation of magnesium. Surf. Interface Anal. 2002, 34, 494–497. [Google Scholar] [CrossRef]
- Blaber, M.G.; Engel, C.J.; Vivekchand, S.R.C.; Lubin, S.M.; Odom, T.W.; Schatz, G.C. Eutectic liquid alloys for plasmonics: Theory and experiment. Nano Lett. 2012, 12, 5275–5280. [Google Scholar] [CrossRef] [PubMed]
- Losurdo, M.; Suvorova, A.; Rubanov, S.; Hingerl, K.; Brown, A.S. Thermally stable coexistence of liquid and solid phases in gallium nanoparticles. Nat. Mater. 2016, 15, 995–1002. [Google Scholar] [CrossRef] [PubMed]
- Knight, M.W.; Coenen, T.; Yang, Y.; Brenny, B.J.M.; Losurdo, M.; Brown, A.S.; Everitt, H.O.; Polman, A. Gallium Plasmonics: Deep subwavelength spectroscopic imaging of single and interacting gallium nanoparticles. ACS Nano 2015, 9, 2049–2060. [Google Scholar] [CrossRef] [PubMed]
- Alcaraz de la Osa, R.; Sanz, J.M.; Barreda, A.I.; Saiz, J.M.; González, F.; Everitt, H.O.; Moreno, F. Rhodium tripod stars for UV plasmonics. J. Phys. Chem. C 2015, 119, 12572–12580. [Google Scholar] [CrossRef]
- Zhang, X.; Li, P.; Barreda, Á.; Gutiérrez, Y.; González, F.; Moreno, F.; Everitt, H.O.; Liu, J. Size-tunable rhodium nanostructures for wavelength-tunable ultraviolet plasmonics. Nanoscale Horiz. 2016, 1, 75–80. [Google Scholar] [CrossRef]
- Zhang, X.; Li, X.; Zhang, D.; Su, N.Q.; Yang, W.; Everitt, H.O.; Liu, J. Product selectivity in plasmonic photocatalysis for carbon dioxide hydrogenation. Nat. Commun. 2017, 8, 14542. [Google Scholar] [CrossRef] [PubMed]
- Nørskov, J.K.; Studt, F.; Abild-Pedersen, F.; Bligaard, T. Fundamental Concepts in Heterogeneous Catalysis; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Boerigter, C.; Campana, R.; Morabito, M.; Linic, S. Evidence and implications of direct charge excitation as the dominant mechanism in plasmon-mediated photocatalysis. Nat. Commun. 2016, 7, 10545. [Google Scholar] [CrossRef] [PubMed]
- Kale, M.J.; Avanesian, T.; Christopher, P. Direct photocatalysis by plasmonic nanostructures. ACS Catal. 2014, 4, 116–128. [Google Scholar] [CrossRef]
- Chorkendorff, I.; Niemantsverdriet, J.W. Concepts of Modern Catalysis and Kinetics; Wiley-VCH Verlag GmbH & Co. KGaA: Weinheim, Germany, 2003. [Google Scholar]
- COMSOL, Inc. COMSOL Multiphysics; Version 5.2; COMSOL, Inc.: Burlington, MA, USA, 2016. [Google Scholar]
- Albella, P.; Garcia-Cueto, B.; González, F.; Moreno, F.; Wu, P.C.; Kim, T.H.; Brown, A.; Yang, Y.; Everitt, H.O.; Videen, G. Shape matters: Plasmonic nanoparticle shape enhances interaction with dielectric substrate. Nano Lett. 2011, 11, 3531–3537. [Google Scholar] [CrossRef] [PubMed]
- Harutyunyan, H.; Martinson, A.B.F.; Rosenmann, D.; Khorashad, L.K.; Besteiro, L.V.; Govorov, A.O.; Wiederrecht, G.P. Anomalous ultrafast dynamics of hot plasmonic electrons in nanostructures with hot spots. Nat. Nanotechnol. 2015, 10, 770–774. [Google Scholar] [CrossRef] [PubMed]
- Palik, E.D. Handbook of Optical Constants of Solids; Academic Press: Cambridge, MA, USA, 1998. [Google Scholar]
- Pei, F.; Wu, S.; Wang, G.; Xu, M.; Wang, S.Y.; Chen, L.Y.; Jia, Y. Electronic and Optical Properties of Noble Metal Oxides M2O (M=Cu, Ag and Au): First-principles Study. J. Korean Phys. Soc. 2008, 55, 1243–1249. [Google Scholar]
- Noguez, C. Surface plasmons on metal nanoparticles: The influence of shape and physical environment. J. Phys. Chem. C 2007, 111, 3606–3619. [Google Scholar] [CrossRef]
- Meier, M.; Wokaun, A. Enhanced fields on large metal particles: Dynamic depolarization. Opt. Lett. 1983, 8, 581–583. [Google Scholar] [CrossRef] [PubMed]
- Raziman, T.V.; Martin, O.J.F. Polarisation charges and scattering behaviour of realistically rounded plasmonic nanostructures. Opt. Express 2013, 21, 21500–21507. [Google Scholar] [CrossRef] [PubMed]
- Moreno, F.; Albella, P.; Nieto-Vesperinas, M. Analysis of the spectral behavior of localized plasmon resonances in the near- and far-field regimes. Langmuir 2013, 29, 6715–6721. [Google Scholar] [CrossRef] [PubMed]
- Alonso-González, P.; Albella, P.; Neubrech, F.; Huck, C.; Chen, J.; Golmar, F.; Casanova, F.; Hueso, L.E.; Pucci, A.; Aizpurua, J.; et al. Experimental verification of the spectral shift between near- and far-field peak intensities of plasmonic infrared nanoantennas. Phys. Rev. Lett. 2013, 110, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Liao, P.F. Lightning rod effect in surface enhanced Raman scattering. J. Chem. Phys. 1982, 76, 751. [Google Scholar] [CrossRef]
- Romo-Herrera, J.M.; González, A.L.; Guerrini, L.; Castiello, F.R.; Alonso-Nuñez, G.; Contreras, O.E.; Alvarez-Puebla, R.A. A study of the depth and size of concave cube Au nanoparticles as highly sensitive SERS probes. Nanoscale 2016, 8, 7326–7333. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Akozbek, N.; Kim, T.H.; Sanz, J.M.; Moreno, F.; Losurdo, M.; Brown, A.S.; Everitt, H.O. Ultraviolet–Visible plasmonic properties of gallium nanoparticles investigated by Variable-Angle spectroscopic and mueller matrix ellipsometry. ACS Photonics 2014, 1, 582–589. [Google Scholar] [CrossRef]
- Sherry, L.J.; Chang, S.H.; Schatz, G.C.; Van Duyne, R.P.; Wiley, B.J.; Xia, Y. Localized surface plasmon resonance spectroscopy of single silver nanocubes. Nano Lett. 2005, 5, 2034–2038. [Google Scholar] [CrossRef] [PubMed]
- Nicoletti, O.; de la Peña, F.; Leary, R.K.; Holland, D.J.; Ducati, C.; Midgley, P.A. Three-dimensional imaging of localized surface plasmon resonances of metal nanoparticles. Nature 2013, 502, 80–84. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Zheng, Z.; Ke, X.; Jaatinen, E.; Xie, T.; Wang, D.; Guo, C.; Zhao, J.; Zhu, H. Supported silver nanoparticles as photocatalysts under ultraviolet and visible light irradiation. Green Chem. 2010, 12, 414. [Google Scholar] [CrossRef]
- Yuan, Y.; Yan, N.; Dyson, P.J. Advances in the rational design of rhodium nanoparticle catalysts: Control via manipulation of the nanoparticle core and stabilizer. ACS Catal. 2012, 2, 1057–1069. [Google Scholar] [CrossRef]
- Shuang, S.; Lv, R.; Xie, Z.; Zhang, Z. Surface plasmon enhanced photocatalysis of Au/Pt-decorated TiO2 Nanopillar Arrays. Sci. Rep. 2016, 6, 26670. [Google Scholar] [CrossRef] [PubMed]




© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gutiérrez, Y.; Ortiz, D.; Saiz, J.M.; González, F.; Everitt, H.O.; Moreno, F. The UV Plasmonic Behavior of Distorted Rhodium Nanocubes. Nanomaterials 2017, 7, 425. https://doi.org/10.3390/nano7120425
Gutiérrez Y, Ortiz D, Saiz JM, González F, Everitt HO, Moreno F. The UV Plasmonic Behavior of Distorted Rhodium Nanocubes. Nanomaterials. 2017; 7(12):425. https://doi.org/10.3390/nano7120425
Chicago/Turabian StyleGutiérrez, Yael, Dolores Ortiz, José M. Saiz, Francisco González, Henry O. Everitt, and Fernando Moreno. 2017. "The UV Plasmonic Behavior of Distorted Rhodium Nanocubes" Nanomaterials 7, no. 12: 425. https://doi.org/10.3390/nano7120425
APA StyleGutiérrez, Y., Ortiz, D., Saiz, J. M., González, F., Everitt, H. O., & Moreno, F. (2017). The UV Plasmonic Behavior of Distorted Rhodium Nanocubes. Nanomaterials, 7(12), 425. https://doi.org/10.3390/nano7120425





