Modeling of Interactions between the Zebrafish Hatching Enzyme ZHE1 and A Series of Metal Oxide Nanoparticles: Nano-QSAR and Causal Analysis of Inactivation Mechanisms
Abstract
:1. Introduction
2. Results
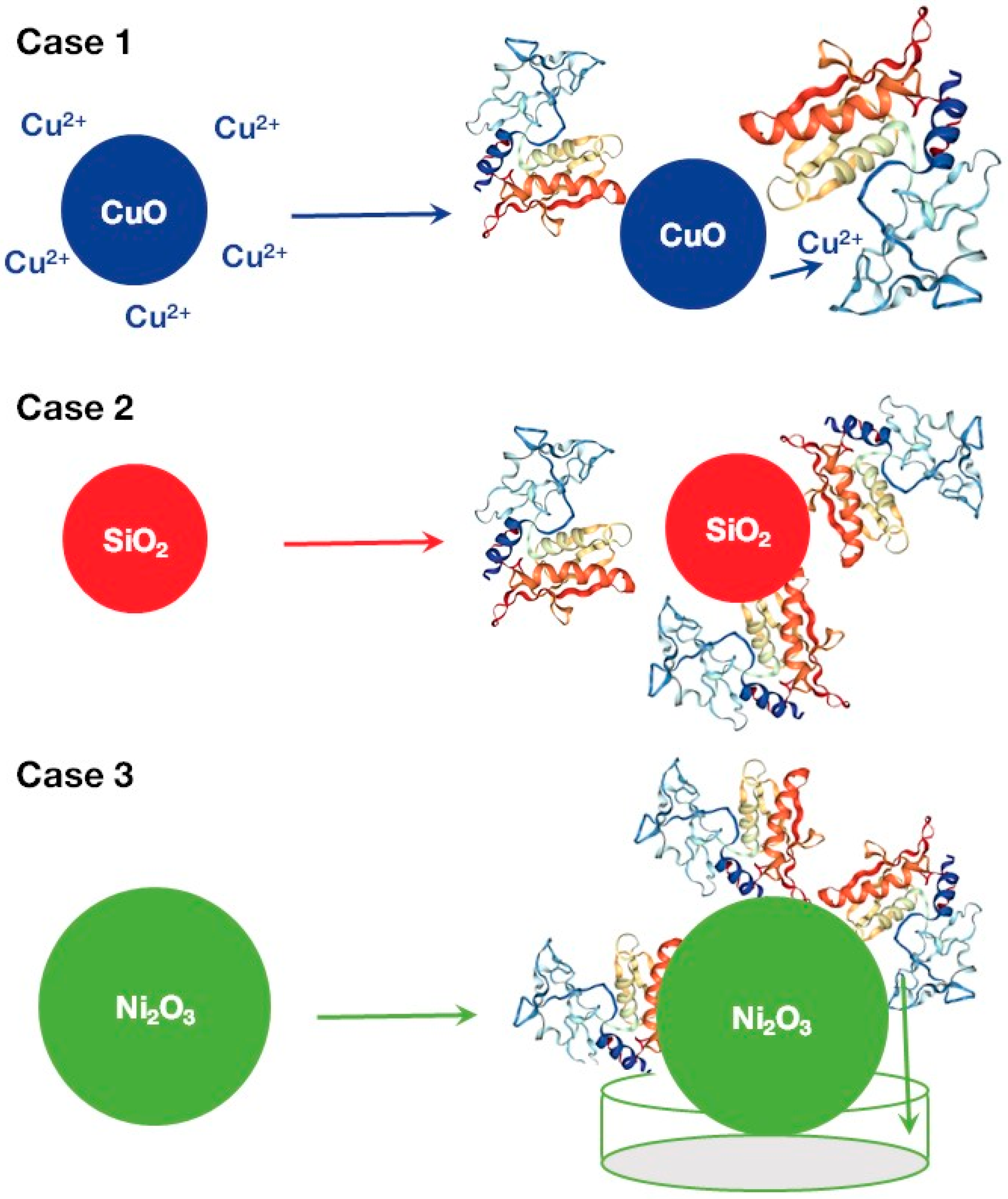
3. Discussion
4. Materials and Methods
4.1. Biological Activity Data
4.2. Theoretical Descriptors
4.3. QSAR Modeling
4.4. Causal Relationships Modeling
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Islam, N.; Miyazaki, K. An Empirical Analysis of Nanotechnology Research Domains. Technovation 2010, 30, 229–237. [Google Scholar] [CrossRef]
- Roco, M.C. The Long View of Nanotechnology Development: The National Nanotechnology Initiative at 10 Years. J. Nanoparticle Res. 2011, 13, 427–445. [Google Scholar] [CrossRef]
- Allarakhia, M.; Walsh, S. Analyzing and Organizing Nanotechnology Development: Application of the Institutional Analysis Development Framework to Nanotechnology Consortia. Technovation 2012, 32, 216–226. [Google Scholar] [CrossRef]
- Caballero-Guzman, A.; Nowack, B. A Critical Review of Engineered Nanomaterial Release Data: Are Current Data Useful for Material Flow Modeling? Environ. Pollut. 2016, 213, 502–517. [Google Scholar] [CrossRef] [PubMed]
- Chapman, K.L.; Holzgrefe, H.; Black, L.E.; Brown, M.; Chellman, G.; Copeman, C.; Couch, J.; Creton, S.; Gehen, S.; Hoberman, A.; et al. Pharmaceutical Toxicology: Designing Studies to Reduce Animal Use, While Maximizing Human Translation. Regul. Toxicol. Pharmacol. 2013, 66, 88–103. [Google Scholar] [CrossRef] [PubMed]
- Auffan, M.; Rose, J.; Bottero, J.-Y.; Lowry, G.V.; Jolivet, J.-P.; Wiesner, M.R. Towards a Definition of Inorganic Nanoparticles from an Environmental, Health and Safety Perspective. Nat. Nanotechnol. 2009, 4, 634–641. [Google Scholar] [CrossRef] [PubMed]
- Gonzalez, L.; Lison, D.; Kirsch-Volders, M. Genotoxicity of Engineered Nanomaterials: A Critical Review. Nanotoxicology 2008, 2, 252–273. [Google Scholar] [CrossRef]
- Jiang, S.; Gao, Q.; Chen, H.; Roco, M.C. The Roles of Sharing, Transfer, and Public Funding in Nanotechnology Knowledge-Diffusion Networks. J. Assoc. Inf. Sci. Technol. 2015, 66, 1017–1029. [Google Scholar] [CrossRef]
- Doke, S.K.; Dhawale, S.C. Alternatives to Animal Testing: A Review. Saudi Pharm. J. 2015, 23, 223–229. [Google Scholar] [CrossRef] [PubMed]
- Couvreur, P.; Vauthier, C. Nanotechnology: Intelligent Design to Treat Complex Disease. Pharm. Res. 2006, 23, 1417–1450. [Google Scholar] [CrossRef] [PubMed]
- George, S.; Xia, T.; Rallo, R.; Zhao, Y.; Ji, Z.; Lin, S.; Wang, X.; Zhang, H.; France, B.; Schoenfeld, D.; et al. Use of a High-Throughput Screening Approach Coupled with In Vivo Zebrafish Embryo Screening To Develop Hazard Ranking for Engineered Nanomaterials. ACS Nano 2011, 5, 1805–1817. [Google Scholar] [CrossRef] [PubMed]
- Lin, S.; Zhao, Y.; Ji, Z.; Ear, J.; Chang, C.H.; Zhang, H.; Low-Kam, C.; Yamada, K.; Meng, H.; Wang, X.; et al. Zebrafish High-Throughput Screening to Study the Impact of Dissolvable Metal Oxide Nanoparticles on the Hatching Enzyme, ZHE1. Small 2013, 9, 1776–1785. [Google Scholar] [CrossRef] [PubMed]
- Rasulev, B.; Gajewicz, A.; Puzyn, T.; Leszczynska, D.; Leszczynski, J. Chapter 10. Nano-QSAR: Advances and Challenges. In Towards Efficient Designing of Safe Nanomaterials: Innovative Merge of Computational Approaches and Experimental Techniques; The Royal Society of Chemistry: London, UK, 2012; pp. 220–256. [Google Scholar]
- Berhanu, W.M.; Pillai, G.G.; Oliferenko, A.A.; Katritzky, A.R. Quantitative Structure–Activity/Property Relationships: The Ubiquitous Links between Cause and Effect. Chempluschemistry 2012, 77, 507–517. [Google Scholar] [CrossRef]
- Tropsha, A. Best Practices for QSAR Model Development, Validation, and Exploitation. Mol. Inform. 2010, 29, 476–488. [Google Scholar] [CrossRef] [PubMed]
- Tropsha, A.; Abraham, D.J. Recent Advances in Development, Validation, and Exploitation of QSAR Models. In Burger’s Medicinal Chemistry and Drug Discovery; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2003. [Google Scholar]
- Consonni, V.; Todeschini, R. Molecular Descriptors. In Recent Advances in QSAR Studies: Methods and Applications; Puzyn, T., Leszczynski, J., Cronin, T.M., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 29–102. [Google Scholar]
- Tantra, R.; Oksel, C.; Puzyn, T.; Wang, J.; Robinson, K.N.; Wang, X.Z.; Ma, C.Y.; Wilkins, T. Nano(Q)SAR: Challenges, Pitfalls and Perspectives. Nanotoxicology 2015, 9, 636–642. [Google Scholar] [CrossRef] [PubMed]
- Panneerselvam, S.; Choi, S. Nanoinformatics: Emerging Databases and Available Tools. Int. J. Mol. Sci. 2014, 15, 7158–7182. [Google Scholar] [CrossRef] [PubMed]
- Sizochenko, N.; Majumdar, D.; Roszak, S.; Leszczynski, J. Application of Quantum Mechanics and Molecular Mechanics in Chemoinformatics. In Handbook of Computational Chemistry; Leszczynski, J., Ed.; Springer: Dordrecht, The Netherlands, 2017; pp. 2041–2063. [Google Scholar]
- Cho, W.-S.; Thielbeer, F.; Duffin, R.; Johansson, E.M.V.; Megson, I.L.; MacNee, W.; Bradley, M.; Donaldson, K. Surface Functionalization Affects the Zeta Potential, Coronal Stability and Membranolytic Activity of Polymeric Nanoparticles. Nanotoxicology 2014, 8, 202–211. [Google Scholar] [CrossRef] [PubMed]
- Oksel, C.; Ma, C.Y.; Wang, X.Z. Current Situation on the Availability of Nanostructure–biological Activity Data. SAR QSAR Environ. Res. 2015, 26, 79–94. [Google Scholar] [CrossRef] [PubMed]
- Sizochenko, N.; Rasulev, B.; Gajewicz, A.; Kuz’min, V.; Puzyn, T.; Leszczynski, J. From Basic Physics to Mechanisms of Toxicity: The “liquid Drop” approach Applied to Develop Predictive Classification Models for Toxicity of Metal Oxide Nanoparticles. Nanoscale 2014, 6, 13986–13993. [Google Scholar] [CrossRef] [PubMed]
- Mikolajczyk, A.; Sizochenko, N.; Mulkiewicz, E.; Malankowska, A.; Nischk, M.; Jurczak, P.; Hirano, S.; Nowaczyk, G.; Zaleska-Medynska, A.; Leszczynski, J.; et al. Evaluating the Toxicity of TiO2-Based Nanoparticles to Chinese Hamster Ovary Cells and Escherichia Coli: A Complementary Experimental and Computational Approach. Beilstein J. Nanotechnol. 2017. accepted. [Google Scholar]
- Holt, D.; Magos, L.; Webb, M. The Interaction of Cadium-Induced Rat Renal Metallothionein with Bivalent Mercury in Vitro. Chem. Biol. Interact. 1980, 32, 125–135. [Google Scholar] [CrossRef]
- Holland, D.R.; Hausrath, A.C.; Juers, D.; Matthews, B.W. Structural Analysis of Zinc Substitutions in the Active Site of Thermolysin. Protein Sci. 1995, 4, 1955–1965. [Google Scholar] [CrossRef] [PubMed]
- Gomis-Rüth, F.X.; Grams, F.; Yiallouros, I.; Nar, H.; Küsthardt, U.; Zwilling, R.; Bode, W.; Stöcker, W. Crystal Structures, Spectroscopic Features, and Catalytic Properties of cobalt(II), copper(II), nickel(II), and mercury(II) Derivatives of the Zinc Endopeptidase Astacin. A Correlation of Structure and Proteolytic Activity. J. Biol. Chem. 1994, 269, 17111–17117. [Google Scholar] [PubMed]
- Fukasawa, K.M.; Hata, T.; Ono, Y.; Hirose, J.; Fukasawa, K.M.; Hata, T.; Ono, Y.; Hirose, J. Metal Preferences of Zinc-Binding Motif on Metalloproteases. J. Amino Acids 2011, 2011, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Kooi, C.; Subsin, B.; Chen, R.; Pohorelic, B.; Sokol, P.A. Burkholderia Cenocepacia ZmpB Is a Broad-Specificity Zinc Metalloprotease Involved in Virulence. Infect. Immun. 2006, 74, 4083–4093. [Google Scholar] [CrossRef] [PubMed]
- Sizochenko, N.; Gajewicz, A.; Leszczynski, J.; Puzyn, T. Causation or Only Correlation? Application of Causal Inference Graphs for Evaluating Causality in Nano-QSAR Models. Nanoscale 2016, 8, 7203–7208. [Google Scholar] [CrossRef] [PubMed]
- Sizochenko, N.; Jagiello, K.; Leszczynski, J.; Puzyn, T. How The “liquid Drop” Approach Could Be Efficiently Applied for Quantitative Structure-Property Relationship Modeling of Nanofluids. J. Phys. Chem. C 2015, 119, 25542–25547. [Google Scholar] [CrossRef]
- Sizochenko, N.; Syzochenko, M.; Gajewicz, A.; Leszczynski, J.; Puzyn, T. Predicting Physical Properties of Nanofluids by Computational Modeling. J. Phys. Chem. C 2017, 121, 1910–1917. [Google Scholar] [CrossRef]
- Sizochenko, N.; Rasulev, B.; Gajewicz, A.; Mokshyna, E.; Kuz’min, V.E.; Leszczynski, J.; Puzyn, T. Causal Inference Methods to Assist in Mechanistic Interpretation of Classification Nano-SAR Models. RSC Adv. 2015, 5, 77739–77745. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Quinlan, J. Learning With Continuous Classes. In Proceedings AI’92; Adams, A., Sterling, L., Eds.; World Scientific: Singapore, 1992; pp. 343–348. [Google Scholar]
- Spirtes, P.; Glymour, C.; Scheines, R. Causation, Prediction, and Search; Springer: New York, NY, USA, 1993; pp. 41–86. [Google Scholar]
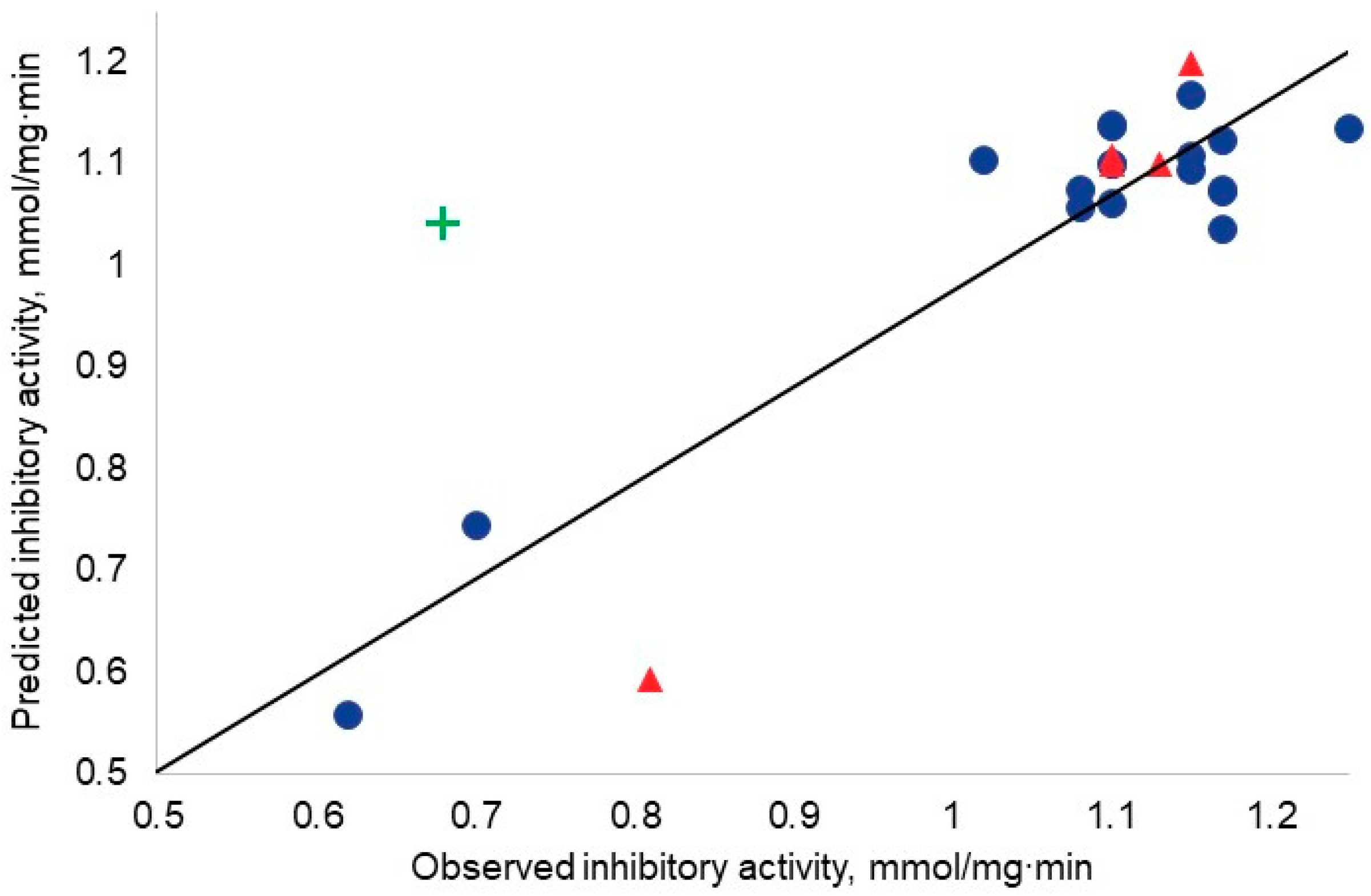
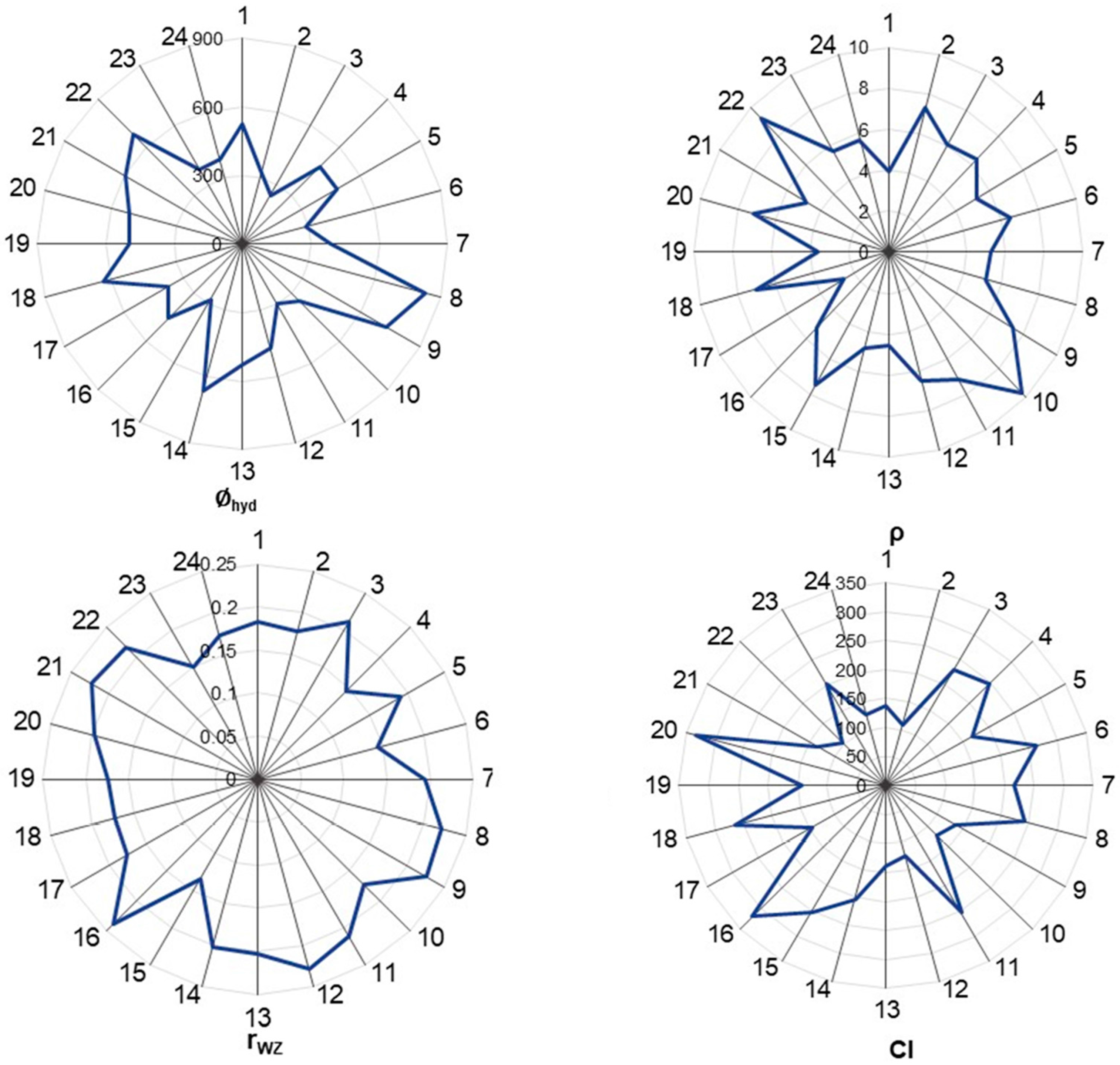
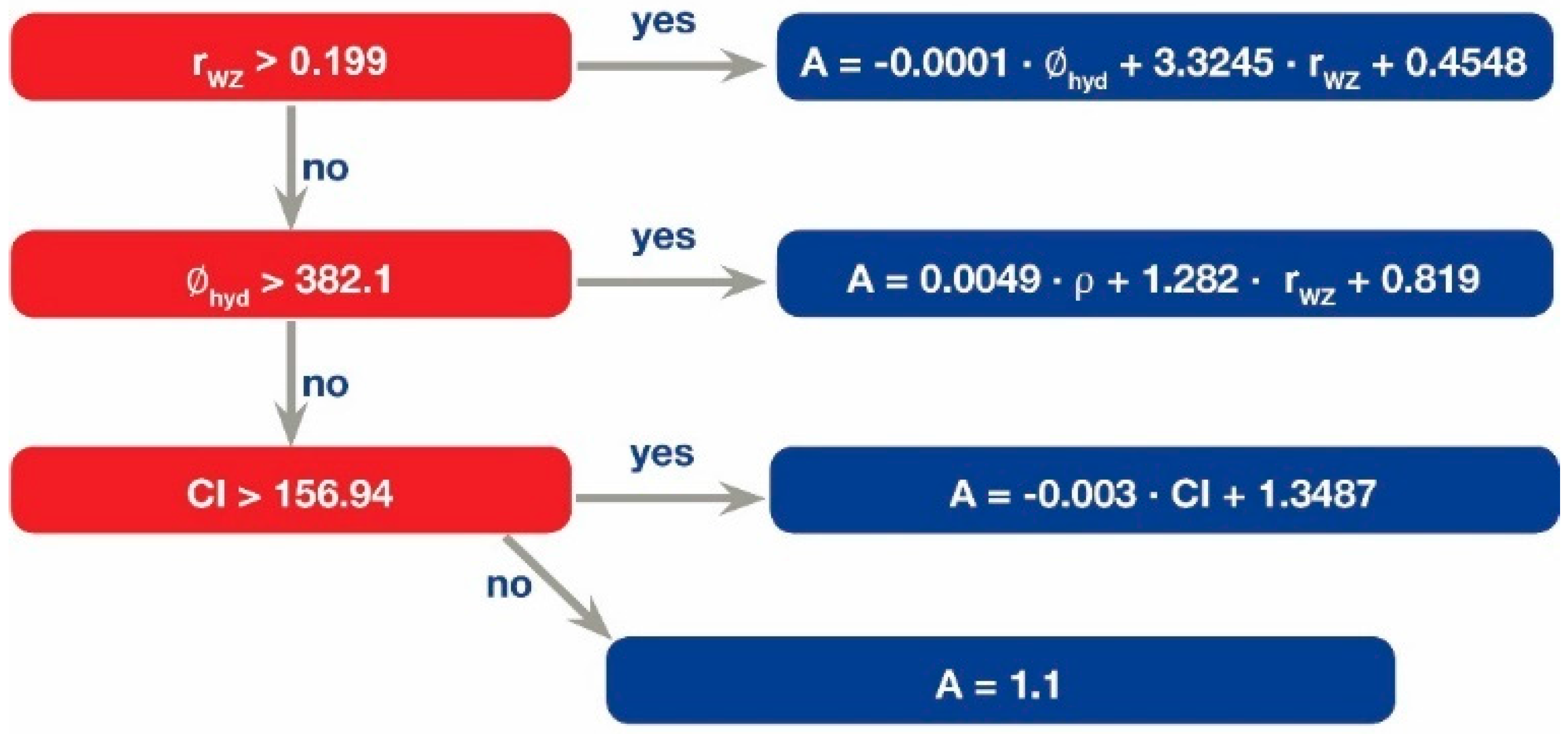
| Descriptor | Symbol | Descriptor Type | RI, % |
|---|---|---|---|
| hydrodynamic size | ∅hyd | experimental | 37.8 |
| density | ρ | LDM | 16.2 |
| Wigner–Seitz radius | rwz | LDM | 37.8 |
| covalent index | CI | ionic | 8.2 |
| NP | Hydrodynamic Size (∅hyd), nm | Density (ρ), g/sm3 | Wigner–Seitz Radius (rwz), a.u. | Covalent Index (CI) | Enzyme Activity (A), mmol/mg∙min |
|---|---|---|---|---|---|
| Al2O3 | 524.8 | 3.96 | 0.183 | 138.68 | 1.17 |
| CeO2 | 321.3 | 7.30 | 0.178 | 109.13 | 1.10 |
| Co3O4 | 247.6 | 6.07 | 0.212 | 229.74 | 1.25 |
| CoO | 378.3 | 6.40 | 0.144 | 247.41 | 1.17 |
| Cr2O3 | 478.5 | 5.21 | 0.191 | 168.09 | 0.68 |
| CuO | 289.5 | 6.45 | 0.143 | 263.53 | 0.62 |
| Fe2O3 | 385.2 | 5.25 | 0.194 | 216.00 | 1.15 |
| Fe3O4 | 831.7 | 5.20 | 0.220 | 241.12 | 1.02 |
| Gd2O3 | 726.7 | 7.41 | 0.227 | 134.64 | 1.10 |
| HfO2 | 349.9 | 9.68 | 0.173 | 119.99 | 1.10 |
| In2O3 | 303.2 | 7.18 | 0.210 | 253.47 | 1.17 |
| La2O3 | 471.2 | 6.51 | 0.229 | 124.87 | 1.15 |
| Mn2O3 | 525.9 | 4.55 | 0.202 | 139.35 | 1.08 |
| Ni2O3 | 665.8 | 4.83 | 0.201 | 204.29 | 1.08 |
| NiO | 277.5 | 7.45 | 0.134 | 251.72 | 0.81 |
| Sb2O3 | 459.9 | 5.19 | 0.238 | 319.39 | 1.15 |
| SiO2 | 374.9 | 2.65 | 0.176 | 144.40 | 1.10 |
| SnO2 | 635.0 | 7.01 | 0.173 | 265.07 | 1.17 |
| TiO2 | 497.0 | 3.60 | 0.174 | 143.48 | 1.10 |
| WO3 | 511.9 | 7.20 | 0.197 | 334.18 | 1.15 |
| Y2O3 | 594.5 | 4.84 | 0.223 | 133.96 | 1.10 |
| Yb2O3 | 682.6 | 9.25 | 0.217 | 105.03 | 1.10 |
| ZnO | 379 | 5.70 | 0.150 | 201.47 | 0.70 |
| ZrO2 | 384.4 | 5.68 | 0.173 | 127.36 | 1.13 |
| Control value | - | - | - | - | 1.25 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sizochenko, N.; Leszczynska, D.; Leszczynski, J. Modeling of Interactions between the Zebrafish Hatching Enzyme ZHE1 and A Series of Metal Oxide Nanoparticles: Nano-QSAR and Causal Analysis of Inactivation Mechanisms. Nanomaterials 2017, 7, 330. https://doi.org/10.3390/nano7100330
Sizochenko N, Leszczynska D, Leszczynski J. Modeling of Interactions between the Zebrafish Hatching Enzyme ZHE1 and A Series of Metal Oxide Nanoparticles: Nano-QSAR and Causal Analysis of Inactivation Mechanisms. Nanomaterials. 2017; 7(10):330. https://doi.org/10.3390/nano7100330
Chicago/Turabian StyleSizochenko, Natalia, Danuta Leszczynska, and Jerzy Leszczynski. 2017. "Modeling of Interactions between the Zebrafish Hatching Enzyme ZHE1 and A Series of Metal Oxide Nanoparticles: Nano-QSAR and Causal Analysis of Inactivation Mechanisms" Nanomaterials 7, no. 10: 330. https://doi.org/10.3390/nano7100330
APA StyleSizochenko, N., Leszczynska, D., & Leszczynski, J. (2017). Modeling of Interactions between the Zebrafish Hatching Enzyme ZHE1 and A Series of Metal Oxide Nanoparticles: Nano-QSAR and Causal Analysis of Inactivation Mechanisms. Nanomaterials, 7(10), 330. https://doi.org/10.3390/nano7100330






