Performance Evaluation of a Nanofluid-Based Direct Absorption Solar Collector with Parabolic Trough Concentrator
Abstract
:1. Introduction

2. Results and Discussion
2.1. Solar Collection Principles and Theoretical Evaluation of Heat Transfer
2.1.1. Solar Collection Principles
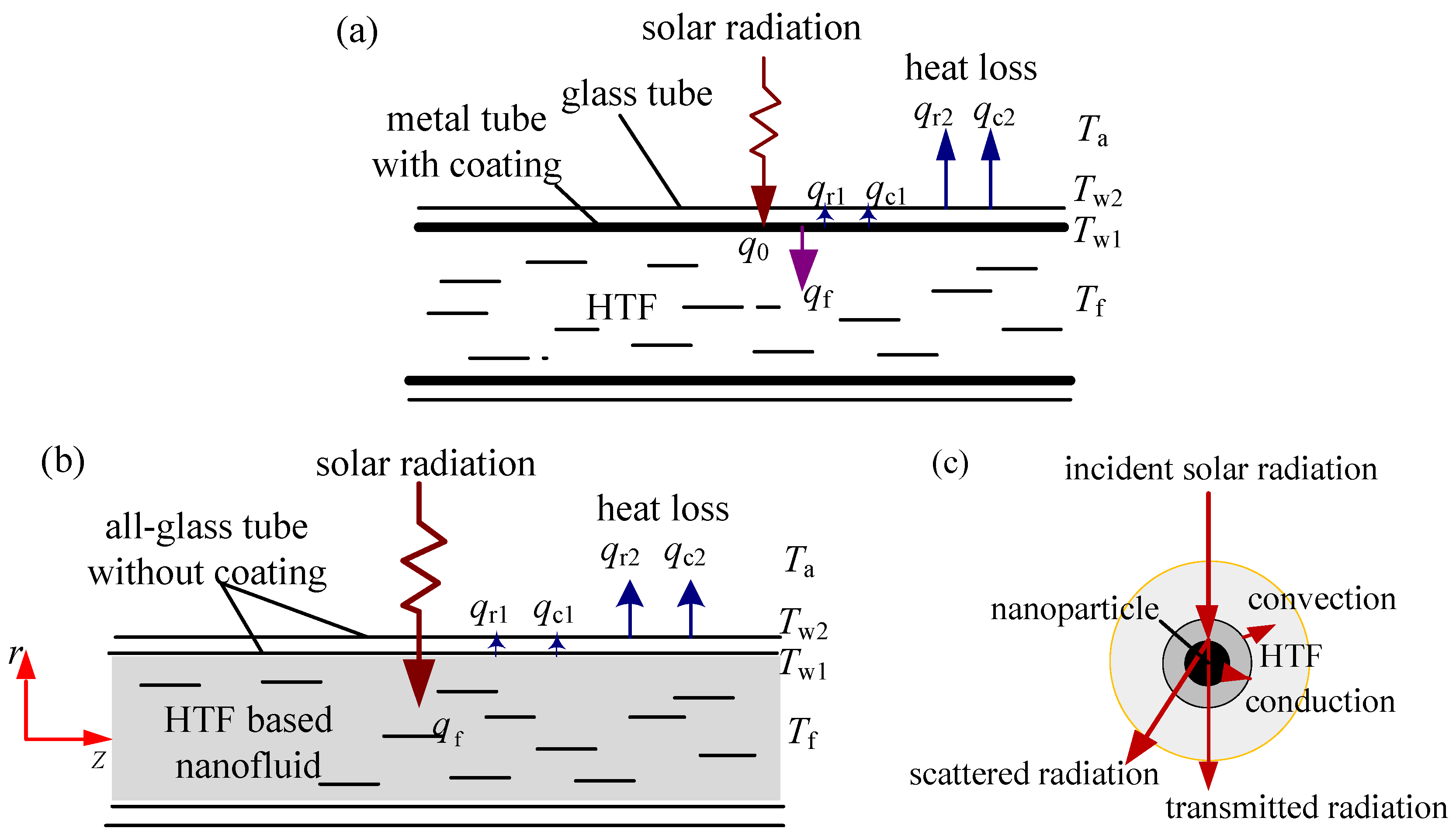
2.1.2. Theoretical Evaluation of Heat Transfer in the Novel NDASC
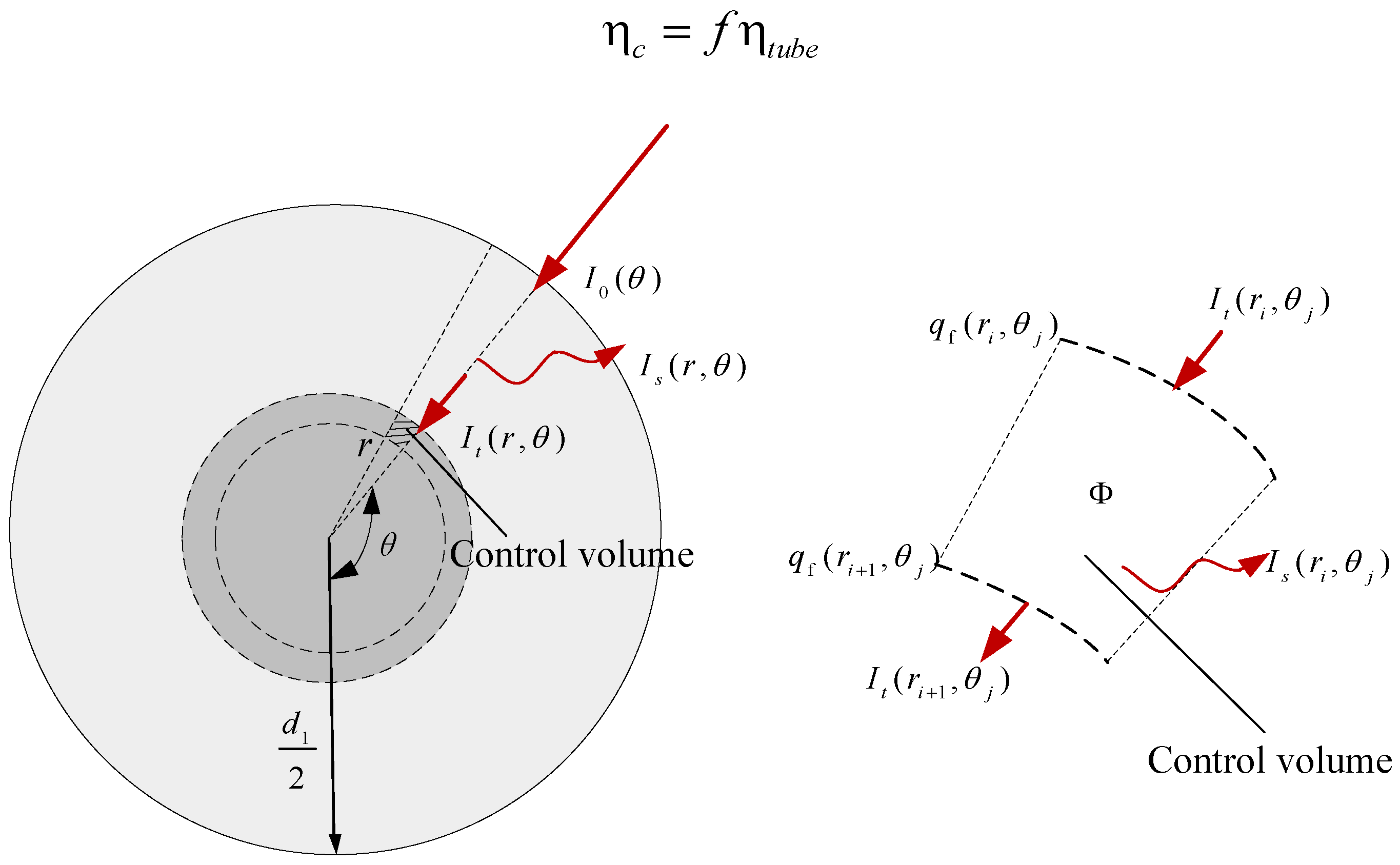
2.1.3. Theoretical Evaluation of Heat Transfer in an IASC
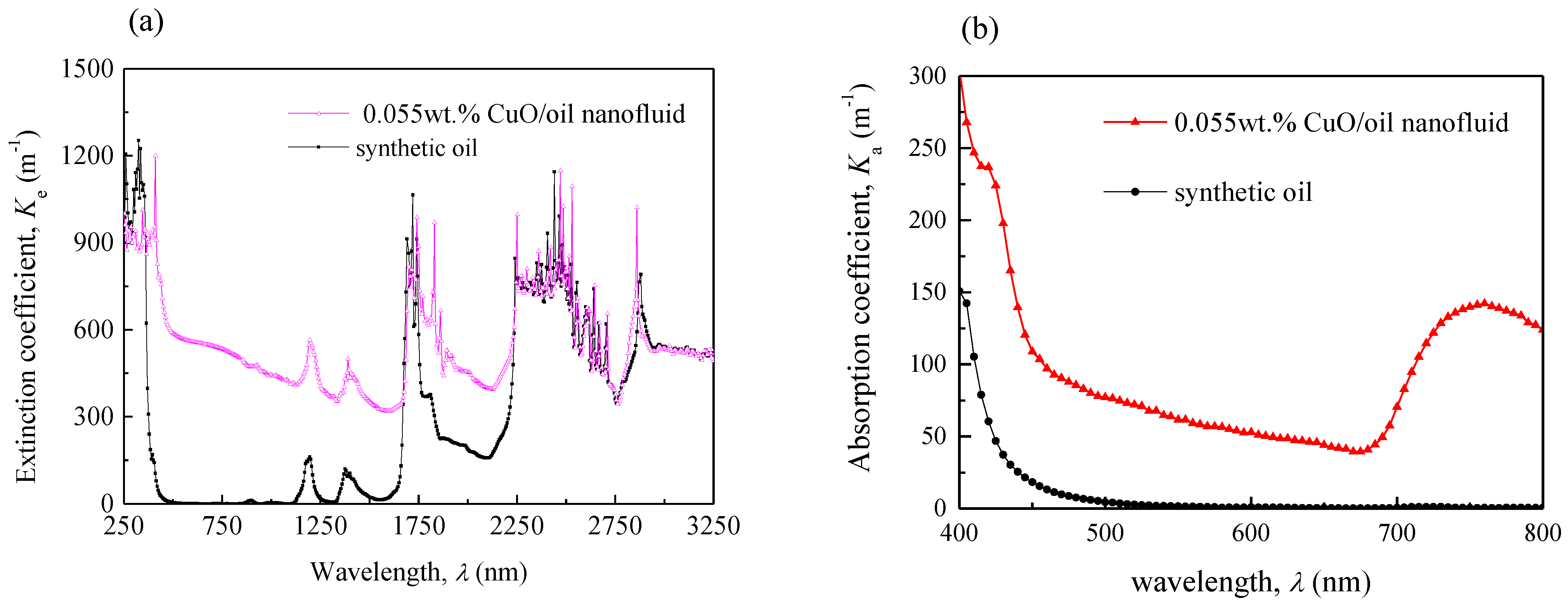
2.2. Properties of CuO/Oil Nanofluid

| Parameters | Cp | ρ | k | μ | Ke | Ka |
|---|---|---|---|---|---|---|
| Unit | J·(kg·K)−1 | kg·m−3 | W·(m·K)−1 | Pa·s | m−1 | m−1 |
| CuO nanoparticles | 475 | 6300 | 33 | - | - | - |
| synthetic oil | 2.14 × 103 | 814.7 | 0.12 | 6.2 × 10−3 | 2 | 2 |
| 0.055 wt % CuO/oil nanofluid | 2.139 × 103 | 815.1 | 0.1201 | 6.2 × 10−3 | 514 | 103 |
2.3. Theoretical Analysis on the Characteristics of the NDASC and the IASC.
2.3.1. Calculation Conditions
| Parameters | Values | Parameters | Values |
|---|---|---|---|
| Diameter of inner tube, d1 | 0.045 m | Absorption ratio of coating, α | 0.86 |
| Diameter of outer tube, d2 | 0.058 m | Transmittance of glass, τg | 0.93 |
| Collector tube length, L | 1.8 m | Dirt coefficient, τd | 0.97 |
| Concentrator’s aperture width, W | 1.04 m | Emissivity of glass, εg | 0.89 |
| Optical efficiency factor, f | 0.73 | Emissivity of coating, εco | 0.09 |

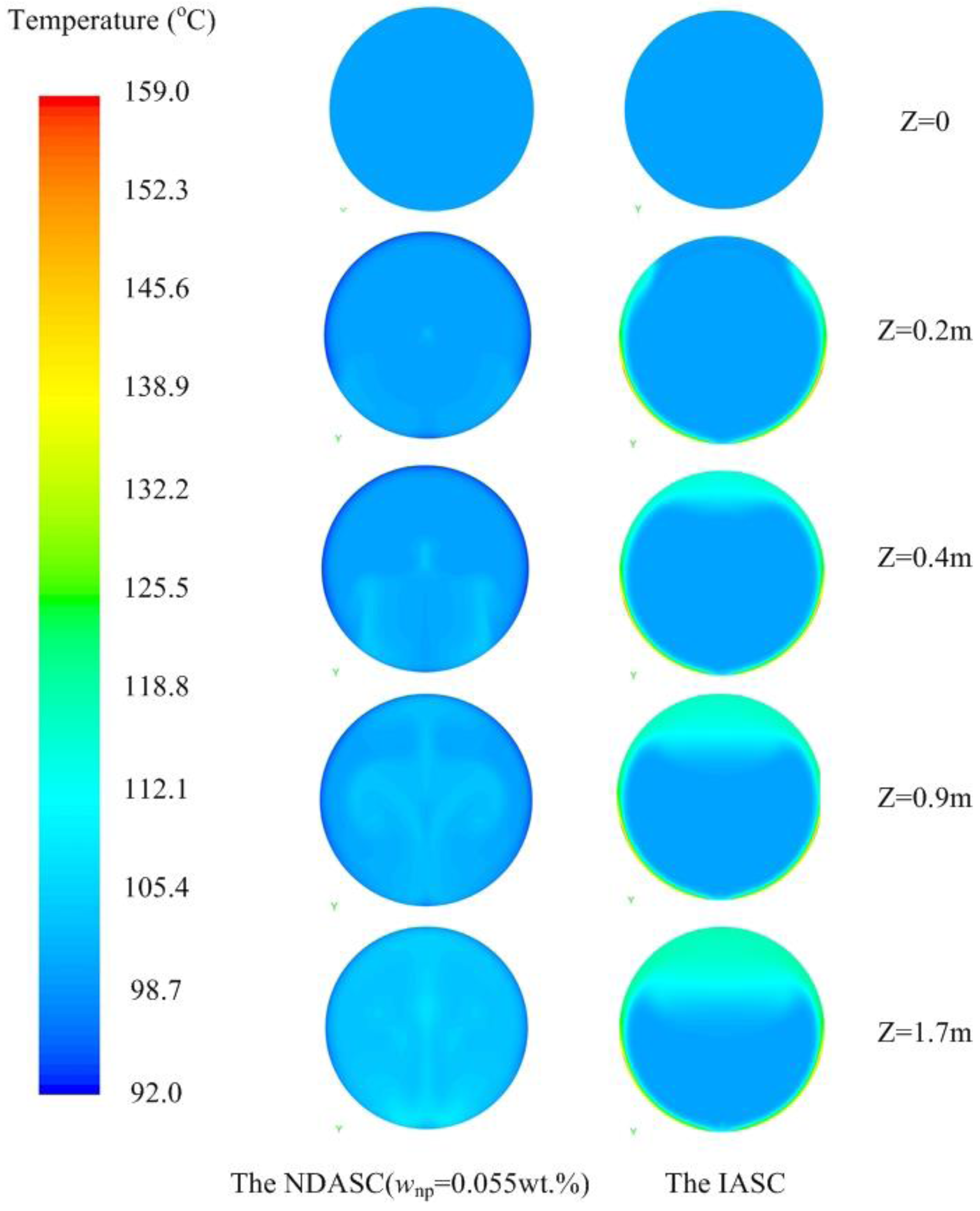
2.3.2. Temperature Distributions inside Collector Tubes

2.3.3 Solar Collection Efficiencies

3. Experimental Section
3.1. Experimental Setups for Solar Collection

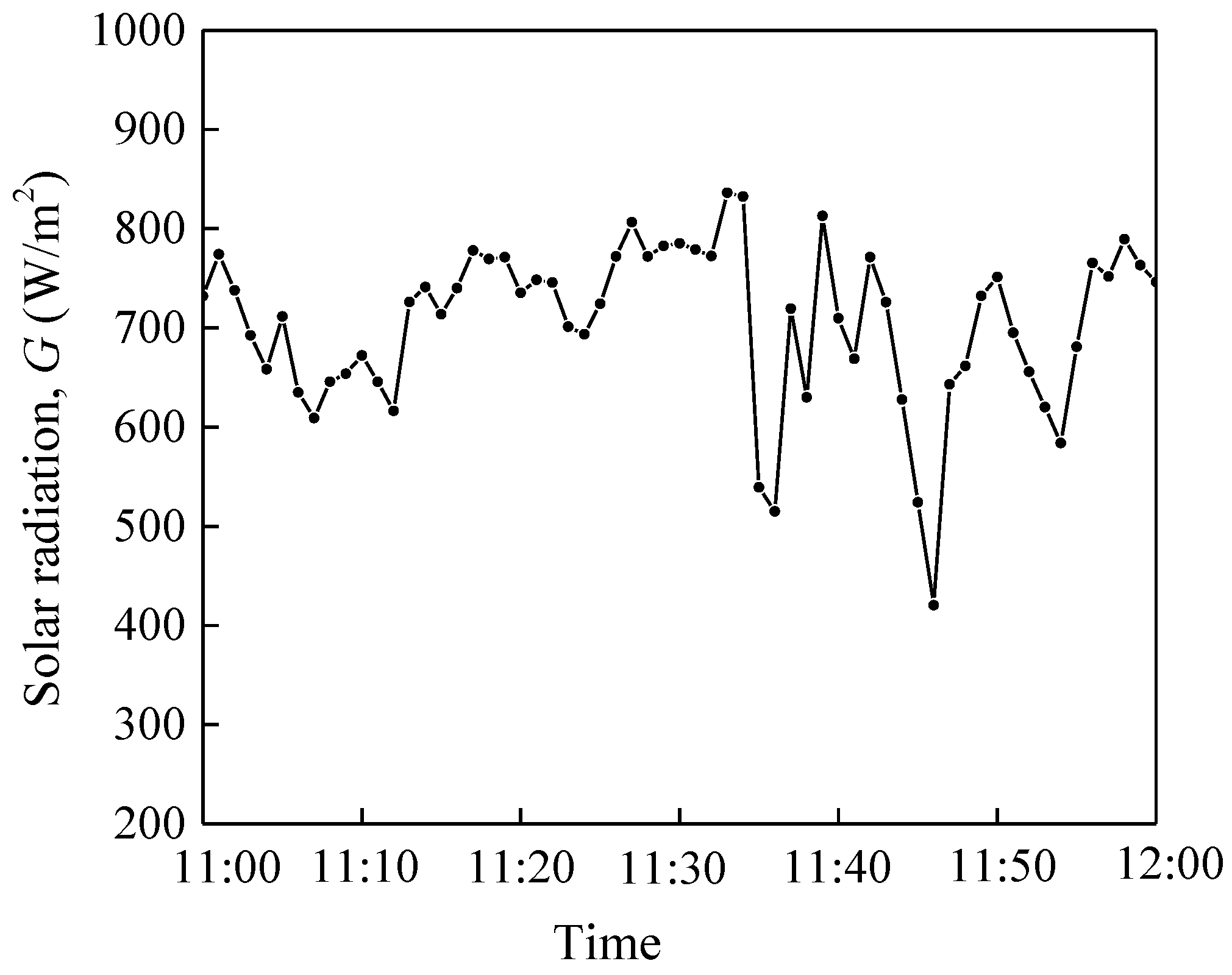
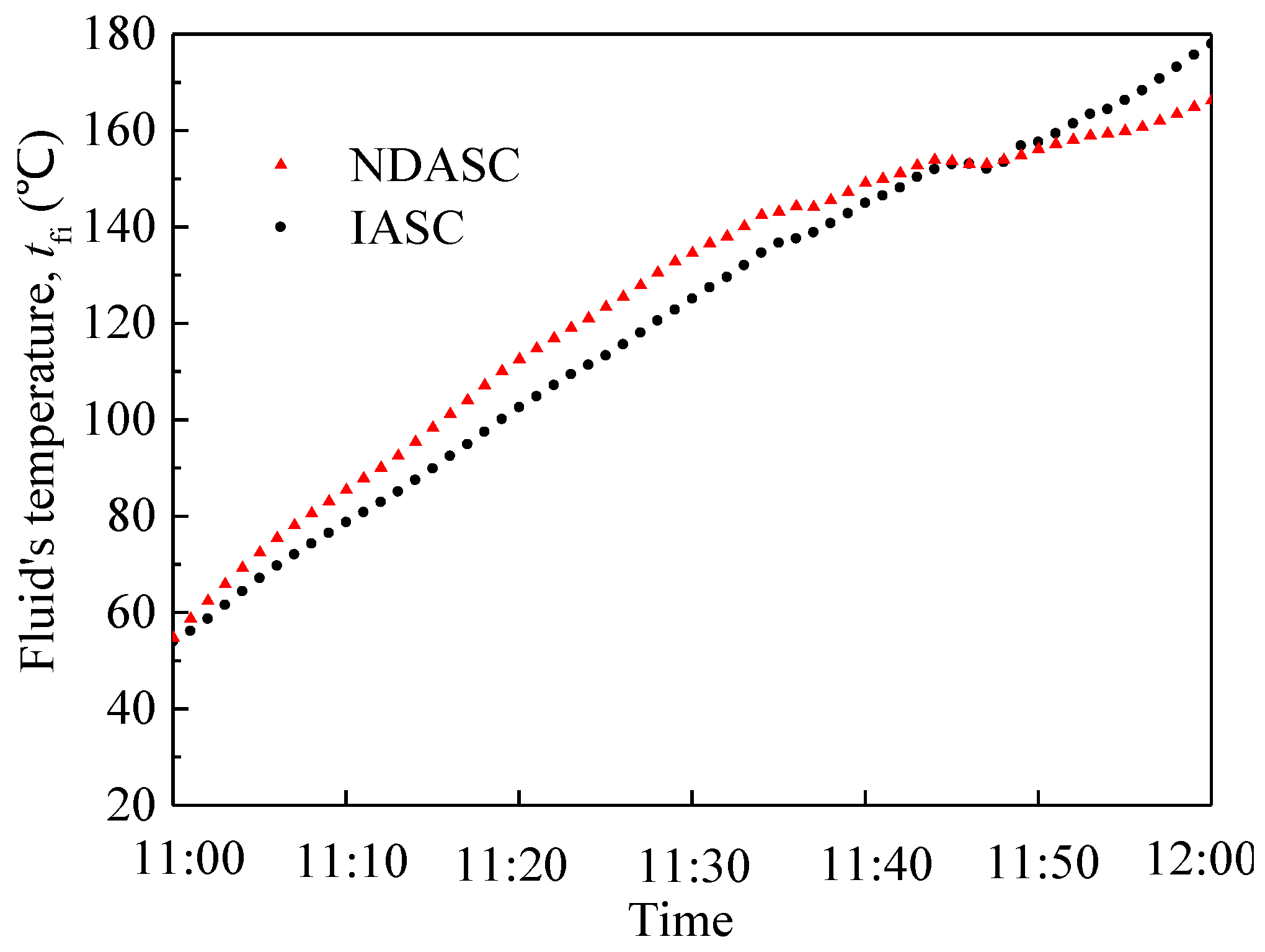
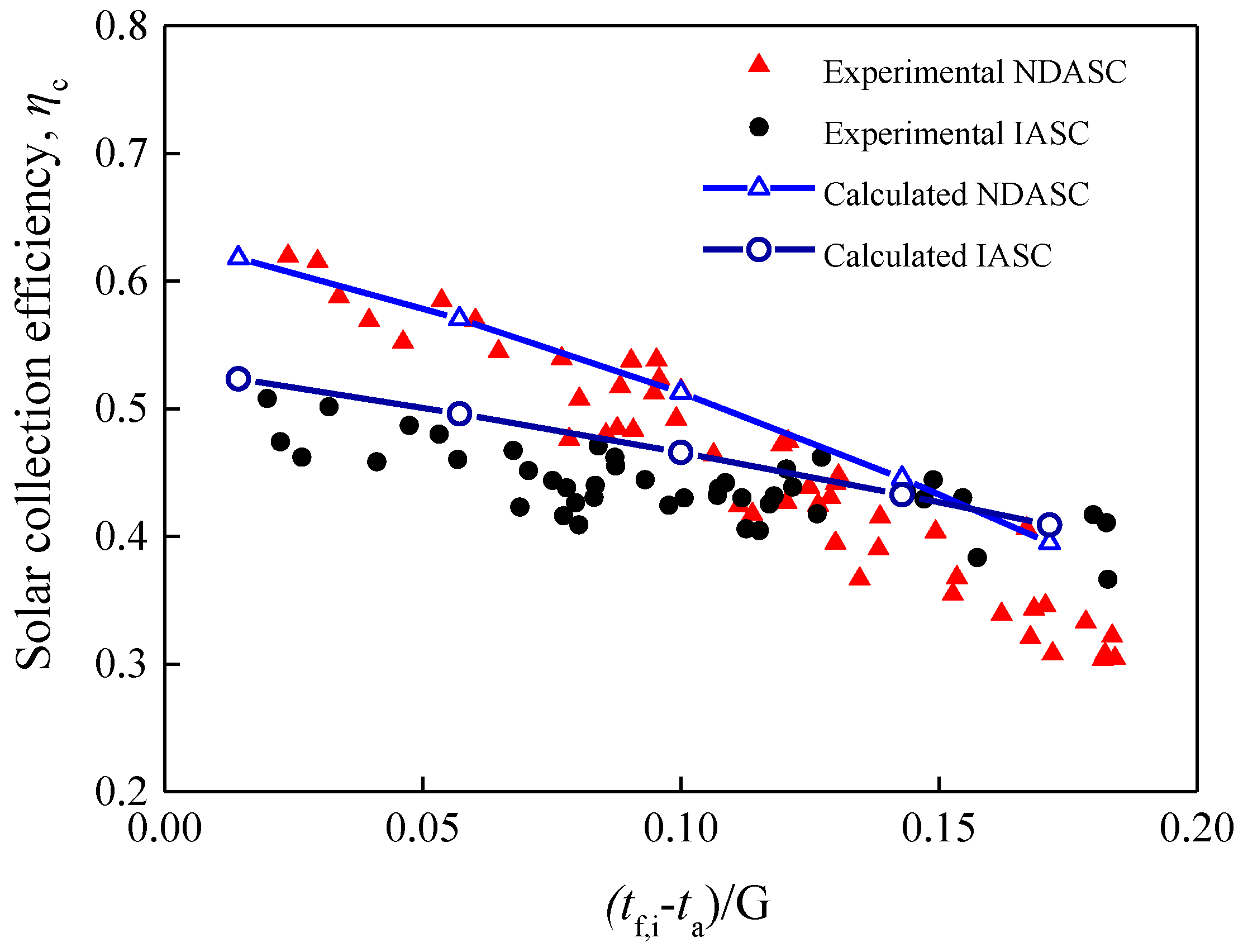
3.2. Experimental Comparison of Solar Collection Efficiencies
4. Conclusions
- By adding nanoparticles, the solar absorptivity of a heat-transfer fluid can be significantly improved. Heat transfer in uncoated tube in the NDASC was more efficient than that in the IASC.
- The fluid’s temperature distribution in the tube cross section of the NDASC was much more uniform than that of the IASC. For a conventional IASC with concentrator, the maximum temperature always occurred on the tube wall, and the temperature in focal lines was much higher. By contrast, the temperature of the nanofluid inside uncoated tube was even higher than the tube wall temperature under certain condition for the NDASC.
- Theoretical and experimental results demonstrated that the proposed NDASC with a geometrical concentrating ratio of 7.36 obtained higher collection efficiencies than the IASC, when operated below a critical temperature value at 139 °C in theoretical analysis and 128 °C in experiments, respectively. The critical temperature may vary with the ambient conditions and solar collector’s structure.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- REN21. Renewables 2014 Global Status Report. Available online: http://www.ren21.net/status-of-renewables/global-status-report/ (accessed on 10 April 2015).
- Zhu, Q.Z.; Cui, Y.; Mu, L.J.; Tang, L.Q. Characterization of thermal radiative properties of nanofluids for selective absorption of solar radiation. Int. J. Thermophys. 2013, 34, 2307–2321. [Google Scholar] [CrossRef]
- Taylor, R.A.; Phelan, P.E.; Otanicar, T.P.; Adrian, R.; Prasher, R. Nanofluid optical property characterization: Towards efficient direct absorption solar collectors. Nanoscale Res. Lett. 2011, 6. [Google Scholar] [CrossRef] [PubMed]
- Lee, B.J.; Park, K.; Walsh, T.; Xu, L. Radiative heat transfer analysis in plasmonic nanofluid for direct solar thermal absorption. J. Sol. Energy Eng. Trans Asme 2012, 134. [Google Scholar] [CrossRef]
- Otanicar, T.P.; Phelan, P.E.; Golden, J.S. Optical properties of liquids for direct absorption solar thermal energy systems. Sol. Energy 2009, 83, 969–977. [Google Scholar] [CrossRef]
- Nasrin, R.; Alim, M.; Chamkha, A.J. Effects of physical parameters on natural convection in a solar collector filled with nanofluid. Heat Trans. Asian Res. 2013, 42, 73–88. [Google Scholar] [CrossRef]
- Karami, M.; Bahabadi, M.A.; Delfani, S.; Ghozatloo, A. A new application of carbon nanotubes nanofluid as working fluid of low-temperature direct absorption solar collector. Sol. Energy Mater. Sol. Cells 2014, 121, 114–118. [Google Scholar] [CrossRef]
- Sani, E.; Mercatelli, L.; Barison, S.; Pagura, C.; Agresti, F.; Colla, L.; Sansoni, P. Potential of carbon nanohorn-based suspensions for solar thermal collectors. Sol. Energy Mater. Sol. Cells 2011, 95, 2994–3000. [Google Scholar] [CrossRef]
- Otanicar, T.P.; Phelan, P.E.; Prasher, R.S.; Rosengarten, G.; Taylor, R.A. Nanofluid-based direct absorption solar collector. J. Renew. Sustain. Energy 2010, 2, 102–115. [Google Scholar] [CrossRef]
- Tyagi, H.; Phelan, P.E.; Prasher, R.S. Predicted efficiency of a low temperature nanofluid based direct absorption solar collector. J. Sol. Energy Eng. Trans Asme 2009, 131. [Google Scholar] [CrossRef]
- Verma, S.K.; Tiwari, A.K. Progress of nanofluid application in solar collectors: A review. Energy Convers. Manag. 2015, 100, 324–346. [Google Scholar] [CrossRef]
- Kasaeian, A.; Eshghi, A.T.; Sameti, M. A review on the applications of nanofluids in solar energy systems. Renew. Sustain. Energy Rev. 2015, 43, 584–598. [Google Scholar] [CrossRef]
- Luo, Z.Y.; Wang, C.; Wei, W.; Xiao, G.; Ni, M.J. Performance improvement of a nanofluid solar collector based on direct absorption collection (DAC) concepts. Int. J. Heat Mass Transf. 2014, 75, 262–271. [Google Scholar] [CrossRef]
- Said, Z.; Saidur, R.; Rahim, N.A.; Alim, M.A. Analyses of exergy efficiency and pumping power for a conventional flat plate solar collector using SWCNTs based nanofluid. Energy Build. 2014, 78, 1–9. [Google Scholar] [CrossRef]
- Bandarra, E.; Mendoza, O.; Beicker, C.; Menezes, A.; Wen, D. Experimental investigation of a silver nanoparticle-based direct absorption solar thermal system. Energy Convers. Manag. 2014, 84, 261–267. [Google Scholar] [CrossRef]
- De Risi, A.; Milanese, M.; Laforgia, D. Modelling and optimization of transparent parabolic trough collector based on gas-phase nanofluids. Renew. Energy 2013, 58, 134–139. [Google Scholar] [CrossRef]
- Taylor, R.A.; Phelan, P.E.; Otanicar, T.P.; Walker, C.A.; Nguyen, M.; Trimble, S.; Prasher, R. Applicability of nanofluid in high flux solar collectors. J. Renew. Sustain. Energy 2011, 3. [Google Scholar] [CrossRef]
- Barlev, D.; Vidu, R.; Stroeve, P. Innovation in concentrated solar power. Sol. Energy Mater. Sol. Cells 2011, 95, 2703–2725. [Google Scholar] [CrossRef]
- Forristall, R. Heat Transfer Analysis and Modeling of a Parabolic Trough Solar Receiver Implemented in Engineering Equation Solver. In National Renewable Energy Laboratory/Technical Refort-550-34169; NREL Publication Database: Golden, CO, USA, 2003. [Google Scholar]
- Kalogirou, S.A. A detailed thermal model of a parabolic trough collector receiver. Energy 2012, 48, 298–306. [Google Scholar] [CrossRef]
- Jeter, S.M. Calculation of the concentrated flux density distribution in parabolic trough collectors by a semifinite formulation. Sol. Energy 1986, 37, 335–345. [Google Scholar] [CrossRef]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, G.; Chen, W.; Deng, S.; Zhang, X.; Zhao, S. Performance Evaluation of a Nanofluid-Based Direct Absorption Solar Collector with Parabolic Trough Concentrator. Nanomaterials 2015, 5, 2131-2147. https://doi.org/10.3390/nano5042131
Xu G, Chen W, Deng S, Zhang X, Zhao S. Performance Evaluation of a Nanofluid-Based Direct Absorption Solar Collector with Parabolic Trough Concentrator. Nanomaterials. 2015; 5(4):2131-2147. https://doi.org/10.3390/nano5042131
Chicago/Turabian StyleXu, Guoying, Wei Chen, Shiming Deng, Xiaosong Zhang, and Sainan Zhao. 2015. "Performance Evaluation of a Nanofluid-Based Direct Absorption Solar Collector with Parabolic Trough Concentrator" Nanomaterials 5, no. 4: 2131-2147. https://doi.org/10.3390/nano5042131
APA StyleXu, G., Chen, W., Deng, S., Zhang, X., & Zhao, S. (2015). Performance Evaluation of a Nanofluid-Based Direct Absorption Solar Collector with Parabolic Trough Concentrator. Nanomaterials, 5(4), 2131-2147. https://doi.org/10.3390/nano5042131





