Modeling the Dispersibility of Single Walled Carbon Nanotubes in Organic Solvents by Quantitative Structure-Activity Relationship Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Set
| No | Name | C (mg/mL) | LogC(exp) ** | LogC(cal) |
|---|---|---|---|---|
| 1 | N-Cyclohexyl-pyrrolidinone | 3.5 | 0.544 | 0.317 |
| 2 * | 1,3-Dimethyltetrahydro-2(1H)-pyrimidinone | 0.65 | −0.187 | −0.617 |
| 3 | 1-Butylpyrrolidin-2-one | 0.279 | −0.554 | −0.480 |
| 4 | 1-Benzylpyrrolidin-2-one | 0.18 | −0.745 | −0.566 |
| 5 * | 1-Methylpyrrolidin-2-one | 0.116 | −0.935 | −0.972 |
| 6 | 3-(2-Oxo-1-pyrrolidinyl)propanenitrile | 0.115 | −0.939 | −0.510 |
| 7 | N-Ethyl-pyrrolidinone | 0.101 | −0.996 | −1.200 |
| 8 | N-Octyl-pyrrolidone | 0.092 | −1.036 | −1.241 |
| 9 | N-Vinyl-pyrrolidinone | 0.084 | −1.076 | −1.459 |
| 10 | Dimethyl-imidazolidinone | 0.083 | −1.080 | −1.111 |
| 11 | Dimethylacetamide | 0.041 | −1.387 | −1.534 |
| 12 * | N-Formyl-piperidine | 0.039 | −1.409 | −1.126 |
| 13 | N-Dodecyl-pyrrolidone | 0.03 | −1.553 | −1.157 |
| 14 | Dimethylformamide | 0.023 | −1.638 | −2.374 |
| 15 | Benzyl acetate | 0.0192 | −1.717 | −2.040 |
| 16 | Propionitrile | 0.015 | −1.824 | −1.850 |
| 17 | Acrylic acid | 0.0138 | −1.860 | −2.345 |
| 18 | 2,2'-thiodiethanol | 0.0136 | −1.866 | −2.100 |
| 19 * | Ethanolamine | 0.0133 | −1.876 | −1.424 |
| 20 * | Cyclopentanone | 0.0129 | −1.889 | −1.757 |
| 21 * | Chlorophenol | 0.012 | −1.921 | −2.064 |
| 22 | Acetone | 0.011 | −1.959 | −1.530 |
| 23 | Benzyl benzoate | 0.0109 | −1.963 | −2.160 |
| 24 | Isopropyl alcohol | 0.0105 | −1.979 | −2.038 |
| 25 * | Cyclohexanone | 0.0068 | −2.168 | −2.330 |
| 26 | Toluene | 0.005 | −2.301 | −2.056 |
| 27 | Triethyleneglycol | 0.0037 | −2.432 | −2.647 |
| 28 | Formamide | 3.00 ×10−4 | −3.523 | −2.374 |
| 29 | Benzyl alcohol | 2.79×10−4 | −3.554 | −3.007 |
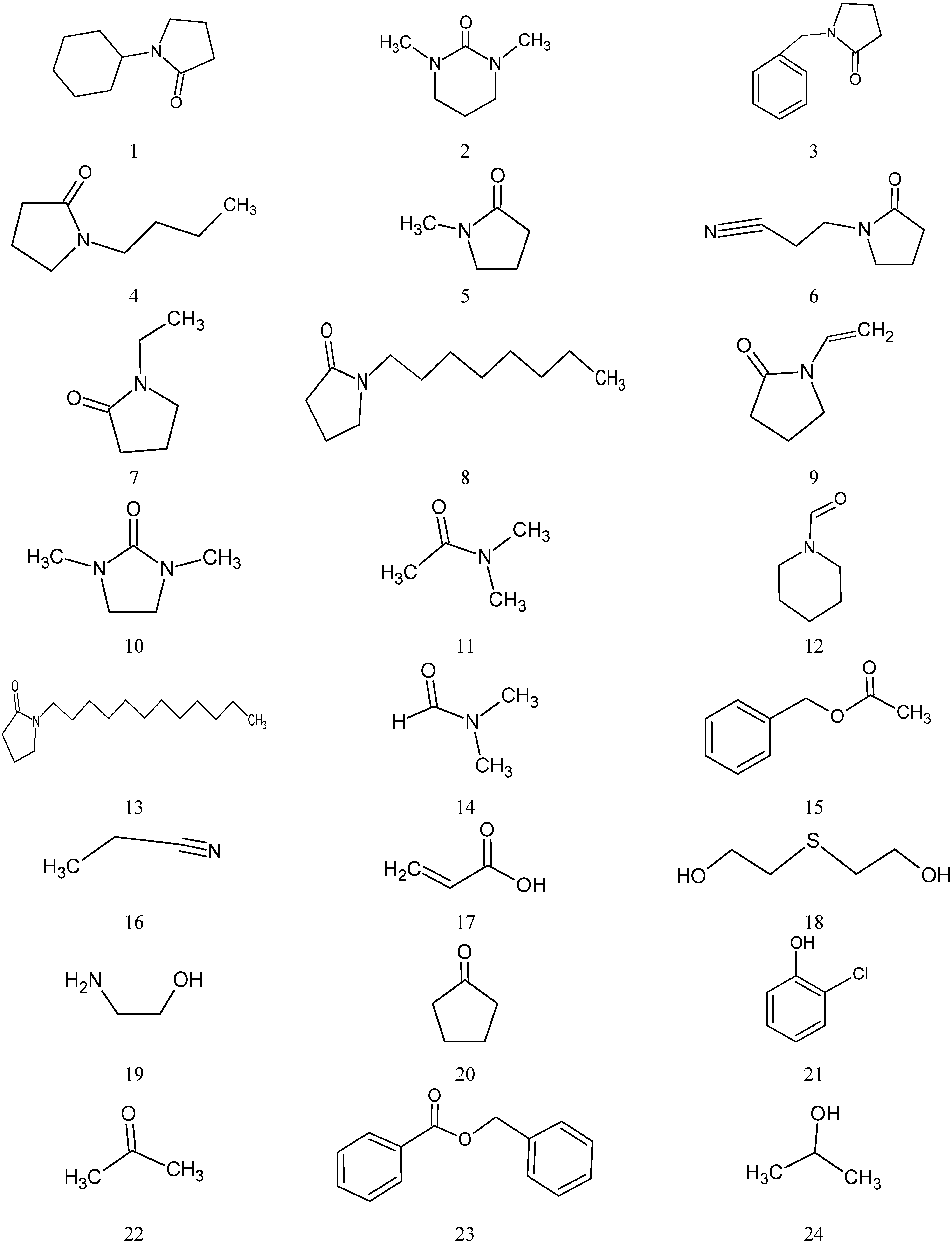
2.2. Quantum Chemical Calculations
2.3. QSAR Modeling and Statistical Analysis
3. Results and Discussion
| Descriptor | SRW09 | Dipole Z | piPC05 | Ram | X0Av | ATS6m | LogC(cal) |
|---|---|---|---|---|---|---|---|
| SRW09 | 1 | ||||||
| Dipole Z | −0.004 | 1 | |||||
| piPC05 | −0.002 | 0.009 | 1 | ||||
| Ram | 0.567 | 0.068 | 0.631 | 1 | |||
| X0Av | 0.053 | −0.112 | −0.275 | 0.075 | 1 | ||
| ATS6m | 0.427 | 0.118 | 0.532 | 0.545 | 0.042 | 1 | |
| LogC(cal) | 0.706 | 0.377 | −0.037 | 0.530 | 0.159 | 0.276 | 1 |
| No. | Descriptors | Training Set | Test Set | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| N | R2 | Q2 | F | SDEP | Spress | N | R2 | Rm(avr)2 | ΔR2 | ||
| 1 | SRW09 | 22 | 0.548 | 0.453 | 24.249 | 0.674 | 0.690 | 7 | 0.830 | 0.773 | 0.112 |
| 2 | SRW09, Dipole Z | 22 | 0.679 | 0.573 | 20.080 | 0.595 | 0.626 | 7 | 0.786 | 0.717 | 0.137 |
| 3 | Ram,piPC05, Dipole Z | 22 | 0.736 | 0.601 | 16.687 | 0.575 | 0.621 | 7 | 0.813 | 0.751 | 0.122 |
| 4 | ATS6m,SRW09, X0Av, Dipole Z | 22 | 0.797 | 0.666 | 16.722 | 0.527 | 0.585 | 7 | 0.807 | 0.744 | 0.125 |
| 5 | X3A,ATS6m, SRW09, X0Av, Dipole Z | 22 | 0.817 | 0.632 | 14.366 | 0.552 | 0.633 | 7 | 0.736 | 0.702 | 0.162 |
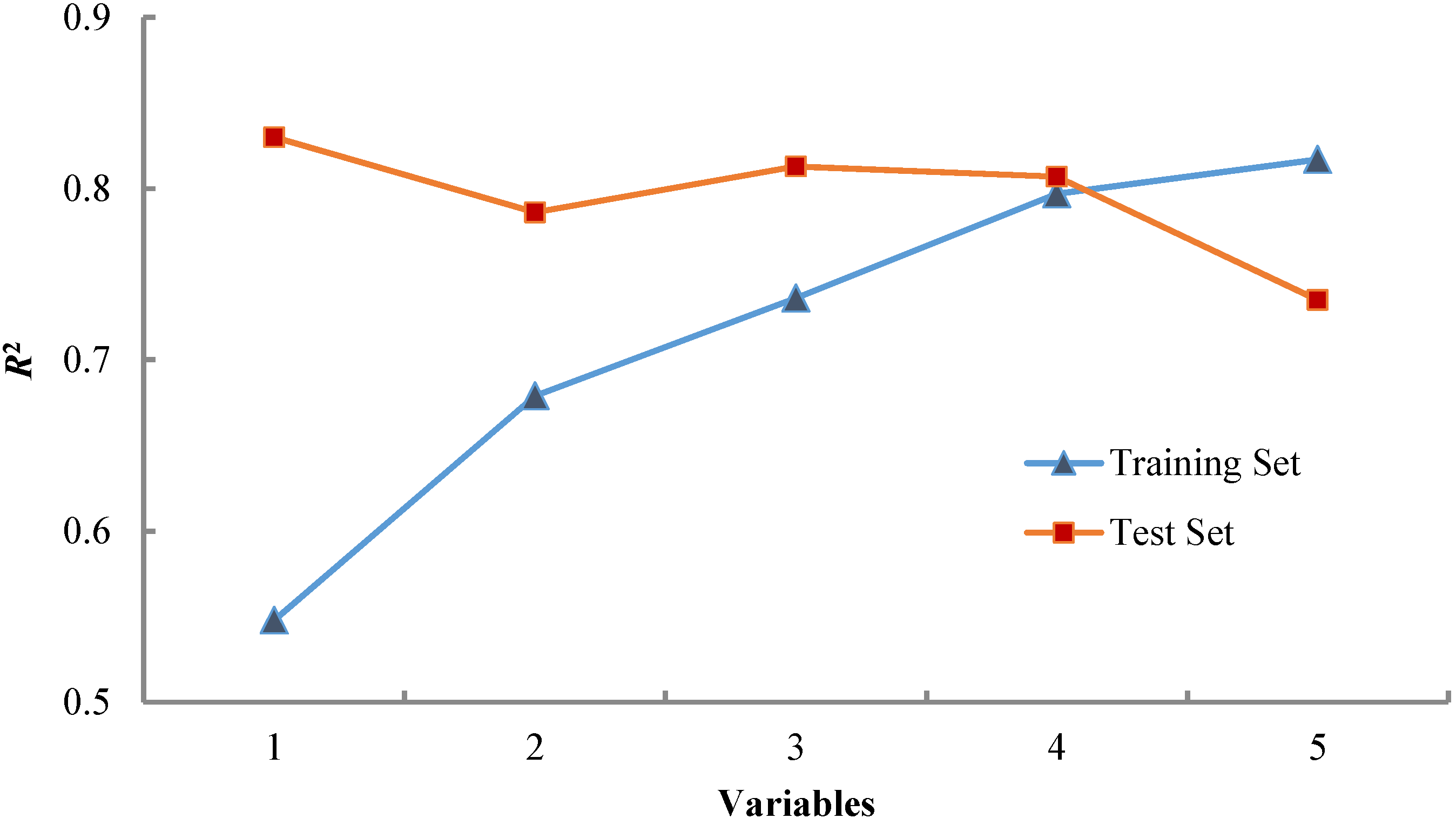
| No. | SRW09 | Dipole Z | piPC05 | Ram | X0Av | ATS6m |
|---|---|---|---|---|---|---|
| 1 | 702 | 2.225 | 30 | 3 | 0.632 | 6.731 |
| 2 | 0 | −0.166 | 10 | 1 | 0.576 | 0.000 |
| 3 | 684 | 1.312 | 78 | 3 | 0.582 | 7.343 |
| 4 | 684 | 0.459 | 14 | 2 | 0.660 | 6.580 |
| 5 | 504 | 0.515 | 4 | 1 | 0.588 | 0.000 |
| 6 | 684 | 1.110 | 18 | 2 | 0.584 | 6.472 |
| 7 | 684 | −1.214 | 8 | 2 | 0.648 | 2.583 |
| 8 | 684 | −0.743 | 18 | 2 | 0.673 | 7.406 |
| 9 | 684 | −1.345 | 10 | 2 | 0.595 | 2.215 |
| 10 | 504 | −0.006 | 4 | 1 | 0.554 | 0.000 |
| 11 | 0 | 0.000 | 0 | 2 | 0.726 | 0.000 |
| 12 | 0 | 2.665 | 12 | 1 | 0.621 | 3.566 |
| 13 | 684 | −0.590 | 22 | 2 | 0.681 | 7.797 |
| 14 | 0 | 0.000 | 0 | 0 | 0.521 | 0.000 |
| 15 | 0 | 1.192 | 63 | 2 | 0.583 | 6.898 |
| 16 | 0 | 0.000 | 0 | 0 | 0.649 | 0.000 |
| 17 | 0 | 0.000 | 0 | 1 | 0.528 | 0.000 |
| 18 | 0 | 0.001 | 2 | 0 | 0.707 | 5.869 |
| 19 | 0 | 0.887 | 0 | 0 | 0.610 | 0.000 |
| 20 | 504 | 0.454 | 4 | 1 | 0.623 | 0.000 |
| 21 | 0 | 0.000 | 52 | 2 | 0.611 | 0.703 |
| 22 | 0 | 0.000 | 0 | 1 | 0.727 | 0.000 |
| 23 | 0 | −0.763 | 132 | 3 | 0.550 | 7.631 |
| 24 | 0 | −1.142 | 0 | 1 | 0.756 | 0.000 |
| 25 | 0 | 1.892 | 10 | 1 | 0.635 | 0.000 |
| 26 | 0 | 0.000 | 44 | 1 | 0.627 | 1.401 |
| 27 | 0 | 0.000 | 5 | 0 | 0.595 | 6.923 |
| 28 | 0 | 0.000 | 0 | 0 | 0.521 | 0.000 |
| 29 | 0 | −0.973 | 50 | 1 | 0.568 | 3.508 |
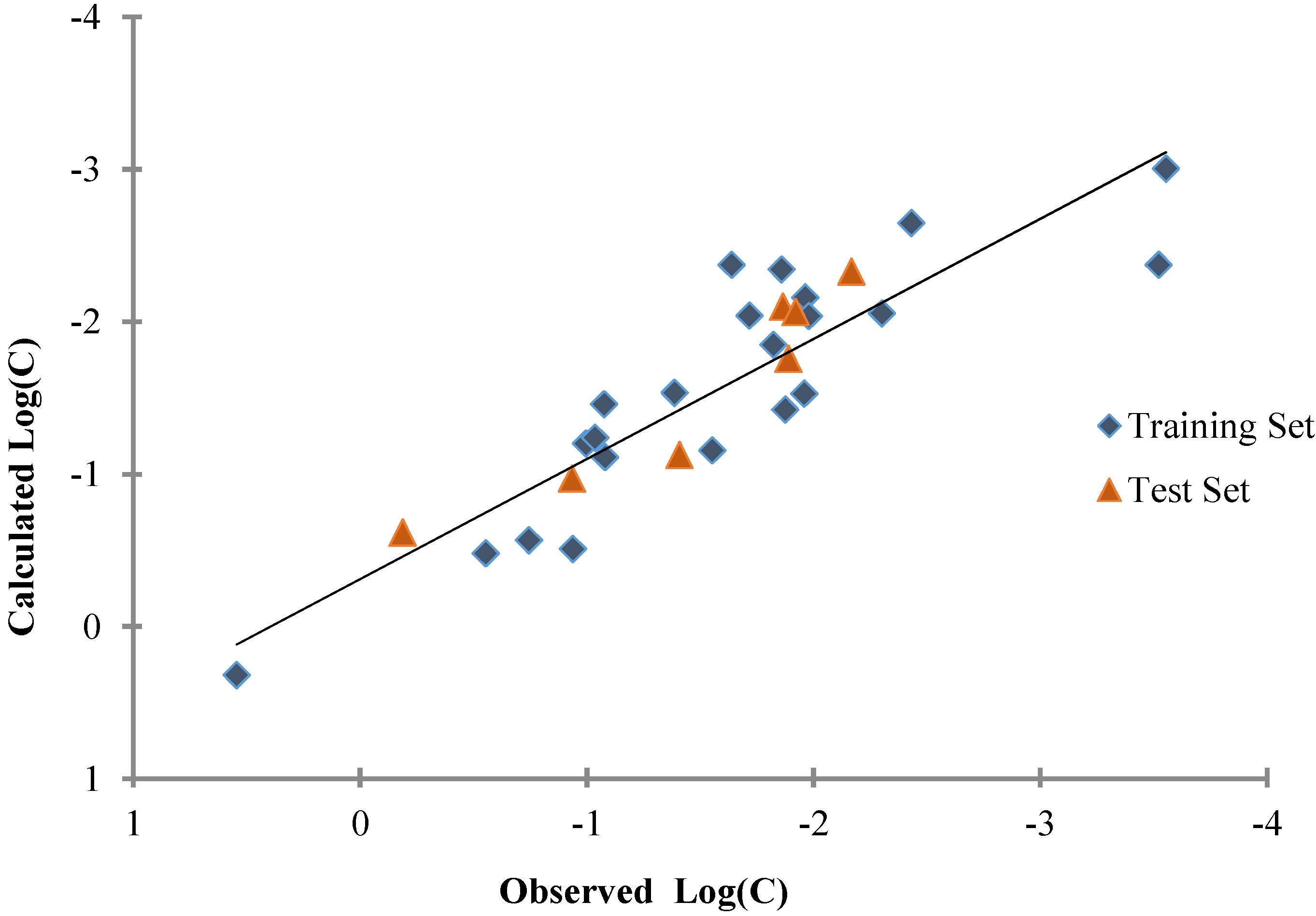
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Lijima, S.; Ichihashio, T. Single-shell carbon nanotubes of 1-nm diameter. Nature 1993, 363, 603–605. [Google Scholar] [PubMed]
- Nakashima, N. Soluble carbon nanotubes: Fundamental and applications. Int. J. Nanosci. 2005, 4, 119–137. [Google Scholar] [CrossRef]
- Britz, D.A.; Khlobystov, A.N. Noncovalent interactions of molecules with single walled carbon nanotubes. Chem. Soc. Rev. 2006, 35, 637–659. [Google Scholar] [CrossRef] [PubMed]
- Girifalco, L.A.; Hodak, M.; Lee, R.S. Carbon nanotubes, buckyballs, ropes, and a universal graphitic potential. Phys. Rev. B. 2000, 62, 13104. [Google Scholar] [CrossRef]
- Liu, J.; Rinzler, A.G.; Dai, H.; Hafner, J.H.; Bradley, R.K.; Boul, P.J.; Lu, A.; Iverson, T.; Shelimov, K.; Huffman, C.B.; et al. Fullerene pipes. Science 1998, 280, 1253–1256. [Google Scholar] [CrossRef] [PubMed]
- Pavese, M.; Musso, S.; Bianco, S.; Giorcelli, M.; Pugno, N. An analysis of carbon nanotube structure wettability before and after oxidation treatment. J. Phys. Condens. Matter 2008, 20. [Google Scholar] [CrossRef]
- Ziegler, K.J.; Gu, Z.; Peng, H.; Flor, E.L.; Hauge, R.H.; Smalley, R.E. Controlled oxidative cutting of single-walled carbon nanotubes. J. Am. Chem. Soc. 2005, 127, 1541–1547. [Google Scholar] [CrossRef] [PubMed]
- Worsley, K.A.; Kalinina, I.; Bekyarova, E.; Haddon, R.C. Functionalization and dissolution of nitric acid treated single-walled carbon nanotubes. J. Am. Chem. Soc. 2009, 131, 18153–18158. [Google Scholar] [CrossRef] [PubMed]
- Ausman, K.D.; Piner, R.; Lourie, O.; Ruoff, R.S.; Korobov, M. Organic solvent dispersions of single-walled carbon nanotubes: Toward solutions of pristine nanotubes. J. Phys. Chem. B 2000, 104, 8911–8915. [Google Scholar] [CrossRef]
- Bahr, J.L.; Mickelson, E.T.; Bronikowski, M.J.; Smalley, R.E.; Tour, J.M. Dissolution of small diameter single-wall carbon nanotubes in organic solvents. Chem. Commun. 2001, 2, 193–194. [Google Scholar] [CrossRef]
- Furtado, C.A.; Kim, U.J.; Gutierrez, H.R.; Pan, L.; Dickey, E.C.; Eklund, P.C. Debundling and dissolution of single walled carbon nanotubes in amide solvents. J. Am. Chem. Soc. 2004, 126, 6095–6105. [Google Scholar] [CrossRef] [PubMed]
- Landi, B.J.; Ruf, H.J.; Worman, J.J.; Raffaelle, R.P. Effects of alkyl amide solvents on the dispersion of single-wall carbon nanotubes. J. Phys. Chem. B 2004, 108, 17089–17095. [Google Scholar] [CrossRef]
- Maeda, Y.; Kimura, S.; Hirashima, Y.; Kanda, M.; Lian, Y.F.; Wakahara, T.; Akasaka, T.; Hasegawa, T.; Tokumoto, H.; Shimizu, T.; et al. Dispersion of single-walled carbon nanotube bundles in nonaqueous solution. J. Phys. Chem. B 2004, 108, 18395–18397. [Google Scholar] [CrossRef]
- Umek, P.; Vrbanic, D.; Remskar, M.; Mertelj, T.; Venturini, P.; Pejovnik, S.; Mihailovic, D. An effective surfactant-free isolation procedure for single-wall carbon nanotubes. Carbon 2002, 40, 2581–2585. [Google Scholar] [CrossRef]
- Bergin, S.D.; Nicolosi, V.; Streich, P.V.; Giordani, S.; Sun, Z.; Windle, A.H.; Ryan, P.; Peter, N.; Niraj, P.; Wang, Z.-T.T.; et al. Towards solutions of single-walled carbon nanotubes in common solvents. Adv. Mater. 2008, 20, 1876–1881. [Google Scholar] [CrossRef]
- Giordani, S.; Bergin, S.D.; Nicolosi, V.; Lebedkin, S.; Kappes, M.M.; Blau, W.J.; Coleman, J.N. Debundling of single walled nanotubes by dilution: Observation of large populations of individual nanotubes in amide solvent. J. Phys. Chem. B 2006, 110, 15708–15718. [Google Scholar] [CrossRef] [PubMed]
- Usrey, M.L.; Chaffee, A.; Jeng, E.S.; Strano, M.S. Application of polymer solubility theory to solution phase dispersion of single-walled carbon nanotubes. J. Phys. Chem. C 2009, 113, 9532–9540. [Google Scholar] [CrossRef]
- Maiti, A.; Wescott, J.; Kung, P. Nanotube-polymer composites: Insights from Flory-Huggins theory and mesoscale simulations. Mol. Simul. 2005, 31, 143–149. [Google Scholar] [CrossRef]
- Detriche, S.; Zorzini, G.; Colomer, J.F.; Fonseca, A.; Nagy, J.B. Application of the Hansen solubility parameters theory to carbon nanotubes. J. Nanosci. Nanotechnol. 2007, 8, 6082–6092. [Google Scholar] [CrossRef]
- Ham, H.T.; Choi, Y.S.; Chung, I.J. An explanation of dispersion states of single-walled carbon nanotubes in solvents and aqueous surfactant solutions using solubility parameters. J. Colloid Interface Sci. 2005, 286, 216–223. [Google Scholar] [CrossRef] [PubMed]
- Turabekova, M.; Rasulev, B.; Theodore, M.; Jackman, J.; Leszczynska, D.; Leszczynski, J. Immunotoxicity of nanoparticles: A computational study suggests that CNTs and C60 fullerenes might be recognized as pathogens by Toll-like receptors. Nanoscale 2014, 7, 3488–3495. [Google Scholar] [CrossRef]
- Rasulev, B.; Gajewicz, A.; Puzyn, T.; Leszczynska, D.; Leszczynski, J. Nano-QSAR: Advances and challenges. RSC Nanosci. Nanotechnol. 2012, 25, 220–256. [Google Scholar]
- Petrova, T.; Rasulev, B.F.; Toropov, A.A.; Leszczynska, D.; Leszczynski, J. Improved model for fullerene C60 solubility in organic solvents based on quantum-chemical and topological descriptors. J. Nanopart. Res. 2011, 13, 3235–3247. [Google Scholar] [CrossRef]
- Cook, S.M.; Aker, W.G.; Rasulev, B.F.; Hwang, H.-M.; Leszczynski, J.; Jenkins, J.J.; Shockley, V. Choosing safe dispersing media for C60 fullerenes by using cytotoxicity tests on the bacterium Escherichia coli. J. Hazard. Mater. 2010, 176, 367–373. [Google Scholar] [CrossRef] [PubMed]
- Toropov, A.A.; Rasulev, B.F.; Leszczynska, D.; Leszczynski, J. Multiplicative SMILES-based optimal descriptors: QSPR modeling of fullerene C60 solubility in organic solvents. Chem. Phys. Lett. 2008, 457, 332–336. [Google Scholar] [CrossRef]
- Toropov, A.A.; Rasulev, B.F.; Leszczynska, D.; Leszczynski, J. Additive SMILES based optimal descriptors: QSPR modeling of fullerene C60 solubility in organic solvents. Chem. Phys. Lett. 2007, 444, 209–214. [Google Scholar] [CrossRef]
- Rofouei, M.K.; Salahinejad, M.; Ghasemi, J.B. An alignment independent 3D-QSAR modeling of dispersibility of single-walled carbon nanotubes in different organic solvents. Fuller. Nanotub. Carbon Nanostruct. 2014, 22, 605–617. [Google Scholar] [CrossRef]
- Salahinejad, M.; Zolfonoun, E. QSAR studies of the dispersion of SWNTs in different organic solvents. J. Nanopart. Res. 2013, 15, 2028–2039. [Google Scholar] [CrossRef]
- Bergin, S.D.; Sun, Z.Y.; Rickard, D.; Streich, P.V.; Hamilton, J.P.; Coleman, J.N. Multicomponent solubility parameters for single-walled carbon nanotube-solvent mixtures. ACS Nano 2009, 3, 2340–2350. [Google Scholar] [CrossRef] [PubMed]
- HyperChem (HyperCube) Homepage. Available online: http://www.hyper.com (accessed on 2 June 2009).
- DRAGON 6.0. Available online: http://www.disat.unimib.it/chm (accessed on 11 December 2014).
- Todeschini, R.; Consonni, V. DRAGON Software for the Calculation of Molecular Descriptors, web version 3.0 for Windows; TALETE S.R.L.: Milano, Italy, 2003.
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley-VCH: Weinheim, Germany; New York, NY, USA, 2000. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, kinetics, noncovalent interactions, excited states, and transition elements: Two new functionals and systematic testing of four M06 functionals and twelve other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A.; et al. Gaussian 09, Revision B.01; Gaussian Inc: Wallingford, CT, USA, 2009. [Google Scholar]
- Devillers, J. Genetic Algorithms in Molecular Modeling; Academic Press: London, UK, 1996. [Google Scholar]
- Rasulev, B.F.; Saidkhodzhaev, A.I.; Nazrullaev, S.S.; Akhmedkhodzhaeva, K.S.; Khushbaktova, Z.A.; Leszczynski, J. Molecular modelling and QSAR analysis of the estrogenic activity of terpenoids isolated from Ferula plants. SAR QSAR Environ. Res. 2007, 18, 663–673. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, L.; Rasulev, B.; Turabekova, M.; Leszczynska, D.; Leszczynski, J. Receptor and ligand-based study of fullerene analogues: Comprehensive computational approach including quantum-chemical, QSAR and molecular docking simulations. Org. Biomol. Chem. 2013, 11, 5798–5808. [Google Scholar] [CrossRef] [PubMed]
- De Oliveira, D.B.; Gaudio, A.C. BuildQSAR: A new computer program for QSAR analysis. Quant. Struct. Act. Relat. 2003, 19, 599–604. [Google Scholar] [CrossRef]
- Hayriye, Y.; Yahya, G.; Zulbiye, O.; Gokce, A.; Safak Ozhan, K. 4D-QSAR study of p56lck protein tyrosine kinase inhibitory activity of flavonoid derivatives using MCET method. Bull. Korean Chem. Soc. 2012, 32, 4352–4360. [Google Scholar]
- Yilmaz, H.; Güzel, Y.; Boz, M.; Türkmenoğlu, B. Pharmacophore and functional group identification of 4,4'-dihydroxydiphenylmethane as bisphenol-A (BSA) derivative. Trop. J. Pharm. Res. 2014, 13, 117–129. [Google Scholar] [CrossRef]
- Roy, K.; Mitra, I.; Kar, S.; Ojha, P.; Das, R.N.; Kabir, H. Comparative studies on some metrics for external validation of QSPR models. J. Chem. Inf. Model. 2012, 52, 396–408. [Google Scholar] [CrossRef] [PubMed]
- Ojha, P.K.; Mitra, I.; Das, R.N.; Roy, K. Further exploring rm2 metrics for validation of QSPR models dataset. Chemom. Intell. Lab. Syst. 2011, 107, 194–205. [Google Scholar] [CrossRef]
- Gutman, I.; Rücker, C.; Rücker, G. On walks in molecular graphs. J. Chem. Inf. Comput. Sci. 2001, 41, 739–745. [Google Scholar] [CrossRef] [PubMed]
- Devinyak, O.; Zimenkovsky, B.; Lesyk, R. Biologically active 4-thiazolidinones: A review of QSAR studies and QSAR modeling of antitumor activity. Curr. Top. Med. Chem. 2012, 12, 2763–2784. [Google Scholar] [CrossRef] [PubMed]
- Sharmaa, B.K.; Singha, P.; Sarbhaia, K.; Prabhakar, Y.S. A QSAR study on serotonin 5-HT6 receptor ligands: Indolyl and piperidinyl sulfonamides. SAR QSAR Environ. Res. 2010, 21, 369–388. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yilmaz, H.; Rasulev, B.; Leszczynski, J. Modeling the Dispersibility of Single Walled Carbon Nanotubes in Organic Solvents by Quantitative Structure-Activity Relationship Approach. Nanomaterials 2015, 5, 778-791. https://doi.org/10.3390/nano5020778
Yilmaz H, Rasulev B, Leszczynski J. Modeling the Dispersibility of Single Walled Carbon Nanotubes in Organic Solvents by Quantitative Structure-Activity Relationship Approach. Nanomaterials. 2015; 5(2):778-791. https://doi.org/10.3390/nano5020778
Chicago/Turabian StyleYilmaz, Hayriye, Bakhtiyor Rasulev, and Jerzy Leszczynski. 2015. "Modeling the Dispersibility of Single Walled Carbon Nanotubes in Organic Solvents by Quantitative Structure-Activity Relationship Approach" Nanomaterials 5, no. 2: 778-791. https://doi.org/10.3390/nano5020778
APA StyleYilmaz, H., Rasulev, B., & Leszczynski, J. (2015). Modeling the Dispersibility of Single Walled Carbon Nanotubes in Organic Solvents by Quantitative Structure-Activity Relationship Approach. Nanomaterials, 5(2), 778-791. https://doi.org/10.3390/nano5020778







