DNA under Force: Mechanics, Electrostatics, and Hydration
Abstract
:1. Introduction
2. Mechanical Forces in DNA
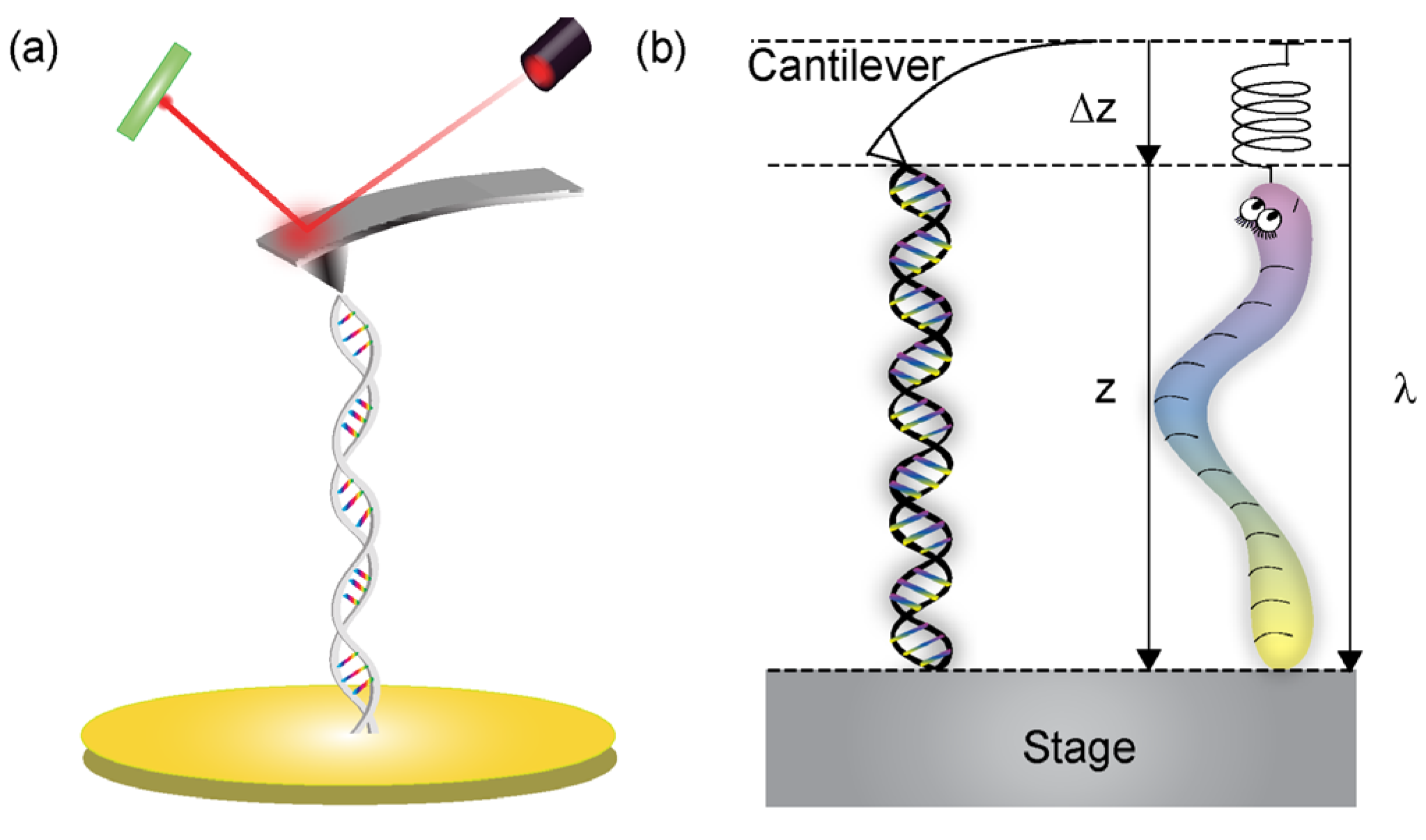
2.1. Mechanics of Double-Stranded DNA
2.1.1. Short dsDNA
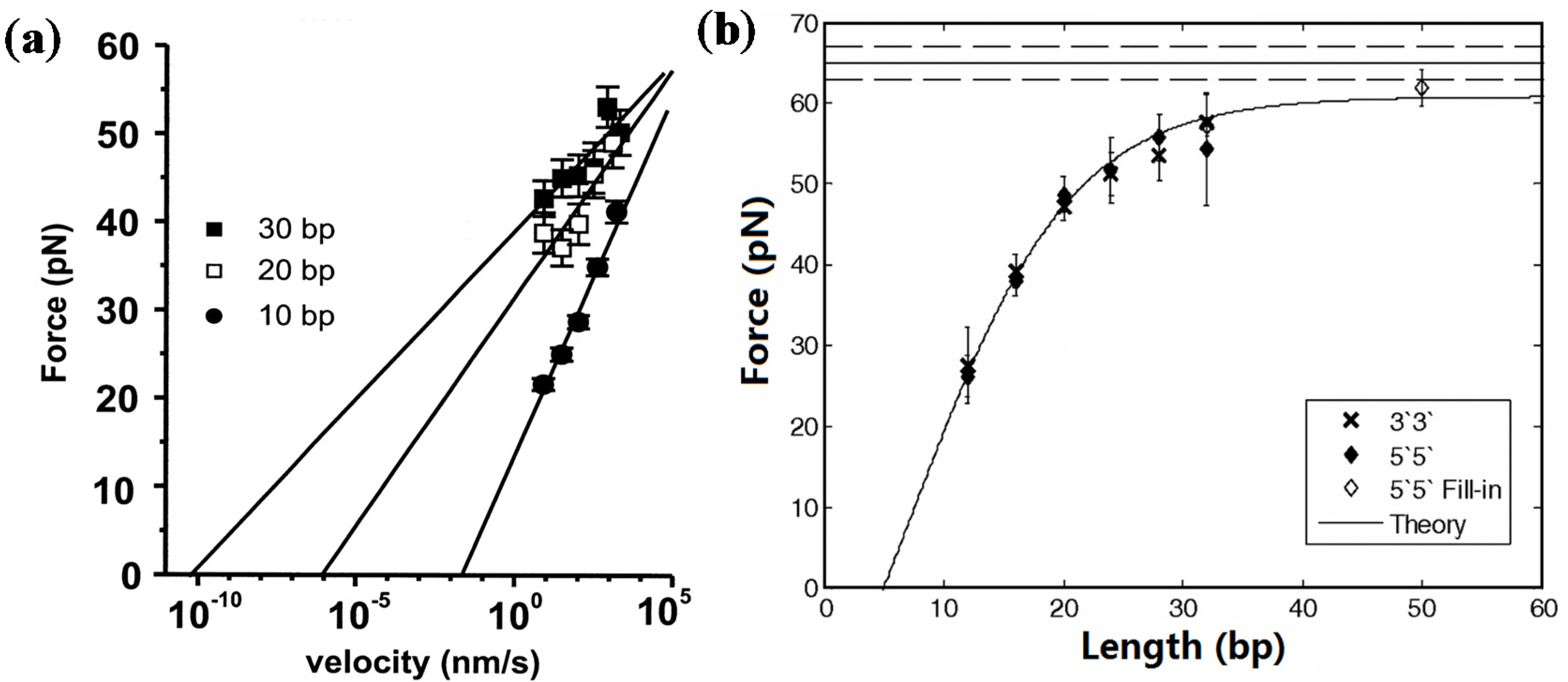
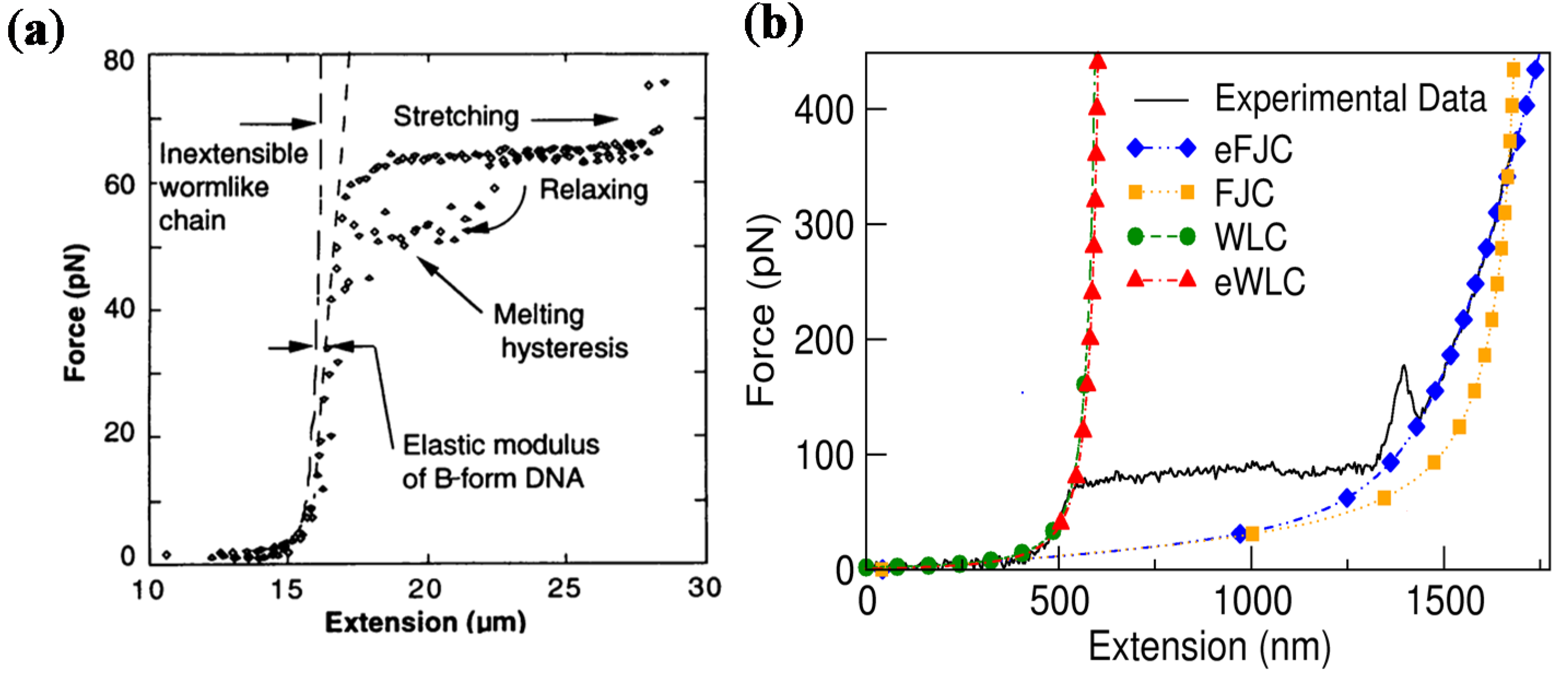
2.1.2. Long dsDNA
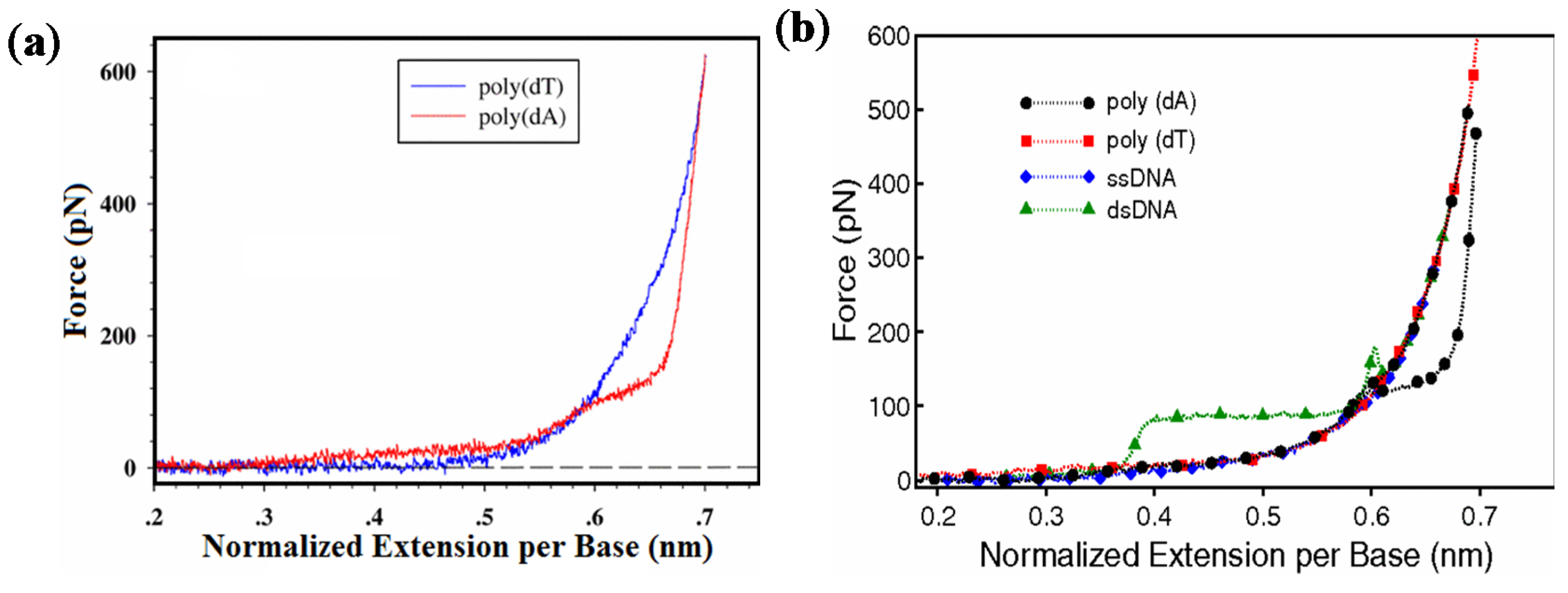
2.2. Mechanics of Single-Stranded DNA
3. Electrostatic and Hydration Forces in DNA
- (1)
- Bjerrum length , where e is the electron charge, ε is the dielectric constant of the solvent (e.g., 78.3 for water at 25 °C), and kBT is the thermal energy. Mathematically, when two ions of elemental charge are separated by Bjerrum length, the electric potential energy is the same as the thermal energy, giving a measure of the length scale of ion–ion correlations which is about 0.7 nm in water at 25 °C. It is worth noting that for ions of higher valence, the effective Bjerrum length is reduced by a factor of the product of the valences of the ion pairs.
- (2)
- Ionic strength , where the sum runs over all ionic species; zi is the valence of ion; i, and ni is the concentration of ion i. To put the role of ionic valence in perspective, 100 mM NaCl and MgCl2 solutions will give an ionic strength of 100 mM and 300 mM, respectively. Without resorting to any physical formalism, ionic strength can be considered as an empirical way to characterize the effect of ion screening.
- (3)
- Screening Debye length . Debye length thus considers the roles of both thermal motion and ion screening. Mathematically, it is the decay length of the electrostatic field in ionic solutions that takes on an exponential form rather than a power law in dielectric medium as a result of ionic screening. For example, λD is ~1 nm at 100 mM monovalent salt. However, it should be noted that Debye length is strictly speaking only applicable to weak electrostatic fields, as it is derived from a linearized version of the Poisson-Boltzmann (PB) mean-field treatment of electrostatic interactions.
- (4)
- Charge densities of charged biomolecules, linear charge density η, and surface charge density σ. In the case of dsDNA of 1 nm radius and 2 e per 0.34 nm, η is 5.88 e/nm and σ is 0.94 e/nm2.
3.1. The Role of Ions
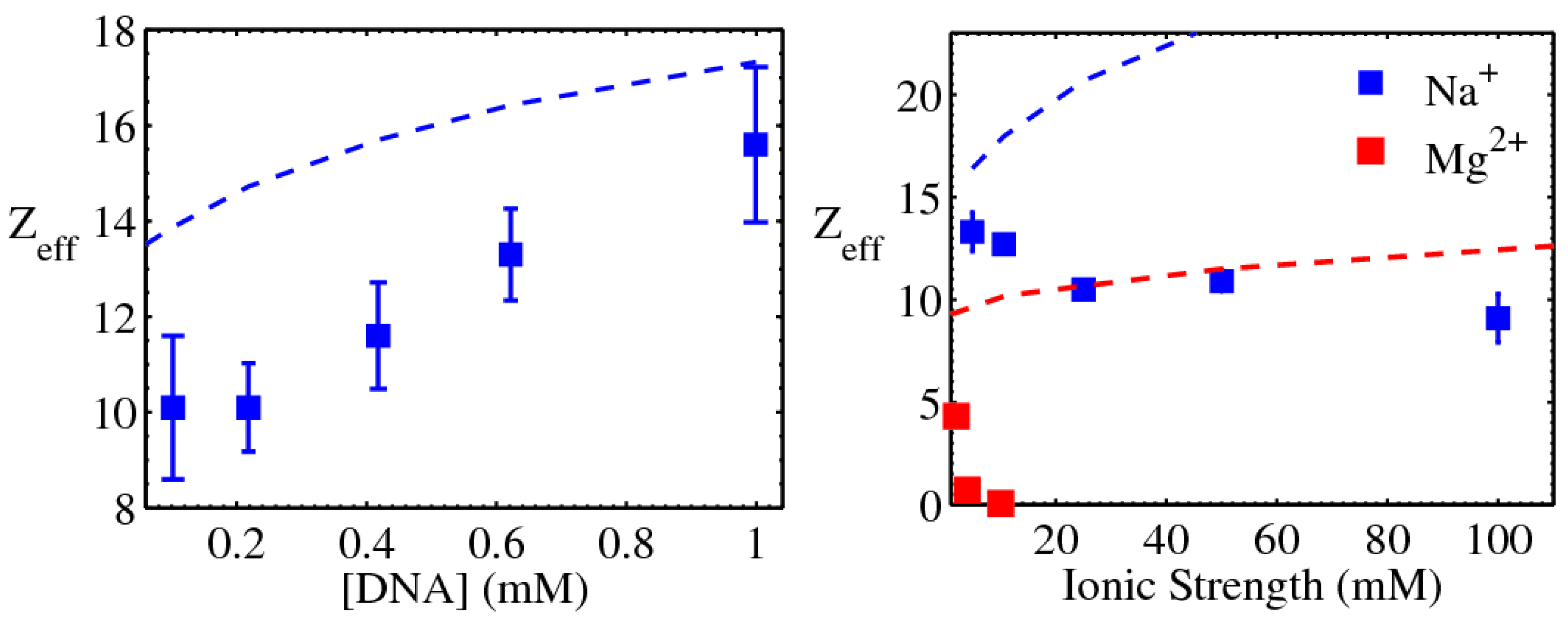
3.1.1. Screening of DNA–DNA repulsion


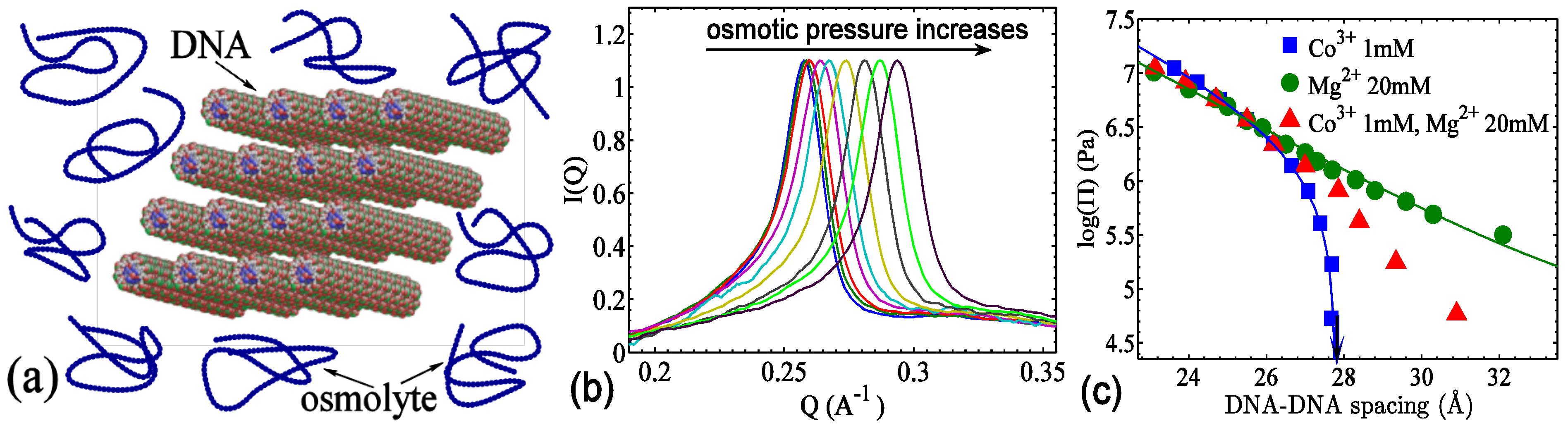
3.1.2. Mediation of DNA–DNA attraction

3.2. The Role of Solvent
3.3. The Role of DNA’s Structure
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Smith, S.B.; Cui, Y.J.; Bustamante, C. Overstretching B-DNA: The elastic response of individual double-stranded and single-stranded DNA molecules. Science 1996, 271, 795–799. [Google Scholar] [CrossRef] [PubMed]
- Rief, M.; Clausen-Schaumann, H.; Gaub, H.E. Sequence-dependent mechanics of single DNA molecules. Nat. Struct. Biol. 1999, 6, 346–349. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.S.; Chen, W.H.; Chen, Z.P.; Gooding, A.A.; Lin, K.J.; Kiang, C.H. Direct observation of multiple pathways of single-stranded DNA stretching. Phys. Rev. Lett. 2010, 105, 218104:1–218104:5. [Google Scholar]
- Livolant, F.; Leforestier, A. Condensed phases of DNA: Structures and phase transitions. Prog. Polym. Sci. 1996, 21, 1115–1164. [Google Scholar] [CrossRef]
- Parsegian, V.A.; Rand, R.P.; Rau, D.C. Macromolecules and water: Probing with osmotic stress. Meth. Enzymol. 1995, 259, 43–94. [Google Scholar] [PubMed]
- Bloomfield, V.A. DNA condensation. Curr. Opin. Struct. Biol. 1996, 6, 334–341. [Google Scholar] [CrossRef] [PubMed]
- Gelbart, W.M.; Bruinsma, R.F.; Pincus, P.A.; Parsegian, V.A. DNA-inspired electrostatics. Phys. Today 2000, 53, 38–44. [Google Scholar] [CrossRef]
- Solis, F.J.; de la Cruz, M.O. Flexible polymers also counterattract. Phys. Today 2001, 54, 71–72. [Google Scholar] [CrossRef]
- Parsegian, V.A.; Zemb, T. Hydration forces: Observations, explanations, expectations, questions. Curr. Opin. Colloid Interface Sci. 2011, 16, 618–624. [Google Scholar] [CrossRef]
- Modi, S.; Bhatia, D.; Simmel, F.C.; Krishnan, Y. Structural DNA nanotechnology: From bases to bricks, from structure to function. J. Phys. Chem. Lett. 2010, 1, 1994–2005. [Google Scholar] [CrossRef]
- Seeman, N.C. DNA in a material world. Nature 2003, 421, 427–431. [Google Scholar] [CrossRef] [PubMed]
- Zhang, F.; Nangreave, J.; Liu, Y.; Yan, H. Structural DNA nanotechnology: State of the art and future perspective. J. Am. Chem. Soc. 2014, 136, 11198–11211. [Google Scholar] [CrossRef] [PubMed]
- Shih, W.M.; Douglas, S.M.; Dietz, H.; Liedl, T.; Hogberg, B.; Graf, F. Self-assembly of DNA into nanoscale three-dimensional shapes. J. Biomol. Struct. Dyn. 2009, 26, 414–418. [Google Scholar]
- Liu, Q.H.; Wang, L.M.; Frutos, A.G.; Condon, A.E.; Corn, R.M.; Smith, L.M. DNA computing on surfaces. Nature 2000, 403, 175–179. [Google Scholar] [CrossRef] [PubMed]
- Adleman, L.M. Molecular computation of solutions to combinatorial problems. Science 1994, 266, 1021–1024. [Google Scholar] [CrossRef] [PubMed]
- Fu, J.L.; Yang, Y.R.; Johnson-Buck, A.; Liu, M.H.; Liu, Y.; Walter, N.G.; Woodbury, N.W.; Yan, H. Multi-enzyme complexes on DNA scaffolds capable of substrate channelling with an artificial swinging arm. Nat. Nanotechnol. 2014, 9, 531–536. [Google Scholar] [CrossRef] [PubMed]
- Han, D.R.; Pal, S.; Yang, Y.; Jiang, S.X.; Nangreave, J.; Liu, Y.; Yan, H. DNA gridiron nanostructures based on four-arm junctions. Science 2013, 339, 1412–1415. [Google Scholar] [CrossRef] [PubMed]
- Bustamante, C.; Marko, J.F.; Siggia, E.D.; Smith, S. Entropic elasticity of lambda-phage DNA. Science 1994, 265, 1599–1600. [Google Scholar] [CrossRef] [PubMed]
- Liphardt, J.; Onoa, B.; Smith, S.B.; Tinoco, I.; Bustamante, C. Reversible unfolding of single RNA molecules by mechanical force. Science 2001, 292, 733–737. [Google Scholar] [CrossRef] [PubMed]
- Wijeratne, S.S.; Botello, E.; Yeh, H.C.; Zhou, Z.; Bergeron, A.L.; Frey, E.W.; Patel, J.M.; Nolasco, L.; Turner, N.A.; Moake, J.L.; et al. Mechanical activation of a multimeric adhesive protein through domain conformational change. Phys. Rev. Lett. 2013, 110, 108102:1–108102:9. [Google Scholar]
- Moy, V.T.; Florin, E.L.; Gaub, H.E. Intermolecular forces and energies between ligands and receptors. Science 1994, 266, 257–259. [Google Scholar] [CrossRef] [PubMed]
- Harris, N.C.; Song, Y.; Kiang, C.H. Experimental free energy surface reconstruction from single-molecule force spectroscopy using Jarzynski’s equality. Phys. Rev. Lett. 2007, 99, 068101:1–068101:4. [Google Scholar]
- Wang, M.D.; Yin, H.; Landick, R.; Gelles, J.; Block, S.M. Stretching DNA with optical tweezers. Biophys. J. 1997, 72, 1335–1346. [Google Scholar] [CrossRef] [PubMed]
- Smith, S.B.; Finzi, L.; Bustamante, C. Direct mechanical measurements of the elasticity of single DNA-molecules by using magnetic beads. Science 1992, 258, 1122–1126. [Google Scholar] [CrossRef] [PubMed]
- Cluzel, P.; Lebrun, A.; Heller, C.; Lavery, R.; Viovy, J.L.; Chatenay, D.; Caron, F. DNA: An extensible molecule. Science 1996, 271, 792–794. [Google Scholar] [CrossRef] [PubMed]
- Evans, E.; Ritchie, K.; Merkel, R. Sensitive force technique to probe molecular adhesion and structural linkages at biological interfaces. Biophys. J. 1995, 68, 2580–2587. [Google Scholar] [CrossRef] [PubMed]
- Calderon, C.P.; Chen, W.H.; Lin, K.J.; Harris, N.C.; Kiang, C.H. Quantifying DNA melting transitions using single-molecule force spectroscopy. J. Phys.: Condens. Matter 2009, 21, 034114:1–034114:12. [Google Scholar] [CrossRef]
- Bryant, Z.; Stone, M.D.; Gore, J.; Smith, S.B.; Cozzarelli, N.R.; Bustamante, C. Structural transitions and elasticity from torque measurements on DNA. Nature 2003, 424, 338–341. [Google Scholar] [CrossRef] [PubMed]
- Gore, J.; Bryant, Z.; Nollmann, M.; Le, M.U.; Cozzarelli, N.R.; Bustamante, C. DNA overwinds when stretched. Nature 2006, 442, 836–839. [Google Scholar] [CrossRef] [PubMed]
- Celedon, A.; Nodelman, I.M.; Wildt, B.; Dewan, R.; Searson, P.; Wirtz, D.; Bowman, G.D.; Sun, S.X. Magnetic tweezers measurement of single molecule torque. Nano Lett. 2009, 9, 1720–1725. [Google Scholar] [CrossRef] [PubMed]
- Mosconi, F.; Allemand, J.F.; Bensimon, D.; Croquette, V. Measurement of the torque on a single stretched and twisted DNA using magnetic tweezers. Phys. Rev. Lett. 2009, 102. doi:http://dx.doi.org/10.1103/PhysRevLett.102.078301. [Google Scholar] [CrossRef] [PubMed]
- Gross, P.; Laurens, N.; Oddershede, L.B.; Bockelmann, U.; Peterman, E.J.G.; Wuite, G.J.L. Quantifying how DNA stretches, melts and changes twist under tension. Nat. Phys. 2011, 7, 731–736. [Google Scholar] [CrossRef]
- Wijeratne, S.S.; Harris, N.C.; Kiang, C.-H. Principles Involved in Interpreting Single-Molecule Force Measurement of Biomolecules. In MEMS and Nanotechnology; Shaw, G.A., Prorok, B., Starman, L.A., Eds.; Springer: New York, NY, USA, 2012; Volume 6, pp. 19–23. [Google Scholar]
- Frey, E.W.; Gooding, A.A.; Wijeratne, S.; Kiang, C.H. Understanding the physics of DNA using nanoscale single-molecule manipulation. Front. Phys. 2012, 7, 576–581. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J. Statistical Mechanics of Chain Molecules; Interscience Publishers: New York, NY, USA, 1969. [Google Scholar]
- Marko, J.F.; Siggia, E.D. Stretching DNA. Macromolecules 1995, 28, 8759–8770. [Google Scholar] [CrossRef]
- Odijk, T. Stiff chains and filaments under tension. Macromolecules 1995, 28, 7016–7018. [Google Scholar] [CrossRef]
- Cocco, S.; Yan, J.; Leger, J.F.; Chatenay, D.; Marko, J.F. Overstretching and force-driven strand separation of double-helix DNA. Phys. Rev. E 2004, 70, 011910:1–011910:18. [Google Scholar] [CrossRef]
- Hatch, K.; Danilowicz, C.; Coljee, V.; Prentiss, M. Demonstration that the shear force required to separate short double-stranded DNA does not increase significantly with sequence length for sequences longer than 25 base pairs. Phys. Rev. E 2008, 78, 011920. [Google Scholar] [CrossRef]
- Ho, D.; Zimmermann, J.L.; Dehmelt, F.A.; Steinbach, U.; Erdmann, M.; Severin, P.; Falter, K.; Gaub, H.E. Force-driven separation of short double-stranded DNA. Biophys. J. 2009, 97, 3158–3167. [Google Scholar] [CrossRef] [PubMed]
- Pope, L.H.; Davies, M.C.; Laughton, C.A.; Roberts, C.J.; Tendler, S.J.B.; Williams, P.M. Force-induced melting of a short DNA double helix. Eur. Biophys. J. 2001, 30, 53–62. [Google Scholar] [CrossRef] [PubMed]
- Sattin, B.D.; Pelling, A.E.; Goh, M.C. DNA base pair resolution by single molecule force spectroscopy. Nucleic Acids Res. 2004, 32, 4876–4883. [Google Scholar] [CrossRef] [PubMed]
- Lee, G.U.; Chrisey, L.A.; Colton, R.J. Direct measurement of the forces between complementary strands of DNA. Science 1994, 266, 771–773. [Google Scholar] [CrossRef] [PubMed]
- Clausen-Schaumann, H.; Rief, M.; Tolksdorf, C.; Gaub, H.E. Mechanical stability of single DNA molecules. Biophys. J. 2000, 78, 1997–2007. [Google Scholar] [CrossRef] [PubMed]
- Scholl, Z.N.; Rabbi, M.; Lee, D.; Manson, L.; S-Gracz, H.; Marszalek, P.E. Origin of overstretching transitions in single-stranded nucleic acids. Phys. Rev. Lett. 2013, 111, 188302. [Google Scholar] [CrossRef] [PubMed]
- Bustamante, C.; Smith, S.B.; Liphardt, J.; Smith, D. Single-molecule studies of DNA mechanics. Curr. Opin. Struct. Biol. 2000, 10, 279–285. [Google Scholar] [CrossRef] [PubMed]
- Bustamante, C.; Bryant, Z.; Smith, S.B. Ten years of tension: Single-molecule DNA mechanics. Nature 2003, 421, 423–427. [Google Scholar] [CrossRef] [PubMed]
- Strunz, T.; Oroszlan, K.; Schafer, R.; Guntherodt, H.J. Dynamic force spectroscopy of single DNA molecules. Proc. Natl. Acad. Sci. USA 1999, 96, 11277–11282. [Google Scholar] [CrossRef] [PubMed]
- Grange, W.; Strunz, T.; Schumakovitch, I.; Guntherodt, H.J.; Hegner, M. Molecular recognition and adhesion of individual DNA strands studied by dynamic force microscopy. Single Mol. 2001, 2, 75–78. [Google Scholar] [CrossRef]
- Van Mameren, J.; Gross, P.; Farge, G.; Hooijman, P.; Modesti, M.; Falkenberg, M.; Wuite, G.J.L.; Peterman, E.J.G. Unraveling the structure of DNA during overstretching by using multicolor, single-molecule fluorescence imaging. Proc. Natl. Acad. Sci. USA 2009, 106, 18231–18236. [Google Scholar] [CrossRef] [PubMed]
- Bosaeus, N.; El-Sagheer, A.H.; Brown, T.; Smith, S.B.; Akerman, B.; Bustamante, C.; Norden, B. Tension induces a base-paired overstretched DNA conformation. Proc. Natl. Acad. Sci. USA 2012, 109, 15179–15184. [Google Scholar] [CrossRef] [PubMed]
- Bongini, L.; Melli, L.; Lombardi, V.; Bianco, P. Transient kinetics measured with force steps discriminate between double-stranded DNA elongation and melting and define the reaction energetics. Nucleic Acids Res. 2014, 42, 3436–3449. [Google Scholar] [CrossRef] [PubMed]
- Fu, H.X.; Chen, H.; Marko, J.F.; Yan, J. Two distinct overstretched DNA states. Nucleic Acids Res. 2010, 38, 5594–5600. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Chen, H.; Fu, H.; Doyle, P.S.; Yan, J. Two distinct overstretched DNA structures revealed by single-molecule thermodynamics measurements. Proc. Natl. Acad. Sci. USA 2012, 109, 8103–8108. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.H.; Chen, H.; Le, S.M.; Rouzina, I.; Doyle, P.S.; Yan, J. Revealing the competition between peeled ssDNA, melting bubbles, and s-DNA during DNA overstretching by single-molecule calorimetry. Proc. Natl. Acad. Sci. USA 2013, 110, 3865–3870. [Google Scholar] [CrossRef] [PubMed]
- Goddard, N.L.; Bonnet, G.; Krichevsky, O.; Libchaber, A. Sequence dependent rigidity of single stranded DNA. Phys. Rev. Lett. 2000, 85, 2400–2403. [Google Scholar] [CrossRef] [PubMed]
- Turner, N.A. Conformational Changes. In Nucleic Acids: Structure Properties and Functions; Bloomfield, V.A., Crothers, D.M., Tinoco, I., Eds.; University Science Books: Sausalito, CA, USA, 2000; pp. 259–334. [Google Scholar]
- Buhot, A.; Halperin, A. Effects of stacking on the configurations and elasticity of single-stranded nucleic acids. Phys. Rev. E 2004, 70, 020902:1–020902:4. [Google Scholar] [CrossRef]
- Seol, Y.; Skinner, G.M.; Visscher, K.; Buhot, A.; Halperin, A. Stretching of homopolymeric RNA reveals single-stranded helices and base-stacking. Phys. Rev. Lett. 2007, 98, 158103. [Google Scholar] [CrossRef] [PubMed]
- Ke, C.; Humeniuk, M.; S-Gracz, H.; Marszalek, P.E. Direct measurements of base stacking interactions in DNA by single-molecule atomic-force spectroscopy. Phys. Rev. Lett. 2007, 99. doi:http://dx.doi.org/10.1103/PhysRevLett.99.018302. [Google Scholar] [CrossRef] [PubMed]
- Segal, E.; Widom, J. Poly(da:Dt) tracts: Major determinants of nucleosome organization. Curr. Opin. Struct. Biol. 2009, 19, 65–71. [Google Scholar] [CrossRef] [PubMed]
- Hopkins, J.C.; Dryden, D.M.; Ching, W.Y.; French, R.H.; Parsegian, V.A.; Podgornik, R. Dielectric response variation and the strength of van der waals interactions. J. Colloid Interface Sci. 2014, 417, 278–284. [Google Scholar] [CrossRef] [PubMed]
- Lorman, V.; Podgornik, R.; Zeks, B. Positional, reorientational, and bond orientational order in DNA mesophases. Phys. Rev. Lett. 2001, 87, 218101:1–218101:4. [Google Scholar] [CrossRef]
- Strey, H.H.; Wang, J.; Podgornik, R.; Rupprecht, A.; Yu, L.; Parsegian, V.A.; Sirota, E.B. Refusing to twist: Demonstration of a line hexatic phase in DNA liquid crystals. Phys. Rev. Lett. 2000, 84, 3105–3108. [Google Scholar] [CrossRef] [PubMed]
- Van Dam, L.; Korolev, N.; Nordenskiold, L. Polyamine-nucleic acid interactions and the effects on structure in oriented DNA fibers. Nucleic Acids Res. 2002, 30, 419–428. [Google Scholar] [CrossRef] [PubMed]
- Strey, H.H.; Podgornik, R.; Rau, D.C.; Parsegian, V.A. DNA–DNA interactions. Curr. Opin. Struct. Biol. 1998, 8, 309–313. [Google Scholar] [CrossRef] [PubMed]
- Wong, G.C.; Pollack, L. Electrostatics of strongly charged biological polymers: Ion-mediated interactions and self-organization in nucleic acids and proteins. Annu. Rev. Phys. Chem. 2010, 61, 171–189. [Google Scholar] [CrossRef] [PubMed]
- Tan, Z.J.; Chen, S.J. Predicting electrostatic forces in RNA folding. Method Enzymol. 2009, 469, 465–487. [Google Scholar]
- Kanduc, M.; Dobnikar, J.; Podgornik, R. Counterion-mediated electrostatic interactions between helical molecules. Soft Matter 2009, 5, 868–877. [Google Scholar] [CrossRef]
- Dong, F.; Olsen, B.; Baker, N.A. Computational methods for biomolecular electrostatics. Methods Cell Biol. 2008, 84, 843–870. [Google Scholar] [PubMed]
- Wong, G.C.L. Electrostatics of rigid polyelectrolytes. Curr. Opin. Colloid Interface Sci. 2006, 11, 310–315. [Google Scholar] [CrossRef]
- Baker, N.A.; McCammon, J.A. Electrostatic interactions. Methods Biochem. Anal. 2003, 44, 427–440. [Google Scholar] [PubMed]
- Levin, Y. Electrostatic correlations: From plasma to biology. Rep. Prog. Phys. 2002, 65, 1577–1632. [Google Scholar] [CrossRef]
- Belloni, L. Colloidal interactions. J. Phys. Condens. Matter. 2000, 12, 549–587. [Google Scholar] [CrossRef]
- Lof, D.; Schillen, K.; Jonsson, B.; Evilevitch, A. Dynamic and static light scattering analysis of DNA ejection from the phage lambda. Phys. Rev. E 2007, 76, 011914:1–011914:11. [Google Scholar] [CrossRef]
- Fuller, D.N.; Raymer, D.M.; Rickgauer, J.P.; Robertson, R.M.; Catalano, C.E.; Anderson, D.L.; Grimes, S.; Smith, D.E. Measurements of single DNA molecule packaging dynamics in bacteriophage lambda reveal high forces, high motor processivity, and capsid transformations. J. Mol. Biol. 2007, 373, 1113–1122. [Google Scholar] [CrossRef] [PubMed]
- Bloomfield, V.A. DNA condensation by multivalent cations. Biopolymers 1997, 44, 269–282. [Google Scholar] [CrossRef] [PubMed]
- Li, G.-Y.; Guan, R.-L.; Ji, L.-N.; Chao, H. DNA condensation induced by metal complexes. Coord. Chem. Rev. 2014, 281, 100–113. [Google Scholar] [CrossRef]
- Verwey, E.J.W.; Overbeek, J.T.G. Theory of the Stability of Lyophobic Colloids; Elsevier: Amsterdam, The Netherland, 1948. [Google Scholar]
- Deserno, M.; Holm, C. Theory and simulations of rigid polyelectrolytes. Mol. Phys. 2002, 100, 2941–2956. [Google Scholar] [CrossRef]
- Manning, G.S.; Ray, J. Counterion condensation revisited. J. Biomol. Struct. Dyn. 1998, 16, 461–476. [Google Scholar] [CrossRef] [PubMed]
- Manning, G.S. Limiting laws and counterion condensation in polyelectrolyte solutions I. Colligative properties. J. Chem. Phys. 1969, 51, 924–933. [Google Scholar]
- Borukhov, I. Charge renormalization of cylinders and spheres: Ion size effects. J. Polym. Sci. Polym. Phys. 2004, 42, 3598–3615. [Google Scholar] [CrossRef]
- Hsin, W.L.; Wang, T.Y.; Sheng, Y.J.; Tsao, H.K. Charge renormalization of charged spheres based on thermodynamic properties. J. Chem. Phys. 2004, 121, 5494–5504. [Google Scholar] [CrossRef] [PubMed]
- Trizac, E.; Bocquet, L.; Aubouy, M.; von Grunberg, H.H. Alexander’s prescription for colloidal charge renormalization. Langmuir 2003, 19, 4027–4033. [Google Scholar] [CrossRef]
- Alexander, S.; Chaikin, P.M.; Grant, P.; Morales, G.J.; Pincus, P.; Hone, D. Charge renormalization, osmotic-pressure, and bulk modulus of colloidal crystals—Theory. J. Chem. Phys. 1984, 80, 5776–5781. [Google Scholar] [CrossRef]
- Podgornik, R.; Hansen, P.L.; Parsegian, V.A. Elastic moduli renormalization in self-interacting stretchable polyelectrolytes. J. Chem. Phys. 2000, 113, 9343–9350. [Google Scholar] [CrossRef]
- Savelyev, A. Do monovalent mobile ions affect DNA’s flexibility at high salt content? Phys. Chem. Chem. Phys. 2012, 14, 2250–2254. [Google Scholar] [CrossRef] [PubMed]
- Raspaud, E.; da Conceicao, M.; Livolant, F. Do free DNA counterions control the osmotic pressure? Phys. Rev. Lett. 2000, 84, 2533–2536. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.; Andresen, K.; Kwok, L.W.; Lamb, J.S.; Park, H.Y.; Pollack, L. Inter-DNA attraction mediated by divalent counterions. Phys. Rev. Lett. 2007, 99, 038104:1–038104:4. [Google Scholar] [CrossRef]
- Qiu, X.; Kwok, L.W.; Park, H.Y.; Lamb, J.S.; Andresen, K.; Pollack, L. Measuring inter-DNA potentials in solution. Phys. Rev. Lett. 2006, 96, 138101:1–138101:4. [Google Scholar] [CrossRef]
- Qiu, X.Y.; Parsegian, V.A.; Rau, D.C. Divalent counterion-induced condensation of triple-strand DNA. Proc. Natl. Acad. Sci. USA 2010, 107, 21482–21486. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Pabit, S.A.; Lamb, J.S.; Park, H.Y.; Pollack, L. Closing the lid on DNA end-to-end stacking interactions. Appl. Phys. Lett. 2008, 92, 22390:1–22390:13. [Google Scholar] [CrossRef]
- Pelta, J.; Livolant, F.; Sikorav, J.L. DNA aggregation induced by polyamines and cobalthexamine. J. Biol. Chem. 1996, 271, 5656–5662. [Google Scholar] [CrossRef] [PubMed]
- Podgornik, R.; Strey, H.H.; Parsegian, V.A. Colloidal DNA. Curr. Opin. Colloid Interface Sci. 1998, 3, 534–539. [Google Scholar] [CrossRef]
- Saminathan, M.; Antony, T.; Shirahata, A.; Sigal, L.H.; Thomas, T.; Thomas, T.J. Ionic and structural specificity effects of natural and synthetic polyamines on the aggregation and resolubilization of single-, double-, and triple-stranded DNA. Biochemistry 1999, 38, 3821–3830. [Google Scholar] [CrossRef] [PubMed]
- Korolev, N.; Lyubartsev, A.P.; Rupprecht, A.; Nordenskiold, L. Competitive substitution of hexammine cobalt(III) for Na+ and K+ ions in oriented DNA fibers. Biopolymers 2001, 58, 268–278. [Google Scholar] [CrossRef] [PubMed]
- Dai, L.; Mu, Y.G.; Nordenskiold, L.; van der Maarel, J.R.C. Molecular dynamics simulation of multivalent-ion mediated attraction between DNA molecules. Phys. Rev. Lett. 2008, 100, 118301:1–118301:4. [Google Scholar] [CrossRef]
- Raspaud, E.; de la Cruz, M.O.; Sikorav, J.L.; Livolant, F. Precipitation of DNA by polyamines: A polyelectrolyte behavior. Biophys. J. 1998, 74, 381–393. [Google Scholar] [CrossRef] [PubMed]
- Raspaud, E.; Durand, D.; Livolant, F. Interhelical spacing in liquid crystalline spermine and spermidine-DNA precipitates. Biophys. J. 2005, 88, 392–403. [Google Scholar] [CrossRef] [PubMed]
- Yang, J.; Rau, D.C. Incomplete ion dissociation underlies the weakened attraction between DNA helices at high spermidine concentrations. Biophys. J. 2005, 89, 1932–1940. [Google Scholar] [CrossRef] [PubMed]
- Qiu, X.Y.; Giannini, J.; Howell, S.C.; Xia, Q.; Ke, F.Y.; Andresen, K. Ion competition in condensed DNA arrays in the attractive regime. Biophys. J. 2013, 105, 984–992. [Google Scholar] [CrossRef] [PubMed]
- Liu, A.J.; Ha, B.Y. When like-charged chains attract—Physical questions posed by DNA condensation. Abstr. Pap. Am. Chem. Soc. 1999, 217, U295–U295. [Google Scholar]
- Ha, B.Y.; Liu, A.J. Effect of non-pairwise-additive interactions on bundles of rodlike polyelectrolytes. Phys. Rev. Lett. 1998, 81, 1011–1014. [Google Scholar] [CrossRef]
- Ha, B.Y.; Liu, A.J. Counterion-mediated attraction between two like-charged rods. Phys. Rev. Lett. 1997, 79, 1289–1292. [Google Scholar] [CrossRef]
- Angelini, T.E.; Liang, H.; Wriggers, W.; Wong, G.C.L. Like-charge attraction between polyelectrolytes induced by counterion charge density waves. Proc. Natl. Acad. Sci. USA 2003, 100, 8634–8637. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.T.; Rouzina, I.; Shklovskii, B.I. Reentrant condensation of DNA induced by multivalent counterions. J. Chem. Phys. 2000, 112, 2562–2568. [Google Scholar] [CrossRef]
- Shklovskii, B.I. Wigner crystal model of counterion induced bundle formation of rodlike polyelectrolytes. Phys. Rev. Lett. 1999, 82, 3268–3271. [Google Scholar] [CrossRef]
- Rouzina, I.; Bloomfield, V.A. Competitive electrostatic binding of charged ligands to polyelectrolytes: Practical approach using the non-linear poisson-boltzmann equation. Biophys. Chem. 1997, 64, 139–155. [Google Scholar] [CrossRef] [PubMed]
- Rouzina, I.; Bloomfield, V.A. Influence of ligand spatial organization on competitive electrostatic binding to DNA. J. Phys. Chem. 1996, 100, 4305–4313. [Google Scholar] [CrossRef]
- Grosberg, A.Y.; Nguyen, T.T.; Shklovskii, B.I. Colloquium: The physics of charge inversion in chemical and biological systems. Rev. Mod. Phys. 2002, 74, 329–345. [Google Scholar] [CrossRef]
- Naji, A.; Netz, R.R. Attraction of like-charged macroions in the strong-coupling limit. Eur. Phys. J. E 2004, 13, 43–59. [Google Scholar] [CrossRef] [PubMed]
- Kanduc, M.; Naji, A.; Podgornik, R. Counterion-mediated weak and strong coupling electrostatic interaction between like-charged cylindrical dielectrics. J. Chem. Phys. 2010, 132, 224703:1–224703:19. [Google Scholar]
- Chen, Y.G.; Weeks, J.D. Local molecular field theory for effective attractions between like charged objects in systems with strong coulomb interactions. Proc. Natl. Acad. Sci. USA 2006, 103, 7560–7565. [Google Scholar] [CrossRef] [PubMed]
- Rodgers, J.M.; Kaur, C.; Chen, Y.G.; Weeks, J.D. Attraction between like-charged walls: Short-ranged simulations using local molecular field theory. Phys. Rev. Lett. 2006, 97, 097801:1–097801:5. [Google Scholar] [CrossRef]
- Tan, Z.J.; Chen, S.J. Nucleic acid helix stability: Effects of salt concentration, cation valence and size, and chain length. Biophys. J. 2006, 90, 1175–1190. [Google Scholar] [CrossRef] [PubMed]
- Tan, Z.J.; Chen, S.J. Ion-mediated nucleic acid helix-helix interactions. Biophys. J. 2006, 91, 518–536. [Google Scholar] [CrossRef] [PubMed]
- Kornyshev, A.A.; Leikin, S. Electrostatic zipper motif for DNA aggregation. Phys. Rev. Lett. 1999, 82, 4138–4141. [Google Scholar] [CrossRef]
- Kornyshev, A.A.; Wynveen, A. The homology recognition well as an innate property of DNA structure. Proc. Natl. Acad. Sci. USA 2009, 106, 4683–4688. [Google Scholar] [CrossRef] [PubMed]
- Rau, D.C.; Parsegian, V.A. Direct measurement of the intermolecular forces between counterion-condensed DNA double helices—Evidence for long-range attractive hydration forces. Biophys. J. 1992, 61, 246–259. [Google Scholar] [CrossRef] [PubMed]
- Rau, D.C.; Lee, B.; Parsegian, V.A. Measurement of the repulsive force between poly-electrolyte molecules in ionic solution—Hydration forces between parallel DNA double helices. Proc. Natl. Acad. Sci. USA 1984, 81, 2621–2625. [Google Scholar] [CrossRef] [PubMed]
- Podgornik, R.; Strey, H.H.; Rau, D.C.; Parsegian, V.A. Watching molecules crowd—DNA double helices under osmotic-stress. Biophys. Chem. 1995, 57, 111–121. [Google Scholar] [CrossRef] [PubMed]
- Leikin, S.; Parsegian, V.A.; Rau, D.C.; Rand, R.P. Hydration forces. Annu. Rev. Phys. Chem. 1993, 44, 369–395. [Google Scholar] [CrossRef] [PubMed]
- Stanley, C.; Rau, D.C. Evidence for water structuring forces between surfaces. Curr. Opin. Colloid Interface Sci. 2011, 16, 551–556. [Google Scholar] [CrossRef] [PubMed]
- Li, W.F.; Nordenskiold, L.; Zhou, R.H.; Mu, Y.G. Conformation-dependent DNA attraction. Nanoscale 2014, 6, 7085–7092. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Pabit, S.A.; Meisburger, S.P.; Pollack, L. Double-stranded RNA resists condensation. Phys. Rev. Lett. 2011, 106, 108101:1–108101:9. [Google Scholar]
- Tolokh, I.S.; Pabit, S.A.; Katz, A.M.; Chen, Y.; Drozdetski, A.; Baker, N.; Pollack, L.; Onufriev, A.V. Why double-stranded RNA resists condensation. Nucleic Acids Res. 2014, 42, 10823–10831. [Google Scholar] [CrossRef] [PubMed]
- Kornyshev, A.A.; Leikin, S. Helical structure determines different susceptibilities of dsDNA, dsRNA, and tsDNA to counterion-induced condensation. Biophys. J. 2013, 104, 2031–2041. [Google Scholar] [CrossRef] [PubMed]
- He, Z.J.; Chen, S.J. Quantifying coulombic and solvent polarization-mediated forces between DNA helices. J. Phys. Chem. B 2013, 117, 7221–7227. [Google Scholar] [CrossRef] [PubMed]
© 2015 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Wijeratne, S.S.; Qiu, X.; Kiang, C.-H. DNA under Force: Mechanics, Electrostatics, and Hydration. Nanomaterials 2015, 5, 246-267. https://doi.org/10.3390/nano5010246
Li J, Wijeratne SS, Qiu X, Kiang C-H. DNA under Force: Mechanics, Electrostatics, and Hydration. Nanomaterials. 2015; 5(1):246-267. https://doi.org/10.3390/nano5010246
Chicago/Turabian StyleLi, Jingqiang, Sithara S. Wijeratne, Xiangyun Qiu, and Ching-Hwa Kiang. 2015. "DNA under Force: Mechanics, Electrostatics, and Hydration" Nanomaterials 5, no. 1: 246-267. https://doi.org/10.3390/nano5010246
APA StyleLi, J., Wijeratne, S. S., Qiu, X., & Kiang, C.-H. (2015). DNA under Force: Mechanics, Electrostatics, and Hydration. Nanomaterials, 5(1), 246-267. https://doi.org/10.3390/nano5010246





