Accurate Size and Size-Distribution Determination of Polystyrene Latex Nanoparticles in Aqueous Medium Using Dynamic Light Scattering and Asymmetrical Flow Field Flow Fractionation with Multi-Angle Light Scattering
Abstract
:1. Introduction
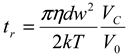
| Sample name | Official diameter a) | CV value b) |
|---|---|---|
| (nm) | % | |
| a) The official values of official diameter are determined by DMA or TEM; b) CV values are calculated from the standard deviation of the size distribution by DMA, and the observed size distributions are divided by size. | ||
| STADEX SC-0070-D | 70 | 7.30 |
| STADEX SC-0080-D | 80 | 4.80 |
| STADEX SC-0100-D | 100 | 2.47 |
| STADEX SC-0110-D | 107 | 3.10 |
| STADEX SC-0140-D | 144 | 1.42 |
| STADEX SC-016-S | 152 | 2.46 |
| F0223 | 140 | - |
| T2112 | 147 | - |
| T0622 | 128 | - |
| T0021 | 90 | - |
| T0118 | 91 | - |
| T0408 | 88 | - |
| T0625 | 103 | - |
2. Experimental Section
2.1. Materials
2.2. DLS Measurements
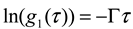
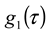 is the homodyne correlation function in DLS and Γ is the decay rate related to the translational diffusion coefficient (D) of the particles in the medium by
is the homodyne correlation function in DLS and Γ is the decay rate related to the translational diffusion coefficient (D) of the particles in the medium by 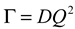
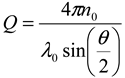
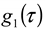 thus obtained was analyzed by the first cumulant method described in ISO 13321 to determine the average decay rate Γ [19]. The apparent diffusion coefficient obtained from DLS was used in the Stokes–Einstein relation of the following form to determine the hydrodynamic particle size of the PS-latex secondary nanoparticles:
thus obtained was analyzed by the first cumulant method described in ISO 13321 to determine the average decay rate Γ [19]. The apparent diffusion coefficient obtained from DLS was used in the Stokes–Einstein relation of the following form to determine the hydrodynamic particle size of the PS-latex secondary nanoparticles:
2.3. AFFFF-MALS Measurement
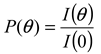
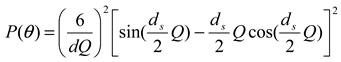
3. Results and Discussion
3.1. DLS
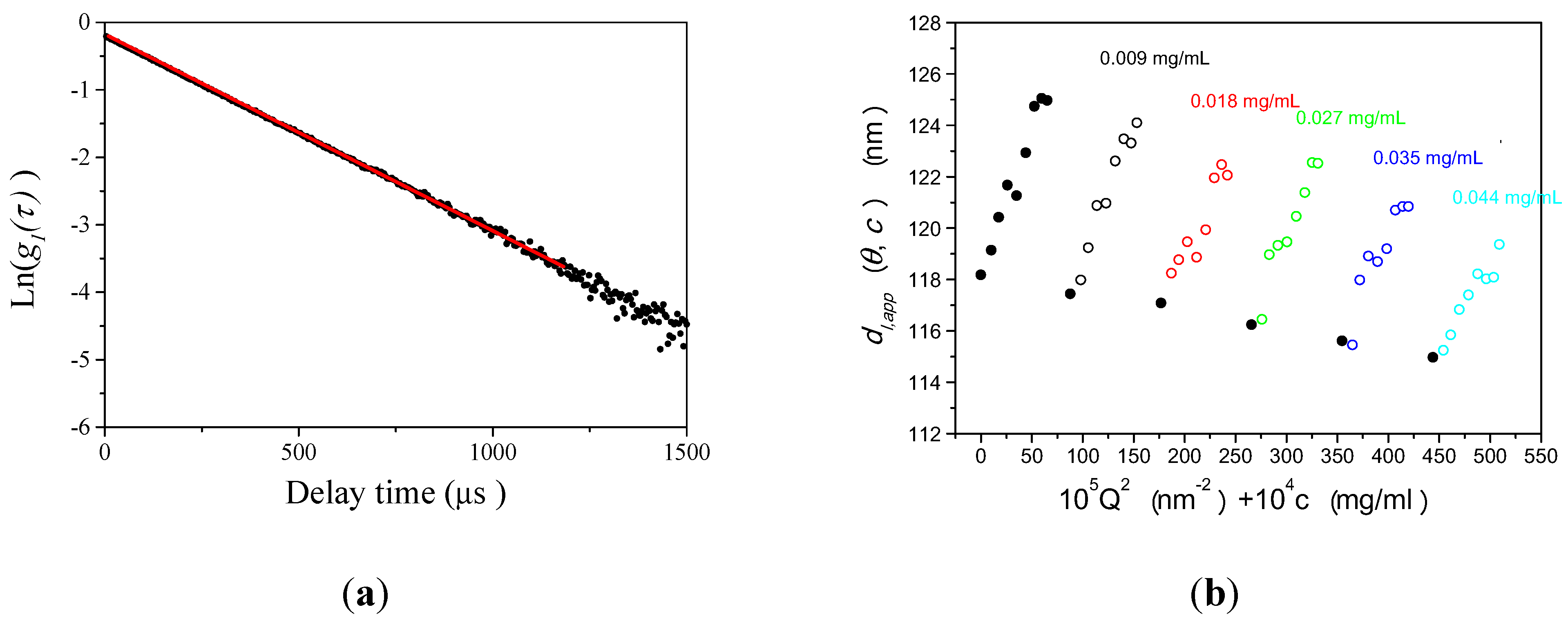
3.1.1. Calculation Method for Reliable Size Determination by DLS
3.1.2. Size Determination of PS-Latex by DLS
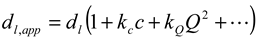
3.1.3. Concept of Identifying and Analyzing Sources of Uncertainty in DLS
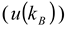 ) [22], the temperature (
) [22], the temperature ( 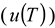 ), the solvent viscosity (
), the solvent viscosity (  ) [20,23], the delay rate (
) [20,23], the delay rate (  ), the solvent refractive index (
), the solvent refractive index (  ) [24,25], the wavelength (
) [24,25], the wavelength ( 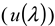 ), the observed scattering angle (
), the observed scattering angle ( 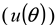 ), the repeatability of DLS measurements (
), the repeatability of DLS measurements ( 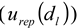 ), and the extrapolation to infinite dilution and to zero angle in the Zimm plot (
), and the extrapolation to infinite dilution and to zero angle in the Zimm plot ( 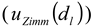 ).
).3.2. AFFFF-MALS
3.2.1. Calculation Method for Determining Size and Size Distribution by AFFFF-MALS


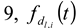 is a Gaussian function for truly monodisperse PS-latex nanoparticles assumed to have a standard deviation factor caused by band broadening (
is a Gaussian function for truly monodisperse PS-latex nanoparticles assumed to have a standard deviation factor caused by band broadening ( 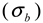 ) and to have a center of diameter from the set of positive integers.
) and to have a center of diameter from the set of positive integers.  is composed of
is composed of 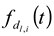 and
and 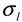 , which are in the set of positive integers. In
, which are in the set of positive integers. In 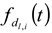 ,
, 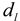 is the intensity-average diameter, and
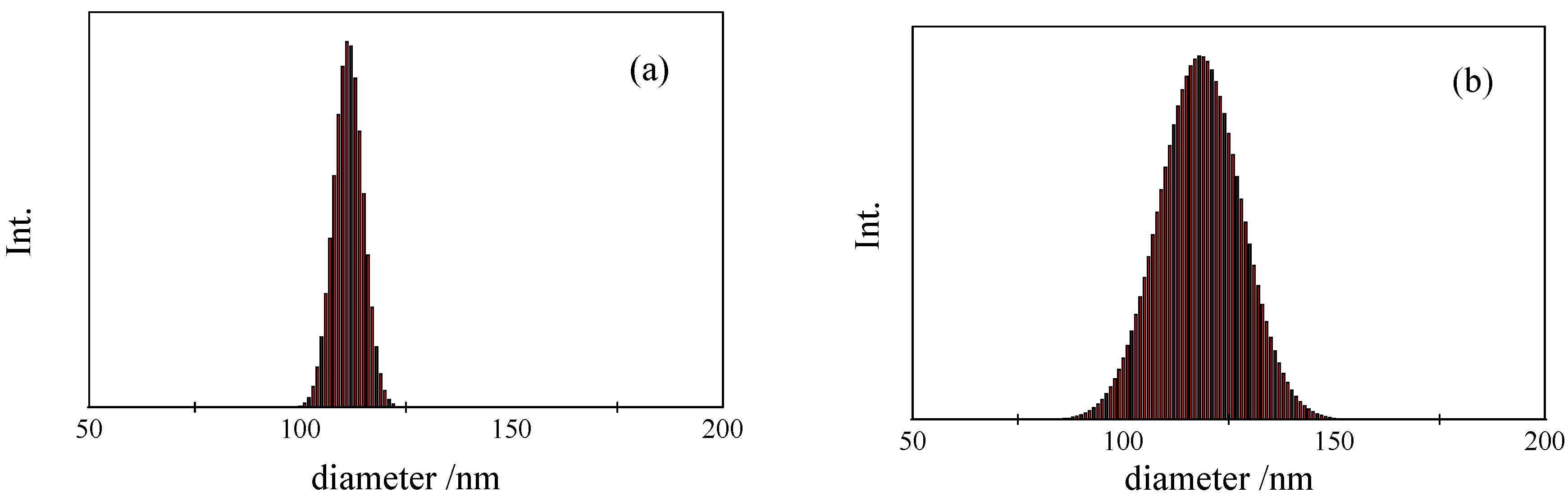
is the intensity-average diameter, and 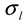 is the standard deviation of size distribution of PS-latex. Using these equations, the size distribution of PS-latex nanoparticles in an aqueous suspension is therefore assumed to be a Gaussian distribution and the fractogram can be represented as a function of the elution time for corresponding diameters of PS-latex nanoparticles. Under this assumption, the plot in Figure 2a changes to the one in Figure 2b.
is the standard deviation of size distribution of PS-latex. Using these equations, the size distribution of PS-latex nanoparticles in an aqueous suspension is therefore assumed to be a Gaussian distribution and the fractogram can be represented as a function of the elution time for corresponding diameters of PS-latex nanoparticles. Under this assumption, the plot in Figure 2a changes to the one in Figure 2b.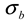 by using a PS-latex nanoparticle standard whose size distribution has already been well characterized by the DMA method [13]. Under this assumption,
by using a PS-latex nanoparticle standard whose size distribution has already been well characterized by the DMA method [13]. Under this assumption, 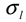 and
and 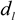 are then determined from the AFFFF-MALS results.
are then determined from the AFFFF-MALS results.3.2.2. Determination of Size and Size Distribution by AFFFF-MALS
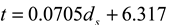
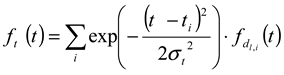
| Sample name | Official CV value | Calculated CV value |
|---|---|---|
| % | % | |
| STADEX SC-0080-D | 4.80 | 4.60 |
| STADEX SC-0100-D | 2.47 | 2.20 |
| STADEX SC-0110-D | 3.10 | 3.30 |
| STADEX SC-0140-D | 1.42 | 1.30 |
| STADEX SC-016-S | 2.46 | 2.20 |
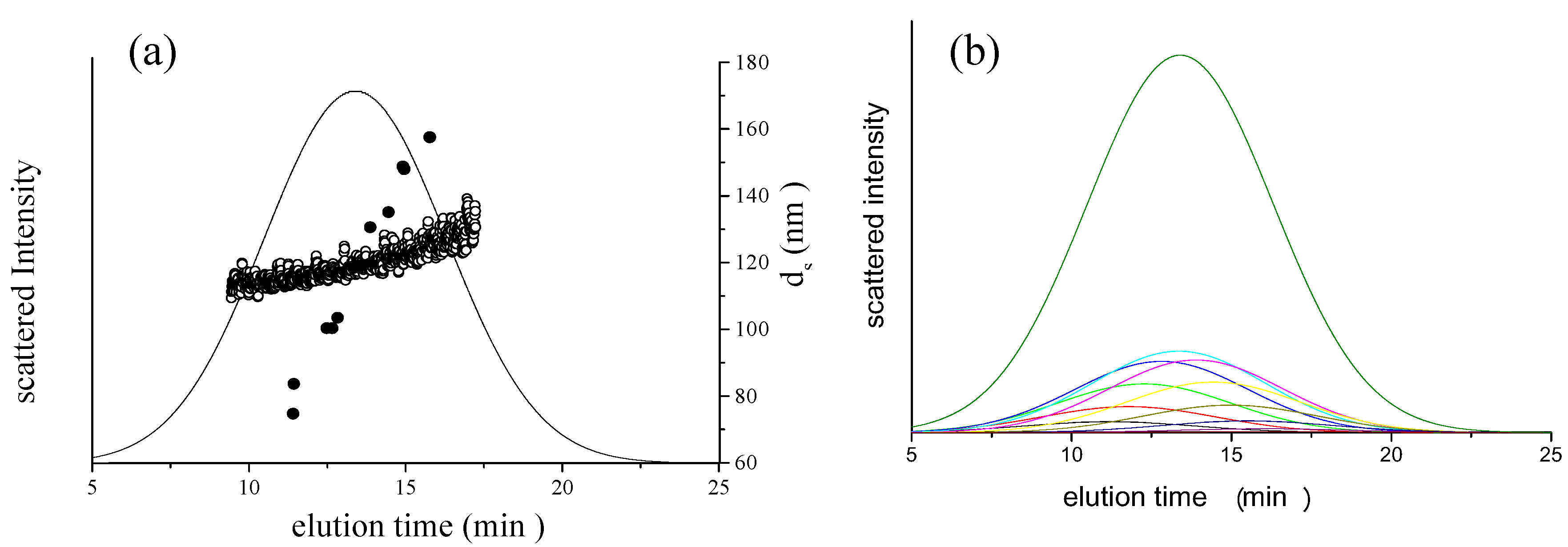
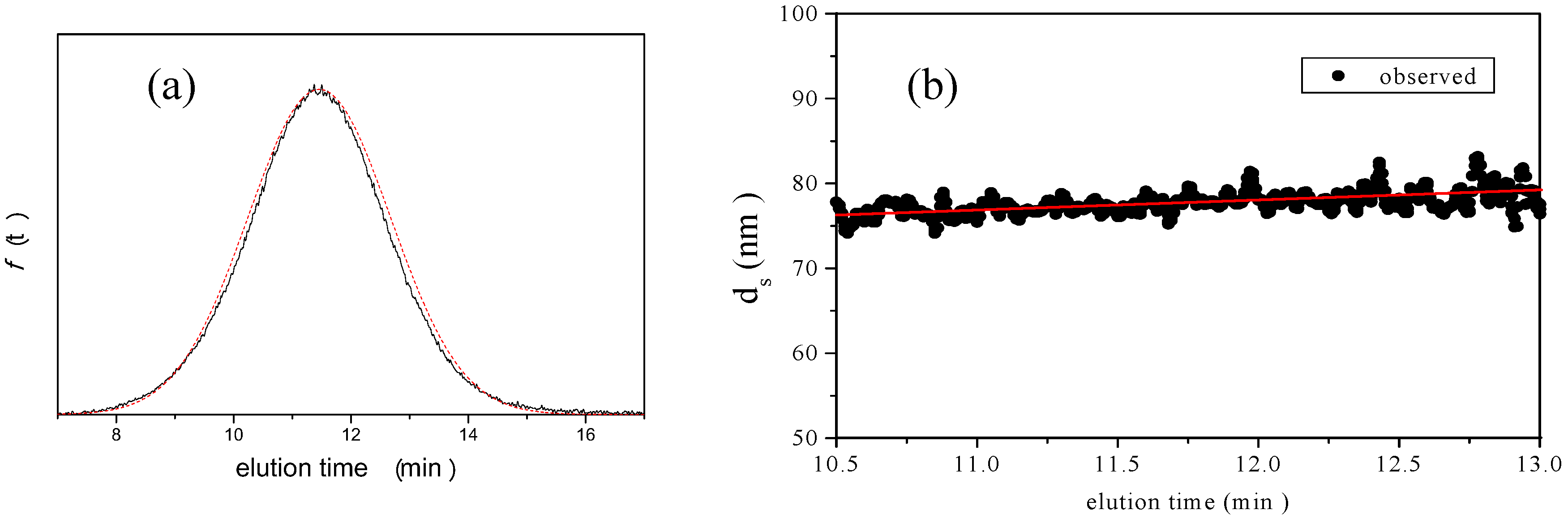
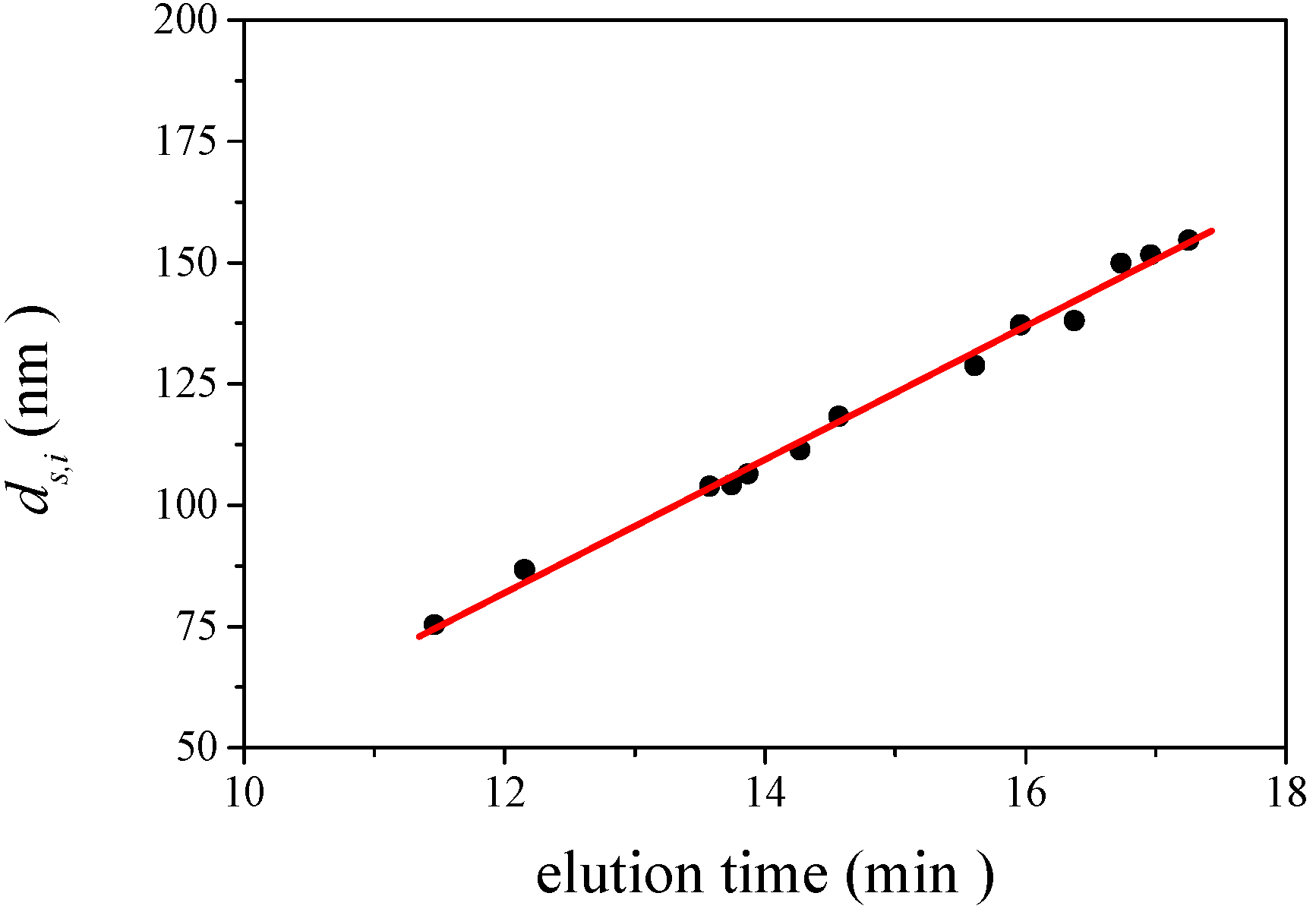
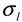 is 11.5 nm from Equation 15. (a) Apparent l ight scattering intensity ( black solid curve) fractogram and fitting curve expressed by Equation 12 (red solid curve). ( b)Apparent diameter of PS-latex (T0625) nanoparticles measured by MALS at corresponding elution times (filled black circles) and theoretical relationship between diameter and elution time (red line) .
is 11.5 nm from Equation 15. (a) Apparent l ight scattering intensity ( black solid curve) fractogram and fitting curve expressed by Equation 12 (red solid curve). ( b)Apparent diameter of PS-latex (T0625) nanoparticles measured by MALS at corresponding elution times (filled black circles) and theoretical relationship between diameter and elution time (red line) .
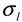 is 11.5 nm from Equation 15. (a) Apparent l ight scattering intensity ( black solid curve) fractogram and fitting curve expressed by Equation 12 (red solid curve). ( b)Apparent diameter of PS-latex (T0625) nanoparticles measured by MALS at corresponding elution times (filled black circles) and theoretical relationship between diameter and elution time (red line) .
is 11.5 nm from Equation 15. (a) Apparent l ight scattering intensity ( black solid curve) fractogram and fitting curve expressed by Equation 12 (red solid curve). ( b)Apparent diameter of PS-latex (T0625) nanoparticles measured by MALS at corresponding elution times (filled black circles) and theoretical relationship between diameter and elution time (red line) . 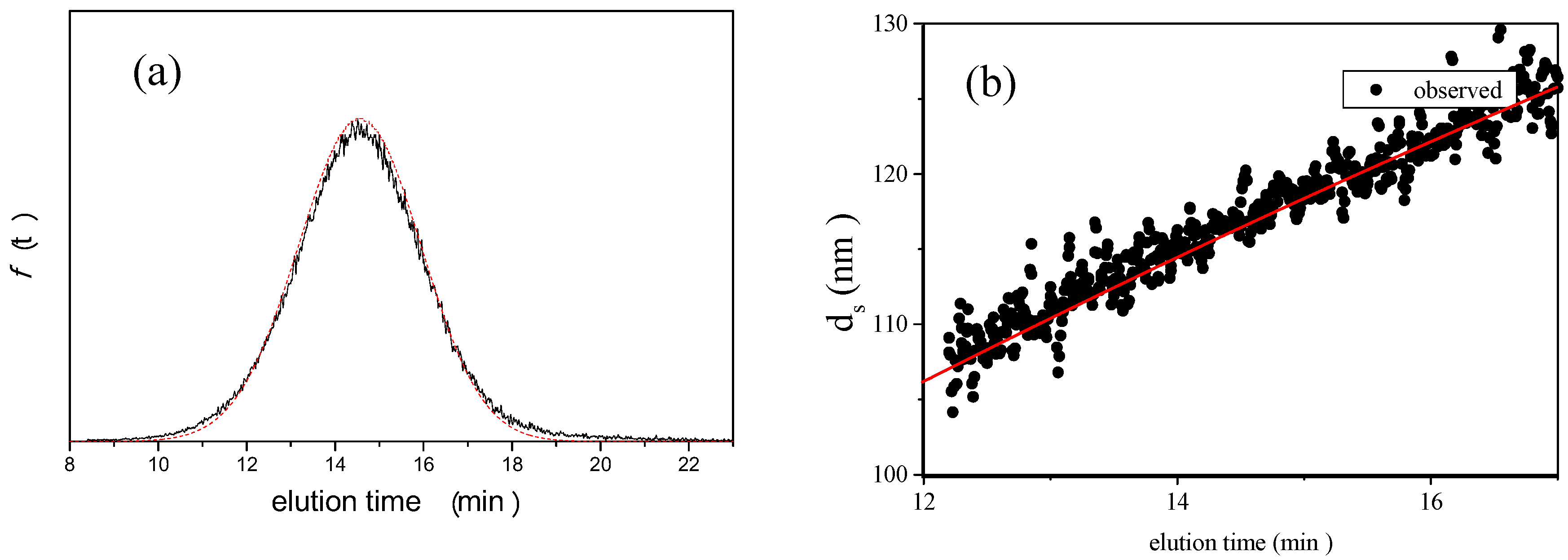
3.2.3. Concept of Identifying and Analyzing Sources of Uncertainty in AFFFF-MALS
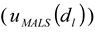 ), the procedure for determining the baseline for AFFFF-MALS measurement (
), the procedure for determining the baseline for AFFFF-MALS measurement (  and
and 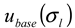 ), the procedure for determining the band broadening factor (
), the procedure for determining the band broadening factor ( 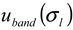 ), the calibration line in Equation 11 (
), the calibration line in Equation 11 ( 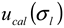 ), and the repeatability of the AFFFF-MALS measurements (
), and the repeatability of the AFFFF-MALS measurements (  and
and 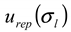 ). The results of separate uncertainty analyses are summarized in Tables S-4 and S-5 (see Supplementary Information). The combined standard uncertainty values calculated for dl and
). The results of separate uncertainty analyses are summarized in Tables S-4 and S-5 (see Supplementary Information). The combined standard uncertainty values calculated for dl and 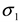 for PS-latex (T0625) are 3.48 and 0.38 nm, respectively.
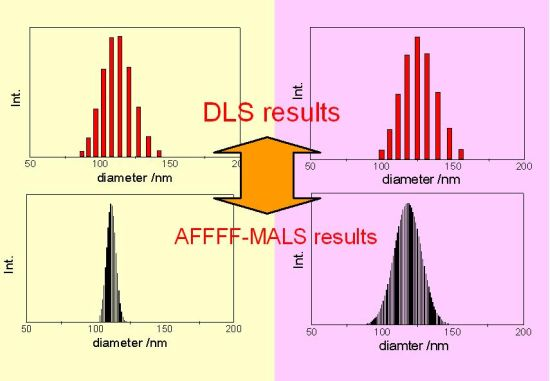
for PS-latex (T0625) are 3.48 and 0.38 nm, respectively.3.3. Comparison of DLS and AFFFF-MALS Results

4. Conclusions
Supplementary Materials
Supplementary File 1References
- Freund, H.; Shaikhutdinov, S.K.; Doyle, A.M. Surface bonded precursor determines particle size effects for alkene hydrogenation on palladium. Angew. Chem. Int. Ed. 2005, 44, 629–631. [Google Scholar] [CrossRef]
- Shinoda, K.; Jeyadevan, B.; Tohji, K.; Liu, X.; Perales, O.; Czajka, R.; Barnakov, Y.; Dmitruk, I.; Milczarek, G.; Kasuya, A.; et al. Size- and shape-controls and electronic functions of nanometer-scale semiconductors and oxides. Colloids Surf. A 2002, 202, 291–296. [Google Scholar] [CrossRef]
- Chan, C.K.; Yue, P.L.; Lee, C.Y.; Yeung, K.L.; Maira, A.J. Size effects in gas-phase photo-oxidation of trichloroethylene using nanometer-sized TiO2 catalysts. J. Catal. 2000, 192, 185–196. [Google Scholar] [CrossRef]
- Talapatra, G.B.; Pal, P.; Sarkar, J. Self-assembly of silver nano-particles on stearic acid Langmuir–Blodgett film: Evidence of fractal growth. Chem. Phys. Lett. 2005, 401, 400–404. [Google Scholar] [CrossRef]
- Wieckowski, A.; Oldfield, E.; Chung, J.H.; Kobayashi, T.; Babu, P.K.; Watanabe, M.; Uchida, H.; Inukai, J.; Yano, H. Particle-size effect of nanoscale platinum catalysts in oxygen reduction reaction: An electrochemical and 195Pt EC-NMR study. Phys. Chem. Chem. Phys. 2006, 8, 4932–4939. [Google Scholar] [PubMed]
- Grassian, V.H.; Jayaweera, P.M.; Baltrusaitis, J. Sulfur dioxide adsorption on TiO2 nanoparticles: Influence of particle size, co-adsorbates, sample pretreatment, and light on surface speciation and surface coverage. J. Phys. Chem. C 2011, 115, 492–500. [Google Scholar] [CrossRef]
- Nel, A.E.; Xia, T.; Li, N. The role of oxidative stress in ambient particulate matter- induced lung diseases and its implications in the toxicity of engineered nanoparticles. Free Radic. Biol. Med. 2008, 44, 1689–1699. [Google Scholar] [CrossRef] [PubMed]
- Lyng, F.M.; Byrne, H.J.; Chamber, G.; Cottineau, B.; Casey, A.; Herzog, E.; Davoren, M. In vitro toxicity evaluation of single walled carbon nanotubes on human A549 lung cells. Toxicol. In Vitro 2007, 21, 438–448. [Google Scholar] [CrossRef] [PubMed]
- Lai, D.; Kreyling, W.; Karn, B.; Carter, J.; Ausman, K.; Fitzpartrick, J.; Castranova, V.; Donaldson, K.; Maynard, A.; Oberdörster, G.; et al. Principles for characterizing the potential human health effects from exposure to nanomaterials: Elements of a screening strategy. Part. Fibre Toxicol. 2005, 2, 1–35. [Google Scholar] [CrossRef] [PubMed]
- Holian, A., Jr.; Hamilton, R.F., Jr.; Buford, M.C. A comparison of dispersing media for various engineered carbon nanoparticles. Part. Fibre Toxicol. 2007, 4, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Commission Recommendation on the definition of nanomaterial. European Commission Website. 2011. Available online: http://ec.europa.eu/environment/chemicals/nanotech/pdf/commission_recommendation.pdf (accessed on 26 October 2011).
- Pecora, R.; Berne, B.J. Dynamic Light Scattering: With Applications to Chemistry,Biology,and Physics; 2000; Dover Publications: Mineola, NY, USA. [Google Scholar]
- Kinugasa, S.; Nakamura, A.; Takahashi, K.; Iwahashi, H.; Yoshida, Y.; Endoh, S.; Horie, M.; Fujita, K.; Suzuki, M.; Kato, H. Reliable size determination of nanoparticles using dynamic light scattering method for in vitro toxicology assessment. Toxicol. In Vitro 2009, 23, 927–934. [Google Scholar] [CrossRef] [PubMed]
- Caldwell, J.C.; Schimpf, K. Caldwell,J.C. Giddings Field-Flow Fractionation Handbook; 2000; John Wiley : Hoboken, NJ, USA. [Google Scholar]
- Burchard, W.; Schmidt, M.; Bantle, S. Simultaneous static and dynamic light scattering. Macromolecules 1982, 15, 1604–1609. [Google Scholar] [CrossRef]
- Schätzel, K.; Burchard, W.; Wenzel, M. Dynamic light scattering from semidilute cellulose-tri-carbanilate solutions. Polymer 1986, 27, 195–201. [Google Scholar] [CrossRef]
- Kinugasa, S.; Matsuyama, S.; Saito, T.; Kato, H.; Takahashi, K. Precise measurement of the size of nanoparticles by dynamic light scattering with uncertainty analysis. Part. Part. Syst. Charact. 2008, 25, 31–38. [Google Scholar] [CrossRef]
- Hagwood, R.C.; Mulholland, G.W.; Ehara, K. Determination of arbitrary moments of aerosol size distributions from measurements with a differential mobility analyzer. Aerosol Sci. Technol. 2000, 32, 434–452. [Google Scholar] [CrossRef]
- Particle size analysis—Photon correlation spectroscopy. ISO 13321. International Organization for Standardization, Geneva, Switzerland, 1996.
- Sakano, T.K.; Bunger, W.B.; Riddick, J.A. Organic Solvents: Physical Properties and methods of Purification1986, 4th ed; John Wiley : New York, NY, USA. [Google Scholar]
- Felderhof, B.U.; Cichocki, B. Self-diffusion of Brownian particles with hydrodynamic interaction and square step or well potential. J. Chem. Phys. 1991, 94, 563–568. [Google Scholar] [CrossRef]
- Glossary of terms in quantities and units in Clinical Chemistry PAC. Pure Appl. Chem. 1996, 68, 957–1000. [CrossRef]
- Wakeham, A.; Sokolov, M.; Kestin, J. Viscosity of liquid water in the range −8 °C to 150 °C. J. Phys. Chem. Ref. Data 1978, 7, 941–948. [Google Scholar] [CrossRef]
- Radwan, M.A.; O’Donohue, S.J.; Huglin, M.B. Refractometric and light scattering parameters at 633 nm for polystyrene solutions. Eur. Polym. J. 1989, 25, 543–547. [Google Scholar] [CrossRef]
- Finsy, R.; Greef, C.; Moreels, E. Laser light refractometer. Appl. Opt. 1984, 23, 3010–3013. [Google Scholar] [CrossRef] [PubMed]
- Ehara, K.; Takahata, K. Accurate particle size measurements for development of particle size standards in the range of 30 to 100 nm. In. In Proceedings of the 7th International Aerosol Conference, St. Paul, MI, USA, 10–15 September 2006, Mt. Laurel, NJ, USA, 10–15 September 2006; American Association for Aerosol Reseach, 2006; pp. 395–396. [Google Scholar]
- Kinugasa, S.; Saito, T.; Takahashi, K.; Kato, H. Characterization of nanoparticles in an aqueous solution with bound water molecules using pulsed field gradient nuclear magnetic resonance spectroscopy. Chem. Lett. 2008, 37, 1128–1129. [Google Scholar] [CrossRef]
- Vass, S.; Grimm, H.; Bányai, I.; Meier G., *REPLACE*; Gilányi, T. Slow water diffusion in micellar solutions. J. Phys. Chem. B 2005, 109, 11870–11874. [Google Scholar] [PubMed]
- Kullcke, W.; Roessner, D.; Thielking, H. On-line coupling of flow field-flow fractionation and multiangle laser light scattering for the characterization of polystyrene particles. Anal. Chem. 1995, 67, 3229–3233. [Google Scholar] [CrossRef]
- Giddings, J.C.; Moon, M.H.; Rao, S.P.; Lee, S. Determination of mean diameter and PSD of acrylate latex using flow FFF, PCS, EM. Anal. Chem. 1996, 68, 1545–1549. [Google Scholar] [CrossRef] [PubMed]
- Maskos, M.; Schmidt, M.; Jungmann, N. Characterization of polyorganosiloxane nanoparticles in aqueous dispersion by asymmetrical flow field-flow fractionation. Macromolecules 2001, 34, 8347–8353. [Google Scholar] [CrossRef]
- Lee, D.W.; Kim, W.S.; Park, Y.H. Size analysis of industrial carbon blacks by field-flow fractionation. Anal. Bioanal. Chem. 2003, 375, 489–495. [Google Scholar] [PubMed]
© 2012 by the authors. This article is an open-access article distributed under the terms and conditions of the Creative Commons Attribution license ( http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Kato, H.; Nakamura, A.; Takahashi, K.; Kinugasa, S. Accurate Size and Size-Distribution Determination of Polystyrene Latex Nanoparticles in Aqueous Medium Using Dynamic Light Scattering and Asymmetrical Flow Field Flow Fractionation with Multi-Angle Light Scattering. Nanomaterials 2012, 2, 15-30. https://doi.org/10.3390/nano2010015
Kato H, Nakamura A, Takahashi K, Kinugasa S. Accurate Size and Size-Distribution Determination of Polystyrene Latex Nanoparticles in Aqueous Medium Using Dynamic Light Scattering and Asymmetrical Flow Field Flow Fractionation with Multi-Angle Light Scattering. Nanomaterials. 2012; 2(1):15-30. https://doi.org/10.3390/nano2010015
Chicago/Turabian StyleKato, Haruhisa, Ayako Nakamura, Kayori Takahashi, and Shinichi Kinugasa. 2012. "Accurate Size and Size-Distribution Determination of Polystyrene Latex Nanoparticles in Aqueous Medium Using Dynamic Light Scattering and Asymmetrical Flow Field Flow Fractionation with Multi-Angle Light Scattering" Nanomaterials 2, no. 1: 15-30. https://doi.org/10.3390/nano2010015
APA StyleKato, H., Nakamura, A., Takahashi, K., & Kinugasa, S. (2012). Accurate Size and Size-Distribution Determination of Polystyrene Latex Nanoparticles in Aqueous Medium Using Dynamic Light Scattering and Asymmetrical Flow Field Flow Fractionation with Multi-Angle Light Scattering. Nanomaterials, 2(1), 15-30. https://doi.org/10.3390/nano2010015