Chromotropism of Iron(II) Complexes with Non-Symmetric Heterocyclic Ligands: Polarity Sensing in Aqueous Urea Solutions
Abstract
1. Introduction
2. Results and Discussion
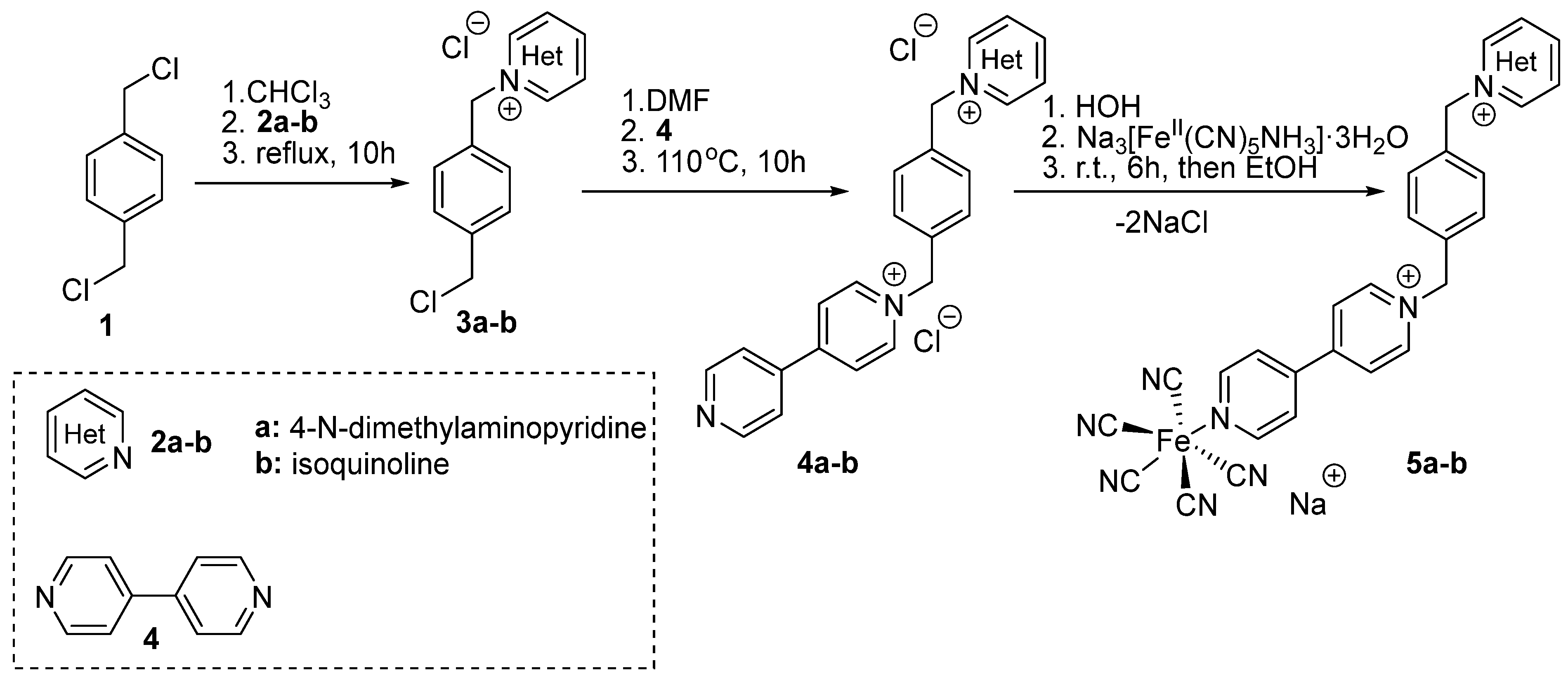
2.1. Synthesis and Characterization
2.2. Solvatochromism
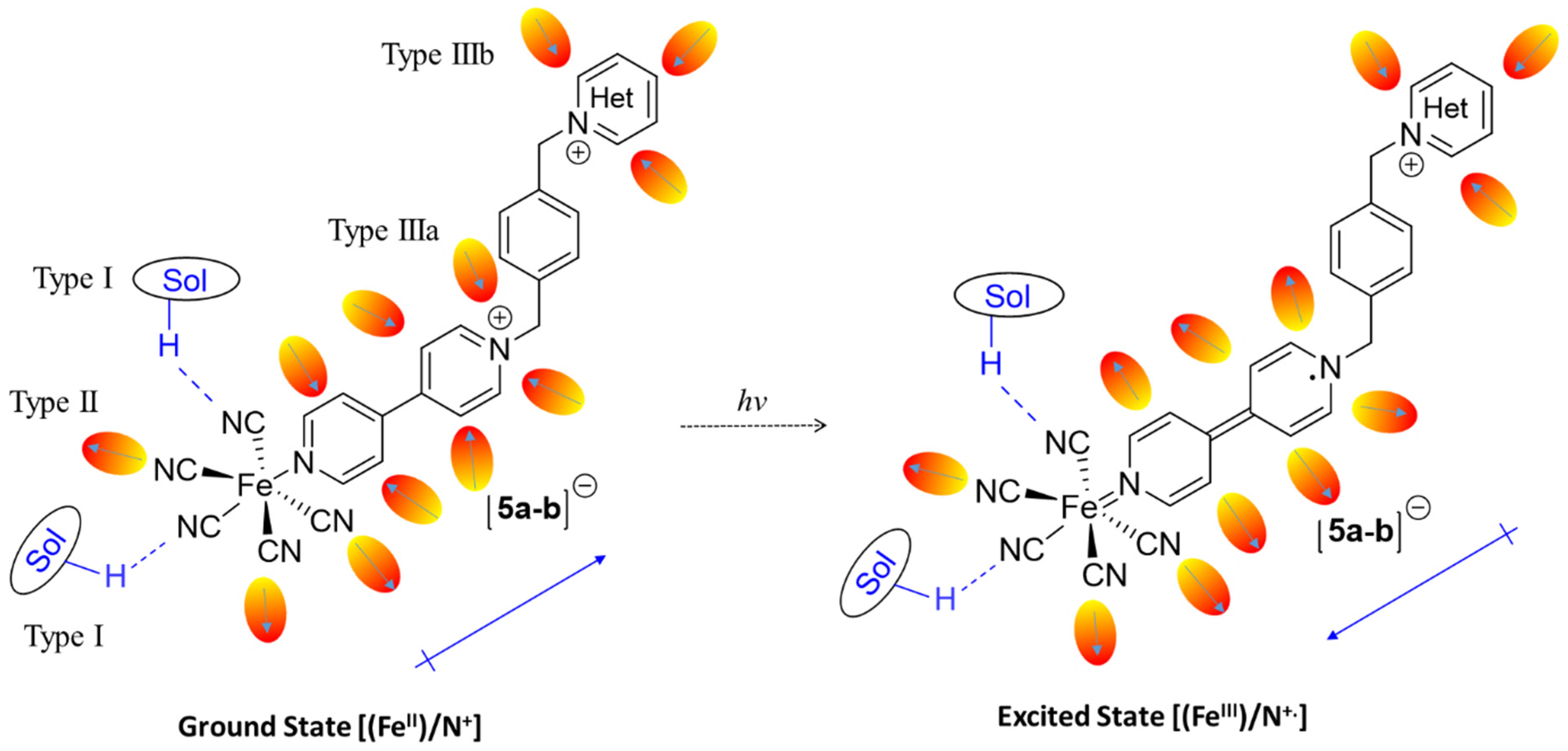
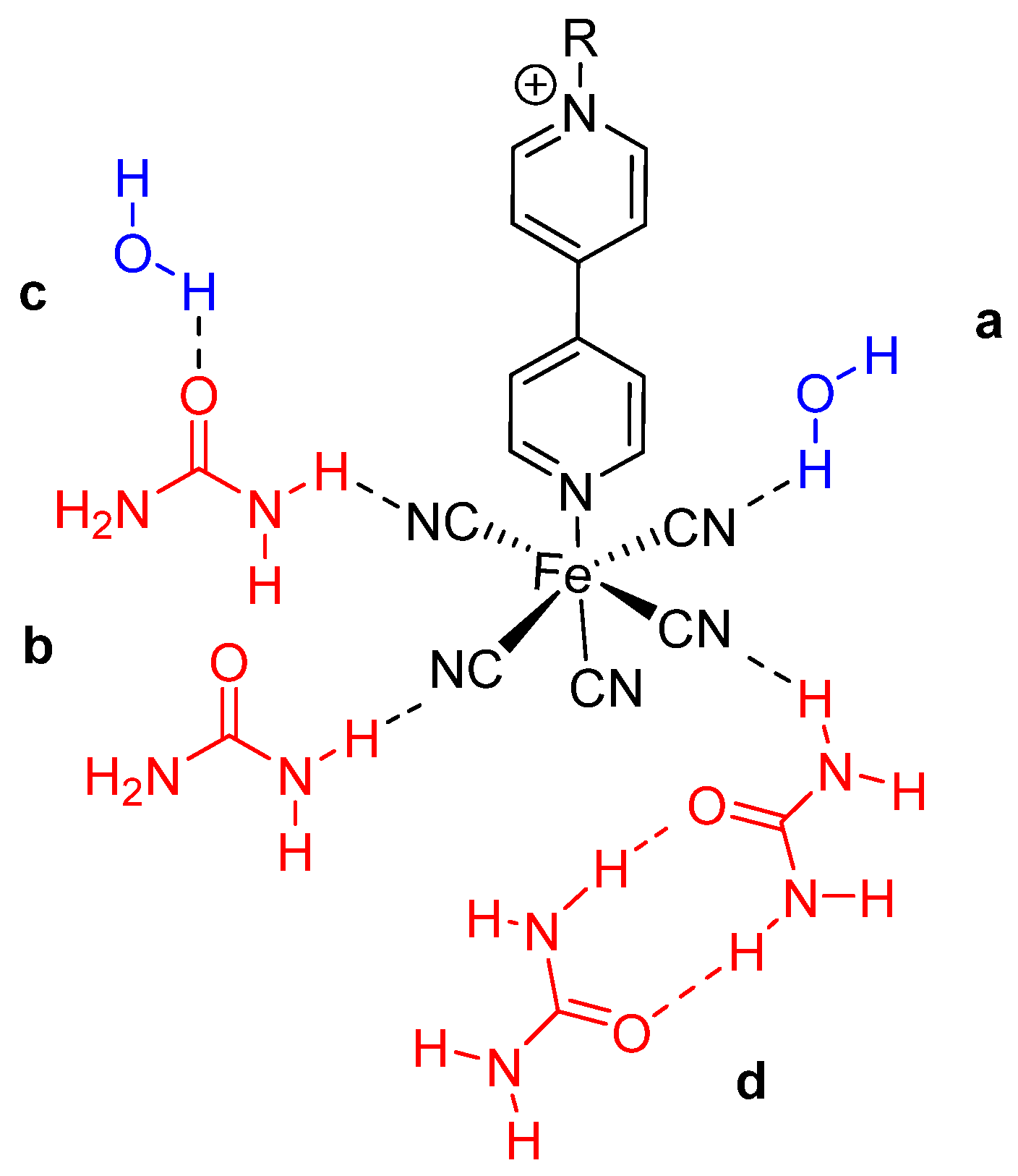
2.3. Types of Solute–Solvent Interactions
2.4. Using LSERs to Rationalize the Solvatochromic Effects
2.5. Determination of Electronic Ground and Excited State Dipole Moments
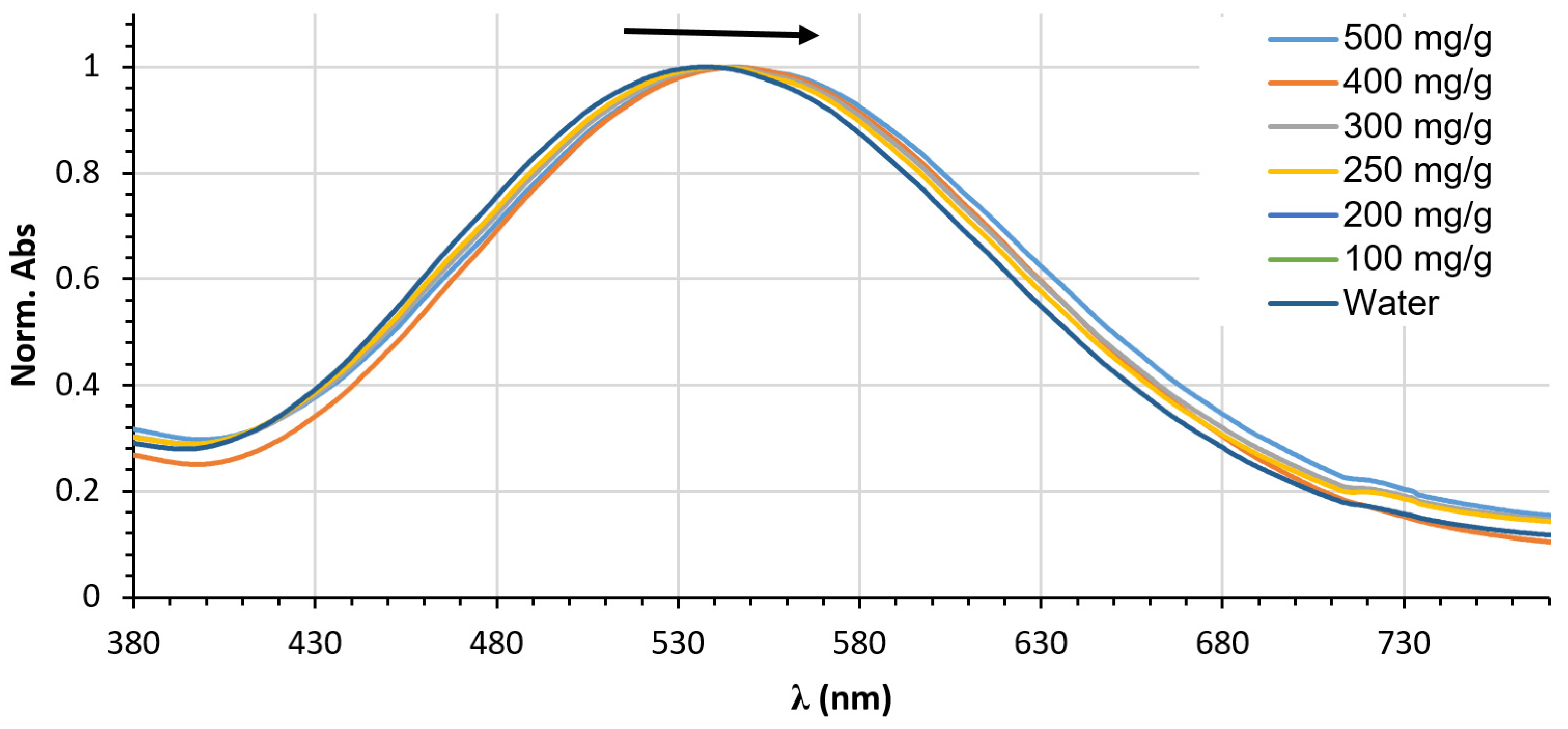
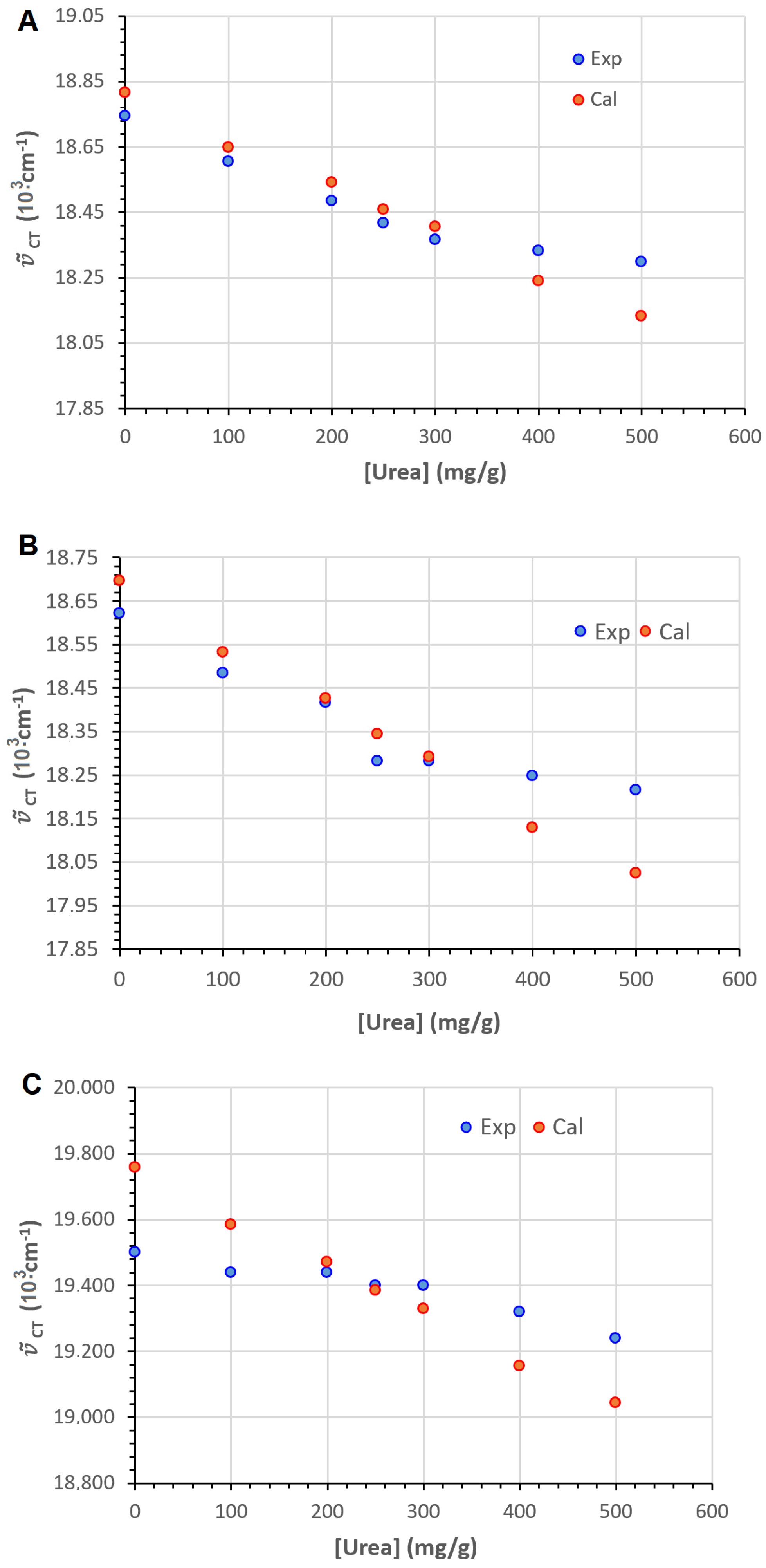
2.6. Polarity Sensing in Aqueous Urea
2.7. An Inverted Solvatochromic Effect or a Pronounced Specific Effect?
2.8. Setting a Suitable Equation Describing Aqueous Urea Polarity Sensing
3. Conclusions
4. Materials and Methods
4.1. Materials
4.2. Model Compounds
4.3. Computations
4.3.1. Linear Solvation Energy Relationships (LSERs)
4.3.2. Dipole Moment Calculations
4.3.3. Determination of Relative Importance (Contribution) of Each of the Parameters Involved in the LSERs
4.3.4. Model Describing Aqueous Urea Solvatochromic Sensing
- and
4.3.5. Spectroscopic and Analytical Methods
4.4. Syntheses
4.4.1. General Method for the Synthesis of Products (3a-b)
4.4.2. 2-(4-(Chloromethyl)benzyl)isoquinolin-2-ium (3b)
4.4.3. Preparation of Products (4a-b)
4.4.4. 2-(4-([4,4′-Bipyridin]-1-ium-1-ylmethyl)benzyl)isoquinolin-2-ium: Ligand: Ligand 4b
4.4.5. General Method for the Synthesis of Solvatochromic Products (5a-b)
4.4.6. Solvatochromic Complex 5b
Supplementary Materials
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| ar | Van der Waals cavity parameter of a solvatochromic compound |
| α | HBD acidity parameter (involved in KAT equation) |
| a | Coefficient of parameter α |
| β | HBA basicity parameter (involved in KAT equation) |
| b | |
| bpy | 4,4′-Bipyridine |
| δ | Chemical shift (NMR) |
| e | in Equations (1) and (4) (does not correspond to the mathematical constant: Euler’s number) |
| EG | Ethylene glycol |
| Normalized Reichardt’s polarity scale | |
| Dimroth–Reichardt’s polarity scale | |
| Permittivity of the medium | |
| Vacuum permittivity | |
| Dipolarity function | |
| Polarizability function | |
| FA | Formamide |
| Dipolarity function in Suppan–Tsiamis equation | |
| Polarizability function in Suppan–Tsiamis equation | |
| “Pure dipolarity” function: φ= | |
| HBD | Hydrogen Bond Donor |
| HBA | Hydrogen Bond Acceptor |
| J | Coupling constant in 1H-NMR |
| KAT | Kamlet–Taft–Abboud (Equation) |
| LSER | Linear solvation energy relationship |
| MLCT maximum wavelength of comound 5a, 5b and 7 respectively | |
| Intercept and two coefficients involved in Equation (10) | |
| Ground state dipole moment | |
| Excited state dipole moment | |
| MLCT maximum wavenumber of comound 5a, 5b and 7 respectively | |
| Intercept MLCT wavenumber involved in LSERs: 1–4 | |
| Polarizability of the medium | |
| Refractive index of the medium | |
| NMF | N-methyl formamide |
| π* | Dipolarity/polarizability parameter involved in KAT equation |
| Physicochemical parameter involved in the generic LSER equation: | |
| Intercept involved in the generic LSER equation: | |
| Ρ | Density of an aqueous urea solution |
| s | Coefficient of parameter π* (KAT equation) |
| TFE | 2,2,2-Trifluoroethanol |
| Parameter involved in the generic LSER model |
References
- Macartney, D.H. Properties and reactions of substituted pentacyanoferrate (II) complexes. Rev. Inorg. Chem. 1988, 9, 101–152. [Google Scholar] [CrossRef]
- Pires, B.M.; Galdino, F.E.; Bonacin, J.A. Electrocatalytic reduction of oxygen by metal coordination polymers produced from pentacyanidoferrate(II) complex. Inorg. Chim. Acta 2017, 466, 166–173. [Google Scholar] [CrossRef]
- MPires, B.; Hegner, F.S.; Bonacin, J.A.; Galán-Mascarós, J.R. Ligand effects of penta- and hexacyanidoferrate-derived water oxidation catalysts on BiVO4 photoanodes. ACS Appl. Energy Mater. 2020, 3, 8448–8456. [Google Scholar] [CrossRef]
- Bratskaya, S.Y.; Privar, Y.O.; Korjakova, O.V.; Mechaev, A.V.; Pestov, A.V. Pentacyanoferrate(II) complexes with chitosan. Polym. Eng. Sci. 2014, 54, 2392–2397. [Google Scholar] [CrossRef]
- Bratskaya, S.Y.; Zheleznov, V.V.; Privar, Y.O.; Mechaev, A.V.; Zub, Y.L.; Pestov, A.V. Pentacyanoferrate(II) complexes with N-containing derivatives of chitosan and polyallylamine: Synthesis and cesium uptake properties. Colloids Surf. A Physicochem. Eng. Asp. 2014, 460, 145–150. [Google Scholar] [CrossRef]
- Zakaria, M.B.; Chikyow, T. Recent advances in Prussian blue and Prussian blue analogues: Synthesis and thermal treatments. Coord. Chem. Rev. 2017, 352, 328–345. [Google Scholar] [CrossRef]
- Carvalho, E.M.; Paulo, T.d.F.; Saquet, A.S.; Abbadi, B.L.; Macchi, F.S.; Bizarro, C.V.; Campos, R.d.M.; Ferreira, T.L.A.; Nascimento, N.R.F.D.; Lopes, L.G.F.; et al. Pentacyanoferrate(II) complex of pyridine-4- and pyrazine-2-hydroxamic acid as source of HNO: Investigation of anti-tubercular and vasodilation activities. J. Biol. Inorg. Chem. 2020, 25, 887–901. [Google Scholar] [CrossRef]
- Toma, H.E.; Malin, J.M. Properties and reactivity of some pentacyanoferrate(II) complexes of aromatic nitrogen heterocycles. Inorg. Chem. 1973, 12, 1039–1045. [Google Scholar] [CrossRef]
- Naik, R.M.; Kumar, B. The palladium(ii)-catalysed ligand exchange between hexacyanoferrate(ii) and 4-Cyanopyridine in aqueous acidic medium. Prog. React. Kinet. Mech. 2012, 37, 147–160. [Google Scholar] [CrossRef]
- Gou, S.; Renz, F.; Fukuda, Y.; Linert, W. Cyano-bridged dinuclear iron complexes in different oxidation states. Inorg. Chim. Acta 1999, 287, 95–100. [Google Scholar] [CrossRef]
- Coe, B.J.; Foxon, S.P.; Harper, E.C.; Raftery, J.; Shaw, R.; Swanson, C.A.; Asselberghs, I.; Clays, K.; Brunschwig, B.S.; Fitch, A.G. Nonlinear optical and related properties of iron(II) pentacyanide complexes with quaternary nitrogen electron acceptor units. Inorg. Chem. 2009, 48, 1370–1379. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, R. Mono- and Di-quaternized 4,4′-bipyridine derivatives as key building blocks for medium- and environment-responsive compounds and materials. Molecules 2019, 25, 1. [Google Scholar] [CrossRef]
- Papadakis, R. Preferential solvation of a highly medium responsive pentacyanoferrate(II) complex in binary solvent mixtures: Understanding the role of dielectric enrichment and the specificity of solute–solvent interactions. J. Phys. Chem. B 2016, 120, 9422–9433. [Google Scholar] [CrossRef] [PubMed]
- Papadakis, R. Solute-centric versus indicator-centric solvent polarity parameters in binary solvent mixtures. Determining the contribution of local solvent basicity to the solvatochromism of a pentacyanoferrate(II) dye. J. Mol. Liq. 2017, 241, 211–221. [Google Scholar] [CrossRef]
- Papadakis, R.; Deligkiozi, I.; Nowak, K.E. Study of the preferential solvation effects in binary solvent mixtures with the use of intensely solvatochromic azobenzene involving [2]rotaxane solutes. J. Mol. Liq. 2019, 274, 715–723. [Google Scholar] [CrossRef]
- Papadakis, R.; Deligkiozi, I.; Giorgi, M.; Faure, B.; Tsolomitis, A. Supramolecular complexes involving non-symmetric viologen cations and hexacyanoferrate(II) anions. A spectroscopic, crystallographic and computational study. RSC Adv. 2016, 6, 575–585. [Google Scholar] [CrossRef]
- Deligkiozi, I.; Papadakis, R. Probing solvation effects in binary solvent mixtures with the use of solvatochromic dyes. In Dyes and Pigments—Novel Applications and Waste Treatment; IntechOpen: London, UK, 2021. [Google Scholar] [CrossRef]
- Papadakis, R. The solvatochromic behavior and degree of ionicity of a synthesized pentacyano (N-substituted-4,4′-bipyridinium) ferrate(II) complex in different media. Tuning the solvatochromic intensity in aqueous glucose solutions. Chem. Phys. 2014, 430, 29–39. [Google Scholar] [CrossRef]
- Papadakis, R.; Tsolomitis, A. Solvatochromism and preferential solvation of 4-pentacyanoferrate 4′-aryl substituted bipyridinium complexes in binary mixtures of hydroxylic and non-hydroxylic solvents. J. Solut. Chem. 2011, 40, 1108–1125. [Google Scholar] [CrossRef]
- Papadakis, R.; Tsolomitis, A. Study of the correlations of the MLCT Vis absorption maxima of 4-pentacyanoferrate- 4′-arylsubstituted bispyridinium complexes with the Hammett substituent parameters and the solvent polarity parameters E and AN. J. Phys. Org. Chem. 2009, 22, 515–521. [Google Scholar] [CrossRef]
- Foretić, B.; Klaser, T.; Ovčar, J.; Lončarić, I.; Žilić, D.; Šantić, A.; Štefanić, Z.; Bjelopetrović, A.; Popović, J.; Picek, I. The reversible electron transfer within stimuli-responsive hydrochromic supramolecular material containing pyridinium oxime and hexacyanoferrate (II) ions. Molecules 2024, 29, 5611. [Google Scholar] [CrossRef]
- Tanaka, R.; Okazawa, A.; Konaka, H.; Sasaki, A.; Kojima, N.; Matsushita, N. Unique hydration/dehydration-induced vapochromic behavior of a charge-transfer salt comprising viologen and hexacyanidoferrate(II). Inorg. Chem. 2018, 57, 2209–2217. [Google Scholar] [CrossRef]
- Abouelwafa, A.S.; Mereacre, V.; Balaban, T.S.; Anson, C.E.; Powell, A.K. Photo- and thermally-enhanced charge separation in supramolecular viologen–hexacyanoferrate complexes. CrystEngComm 2010, 12, 94–99. [Google Scholar] [CrossRef]
- Deligkiozi, I.; Voyiatzis, E.; Tsolomitis, A.; Papadakis, R. Synthesis and characterization of new azobenzene-containing bis pentacyanoferrate(II) stoppered push–pull [2]rotaxanes, with α- and β-cyclodextrin. Towards highly medium responsive dyes. Dye. Pigment. 2015, 113, 709–722. [Google Scholar] [CrossRef]
- Li, M.H.; You, M.H.; Lin, M.J. Photochromism- and photoluminescence-tunable heterobimetallic supramolecular hybrid isomers. Cryst. Growth Des. 2021, 21, 2856–2867. [Google Scholar] [CrossRef]
- Parra-Alfambra, A.M.; Casero, E.; Ruiz, M.A.; Vázquez, L.; Pariente, F.; Lorenzo, E. Carbon nanotubes/pentacyaneferrate-modified chitosan nanocomposites platforms for reagentless glucose biosensing. Anal. Bioanal. Chem. 2011, 401, 883–889. [Google Scholar] [CrossRef] [PubMed]
- Filho, U.P.R.; Gushikem, Y.; Fujiwara, F.Y.; Stadler, E.; Drago, V. Pentacyanoferrates(II) on the surface of organomodified silica gel: The matrix effect. Struct. Chem. 1994, 5, 129–133. [Google Scholar] [CrossRef]
- Li, J.; Robison, T. Application of linear solvation energy relationships to guide selection of polar modifiers in normal-phase liquid chromatographic separations. Anal. Chim. Acta 1999, 395, 85–99. [Google Scholar] [CrossRef]
- Spange, S.; Keutel, D. Untersuchungen zur Polarität wäßriger Harnstoff- und Zucker-Lösungen mit der Methode der vergleichenden Solvatochromie. Liebigs Ann. Chem. 1993, 1993, 981–985. [Google Scholar] [CrossRef]
- Wibowo, E.S.; Park, B.D.; Causin, V. Recent advances in urea–formaldehyde resins: Converting crystalline thermosetting polymers back to amorphous ones. Polym. Rev. 2022, 62, 722–756. [Google Scholar] [CrossRef]
- Dorieh, A.; Selakjani, P.P.; Shahavi, M.H.; Pizzi, A.; Movahed, S.G.; Pour, M.F.; Aghaei, R. Recent developments in the performance of micro/nanoparticle-modified urea-formaldehyde resins used as wood-based composite binders: A review. Int. J. Adhes. Adhes. 2022, 114, 103106. [Google Scholar] [CrossRef]
- Tomita, B.; Hse, C.Y. Phenol–urea–formaldehyde (PUF) co-condensed wood adhesives. Int. J. Adhes. Adhes. 1998, 18, 69–79. [Google Scholar] [CrossRef]
- Laskowska, A. Characteristics of the pressing process and density profile of MUPF-bonded particleboards produced from waste plywood. Materials 2024, 17, 850. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Q.; Yang, C.; Zhuo, H.; Lu, W.; Lu, W. Study on the effect of urea-formaldehyde adhesive on the properties and microscopic characteristics of UF solidified foam. Constr. Build. Mater. 2024, 450, 138704. [Google Scholar] [CrossRef]
- Yang, H.; Wang, H.; Du, G.; Ni, K.; Wu, Y.; Su, H.; Gao, W.; Tan, X.; Yang, Z.; Yang, L.; et al. Ureido hyperbranched polymer modified urea-formaldehyde resin as high-performance particleboard adhesive. Materials 2023, 16, 4021. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Wang, C.; Fang, M.; Li, B.; Jia, J.; Yu, B.; Wang, L. Highly effective flame-retardant coatings consisting of urea-formaldehyde resin/aluminium hydroxide/boric acid for polystyrene foam: Properties and mechanisms investigation. Prog. Org. Coat. 2024, 196, 108766. [Google Scholar] [CrossRef]
- Zotiadis, C.; Patrikalos, I.; Loukaidou, V.; Korres, D.M.; Karantonis, A.; Vouyiouka, S. Self-healing coatings based on poly(urea-formaldehyde) microcapsules: In situ polymerization, capsule properties and application. Prog. Org. Coat. 2021, 161, 106475. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Q.; Lei, H.; Zhou, X.; Zhao, D.; Du, G.; Pizzi, A.; Xi, X. A formaldehyde-free amino resin alternative to urea-formaldehyde adhesives: A bio-based oxidized glucose—Urea resin. Ind. Crops Prod. 2024, 218, 119037. [Google Scholar] [CrossRef]
- Reichardt, C.; Welton, T. Solvents and Solvent Effects in Organic Chemistry; Wiley-VCH Verlag GmbH & Co., KGaA: Hoboken, NJ, USA, 2010. [Google Scholar]
- Lide, D.R. (Ed.) Handbook of Chemistry and Physics, 76th ed.; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Budavari, S. The Merck Index, 11th ed.; Merck and Co.: Rahway, NJ, USA, 1989. [Google Scholar]
- Coe, B.J.; Harries, J.L.; Helliwell, M.; Jones, L.A.; Asselberghs, I.; Clays, K.; Brunschwig, B.S.; Harris, J.A.; Garín, J.; Orduna, J. Pentacyanoiron(II) as an electron donor group for nonlinear optics: Medium-responsive properties and comparisons with related pentaammineruthenium(II) complexes. J. Am. Chem. Soc. 2006, 128, 12192–12204. [Google Scholar] [CrossRef]
- Janjua, N.K.; Qureshi, R.; Ahmed, S.; Khan, A.Y.; Muhammad, M.; Subhani, M.S.; Iqbal, R. Solvent-oriented 1H NMR chemical shifts of pyridinium iodide and application of Buckingham equation. J. Mol. Struct. 2009, 919, 321–324. [Google Scholar] [CrossRef]
- Kamlet, M.J.; Abboud, J.M.; Taft, R.W. An examination of linear solvation energy relationships. Prog. Phys. Org. Chem. 1981, 13, 485. [Google Scholar] [CrossRef]
- Marcus, Y. The properties of organic liquids that are relevant to their use as solvating solvents. Chem. Soc. Rev. 1993, 22, 409–416. [Google Scholar] [CrossRef]
- Krygowski, T.M.; Fawcett, W.R. Complementary Lewis acid-base description of solvent effects. I. Ion-ion and ion-dipole interactions. J. Am. Chem. Soc. 1975, 97, 2143–2148. [Google Scholar] [CrossRef]
- Mulla, B.B.A.; Nesaragi, A.R.; M, M.P.K.; Kamble, R.R.; Sidarai, A.H. Exploration of coumarin derivative: Experimental and computational modeling for dipole moment estimation and thermal sensing application. J. Fluoresc. 2024, 34, 1719–1735. [Google Scholar] [CrossRef]
- Gsänger, M.; Bialas, D.; Huang, L.; Stolte, M.; Würthner, F. Organic Semiconductors based on Dyes and Color Pigments. Adv. Mater. 2016, 28, 3615–3645. [Google Scholar] [CrossRef] [PubMed]
- Carsten, B.; Szarko, J.M.; Son, H.J.; Wang, W.; Lu, L.; He, F.; Rolczynski, B.S.; Lou, S.J.; Chen, L.X.; Yu, L. Examining the effect of the dipole moment on charge separation in donor-acceptor polymers for organic photovoltaic applications. J. Am. Chem. Soc. 2011, 133, 20468–20475. [Google Scholar] [CrossRef] [PubMed]
- Suppan, P.; Tsiamis, C. Absolute excited state dipole moments from solvatochromic shifts. Spectrochim. Acta. Part A Mol. Spectrosc. 1980, 36, 971–974. [Google Scholar] [CrossRef]
- Párkányi, C. Theoretical Organic Chemistry; Elsevier: Amsterdam, The Netherlands, 1998; Volume 5, p. 248. [Google Scholar]
- Hayashi, Y.; Katsumoto, Y.; Omori, S.; Kishii, N.; Yasuda, A. Liquid structure of the urea-water system studied by dielectric spectroscopy. J. Phys. Chem. B 2007, 111, 1076–1080. [Google Scholar] [CrossRef]
- Bandyopadhyay, D.; Mohan, S.; Ghosh, S.K. Molecular Dynamics Simulation of Aqueous Urea Solution: Is Urea a Structure Breaker? J. Phys. Chem. B 2014, 118, 11579–11589. [Google Scholar] [CrossRef]
- Rezus, Y.L.A.; Bakker, H.J. Effect of urea on the structural dynamics of water. Proc. Natl. Acad. Sci. USA 2006, 103, 18417–18420. [Google Scholar] [CrossRef]
- Soper, A.K.; Castner, E.W., Jr.; Luzar, A. Impact of urea on water structure: A clue to its properties as a denaturant? Biophys. Chem. 2003, 105, 649–666. [Google Scholar] [CrossRef]
- Warren, J.R.; Gordon, J.A. On the Refractive Indices of Aqueous Solutions of Urea. J. Chem. Educ. 1951, 28, 291–293. [Google Scholar] [CrossRef]
- Alvarez, S.; López, C.; Bermejo, M.J. C-N stretching force constants in cyano complexes: General trends for polycyano, mixed-ligand and cyano-bridged complexes. Transit. Met. Chem. 1984, 9, 123–126. [Google Scholar] [CrossRef]
- Marcus, Y. The Properties of Solvents; Wiley: Hoboken, NJ, USA, 1998. [Google Scholar]
- Armarego, W.L.F.; Perrin, D.D. Purification of Laboratory Chemicals, 4th ed.; Butterworth-Heinemann: Oxford, UK, 1988. [Google Scholar]
- Papadakis, R.; Deligkiozi, I.; Tsolomitis, A. Spectroscopic investigation of the solvatochromic behavior of a new synthesized non symmetric viologen dye: Study of the solvent-solute interactions. Anal. Bioanal. Chem. 2010, 397, 2253–2259. [Google Scholar] [CrossRef] [PubMed]
- Gottlieb, H.E. NMR Chemical Shifts of Common Laboratory Solvents as Trace Impurities. J. Org. Chem. 1997, 62, 7512–7515. [Google Scholar] [CrossRef]





| Solvent | α [39] | β [39] | π* [39] | ET(30) [39] (kcal/mol) | ■ | ϵ [40] | n [41] | φ(ϵ) † | φ(n2) † |
|---|---|---|---|---|---|---|---|---|---|
| HOH | 1.17 | 0.47 | 1.09 | 63.1 | 1.000 | 78.5 | 1.3325 | 0.9810 | 0.3408 |
| TFE | 1.51 | 0.00 | 0.73 | 59.8 | 0.898 | 26.7 | 1.2907 | 0.9449 | 0.3074 |
| Glycerol | 1.14 | 0.87 | 0.92 | 57.0 | 0.812 | 42.5 | 1.4746 | 0.9651 | 0.4391 |
| ‡ EtOH50% | 1.10 | 0.54 | 0.96 | 56.5 | 0.796 | 38.1 | 1.3617 | 0.9611 | 0.3628 |
| EG | 0.90 | 0.52 | 0.92 | 56.3 | 0.790 | 41.4 | 1.4318 | 0.9642 | 0.4118 |
| FA | 0.71 | 0.48 | 0.97 | 55.8 | 0.775 | 109.5 | 1.4475 | 0.9864 | 0.4220 |
| MeOH | 0.98 | 0.66 | 0.60 | 55.4 | 0.762 | 33.8 | 1.3264 | 0.9563 | 0.3361 |
| ‡ AcMe50% | 0.96 | 0.47 | 1.00 | 54.9 | 0.747 | 30.0 | 1.3583 | 0.9508 | 0.3603 |
| NMF | 0.62 | 0.80 | 0.90 | 54.1 | 0.722 | 182.4 | 1.4319 | 0.9918 | 0.4118 |
| Solvent | (nm) * | (nm) ‡ | ) | ) |
|---|---|---|---|---|
| HOH | 534 | 537 | 18.744 | 18.622 |
| TFE | 572 † | 577 | 17.470 | 17.341 |
| Glycerol | 605 | 610 | 16.529 | 16.389 |
| EtOH50% | 585 | 585 | 17.094 | 17.094 |
| EG | 600 | 599 | 16.667 | 16.705 |
| FA | 628 | 638 | 15.923 | 15.664 |
| MeOH | 671 | 690 | 14.903 | 14.497 |
| AcMe50% | 599 | 604 | 16.694 | 16.564 |
| NMF | 626 | 625 | 15.978 | 16.009 |
| Solvent Parameter/Correlation Coefficient | |||||||
|---|---|---|---|---|---|---|---|
| Compound/Equation # | π* | a | β | ||||
| (103·cm−1) | e(103·cm−1) | s(103·cm−1) | a(103·cm−1) | b(103·cm−1) | r2 | rse | |
| 5a/1 | 8.119 2.064 | 10.54 2.531 | - | - | - | 0.712 | 0.618 |
| 5a/2 | 9.547 1.636 | - | 5.486 1.151 | 9.547 1.636 | −0.730 0.839 | 0.881 | 0.470 |
| 5a/3 | 8.733 1.314 | - | 5.487 1.127 | 2.972 0.630 | - | 0.864 | 0.460 |
| 5a/4 | 8.594 2.833 | 10.14 3.090 | - | - | −0.288 1.072 | 0.716 | 0.664 |
| 5b/1 | 8.121 2.525 | 10.39 3.096 | - | - | - | 0.617 | 0.756 |
| 5b/2 | 9.052 1.971 | - | 5.958 1.387 | 2.509 0.968 | −0.731 1.012 | 0.847 | 0.566 |
| 5b/3 | 8.238 1.551 | - | 5.959 1.330 | 2.928 0.743 | - | 0.831 | 0.543 |
| 5b/4 | 8.513 3.477 | 10.06 3.792 | - | - | −0.238 1.315 | 0.619 | 0.815 |
| Compound/Equation # | ||||
|---|---|---|---|---|
| 5a/2 | - | 0.52 | 0.34 | 0.14 |
| 5a/3 | - | 0.52 | 0.48 | - |
| 5a/4 | 0.85 | - | - | 0.15 |
| 5b/2 | - | 0.58 | 0.29 | 0.13 |
| 5b/3 | - | 0.58 | 0.42 | - |
| 5b/4 | 0.86 | - | - | 0.14 |
| (Å) | (D) | r2 | |||||
|---|---|---|---|---|---|---|---|
| 5a | 5.01 | 15.1 | 21.5 | 0.997 | |||
| 5b | 5.03 | 14.8 | 21.9 | 0.996 |
| Urea Conc. (mg/g) | ρ (g/L) [52] | [Urea] (mol/L) | ET(30) [29] (kcal/mol) | ) | [52] | [56] | ♠ | ♠ |
|---|---|---|---|---|---|---|---|---|
| 0 | 998.68 | 0.00 | 63.1 | 19.50 | 78.48 | 1.3310 | 0.4905 | 0.1706 |
| 100 | 1023.4 | 1.70 | 62.5 | 19.44 | 83.74 | 1.3472 | 0.4911 | 0.1760 |
| 200 | 1049.7 | 3.50 | 62.1 | 19.44 | 87.76 | 1.3621 | 0.4915 | 0.1816 |
| 250 | 1063.5 | 4.43 | 61.8 | 19.40 | 90.10 | 1.3698 | 0.4917 | 0.1844 |
| 300 | 1077.7 | 5.38 | 61.6 | 19.40 | 92.48 | 1.3778 | 0.4919 | 0.1873 |
| 400 | 1107.2 | 7.37 | 61.4 | 19.32 | 96.45 | 1.3943 | 0.4923 | 0.1931 |
| 500 | 1138.3 | 9.48 | 61.2 | 19.24 | 102.1 | 1.4118 | 0.4927 | 0.1992 |
| Urea Concentration (mg/g) | ||||
|---|---|---|---|---|
| 0 | 533.5 | 18.744 | 537.0 | 18.622 |
| 100 | 537.5 | 18.605 | 541.0 | 18.484 |
| 200 | 541.0 | 18.484 | 543.0 | 18.416 |
| 250 | 543.0 | 18.416 | 547.0 | 18.282 |
| 300 | 544.5 | 18.365 | 547.0 | 18.282 |
| 400 | 545.5 | 18.332 | 548.0 | 18.248 |
| 500 | 546.5 | 18.298 | 549.0 | 18.215 |
| (103cm−1) | (103cm−1·mol·kcal−1) | (103cm−1) | * r2 | %RET(30) | %Rf(ϵ) − f(n2) | |
|---|---|---|---|---|---|---|
| 5a | 0.988 | 0.291 | 1.750 | 0.849 | 63 | 37 |
| 5b | 1.168 | 0.286 | 1.621 | 0.898 | 59 | 41 |
| 7 | 1.182 | 0.302 | 1.580 | 0.556 | 11 | 88 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papadakis, R. Chromotropism of Iron(II) Complexes with Non-Symmetric Heterocyclic Ligands: Polarity Sensing in Aqueous Urea Solutions. Nanomaterials 2025, 15, 598. https://doi.org/10.3390/nano15080598
Papadakis R. Chromotropism of Iron(II) Complexes with Non-Symmetric Heterocyclic Ligands: Polarity Sensing in Aqueous Urea Solutions. Nanomaterials. 2025; 15(8):598. https://doi.org/10.3390/nano15080598
Chicago/Turabian StylePapadakis, Raffaello. 2025. "Chromotropism of Iron(II) Complexes with Non-Symmetric Heterocyclic Ligands: Polarity Sensing in Aqueous Urea Solutions" Nanomaterials 15, no. 8: 598. https://doi.org/10.3390/nano15080598
APA StylePapadakis, R. (2025). Chromotropism of Iron(II) Complexes with Non-Symmetric Heterocyclic Ligands: Polarity Sensing in Aqueous Urea Solutions. Nanomaterials, 15(8), 598. https://doi.org/10.3390/nano15080598






