Instability by Extension of an Elastic Nanorod
Abstract
1. Introduction
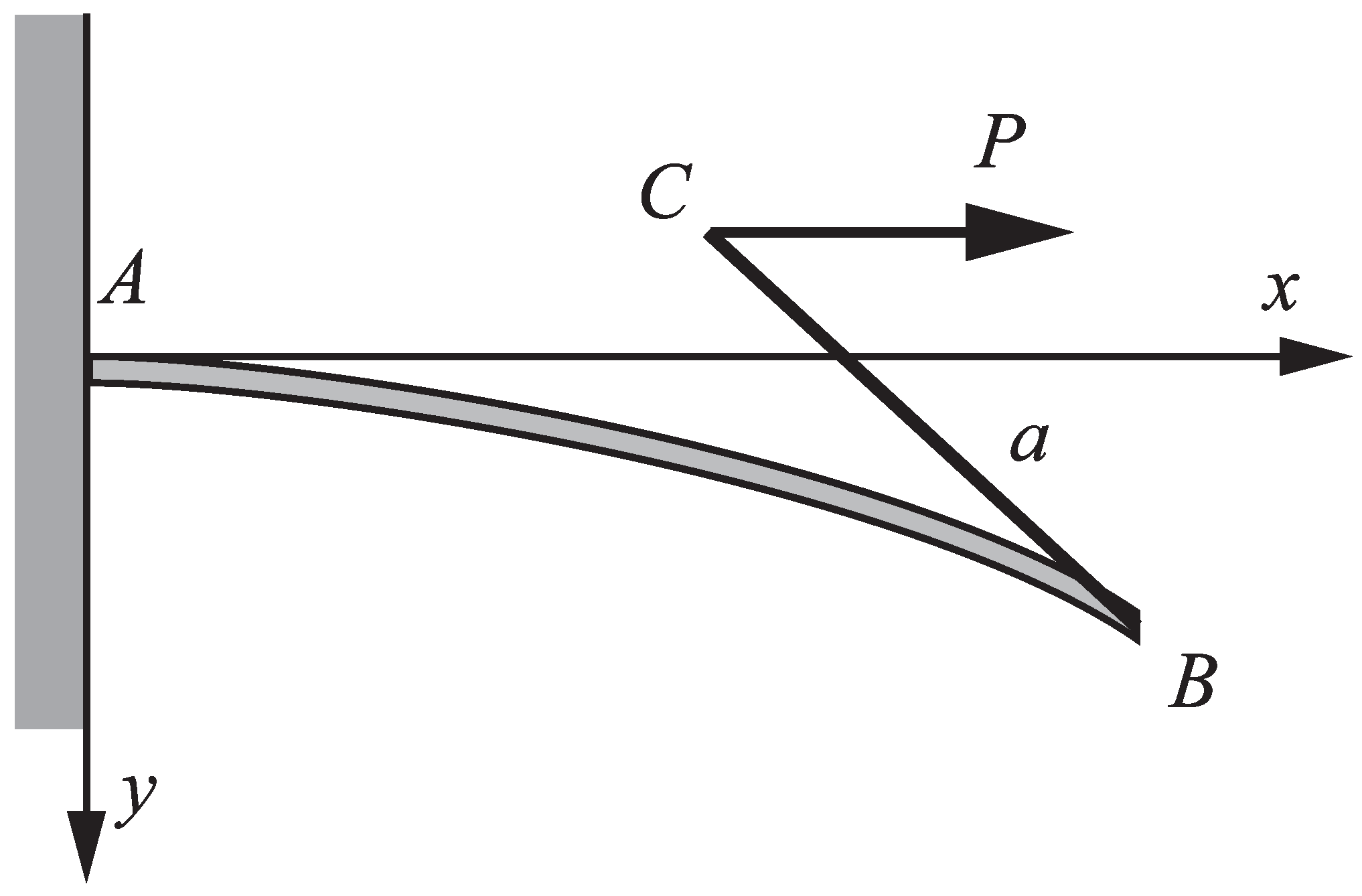
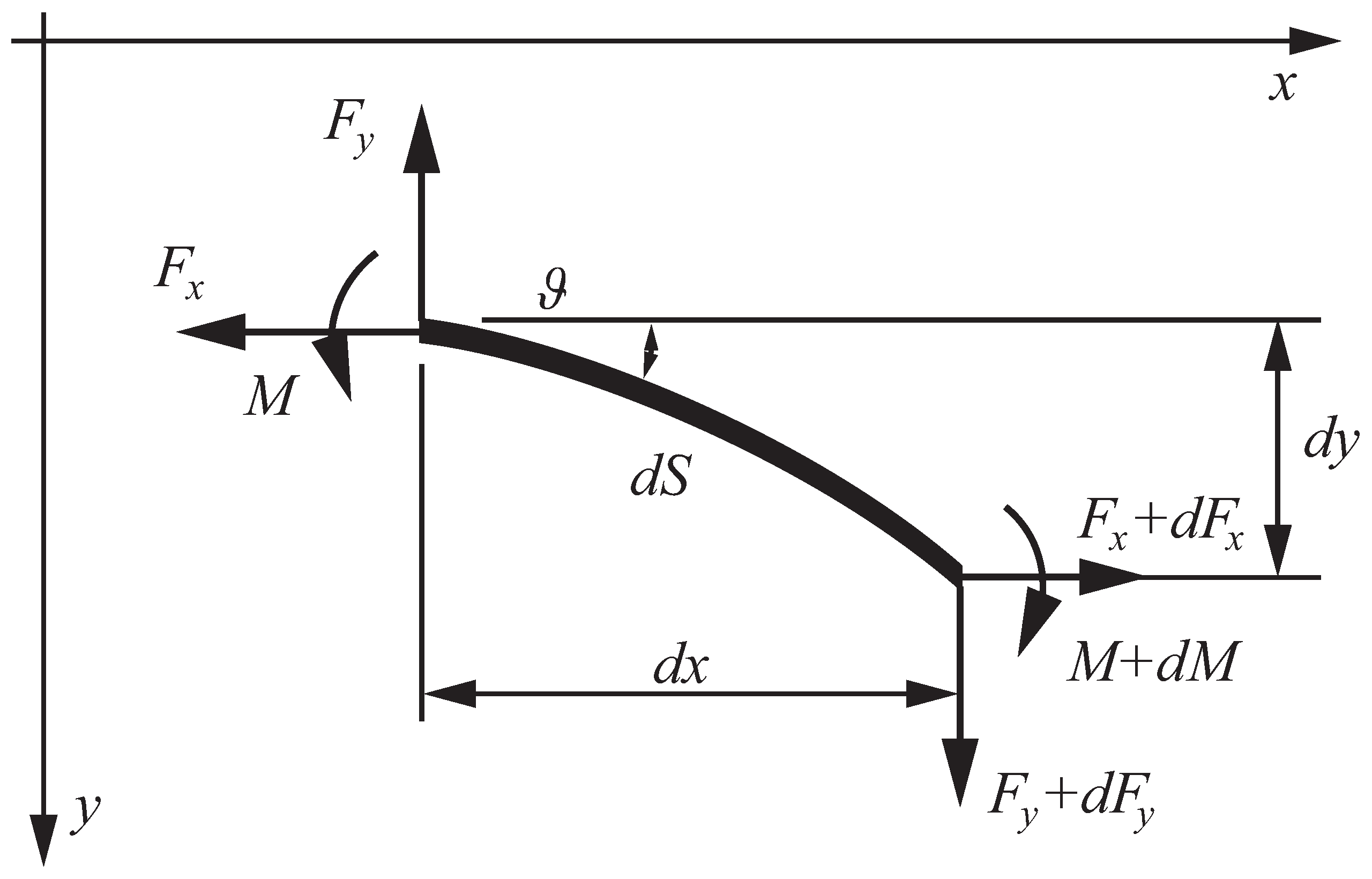
2. Governing Equations
3. Buckling Loads
4. Post-Buckling Analysis
5. Numerical Results and Discussion
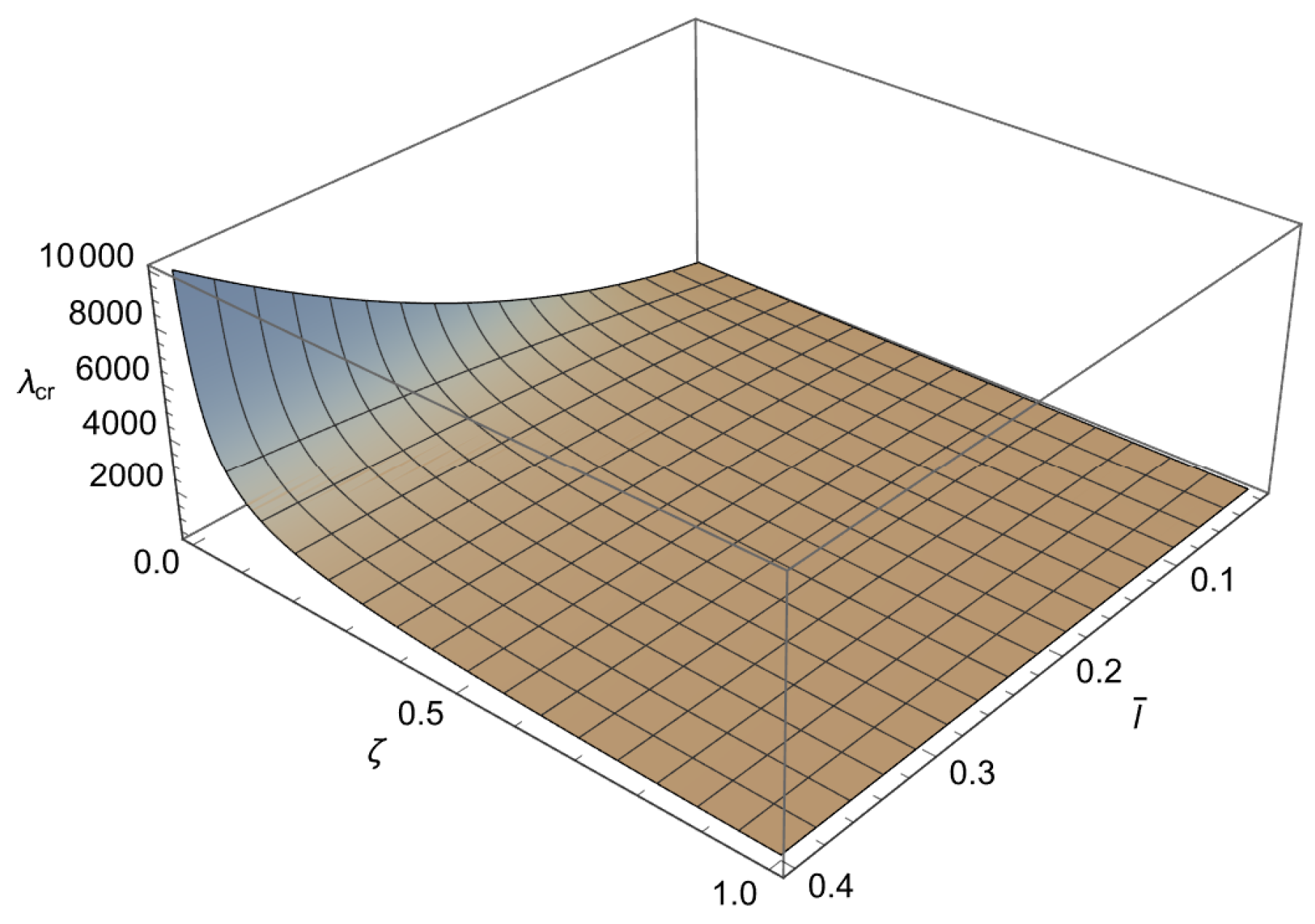
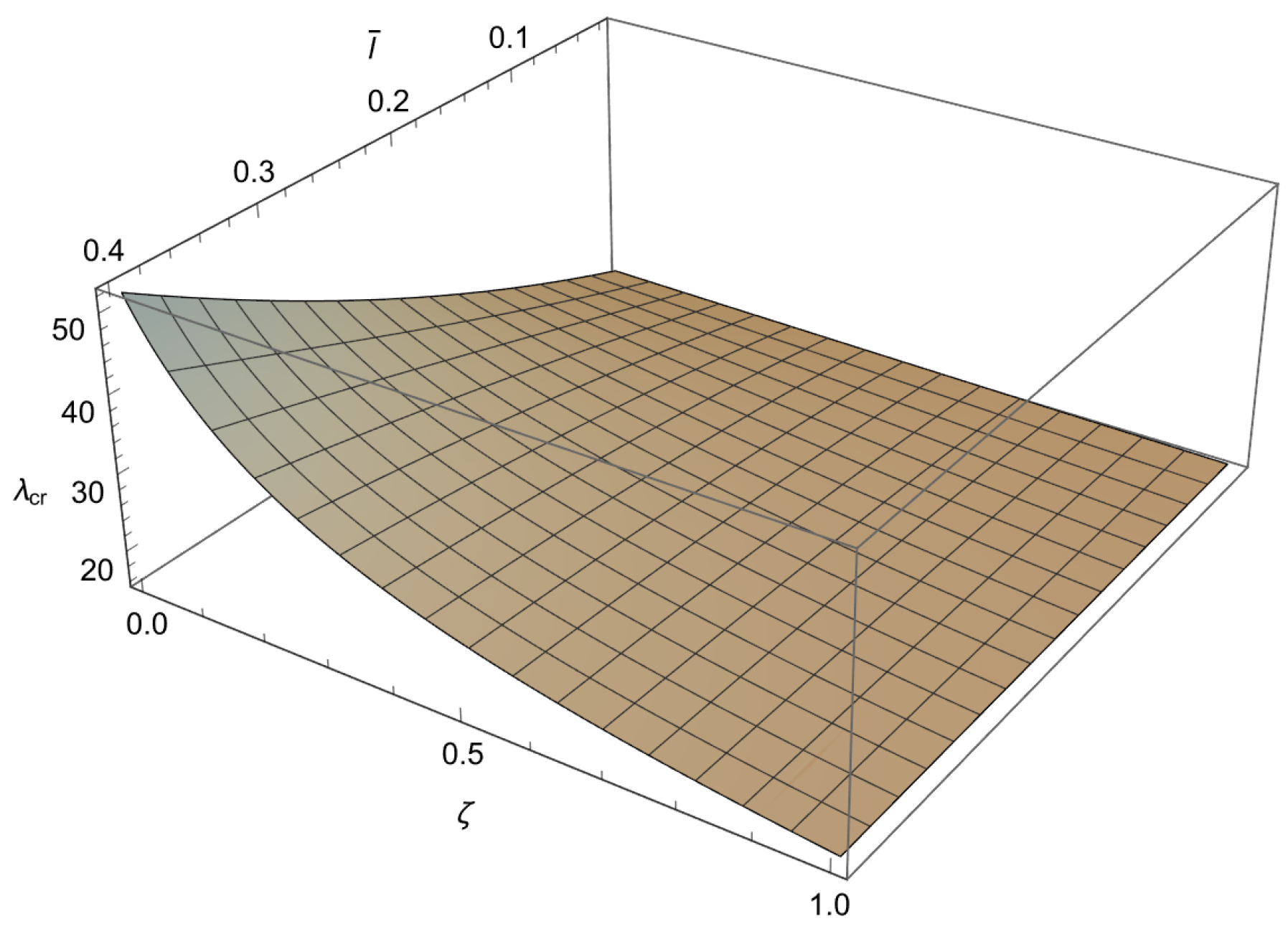
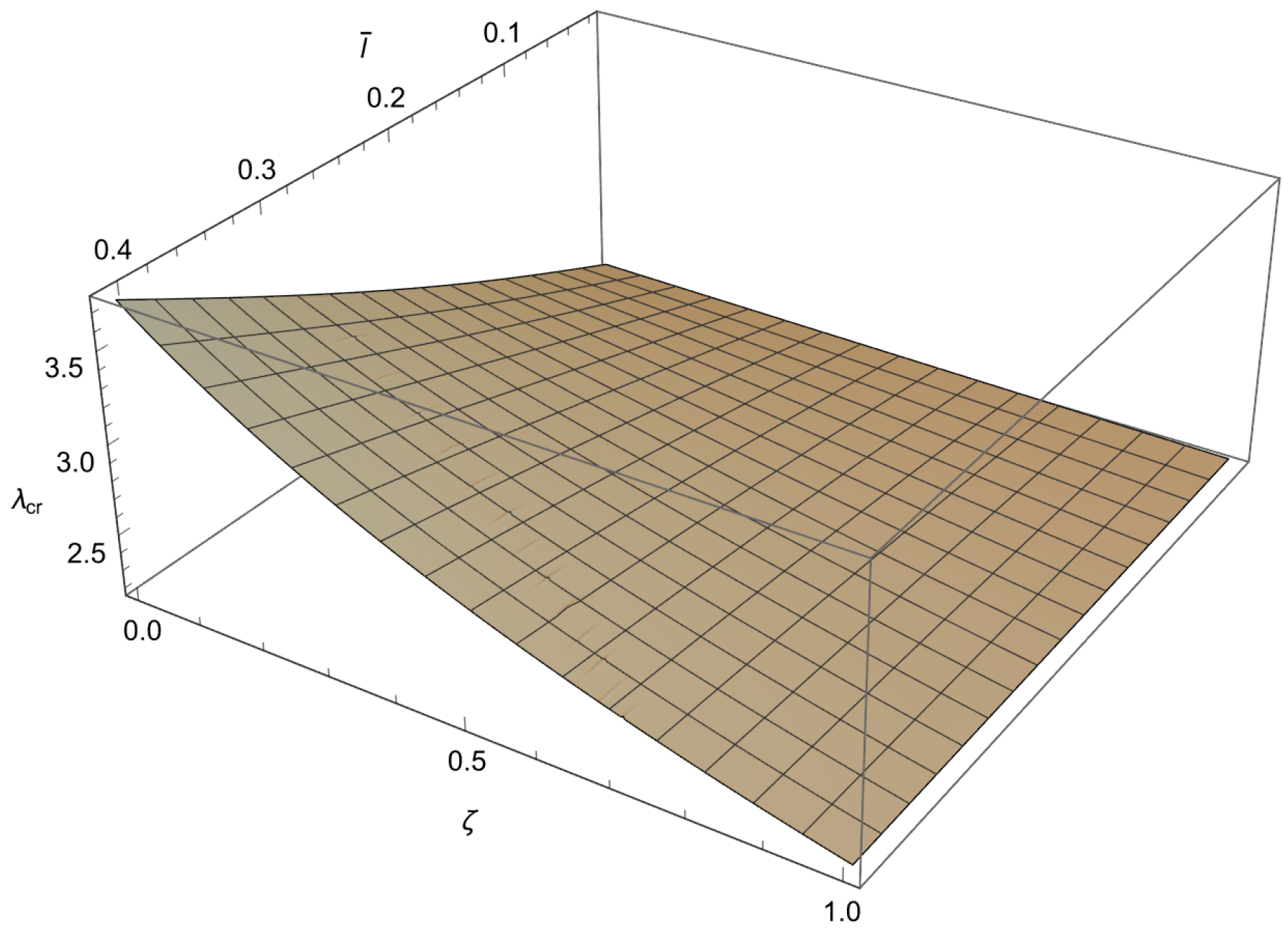
5.1. Buckling Loads of Nanorod
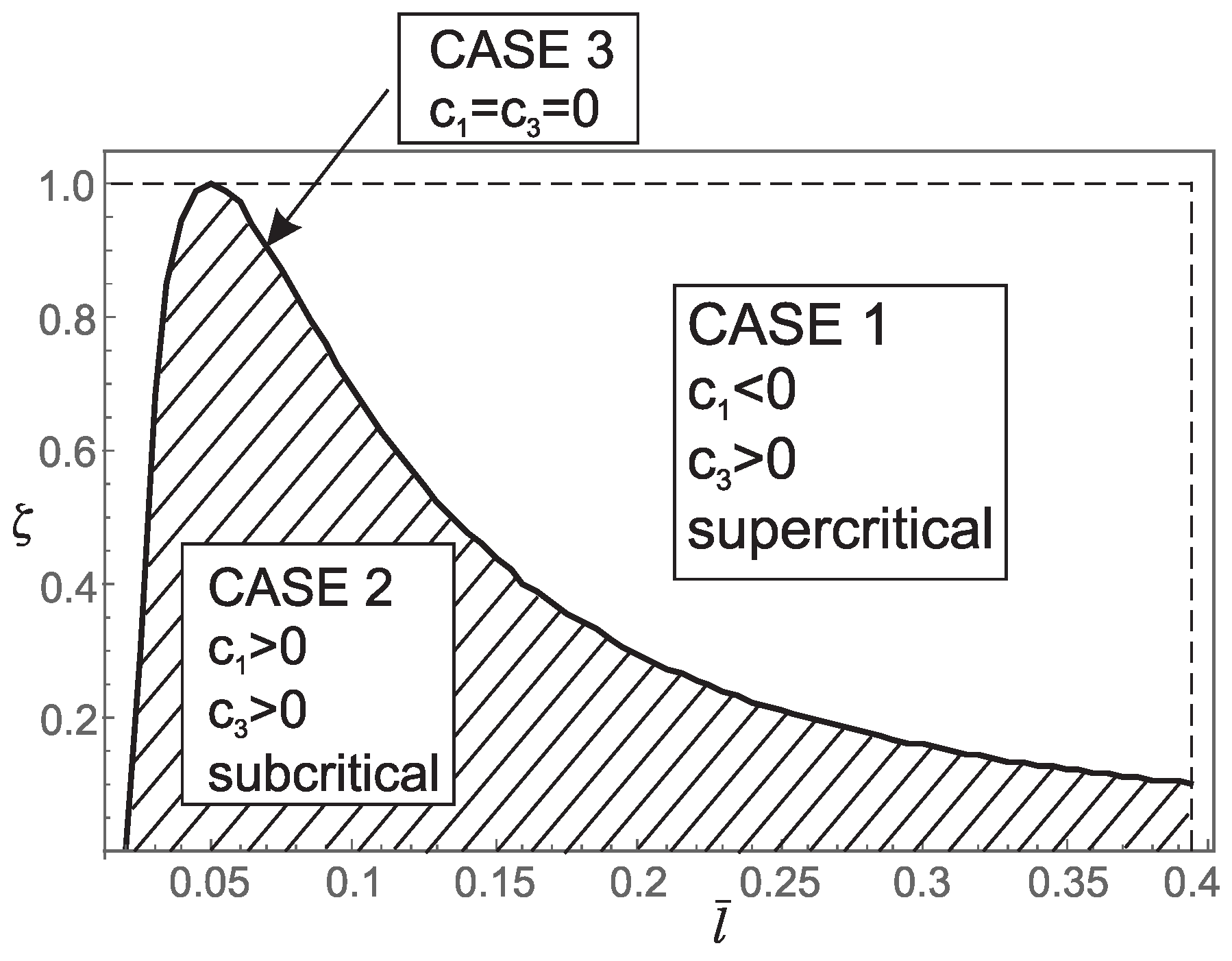
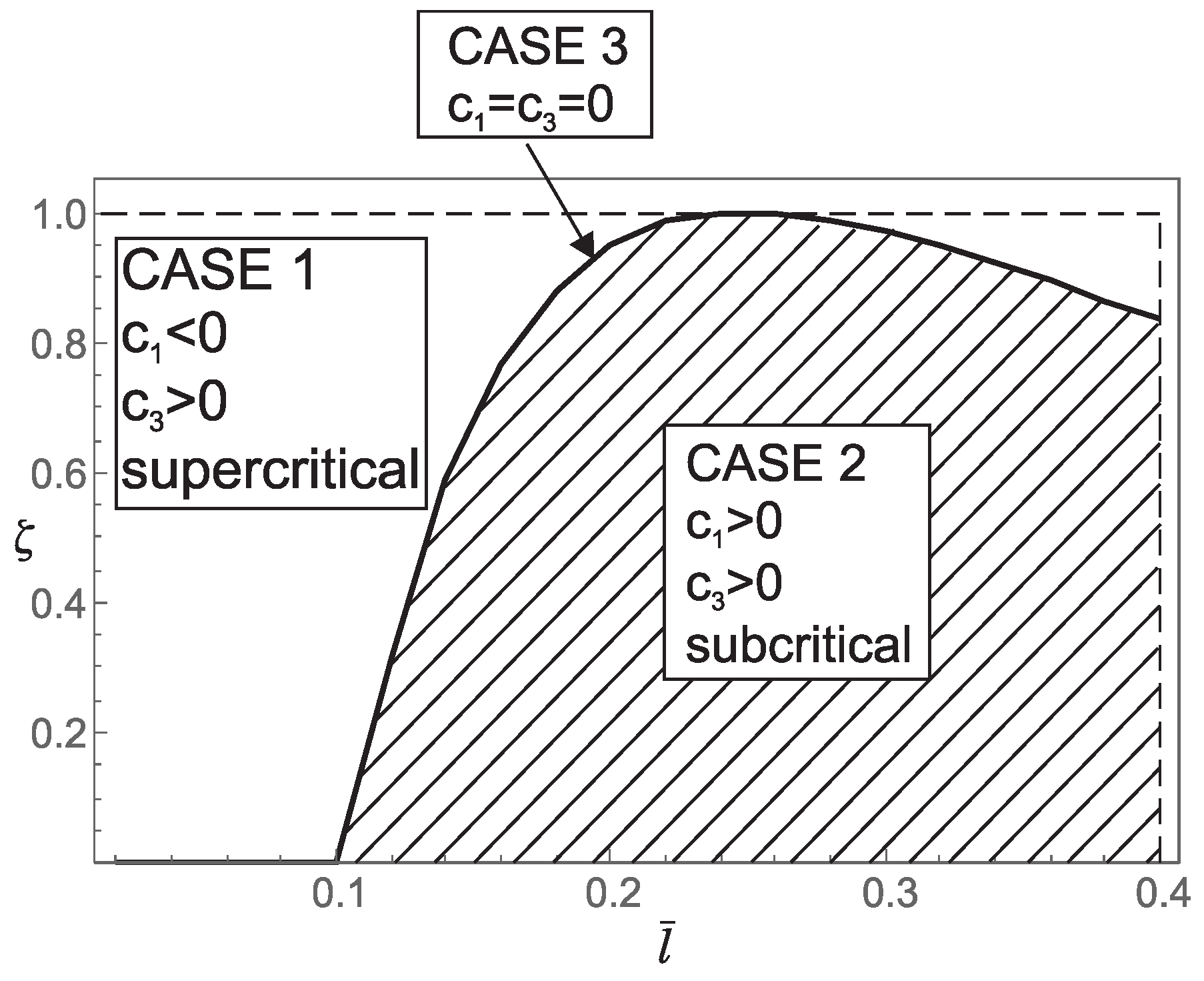
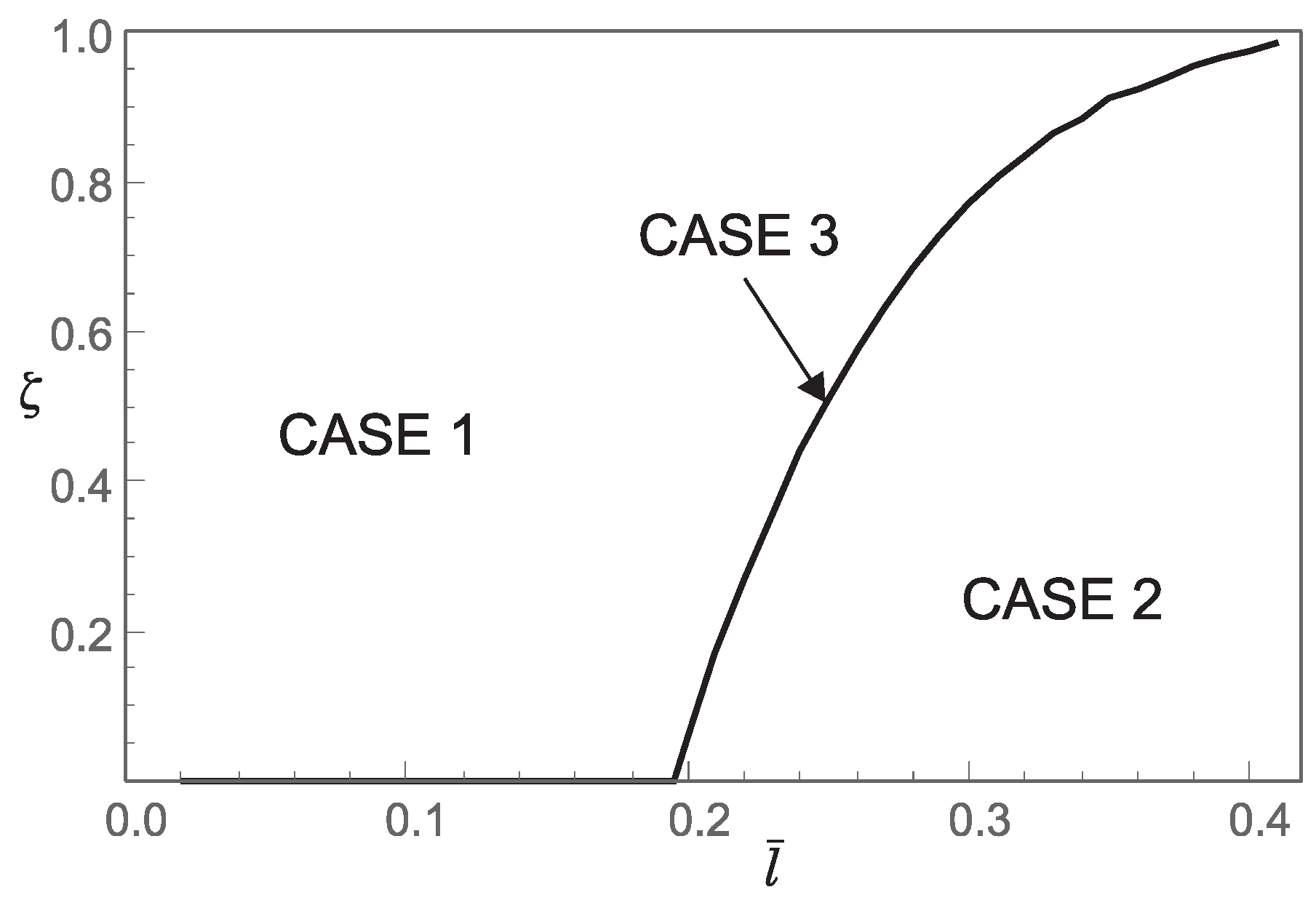
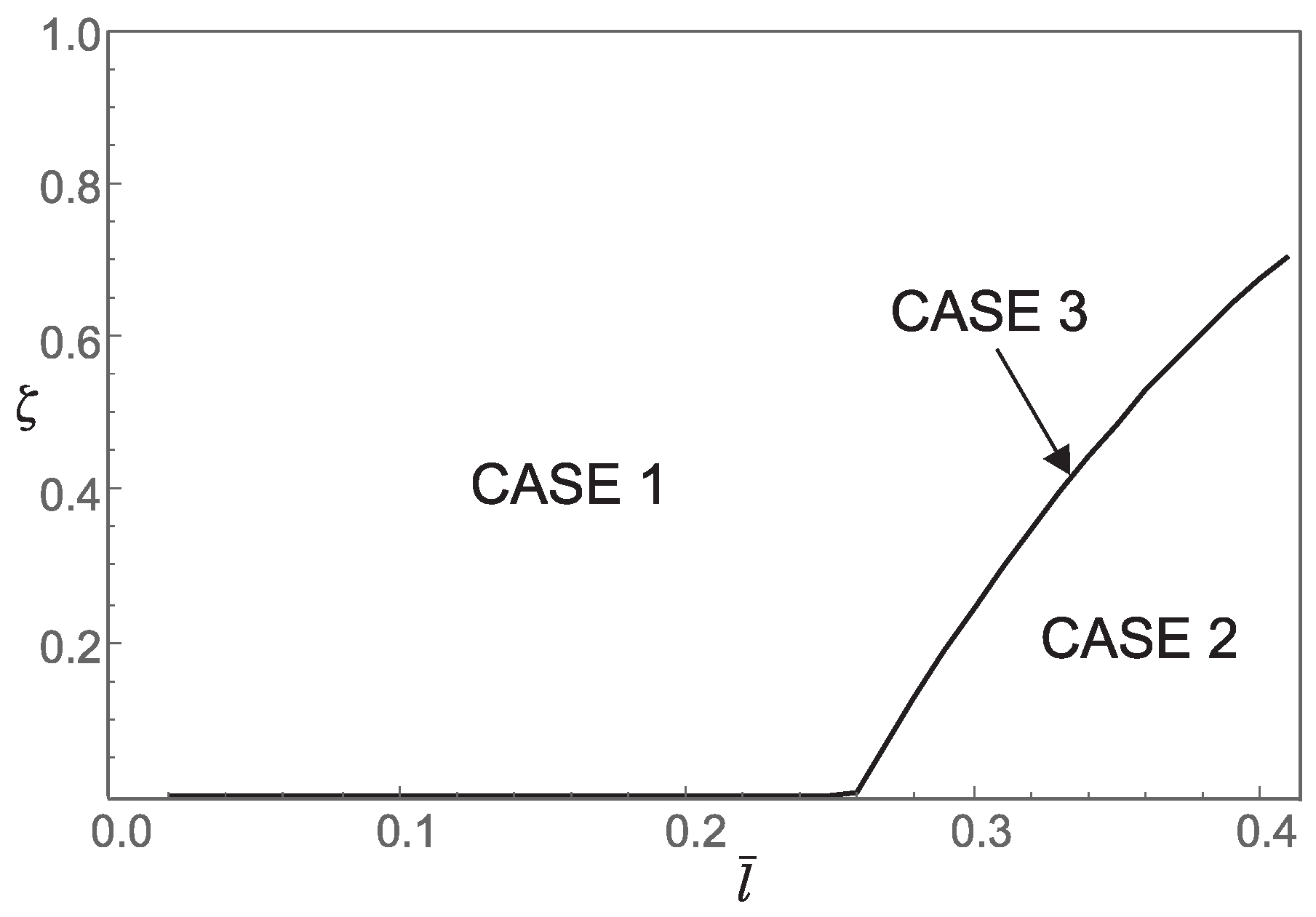
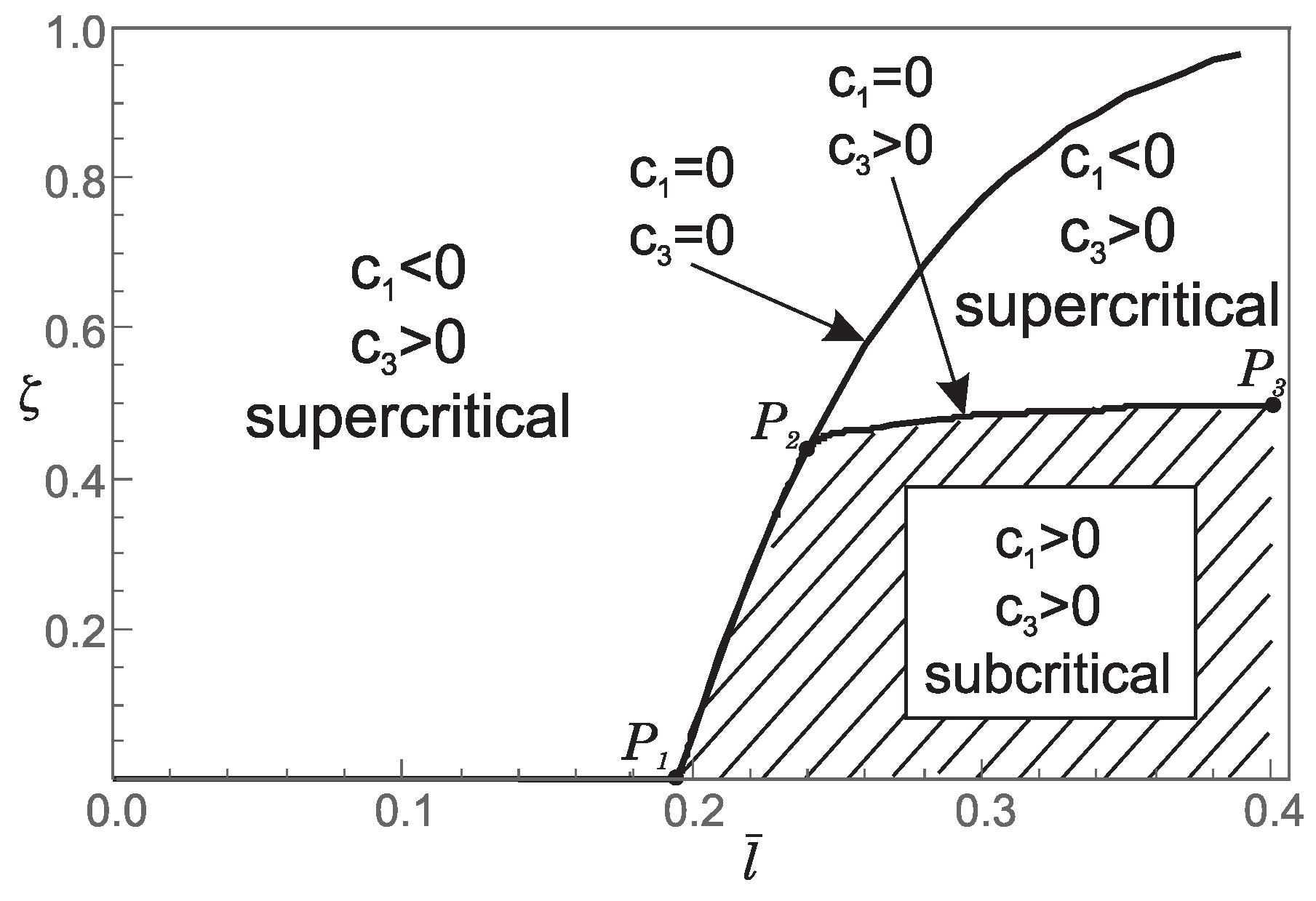
5.2. Post-Buckling Behavior of Nanorod
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Feynman, R.P. There’s Plenty of Room at the Bottom. Eng. Sci. 1960, 23, 22–36. [Google Scholar]
- Baig, N.; Kammakakam, I.; Falath, W. Nanomaterials: A review of synthesis methods, properties, recent progress, and challenges. Mater. Adv. 2021, 2, 1821–1871. [Google Scholar] [CrossRef]
- Chen, G.; Tang, D.-M. Advances in Carbon Nanotubes: Synthesis, Properties, and Cutting-Edge Application. Nanomaterials 2025, 15, 1595. [Google Scholar] [CrossRef] [PubMed]
- Biezeno, C.B.; Grammel, R. Technische Dynamik; Springer: Berlin/Heidelberg, Germany, 1953. [Google Scholar]
- Atanackovic, T.M.; Djukic, D.S. Buckling by extension: Stability boundary and post-critical behaviour. Dyn. Stab. Syst. Int. J. 1989, 4, 81–94. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Djukic, D.S.; Strauss, A.M. Instability by Extension of an Extensible Elastic Column. Z. Angew. Math. Mech. 1992, 72, 209–218. [Google Scholar] [CrossRef]
- Jelicic, Z.D.; Atanackovic, T.M. On an optimization problem for elastic rods. Struct. Multidisc. Optim. 2006, 32, 59–64. [Google Scholar] [CrossRef]
- Kröner, E. Elasticity theory of materials with long range cohesive forces. Int. J. Solids Struct. 1967, 3, 731–742. [Google Scholar] [CrossRef]
- Krumhansl, J. Some considerations of the relation between solid state physics and generalized continuum mechanics. In Mechanics of Generalized Continua; Kröner, E., Ed.; Springer: Berlin/Heidelberg, Germany, 1968; pp. 298–311. [Google Scholar]
- Kunin, I.A. The theory of elastic media with microstructure and the theory of dislocations. In Mechanics of Generalized Continua; Kröner, E., Ed.; Springer: Berlin/Heidelberg, Germany, 1968; pp. 321–329. [Google Scholar]
- Eringen, A.C. On differential-equations of nonlocal elasticity and solutions of screw dislocation and surface-waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Eringen, A.C. Linear theory of nonlocal elasticity and dispersion of plane waves. Int. J. Eng. Sci. 1972, 10, 425–435. [Google Scholar] [CrossRef]
- Eringen, A.C. Theory of nonlocal elasticity and some applications. Res. Mech. 1987, 21, 313–342. [Google Scholar]
- Altan, S.B. Uniqueness of initial-boundary value problems in nonlocal elasticity. Int. J. Solids Struct. 1989, 25, 1271–1278. [Google Scholar] [CrossRef]
- Eringen, A.C. Nonlocal Continuum Field Theories; Springer: New York, NY, USA, 2002. [Google Scholar]
- Polizzotto, C. Nonlocal elasticity and related variational principles. Int. J. Solids Struct. 2001, 38, 7359–7380. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R. Nonlocal elasticity in nanobeams: The stress-driven integral model. Int. J. Eng. Sci. 2017, 115, 14–27. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M. On nonlocal integral models for elastic nano-beams. Int. J. Mech. Sci. 2017, 131–132, 490–499. [Google Scholar] [CrossRef]
- Romano, G.; Barretta, R.; Diaco, M.; Marotti de Sciarra, F. Constitutive boundary conditions and paradoxes in nonlocal elastic nanobeams. Int. J. Mech. Sci. 2017, 121, 151–156. [Google Scholar] [CrossRef]
- Barretta, R.; Fabbrocino, F.; Luciano, R.; Marotti de Sciarra, F. Closed-form solutions in stress-driven two-phase integral elasticity for bending of functionally graded nano-beams. Phys. E Low-Dimens. Syst. Nanostruct. 2018, 97, 13–30. [Google Scholar] [CrossRef]
- Barretta, R.; de Sciarra, F.M.; Vaccaro, M.S. Nonlocal Elasticity for Nanostructures: A Review of Recent Achievements. Encyclopedia 2023, 3, 279–310. [Google Scholar] [CrossRef]
- Singh, C.V.; Guannan, W.; Mohammad, T. Advances in modelling and analysis of nano structures: A review. Nanotechnol. Rev. 2020, 9, 230–258. [Google Scholar] [CrossRef]
- Shariati, M.; Shishehsaz, M.; Hossein Sahbafar, H.; Pourabdy, M.; Mohammad Hosseini, M. A review on stress-driven nonlocal elasticity theory. J. Comput. Appl. Mech. 2021, 52, 535–552. [Google Scholar] [CrossRef]
- Peddieson, J.; Buchanan, G.R.; McNitt, R.P. Application of nonlocal continuum models to nanotechnology. Int. J. Eng. Sci. 2003, 41, 305–312. [Google Scholar] [CrossRef]
- Barretta, R.; Fabbrocino, F.; Luciano, R.; de Sciarra, F.M.; Ruta, G. Buckling loads of nano-beams in stress-driven nonlocal elasticity. Mech. Adv. Mater. Struct. 2020, 27, 869–875. [Google Scholar] [CrossRef]
- Jiang, P.; Qing, H.; Gao, C. Theoretical analysis on elastic buckling of nanobeams based on stress-driven nonlocal integral model. Appl. Math. Mech. 2020, 41, 207–232. [Google Scholar] [CrossRef]
- Oskouie, M.F.; Ansari, R.; Rouhi, H. A numerical study on the buckling and vibration of nanobeams based on the strain and stress-driven nonlocal integral models. Int. J. Comput. Mater. Sci. Eng. 2018, 7, 1850016. [Google Scholar] [CrossRef]
- Darban, H.; Luciano, R.; Darban, R. Buckling of cracked micro- and nanocantilevers. Acta Mech. 2023, 234, 693–704. [Google Scholar] [CrossRef]
- Zhang, P.; Qing, H. Stress-driven nonlocal integral model with discontinuity for size-dependent buckling and bending of cracked nanobeams using Laplace transform. Mech. Based Des. Struct. Mach. 2024, 52, 8063–8085. [Google Scholar] [CrossRef]
- Benvenuti, E.; Simone, A. One-dimensional nonlocal and gradient elasticity: Closed-form solution and size effect. Mech. Res. Commun. 2013, 48, 46–51. [Google Scholar] [CrossRef]
- Zhang, P.; Schiavone, P.; Qing, H. Stress-driven local/nonlocal mixture model for buckling and free vibration of FG sandwich Timoshenko beams resting on a nonlocal elastic foundation. Compos. Struct. 2022, 289, 115473. [Google Scholar] [CrossRef]
- Apuzzo, A.; Bartolomeo, C.; Luciano, R.; Scorza, D. Novel local/nonlocal formulation of the stress-driven model through closed form solution for higher vibrations modes. Compos. Struct. 2020, 252, 112688. [Google Scholar] [CrossRef]
- Zhang, P.; Schiavone, P.; Qing, H. Local/nonlocal mixture integral models with bi-Helmholtz kernel for free vibration of Euler-Bernoulli beams under thermal effect. J. Sound Vib. 2022, 525, 116798. [Google Scholar] [CrossRef]
- Behdad, S.; Arefi, M. A mixed two-phase stress/strain driven elasticity: In applications on static bending, vibration analysis and wave propagation. Eur. J. Mech. A Solids 2022, 94, 104558. [Google Scholar] [CrossRef]
- Zhang, P.; Schiavone, P.; Qing, H. Unified two-phase nonlocal formulation for vibration of functionally graded beams resting on nonlocal viscoelastic Winkler-Pasternak foundation. Appl. Math. Mech. 2023, 44, 89–108. [Google Scholar] [CrossRef]
- Vaccaro, M.S.; Pinnola, F.P.; de Sciarra, F.M.; Barretta, R. Dynamics of Stress-Driven Two-Phase Elastic Beams. Nanomaterials 2021, 11, 1138. [Google Scholar] [CrossRef]
- Barretta, R.; Caporale, A.; Ali Faghidian, S.; Luciano, R.; de Sciarra, F.M.; Medaglia, C.A. A stress-driven local-nonlocal mixture model for Timoshenko nano-beams. Compos. Part B Eng. 2019, 164, 590–598. [Google Scholar] [CrossRef]
- Zhang, P.; Qing, H. On well-posedness of two-phase nonlocal integral models for higher-order refined shear deformation beams. Appl. Math. Mech. 2021, 42, 931–950. [Google Scholar] [CrossRef]
- Zhang, P.; Schiavone, P.; Qing, H. Two-phase local/nonlocal mixture models for buckling analysis of higher-order refined shear deformation beams under thermal effect. Mech. Adv. Mater. Struct. 2022, 29, 7605–7622. [Google Scholar] [CrossRef]
- Vaccaro, M.S.; Pinnola, F.P.; de Sciarra, F.M.; Canadija, M.; Barretta, R. Stress-driven two-phase integral elasticity for Timoshenko curved beams. Proc. Inst. Mech. Eng. Part N J. Nanomater. Nanoeng. Nanosyst. 2021, 235, 52–63. [Google Scholar] [CrossRef]
- Scorza, D.; Luciano, R.; Vantadori, S. Fracture behaviour of nanobeams through Two-Phase Local/Nonlocal Stress-Driven model. Compos. Struct. 2022, 280, 114957. [Google Scholar] [CrossRef]
- Tang, Y.; Qing, H. Size-dependent nonlinear post-buckling analysis of functionally graded porous Timoshenko microbeam with nonlocal integral models. Commun. Nonlinear Sci. Numer. Simul. 2023, 116, 106808. [Google Scholar] [CrossRef]
- Rezaiee-Pajand, M.; Rajabzadeh-Safaei, N. Stress-driven nonlinear behavior of curved nanobeams. Int. J. Eng. Sci. 2022, 178, 103724. [Google Scholar] [CrossRef]
- Qing, H.; Cai, Y. Semi-analytical and numerical post-buckling analysis of nanobeam using two-phase nonlocal integral models. Arch. Appl. Mech. 2023, 93, 129–149. [Google Scholar] [CrossRef]
- Atanackovic, T.M.; Oparnica, L.; Zorica, D. Bifurcation analysis of the rotating axially compressed nano-rod with imperfections. Z. Angew. Math. Mech. 2019, 99, e201800284. [Google Scholar] [CrossRef]
- Berecki, A.D.; Glavardanov, V.B.; Grahovac, N.M.; Zigic, M.M. Bifurcation analysis of a nanotube through which passes a nanostring. Acta Mech. 2024, 235, 6867–6888. [Google Scholar] [CrossRef]
- Asghar, U.; Azam Qamar, M.; Hakami, O.; Kashif Ali, S.; Imran, M.; Farhan, A.; Parveen, H.; Sharma, M. Recent Advances in Carbon Nanotube Utilization in Perovskite Solar Cells: A Review. Micromachines 2024, 15, 529. [Google Scholar] [CrossRef]
- Barcelos, K.A.; Garg, J.; Ferreira Soares, D.C.; Branco de Barros, A.L.; Zhao, Y.; Alisaraie, L. Recent advances in the applications of CNT-based nanomaterials in pharmaceutical nanotechnology and biomedical engineering. J. Drug Deliv. Sci. Technol. 2023, 87, 104834. [Google Scholar] [CrossRef]
- Thiruvengadam, M.; Rajakumar, G.; Swetha, V.; Ansari, M.A.; Alghamdi, S.; Almehmadi, M.; Halawi, M.; Kungumadevi, L.; Raja, V.; Sabura Sarbudeen, S.; et al. Recent Insights and Multifactorial Applications of Carbon Nanotubes. Micromachines 2021, 12, 1502. [Google Scholar] [CrossRef] [PubMed]
- Pang, J.; Bachmatiuk, A.; Yang, F.; Liu, H.; Yhou, W.; Rümmeli, M.H.; Cuniberti, G. Applications of Carbon Nanotubes in the Internet of Things Era. Nano-Micro Lett. 2021, 13, 191. [Google Scholar] [CrossRef] [PubMed]
- Kim, K.; Guo, J.; Xu, X.; Fan, D.L. Recent progress on man-made inorganic nanomachines. Small 2015, 11, 4037–4057. [Google Scholar] [CrossRef] [PubMed]
- Barretta, R.; Canadija, M.; Marotti de Sciarra, F.; Skoblar, A. Free Vibrations of Bernoulli-Euler Nanobeams with Point Mass Interacting with Heavy Fluid Using Nonlocal Elasticity. Nanomaterials 2022, 12, 2676. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Manzhirov, A.V. Handbook of Integral Equations, 2nd ed.; Chapman & Hall/CRC: Boca Raton, FL, USA, 2008. [Google Scholar]
- Chow, S.-N.; Hale, J.K. Methods of Bifurcation Theory; Springer: New York, NY, USA, 1982. [Google Scholar]
- Troger, H.; Steindl, A. Nonlinear Stability and Bifurcation Theory; Springer: Vienna, Austria, 1991. [Google Scholar]
- Chen, Y.; Leung Andrew, Y.T. Bifurcation and Chaos in Engineering; Springer: London, UK, 1998. [Google Scholar]
- Kielhöfer, H. Bifurcation Theory: An Introduction with Applications to PDEs; Springer: New York, NY, USA, 2004. [Google Scholar]
- Atanackovic, T.M. Stability Theory of Elastic Rods; World Scientific: Singapore, 1997. [Google Scholar]
- Iooss, G.; Joseph, D.D. Elementary Stability and Bifurcation Theory; Springer: New York, NY, USA, 1990. [Google Scholar]
- Darban, H. MD benchmarks: Size-dependent tension, bending, buckling, and vibration of nanobeams. Int. J. Mech. Sci. 2025, 296, 110316. [Google Scholar] [CrossRef]
- Shariati, M.; Azizi, B.; Hosseini, M.; Shishesaz, M. On the calibration of size parameters related to non-classical continuum theories using molecular dynamics simulations. Int. J. Eng. Sci. 2021, 168, 103544. [Google Scholar] [CrossRef]
- Kent Nagle, R.; Edward, B.; Saff, E.B.; David Snider, A. Fundamentals of Differential Equations and Boundary Value Problems, 7th ed.; Pearson: Boston, MA, USA, 2018. [Google Scholar]
- Chen, W.-F.; Atsuta, T. Theory of Beam-Columns; McGraw-Hill Inc.: New York, NY, USA, 1976; Volume 1. [Google Scholar]

| / | |||||
|---|---|---|---|---|---|
| 1 | 400 | 400 | 400 | 400 | 400 |
| 468.9498 | 611.1456 | 678.8897 | 711.1087 | 729.8253 | |
| 574.6217 | 1568.7782 | 3398.9511 | 5730.7799 | 8392.8216 |
| / | |||||
|---|---|---|---|---|---|
| 1 | 16.0213 | 16.0213 | 16.0213 | 16.0213 | 16.0213 |
| 16.6414 | 18.7717 | 20.8000 | 22.3237 | 23.4916 | |
| 17.3176 | 22.9900 | 31.1948 | 40.6795 | 51.4316 |
| / | |||||
|---|---|---|---|---|---|
| 1 | 4.5865 | 4.5865 | 4.5865 | 4.5865 | 4.5865 |
| 4.6799 | 5.021 | 5.3904 | 5.7124 | 5.9923 | |
| 4.7771 | 5.5625 | 6.6052 | 7.7228 | 8.8971 |
| / | |||||
|---|---|---|---|---|---|
| 1 | 2.1882 | 2.1882 | 2.1882 | 2.1882 | 2.1882 |
| 2.2205 | 2.3427 | 2.4866 | 2.6225 | 2.7472 | |
| 2.2534 | 2.5215 | 2.8827 | 3.2783 | 3.6984 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Berecki, A.; Glavardanov, V.; Mihok, S.; Grahovac, N.; Zigic, M. Instability by Extension of an Elastic Nanorod. Nanomaterials 2025, 15, 1689. https://doi.org/10.3390/nano15221689
Berecki A, Glavardanov V, Mihok S, Grahovac N, Zigic M. Instability by Extension of an Elastic Nanorod. Nanomaterials. 2025; 15(22):1689. https://doi.org/10.3390/nano15221689
Chicago/Turabian StyleBerecki, Armin, Valentin Glavardanov, Sanja Mihok, Nenad Grahovac, and Miodrag Zigic. 2025. "Instability by Extension of an Elastic Nanorod" Nanomaterials 15, no. 22: 1689. https://doi.org/10.3390/nano15221689
APA StyleBerecki, A., Glavardanov, V., Mihok, S., Grahovac, N., & Zigic, M. (2025). Instability by Extension of an Elastic Nanorod. Nanomaterials, 15(22), 1689. https://doi.org/10.3390/nano15221689






