Scatterers of Non-Electric-Dipole Radiation
Abstract
1. Introduction
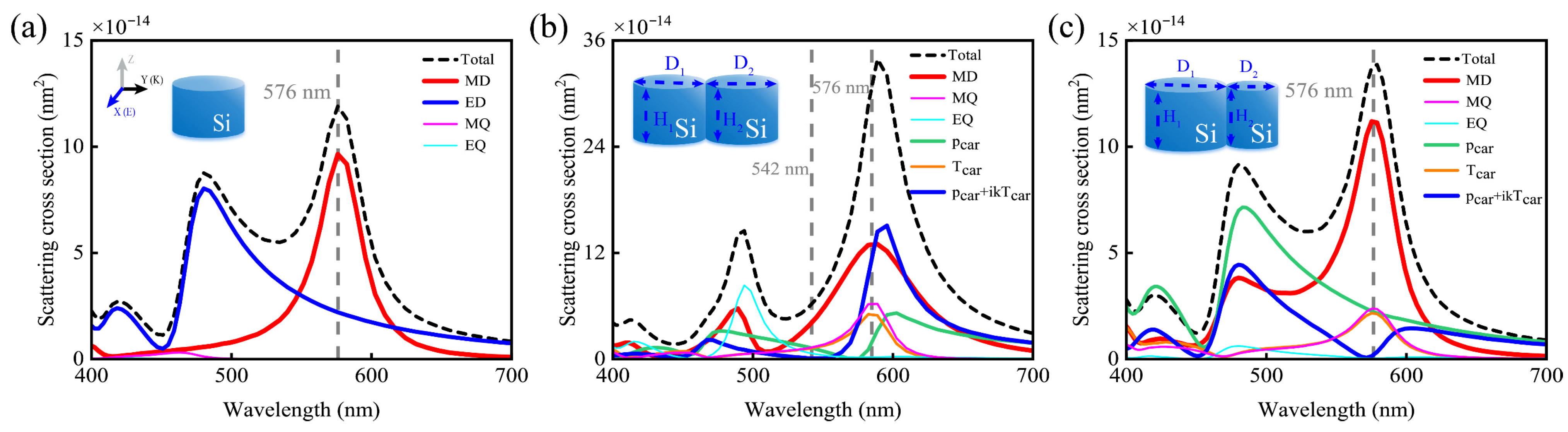
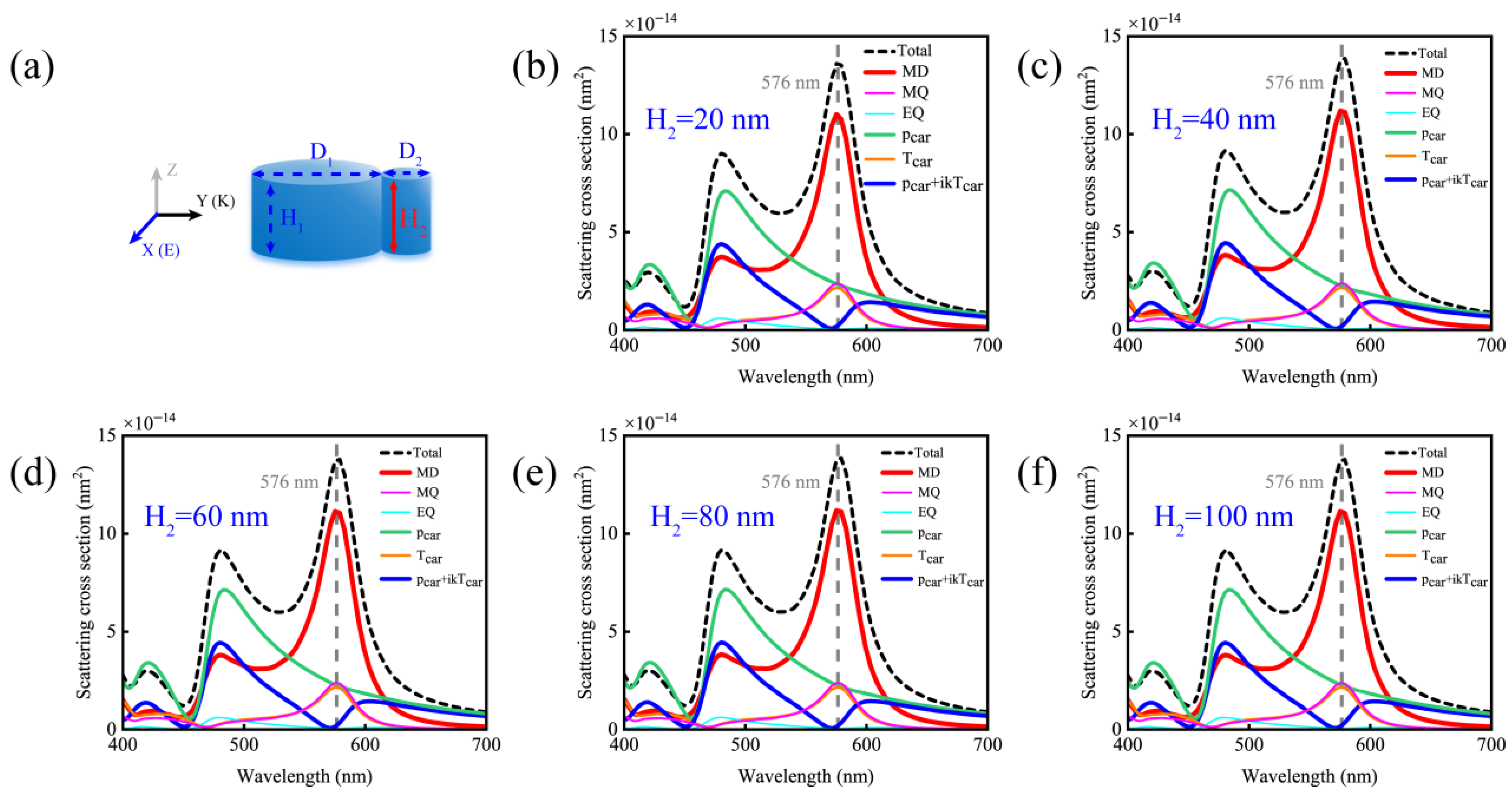
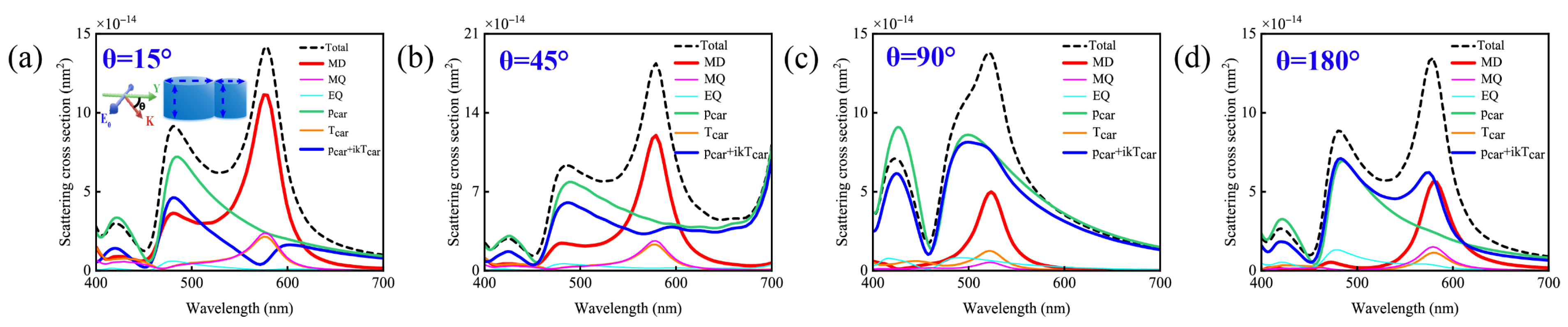
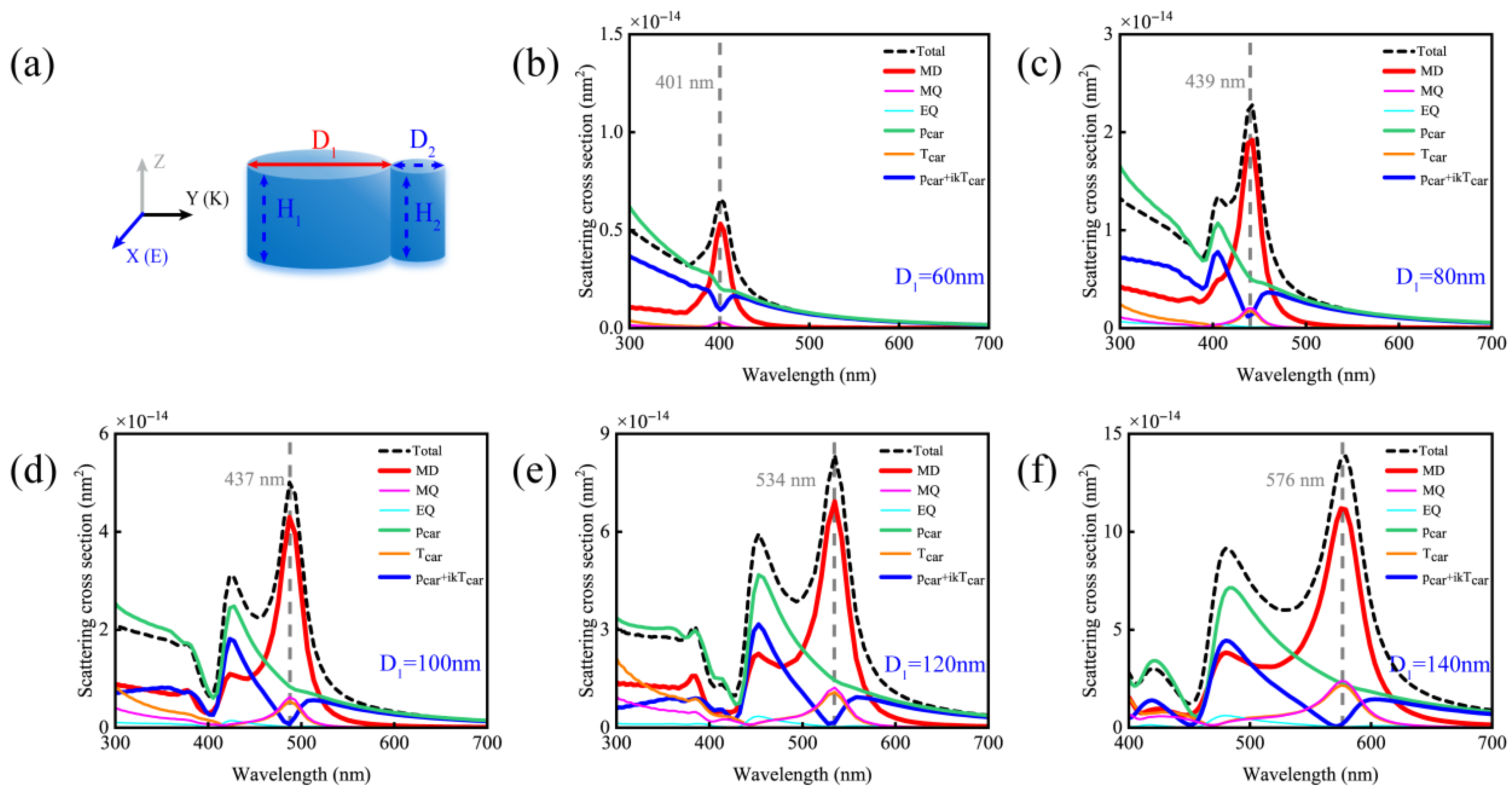
2. Results and Discussion
3. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Aigouy, L.; Cazé, A.; Gredin, P.; Mortier, M.; Carminati, R. Mapping and Quantifying Electric and Magnetic Dipole Luminescence at the Nanoscale. Phys. Rev. Lett. 2014, 113, 076101. [Google Scholar] [CrossRef] [PubMed]
- Feng, T.; Xu, Y.; Zhang, W.; Miroshnichenko, A.E. Ideal Magnetic Dipole Scattering. Phys. Rev. Lett. 2017, 118, 173901. [Google Scholar] [CrossRef] [PubMed]
- Karaveli, S.; Zia, R. Spectral Tuning by Selective Enhancement of Electric and Magnetic Dipole Emission. Phys. Rev. Lett. 2011, 106, 193004. [Google Scholar] [CrossRef]
- Taminiau, T.H.; Karaveli, S.; van Hulst, N.F.; Zia, R. Quantifying the Magnetic Nature of Light Emission. Nat. Commun. 2012, 3, 979. [Google Scholar] [CrossRef] [PubMed]
- Burresi, M.; Kampfrath, T.; van Oosten, D.; Prangsma, J.C.; Song, B.S.; Noda, S.; Kuipers, L. Magnetic Light-Matter Interactions in a Photonic Crystal Nanocavity. Phys. Rev. Lett. 2010, 105, 123901. [Google Scholar] [CrossRef]
- Burresi, M.; Oosten, D.v.; Kampfrath, T.; Schoenmaker, H.; Heideman, R.; Leinse, A.; Kuipers, L. Probing the Magnetic Field of Light at Optical Frequencies. Science 2009, 23, 326. [Google Scholar] [CrossRef]
- Moreau, A.; Ciracì, C.; Mock, J.J.; Hill, R.T.; Wang, Q.; Wiley, B.J.; Chilkoti, A.; Smith, D.R. Controlled-Reflectance Surfaces with Film-Coupled Colloidal Nanoantennas. Nature 2012, 492, 86–89. [Google Scholar]
- Shafiei, F.; Monticone, F.; Le, K.Q.; Liu, X.-X.; Hartsfield, T.; Alù, A.; Li, X. A Subwavelength Plasmonic Metamolecule Exhibiting Magnetic-Based Optical Fano Resonance. Nat. Nanotechnol. 2013, 8, 95–99. [Google Scholar]
- Meng, Y.; Zhang, Q.; Lei, D.; Li, Y.; Li, S.; Liu, Z.; Xie, W.; Leung, C.W. Plasmon-Induced Optical Magnetism in an Ultrathin Metal Nanosphere-Based Dimer-on-Film Nanocavity. Laser Photonics Rev. 2020, 14, 2000068. [Google Scholar] [CrossRef]
- Verslegers, L.; Yu, Z.; Ruan, Z.; Catrysse, P.B.; Fan, S. From Electromagnetically Induced Transparency to Superscattering with a Single Structure: A Coupled-Mode Theory for Doubly Resonant Structures. Phys. Rev. Lett. 2012, 108, 083902. [Google Scholar] [CrossRef]
- Li, Z.; Li, Y.; You, Q.; Wang, M.; Zhu, C.; Yang, Y.; Luan, H.; Wang, P. Magnetic Purcell Enhancement by Plasmon-Induced Magnetic Resonance of the Nanoparticle-on-Mirror Configuration. Phys. Rev. A 2024, 110, 013516. [Google Scholar] [CrossRef]
- Wu, H.-W.; Li, Y.; Chen, H.-J.; Sheng, Z.-Q.; Jing, H.; Fan, R.-H.; Peng, R.-W. Strong Purcell Effect for Terahertz Magnetic Dipole Emission with Spoof Plasmonic Structure. ACS Appl. Nano Mater. 2019, 2, 1045–1052. [Google Scholar] [CrossRef]
- Hein, S.M.; Giessen, H. Tailoring Magnetic Dipole Emission with Plasmonic Split-Ring Resonators. Phys. Rev. Lett. 2013, 111, 026803. [Google Scholar] [CrossRef] [PubMed]
- Alù, A.; Engheta, N. Dynamical Theory of Artificial Optical Magnetism Produced by Rings of Plasmonic Nanoparticles. Phys. Rev. B 2008, 78, 085112. [Google Scholar] [CrossRef]
- Nazir, A.; Panaro, S.; Proietti Zaccaria, R.; Liberale, C.; De Angelis, F.; Toma, A. Fano Coil-Type Resonance for Magnetic Hot-Spot Generation. Nano Lett. 2014, 14, 3166–3171. [Google Scholar] [CrossRef]
- Chen, S.; Zhang, Y.; Shih, T.M.; Yang, W.; Hu, S.; Hu, X.; Li, J.; Ren, B.; Mao, B.; Yang, Z.; et al. Plasmon-Induced Magnetic Resonance Enhanced Raman Spectroscopy. Nano Lett. 2018, 18, 2209–2216. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, T.M.; Cho, Y.; Huh, J.H.; Ahn, H.; Kim, N.; Rho, K.H.; Lee, J.; Kwon, M.; Park, S.H.; Kim, C.; et al. Ultralow-Loss Substrate for Nanophotonic Dark-Field Microscopy. Nano Lett. 2023, 23, 1546–1554. [Google Scholar] [CrossRef]
- Ren, Y.; Li, Y.; Xu, Z.; Li, X.-F.; Li, J.; Gu, S.; Wang, P.; Wang, M.; Li, Z. Magnetic Radiative Purcell Enhancement by Magnetic Anapole in the Gap of Nanodisk on Metal Mirror Structure. Opt. Express 2025, 33, 29146–29153. [Google Scholar] [CrossRef]
- Landy, N.I.; Sajuyigbe, S.; Mock, J.J.; Smith, D.R.; Padilla, W.J. Perfect Metamaterial Absorber. Phys. Rev. Lett. 2008, 100, 207402. [Google Scholar] [CrossRef]
- Khurgin, J.B. How to Deal with the Loss in Plasmonics and Metamaterials. Nat. Nanotechnol. 2015, 10, 2–6. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Brongersma, M.L.; Kivshar, Y.S.; Luk’yanchuk, B. Optically Resonant Dielectric Nanostructures. Science 2016, 354, 2742. [Google Scholar] [CrossRef]
- Yao, R.; Sugimoto, H.; Feng, T.; Fujii, M.; Liu, S.; Li, X.; Lan, S.; Li, G.-C. Achieving Ideal Magnetic Light Emission with Electric-Type Emitters. Nano Lett. 2024, 24, 13315–13323. [Google Scholar] [CrossRef]
- Evlyukhin, A.B.; Fischer, T.; Reinhardt, C.; Chichkov, B.N. Optical Theorem and Multipole Scattering of Light by Arbitrarily Shaped Nanoparticles. Phys. Rev. B 2016, 94, 205434. [Google Scholar] [CrossRef]
- Sugimoto, H.; Fujii, M. Magnetic Purcell Enhancement by Magnetic Quadrupole Resonance of Dielectric Nanosphere Antenna. ACS Photonics 2021, 8, 1794–1800. [Google Scholar] [CrossRef]
- Kuznetsov, A.I.; Miroshnichenko, A.E.; Fu, Y.H.; Zhang, J.; Luk’yanchuk, B. Magnetic Light. Sci. Rep. 2012, 2, 492. [Google Scholar] [CrossRef] [PubMed]
- Basharin, A.A.; Kafesaki, M.; Economou, E.N.; Soukoulis, C.M.; Fedotov, V.A.; Savinov, V.; Zheludev, N.I. Dielectric Metamaterials with Toroidal Dipolar Response. Phys. Rev. X 2015, 5, 011036. [Google Scholar] [CrossRef]
- Liu, T.; Xu, R.; Yu, P.; Wang, Z.; Takahara, J. Multipole and multimode engineering in Mie resonance-based metastructures. Nanophotonics 2020, 9, 1115–1137. [Google Scholar] [CrossRef]
- Tang, Y.-L.; Yen, T.-H.; Nishida, K.; Li, C.-H.; Chen, Y.-C.; Zhang, T.; Pai, C.-K.; Chen, K.-P.; Li, X.; Takahara, J.; et al. Multipole engineering by displacement resonance: A new degree of freedom of Mie resonance. Nat. Commun. 2023, 14, 7213. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Li, Y.; Wang, M.; Li, M.; Zhao, L.; Rong, J.; Wang, P.; Li, Z. Ideal Magnetic-Resonance Scatterers in the Visible Range. Phys. Rev. A 2025, 112, L021502. [Google Scholar] [CrossRef]
- Jiang, T.; Li, Y.; Xu, Z.; Qian, X.; Shi, R.; Li, X.; Wang, M.; Li, Z. Tunable Dual-Mode Resonant Excitation of Dumbbell-Shaped Structures in the Mid-Infrared Band. Nanomaterials 2025, 15, 1181. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Evlyukhin, A.B.; Yu, Y.F.; Bakker, R.M.; Chipouline, A.; Kuznetsov, A.I.; Luk’yanchuk, B.; Chichkov, B.N.; Kivshar, Y.S. Nonradiating Anapole Modes in Dielectric Nanoparticles. Nat. Commun. 2015, 6, 8069. [Google Scholar] [CrossRef] [PubMed]
- Parker, J.A.; Sugimoto, H.; Coe, B.; Eggena, D.; Fujii, M.; Scherer, N.F.; Gray, S.K.; Manna, U. Excitation of Nonradiating Anapoles in Dielectric Nanospheres. Phys. Rev. Lett. 2020, 124, 097402. [Google Scholar] [CrossRef]
- Luk’yanchuk, B.; Paniagua-Domínguez, R.; Kuznetsov, A.I.; Miroshnichenko, A.E.; Kivshar, Y.S. Hybrid Anapole Modes of High-Index Dielectric Nanoparticles. Phys. Rev. A 2017, 95, 063820. [Google Scholar] [CrossRef]
- Basharin, A.A.; Chuguevsky, V.; Volsky, N.; Kafesaki, M.; Economou, E.N. Extremely High Q-Factor Metamaterials Due to Anapole Excitation. Phys. Rev. B 2017, 95, 035104. [Google Scholar] [CrossRef]
- Li, Z.; You, Q.; Li, J.; Zhu, C.; Zhang, L.; Yang, L.; Fang, Y.; Wang, P. Boosting Light–Matter Interaction in a Longitudinal Bonding Dipole Plasmon Hybrid Anapole System. J. Phys. Chem. C 2023, 127, 3594–3601. [Google Scholar] [CrossRef]
- Roller, E.-M.; Khorashad, L.K.; Fedoruk, M.; Schreiber, R.; Govorov, A.O.; Liedl, T. DNA-Assembled Nanoparticle Rings Exhibit Electric and Magnetic Resonances at Visible Frequencies. Nano Lett. 2015, 15, 1368–1373. [Google Scholar] [CrossRef]
- Alaee, R.; Rockstuhl, C.; Fernandez-Corbaton, I. An Electromagnetic Multipole Expansion Beyond the Long-Wavelength Approximation. Opt. Commun. 2018, 407, 17–21. [Google Scholar] [CrossRef]
- Radescu, E.E.; Vaman, G. Exact Calculation of the Angular Momentum Loss, Recoil Force, and Radiation Intensity for an Arbitrary Source in Terms of Electric, Magnetic, and Toroid Multipoles. Phys. Rev. E 2002, 65, 046609. [Google Scholar] [CrossRef]
- Baryshnikova, K.V.; Smirnova, D.A.; Luk’yanchuk, B.S.; Kivshar, Y.S. Optical Anapoles: Concepts and Applications. Adv. Opt. Mater. 2019, 7, 1801350. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Liu, Z.; Cheng, S.; Li, M.; Meng, J.; Jiang, T.; Li, J.; Xu, Z.; Qian, X.; Wang, M.; et al. Scatterers of Non-Electric-Dipole Radiation. Nanomaterials 2025, 15, 1584. https://doi.org/10.3390/nano15201584
Li Y, Liu Z, Cheng S, Li M, Meng J, Jiang T, Li J, Xu Z, Qian X, Wang M, et al. Scatterers of Non-Electric-Dipole Radiation. Nanomaterials. 2025; 15(20):1584. https://doi.org/10.3390/nano15201584
Chicago/Turabian StyleLi, Yafei, Zhihui Liu, Shuanglong Cheng, Mansha Li, Jianchao Meng, Tao Jiang, Jiani Li, Zhuangzhuang Xu, Xike Qian, Meng Wang, and et al. 2025. "Scatterers of Non-Electric-Dipole Radiation" Nanomaterials 15, no. 20: 1584. https://doi.org/10.3390/nano15201584
APA StyleLi, Y., Liu, Z., Cheng, S., Li, M., Meng, J., Jiang, T., Li, J., Xu, Z., Qian, X., Wang, M., & Li, Z. (2025). Scatterers of Non-Electric-Dipole Radiation. Nanomaterials, 15(20), 1584. https://doi.org/10.3390/nano15201584





