Nanomechanical Properties of Rib Bones in Diabetic vs. Healthy Rat Models
Abstract
1. Introduction
2. Materials and Methods
2.1. Animal Model and Sample Preparation
2.2. Nanoindentation Protocol
2.3. Surface Morphology and Characterization
2.4. Statistical Evaluation
3. Results
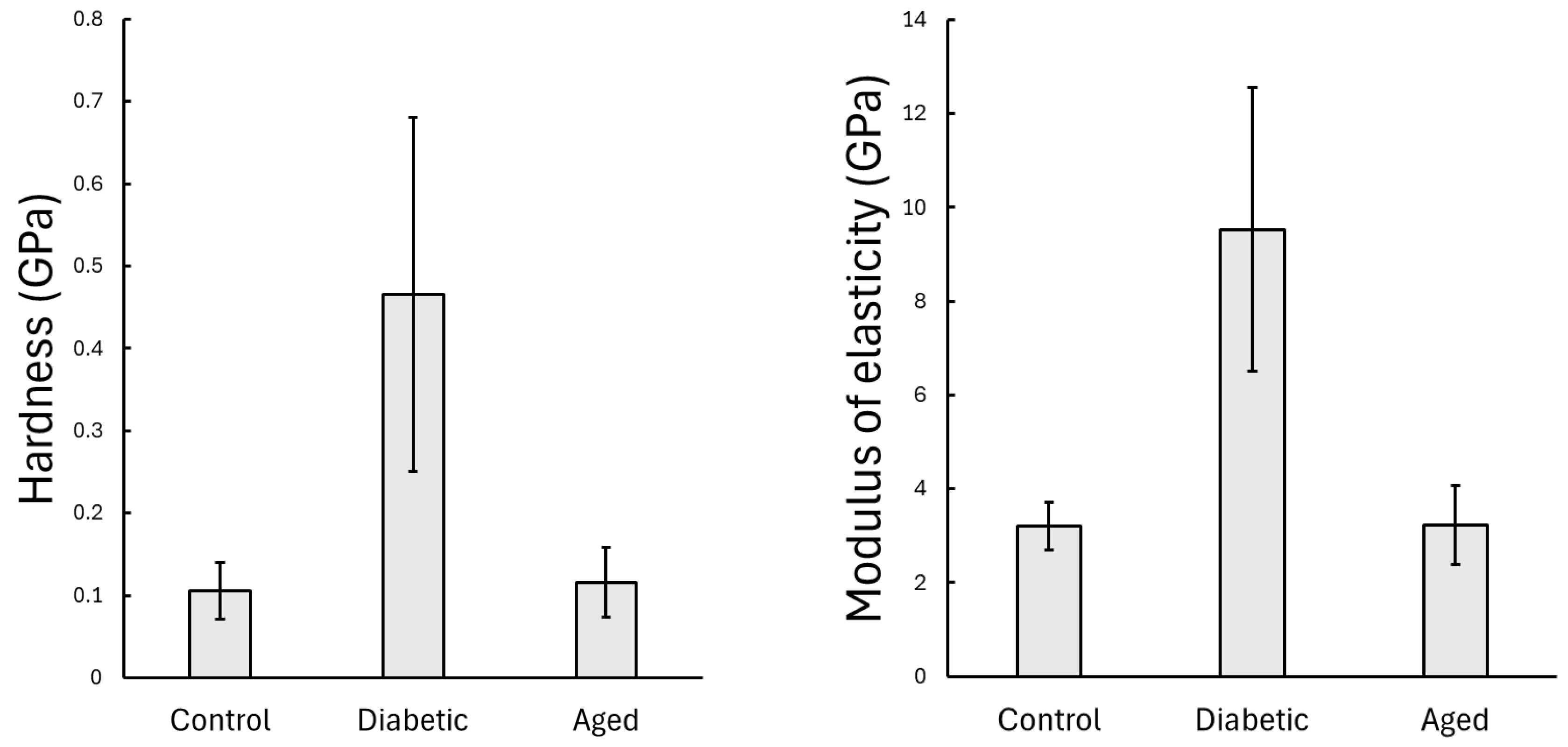
3.1. Results of the Static Nanoindentation
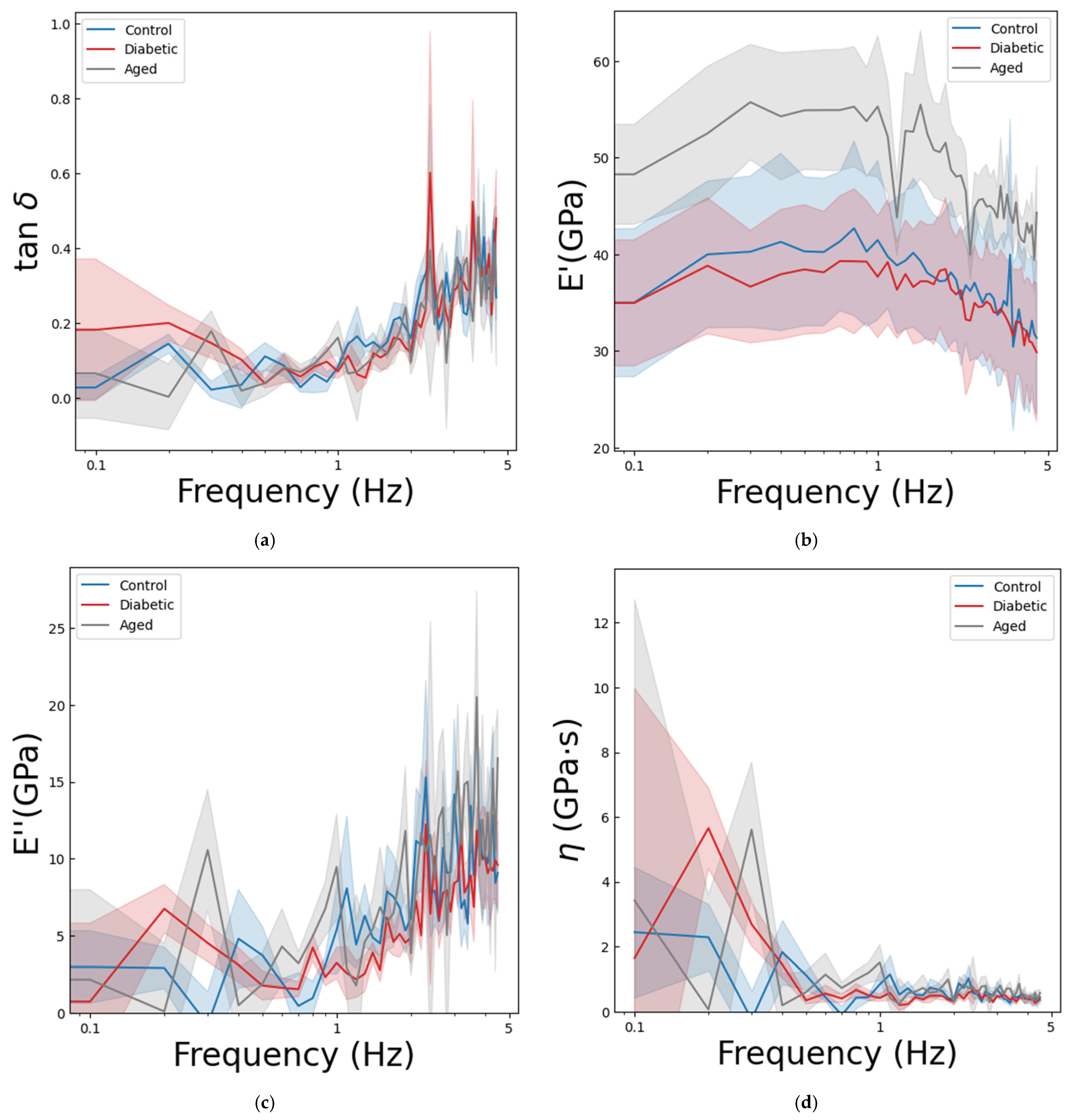
3.2. Results of the Dynamic Nanoindentation
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Representative Load–Displacement Curves

Appendix B. Supplementary Nanoindentation Parameters
References
- Kamml, J.; Acevedo, C.; Kammer, D.S. Mineral and cross-linking in collagen fibrils: The mechanical behavior of bone tissue at the nano-scale. J. Mech. Behav. Biomed. Mater. 2024, 159, 106697. [Google Scholar] [CrossRef]
- Stock, S.R. The Mineral-Collagen Interface in Bone. Calcif. Tissue Int. 2015, 97, 262–280. [Google Scholar] [CrossRef]
- Garcia-Giner, V.; Han, Z.; Giuliani, F.; Porter, A.E. Nanoscale Imaging and Analysis of Bone Pathologies. Appl. Sci. 2021, 11, 12033. [Google Scholar] [CrossRef]
- Rho, J.Y.; Tsui, T.Y.; Pharr, G.M. Elastic properties of human cortical and trabecular lamellar bone measured by nanoindentation. Biomaterials 1997, 18, 1325–1330. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Nanoindentation, 2nd ed.; Springer: New York, NY, USA, 2004; p. xxii. 263p. [Google Scholar]
- Rho, J.Y.; Roy, M.E., 2nd; Tsui, T.Y.; Pharr, G.M. Elastic properties of microstructural components of human bone tissue as measured by nanoindentation. J. Biomed. Mater. Res. 1999, 45, 48–54. [Google Scholar] [CrossRef]
- Kasperk, C.; Georgescu, C.; Nawroth, P. Diabetes Mellitus and Bone Metabolism. Exp. Clin. Endocrinol. Diabetes 2017, 125, 213–217. [Google Scholar] [CrossRef]
- Wang, L.X.; Wang, G.Y.; Su, N.; Ma, J.; Li, Y.K. Effects of different doses of metformin on bone mineral density and bone metabolism in elderly male patients with type 2 diabetes mellitus. World J. Clin. Cases 2020, 8, 4010–4016. [Google Scholar] [CrossRef]
- Murray, C.E.; Coleman, C.M. Impact of Diabetes Mellitus on Bone Health. Int. J. Mol. Sci. 2019, 20, 4873. [Google Scholar] [CrossRef]
- Sharma, P.; Sharma, R.K.; Gaur, K. Understanding the impact of diabetes on bone health: A clinical review. Metab. Open 2024, 24, 100330. [Google Scholar] [CrossRef]
- Furst, J.R.; Bandeira, L.C.; Fan, W.W.; Agarwal, S.; Nishiyama, K.K.; McMahon, D.J.; Dworakowski, E.; Jiang, H.; Silverberg, S.J.; Rubin, M.R. Advanced Glycation Endproducts and Bone Material Strength in Type 2 Diabetes. J. Clin. Endocrinol. Metab. 2016, 101, 2502–2510. [Google Scholar] [CrossRef]
- Singleton, R.C.; Pharr, G.M.; Nyman, J.S. Increased tissue-level storage modulus and hardness with age in male cortical bone and its association with decreased fracture toughness. Bone 2021, 148, 115949. [Google Scholar] [CrossRef]
- Farr, J.N.; Khosla, S. Skeletal changes through the lifespan–from growth to senescence. Nat. Rev. Endocrinol. 2015, 11, 513–521. [Google Scholar] [CrossRef]
- Osterhoff, G.; Morgan, E.F.; Shefelbine, S.J.; Karim, L.; McNamara, L.M.; Augat, P. Bone mechanical properties and changes with osteoporosis. Injury 2016, 47 (Suppl. 2), S11–S20. [Google Scholar] [CrossRef]
- Casanova, M.; Balmelli, A.; Carnelli, D.; Courty, D.; Schneider, P.; Muller, R. Nanoindentation analysis of the micromechanical anisotropy in mouse cortical bone. R. Soc. Open Sci. 2017, 4, 160971. [Google Scholar] [CrossRef]
- Shih, K.S.; Truong, T.A.; Hsu, C.C.; Hou, S.M. Biomechanical investigation of different surgical strategies for the treatment of rib fractures using a three-dimensional human respiratory model. Biomed. Tech. 2019, 64, 93–102. [Google Scholar] [CrossRef]
- Agnew, A.M.; Dominguez, V.M.; Sciulli, P.W.; Stout, S.D. Variability of in vivo linear microcrack accumulation in the cortex of elderly human ribs. Bone Rep. 2017, 6, 60–63. [Google Scholar] [CrossRef] [PubMed]
- Bajaj, D.; Geissler, J.R.; Allen, M.R.; Burr, D.B.; Fritton, J.C. The resistance of cortical bone tissue to failure under cyclic loading is reduced with alendronate. Bone 2014, 64, 57–64. [Google Scholar] [CrossRef]
- Cohen, S.R.; Kalfon-Cohen, E. Dynamic nanoindentation by instrumented nanoindentation and force microscopy: A comparative review. Beilstein J. Nanotechnol. 2013, 4, 815–833. [Google Scholar] [CrossRef]
- Toledano, M.; Toledano-Osorio, M.; Guerado, E.; Caso, E.; Osorio, E.; Osorio, R. Assessing bone quality through mechanical properties in postmenopausal trabecular bone. Injury 2018, 49 (Suppl. 2), S3–S10. [Google Scholar] [CrossRef]
- Fischer-Cripps, A.C. Multiple-frequency dynamic nanoindentation testing. J. Mater. Res. 2004, 19, 2981–2988. [Google Scholar] [CrossRef]
- Sudy, R.; Schranc, A.; Fodor, G.H.; Tolnai, J.; Babik, B.; Petak, F. Lung volume dependence of respiratory function in rodent models of diabetes mellitus. Respir. Res. 2020, 21, 82. [Google Scholar] [CrossRef]
- ISO 14577-1:2015; Metallic Materials—Instrumented Indentation Test for Hardness and Materials Parameters—Part 1: Test Method. International Organization for Standardization: Geneva, Switzerland, 2015.
- Oliver, W.C.; Pharr, G.M. An improved technique for determining hardness and elastic modulus using load and displacement sensing indentation experiments. J. Mater. Res. 1992, 7, 1564–1583. [Google Scholar] [CrossRef]
- Frater, M.; Grosz, J.; Jakab, A.; Braunitzer, G.; Tarjanyi, T.; Gulyas, G.; Bali, K.; Villa-Machado, P.A.; Garoushi, S.; Forster, A. Evaluation of microhardness of short fiber-reinforced composites inside the root canal after different light curing methods—An in vitro study. J. Mech. Behav. Biomed. Mater. 2024, 150, 106324. [Google Scholar] [CrossRef] [PubMed]
- Tarjanyi, T.; Jakab, A.G.; Sami, M.; Bali, K.; Rarosi, F.; Jarabik, M.L.; Braunitzer, G.; Palkovics, D.; Lassila, L.; Lempel, E.; et al. The Nanomechanical Performance and Water Uptake of a Flowable Short Fiber Composite: The Influence of Bulk and Layering Restorative Techniques. Polymers 2025, 17, 1553. [Google Scholar] [CrossRef]
- Hu, S.; Li, J.; Liu, L.; Dai, R.; Sheng, Z.; Wu, X.; Feng, X.; Yao, X.; Liao, E.; Keller, E.; et al. Micro/Nanostructures and Mechanical Properties of Trabecular Bone in Ovariectomized Rats. Int. J. Endocrinol. 2015, 2015, 252503. [Google Scholar] [CrossRef]
- Sun, L.W.; Fan, Y.B.; Li, D.Y.; Zhao, F.; Xie, T.; Yang, X.; Gu, Z.T. Evaluation of the mechanical properties of rat bone under simulated microgravity using nanoindentation. Acta Biomater. 2009, 5, 3506–3511. [Google Scholar] [CrossRef]
- Faienza, M.F.; Pontrelli, P.; Brunetti, G. Type 2 diabetes and bone fragility in children and adults. World J. Diabetes 2022, 13, 900–911. [Google Scholar] [CrossRef] [PubMed]
- Hofbauer, L.C.; Busse, B.; Eastell, R.; Ferrari, S.; Frost, M.; Muller, R.; Burden, A.M.; Rivadeneira, F.; Napoli, N.; Rauner, M. Bone fragility in diabetes: Novel concepts and clinical implications. Lancet Diabetes Endocrinol. 2022, 10, 207–220. [Google Scholar] [CrossRef]
- Fan, Z.F.; Smith, P.; Rauch, F.; Harris, G.F. Nanoindentation as a means for distinguishing clinical type of osteogenesis imperfecta. Compos. Part B Eng. 2007, 38, 411–415. [Google Scholar] [CrossRef]
- Moayeri, A.; Mohamadpour, M.; Mousavi, S.F.; Shirzadpour, E.; Mohamadpour, S.; Amraei, M. Fracture risk in patients with type 2 diabetes mellitus and possible risk factors: A systematic review and meta-analysis. Ther. Clin. Risk Manag. 2017, 13, 455–468. [Google Scholar] [CrossRef] [PubMed]
- Tang, S.Y.; Zeenath, U.; Vashishth, D. Effects of non-enzymatic glycation on cancellous bone fragility. Bone 2007, 40, 1144–1151. [Google Scholar] [CrossRef]
- Saito, M.; Kida, Y.; Kato, S.; Marumo, K. Diabetes, collagen, and bone quality. Curr. Osteoporos. Rep. 2014, 12, 181–188. [Google Scholar] [CrossRef]
- Gao, Q.; Jiang, Y.; Zhou, D.; Li, G.; Han, Y.; Yang, J.; Xu, K.; Jing, Y.; Bai, L.; Geng, Z.; et al. Advanced glycation end products mediate biomineralization disorder in diabetic bone disease. Cell Rep. Med. 2024, 5, 101694. [Google Scholar] [CrossRef]
- Parle, E.; Tio, S.; Behre, A.; Carey, J.J.; Murphy, C.G.; O’Brien, T.F.; Curtin, W.A.; Kearns, S.R.; McCabe, J.P.; Coleman, C.M.; et al. Bone Mineral Is More Heterogeneously Distributed in the Femoral Heads of Osteoporotic and Diabetic Patients: A Pilot Study. JBMR Plus 2020, 4, e10253. [Google Scholar] [CrossRef] [PubMed]
- Bolger, M.W.; Tekkey, T.; Kohn, D.H. The Contribution of Perilacunar Composition and Mechanical Properties to Whole-Bone Mechanical Outcomes in Streptozotocin-Induced Diabetes. Calcif. Tissue Int. 2023, 113, 229–245. [Google Scholar] [CrossRef] [PubMed]
- Lekkala, S.; Taylor, E.A.; Hunt, H.B.; Donnelly, E. Effects of Diabetes on Bone Material Properties. Curr. Osteoporos. Rep. 2019, 17, 455–464. [Google Scholar] [CrossRef] [PubMed]
- Lekkala, S.; Sacher, S.E.; Taylor, E.A.; Williams, R.M.; Moseley, K.F.; Donnelly, E. Increased Advanced Glycation Endproducts, Stiffness, and Hardness in Iliac Crest Bone from Postmenopausal Women with Type 2 Diabetes Mellitus on Insulin. J. Bone Miner. Res. 2023, 38, 261–277. [Google Scholar] [CrossRef]
- Wolfel, E.M.; Fiedler, I.A.K.; Dragoun Kolibova, S.; Krug, J.; Lin, M.C.; Yazigi, B.; Siebels, A.K.; Mushumba, H.; Wulff, B.; Ondruschka, B.; et al. Human tibial cortical bone with high porosity in type 2 diabetes mellitus is accompanied by distinctive bone material properties. Bone 2022, 165, 116546. [Google Scholar] [CrossRef]
- Minami, M.; Ikoma, K.; Onishi, O.; Horii, M.; Itoh, K.; Takahashi, K. Histological assessment of cortical bone changes in diabetic rats. J. Orthop. Surg. Res. 2022, 17, 568. [Google Scholar] [CrossRef]
- Qian, W.; Gamsjaeger, S.; Paschalis, E.P.; Graeff-Armas, L.A.; Bare, S.P.; Turner, J.A.; Lappe, J.M.; Recker, R.R.; Akhter, M.P. Bone intrinsic material and compositional properties in postmenopausal women diagnosed with long-term Type-1 diabetes. Bone 2023, 174, 116832. [Google Scholar] [CrossRef]
- Ravazzano, L.; Colaianni, G.; Tarakanova, A.; Xiao, Y.B.; Grano, M.; Libonati, F. Multiscale and multidisciplinary analysis of aging processes in bone. NPJ Aging 2024, 10, 28. [Google Scholar] [CrossRef]
- Kamml, J.; Acevedo, C.; Kammer, D.S. Advanced-Glycation Endproducts: How cross-linking properties affect the collagen fibril behavior. J. Mech. Behav. Biomed. Mater. 2023, 148, 106198. [Google Scholar] [CrossRef]
- Farlay, D.; Falgayrac, G.; Poncon, C.; Rizzo, S.; Cortet, B.; Chapurlat, R.; Penel, G.; Badoud, I.; Ammann, P.; Boivin, G. Material and nanomechanical properties of bone structural units of cortical and trabecular iliac bone tissues from untreated postmenopausal osteoporotic women. Bone Rep. 2022, 17, 101623. [Google Scholar] [CrossRef]
- Ojanen, X.; Isaksson, H.; Toyras, J.; Turunen, M.J.; Malo, M.K.; Halvari, A.; Jurvelin, J.S. Relationships between tissue composition and viscoelastic properties in human trabecular bone. J. Biomech. 2015, 48, 269–275. [Google Scholar] [CrossRef] [PubMed]
- Saito, M.; Marumo, K. Collagen cross-links as a determinant of bone quality: A possible explanation for bone fragility in aging, osteoporosis, and diabetes mellitus. Osteoporos. Int. 2010, 21, 195–214. [Google Scholar] [CrossRef]
- Bracher, S.; Voumard, B.; Simon, M.; Kochetkova, T.; Pretterklieber, M.; Zysset, P. Bone collagen tensile properties of the aging human proximal femur. Bone Rep. 2024, 21, 101773. [Google Scholar] [CrossRef] [PubMed]
- Pathak, S.; Swadener, J.G.; Kalidindi, S.R.; Courtland, H.W.; Jepsen, K.J.; Goldman, H.M. Measuring the dynamic mechanical response of hydrated mouse bone by nanoindentation. J. Mech. Behav. Biomed. Mater. 2011, 4, 34–43. [Google Scholar] [CrossRef]
- Guidoni, G.; Swain, M.; Jäger, I. Nanoindentation of wet and dry compact bone: Influence of environment and indenter tip geometry on the indentation modulus. Philos. Mag. 2010, 90, 553–565. [Google Scholar] [CrossRef]
- Lee, K.L.; Baldassarri, M.; Gupta, N.; Pinisetty, D.; Janal, M.N.; Tovar, N.; Coelho, P.G. Nanomechanical Characterization of Canine Femur Bone for Strain Rate Sensitivity in the Quasistatic Range under Dry versus Wet Conditions. Int. J. Biomater. 2012, 2012, 415230. [Google Scholar] [CrossRef] [PubMed]
- Oyen, M.L. Nanoindentation of hydrated materials and tissues. Curr. Opin. Solid State Mater. Sci. 2015, 19, 317–323. [Google Scholar] [CrossRef]
- Bembey, A.K.; Bushby, A.J.; Boyde, A.; Ferguson, V.L.; Oyen, M.L. Hydration effects on the micro-mechanical properties of bone. J. Mater. Res. 2006, 21, 1962–1968. [Google Scholar] [CrossRef]
- Granke, M.; Does, M.D.; Nyman, J.S. The Role of Water Compartments in the Material Properties of Cortical Bone. Calcif. Tissue Int. 2015, 97, 292–307. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tarjányi, T.; Rosztóczy, C.; Peták, F.; Kun-Szabó, F.; Gulyás, G.; Tolnai, J.; Bali, K.; Somogyi, P.; Kiss, R.A.; Fodor, G.H. Nanomechanical Properties of Rib Bones in Diabetic vs. Healthy Rat Models. Nanomaterials 2025, 15, 1582. https://doi.org/10.3390/nano15201582
Tarjányi T, Rosztóczy C, Peták F, Kun-Szabó F, Gulyás G, Tolnai J, Bali K, Somogyi P, Kiss RA, Fodor GH. Nanomechanical Properties of Rib Bones in Diabetic vs. Healthy Rat Models. Nanomaterials. 2025; 15(20):1582. https://doi.org/10.3390/nano15201582
Chicago/Turabian StyleTarjányi, Tamás, Csaba Rosztóczy, Ferenc Peták, Fruzsina Kun-Szabó, Gábor Gulyás, József Tolnai, Krisztián Bali, Petra Somogyi, Rebeka Anna Kiss, and Gergely H. Fodor. 2025. "Nanomechanical Properties of Rib Bones in Diabetic vs. Healthy Rat Models" Nanomaterials 15, no. 20: 1582. https://doi.org/10.3390/nano15201582
APA StyleTarjányi, T., Rosztóczy, C., Peták, F., Kun-Szabó, F., Gulyás, G., Tolnai, J., Bali, K., Somogyi, P., Kiss, R. A., & Fodor, G. H. (2025). Nanomechanical Properties of Rib Bones in Diabetic vs. Healthy Rat Models. Nanomaterials, 15(20), 1582. https://doi.org/10.3390/nano15201582






