A Small-Angle Neutron Scattering Methodology for Quantitative Characterization of Channel Width in Gamma Matrix Phase
Abstract
1. Introduction
2. Materials and Methods
3. Results
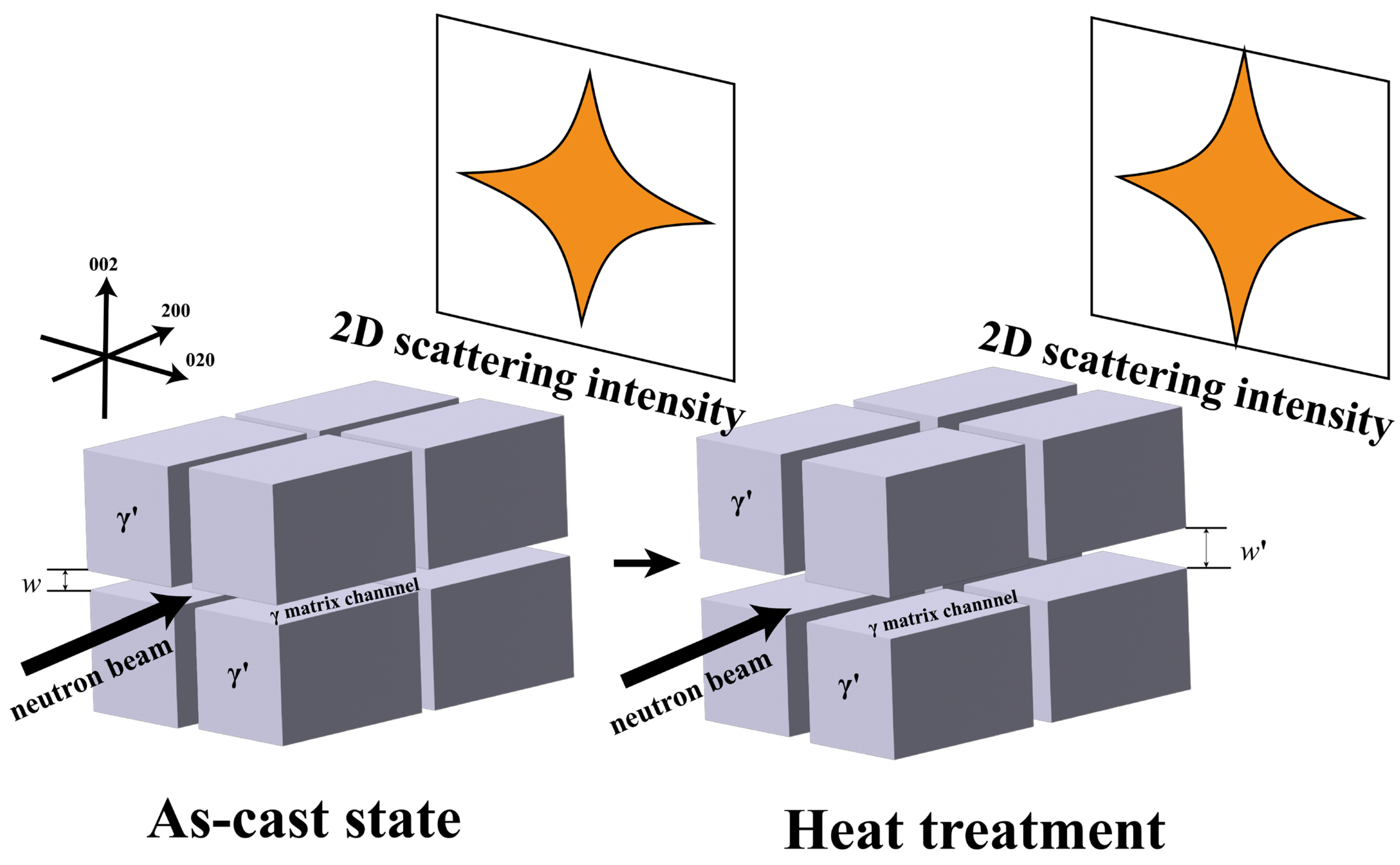
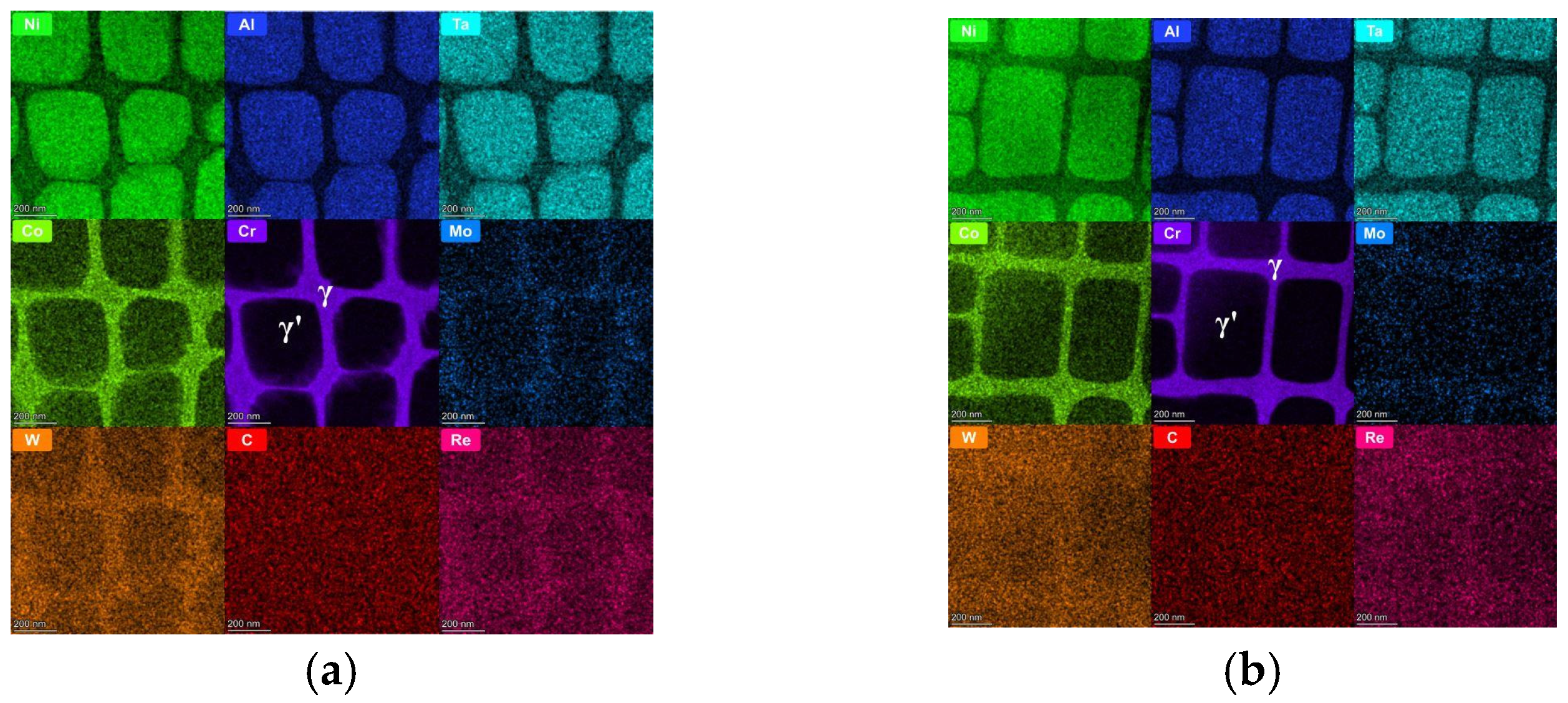
3.1. Microstructural Characterization via TEM and SANS
3.2. Quantitative Analysis of γ Matrix Channel Width
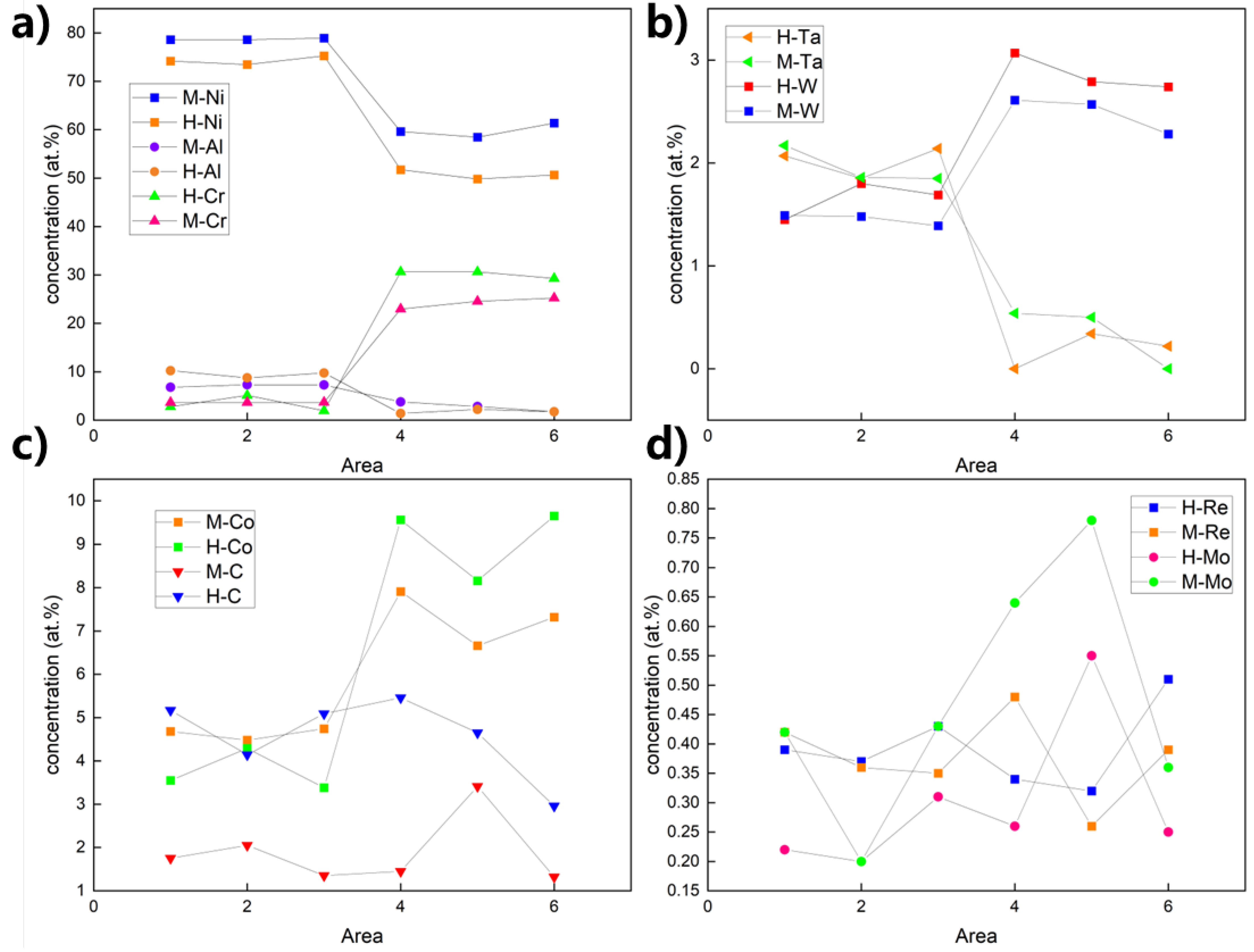
3.3. Elemental Partitioning Behavior and Evolution upon Heat Treatment
4. Discussion
4.1. SANS as a Quantitative Tool for Channel Width Characterization
4.2. Anisotropic Channel Widening and Rafting Mechanisms
4.3. Implications for Diffusion and Microstructural Evolution
4.4. Comparison with Prior Work
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| APT | Atom Probe Tomography |
| SANS | Small-Angle Neutron Scattering |
| TEM | Transmission Electron Microscopy |
| γ | gamma matrix phase |
| γ’ | gamma prime precipitate phase |
| HRTEM | High-Resolution Transmission Electron Microscopy |
| DD10 | A specific first-generation Ni-based single-crystal superalloy |
| L12 | A type of ordered crystal structure (e.g., Ni3Al) |
| SC | Single Crystal |
| Q | Scattering vector |
| I(Q) | Scattering intensity |
| Δρ | Neutron scattering length density contrast |
| w | Width of the γ matrix channel |
| w_med | Median channel width (from lognormal fit) |
| σ | Width parameter of the lognormal distribution |
| [hkl] | Miller indices denoting a crystallographic direction |
| (hkl) | Miller indices denoting a crystallographic plane |
| nm | Nanometer |
References
- Reed, R.C. The Superalloys: Fundamentals and Applications, 1st ed.; Cambridge University Press: Cambridge, UK, 2006; ISBN 978-0-521-85904-2. [Google Scholar]
- Pollock, T.M.; Tin, S. Nickel-Based Superalloys for Advanced Turbine Engines: Chemistry, Microstructure and Properties. J. Propuls. Power 2006, 22, 361–374. [Google Scholar] [CrossRef]
- Locq, D.; Caron, P.; Raujol, S.; Pettinari-Sturmel, F.; Coujou, A.; Clement, N. On the Role of Tertiary γ’ Precipitates in the Creep Behaviour at 700C of a PM Disk Superalloy. In Proceedings of the Superalloys 2004 (Tenth International Symposium), Champion, PA, USA, 19–23 September 2004; TMS: Pittsburgh, PA, USA, 2004; pp. 179–187. [Google Scholar]
- Giese, S.; Bezold, A.; Pröbstle, M.; Heckl, A.; Neumeier, S.; Göken, M. The Importance of Diffusivity and Partitioning Behavior of Solid Solution Strengthening Elements for the High Temperature Creep Strength of Ni-Base Superalloys. Metall. Mater. Trans. A 2020, 51, 6195–6206. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, T.; Lu, F.; Cao, K.; Wang, D.; Zhang, J.; Zhang, J.; Su, H.; Liu, L. The Effect of Rhenium on the Microstructure Stability and γ/γ′ Interfacial Characteristics of Ni-Based Single Crystal Superalloys during Long-Term Aging. J. Alloys Compd. 2021, 876, 160114. [Google Scholar] [CrossRef]
- Guo, Z.; Song, Z.; Huang, D.; Yan, X. Matrix Channel Width Evolution of Single Crystal Superalloy Under Creep and Thermal Mechanical Fatigue: Experimental and Modeling Investigations. Met. Mater. Int. 2022, 28, 2972–2986. [Google Scholar] [CrossRef]
- Tiley, J.; Viswanathan, G.B.; Srinivasan, R.; Banerjee, R.; Dimiduk, D.M.; Fraser, H.L. Coarsening Kinetics of γ′ Precipitates in the Commercial Nickel Base Superalloy René 88 DT. Acta Mater. 2009, 57, 2538–2549. [Google Scholar] [CrossRef]
- Saksena, A.; Kubacka, D.; Gault, B.; Spiecker, E.; Kontis, P. The Effect of γ Matrix Channel Width on the Compositional Evolution in a Multi-Component Nickel-Based Superalloy. Scr. Mater. 2022, 219, 114853. [Google Scholar] [CrossRef]
- Yu, T.; Hope, A.; Mason, P. Implementing Numerical Algorithms to Optimize the Parameters in Kampmann–Wagner Numerical (KWN) Precipitation Models. npj Comput. Mater. 2024, 10, 235. [Google Scholar] [CrossRef]
- Williams, D.B.; Carter, C.B. Transmission Electron Microscopy; Springer: Boston, MA, USA, 2009; ISBN 978-0-387-76500-6. [Google Scholar]
- Peters, J.J.P.; Beanland, R.; Alexe, M.; Cockburn, J.W.; Revin, D.G.; Zhang, S.Y.; Sanchez, A.M. Artefacts in Geometric Phase Analysis of Compound Materials. Ultramicroscopy 2015, 157, 91–97. [Google Scholar] [CrossRef]
- Kareh, K.M. Atom Probe Tomography. Nat. Rev. Methods Primer 2021, 1, 52. [Google Scholar] [CrossRef]
- Pan, Q.; Zhao, X.; Cheng, Y.; Yue, Q.; Gu, Y.; Bei, H.; Zhang, Z. Effects of Co on Microstructure Evolution of a 4th Generation Nickel-Based Single Crystal Superalloys. Intermetallics 2023, 153, 107798. [Google Scholar] [CrossRef]
- Ardell, A.J. Trans-Interface-Diffusion-Controlled Coarsening of γ′ Precipitates in Ternary Ni–Al–Cr Alloys. Acta Mater. 2013, 61, 7828–7840. [Google Scholar] [CrossRef]
- Wang, T.; Sheng, G.; Liu, Z.-K.; Chen, L.-Q. Coarsening Kinetics of γ′ Precipitates in the Ni–Al–Mo System. Acta Mater. 2008, 56, 5544–5551. [Google Scholar] [CrossRef]
- Reed, R.C.; Matan, N.; Cox, D.C.; Rist, M.A.; Rae, C.M.F. Creep of CMSX-4 Superalloy Single Crystals: Effects of Rafting at High Temperature. Acta Mater. 1999, 47, 3367–3381. [Google Scholar] [CrossRef]
- Matan, N.; Cox, D.C.; Rae, C.M.F.; Reed, R.C. On the Kinetics of Rafting in CMSX-4 Superalloy Single Crystals. Acta Mater. 1999, 47, 2031–2045. [Google Scholar] [CrossRef]
- Caccuri, V.; Cormier, J.; Desmorat, R. γ′-Rafting Mechanisms under Complex Mechanical Stress State in Ni-Based Single Crystalline Superalloys. Mater. Des. 2017, 131, 487–497. [Google Scholar] [CrossRef]
- Brass, A.M.; Chêne, J. Sans Analysis of γ′ Precipitation in the γ Matrix of Ni Base Superalloy Single Crystals. Scr. Mater. 2000, 43, 913–918. [Google Scholar] [CrossRef]
- Bellet, D.; Bastie, P.; Royer, A.; Lajzerowicz, J.; Legrand, J.F.; Bonnet, R. Small Angle Neutron Scattering (SANS) Study of γ’ Precipitates in Single Crystals of AM1 Superalloy. J. Phys. I 1992, 2, 1097–1112. [Google Scholar] [CrossRef]
- Strunz, P.; Šmilauerová, J.; Janeček, M.; Stráský, J.; Harcuba, P.; Pospíšil, J.; Veselý, J.; Lindner, P.; Karge, L. Evaluation of Anisotropic Small-Angle Neutron Scattering Data from Metastable β-Ti Alloy. Philos. Mag. 2018, 98, 3086–3108. [Google Scholar] [CrossRef]
- Strunz, P.; Petrenec, M.; Polák, J.; Gasser, U.; Farkas, G. Formation and Dissolution of γ’ Precipitates in IN792 Superalloy at Elevated Temperatures. Metals 2016, 6, 37. [Google Scholar] [CrossRef]
- Strunz, P.; Petrenec, M.; Gasser, U.; Tobiáš, J.; Polák, J.; Šaroun, J. Precipitate Microstructure Evolution in Exposed IN738LC Superalloy. J. Alloys Compd. 2014, 589, 462–471. [Google Scholar] [CrossRef]
- Zrník, J.; Strunz, P.; Maldini, M.; Davydov, V. SANS Investigation of γ’ Precipitate Morphology Evolution in Creep Exposed Single Crystal Ni Base Superalloy. Mater. Sci. Forum 2010, 636–637, 1475–1482. Available online: https://www.scientific.net/MSF.636-637.1475.
- Rogozhkin, S.V.; Klauz, A.V.; Ke, Y.; Almásy, L.; Nikitin, A.A.; Khomich, A.A.; Bogachev, A.A.; Gorshkova, Y.E.; Bokuchava, G.D.; Kopitsa, G.P.; et al. Study of Precipitates in Oxide Dispersion-Strengthened Steels by SANS, TEM, and APT. Nanomaterials 2024, 14, 194. [Google Scholar] [CrossRef]
- Yan, S.; Wang, Z.; Li, T.; Chen, Z.; Du, X.; Liu, Y.; Chen, D.; Sun, K.; Liu, R.; Bai, B.; et al. In Situ Characterization of 17-4PH Stainless Steel by Small-Angle Neutron Scattering. Materials 2023, 16, 5583. [Google Scholar] [CrossRef]
- Wu, E.; Zhang, J.; Chen, B.; Sun, G.; Ji, V.; Hughes, D.; Pirling, T. Neutron Diffraction Study of Strain and Stress Induced by Thermomechanical Fatigue in a Single Crystal Superalloy. J. Phys. Condens. Matter 2008, 20, 104255. [Google Scholar] [CrossRef]
- Youdao, W.; Erdong, W.; Sucheng, W.; Wuhui, L. X–ray diffraction analysis on the thickness effect of γ/γ ′ lattice mismatche in nickel base single crystal superalloy DD10. Acta Met. Sin. 2011, 47, 1418–1425. [Google Scholar] [CrossRef]
- Berghausen, J.; Zipfel, J.; Lindner, P.; Richtering, W. Influence of Water-Soluble Polymers on the Shear-Induced Structure Formation in Lyotropic Lamellar Phases. J. Phys. Chem. B 2001, 105, 11081–11088. [Google Scholar] [CrossRef]
- Rowan, O.K.; Sisson, R.D. Effect of Alloy Composition on Carburizing Performance of Steel. J. Phase Equilibria Diffus. 2009, 30, 235–241. [Google Scholar] [CrossRef]
- Burada, P.S.; Hänggi, P.; Marchesoni, F.; Schmid, G.; Talkner, P. Diffusion in Confined Geometries. ChemPhysChem 2009, 10, 45–54. [Google Scholar] [CrossRef] [PubMed]
- Berezhkovskii, A.M.; Pustovoit, M.A.; Bezrukov, S.M. Diffusion in a Tube of Varying Cross Section: Numerical Study of Reduction to Effective One-Dimensional Description. J. Chem. Phys. 2007, 126, 134706. [Google Scholar] [CrossRef] [PubMed]



| Name | Most Probable Thickness (nm) |
|---|---|
| [002] virgin | 17.8 ± 0.1 |
| [020] virgin | 20.5 ± 0.1 |
| [002] Heat-treated | 36.8 ± 0.2 |
| [020] Heat-treated | 28.0 ± 0.1 |
| Element | Virgin(M) | Heat-Treated (H) | Change (H − M) | |||
|---|---|---|---|---|---|---|
| γ’ | γ | γ’ | γ | γ’ | γ | |
| Ni | 78.69 | 59.82 | 73.29 | 50.59 | −5.40 | −9.23 |
| Al | 7.14 | 2.01 | 9.74 | 1.66 | +2.60 | −0.35 |
| Cr | 3.68 | 24.24 | 2.96 | 30.18 | −0.72 | +5.94 |
| Co | 4.63 | 7.30 | 3.81 | 9.14 | −0.82 | +1.84 |
| Ta | 1.96 | 0.35 | 2.02 | 0.11 | +0.06 | −0.24 |
| W | 1.45 | 2.49 | 1.65 | 2.87 | +0.20 | +0.38 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, Z.; Li, T.; Wu, E.; Du, X.; Zhang, S.; Yan, S.; Wang, Z.; Sun, K.; Chen, D. A Small-Angle Neutron Scattering Methodology for Quantitative Characterization of Channel Width in Gamma Matrix Phase. Nanomaterials 2025, 15, 1581. https://doi.org/10.3390/nano15201581
Chen Z, Li T, Wu E, Du X, Zhang S, Yan S, Wang Z, Sun K, Chen D. A Small-Angle Neutron Scattering Methodology for Quantitative Characterization of Channel Width in Gamma Matrix Phase. Nanomaterials. 2025; 15(20):1581. https://doi.org/10.3390/nano15201581
Chicago/Turabian StyleChen, Zhong, Tianfu Li, Erdong Wu, Xiaoming Du, Shaohua Zhang, Shibo Yan, Zijun Wang, Kai Sun, and Dongfeng Chen. 2025. "A Small-Angle Neutron Scattering Methodology for Quantitative Characterization of Channel Width in Gamma Matrix Phase" Nanomaterials 15, no. 20: 1581. https://doi.org/10.3390/nano15201581
APA StyleChen, Z., Li, T., Wu, E., Du, X., Zhang, S., Yan, S., Wang, Z., Sun, K., & Chen, D. (2025). A Small-Angle Neutron Scattering Methodology for Quantitative Characterization of Channel Width in Gamma Matrix Phase. Nanomaterials, 15(20), 1581. https://doi.org/10.3390/nano15201581






