Vibration Analysis of Multilayer Stepped Cross-Sectional Carbon Nanotubes
Abstract
1. Introduction
2. Methodology
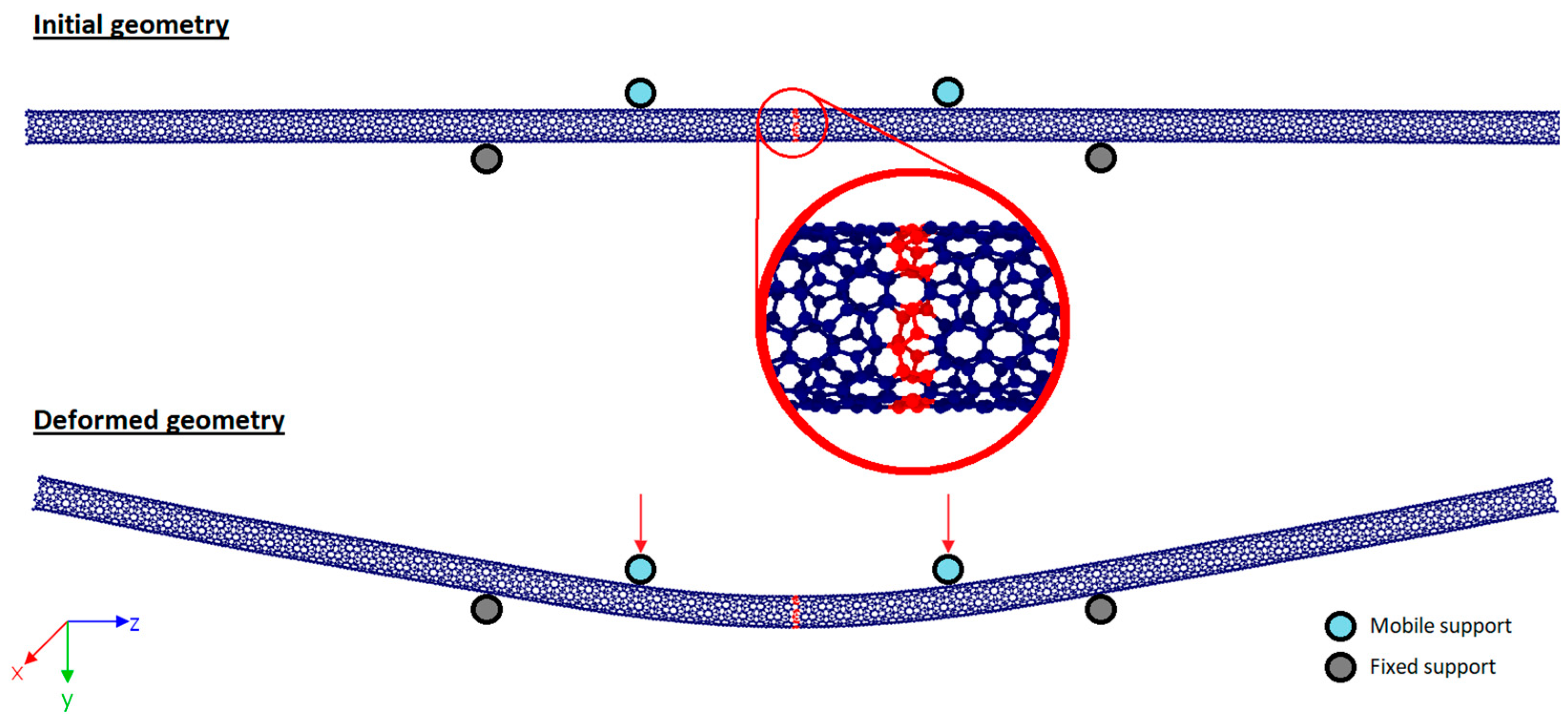
2.1. Molecular Dynamics Analysis
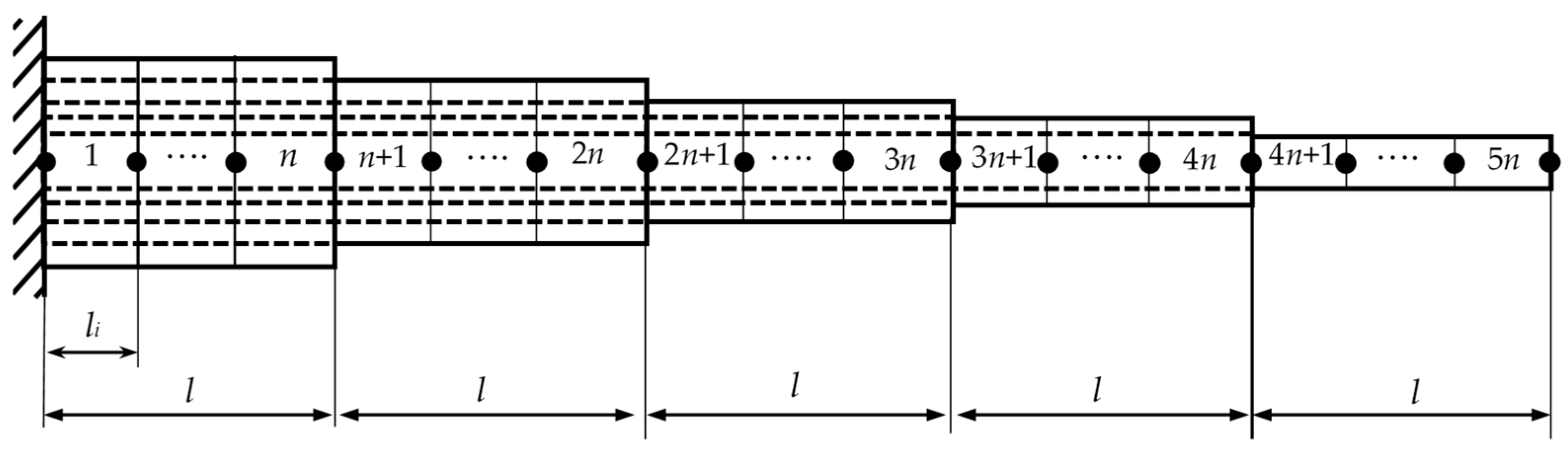
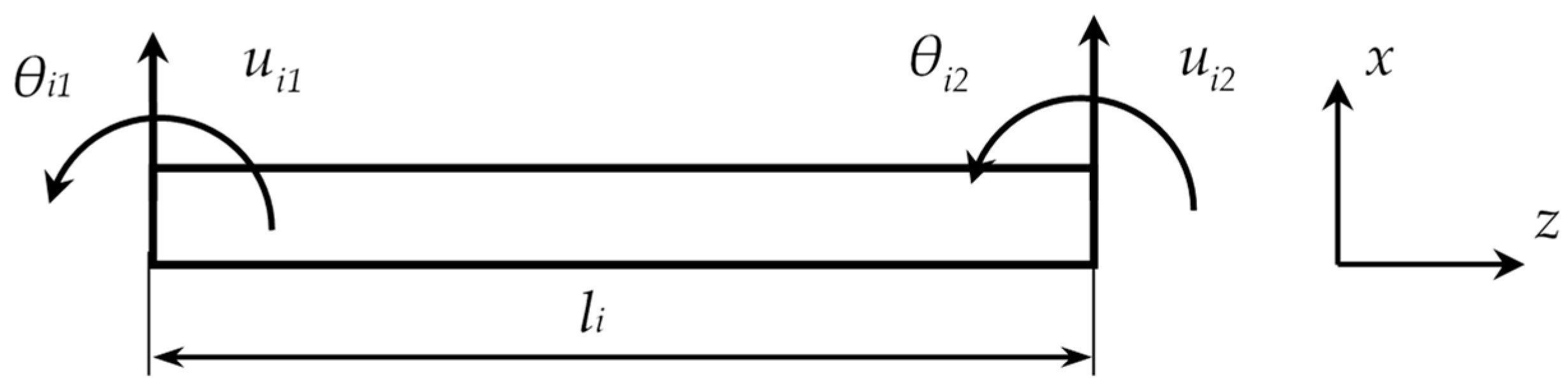
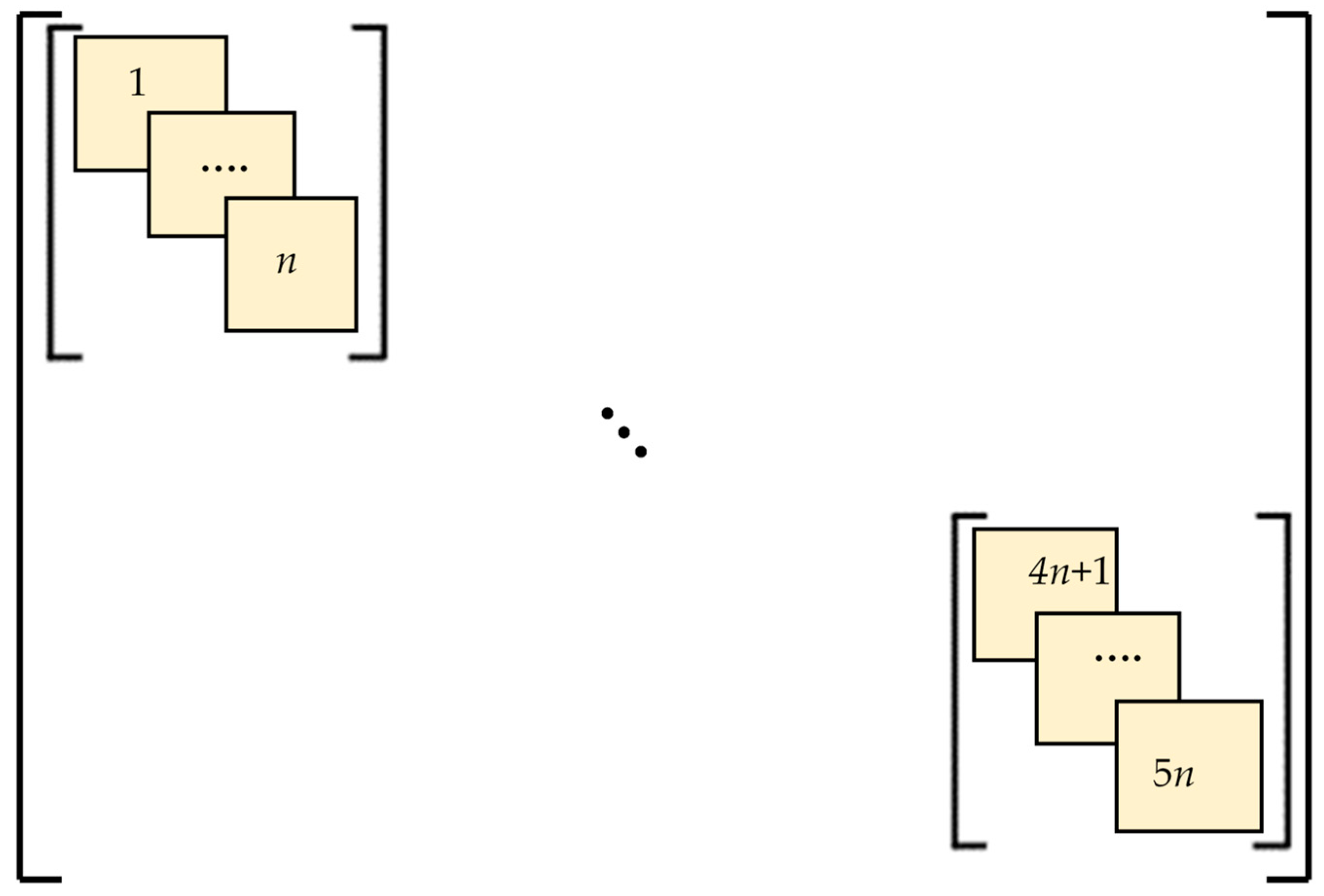
2.2. Numerical Analysis
2.3. The Core of Nonlocal Constitutive Relation
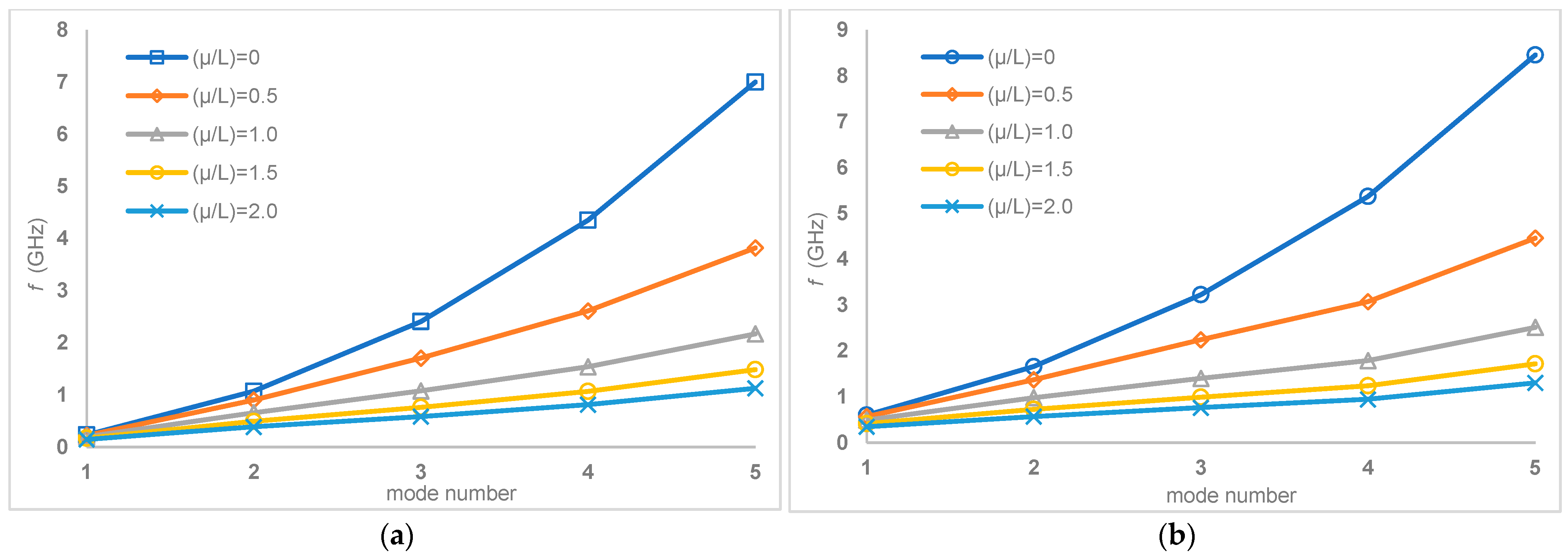
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| VTGSs | Variable-Thickness Graphene Sheets |
| MD | Molecular Dynamics |
| LAMMPS | Large-scale Atomic/Molecular Massively Parallel Simulator |
| FFT | Fast Fourier Transform |
| VACF | Velocity Autocorrelation Function |
| CNTs | Carbon Nanotubes |
| FEM | Finite Element Modeling |
| SWNTs | Single-Walled Carbon Nanotubes |
| SWCNCs | Single-Walled Carbon Nanocones |
| SLGSs | Single-Layered Graphene Sheets |
| DLGSs | Double-Layered Graphene Sheets |
| MWCNTs | Multi-Walled Carbon Nanotubes |
| vdW | Van Der Waals |
| VMD | Visual Molecular Dynamics |
References
- Kireitseu, M.-V.; Tomlinson, J.L.; Altenbach, H.; Rongong, G.; Bochkareva, L.-V.; Hui, D. Preliminary Results on Vibration Damping Properties of Nanoscale-Reinforced Composite Materials. arXiv 2007, arXiv:0708.1821. [Google Scholar] [CrossRef]
- Jia, X.Q.; Li, S.Y.; Miu, H.J.; Yang, T.; Rao, K.; Wu, D.Y.; Cui, B.L.; Ou, J.L.; Zhu, Z.C. Carbon Nanomaterials: A New Sustainable Solution to Reduce the Emerging Environmental Pollution of Turbomachinery Noise and Vibration. Front. Chem. 2020, 8, 683. [Google Scholar] [CrossRef]
- Dresselhaus, M.S.; Dresselhaus, G.; Avouris, P. Carbon Nanotubes: Synthesis, Structure, Properties, and Applications; Springer Nature: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Bhattacharyya, S.; Sinturel, C.; Bahloul, O.; Saboungi, M.L.; Thomas, S.; Salvetat, J.P. Improving Reinforcement of Natural Rubber by Networking of Activated Carbon Nanotubes. Carbon 2008, 46, 1037–1045. [Google Scholar] [CrossRef]
- Liu, K.; Deslippe, J.; Xiao, F.; Capaz, R.B.; Hong, X.; Aloni, S.; Zettl, A.; Wang, W.; Bai, X.; Louie, S.G.; et al. An Atlas of Carbon Nanotube Optical Transitions. Nat. Nanotechnol. 2012, 7, 325–329. [Google Scholar] [CrossRef]
- Zhou, X.; Shin, E.; Wang, K.W.; Bakis, C.E. Interfacial Damping Characteristics of Carbon Nanotube-Based Composites. Compos. Sci. Technol. 2004, 64, 2425–2437. [Google Scholar] [CrossRef]
- Lemay, S.G.; Janssen, J.W.; Van Den Hout, M.; Mooij, M.; Bronikowski, M.J.; Willis, P.A.; Smalley, R.E.; Kouwenhoven, L.P.; Dekker, C. Two-Dimensional Imaging of Electronic Wavefunctions in Carbon Nano-tubes. Nature 2001, 412, 617–620. [Google Scholar] [CrossRef]
- Eatemadi, A.; Daraee, H.; Karimkhanloo, H.; Kouhi, M.; Zarghami, N.; Akbarzadeh, A.; Abasi, M.; Hanifehpour, Y.; Joo, S.W. Carbon Nanotubes: Properties, Synthesis, Purification, and Medical Applications. Nanoscale Res. Lett. 2014, 9, 393. [Google Scholar] [CrossRef]
- Palacios, J.A.; Ganesan, R. Reliability Evaluation Based on Modal Parameters of Car-bon-Nanotube-Reinforced-Polymer-Composite Material Using Multiscale Finite Element Model. Phys. E Low-Dimens. Syst. Nanostruct. 2021, 125, 114318. [Google Scholar] [CrossRef]
- Jiang, S.; Sun, L.; Zhan, H.; Zheng, Z.; Peng, X.; Lü, C. Bending Behavior of Diamane and Twisted Bilayer Graphene: Insights from Four-Point Bending Deformation. Thin-Walled Struct. 2024, 195, 111415. [Google Scholar] [CrossRef]
- Zheng, Z.; Deng, F.; Su, Z.; Zhan, H.; Wang, L. Analysis of the Vibrational Characteristics of Diamane Nanosheet Based on the Kirchhoff Plate Model and Atomistic Simulations. Discov. Nano 2023, 18, 108. [Google Scholar] [CrossRef] [PubMed]
- Izadi, R.; Tuna, M.; Trovalusci, P.; Fantuzzi, N. Bending Characteristics of Carbon Nanotubes: Micropolar Elasticity Models and Molecular Dynamics Simulations. Mech. Adv. Mater. Struct. 2021, 30, 189–206. [Google Scholar] [CrossRef]
- Kulhavy, P.; Petru, M.; Syrovatkova, M. Possibilities of the Additional Damping of Unidirectional Fiber Composites by Implementation of Viscoelastic Neoprene and Rubber Layers. Shock. Vib. 2017, 2017, 4163485. [Google Scholar] [CrossRef]
- Rahman, M.A.; Chung, G.S. Synthesis of PVDF-Graphene Nanocomposites and Their Properties. J. Alloys Compd. 2013, 581, 724–730. [Google Scholar] [CrossRef]
- Şimşek, M. Nonlocal Effects in the Forced Vibration of an Elastically Connected Double-Carbon Nanotube System under a Moving Nanoparticle. Comput. Mater. Sci. 2011, 50, 2112–2123. [Google Scholar] [CrossRef]
- Belhadj, A.; Boukhalfa, A.; Belalia, S.A. Carbon Nanotube Structure Vibration Based on Non-Local Elasticity. J. Mod. Mater. 2016, 3, 9–13. [Google Scholar] [CrossRef]
- Hussain, M.; Naeem, M.N.; Shahzad, A.; He, M. Vibrational Behavior of Single-Walled Carbon Nanotubes Based on Cylindrical Shell Model Using Wave Propagation Approach. AIP Adv. 2017, 7, 045114. [Google Scholar] [CrossRef]
- Liu, R.; Wang, L. Coupling between Flexural Modes in Free Vibration of Single-Walled Carbon Nanotubes. AIP Adv. 2015, 5, 127110. [Google Scholar] [CrossRef]
- Hossain, M.; Lellep, J. Analysis of Free Vibration of Tapered Cracked Double Nanobeams Using Maclaurin Series. Eng. Res. Express 2022, 4, 025034. [Google Scholar] [CrossRef]
- Liu, R.; Wang, L. Thermal Vibration of a Single-Walled Carbon Nanotube Predicted by Semiquantum Molecular Dynamics. Phys. Chem. Chem. Phys. 2015, 17, 5194–5201. [Google Scholar] [CrossRef]
- Shayan-Amin, S.; Dalir, H.; Farshidianfar, A. Molecular Dynamics Simulation of Double-Walled Carbon Nanotube Vibrations: Comparison with Continuum Elastic Theories. J. Mech. 2009, 25, 337–343. [Google Scholar] [CrossRef]
- Horng, T.-L. Analytical Solution of Vibration Analysis on Fixed-Free Single-Walled Carbon Nano-tube-Based Mass Sensor. J. Surf. Eng. Mater. Adv. Technol. 2012, 2, 47–52. [Google Scholar]
- William, H.; Andrew, D.; Klaus, S. VMD—Visual Molecular Dynamics. J. Mol. Graph. 1996, 14, 33–38. [Google Scholar]
- Sakharova, N.A.; André, A.F.; Antunes, J.M.; Fernandes, J.V. Mechanical Characterization of Multiwalled Carbon Nanotubes: Numerical Simulation Study. Materials 2020, 13, 4283. [Google Scholar] [CrossRef] [PubMed]
- Saito, R.; Fujita, M.; Dresselhaus, G.; Dresselhaus, M.S. Electronic Structure of Chiral Graphene Tubules. Appl. Phys. Lett. 1992, 60, 2204–2206. [Google Scholar] [CrossRef]
- Zhang, L.; Xiong, D.; Yin, L.; Zhang, H. Molecular Dynamics Simulation of Tin Whisker Growth in Three-Point Bending Copper-Tin Coating under Multi-Field Coupling. Chem. Phys. Lett. 2023, 811, 140220. [Google Scholar] [CrossRef]
- Liu, Q.; Sadowski, A.J.; Michael Rotter, J. Ovalization Restraint in Four-Point Bending Tests of Tubes. J. Eng. Mech. 2019, 145, 04019009. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comput. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Stuart, S.J.; Tutein, A.B.; Harrison, J.A. A Reactive Potential for Hydrocarbons with Intermolecular Interactions. J. Chem. Phys. 2000, 112, 6472–6486. [Google Scholar] [CrossRef]
- Song, X.; Liu, S.; Gan, Z.; Yan, H.; Ai, Y. Contact Configuration Modification at Carbon Nanotube-Metal Interface during Nanowelding. J. Appl. Phys. 2009, 106, 124308. [Google Scholar] [CrossRef]
- Thamaraikannan, S.; Pradhan, S.C. Atomistic Study of Carbon Nanotubes: Effect of Cut-Off Distance. In TMS 2016: 145th Annual Meeting & Exhibition: Supplemental Proceedings; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2016. [Google Scholar]
- Eringen, A.C. On Differential Equations of Nonlocal Elasticity and Solutions of Screw Dislocation and Surface Waves. J. Appl. Phys. 1983, 54, 4703–4710. [Google Scholar] [CrossRef]
- Claeyssen, J.R.; Tsukazan, T.; Coppeti, R.D. Nonlocal Effects in Modal Analysis of Forced Responses with Single Carbon Nanotubes. Mech. Syst. Signal Process. 2013, 38, 299–311. [Google Scholar] [CrossRef]
- Golub, G.H.; Welsch, J.H. Calculation of Gauss Quadrature Rules. Math. Comput. 1969, 23, 221–230. [Google Scholar] [CrossRef]
- Stukowski, A. Visualization and Analysis of Atomistic Simulation Data with OVITO-the Open Visualization Tool. Model. Simul. Mater. Sci. Eng. 2010, 18, 015012. [Google Scholar] [CrossRef]
- Shimizu, F.; Ogata, S.; Li, J. Theory of Shear Banding in Metallic Glasses and Molecular Dynamics Calculations. Mater. Trans. 2007, 48, 2923–2927. [Google Scholar] [CrossRef]
- Falk, M.L.; Langer, J.S. Dynamics of Viscoplastic Deformation in Amorphous Solids. Phys. Rev. E—Stat. Phys. Plasmas Fluids Relat. Interdiscip. Top. 1998, 57, 7192–7205. [Google Scholar] [CrossRef]
- Zhou, M. A New Look at the Atomic Level Virial Stress: On Continuum-Molecular System Equivalence. Proc. R. Soc. A Math. Phys. Eng. Sci. 2003, 459, 2347–2392. [Google Scholar] [CrossRef]
- Ewins, D.J. Modal Testing: Theory, Practice and Application, 2nd ed.; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Eringen, A.C. Nonlocal Polar Elastic Continua. Int. J. Eng. Sci. 1972, 10, 1–16. [Google Scholar] [CrossRef]
- Wang, Q. Wave Propagation in Carbon Nanotubes via Nonlocal Continuum Mechanics. J. Appl. Phys. 2005, 98, 124301. [Google Scholar] [CrossRef]

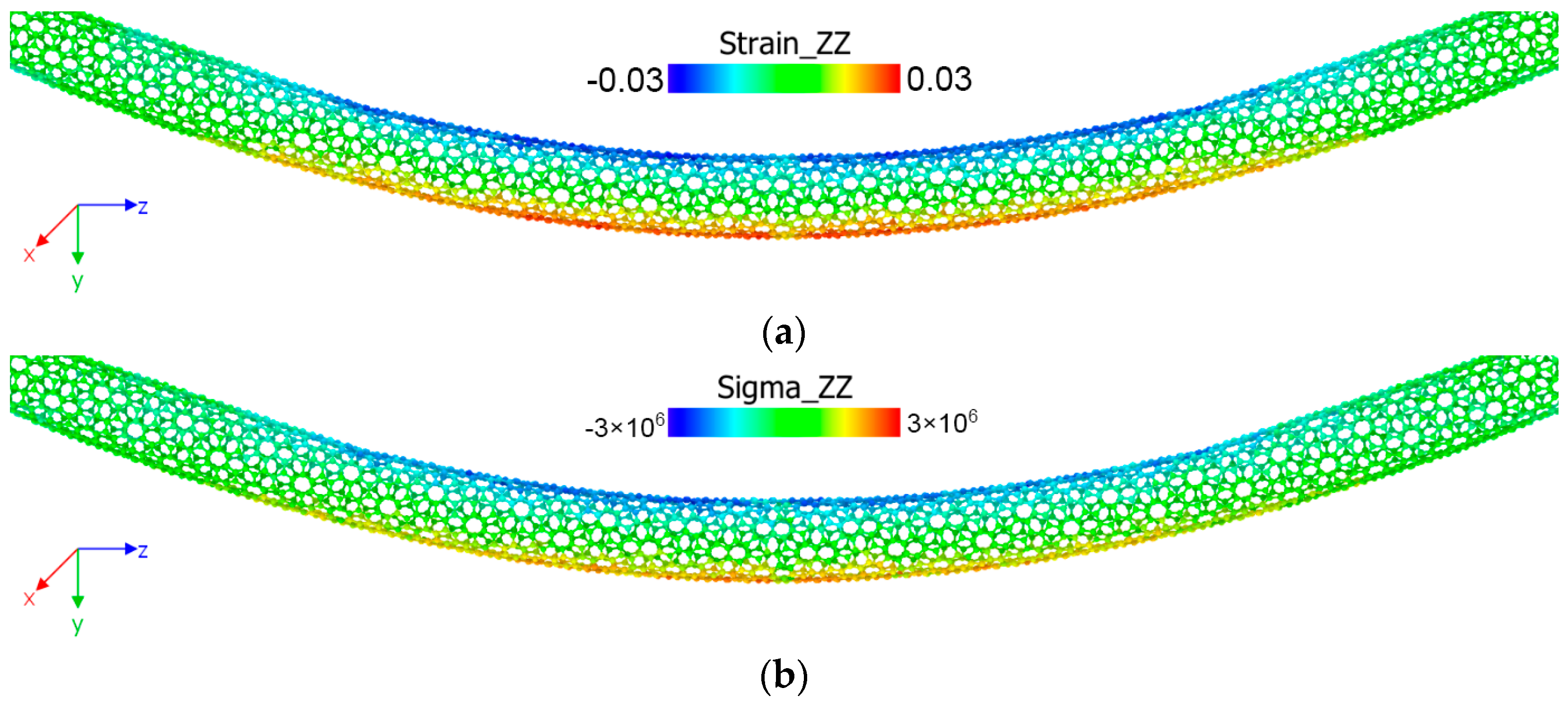
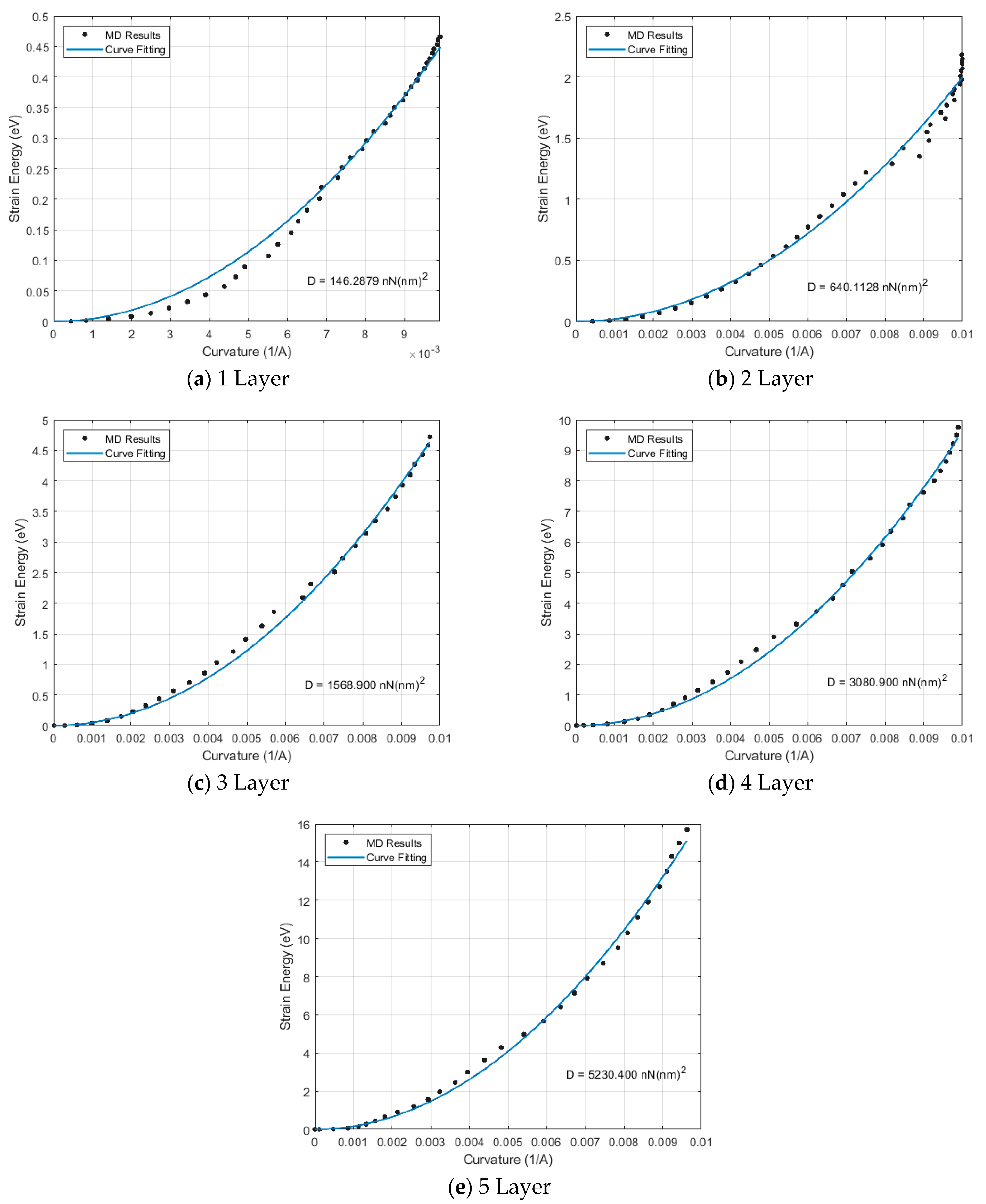
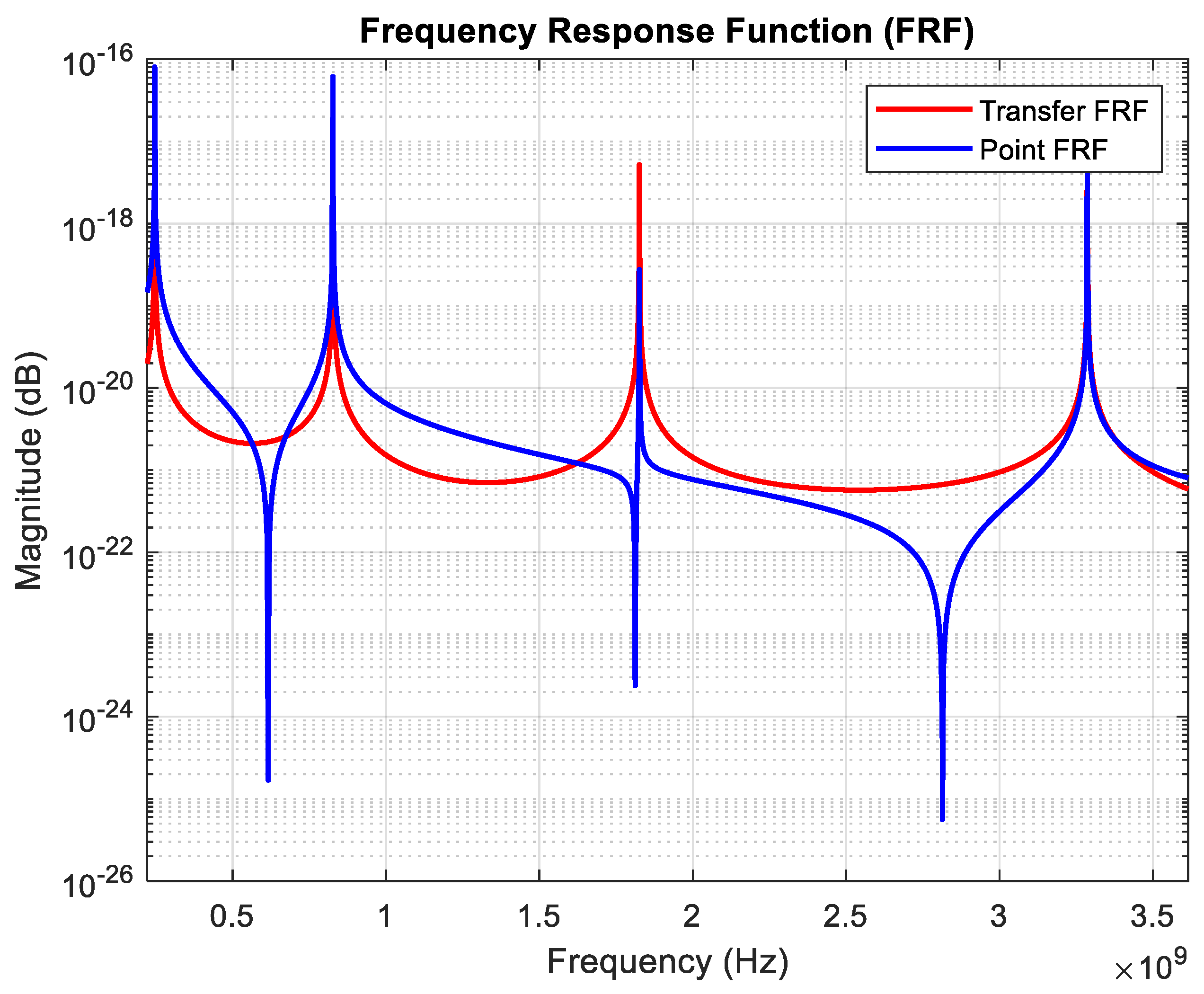
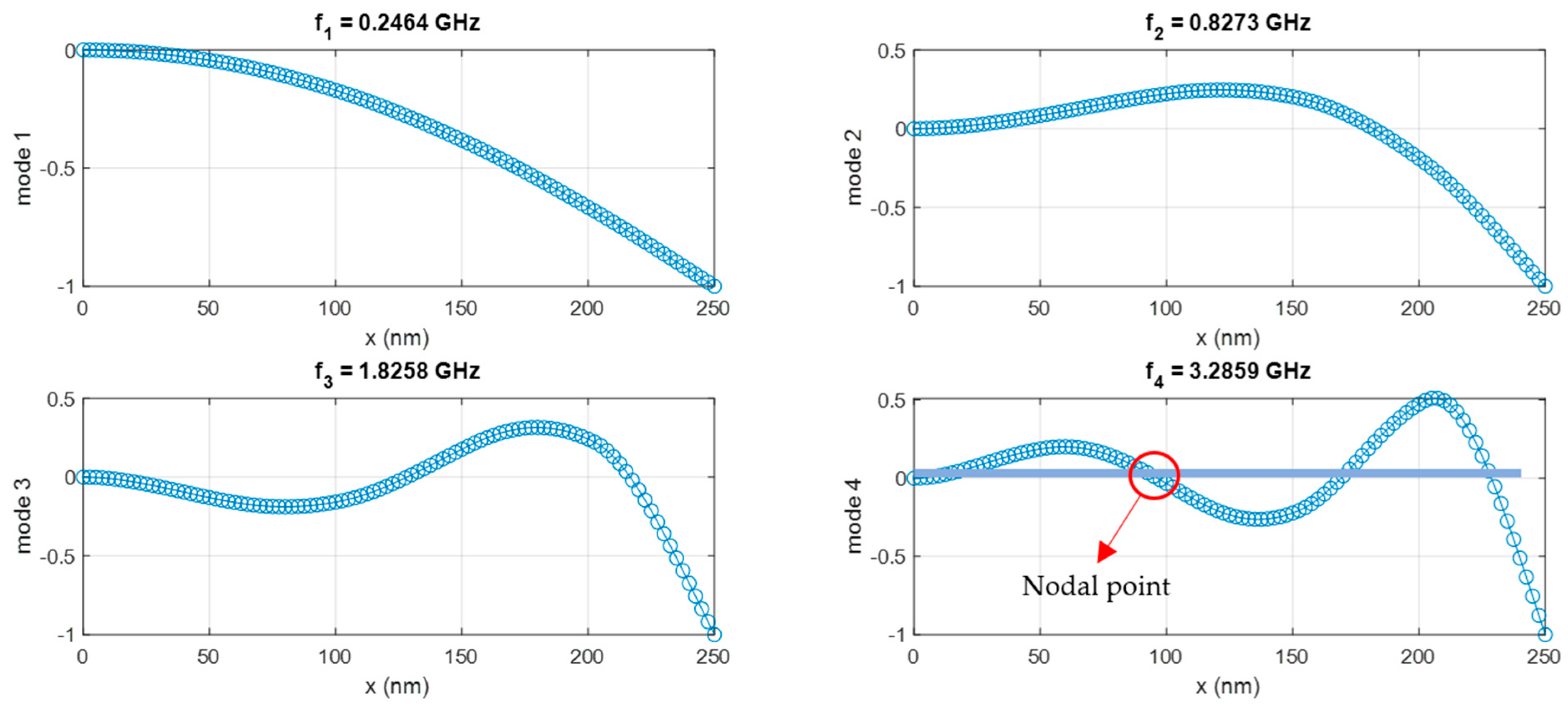


| Model Name | Chirality Vectors | Number of Atoms | Length (nm) | Diameter (Å) [25] | Area (Å2) [25] |
|---|---|---|---|---|---|
| 1 Layer | (5, 10) | 6220 | 50 | 10.36392 | 84.360198 |
| 2 Layer | (5, 10)/(10, 15) | 16,470 | 50 | 17.07464 | 144.61748 |
| 3 Layer | (5, 10)/(10, 15)/(15, 20) | 30,770 | 50 | 23.82734 | 361.54370 |
| 4 Layer | (5, 10)/(10, 15)/(15, 20)/(20, 25) | 49,130 | 50 | 30.59424 | 650.77867 |
| 5 Layer | (5, 10)/(10, 15)/(15, 20)/(20, 25)/(25, 30) | 71,560 | 50 | 37.36762 | 1012.3223 |
| Model Name | Bending Stiffness (EI) | Density (ρ) | |
|---|---|---|---|
| eVÅ | nN (nm)2 | kg/m3 | |
| 1 Layer | 9131.300 | 146.288 | 2938.414 |
| 2 Layer | 39,956.000 | 640.113 | 4538.715 |
| 3 Layer | 97,930.000 | 1568.900 | 3391.773 |
| 4 Layer | 192,310.000 | 3080.900 | 3008.663 |
| 5 Layer | 326,480.000 | 5230.400 | 2817.161 |
| Mode Number | Natural Frequencies (GHz) |
|---|---|
| 1 | 0.246 |
| 2 | 0.827 |
| 3 | 1.826 |
| 4 | 3.286 |
| Mode Number | (μ/L) = 0 | (μ/L) = 0.5 | (μ/L) = 1.0 | (μ/L) = 1.5 | (μ/L) = 2.0 |
|---|---|---|---|---|---|
| 1 | 2.33 × 108 | 2.22 × 108 | 1.97 × 108 | 1.70 × 108 | 1.45 × 108 |
| 2 | 1.07 × 109 | 9.00 × 108 | 6.56 × 108 | 4.91 × 108 | 3.87 × 108 |
| 3 | 2.41 × 109 | 1.70 × 109 | 1.08 × 109 | 7.61 × 108 | 5.83 × 108 |
| 4 | 4.35 × 109 | 2.61 × 109 | 1.54 × 109 | 1.07 × 109 | 8.13 × 108 |
| 5 | 7.00 × 109 | 3.82 × 109 | 2.17 × 109 | 1.49 × 109 | 1.12 × 108 |
| Mode Number | (μ/L) = 0 | (μ/L) = 0.5 | (μ/L) = 1.0 | (μ/L) = 1.5 | (μ/L) = 2.0 |
|---|---|---|---|---|---|
| 1 | 6.02 × 108 | 5.68 × 108 | 4.93 × 108 | 4.14 × 108 | 3.49 × 108 |
| 2 | 1.66 × 109 | 1.37 × 109 | 9.80 × 108 | 7.27 × 108 | 5.69 × 108 |
| 3 | 3.23 × 109 | 2.24 × 109 | 1.40 × 109 | 9.92 × 108 | 7.63 × 108 |
| 4 | 5.37 × 109 | 3.07 × 109 | 1.79 × 109 | 1.24 × 109 | 9.46 × 108 |
| 5 | 8.45 × 109 | 4.46 × 109 | 2.52 × 109 | 1.72 × 109 | 1.30 × 109 |
| Mode Number | (μ/L) = 0 | (μ/L) = 0.5 | (μ/L) = 1.0 | (μ/L) = 1.5 | (μ/L) = 2.0 |
|---|---|---|---|---|---|
| 1 | 4.83 × 108 | 4.56 × 108 | 3.96 × 108 | 3.32 × 108 | 2.79 × 108 |
| 2 | 1.40 × 109 | 1.15 × 109 | 8.12 × 108 | 6.00 × 108 | 4.70 × 108 |
| 3 | 2.86 × 109 | 1.97 × 109 | 1.24 × 109 | 8.77 × 108 | 6.76 × 108 |
| 4 | 4.95 × 109 | 2.93 × 109 | 1.74 × 109 | 1.22 × 109 | 9.29 × 108 |
| 5 | 7.61 × 109 | 4.03 × 109 | 2.24 × 109 | 1.52 × 109 | 1.15 × 109 |
| Mode Number | (μ/L) = 0 | (μ/L) = 0.5 | (μ/L) = 1.0 | (μ/L) = 1.5 | (μ/L) = 2.0 |
|---|---|---|---|---|---|
| 1 | 2.46 × 108 | 2.36 × 108 | 2.10 × 108 | 1.80 × 108 | 1.54 × 108 |
| 2 | 8.27 × 108 | 7.01 × 108 | 5.13 × 108 | 3.87 × 108 | 3.08 × 108 |
| 3 | 1.83 × 109 | 1.31 × 109 | 8.48 × 108 | 6.13 × 108 | 4.77 × 108 |
| 4 | 3.29 × 109 | 2.02 × 109 | 1.24 × 109 | 8.77 × 108 | 6.76 × 108 |
| 5 | 5.37 × 109 | 2.94 × 109 | 1.74 × 109 | 1.22 × 109 | 9.29 × 108 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yildiz, Y.O.; Sen, M.; Yigid, O.; Huseyinoglu, M.; Kara, S.E. Vibration Analysis of Multilayer Stepped Cross-Sectional Carbon Nanotubes. Nanomaterials 2025, 15, 1550. https://doi.org/10.3390/nano15201550
Yildiz YO, Sen M, Yigid O, Huseyinoglu M, Kara SE. Vibration Analysis of Multilayer Stepped Cross-Sectional Carbon Nanotubes. Nanomaterials. 2025; 15(20):1550. https://doi.org/10.3390/nano15201550
Chicago/Turabian StyleYildiz, Yunus Onur, Murat Sen, Osman Yigid, Mesut Huseyinoglu, and Sertac Emre Kara. 2025. "Vibration Analysis of Multilayer Stepped Cross-Sectional Carbon Nanotubes" Nanomaterials 15, no. 20: 1550. https://doi.org/10.3390/nano15201550
APA StyleYildiz, Y. O., Sen, M., Yigid, O., Huseyinoglu, M., & Kara, S. E. (2025). Vibration Analysis of Multilayer Stepped Cross-Sectional Carbon Nanotubes. Nanomaterials, 15(20), 1550. https://doi.org/10.3390/nano15201550






