Negative Differential Conductance Induced by Majorana Bound States Side-Coupled to T-Shaped Double Quantum Dots
Abstract
1. Introduction
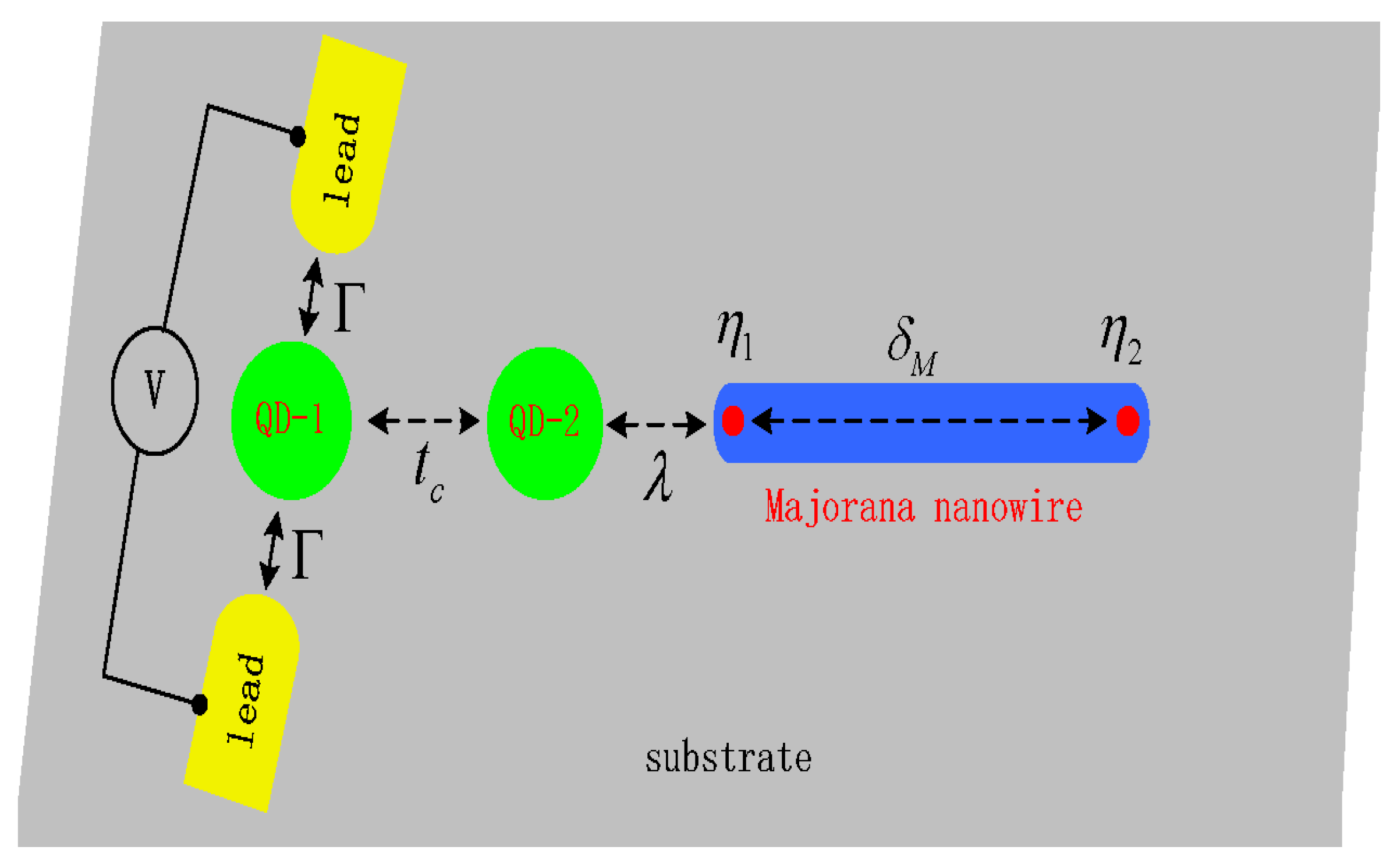
2. Model and Method
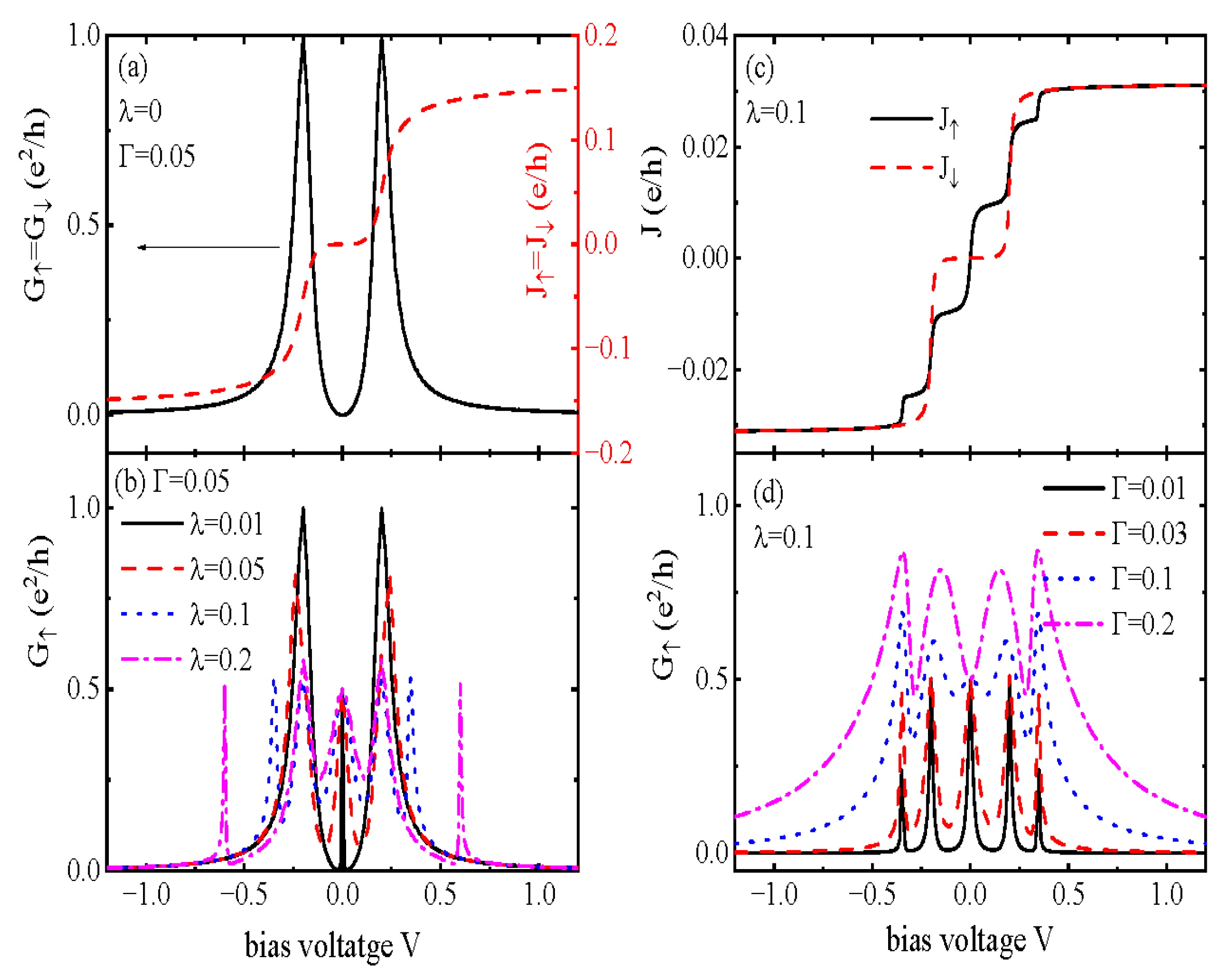
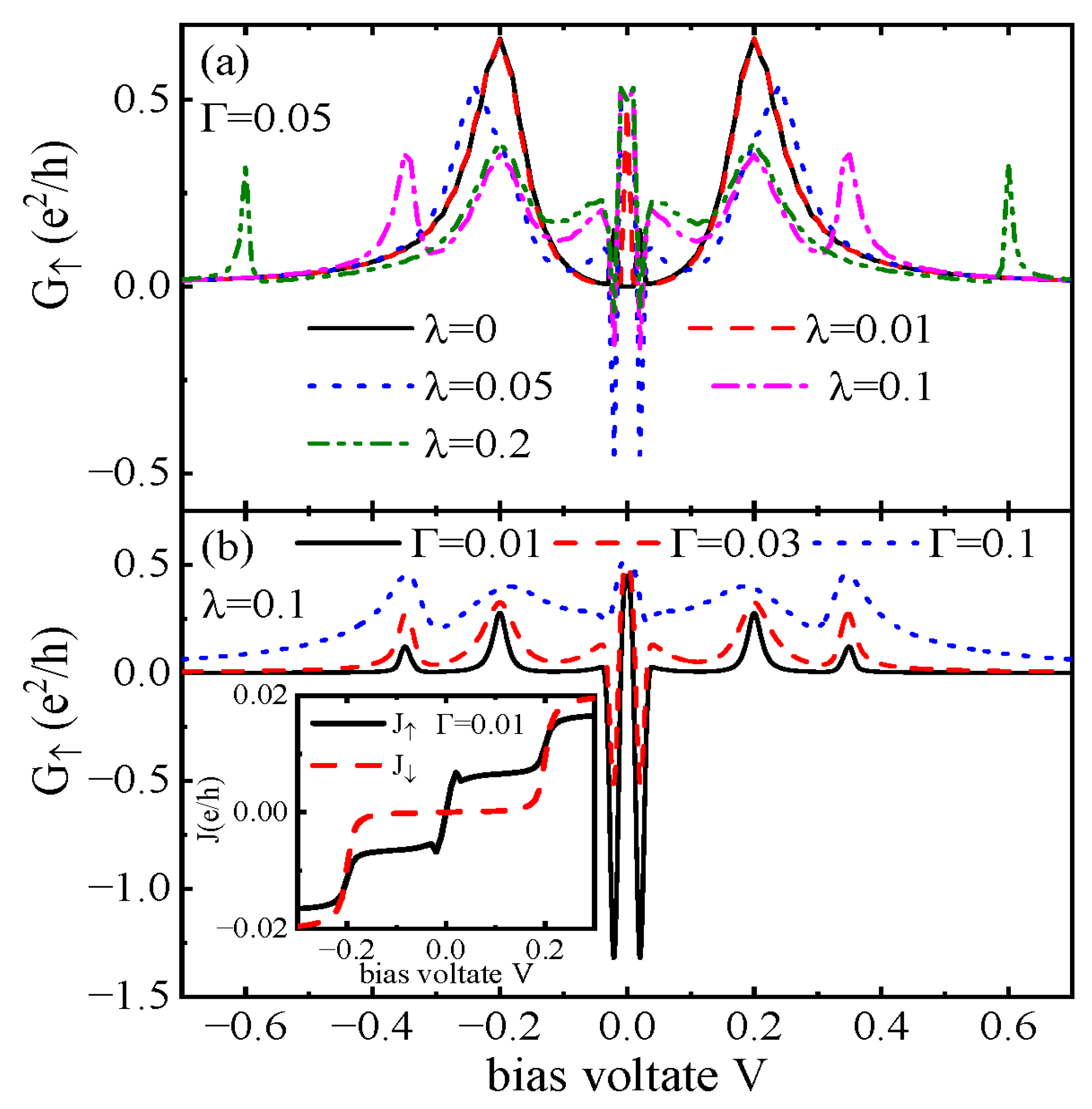
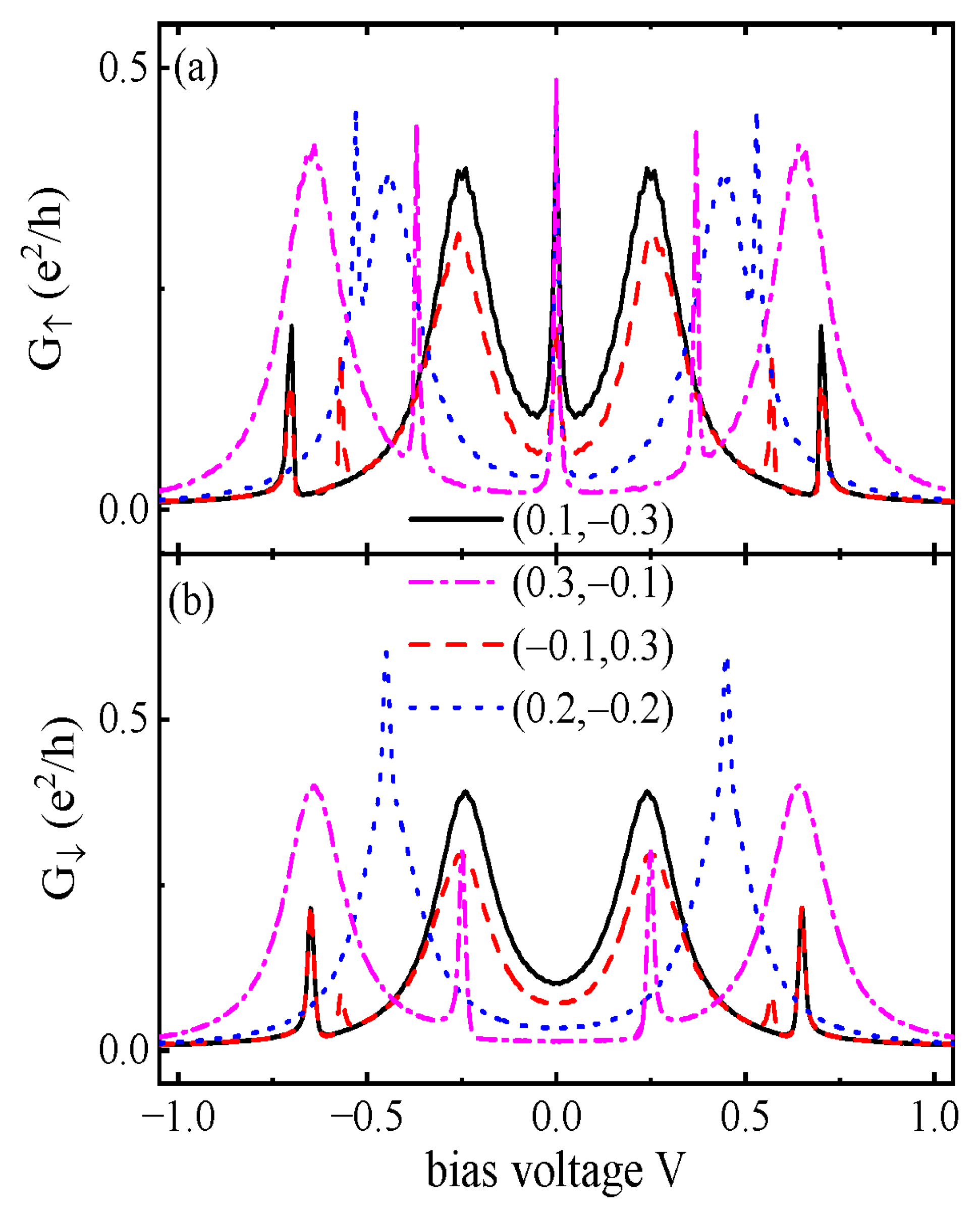
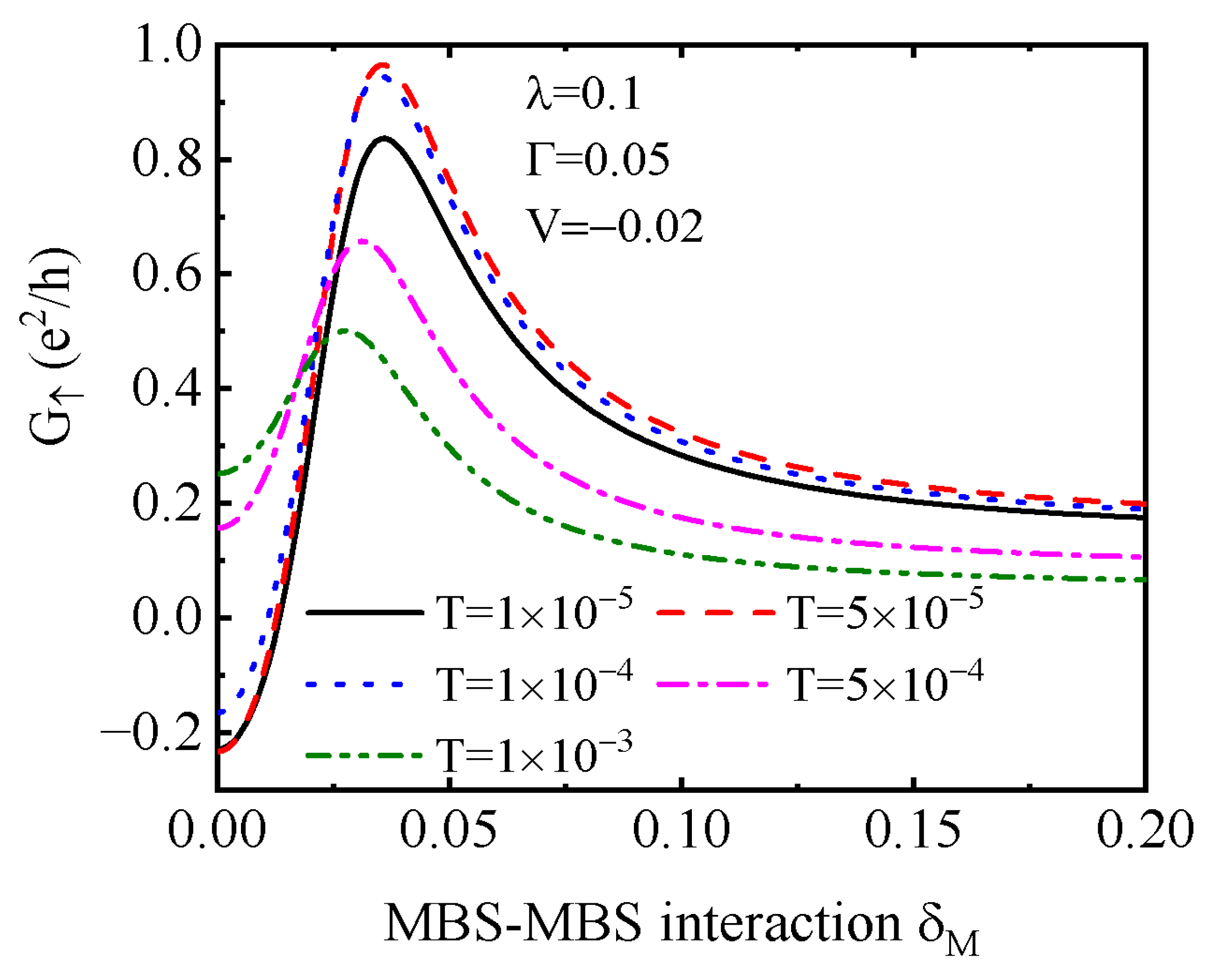
3. Numerical Results
4. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kitaev, A.Y. Unpaired Majorana fermions in quantum wires. Phys.-Usp. 2001, 44, 131–136. [Google Scholar] [CrossRef]
- Qi, X.L.; Zhang, S.C. Topological insulators and superconductors. Rev. Mod. Phys. 2011, 83, 1057. [Google Scholar] [CrossRef]
- Sharma, M.M.; Sharma, P.; Karn, N.K.; Awana, V.P.S. Comprehensive review on topological superconducting materials and interfaces. Supercond. Sci. Technol. 2022, 35, 083003. [Google Scholar] [CrossRef]
- Alicea, J.; Oreg, Y.; Refael, G.; von Oppen, F.; Fisher, M.P.A. Non-abelian statistics and topological quantum information processing in 1d wire networks. Nat. Phys. 2011, 7, 412–417. [Google Scholar] [CrossRef]
- Lian, B.; Sun, X.Q.; Vaezi, A.; Qi, X.L.; Zhang, S.C. Topological quantum computation based on chiral Majorana fermions. Proc. Natl. Acad. Sci. USA 2018, 115, 10938–10942. [Google Scholar] [CrossRef] [PubMed]
- Mourik, V.; Zuo, K.; Frolov, S.M.; Plissard, S.R.; Bakkers, E.P.A.M.; Kouwenhoven, L.P. Signatures of Majorana fermions in hybrid superconductor-semiconductor nanowire devices. Science 2012, 336, 1003–1007. [Google Scholar] [CrossRef] [PubMed]
- Deng, M.T.; Yu, C.L.; Huang, G.Y.; Larsson, M.; Caroff, P.; Xu, H.Q. Anomalous Zero-Bias Conductance Peak in a Nb-InSb Nanowire-Nb Hybrid Device. Nano Lett. 2012, 12, 6414–6419. [Google Scholar] [CrossRef] [PubMed]
- Rokhinson, L.; Liu, X.; Furdyna, J. The fractional a.c. Josephson effect in a semiconductor-superconductor nanowire as a signature of Majorana particles. Nat. Phys. 2012, 8, 795–799. [Google Scholar] [CrossRef]
- Fu, L.; Kane, C.L. Superconducting Proximity Effect and Majorana Fermions at the Surface of a Topological Insulator. Phys. Rev. Lett. 2008, 100, 096407. [Google Scholar] [CrossRef]
- Xu, J.-P.; Wang, M.-X.; Liu, Z.L.; Ge, J.-F.; Yang, X.; Liu, C.; Xu, Z.A.; Guan, D.; Gao, C.L.; Qian, D.; et al. Experimental detection of a Majorana mode in the core of a magnetic vortex inside a topological insulator-superconductor Bi2Te3/NbSe2 heterostructure. Phys. Rev. Lett. 2015, 114, 017001. [Google Scholar] [CrossRef]
- Sau, J.D.; Lutchyn, R.M.; Tewari, S.; Das Sarma, S. Generic new platform for topological quantum computation using semiconductor heterostructures. Phys. Rev. Lett. 2010, 104, 040502. [Google Scholar] [CrossRef]
- Hosur, P.; Ghaemi, P.; Mong, R.S.K.; Vishwanath, A. Majorana modes at the ends of superconductor vortices in doped topological insulators. Phys. Rev. Lett. 2011, 107, 097001. [Google Scholar] [CrossRef]
- Wang, D.; Kong, L.; Fan, P.; Chen, H.; Zhu, S.; Liu, W.; Cao, L.; Sun, Y.; Du, S.; Schneeloch, J.; et al. Evidence for Majorana bound states in an iron-based superconductor. Science 2018, 362, 333–335. [Google Scholar] [CrossRef]
- Das Sarma, S.; Freedman, M.; Nayak, C. Topologically protected qubits from a possible non-Abelian fractional quantum Hall state. Phys. Rev. Lett. 2005, 94, 166802. [Google Scholar] [CrossRef] [PubMed]
- Liu, T.T.; Wan, C.Y.; Yang, H.; Zhao, Y.; Xie, B.; Zheng, W.; Yi, Z.; Guan, D.; Wang, S.; Zheng, H.; et al. Signatures of hybridization of multiple Majorana zero modes in a vortex. Nature 2024, 633, 71–76. [Google Scholar] [CrossRef] [PubMed]
- Vaitiekenas, S.; Winkler, G.W.; van Heck, B.; Karzig, T.; Deng, M.-T.; Flensberg, K.; Glazman, L.I.; Nayak, C.; Krogstrup, P.; Lutchyn, R.M.; et al. Flux-induced topological superconductivity in full-shell nanowires. Science 2020, 367, 3392. [Google Scholar] [CrossRef] [PubMed]
- Pan, X.H.; Chen, L.; Liu, D.E.; Zhang, F.C.; Liu, X. Majorana Zero Modes Induced by the Meissner Effect at Small Magnetic Field. Phys. Rev. Lett. 2024, 132, 036602. [Google Scholar] [CrossRef]
- Laroche, D.; Bouman, D.; van Woerkom, D.J.; Proutski, A.; Murthy, C.; Pikulin, D.I.; Nayak, C.; van Gulik, R.J.J.; Nygard, J.; Krogstrup, P.; et al. Observation of the 4π-periodic Josephson effect in indium arsenide nanowires. Nat. Commun. 2019, 10, 245. [Google Scholar] [CrossRef]
- Lopez, R.; Lee, M.; Serra, L.; Lim, J. Thermoelectrical detection of majorana states. Phys. Rev. B 2014, 89, 205418. [Google Scholar] [CrossRef]
- Chi, F.; Fu, Z.G.; Liu, J.; Li, K.; Wang, Z.; Zhang, P. Thermoelectric effect in a quantum dot side-coupled to majorana bound states. Nanoscale Res. Lett. 2020, 15, 79. [Google Scholar] [CrossRef]
- Hong, L.; Chi, F.; Fu, Z.G.; Hou, Y.F.; Wang, Z.; Li, K.M.; Liu, J.; Yao, H.; Zhang, P. Large enhancement of thermoelectric effect by majorana bound states coupled to a quantum dot. J. Appl. Phys. 2020, 127, 124302. [Google Scholar] [CrossRef]
- Chi, F.; Liu, J.; Fu, Z.G.; Yi, Z.C.; Liu, L.M. Nonlinear Seebeck and Peltier effects in a Majorana nanowire coupled to leads. Chin. Phys. B. 2024, 33, 077301. [Google Scholar] [CrossRef]
- Klees, R.L.; Gresta, D.; Sturm, J.; Molenkamp, L.W.; Hankiewicz, E.M. Majorana-mediated thermoelectric transport in multiterminal junctions. Phys. Rev. B 2024, 110, 064517. [Google Scholar] [CrossRef]
- Chen, H.J.; Zhu, K.D. All-optical scheme for detecting the possible Majorana signature based on QD and nanomechanical resonator systems. Sci. China Phys. Mech. Astron. 2015, 58, 050301. [Google Scholar] [CrossRef]
- Tang, H.Z.; Zhang, Y.T.; Liu, J.J. Photon-assisted tunneling through a topological superconductor with majorana bound states. Aip Adv. 2015, 5, 127129. [Google Scholar] [CrossRef]
- Chi, F.; He, T.Y.; Wang, J.; Fu, Z.G.; Liu, L.M.; Liu, P.; Zhang, P. Photon-assisted transport through a quantum Dot side-coupled to majorana bound states. Front. Phys. 2020, 8, 00254. [Google Scholar] [CrossRef]
- Dmytruk, O.; Trif, M. Microwave detection of gliding Majorana zero modes in nanowires. Phys. Rev. B 2023, 107, 115418. [Google Scholar] [CrossRef]
- Pan, H.N.; Das Sarma, S. Physical mechanisms for zero-bias conductance peaks in Majorana nanowires. Phys. Rev. Res. 2020, 2, 013377. [Google Scholar] [CrossRef]
- Howlader, S.; Mehta, N.S.; Sharma, M.M.; Awana, V.P.S.; Sheet, G. Andreev Reflection Spectroscopy on SnAs Single Crystals. J. Supercond. Nov. Magn. 2022, 35, 1839–1845. [Google Scholar] [CrossRef]
- van der Wiel, W.G.; Franceschi, S.D. Elzerman, J.M.; Fujisawa, T.; Tarucha, S.; Kouwenhoven, L.P. Electron transport through double quantum dots. Rev. Mod. Phys. 2003, 75, 1. [Google Scholar] [CrossRef]
- Liu, D.E.; Baranger, H.U. Detecting a majorana-fermion zero mode using a quantum dot. Phys. Rev. B 2011, 84, 201308R. [Google Scholar] [CrossRef]
- Deng, M.T.; Vaitiekenas, S.; Hansen, E.B.; Danon, J.; Leijnse, M.; Flensberg, K.; Nygard, J.; Krogstrup, P.; Marcus, C.M. Majorana bound state in a coupled quantum-dot hybrid-nanowire system. Science 2016, 354, 1557–1562. [Google Scholar] [CrossRef]
- Das Sarma, S. In search of Majorana. Nat. Phys. 2023, 19, 165–170. [Google Scholar] [CrossRef]
- Yazdani, A.; von Oppen, F.; Halperin, B.I.; Yacoby, A. Hunting for Majoranas. Science 2023, 380, 0850. [Google Scholar] [CrossRef]
- Prada, E.; Aguado, R.; San-Jose, P. Measuring Majorana nonlocality and spin structure with a quantum dot. Phys. Rev. B 2017, 96, 085418. [Google Scholar] [CrossRef]
- Zhao, H.J.; Wang, J.R.; Mao, H.; Jin, J.S. Distinguishing Majorana bound states from Andreev bound states through differential conductance and current noise spectrum. New J. Phys. 2025, 27, 023006. [Google Scholar] [CrossRef]
- Gong, W.J.; Zhang, S.F.; Li, Z.C.; Yi, G.Y.; Zheng, Y.S. Detection of a Majorana-fermion zero mode by a T-shaped quantum-dot structure. Phys. Rev. B 2014, 89, 245413. [Google Scholar] [CrossRef]
- Ivanov, T.I. Coherent tunneling through a double quantum dot coupled to Majorana bound states. Phys. Rev. B 2017, 96, 035417. [Google Scholar] [CrossRef]
- Majek, P.; Gorski, G.; Domanski, T.; Weymann, I. Hallmarks of Majorana mode leaking into a hybrid double quantum dot. Phys. Rev. B 2022, 106, 155123. [Google Scholar] [CrossRef]
- Aksenov, S.V. Probing Majorana bound states through an inhomogeneous Andreev double dot interferometer. Phys. Rev. B 2023, 107, 085417. [Google Scholar] [CrossRef]
- Pino, D.M.; Souto, R.S.; Aguado, R. Minimal Kitaev-transmon qubit based on double quantum dots. Phys. Rev. B 2024, 109, 075101. [Google Scholar] [CrossRef]
- Murugan, B.; Lee, S.Y. Two-dimensional materials based on negative differential transconductance and negative differential resistance for the application of multi valued logic circuit: A review. Carbon Lett. 2023, 33, 59–76. [Google Scholar] [CrossRef]
- Fransson, J. Theory of current-voltage asymmetries in double quantum dots. Phys. Rev. B 2004, 69, 201304(R). [Google Scholar] [CrossRef]
- Chi, F.; Li, S.S. Current voltage characteristics in strongly correlated double quantum dots. J. Appl. Phys. 2005, 97, 123704. [Google Scholar] [CrossRef]
- Perrin, M.L.; Frisenda, R.; Koole, M.; Seldenthuis, J.S.; Gil, J.A.C.; Valkenier, H.; Hummelen, J.C.; Renaud, N.; Grozema, F.C.; Thijssen, J.M.; et al. Large negative differential conductance in single-molecule break junctions. Nat. Nanotechnol. 2014, 9, 830–834. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Astier, H.P.A.G.; Nickle, C.; Soni, S.; Alami, F.A.; Borrini, A.; Zhang, Z.; Honnigfort, C.; Braunschweig, B.; et al. Dynamic molecular switches with hysteretic negative differential conductance emulating synaptic behaviour. Nat. Mater. 2022, 21, 1403–1411. [Google Scholar] [CrossRef]
- Han, K.H.; Kim, S.H.; Kim, S.G.; Kim, J.H.; Song, S.; Yu, H.Y. Charge transfer mechanism for realization of double negative differential transconductance. NPJ 2D Mater. Appl. 2024, 8, 15. [Google Scholar] [CrossRef]
- Yang, K.H.; Guo, H.W.; Wang, H.Y.; Wei, Z.J.; Liang, X.H. Controllable antiresonance and low-bias negative differential conductance in T-shaped double dots with electron-phonon interaction. Phys. E Low Dimens. Syst. Nanostruct. 2024, 163, 116014. [Google Scholar] [CrossRef]
- Wu, B.H.; Cao, J.C. Ahn, K.H. Transport through a strongly correlated quantum dot with Fano interference. Phys. Rev. B 2005, 72, 165313. [Google Scholar] [CrossRef]
- Güçlü, A.D.; Sun, Q.F.; Guo, H. Kondo resonance in a quantum dot molecule. Phys. Rev. B 2002, 68, 245323. [Google Scholar] [CrossRef]
- Wójcik, K.P.; Weymann, I. Two-stage Kondo effect in T-shaped double quantum dots with ferromagnetic leads. Phys. Rev. B 2012, 91, 134422. [Google Scholar] [CrossRef]
- Wójcik, K.P.; Weymann, I. Strong spin Seebeck effect in Kondo T-shaped double quantum dots. J. Phys. Condens. Matter 2017, 29, 055303. [Google Scholar] [CrossRef]
- Gong, W.J.; Zheng, Y.S.; Liu, Y.; Kariuki, F.N.; Lü, T.Q. Fano effect in a T-shaped double quantum dot structure in the presence of Rashba spin-Corbit coupling. Phys. Lett. A 2008, 372, 2934–2940. [Google Scholar] [CrossRef]
- Brown, K.; Crisan, M.; Ţifrea, I. Transport and current noise characteristics of a T-shape double-quantum-dot system. J. Phys. Condens. Matter 2009, 21, 215604. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Gómez-Silva, G.; Orellana, P.A.; Anda, E.V. Enhancement of the thermoelectric efficiency in a T-shaped quantum dot system in the linear and nonlinear regimes. J. Appl. Phys. 2018, 123, 085706. [Google Scholar] [CrossRef]
- Li, Y.X.; Choi, H.Y.; Lee, H.W.; Liu, J.J. Andreev reflection with spin-flip scattering through a T-shaped double quantum dot. J. Appl. Phys. 2007, 101, 103918. [Google Scholar] [CrossRef]
- Bai, L.; Zhang, Z.Z.; Jiang, L.; Tang, F.R. Spin accumulation and spin-dependent Andreev reflection current in a T-shaped double quantum dots. Phys. E 2010, 43, 446–451. [Google Scholar] [CrossRef]
- Barańskij, J.; Domanski, T. Decoherence effect on Fano line shapes in double quantum dots coupled between normal and superconducting leads. Phys. Rev. B 2012, 85, 205451. [Google Scholar] [CrossRef]
- Cheng, S.G.; Sun, Q.F. Josephson current transport through T-shaped double quantum dots. J. Phys. Condens. Matter 2008, 20, 505202. [Google Scholar] [CrossRef]
- Kumar, B.; Verma, S.; Ajay. Josephson and thermophase effect in interacting T-shaped double quantum dots system. Phys. E Low Dimens. Syst. Nanostruct. 2025, 66, 116142. [Google Scholar] [CrossRef]
- Li, Y.X.; Bai, Z.M. Tunneling transport through multi-quantum-dot with Majorana bound states. J. Appl. Phys. 2013, 114, 033703. [Google Scholar] [CrossRef]
- Weymann, I.; Wójcik, K.P.; Majek, P. Majorana-Kondo interplay in T-shaped double quantum dots. Phys. Rev. B 2020, 101, 235404. [Google Scholar] [CrossRef]
- Majek, P.; Wójcik, K.P.; Weymann, I. Spin-resolved thermal signatures of Majorana-Kondo interplay in double quantum dots. Phys. Rev. B 2022, 105, 075418. [Google Scholar] [CrossRef]
- Majek, P.; Weymann, I. Spin-selective transport in a correlated double quantum dot-Majorana wire system. Sci. Rep. 2024, 14, 17762. [Google Scholar] [CrossRef]
- Flensberg, K. Tunneling characteristics of a chain of Majorana bound states. Phys. Rev. B 2010, 82, 180516R. [Google Scholar] [CrossRef]
- Souza, F.M.; Egues, J.C.; Jauho, A.P. Quantum dot as a spin-current diode: A master-equation approach. Phys. Rev. B 2007, 75, 165303. [Google Scholar] [CrossRef]
- Hoffman, S.; Chevallier, D.; Loss, D.; Klinovaja, J. Spin-dependent coupling between quantum dots and topological quantum wires. Phys. Rev. B 2017, 96, 045440. [Google Scholar] [CrossRef]
- Mathe, M.; Sticlet, D.; Zarbo, L.P. Quantum transport through a quantum dot side-coupled to a Majorana bound state pair in the presence of electron-phonon interaction. Phys. Rev. B 2022, 105, 155409. [Google Scholar] [CrossRef]
- Ricco, L.S.; de Souza, M.; Figueira, M.S.; Shelykh, I.A.; Seridonio, A.C. Spin-dependent zero-bias peak in a hybrid nanowire-quantum dot system: Distinguishing isolated Majorana fermions from Andreev bound states. Phys. Rev. B 2017, 99, 155159. [Google Scholar] [CrossRef]
- Calle, A.M.; Pacheco, M.; Martins, G.B.; Apel, V.M.; Lara, G.A.; Orellana, P.A. Fano-Andreev effect in a T-shape double quantum dot in the Kondo regime. J. Phys. Condens. Matter 2017, 29, 135301. [Google Scholar] [CrossRef]
- Sharma, M.M.; Rani, P.; Awana, V.P.S. Probing the topological surface states in superconducting Sn4Au single crystal: A magneto transport study. J. Phys. Condens. Matter 2022, 34, 415701. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.-M.; Huang, Y.-F.; Chi, F.; Yi, Z.-C.; Liu, L.-M. Negative Differential Conductance Induced by Majorana Bound States Side-Coupled to T-Shaped Double Quantum Dots. Nanomaterials 2025, 15, 1359. https://doi.org/10.3390/nano15171359
Gao Y-M, Huang Y-F, Chi F, Yi Z-C, Liu L-M. Negative Differential Conductance Induced by Majorana Bound States Side-Coupled to T-Shaped Double Quantum Dots. Nanomaterials. 2025; 15(17):1359. https://doi.org/10.3390/nano15171359
Chicago/Turabian StyleGao, Yu-Mei, Yi-Fei Huang, Feng Chi, Zi-Chuan Yi, and Li-Ming Liu. 2025. "Negative Differential Conductance Induced by Majorana Bound States Side-Coupled to T-Shaped Double Quantum Dots" Nanomaterials 15, no. 17: 1359. https://doi.org/10.3390/nano15171359
APA StyleGao, Y.-M., Huang, Y.-F., Chi, F., Yi, Z.-C., & Liu, L.-M. (2025). Negative Differential Conductance Induced by Majorana Bound States Side-Coupled to T-Shaped Double Quantum Dots. Nanomaterials, 15(17), 1359. https://doi.org/10.3390/nano15171359






