Tunable Dual-Mode Resonant Excitation of Dumbbell-Shaped Structures in the Mid-Infrared Band
Abstract
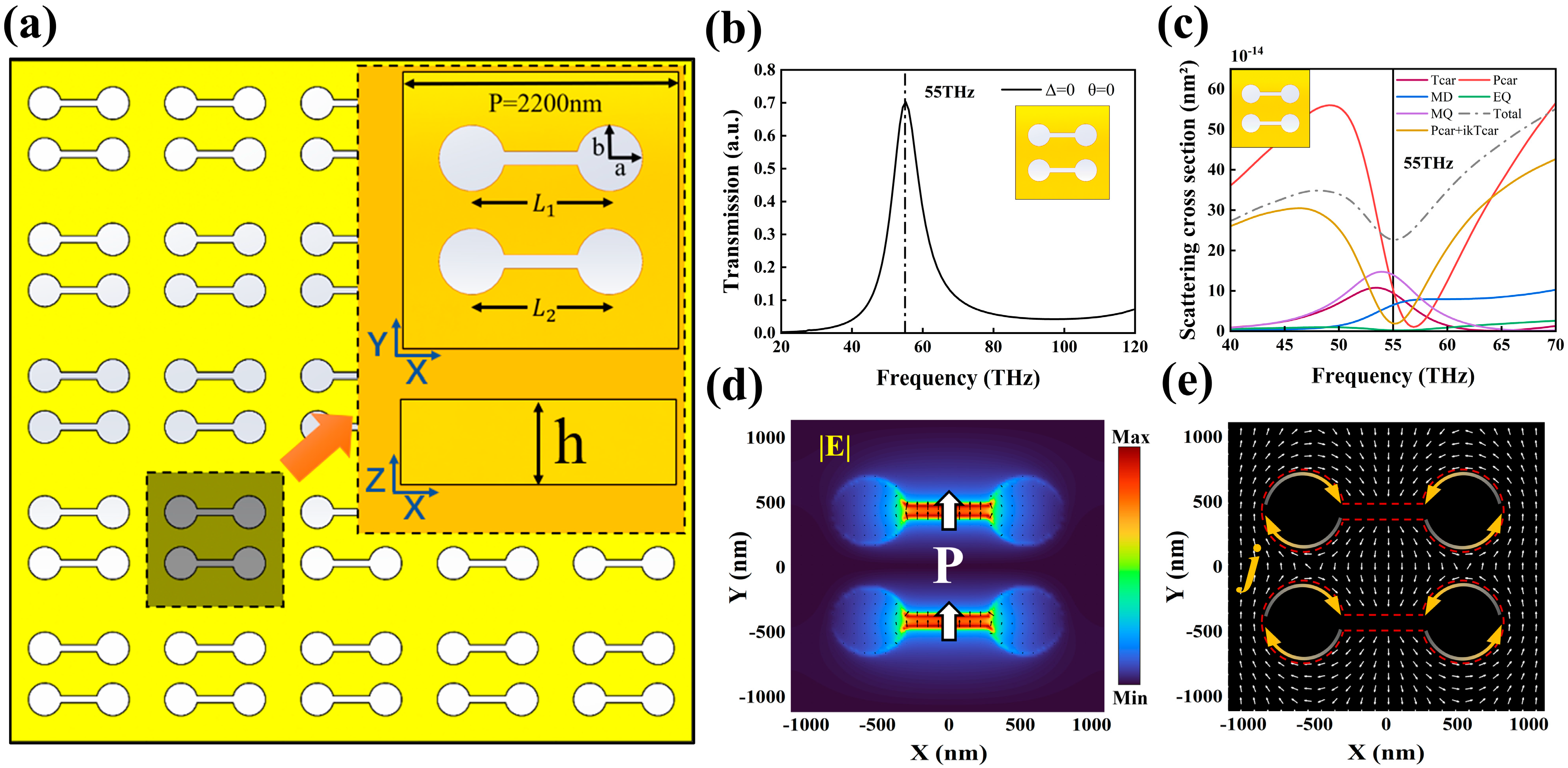
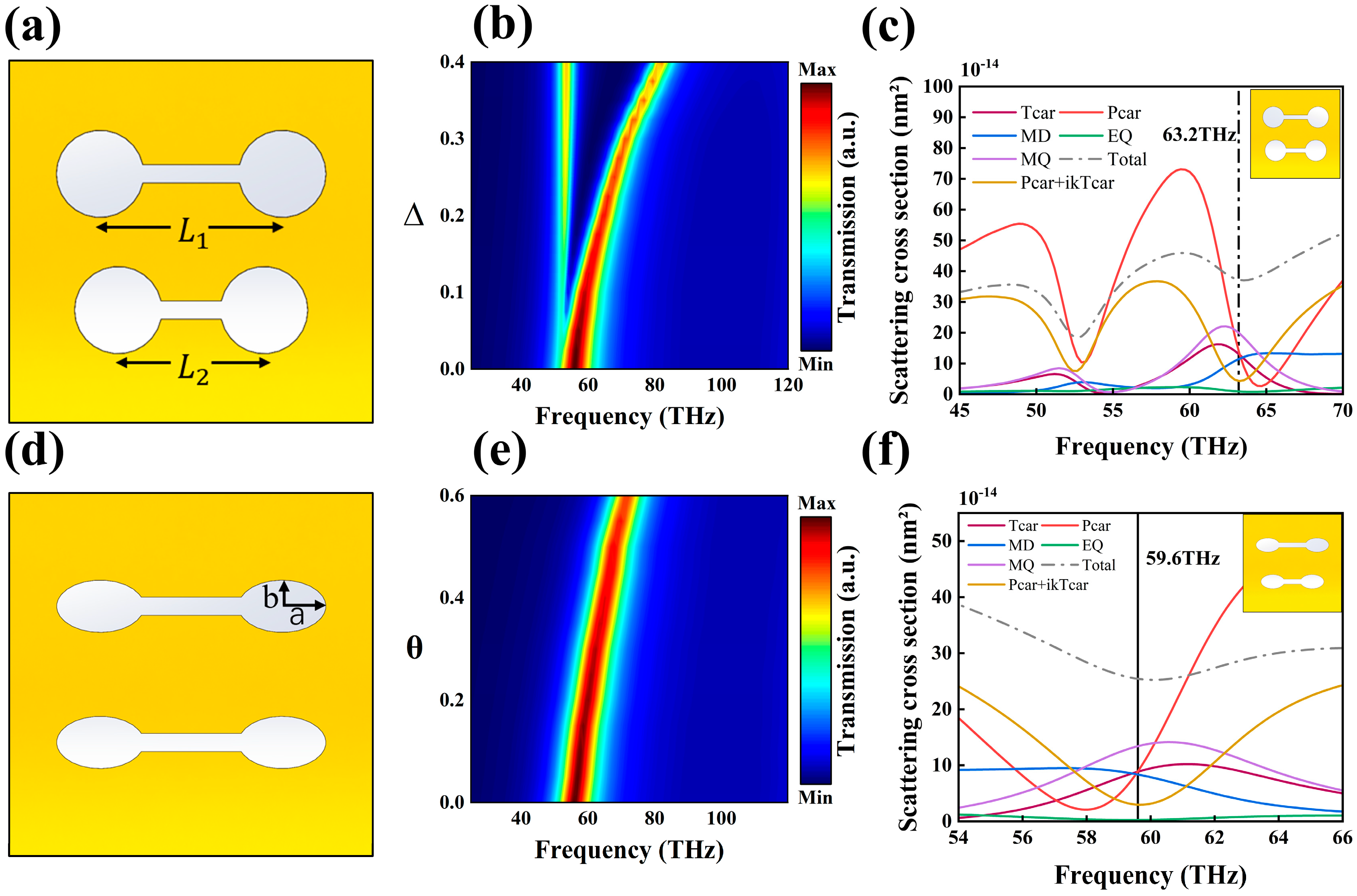
1. Introduction
2. Materials and Methods
3. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Arbabi, A.; Horie, Y.; Bagheri, M.; Faraon, A. Dielectric metasurfaces for complete control of phase and polarization with subwavelength spatial resolution and high transmission. Nat. Nanotechnol. 2015, 10, 937–943. [Google Scholar] [CrossRef]
- Yu, N.; Capasso, F. Flat optics with designer metasurfaces. Nat. Mater. 2014, 13, 139–150. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, B. Square-package arrays for efficient trapping of terahertz waves. J. Chem. Phys. 2023, 159, 014705. [Google Scholar] [CrossRef]
- Hsu, C.W.; Zhen, B.; Lee, J.; Chua, S.-L.; Johnson, S.G.; Joannopoulos, J.D.; Soljačić, M. Bound states in the continuum. Nat. Rev. Mater. 2016, 1, 16048. [Google Scholar] [CrossRef]
- Plotnik, Y.; Peleg, O.; Dreisow, F.; Heinrich, M.; Nolte, S.; Szameit, A.; Segev, M. Experimental observation of optical bound states in the continuum. Phys. Rev. Lett. 2011, 107, 183901. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Yang, W.; He, Y. Strong coupling assisted high-Q and giant chiroptical responses at near-ultraviolet frequency in planar metasurfaces. J. Chem. Phys. 2025, 162, 174704. [Google Scholar] [CrossRef] [PubMed]
- Kim, R.M.; Han, J.H.; Lee, S.M.; Kim, H.; Lim, Y.-C.; Lee, H.-E.; Ahn, H.-Y.; Lee, Y.H.; Ha, I.H.; Nam, K.T. Chiral plasmonic sensing: From the perspective of light–matter interaction. J. Chem. Phys. 2024, 160, 061001. [Google Scholar] [CrossRef]
- Xomalis, A.; Zheng, X.; Chikkaraddy, R.; Koczor-Benda, Z.; Miele, E.; Rosta, E.; Vandenbosch, G.A.E.; Martínez, A.; Baumberg, J.J. Detecting mid-infrared light by molecular frequency upconversion in dual-wavelength nanoantennas. Science 2021, 374, 1268–1271. [Google Scholar] [CrossRef]
- Hu, J.; Lang, T.; Shi, G.H. Simultaneous measurement of refractive index and temperature based on all-dielectric metasurface. Opt. Express 2017, 25, 15241–15251. [Google Scholar] [CrossRef]
- Wang, J.; Kühne, J.; Karamanos, T.; Rockstuhl, C.; Maier, S.A.; Tittl, A. All-dielectric crescent metasurface sensor driven by bound states in the continuum. Adv. Funct. Mater. 2021, 31, 2104652. [Google Scholar] [CrossRef]
- Koshelev, K.; Lepeshov, S.; Liu, M.; Bogdanov, A.; Kivshar, Y. Asymmetric metasurfaces with high-Q resonances governed by bound states in the continuum. Phys. Rev. Lett. 2018, 121, 193903. [Google Scholar] [CrossRef]
- Yang, G.; Dev, S.U.; Allen, M.S.; Allen, J.W.; Harutyunyan, H. Optical Bound States in the Continuum Enabled by Magnetic Resonances Coupled to a Mirror. Nano Lett. 2022, 22, 2001−2008. [Google Scholar] [CrossRef]
- Zhen, B.; Hsu, C.W.; Igarashi, Y.; Lu, L.; Kaminer, I.; Pick, A.; Chua, S.-L.; Joannopoulos, J.D.; Soljačić, M. Topological nature of optical bound states in the continuum. Phys. Rev. X 2014, 4, 031042. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; You, Q.; Li, J.; Zhu, C.; Zhang, L.; Yang, L.; Fang, Y.; Wang, P. Boosting light–matter interaction in a longitudinal bonding dipole plasmon hybrid anapole system. J. Phys. Chem. C 2023, 127, 3594–3601. [Google Scholar] [CrossRef]
- Miroshnichenko, A.E.; Evlyukhin, A.B.; Yu, Y.Y.F.; Bakker, R.M.; Chipouline, A.; Kuznetsov, A.I.; Luk’yanchuk, B.; Chichkov, B.N.; Kivshar, Y.S. Nonradiating anapole modes in dielectric nanoparticles. Nat. Commun. 2015, 6, 8069. [Google Scholar] [CrossRef] [PubMed]
- Terekhov, P.D.; Baryshnikova, K.V.; Greenberg, Y.; Fu, Y.H.; Evlyukhin, A.B.; Shalin, A.S.; Karabchevsky, A. Enhanced absorption in all-dielectric metasurfaces due to magnetic dipole excitation. Sci. Rep. 2019, 9, 3438. [Google Scholar] [CrossRef]
- Wu, M.; Ding, L.; Sabatini, R.P.; Sagar, L.K.; Bappi, G.; Paniagua-Domínguez, R.; Sargent, E.H.; Kuznetsov, A.I. Bound state in the continuum in nanoantenna-coupled slab waveguide enables low-threshold quantum-dot lasing. Nano Lett. 2021, 21, 9754–9760. [Google Scholar] [CrossRef]
- Li, Y.; Zhou, Y.; Liu, Q.; Lu, Z.; Luo, X.-Q.; Liu, W.-M.; Wang, X.-L. Multi-Wavelength Selective and Broadband Near-Infrared Plasmonic Switches in Anisotropic Plasmonic Metasurfaces. Nanomaterials 2023, 13, 3141. [Google Scholar] [CrossRef]
- Zograf, G.; Shalin, A.; Terekhov, P.; Makarov, A.; Krasnok, A. High-harmonic generation from resonant dielectric metasurfaces empowered by bound states in the continuum. ACS Photonics 2022, 9, 567–574. [Google Scholar] [CrossRef]
- Liu, Z.; Xiao, S.; Zhu, Z.; Hu, W.; Gong, Y.; Xu, T. High-Q quasibound states in the continuum for nonlinear metasurfaces. Phys. Rev. Lett. 2019, 123, 253901. [Google Scholar] [CrossRef]
- Moretti, G.Q.; Tittl, A.; Cortés, E.; Maier, S.A.; Bragas, A.V.; Grinblat, G. Introducing a symmetry-breaking coupler into a dielectric metasurface enables robust high-Q quasi-BICs. Adv. Photonics Res. 2022, 3, 2200111. [Google Scholar] [CrossRef]
- Sun, M.; Lin, J.; Xue, Y.; Wang, W.; Shi, S.; Zhang, S.; Shi, Y. A Terahertz Metasurface Sensor Based on Quasi-BIC for Detection of Additives in Infant Formula. Nanomaterials 2024, 14, 883. [Google Scholar] [CrossRef]
- Zito, G.; Siciliano, G.; Seifalinezhad, A.; Miranda, B.; Lanzio, V.; Schwartzberg, A.; Gigli, G.; Turco, A.; Rendina, I.; Mocella, V.; et al. Molecularly imprinted polymer sensor empowered by bound states in the continuum for selective trace-detection of TGF-beta. Adv. Sci. 2024, 11, 2401843. [Google Scholar] [CrossRef]
- Mallick, S.; Rane, S.; Acharyya, N.; Roy Chowdhury, D. Accessing dual toroidal modes in terahertz plasmonic metasurfaces through polarization-sensitive resonance hybridization. New J. Phys. 2023, 25, 053016. [Google Scholar] [CrossRef]
- Yesilkoy, F.; Arvelo, E.R.; Jahani, Y.; Liu, M.; Tittl, A.; Cevher, V.; Kivshar, Y.; Altug, H. Ultrasensitive hyperspectral imaging and biodetection enabled by dielectric metasurfaces. Nat. Photonics 2019, 13, 390–396. [Google Scholar] [CrossRef]
- Ning, T.; Li, X.; Zhang, Z.; Huo, Y.; Yue, Q.; Zhao, L.; Gao, Y. Ultimate conversion efficiency of second harmonic generation in all-dielectric resonators of quasi-BICs in consideration of nonlinear refraction of dielectrics. Opt. Express 2021, 29, 17286–17294. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Chen, Q.; Cao, X.; Ding, J.; Tang, C.; Yan, Z.; Chen, J. Excitation of Tunable Dual Quasi-Bound States in the Continuum in Graphene Metasurface and Terahertz Sensing Application. Plasmonics 2023, 18, 2285–2293. [Google Scholar] [CrossRef]
- Xin, S.; Luo, S.; Luo, Y.; Ye, L. Dual-band flexible plasmonic metasensors for ultrasensitive terahertz biomedical sensing. Sens. Actuators B Chem. 2025, 432, 137480. [Google Scholar] [CrossRef]
- Davis, T.J.; Eftekhari, F.; Gómez, D.E.; Roberts, A. Metasurfaces with asymmetric optical transfer functions for optical signal processing. Phys. Rev. Lett. 2019, 123, 013901. [Google Scholar] [CrossRef]
- Arul, R.; Grys, D.B.; Chikkaraddy, R.; Kussi, A.K.; Baumberg, J.J. Giant mid-IR resonant coupling to molecular vibrations in sub-nm gaps of plasmonic multilayer metafilms. Light Sci. Appl. 2022, 11, 281. [Google Scholar] [CrossRef]
- Paudel, Y.; Chachayma-Farfan, D.J.; Alù, A.; Sfeir, M.Y. Metasurface-enhanced photochemical activity in visible light absorbing semiconductors. J. Chem. Phys. 2024, 160, 144710. [Google Scholar] [CrossRef]
- Song, F.; Wu, X.; Liu, Y.; Yu, K. High-sensitivity multi-gas detection using dual-ridge metasurface emitters with polarization-distinguishable emission spectra. Opt. Express 2024, 32, 41244–41254. [Google Scholar] [CrossRef]
- Zong, X.; Li, L.; Liu, Y. Merging bound states in the continuum in all-dielectric metasurfaces for ultrahigh-Q resonances. Opt. Lett. 2023, 48, 5045–5048. [Google Scholar] [CrossRef]
- Wu, J.; Qing, Y.M. Strong dual-channel nonreciprocal radiation with guided mode resonances. J. Chem. Phys. 2023, 159, 224701. [Google Scholar] [CrossRef]
- Wang, Y.; Li, S.; Wang, H.; Feng, L.; Tan, B.; Tan, Y.; Su, R.; Wu, J.; Zhang, C.; Jin, B.; et al. Broadband and efficient asymmetric wavefront manipulation via terahertz polarization-selective metasurface. Appl. Phys. Lett. 2022, 121, 151701. [Google Scholar] [CrossRef]
- Yang, R.; Dai, M.; Zhao, Y.; Wang, X. Metasurface Design for Dual-Mode Sensors Based on Broken Symmetry Structure. Nanomaterials 2025, 15, 687. [Google Scholar] [CrossRef]
- Schiattarella, C.; Sanità, G.; Guilcapi Alulema, B.; Lanzio, V.; Cabrini, S.; Lamberti, A.; Rendina, I.; Mocella, V.; Zito, G.; Romano, S. High-Q photonic aptasensor based on avoided crossing bound states in the continuum and trace detection of ochratoxin A. Biosens. Bioelectron. X 2022, 12, 100262. [Google Scholar] [CrossRef]
- Wang, Y.; Han, Z.; Du, Y.; Qin, J. Ultrasensitive terahertz sensing with high-Q toroidal dipole resonance governed by bound states in the continuum in all-dielectric metasurface. Nanophotonics 2021, 10, 1295–1307. [Google Scholar] [CrossRef]
- Chen, X.; Fan, W.; Yan, H. Toroidal dipole bound states in the continuum metasurfaces for terahertz nanofilm sensing. Opt. Express 2020, 28, 17102–17112. [Google Scholar] [CrossRef] [PubMed]
- Wu, P.C.; Pala, R.A.; Shirmanesh, G.K.; Cheng, W.H.; Sokhoyan, R.; Grajower, M.; Alam, M.Z.; Lee, D.; Atwater, H.A. Dynamic beam steering with all-dielectric electro-optic III–V multiple-quantum-well metasurfaces. Nat. Commun. 2019, 10, 3654. [Google Scholar] [CrossRef]
- Sun, Y.; Chen, Y.; Qin, X.; Huang, Y.; Xiong, H.; Xu, N.; Wang, B.-X. Tunable metamaterial with quantitatively switchable anapole modes via quasi-BIC using two methods. Appl. Phys. Lett. 2025, 126, 201701. [Google Scholar] [CrossRef]
- Feng, J.; Wang, X.; Shi, W.; Ma, L.; Ji, Y.; Fan, F.; Chang, S. Asymmetric dumbbell dimers simultaneously supporting quasi-bound states in continuum and anapole modes for terahertz biosensing. Nanophotonics 2024, 13, 4007–4017. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Li, Y.; You, Q.; Wang, M.; Zhu, C.; Yang, Y.; Luan, H.; Wang, P. Magnetic Purcell enhancement by plasmon-induced magnetic resonance of the nanoparticle-on-mirror configuration. Phys. Rev. A 2024, 110, 013516. [Google Scholar] [CrossRef]
- Bonino, V.; Angelini, A. Multipolar Analysis in Symmetrical Meta-Atoms Sustaining Fano Resonances. Optics 2024, 5, 238–247. [Google Scholar] [CrossRef]
- Evlyukhin, A.B.; Fischer, T.; Reinhardt, C.; Chichkov, B.N. Optical theorem and multipole scattering of light by arbitrarily shaped nanoparticles. Phys. Rev. B 2016, 94, 205434. [Google Scholar] [CrossRef]
- Alaee, R.; Rockstuhl, C.; Fernandez-Corbaton, I. An electromagnetic multipole expansion beyond the long-wavelength approximation. Opt. Commun. 2018, 407, 17–21. [Google Scholar] [CrossRef]
- Radescu, E.E.; Vaman, G. Exact calculation of the angular momentum loss, recoil force, and radiation intensity for an arbitrary source in terms of electric, magnetic, and toroid multipoles. Phys. Rev. E 2002, 65, 046609. [Google Scholar] [CrossRef]
- Jing, Z.; Jiaxian, W.; Lizhen, G.; Weibin, Q. High-Sensitivity Sensing in All-Dielectric Metasurface Driven by Quasi-Bound States in the Continuum. Nanomaterials 2023, 13, 505. [Google Scholar] [CrossRef]
- Baryshnikova, K.V.; Smirnova, D.A.; Luk’yanchuk, B.S.; Kivshar, Y.S. Optical anapoles: Concepts and applications. Adv. Opt. Mater. 2019, 7, 1801350. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, T.; Li, Y.; Xu, Z.; Qian, X.; Shi, R.; Li, X.; Wang, M.; Li, Z. Tunable Dual-Mode Resonant Excitation of Dumbbell-Shaped Structures in the Mid-Infrared Band. Nanomaterials 2025, 15, 1181. https://doi.org/10.3390/nano15151181
Jiang T, Li Y, Xu Z, Qian X, Shi R, Li X, Wang M, Li Z. Tunable Dual-Mode Resonant Excitation of Dumbbell-Shaped Structures in the Mid-Infrared Band. Nanomaterials. 2025; 15(15):1181. https://doi.org/10.3390/nano15151181
Chicago/Turabian StyleJiang, Tao, Yafei Li, Zhuangzhuang Xu, Xike Qian, Rui Shi, Xiufei Li, Meng Wang, and Ze Li. 2025. "Tunable Dual-Mode Resonant Excitation of Dumbbell-Shaped Structures in the Mid-Infrared Band" Nanomaterials 15, no. 15: 1181. https://doi.org/10.3390/nano15151181
APA StyleJiang, T., Li, Y., Xu, Z., Qian, X., Shi, R., Li, X., Wang, M., & Li, Z. (2025). Tunable Dual-Mode Resonant Excitation of Dumbbell-Shaped Structures in the Mid-Infrared Band. Nanomaterials, 15(15), 1181. https://doi.org/10.3390/nano15151181





