Scaling, Leakage Current Suppression, and Simulation of Carbon Nanotube Field-Effect Transistors
Abstract
1. Introduction
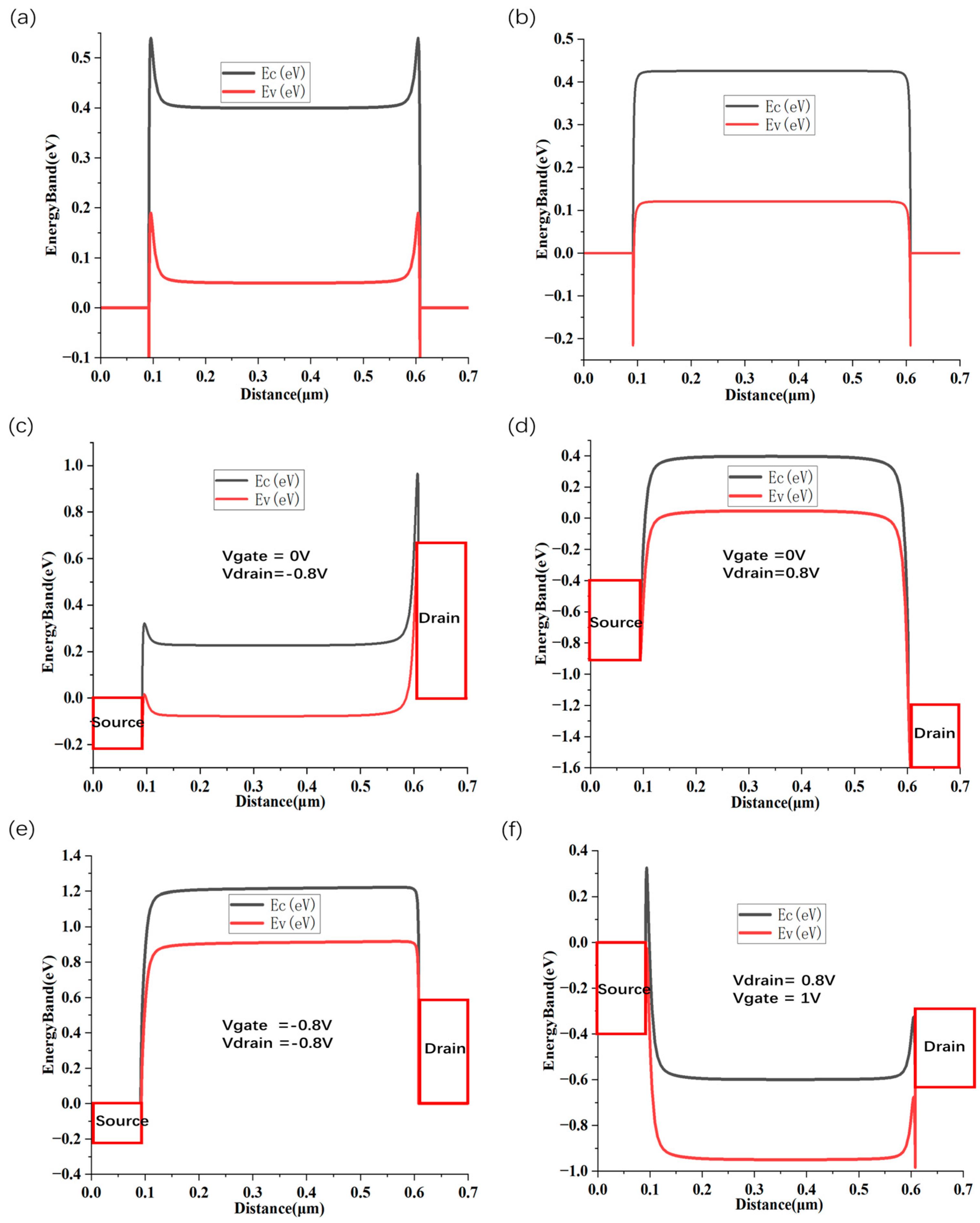
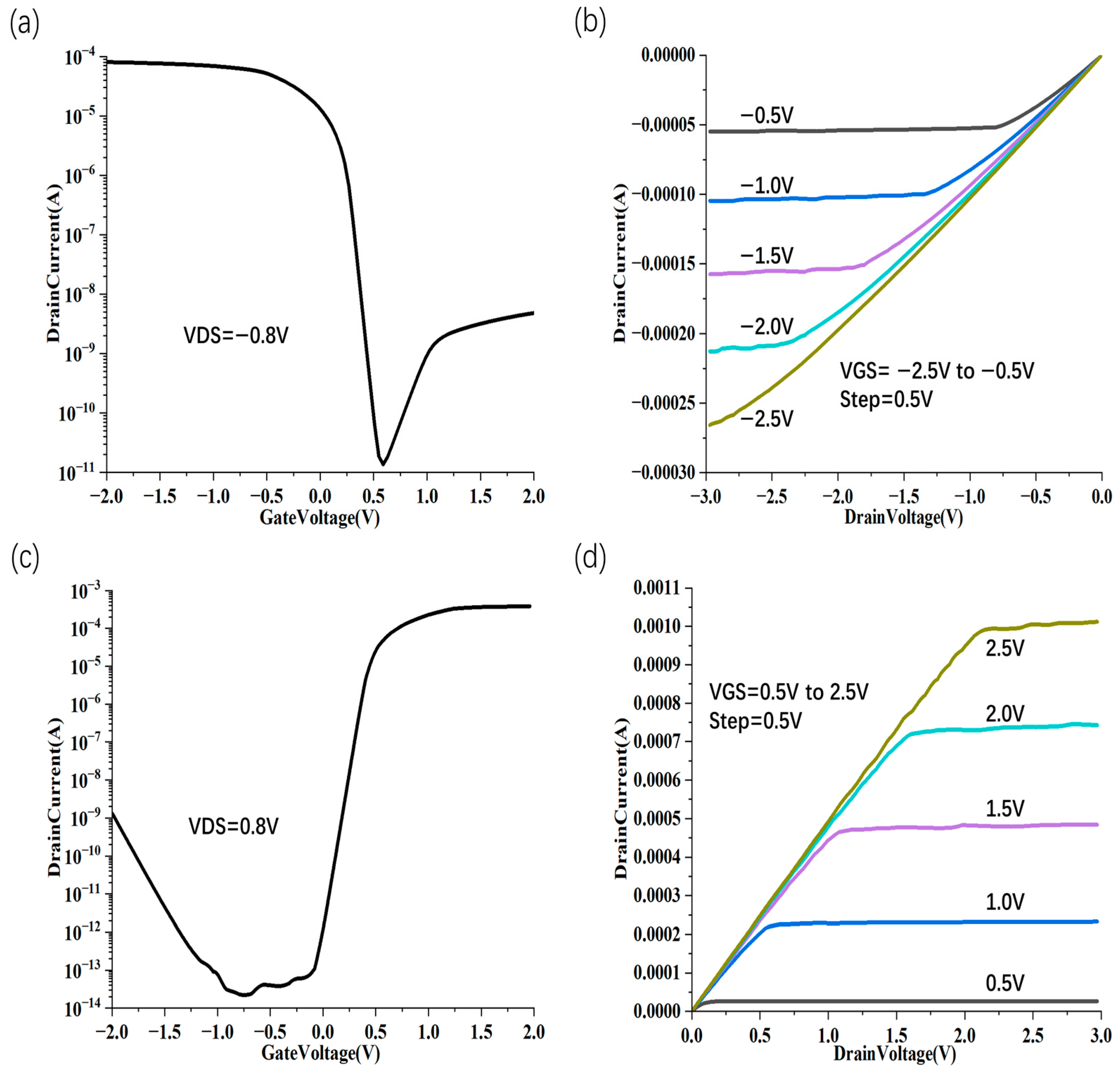
2. Structure, Modeling, and Operation Principle of Self-Aligned Gate CNTFET
3. Proposal of Scaling Structure of CNTFETs and Reduction in Leakage Current
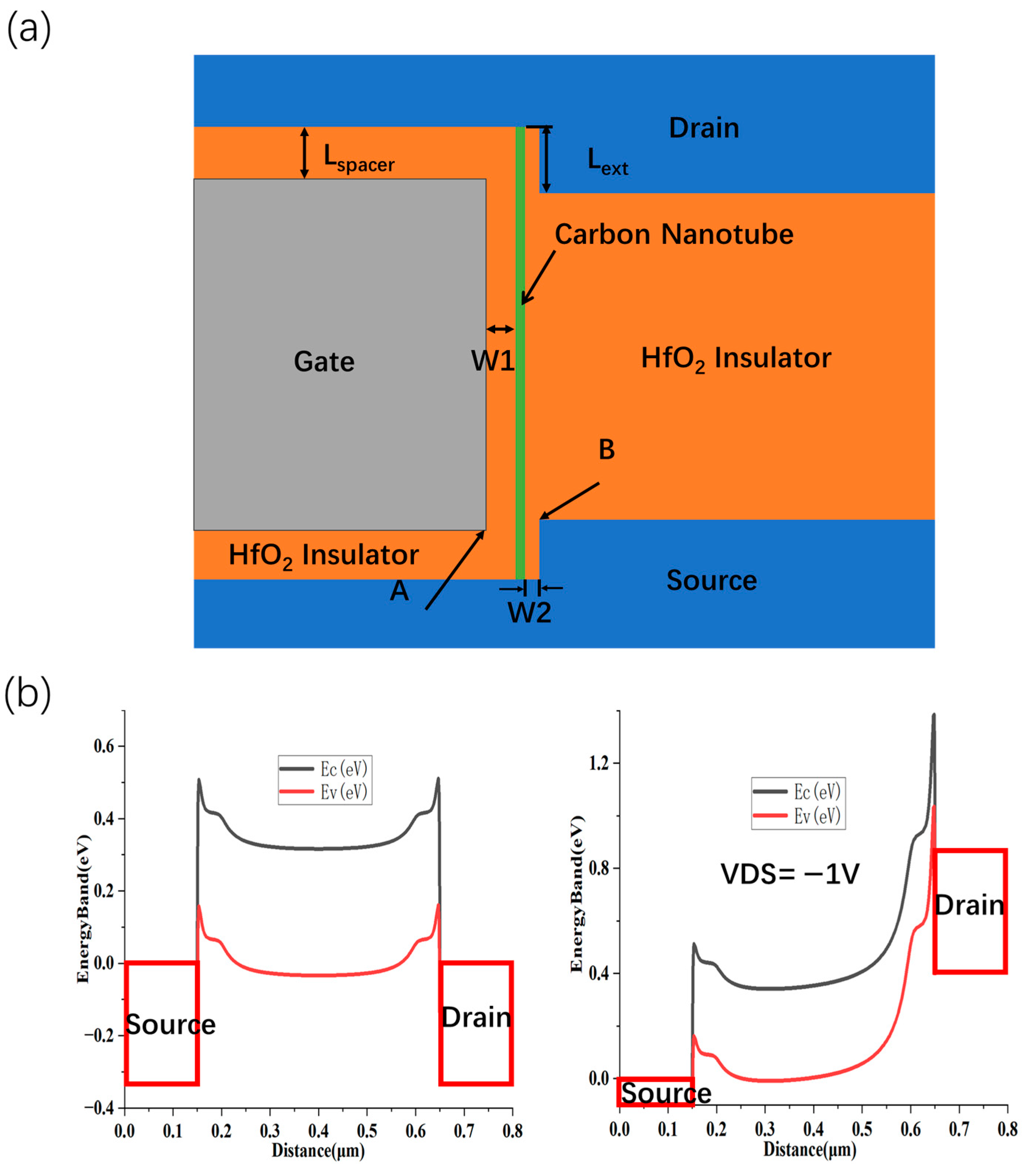
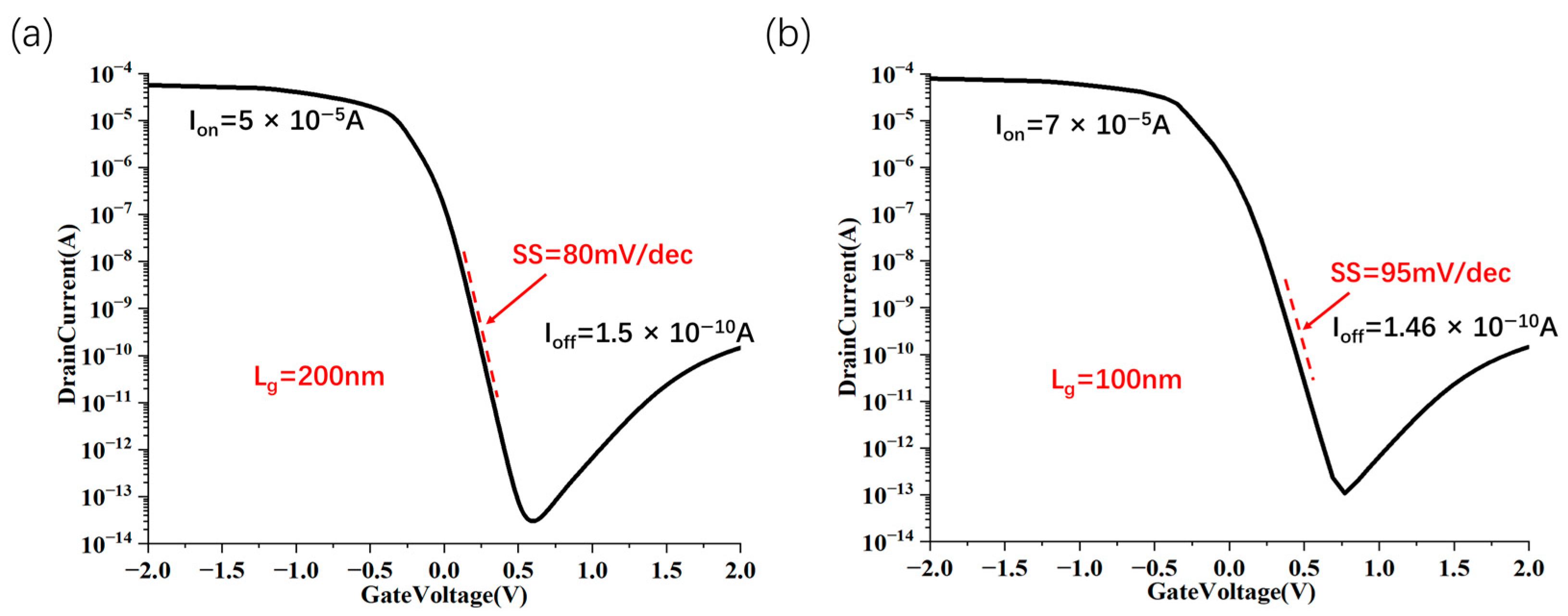
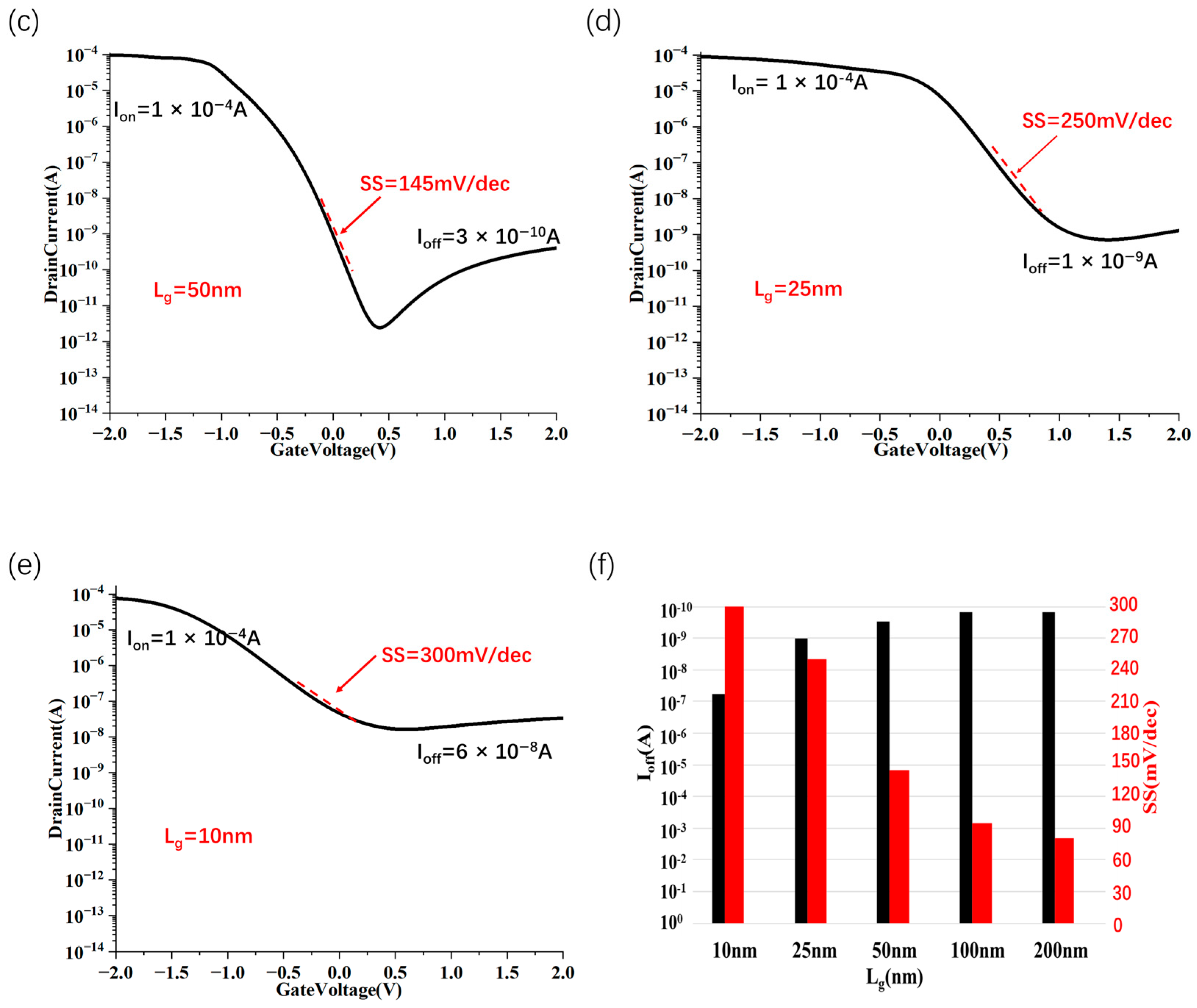
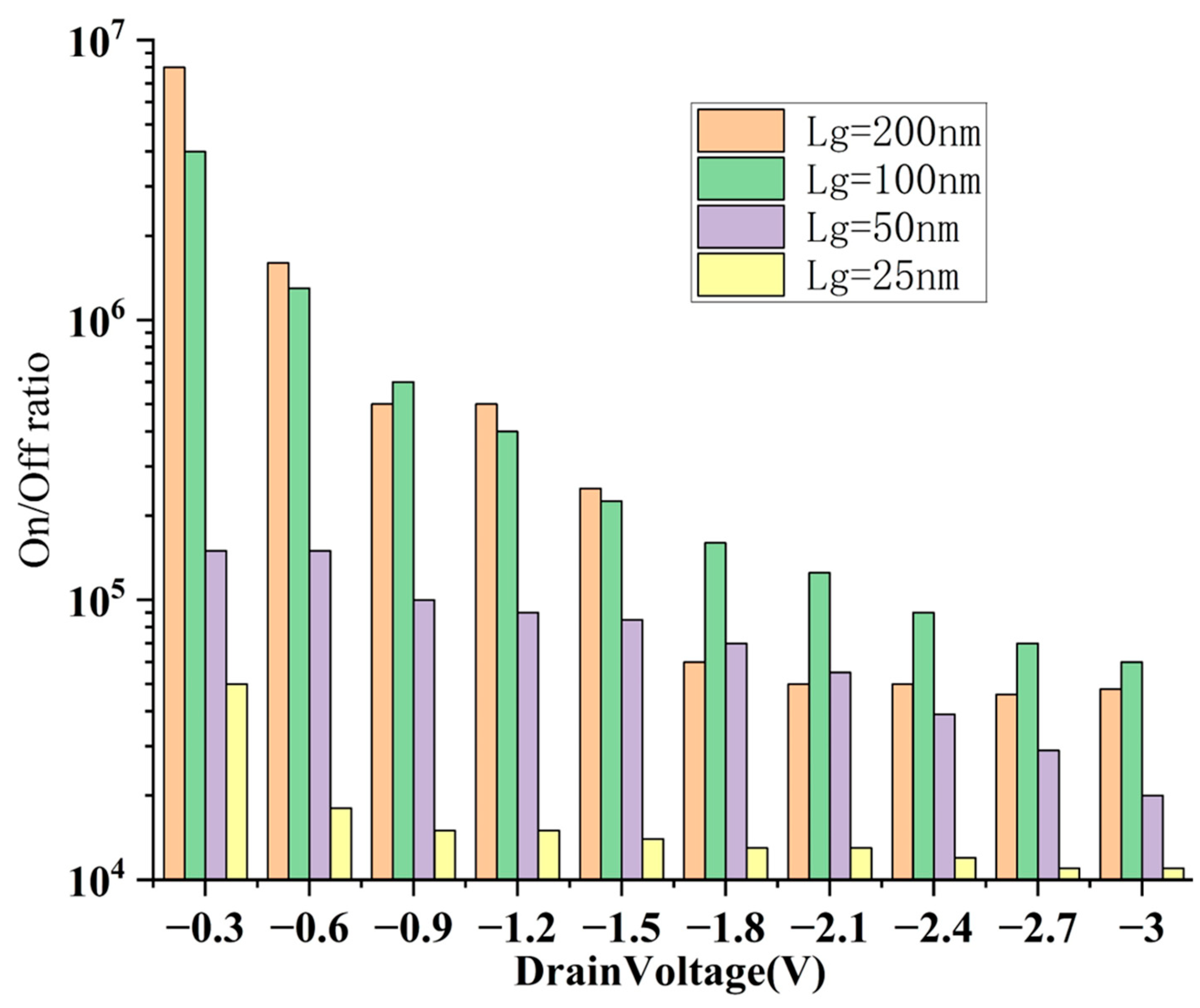
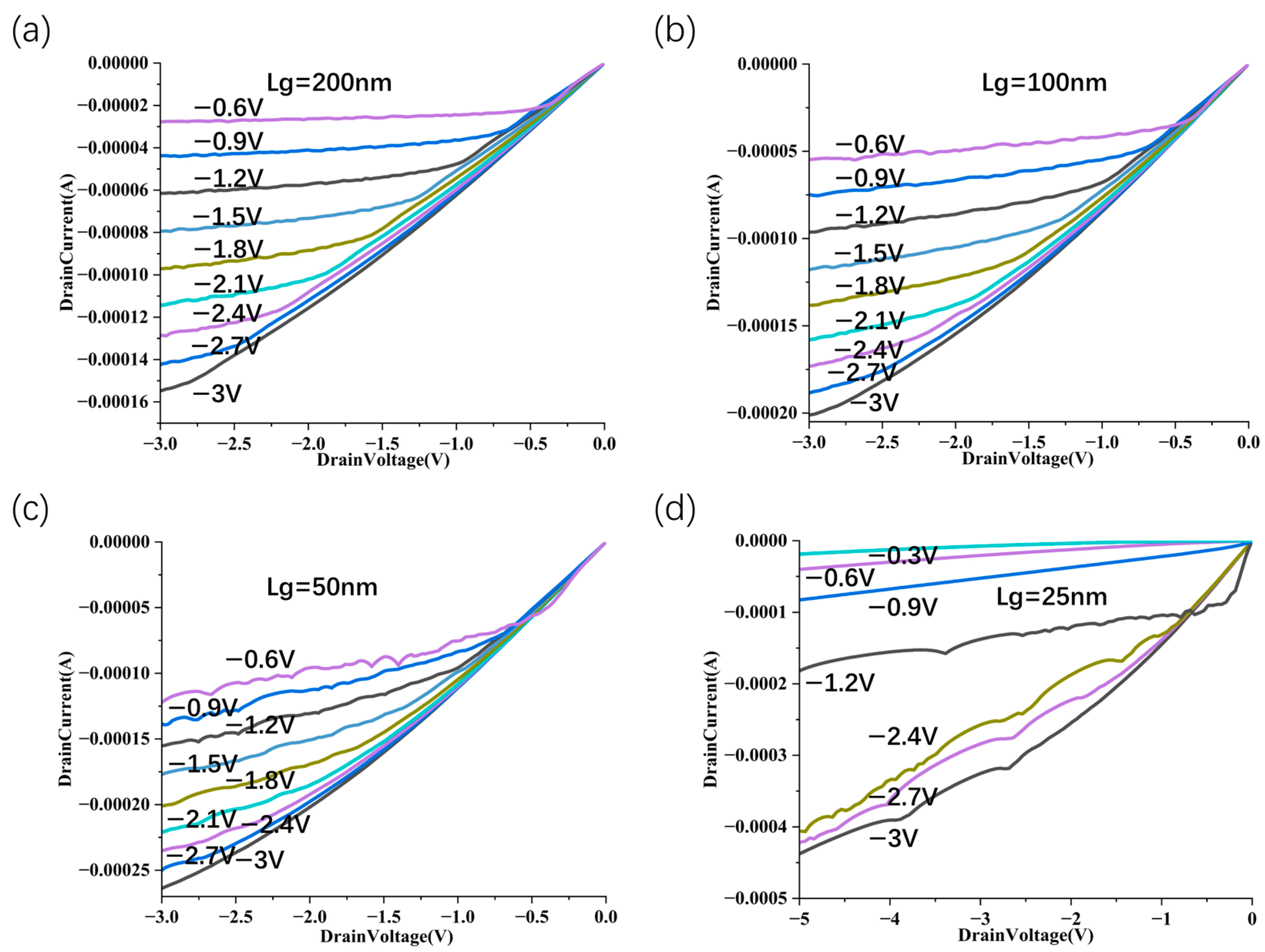
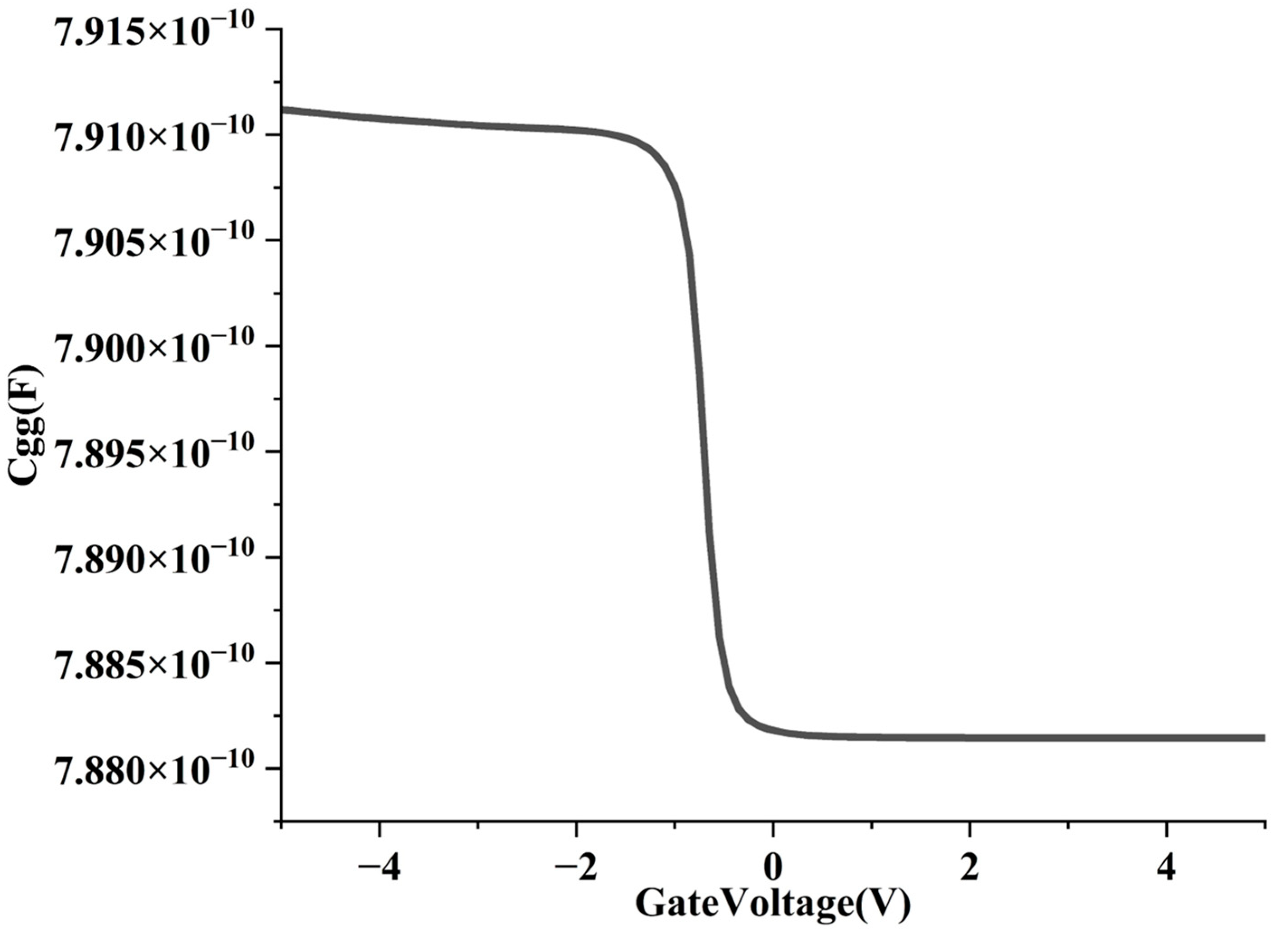
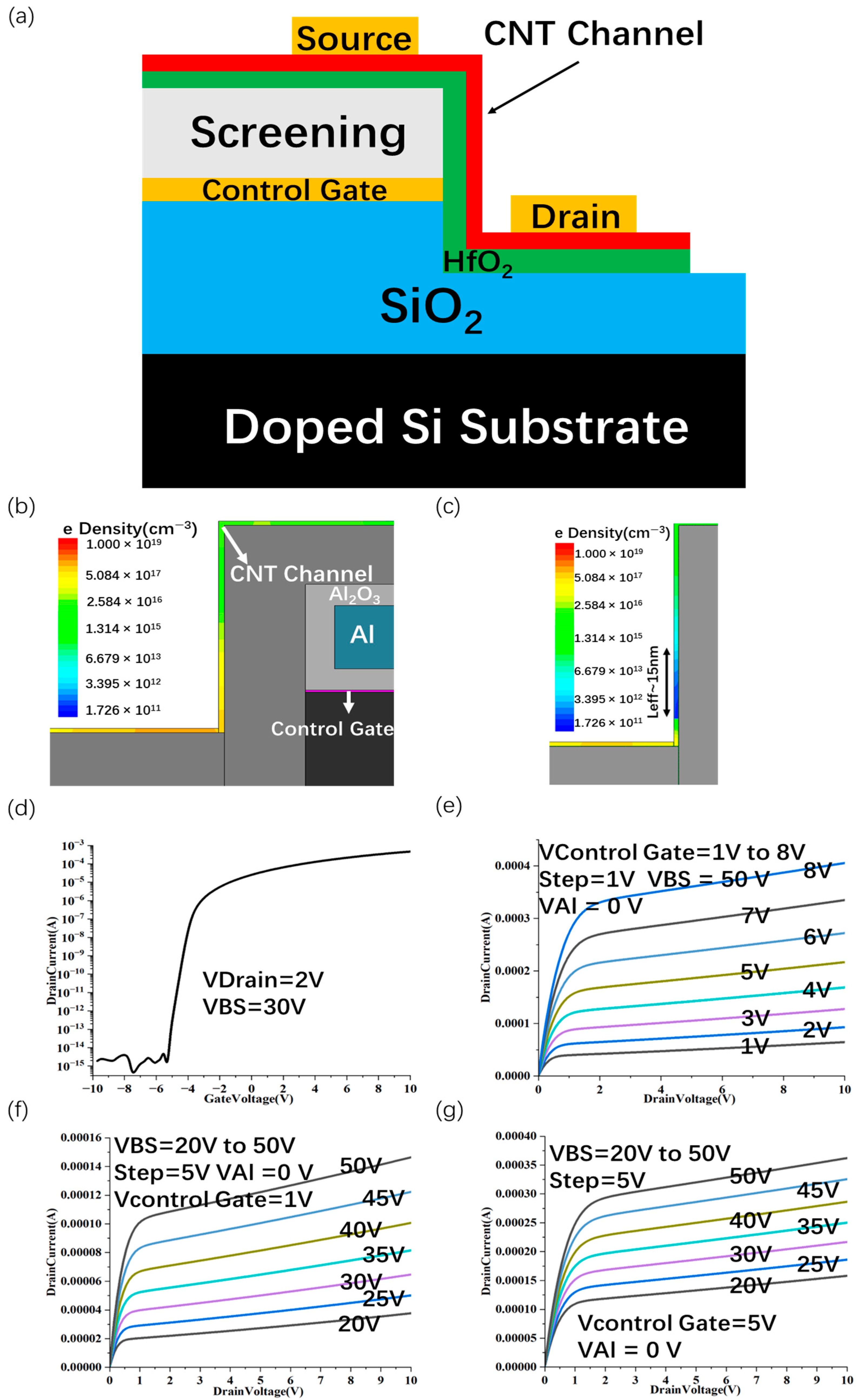
3.1. Vertically Scaling Structure
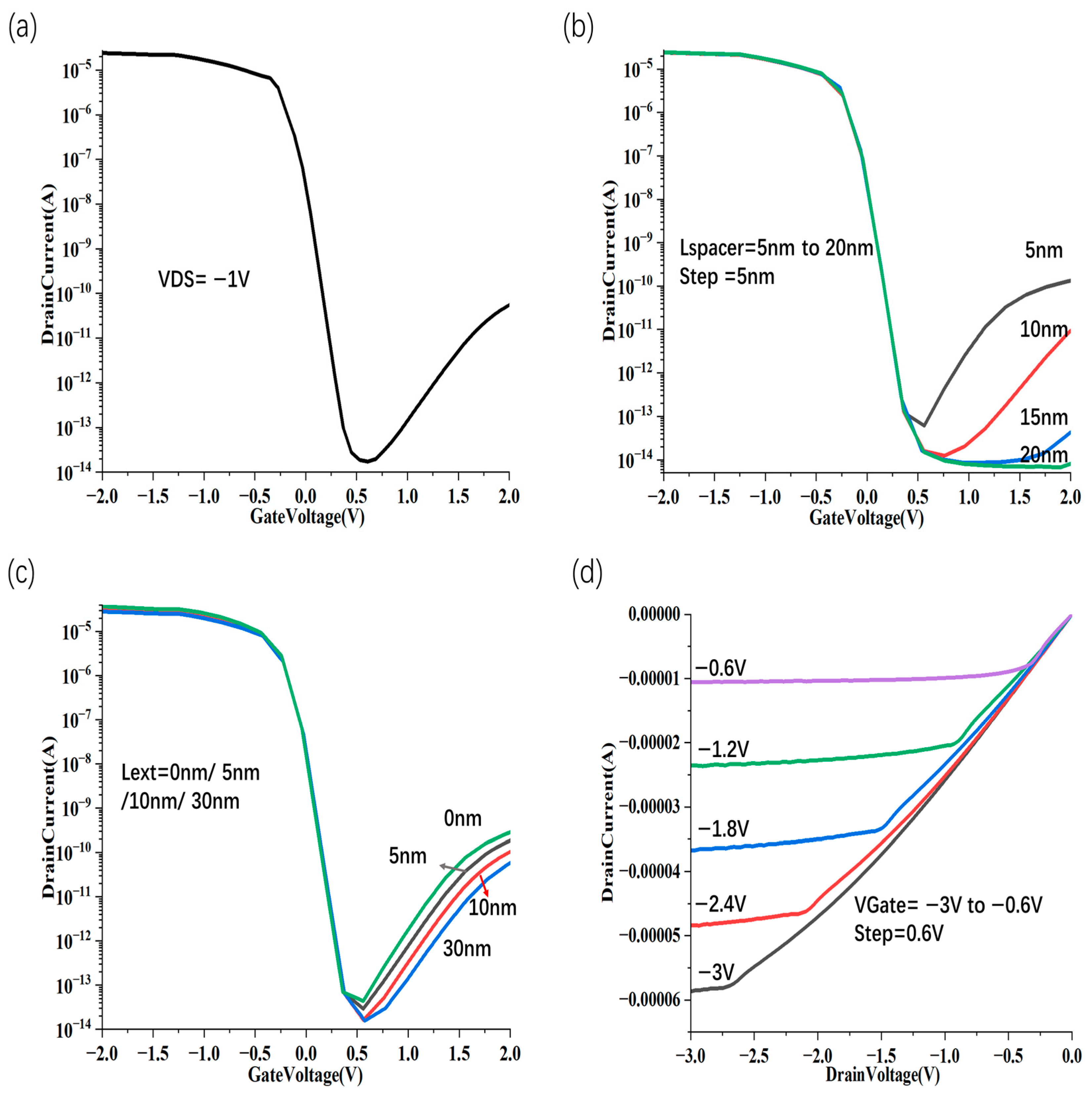
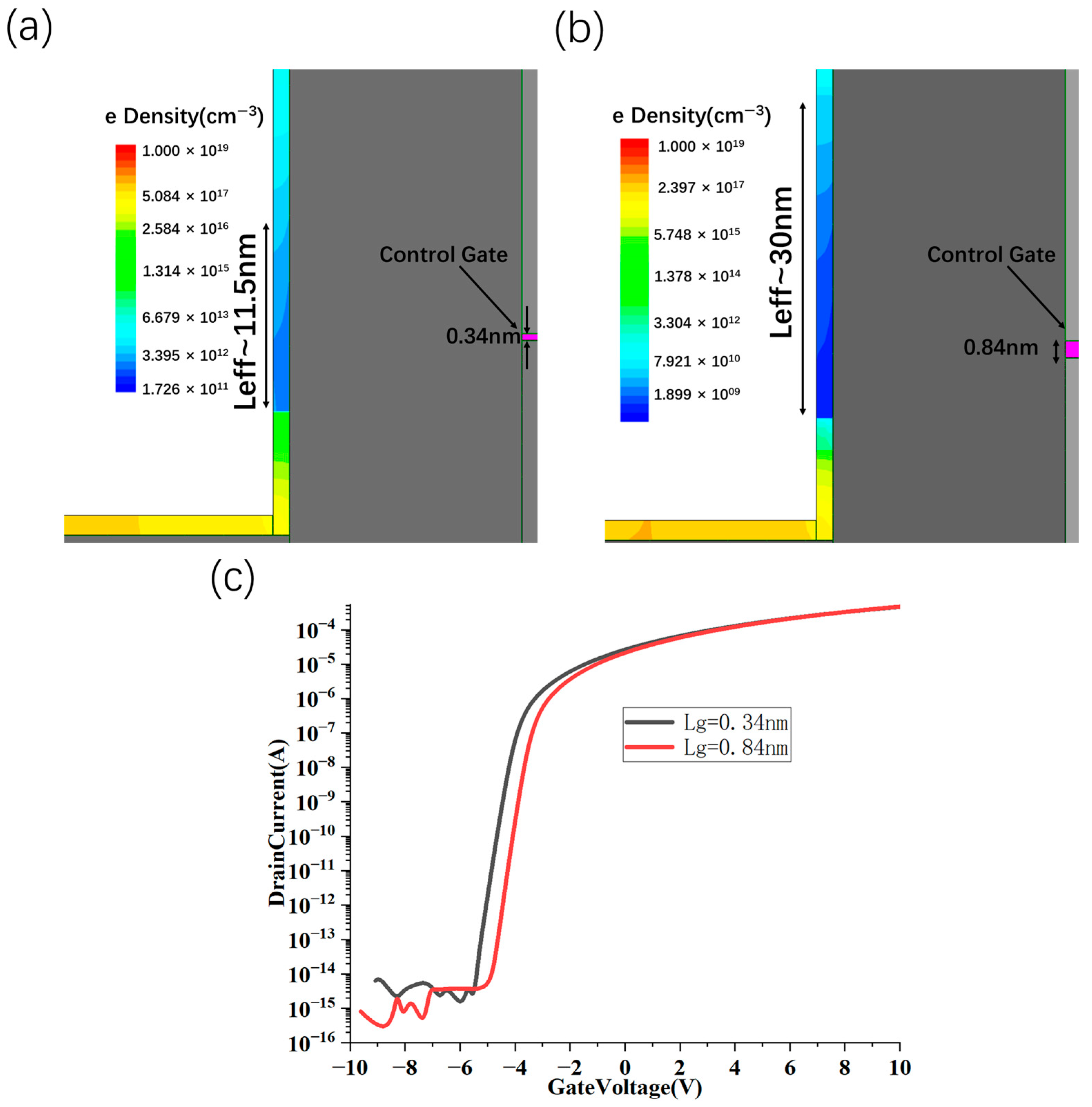
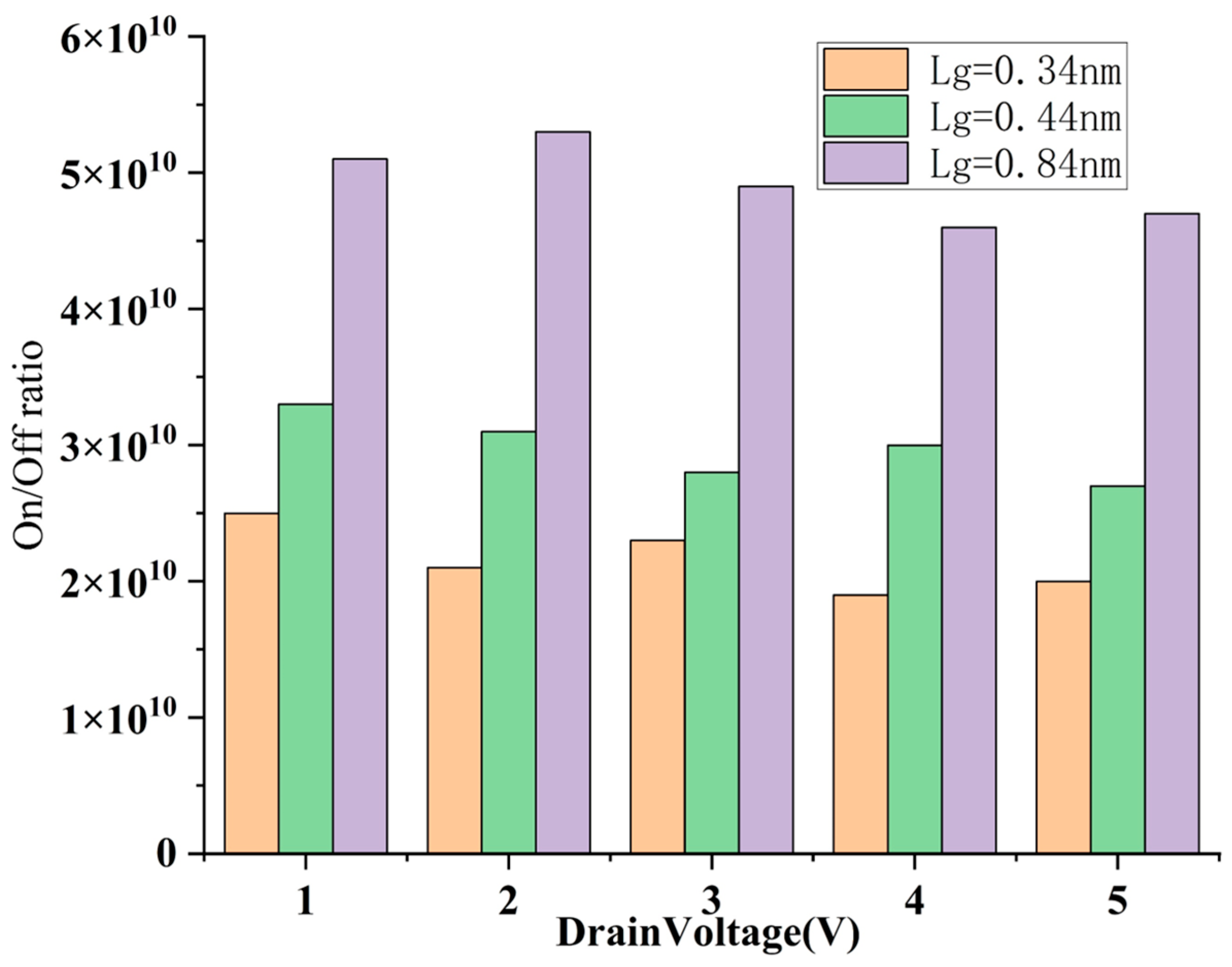
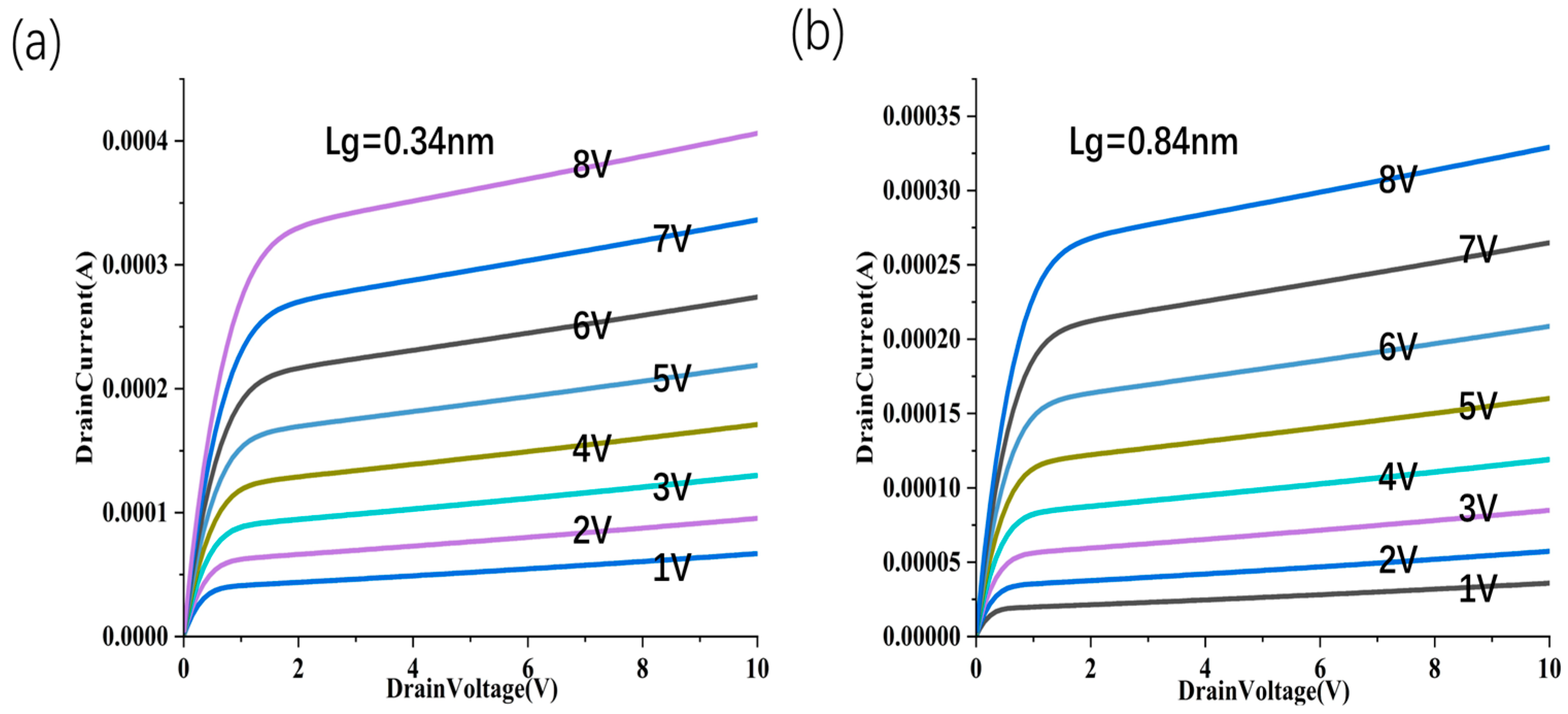
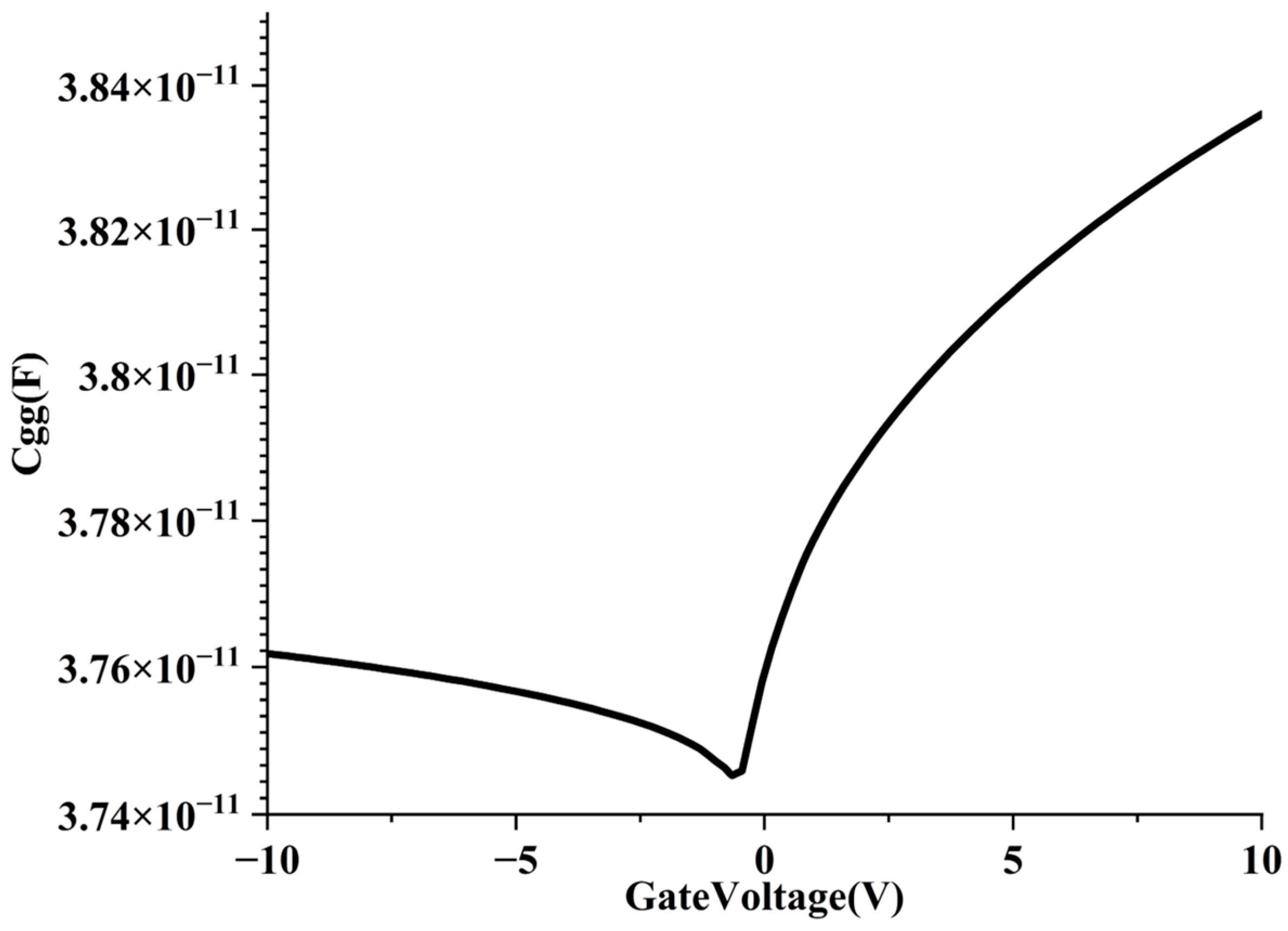
3.2. Scaling Structure with sub-1 nm Sidewall Gate Length
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Haensch, W.; Nowak, E.J.; Dennard, R.H.; Solomon, P.M.; Bryant, A.; Dokumaci, O.H.; Kumar, A.; Wang, X.; Johnson, J.B.; Fischetti, M.V. Silicon CMOS devices beyond scaling. IBM J. Res. Dev. 2006, 50, 339–361. [Google Scholar] [CrossRef]
- Macilwain, C. Computer hardware: Silicon down to the wire. J. Nat. 2005, 436, 22–23. [Google Scholar]
- Amin, A.B.; Ullah, M.S. Performance analysis of squarely packed polymorphic swcnt interconnect. In Proceedings of the 2019 IEEE 10th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 10–12 October 2019; pp. 1199–1203. [Google Scholar]
- Rakheja, S.; Lundstrom, M.; Antoniadis, D. A physics-based compact model for FETs from diffusive to ballistic carrier transport regimes. In Proceedings of the 2014 IEEE International Electron Devices Meeting, San Francisco, CA, USA, 15–17 December 2014; pp. 35.1.1–35.1.4. [Google Scholar]
- Amin, A.B.; Ullah, M.S. Mathematical framework of tetramorphic MWCNT configuration for VLSI interconnect. IEEE Trans. Nanotechnol. 2020, 19, 749–759. [Google Scholar] [CrossRef]
- Shabir, A.; Cao, J.; Fouad, E.; Ullah, M. Prospects of solar cell technology from silicon to carbon nanotube. In Proceedings of the 2022 IEEE 9th International Conference on Sciences of Electronics, Technologies of Information and Telecommunications (SETIT), Genoa, Italy, 28–30 May 2022; pp. 385–391. [Google Scholar]
- Amin, A.B.; Ullah, M.S. Performance analysis of squarely packed dimorphic mwcnt bundle for high speed vlsi interconnect. In Proceedings of the 2020 IEEE Canadian Conference on Electrical and Computer Engineering (CCECE), London, ON, Canada, 30 August–2 September 2020; pp. 1–6. [Google Scholar]
- Rupwate, D.U. FET Biosensors: Breast Cancer Detection. 2025. Available online: https://www.preprints.org/manuscript/202506.0167/v1 (accessed on 26 May 2025).
- Devi, S.; Talukdar, J.; Laskar, N.M.; Choudhury, S. Exploring the Potential of Tunnel Field-Effect Transistors in Biomedical Devices: A Comprehensive Survey. IETE J. Res. 2025, 71, 247–258. [Google Scholar] [CrossRef]
- Shooshtari, M. Ammonia gas sensors based on multi-wall carbon nanofiber field effect transistors by using gate modulation. Colloids Surf. A Physicochem. Eng. Asp. 2025, 704, 135563. [Google Scholar] [CrossRef]
- Shakil, S.M.; Ullah, M.S. Effects of nbti on pmos device with technology scaling. In Proceedings of the 2022 IEEE 13th Annual Ubiquitous Computing, Electronics & Mobile Communication Conference (UEMCON), New York, NY, USA, 26–29 October 2022; pp. 0402–0406. [Google Scholar]
- Dürkop, T.; Getty, S.A.; Cobas, E.; Fuhrer, M.S. Extraordinary mobility in semiconducting carbon nanotubes. Nano Lett. 2004, 4, 35–39. [Google Scholar] [CrossRef]
- Purewal, M.S.; Hong, B.H.; Ravi, A.; Chandra, B.; Hone, J.; Kim, P. Scaling of resistance and electron mean free path of single-walled carbon nanotubes. J. Phys. Rev. Lett. 2007, 98, 186808. [Google Scholar] [CrossRef]
- Jiang, W.F.; Xiao, S.; Zhang, H.; Dong, Y.; Li, X. Capacitive humidity sensing properties of carbon nanotubes grown on silicon nanoporous pillar array. Sci. China Ser. E Technol. Sci. 2007, 50, 510–515. [Google Scholar] [CrossRef]
- Mudimela, P.R.; Grigoras, K.; Anoshkin, I.V.; Varpula, A.; Ermolov, V.; Anisimov, A.S.; Nasibulin, A.G.; Novikov, S.; Kauppinen, E.I. Single-Walled Carbon Nanotube Network Field Effect Transistor as a Humidity Sensor. J. Sens. 2012, 2012, 496546. [Google Scholar] [CrossRef]
- Derycke, V.; Martel, R.; Appenzeller, J.; Avouris, P. Controlling doping and carrier injection in carbon nanotube transistors. Appl. Phys. Lett. 2002, 80, 2773–2775. [Google Scholar] [CrossRef]
- Javey, A.; Guo, J.; Wang, Q.; Lundstrom, M.; Dai, H. Ballistic carbon nanotube field-effect transistors. Nature 2003, 424, 654–657. [Google Scholar] [CrossRef]
- Zhang, Z.; Liang, X.; Wang, S.; Yao, K.; Hu, Y.; Zhu, Y.; Chen, Q.; Zhou, W.; Li, Y.; Yao, Y.; et al. Doping-free fabrication of carbon nanotube based ballistic CMOS devices and circuits. Nano Lett. 2007, 7, 3603–3607. [Google Scholar] [CrossRef]
- Martel, R.; Derycke, V.; Lavoie, C.; Appenzeller, J.; Chan, K.K.; Tersoff, J.; Avouris, P. Ambipolar electrical transport in semiconducting single-wall carbon nanotubes. Phys. Rev. Lett. 2001, 87, 256805. [Google Scholar] [CrossRef]
- Heinze, S.; Tersoff, J.; Martel, R.; Derycke, V.; Appenzeller, J.; Avouris, P. Carbon nanotubes as Schottky barrier transistors. Phys. Rev. Lett. 2002, 89, 106801. [Google Scholar] [CrossRef]
- Appenzeller, J.; Knoch, J.; Derycke, V.; Martel, R.; Wind, S.; Avouris, P. Field-modulated carrier transport in carbon nanotube transistors. Phys. Rev. Lett. 2002, 89, 126801. [Google Scholar] [CrossRef]
- Javey, A.; Farmer, D.; Gordon, R.; Dai, H. Self-aligned 40-nm channel carbon nanotube field-effect transistors with subthreshold swings down to 70 mV/decade. In Quantum Sensing and Nanophotonic Devices II; SPIE: Bellingham, WA, USA; pp. 14–18.
- Cao, Q.; Tersoff, J.; Farmer, D.B.; Zhu, Y.; Han, S.J. Carbon nanotube transistors scaled to a 40-nanometer footprint. Science 2017, 356, 1369–1372. [Google Scholar] [CrossRef] [PubMed]
- Seidel, R.V.; Graham, A.P.; Kretz, J.; Rajasekharan, B.; Duesberg, G.S.; Liebau, M.; Unger, E.; Kreupl, F.; Hoenlein, W. Sub-20 nm short channel carbon nanotube transistors. Nano Lett. 2005, 5, 147–150. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Cao, Y.; Ding, S.; Zhang, P.; Xu, L.; Liu, C. Scaling aligned carbon nanotube transistors to a sub-10 nm node. Nat. Electron. 2023, 6, 506–515. [Google Scholar] [CrossRef]
- Qiu, C.; Zhang, Z.; Xiao, M.; Yang, Y.; Zhong, D.; Peng, L.-M. Scaling carbon nanotube complementary transistors to 5-nm gate lengths. Science 2017, 355, 271–276. [Google Scholar] [CrossRef] [PubMed]
- Guo, J.; Datta, S.; Lundstrom, M. A numerical study of scaling issues for Schottky-barrier carbon nanotube transistors. IEEE Trans. Electron Devices 2004, 51, 172–177. [Google Scholar] [CrossRef]
- Ghoneim, H.; Knoch, J.; Riel, H.; Webb, D.; Björk, M.T.; Karg, S.; Lörtscher, E.; Schmid, H.; Riess, W. Suppression of ambipolar behavior in metallic source/drain metal-oxide-semiconductor field-effect transistors. Appl. Phys. Lett. 2009, 95, 213504. [Google Scholar] [CrossRef]
- Qiu, C.; Zhang, Z.; Zhong, D.; Si, J.; Yang, Y.; Peng, L.M. Carbon nanotube feedback-gate field-effect transistor: Suppressing current leakage and increasing on/off ratio. ACS Nano 2015, 9, 969–977. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Wang, S.; Ding, L.; Liang, X.; Pei, T.; Shen, J.; Xu, H.; Chen, Q.; Cui, R.; Li, Y.; et al. Self-aligned ballistic n-type single-walled carbon nanotube field-effect transistors with adjustable threshold voltage. Nano Lett. 2008, 8, 3696–3701. [Google Scholar] [CrossRef]
- Srimani, T.; Hills, G.; Zhao, X.; Antoniadis, D.; Del Alamo, J.A.; Shulaker, M.M. Asymmetric gating for reducing leakage current in carbon nanotube field-effect transistors. Appl. Phys. Lett. 2019, 115, 063107. [Google Scholar] [CrossRef]
- Pourfath, M.; Ungersboeck, E.; Gehring, A.; Cheong, B.H.; Park, W.; Kosina, H.; Selberherr, S. Improving the ambipolar behavior of schottky barrier carbon nanotube field effect transistors. In Proceedings of the 30th European Solid-State Circuits Conference, Leuven, Belgium, 21–23 September 2004; pp. 429–432. [Google Scholar]
- Nanmeni Bondja, C.; Geng, Z.; Granzner, R.; Pezoldt, J.; Schwierz, F. Simulation of 50-nm gate graphene nanoribbon transistors. Electronics 2016, 5, 3. [Google Scholar] [CrossRef]
- Betti, A.; Fiori, G.; Iannaccone, G. Drift velocity peak and negative differential mobility in high field transport in graphene nanoribbons explained by numerical simulations. Appl. Phys. Lett. 2011, 99, 242108. [Google Scholar] [CrossRef]
- Akinwande, D.; Nishi, Y.; Wong, H.S.P. An analytical derivation of the density of states, effective mass, and carrier density for achiral carbon nanotubes. IEEE Trans. Electron Devices 2007, 55, 289–297. [Google Scholar] [CrossRef]
- Liang, J.; Akinwande, D.; Wong, H.S.P. Carrier density and quantum capacitance for semiconducting carbon nanotubes. Appl. Phys. 2008, 104, 064515. [Google Scholar] [CrossRef]
- Lee, C.S.; Pop, E.; Franklin, A.D.; Haensch, W.; Wong, H.S.P. A compact virtual-source model for carbon nanotube FETs in the sub-10-nm regime—Part I: Intrinsic elements. IEEE Trans. Electron Devices 2015, 62, 3061–3069. [Google Scholar] [CrossRef]
- Wong, H.S.P.; Akinwande, D. Carbon Nanotube and Graphene Device Physics; Cambridge University Press: Cambridge, UK, 2010. [Google Scholar]
- Tseng, A.A.; Chen, K.; Chen, C.D.; Ma, K.J. Electron beam lithography in nanoscale fabrication: Recent development. IEEE Trans. Electron. Packag. Manuf. 2003, 26, 141–149. [Google Scholar] [CrossRef]
- Desai, S.B.; Madhvapathy, S.R.; Sachid, A.B.; Llinas, J.P.; Wang, Q.; Ahn, G.H.; Javey, A.; Pitner, G.; Kim, M.J.; Bokor, J.; et al. MoS2 transistors with 1-nanometer gate lengths. Science 2016, 354, 99–102. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Tian, H.; Shen, Y.; Hou, Z.; Ren, J.; Gou, G.; Sun, Y.; Yang, Y.; Ren, T.-L. Vertical MoS2 transistors with sub-1-nm gate lengths. Nature 2022, 603, 259–264. [Google Scholar] [CrossRef] [PubMed]



| Parameters | Value |
|---|---|
| Diameter (dCNT) (nm) | 2.4 |
| Bandgap (Eg) (eV) | 0.35 |
| CNT Affinity (eV) | 4.4 |
| Effective Mass (m*) | 0.029 |
| Mobility of CNT Channel (μ0) | 1 × 104 |
| NMOS Effective DOS (NC) (cm−3) | 3.4 × 1015 |
| PMOS Effective DOS (NC) (cm−3) | 3.4 × 1011 |
| Effective DOS (NV) (cm−3) | 6.65 × 1015 |
| Saturation Velocity (Vsat) (cm/s) | 1.1 × 107 |
| NMOS Contact Workfunction (Φm) (eV) | 2.9 |
| PMOS Contact Workfunction (Φm) (eV) | 5.1 |
| Gate Workfunction of NMOS (ΦG) (eV) | 4.8 |
| Gate Workfunction of PMOS (ΦG) (eV) | 5.1 |
| Channel Length of CNT (nm) | 516 |
| Thickness of HfO2 (nm) | 8 |
| Parameters | Value |
|---|---|
| Effective DOS (NC) (cm−3) | 3.4 × 1011 |
| Effective DOS (NV) (cm−3) | 6.65 × 1016 |
| Contact Workfunction (Φm) (eV) | 5 |
| Gate Workfunction (ΦG) (eV) | 4.7 |
| Channel Length of CNT (nm) | 500 |
| Gate Length (nm) | 484 |
| Lspacer (nm) | 8 |
| Lext (nm) | 50 |
| W1 (nm) | 8 |
| W2 (nm) | 8 |
| Parameters | Value |
|---|---|
| Effective DOS (NC) (cm−3) | 3.4 × 1014 |
| Effective DOS (Nv) (cm−3) | 6.65 × 1013 |
| Contact work function (ΦM) (eV) | 2.7 |
| Gate work function (ΦG) (eV) | 5.4 |
| Length of Source and Drain (nm) | 30 |
| Thickness of Al2O3 (nm) | 5 |
| Length of Control Gate (nm) | 200 |
| Thickness of Control Gate (nm) | 0.44 |
| Channel Length of CNT (nm) | 800 |
| Thickness of CNT (nm) | 2.4 |
| Thickness of HfO2 (nm) | 14 |
| Thickness of Aluminum Layer (nm) | 15 |
| Thickness of Source side SiO2 (nm) | 50 |
| Thickness of Drain side SiO2 (nm) | 26 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, W.; Cai, Z.; Geng, S.; Gan, Z.; Li, J.; Qiang, T.; Jiang, Y.; Cai, M. Scaling, Leakage Current Suppression, and Simulation of Carbon Nanotube Field-Effect Transistors. Nanomaterials 2025, 15, 1168. https://doi.org/10.3390/nano15151168
Gong W, Cai Z, Geng S, Gan Z, Li J, Qiang T, Jiang Y, Cai M. Scaling, Leakage Current Suppression, and Simulation of Carbon Nanotube Field-Effect Transistors. Nanomaterials. 2025; 15(15):1168. https://doi.org/10.3390/nano15151168
Chicago/Turabian StyleGong, Weixu, Zhengyang Cai, Shengcheng Geng, Zhi Gan, Junqiao Li, Tian Qiang, Yanfeng Jiang, and Mengye Cai. 2025. "Scaling, Leakage Current Suppression, and Simulation of Carbon Nanotube Field-Effect Transistors" Nanomaterials 15, no. 15: 1168. https://doi.org/10.3390/nano15151168
APA StyleGong, W., Cai, Z., Geng, S., Gan, Z., Li, J., Qiang, T., Jiang, Y., & Cai, M. (2025). Scaling, Leakage Current Suppression, and Simulation of Carbon Nanotube Field-Effect Transistors. Nanomaterials, 15(15), 1168. https://doi.org/10.3390/nano15151168








