Abnormal Angle-Dependent Multi-Channel Filtering in Photonic Crystals Containing Hyperbolic Metamaterials
Abstract
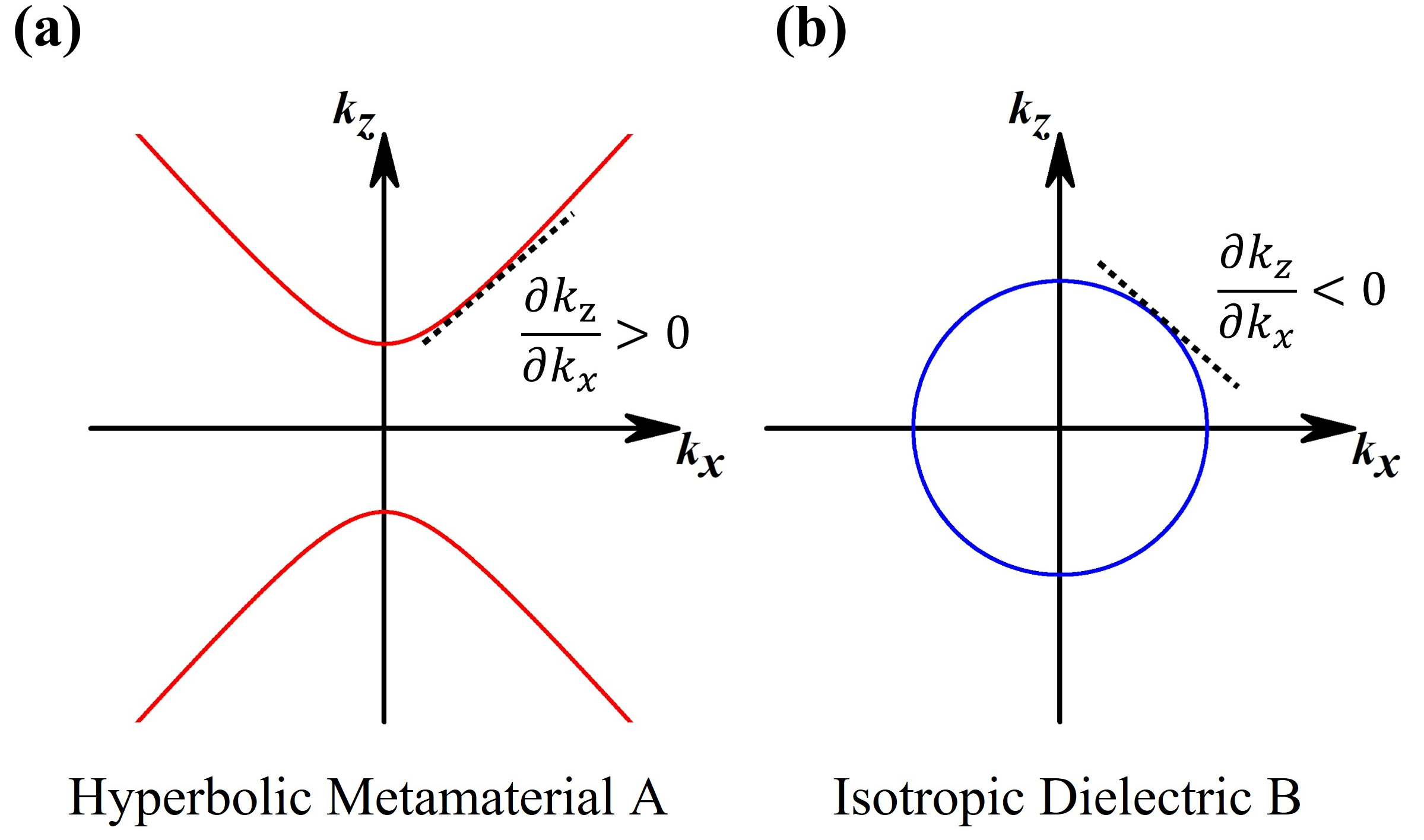
1. Introduction
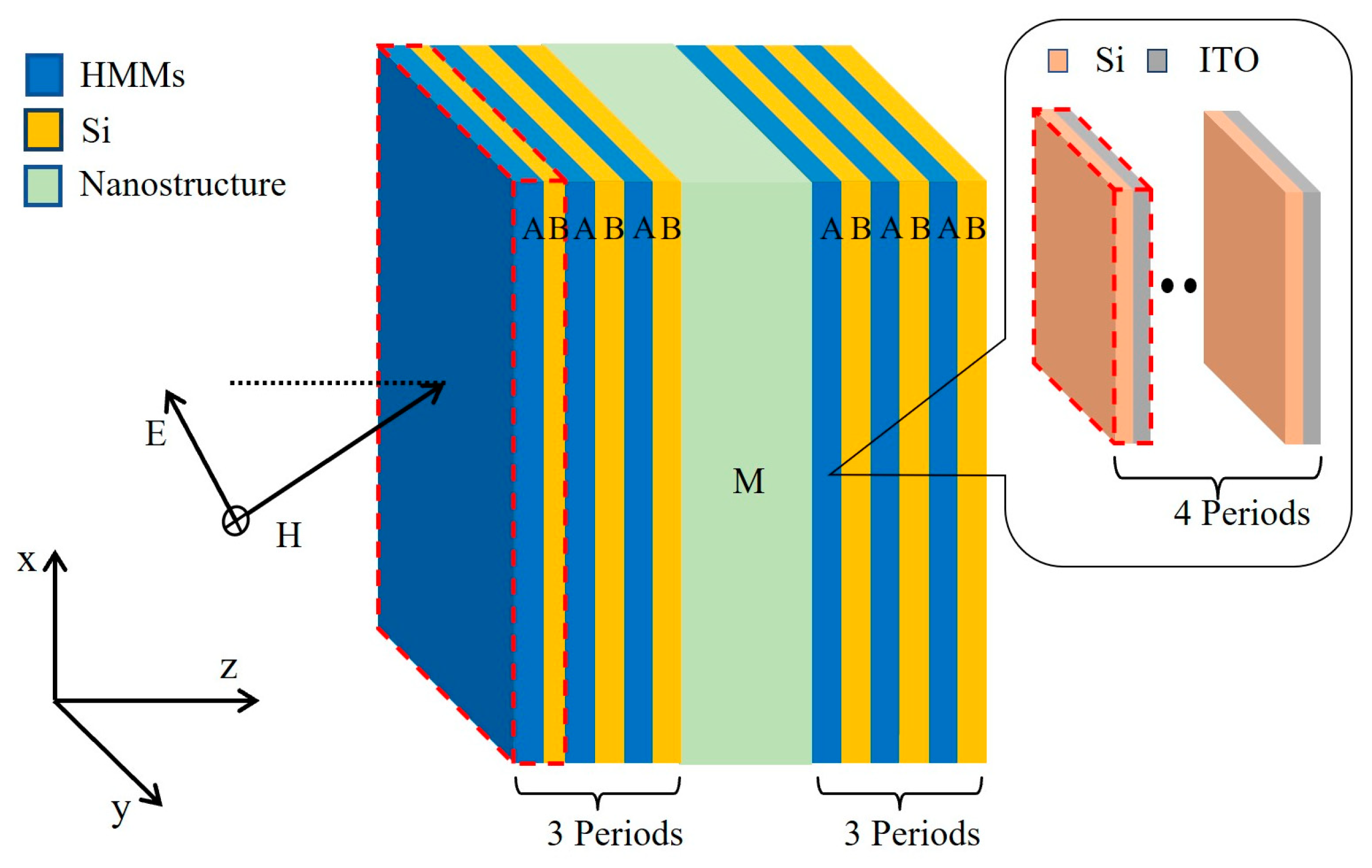
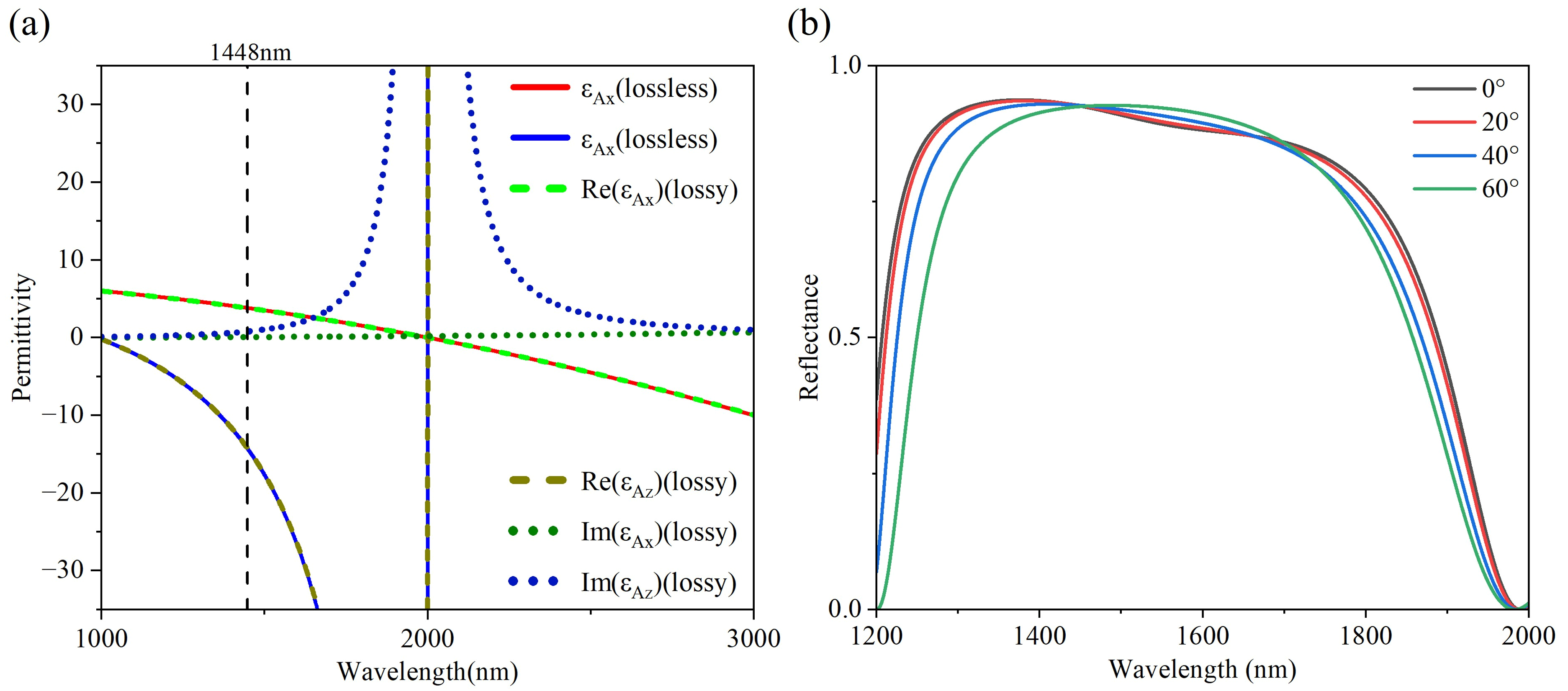
2. HMM-Containing 1D-PC-Based Optical Filters
3. Results
3.1. Multi-Channel Filtering Based on One Type of Angle-Dependence
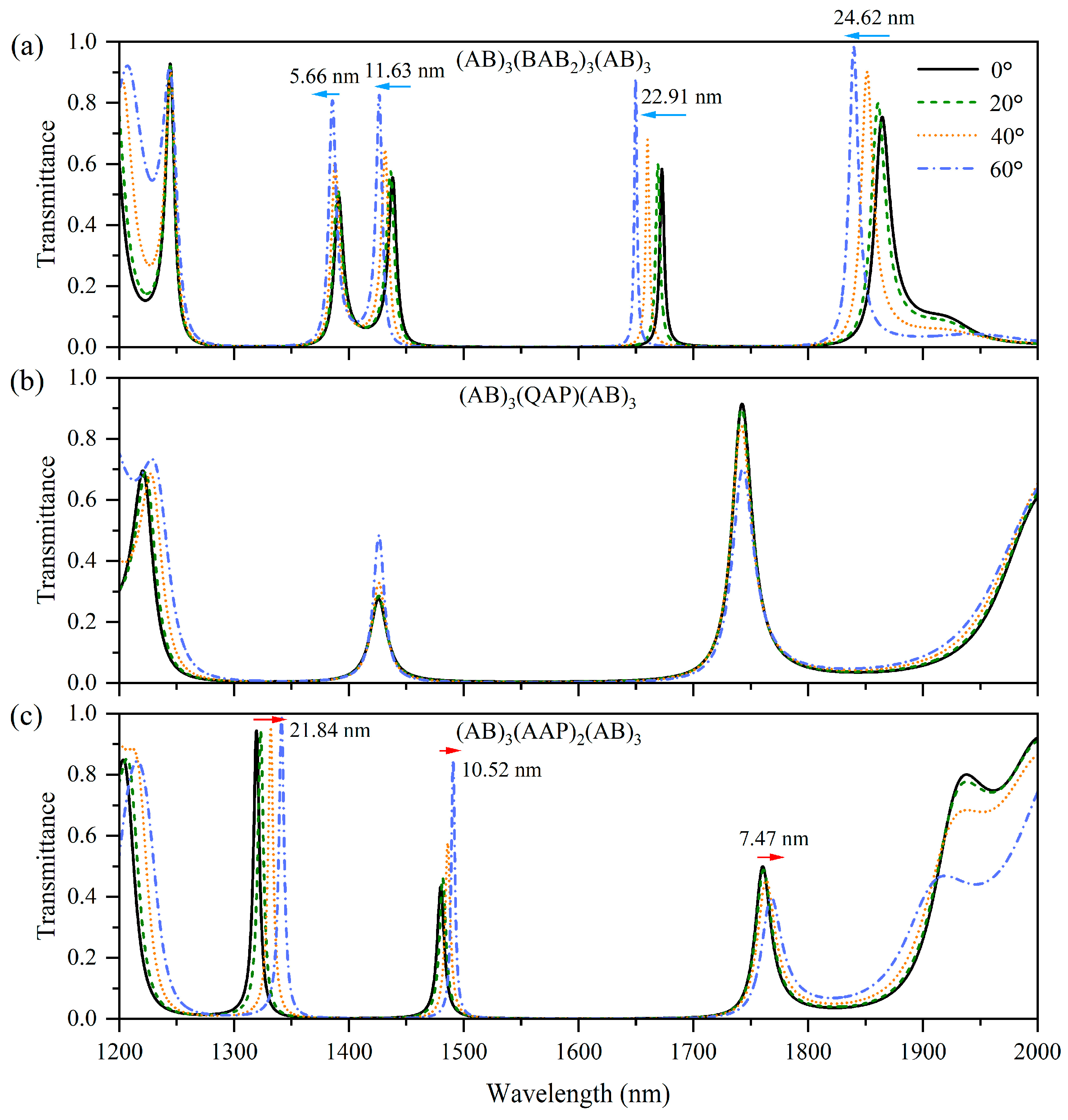
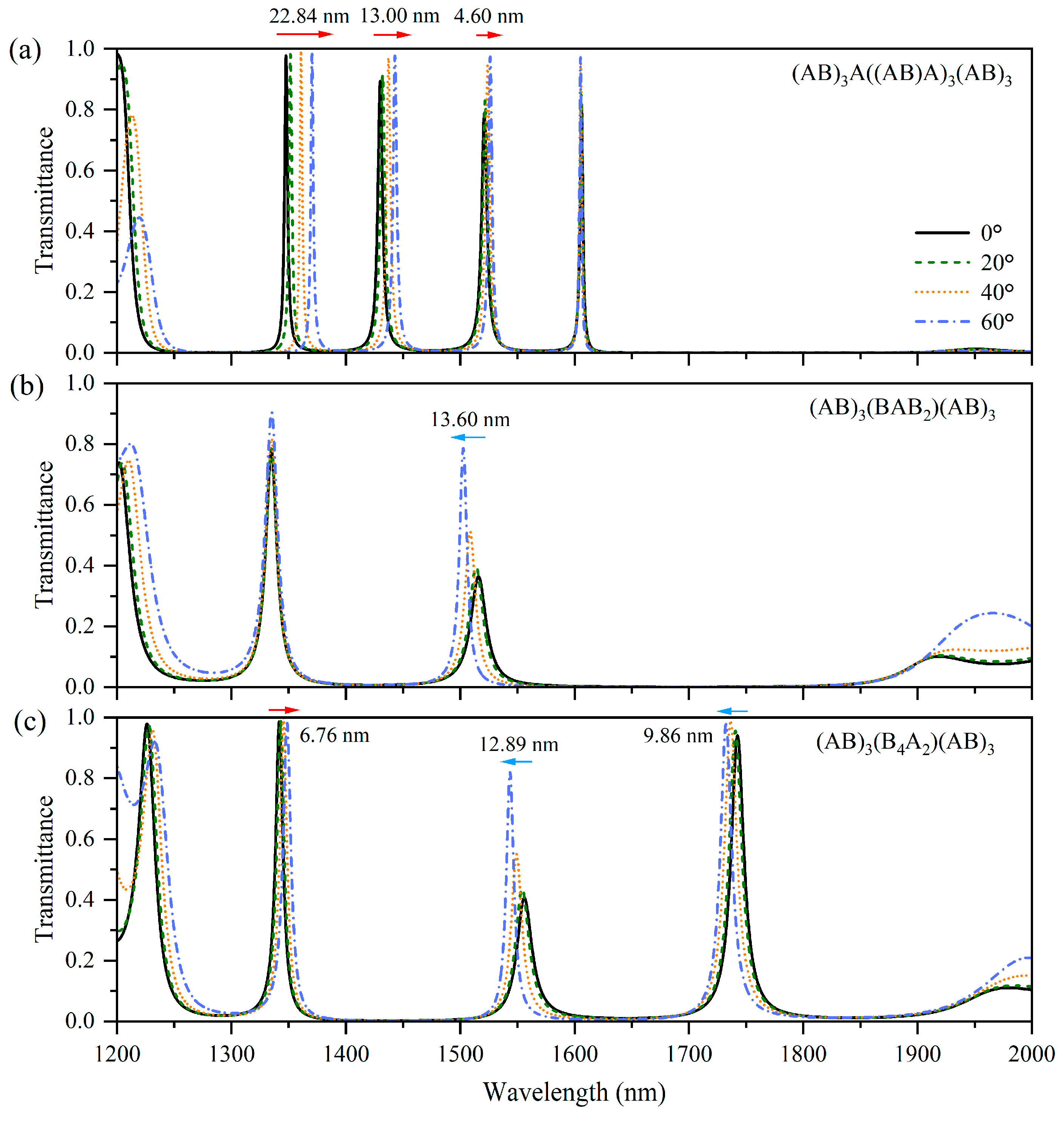
3.2. Multi-Channel Filtering Based on Two Different Angle-Dependencies
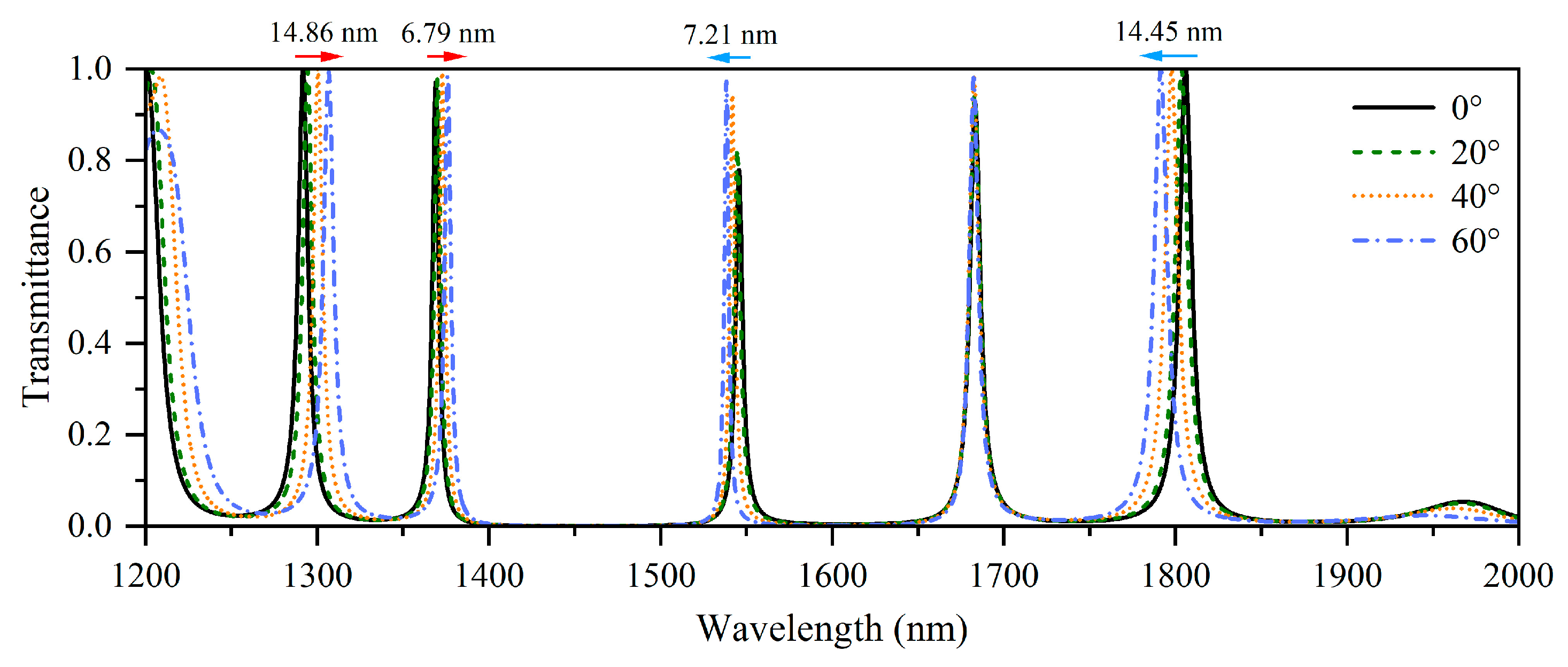
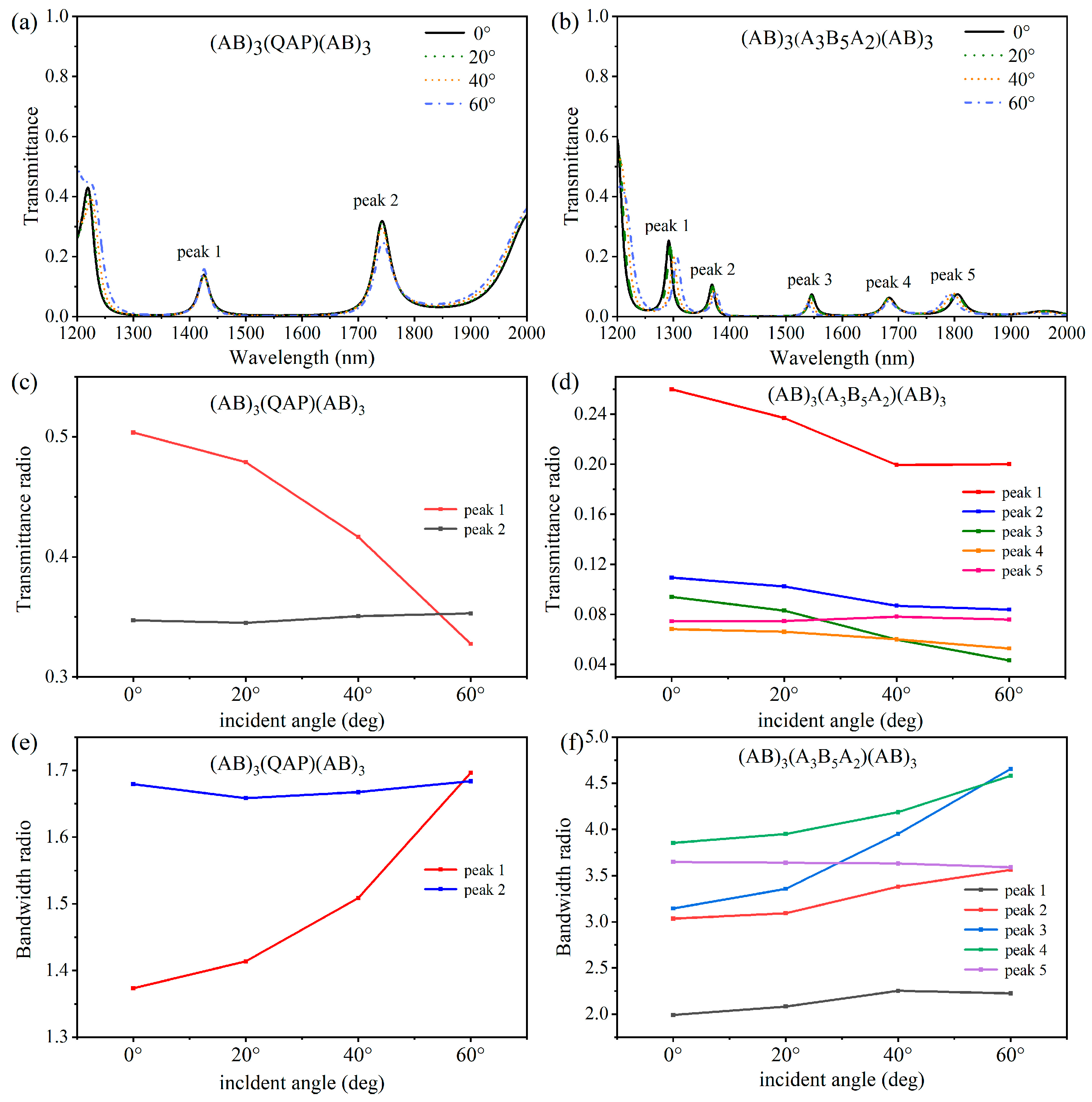
3.3. Multi-Channel Filtering Based on Three Different Angle-Dependences
4. The Influence of Loss on 1D-PCs Filtering
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Tan, R.; Cai, Q.; Wang, J.; Pan, D.; Li, Z.; Chen, D. Highly solar-blind ultraviolet selective metal-semiconductor-metal photodetector based on back-illuminated AlGaN heterostructure with integrated photonic crystal filter. Appl. Phys. Lett. 2021, 118, 142105. [Google Scholar] [CrossRef]
- Qiao, F.; Zhang, C.; Wan, J.; Zi, J. Photonic quantum-well structures: Multiple channeled filtering phenomena. Appl. Phys. Lett. 2000, 77, 3698. [Google Scholar] [CrossRef]
- Zhang, M.; Xing, Y.; Chen, Y. Multichannel filtering properties of quaternary photonic crystals containing single-negative materials. Eur. Phys. J. D 2021, 75, 4. [Google Scholar] [CrossRef]
- Baseri, A.; Keshavarz, A. Wave propagation in an optimized tunable multi channel filter based on one dimensional nano superconductor photonic crystal. Opt. Quant. Electron. 2021, 53, 601. [Google Scholar] [CrossRef]
- Shrestha, V.R.; Lee, S.-S.; Kim, E.-S.; Choi, D.-Y. Aluminum Plasmonics Based Highly Transmissive Polarization-Independent Subtractive Color Filters Exploiting a Nanopatch Array. Nano Lett. 2014, 14, 6672. [Google Scholar] [CrossRef] [PubMed]
- Baek, K.; Kim, Y.; Mohd-Noor, S.; Hyun, J.K. Mie Resonant Structural Colors. ACS Appl. Mater. Interfaces 2020, 12, 5300. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Liu, W.; Li, Z.; Li, Z.; Cheng, H.; Chen, S.; Tian, J. High-quality-factor multiple Fano resonances for refractive index sensing. Opt. Lett. 2018, 43, 1842. [Google Scholar] [CrossRef] [PubMed]
- Dandin, M.; Abshire, P.; Smela, E. Optical filtering technologies for integrated fluorescence sensors. Lab Chip 2007, 7, 955. [Google Scholar] [CrossRef] [PubMed]
- Yablonovitch, E. Inhibited Spontaneous Emission in Solid-State Physics and Electronics. Phys. Rev. Lett. 1987, 58, 2059. [Google Scholar] [CrossRef] [PubMed]
- John, S. Strong localization of photons in certain disordered dielectric superlattices. Phys. Rev. Lett. 1987, 58, 2486. [Google Scholar] [CrossRef] [PubMed]
- Sánchez, A.; Porta, A.V.; Orozco, S. Photonic band-gap and defect modes of a one-dimensional photonic crystal under localized compression. J. Appl. Phys. 2017, 121, 173101. [Google Scholar] [CrossRef]
- Topolancik, J.; Ilic, B.; Vollmer, F. Experimental Observation of Strong Photon Localization in Disordered Photonic Crystal Waveguides. Phys. Rev. Lett. 2007, 99, 253901. [Google Scholar] [CrossRef] [PubMed]
- Xue, C.; Jiang, H.; Chen, H. Highly efficient all-optical diode action based on light-tunneling heterostructures. Opt. Express 2010, 18, 7479. [Google Scholar] [CrossRef] [PubMed]
- Lončar, M.; Yoshie, T.; Scherer, A.; Gogna, P.; Qiu, Y. Low-threshold photonic crystal laser. Appl. Phys. Lett. 2014, 81, 2680. [Google Scholar] [CrossRef]
- Russell, P. Photonic Crystal Fibers. Science 2003, 299, 358. [Google Scholar] [CrossRef] [PubMed]
- Fink, Y.; Winn, J.N.; Fan, S.; Chen, C.; Michel, J.; Joannopoulos, J.D.; Thomas, E.L. A Dielectric Omnidirectional Reflector. Science 1998, 282, 1679. [Google Scholar] [CrossRef] [PubMed]
- Lu, G.; Wu, F.; Zheng, M.; Chen, C.; Zhou, X.; Diao, C.; Liu, F.; Du, G.; Xue, C.; Jiang, H.; et al. Perfect optical absorbers in a wide range of incidence by photonic heterostructures containing layered hyperbolic metamaterials. Opt. Express 2019, 27, 5326. [Google Scholar] [CrossRef] [PubMed]
- Hu, Y.; Tian, Z.; Ma, D.; Qi, C.; Yang, D.; Huang, S. Smart colloidal photonic crystal sensors. Adv. Colloid Interface Sci. 2024, 324, 103089. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Zhang, K.; Pang, C.; Zhao, Y.; Zhou, H.; Chen, H.; Lu, G.; Liu, F.; Du, G.; Akhmadaliev, S.; et al. Tunable structural colors in all-dielectric photonic crystals using energetic ion beams. Opt. Express 2022, 30, 23463. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Wu, J.; Fan, C.; Guo, Z.; Xue, C.; Jiang, H.; Sun, Y.; Li, Y.; Chen, H. Omnidirectional optical filtering based on two kinds of photonic band gaps with different angle-dependent properties. Europhys. Lett. 2020, 129, 34004. [Google Scholar] [CrossRef]
- Xu, K.; Zheng, X.; Li, C.; She, W. Design of omnidirectional and multiple channeled filters using one-dimensional photonic crystals containing a defect layer with a negative refractive index. Phys. Rev. E 2005, 71, 066604. [Google Scholar] [CrossRef] [PubMed]
- Winn, J.N.; Fink, Y.; Fan, S.; Joannopoulos, J.D. Omnidirectional reflection from a one-dimensional photonic crystal. Opt. Lett. 1998, 23, 1573. [Google Scholar] [CrossRef] [PubMed]
- Kaliteevski, M.; Iorsh, I.; Brand, S.; Abram, R.A.; Chamberlain, J.M.; Kavokin, A.V.; Shelykh, I.A. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys. Rev. B 2007, 76, 165415. [Google Scholar] [CrossRef]
- Bijalwan, A.; Singh, B.K.; Rastogi, V. Analysis of one-dimensional photonic crystal based sensor for detection of blood plasma and cancer cells. Optik 2021, 226, 165994. [Google Scholar] [CrossRef]
- Xiong, Y.; Huang, Q.; Canady, T.D.; Barya, P.; Liu, S.; Arogundade, O.H.; Race, C.M.; Che, C.; Wang, X.; Zhou, L.; et al. Photonic crystal enhanced fluorescence emission and blinking suppression for single quantum dot digital resolution biosensing. Nat. Commun. 2022, 13, 4647. [Google Scholar] [CrossRef] [PubMed]
- Semouchkina, E. Superluminal media formed by photonic crystals for transformation optics-based invisibility cloaks. J. Opt. 2016, 18, 044007. [Google Scholar] [CrossRef]
- Qin, H.; Li, J.; Chen, H.; Ren, H.; Lu, G.; Du, G. Angle-insensitive all-optical diodes in a large range of incidence by photonic heterostructure containing hyperbolic metamaterials. Phys. Scr. 2024, 99, 115506. [Google Scholar] [CrossRef]
- Alrowaili, Z.A.; Medhat, M.; Taha, T.A.; Mehaney, A.; Aljoufi, L.S.; Elsayed, H.A. One dimensional photonic crystal structure comprising a hyperbolic metamaterial for optical fltering purpose. Opt. Quant. Electron. 2023, 55, 31. [Google Scholar] [CrossRef]
- Ren, Z.; Chang, Y.; Ma, Y.; Shih, K.; Dong, B.; Lee, C. Leveraging of MEMS Technologies for Optical Metamaterials Applications. Adv. Opt. Mater. 2020, 8, 1900653. [Google Scholar] [CrossRef]
- Xue, C.; Ding, Y.; Jiang, H.; Li, Y.; Wang, Z.; Zhang, Y.; Chen, H. Dispersionless gaps and cavity modes in photonic crystals containing hyperbolic metamaterials. Phys. Rev. B 2016, 93, 125310. [Google Scholar] [CrossRef]
- Yue, X.; Wang, T.; Cai, Y.; Yan, R.; Wang, L.; Wang, H.; Lv, E.; Yuan, X.; Zeng, J.; Shu, X.; et al. Highly sensitive plasmonic nanoridge hyperbolic metamaterial for biosensing. Photonics Res. 2025, 13, 113. [Google Scholar] [CrossRef]
- Mohamed, A.G. Multiplication of photonic band gaps in one-dimensional photonic crystals by using hyperbolic metamaterial in IR range. Sci. Rep. 2023, 13, 324. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.; Guo, Z.; Liu, W.; Chen, S.; Chen, H. Hyperbolic metamaterial empowered controllable photonic Weyl nodal line semimetals. Nat. Commun. 2024, 15, 2773. [Google Scholar] [CrossRef] [PubMed]
- Lu, G.; Zhou, X.; Zhao, Y.; Zhang, K.; Zhou, H.; Li, J.; Diao, C.; Liu, F.; Du, G. Omnidirectional photonic bandgap in one-dimensional photonic crystals containing hyperbolic metamaterials. Opt. Express 2021, 29, 31915. [Google Scholar] [CrossRef] [PubMed]
- Yao, J.; Liu, Z.; Liu, Y.; Wang, Y.; Sun, C.; Bartal, G.; Stacy, A.M.; Zhang, X. Optical Negative Refraction in Bulk Metamaterials of Nanowires. Science 2008, 321, 930. [Google Scholar] [CrossRef] [PubMed]
- High, A.A.; Devlin, R.C.; Dibos, A.; Polking, M.; Wild, D.S.; Perczel, J.; De Leon, N.P.; Lukin, M.D.; Park, H. Visible-frequency hyperbolic metasurface. Nature 2015, 522, 192. [Google Scholar] [CrossRef] [PubMed]
- Peragut, F.; Cerruti, L.; Baranov, A.; Hugonin, J.P.; Taliercio, T.; De Wilde, Y.; Greffet, J.J. Hyperbolic metamaterials and surface plasmon polaritons. Optica 2017, 4, 1409. [Google Scholar] [CrossRef]
- Liu, Z.; Lee, H.; Xiong, Y.; Sun, C.; Zhang, X. Far-Field Optical Hyperlens Magnifying Sub-Diffraction-Limited Objects. Science 2007, 315, 1686. [Google Scholar] [CrossRef] [PubMed]
- Casse, B.D.F.; Lu, W.T.; Huang, Y.J.; Gultepe, E.; Menon, L.; Sridhar, S. Super-resolution imaging using a three-dimensional metamaterials nanolens. Appl. Phys. Lett. 2010, 96, 023114. [Google Scholar] [CrossRef]
- Wei, Q.; Bi, D.; Qi, X.; Ren, M.; Wu, F. Angle-independent topological interface states in one-dimensional photonic crystal heterostructures containing hyperbolic metamaterials. Opt. Lett. 2025, 50, 451. [Google Scholar] [CrossRef] [PubMed]
- Shen, K.; Li, X.; Zheng, Y.; Liu, H.; Dong, S.; Zhang, J.; Xia, S.; Dong, C.; Sun, X.; Zhang, X.; et al. Near-infrared ITO-based photonic hypercrystals with large angle-insensitive bandgaps. Opt. Lett. 2022, 47, 917. [Google Scholar] [CrossRef] [PubMed]
- Wu, F.; Lu, G.; Guo, Z.; Jiang, H.; Xue, C.; Zheng, M.; Chen, C.; Du, G.; Chen, H. Redshift gaps in one-dimensional photonic crystals containing hyperbolic metamaterials. Phys. Rev. Appl. 2018, 10, 064022. [Google Scholar] [CrossRef]
- Wu, F.; Chen, M.; Xiao, S. Wide-angle polarization selectivity based on anomalous defect mode in photonic crystal containing hyperbolic metamaterials. Opt. Lett. 2022, 47, 2153. [Google Scholar] [CrossRef] [PubMed]
- Shen, K.; Xia, S.; Zheng, Y.; Dong, S.; Liu, H.; Dong, C.; Li, X.; Xue, C.; Lu, H. Observation of polarization-dependent optical Tamm states in heterostructures containing hyperbolic metamaterials in the near-infrared region. Results Phys. 2023, 46, 106301. [Google Scholar] [CrossRef]
- Palik, E.D. Handbook of Optical Constants of Solids; Elsevier: New York, NY, USA, 1998. [Google Scholar]
- Du, G.; Jiang, H.; Wang, Z.; Chen, H. Optical nonlinearity enhancement in heterostructures with thick metallic film and truncated photonic crystals. Opt. Lett. 2009, 34, 578. [Google Scholar] [CrossRef] [PubMed]
- Gerfin, T.; Grätzel, M. Optical properties of tin-doped indium oxide determined by spectroscopic ellipsometry. J. Appl. Phys. 1996, 79, 1722. [Google Scholar] [CrossRef]
- Abb, M.; Albella, P.; Aizpurua, J.; Muskens, O.L. All-Optical Control of a Single Plasmonic Nanoantenna–ITO Hybrid. Nano Lett. 2011, 11, 2457. [Google Scholar] [CrossRef] [PubMed]
- Du, G.; Zhou, X.; Pang, C.; Zhang, K.; Zhao, Y.; Lu, G.; Liu, F.; Wu, A.; Akhmadaliev, S.; Zhou, S.; et al. Efficient Modulation of Photonic Bandgap and Defect Modes in All-dielectric Photonic Crystals by Energetic Ion Beams. Adv. Opt. Mater. 2020, 8, 2000426. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, Z. Electron Beam Evaporation Deposition; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Poddubny, A.; Iorsh, I.; Belov, P.; Kivshar, Y. Hyperbolic Matamaterials. Nat. Photonics 2013, 7, 948. [Google Scholar] [CrossRef]
- Ferrari, L.; Wu, C.; Lepage, D.; Zhang, X.; Liu, Z. Hyperbolic metamaterials and their applications. Prog. Quantum Electron. 2015, 40, 1. [Google Scholar] [CrossRef]
- Yeh, P. Optical Waves in Layered Media; Wiley: Hoboken, NJ, USA, 1988. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, M.; Huang, Y.; Qin, H.; Du, G. Abnormal Angle-Dependent Multi-Channel Filtering in Photonic Crystals Containing Hyperbolic Metamaterials. Nanomaterials 2025, 15, 1122. https://doi.org/10.3390/nano15141122
Xie M, Huang Y, Qin H, Du G. Abnormal Angle-Dependent Multi-Channel Filtering in Photonic Crystals Containing Hyperbolic Metamaterials. Nanomaterials. 2025; 15(14):1122. https://doi.org/10.3390/nano15141122
Chicago/Turabian StyleXie, Mingyan, Yuanda Huang, Haoyuan Qin, and Guiqiang Du. 2025. "Abnormal Angle-Dependent Multi-Channel Filtering in Photonic Crystals Containing Hyperbolic Metamaterials" Nanomaterials 15, no. 14: 1122. https://doi.org/10.3390/nano15141122
APA StyleXie, M., Huang, Y., Qin, H., & Du, G. (2025). Abnormal Angle-Dependent Multi-Channel Filtering in Photonic Crystals Containing Hyperbolic Metamaterials. Nanomaterials, 15(14), 1122. https://doi.org/10.3390/nano15141122





